Teil A
1
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1.1
Welchen Anstieg besitzt der Graph der Funktion  mit
mit  an der Stelle
an der Stelle 
1.2
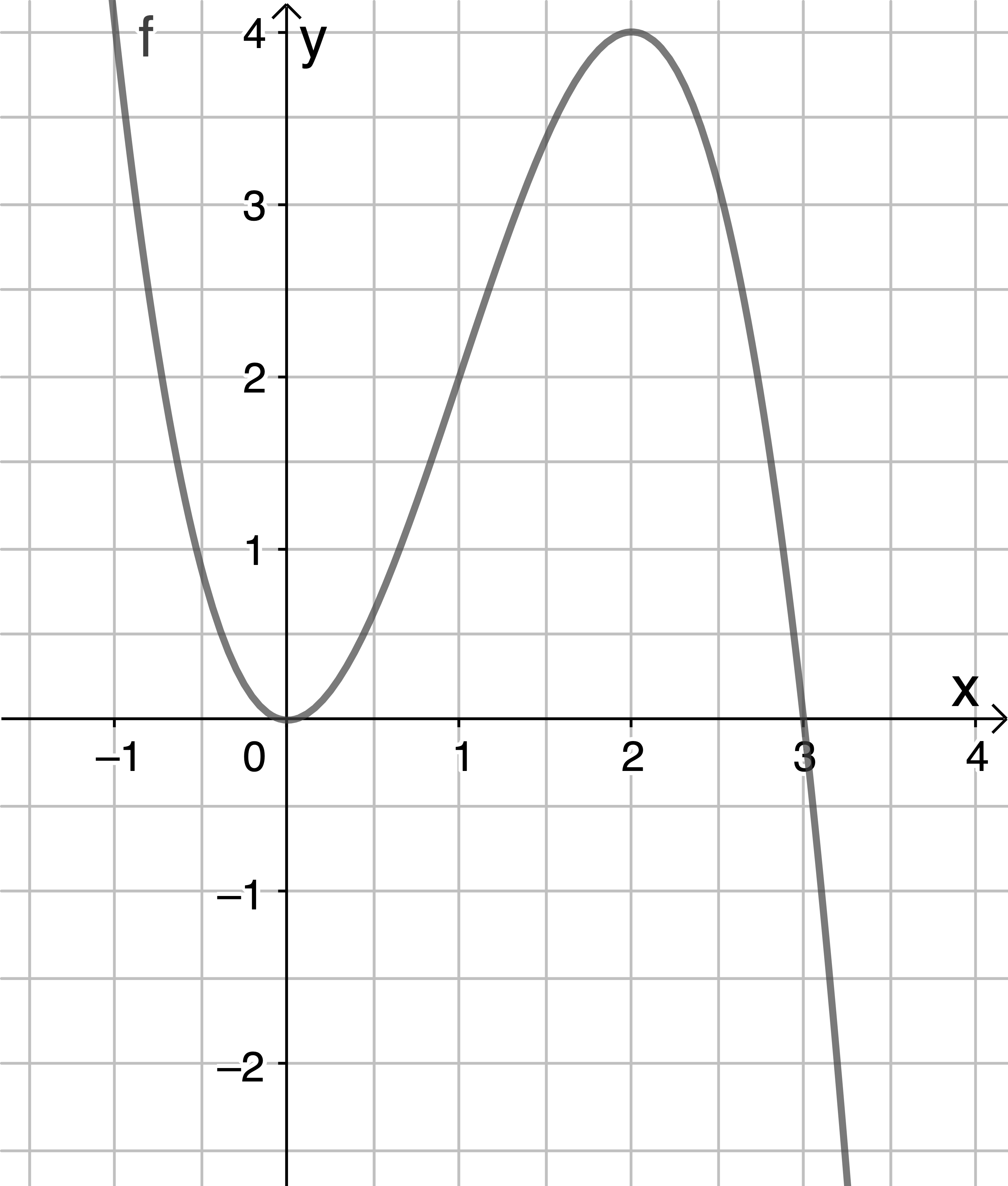
Die Abbildung zeigt den Graphen einer ganzrationalen Funktion 
Welche der folgenden Aussagen ist wahr?
Welche der folgenden Aussagen ist wahr?

1.3
Für welchen Wert von  ist der Vektor
ist der Vektor  senkrecht zum Vektor
senkrecht zum Vektor  ?
?
1.4
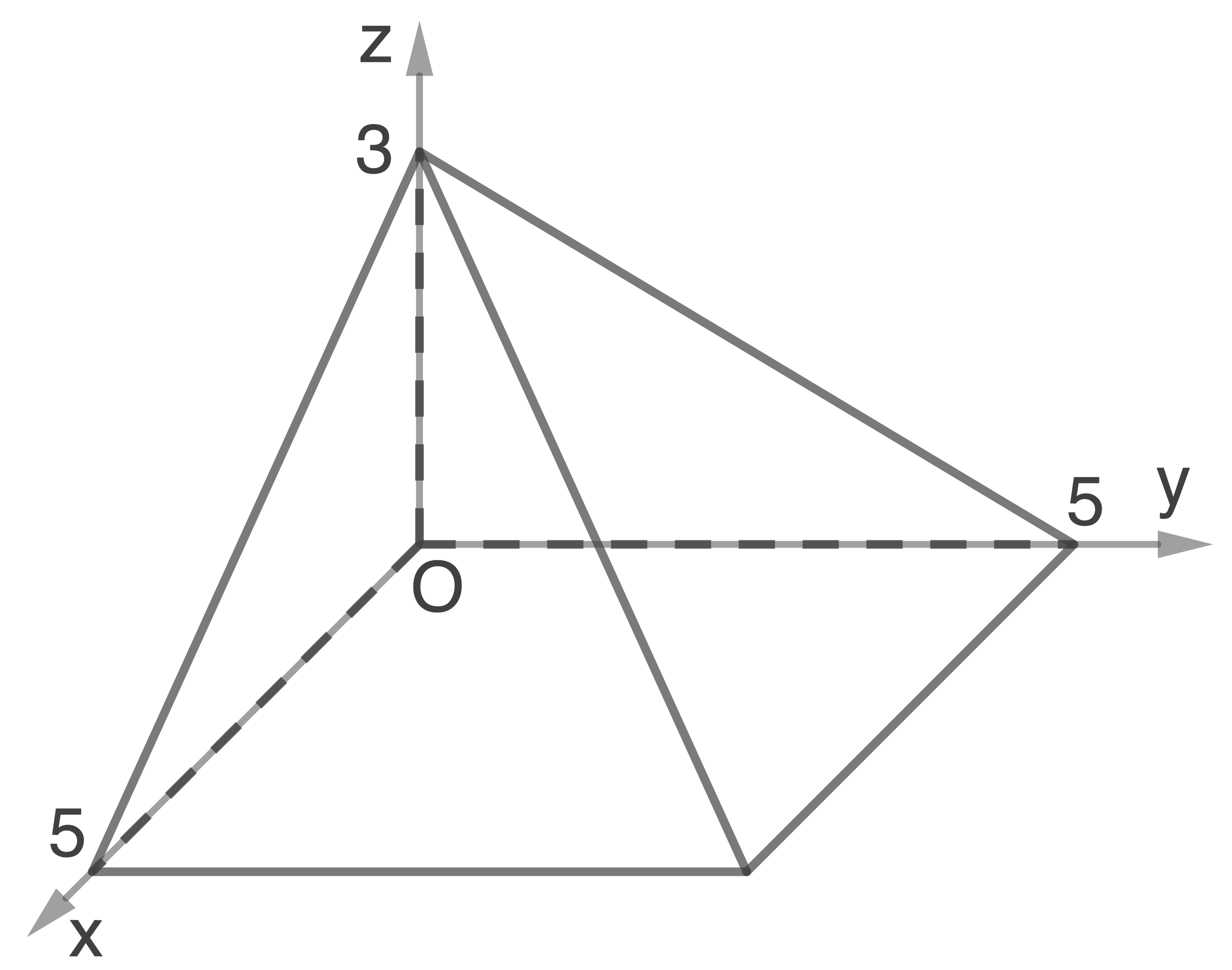
Welche Ebene  teilt die dargestellte quadratische Pyramide in zwei volumengleiche Teile?
teilt die dargestellte quadratische Pyramide in zwei volumengleiche Teile?

1.5
In einer Tüte befinden sich  Gummibärchen:
Gummibärchen:  orange,
orange,  gelbe und
gelbe und  rote. Es werden nacheinander
rote. Es werden nacheinander  Gummibärchen ohne Zurücklegen zufällig entnommen. Die Wahrscheinlichkeit dafür, dass beide Gummibärchen die gleiche Farbe besitzen, kann mit folgendem Term berechnet werden:
Gummibärchen ohne Zurücklegen zufällig entnommen. Die Wahrscheinlichkeit dafür, dass beide Gummibärchen die gleiche Farbe besitzen, kann mit folgendem Term berechnet werden:
Für Aufgabe 1 erreichbare BE-Anzahl: 05
2
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit 
2.1
Zeige, dass  und
und  die Extremstellen von
die Extremstellen von  sind.
sind.
(3 BE)
2.2
Begründe, dass die  -Achse den Graphen von
-Achse den Graphen von  in genau einem Punkt berührt.
in genau einem Punkt berührt.
(2 BE)
3
Der Graph einer quadratischen Funktion  verläuft durch den Koordinatenursprung.
Die Tangente an diesen Graphen im Punkt
verläuft durch den Koordinatenursprung.
Die Tangente an diesen Graphen im Punkt  hat die Gleichung
hat die Gleichung  Bestimme eine Funktionsgleichung von
Bestimme eine Funktionsgleichung von 
(5 BE)
4
ln einem kartesischen Koordinatensystem ist die Gerade
 mit
mit  gegeben.
gegeben.
4.1
Beschreibe die besondere Lage von  in diesem Koordinatensystem.
in diesem Koordinatensystem.
(1 BE)
4.2
Ermittle eine Gleichung der Ebene, die den Punkt  enthält und die Gerade
enthält und die Gerade  senkrecht schneidet.
senkrecht schneidet.
(2 BE)
4.3
Berechne die Koordinaten des Schnittpunkts der Geraden  mit der
mit der  Ebene.
Ebene.
(2 BE)
5
Betrachtet werden die binomialverteilten Zufallsgrößen  und
und 
5.1
Die binomialverteilte Zufallsgröße  hat die Parameter
hat die Parameter  und
und  sowie den Erwartungswert
sowie den Erwartungswert  .
.
Bestimme die Wahrscheinlichkeit .
.
Bestimme die Wahrscheinlichkeit
(2 BE)
5.2
Die binomialverteilte Zufallsgröße  hat die Parameter
hat die Parameter  und
und 
Formuliere dazu eine Aufgabenstellung, die sich mithilfe des Ansatzes lösen lässt.
lösen lässt.
Formuliere dazu eine Aufgabenstellung, die sich mithilfe des Ansatzes
(3 BE)
Lösung 1
1.1
Der Anstieg des Graphen von  wird durch die erste Ableitung
wird durch die erste Ableitung  beschrieben. Mit der Kettenregel folgt:
beschrieben. Mit der Kettenregel folgt:
 Einsetzen von
Einsetzen von  liefert:
liefert:
 Die dritte Antwortauswahl ist somit die richtige.
Die dritte Antwortauswahl ist somit die richtige.
1.2
Die erste Ableitungsfunktion  beschreibt den Anstieg des Graphen von
beschreibt den Anstieg des Graphen von 
 ist die richtige Antwort, da der Graph von
ist die richtige Antwort, da der Graph von  an der Stelle
an der Stelle  ansteigt und an der Stelle
ansteigt und an der Stelle  einen Hochpunkt besitzt, sodass hier die Steigung
einen Hochpunkt besitzt, sodass hier die Steigung  beträgt.
beträgt.
1.3
Zwei Vektoren stehen senkrecht zueinander, wenn ihr Skalarprodukt gleich 0 ist, d.h.
 .
Daraus folgt:
.
Daraus folgt:
![\(\begin{array}[t]{rll}
2a-3a+4 &=& 0 \\[5pt]
-a +4 & = & 0 & \quad \scriptsize \mid \; +a\\[5pt]
4&=& a
\end{array}\)](https://mathjax.schullv.de/ab2295a3fc82a39d8e990395bb560412b81706dba4e4c4368a1d79ba90723c06?color=5a5a5a) Für
Für  stehen die Vektoren senkrecht zueinander.
stehen die Vektoren senkrecht zueinander.
1.4
Die Ebene mit der Gleichung  teilt die Pyramide in der grün markierten Fläche.
teilt die Pyramide in der grün markierten Fläche.
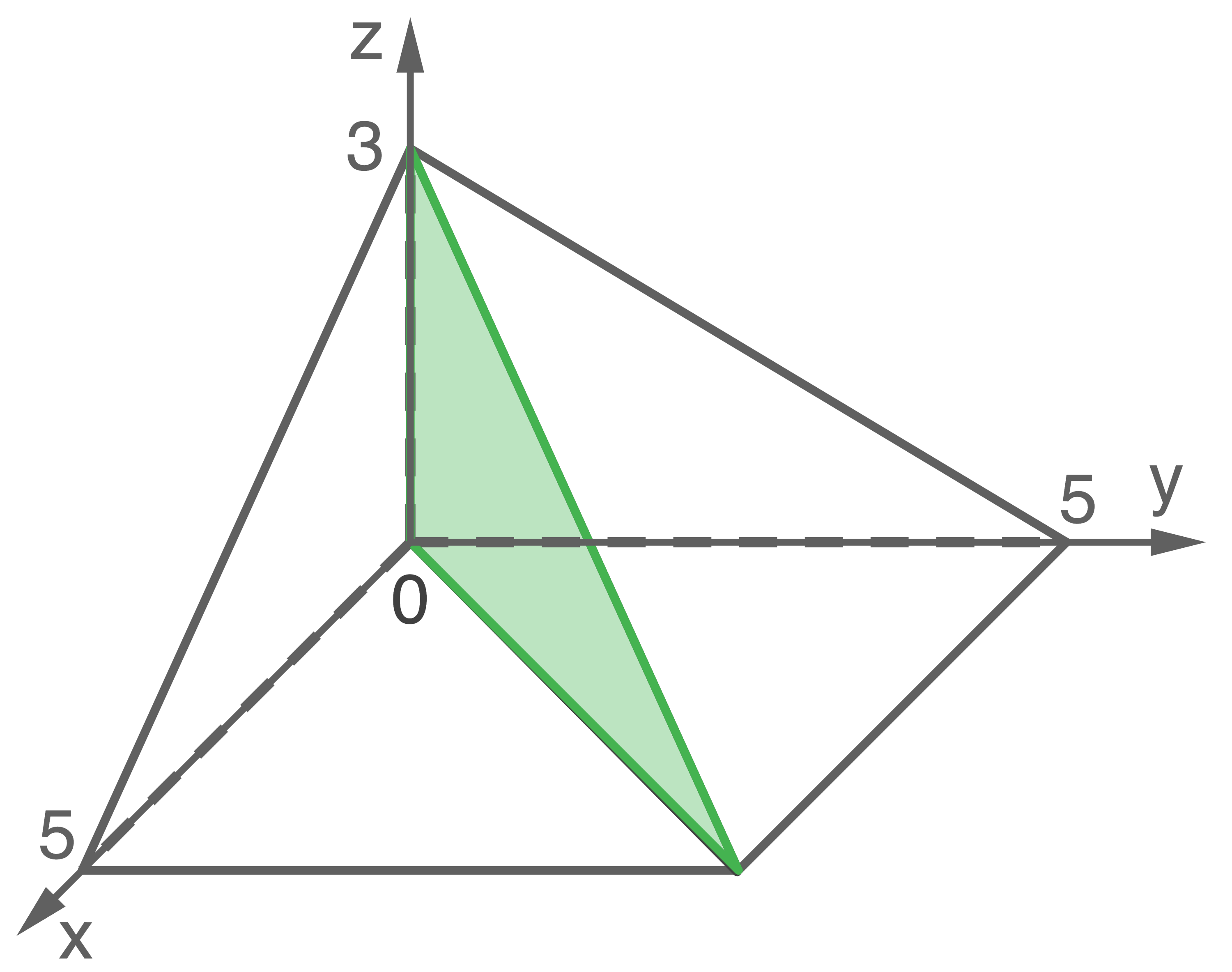 Die letzte Antwort
Die letzte Antwort  ist also richtig.
ist also richtig.

1.5
Mit den Pfadregeln ergibt sich folgender Term:


 Die zweite Antwortmöglichkeit ist also richtig.
Die zweite Antwortmöglichkeit ist also richtig.
Lösung 2
2.1
Bilden der ersten beiden Ableitungsfunktionen von 

 Anwenden des notwendigen Kriteriums für Extremstellen:
Anwenden des notwendigen Kriteriums für Extremstellen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/fe6f76e6d0f9ca44ca45d4b2bac59169824c237bdd3d778365bbb8ca76c4bc74?color=5a5a5a) Überprüfen des hinreichenden Kriteriums für Extremstellen:
Überprüfen des hinreichenden Kriteriums für Extremstellen:


 und
und  sind die einzigen Stellen, die sowohl das notwendige Kriterium, als auch das hinreichende Kriterium für Extremstellen erfüllen. Sie sind also die Extremstellen von
sind die einzigen Stellen, die sowohl das notwendige Kriterium, als auch das hinreichende Kriterium für Extremstellen erfüllen. Sie sind also die Extremstellen von 
2.2
Die x-Achse kann den Graphen von  nur in Extrempunkten berühren. Andernfalls würde sie den Graphen schneiden. Wegen Aufgabe 2.1 besitzt der Graph von
nur in Extrempunkten berühren. Andernfalls würde sie den Graphen schneiden. Wegen Aufgabe 2.1 besitzt der Graph von  genau zwei Extrempunkte.
genau zwei Extrempunkte.
Für die y-Koordinaten gilt:
 Die x-Achse berührt den Graphen von
Die x-Achse berührt den Graphen von  also nur im Punkt
also nur im Punkt 
Für die y-Koordinaten gilt:
Lösung 3
3
Die Gleichung einer quadratischen Funktion hat die Form  Da
Da  durch den Koordinatenursprung verläuft, muss gelten:
durch den Koordinatenursprung verläuft, muss gelten:
![\(\begin{array}[t]{rll}
f(0)&=& 0 & \\[5pt]
a \cdot 0^2 +b \cdot 0+c&=& 0& \\[5pt]
c&=& 0& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c72eb05d0062606584bc132da963ad3107d684612314360a406f6f8c23f27635?color=5a5a5a) Aus der Tangentengleichung am Punkt
Aus der Tangentengleichung am Punkt  ergeben sich folgende Bedingungen:
ergeben sich folgende Bedingungen:
 bilden:
bilden:
 Einsetzen von
Einsetzen von  in die Ableitungsfunktion liefert:
in die Ableitungsfunktion liefert:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d9bdf5e926856b15c804a0e65ae13bdd1bd64b8dcdb70f04d1f16815d449b3a3?color=5a5a5a) Durch Einsetzen von
Durch Einsetzen von  in
in  folgt nun:
folgt nun:
![\(\begin{array}[t]{rll}
f(2)&=& 6 & \\[5pt]
a\cdot 2^2 +b\cdot 2&=& 6& \quad \scriptsize \mid\; b= 4-4a \\[5pt]
4a +2\cdot (4-4a) &=& 6 \\[5pt]
4a +8 -8a &=& 6 &\quad \scriptsize \mid\; -8\\[5pt]
-4a &=& -2 &\quad \scriptsize \mid\; :(-4)\\[5pt]
a &=& \dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/15c74e063fab3c1633d239b58bf28d2ba577506027579bf2bcf7e288ac2bc96d?color=5a5a5a) Für
Für  ergibt sich damit:
ergibt sich damit:
 Eine Funktionsgleichung von
Eine Funktionsgleichung von  lautet also:
lautet also:

Lösung 4
4.1
Da der Richtungsvektor  die
die  -Koordinate
-Koordinate  besitzt, verläuft die Gerade
besitzt, verläuft die Gerade  parallel zur yz-Ebene.
parallel zur yz-Ebene.
4.2
Damit die Ebene  die Gerade
die Gerade  senkrecht schneidet, kann der Richtungsvektor von
senkrecht schneidet, kann der Richtungsvektor von  als Normalenvektor der Ebene gewählt werden:
als Normalenvektor der Ebene gewählt werden:  Damit gilt:
Damit gilt:
 Durch Einsetzen des Punktes
Durch Einsetzen des Punktes  in die Koordinatengleichung der Ebene
in die Koordinatengleichung der Ebene  lässt sich
lässt sich  bestimmen.
bestimmen.
![\(\begin{array}[t]{rll}
y+ z &=& d &\; \scriptsize \mid\; P(1\mid -3 \mid 5) \\[5pt]
-3 +5 &=& d \\[5pt]
2 &=& d
\end{array}\)](https://mathjax.schullv.de/d6b9afe89985b67905722b1d8af46b760a04d5784a4a1a89bcfdd90df1b5714b?color=5a5a5a) Eine Gleichung der Ebene
Eine Gleichung der Ebene  die
die  senkrecht schneidet und
senkrecht schneidet und  enthält, lautet:
enthält, lautet:

4.3
Eine Gleichung der  -
- -Ebene lautet
-Ebene lautet 
Für die -Koordinate von
-Koordinate von  gilt
gilt  Gleichsetzen liefert:
Gleichsetzen liefert:
![\(\begin{array}[t]{rll}
1+k &=& 0 &\; \scriptsize \mid\; -1\\[5pt]
k &=& -1
\end{array}\)](https://mathjax.schullv.de/636f4f0ee1284ea50d7fa4abb6f15f193853dd45d6a44542849138e853ffad29?color=5a5a5a) Einsetzen von
Einsetzen von  in die Geradengleichung liefert die Koordinaten des gesuchten Schnittpunkts
in die Geradengleichung liefert die Koordinaten des gesuchten Schnittpunkts 
 Die Gerade
Die Gerade  schneidet die
schneidet die  -
- -Ebene also im Punkt
-Ebene also im Punkt 
Für die
Lösung 5
5.1
Für  gilt
gilt  und
und 
Mit der Formel für den Erwartungswert einer binomialverteilten Zufallsgröße lässt sich bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
E(X_1)&=&n_1 \cdot p_1 \\[5pt]
2&=& 4 \cdot p_1 &\quad \scriptsize \mid :4\; \\[5pt]
\dfrac{1}{2}&=&p_1
\end{array}\)](https://mathjax.schullv.de/fda008d84bb864ea8c8fdac43c7af944d66aa14524a690da1061a1fb9b454051?color=5a5a5a) Für die Wahrscheinlichkeit folgt mithilfe der Formel für Binomialverteilung:
Für die Wahrscheinlichkeit folgt mithilfe der Formel für Binomialverteilung:



Mit der Formel für den Erwartungswert einer binomialverteilten Zufallsgröße lässt sich
5.2
Daher gilt