Teil B1

Die Abbildung zeigt das Logo eines Geschäfts für Anglerbedarf.
Das Logo stellt u.a. einen Fisch dar, von dem ein Teil aus einer Wasseroberfläche herausragt.
Die obere Spitze der Schwanzflosse des Fisches liegt auf der Wasseroberfläche.
Die Strecke zwischen oberer und unterer Spitze der Schwanzflosse steht senkrecht zur Wasseroberläche.

Grafische Darstellung einer Welle, die auf Wasser trifft, mit verschiedenen Farbtönen und Formen.

In das Logo wird ein Koordinatensystem ( $1$ Längeneinheit entspricht $1$ Dezimeter) gelegt.
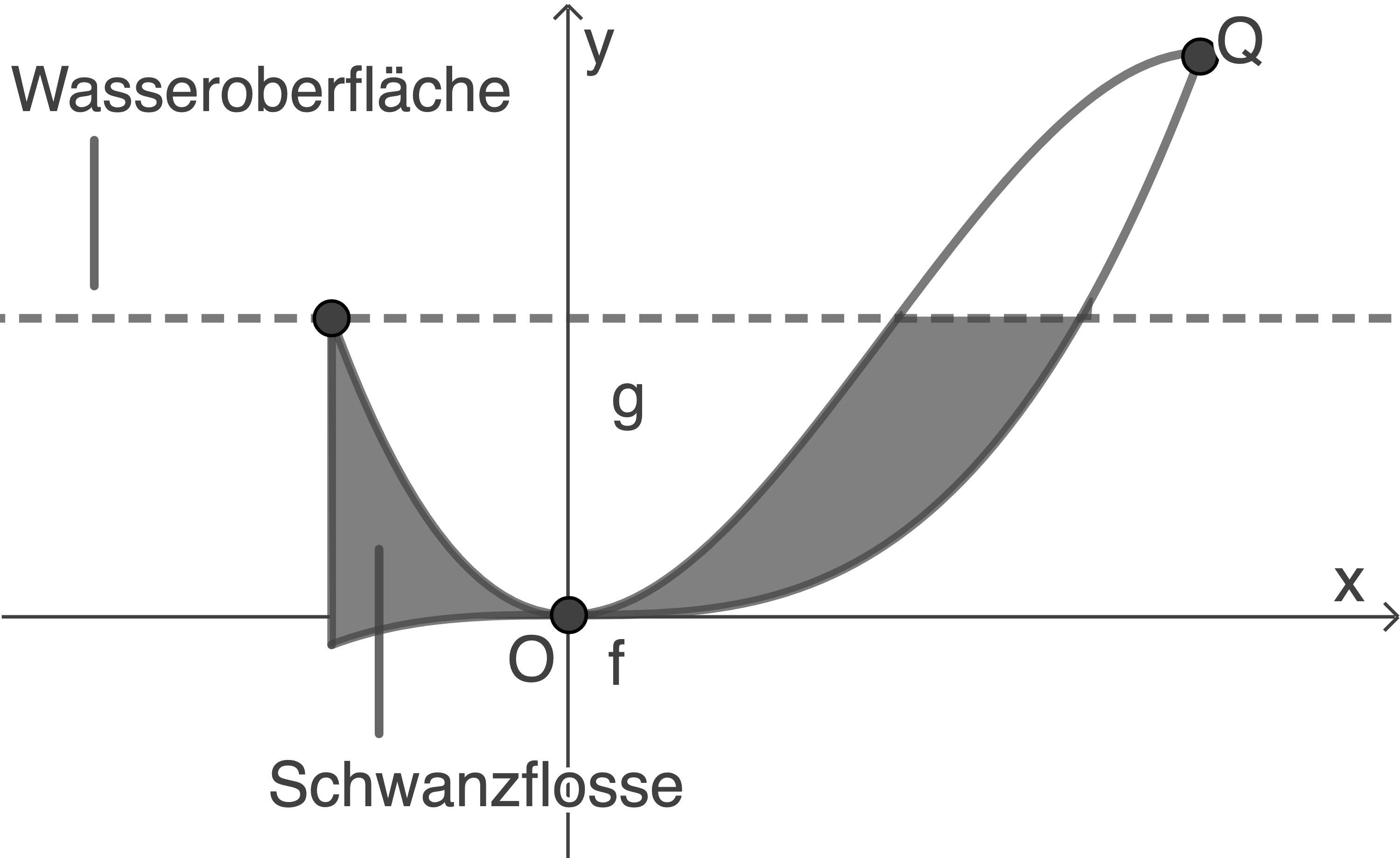
Die untere Begrenzungslinie des Fisches liegt auf dem Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit

$f(x)=\frac{1}{8}\cdot x^{3}.$

Die obere Begrenzungslinie des Fisches liegt auf dem Graphen der in $\mathbb{R}$ definierten Funktion $g$ mit

$g(x)= \frac{1}{4}\cdot x^{2}\cdot(4-x).$

Die Wasseroberfläche liegt auf der Geraden

$y=\frac{5}{4}.$

Diagramm mit Wasseroberfläche, Schwanzflosse und Kurvenverlauf, beschriftet mit Punkten O, f, g und Q.

1.1

Zeige, dass die Graphen von $f$ und $g$ die Punkte $O (0|0)$ und $Q (\frac{8}{3}\mid y_Q)$ gemeinsam haben.
Gib $y_Q$ an.

Erreichbare BE-Anzahl: 04

1.2

Weise nach, dass der Punkt $Q$ ein Extrempunkt des Graphen von $g$ ist. Gib die Art dieses Extrempunktes an.

(4 BE)

1.3

Entscheide, ob folgende Aussage wahr oder falsch ist.
Für jeden Wert von $x$ mit $0\lt x\lt \dfrac{8}{3}$ ist der Anstieg des Graphen von $g$ größer als der Anstieg des Graphen von $f.$
Begründe deine Entscheidung.

(3 BE)

1.4

Der Fisch soll durch ein achsenparalleles Rechteck umrahmt werden. Bestimme die Seitenlängen des kleinstmöglichen Rechtecks, welches diese Bedingungen erfüllt.

(7 BE)

1.5

Die dunkelgrau markierte Fläche stellt den Teil des Fisches dar, der sich unter der Wasseroberfläche befindet.
Bestimme den Flächeninhalt dieses Teils des Fisches.

(9 BE)

Der Verlauf der unteren Begrenzungslinie des Fisches soll so variiert werden, dass diese auf einem der Graphen der Funktion $f_{k}$ mit

$f_{k}(x)=\displaystyle \frac{1}{8}\cdot k\cdot x^{3}$ $(x\in \mathbb{R};k\in \mathbb{R},k\gt 1)$ liegt.
Der gemeinsame Punkt der Graphen von $f_{k}$ und $g$ , der die $x$ -Koordinate $\dfrac{8}{k+2}$ hat, stellt die Kopfspitze des Fisches dar.

1.6

Zeige, dass sich für $k=2$ die Kopfspitze des Fisches oberhalb der Wasseroberfläche befindet.

(4 BE)

1.7

Bestimme alle Werte von $k$ , für welche sich die Kopfspitze des Fisches oberhalb der Wasseroberfläche befindet.

(4 BE)

Das Geschäft verkauft Anglerbekleidung und Anglerzubehör.

1.8

Erfahrungsgemäß kauft ein Kunde mit einer Wahrscheinlichkeit von
$10\,\%$ Anglerbekleidung, aber kein Anglerzubehör;
$13\,\%$ keine Anglerbekleidung, aber Anglerzubehör;
$19\,\%$ weder Anglerbekleidung noch Anglerzubehör.

Ein Kunde wird zufällig ausgewählt. Betrachtet werden die Ereignisse $\mathrm{E}_{1}$ und $\mathrm{E}_{2}$ :
$\mathrm{E}_{1}$ : Der Kunde kauft Anglerbekleidung.
$\mathrm{E}_{2}$ : Der Kunde kauft Anglerzubehör.
Bestimme die Wahrscheinlichkeit dafür, dass höchstens eines der beiden betrachteten Ereignisse eintreten wird.
Untersuche, ob die Ereignisse $\mathrm{E}_{1}$ und $\mathrm{E}_{2}$ stochastisch abhängig sind.

(6 BE)

1.9

Jeder zufällig ausgewählte Kunde kauft mit einer Wahrscheinlichkeit von $68\,\%$ Anglerbekleidung.
Berechne die Wahrscheinlichkeit dafür, dass von $100$ zufällig ausgewählten Kunden mindestens $75$ Anglerbekleidung kaufen werden.
Berechne die Wahrscheinlichkeit dafür, dass von $100$ zufällig ausgewählten Kunden weniger als zu erwarten Anglerbekleidung kaufen werden.

(5 BE)

1.1

Berechnen der Funktionswerte an den Stellen $x=0$ und $x = \frac{8}{3}$ liefert:

$f(0)=\dfrac{1}{8} \cdot 0^3 =0$

$g(0)= \dfrac{1}{4}\cdot 0^2 \cdot (4-0) = 0$

$f\left(\dfrac{8}{3}\right)=\dfrac{1}{8} \cdot \left(\dfrac{8}{3}\right)^3 = \dfrac{64}{27}$

$g\left(\dfrac{8}{3}\right)= \dfrac{1}{4}\cdot \left(\dfrac{8}{3}\right)^2 \cdot \left(4-\dfrac{8}{3}\right) = \dfrac{64}{27}$

Da $f(0)=g(0)=0$ gilt und $f\left(\frac{8}{3}\right) = g\left(\frac{8}{3}\right) = \frac{64}{27},$ haben die beiden Graphen von $f$ und $g$ die Punkte $O(0\mid 0)$ und $Q\left(\frac{8}{3}\mid y_Q = \frac{64}{27}\right)$ gemeinsam.

1.2

1. Schritt: Ableitungen bestimmen

$\(\begin{array}[t]{rll} g(x)&=& \dfrac{1}{4} x^2 \cdot (4-x) \\[5pt] &=& - \dfrac{1}{4} x^3 +x^2 \\[5pt] g$

2. Schritt: Notwendiges Kriterium für Extremstellen überprüfen

$\( g$ $= -\dfrac{16}{3}+ \dfrac{16}{3} =0$

3. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

$\(g$

Da $x_Q = \frac{8}{3}$ sowohl das notwendige, als auch das hinreichende Kriterium für Extremstellen von $g$ erfüllt und der Punkt $Q$ auf dem Graphen von $g$ liegt, ist $Q$ ein Extrempunkt des Graphen von $g.$
Da $\(g$ gilt, handelt es sich dabei um einen Hochpunkt.

1.3

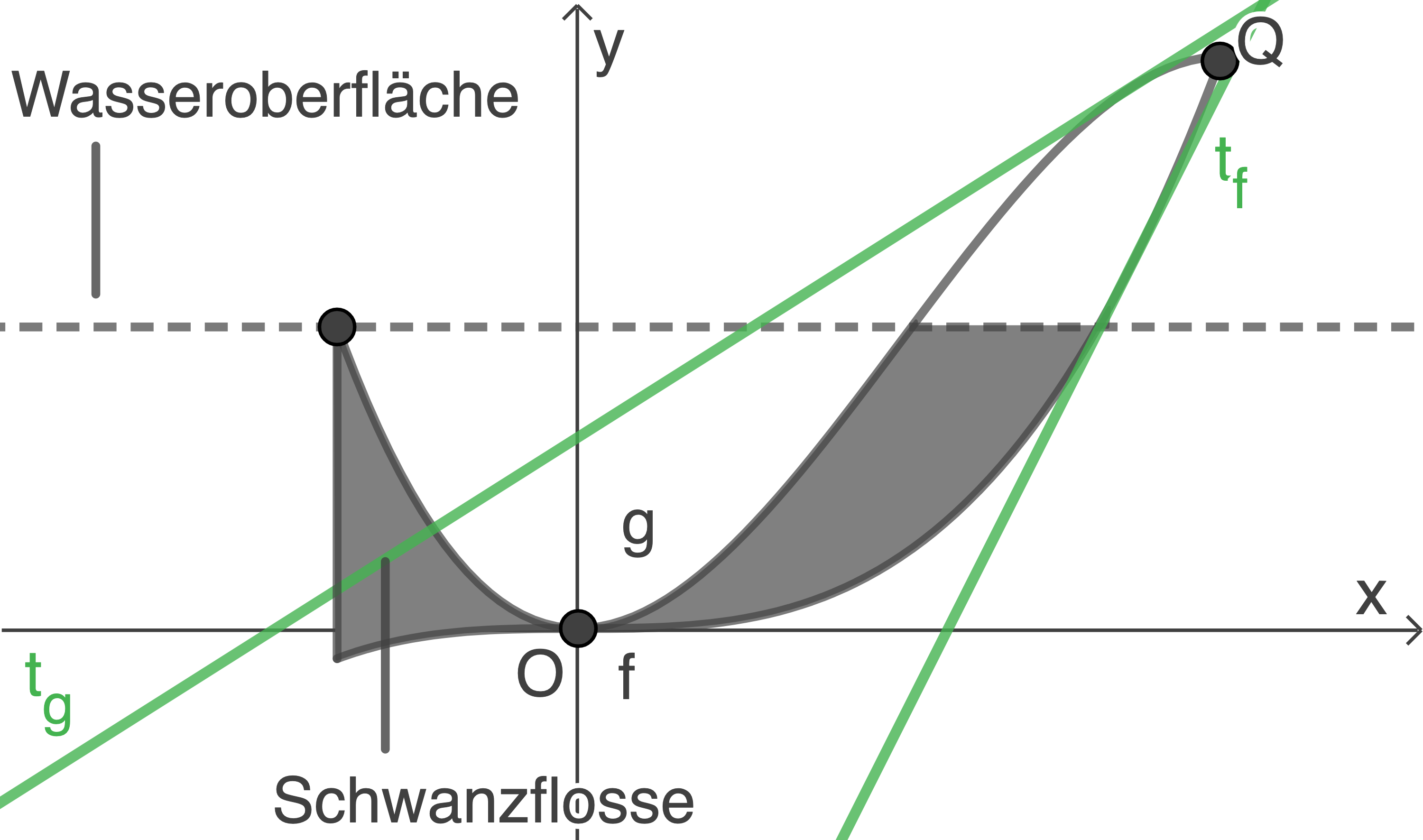
Der Anstieg eines Graphen entspricht der Steigung der Tangente an den Graphen an der jeweiligen Stelle.
In die Abbildung lässt sich in der Nähe des Punktes $Q$ an derselben Stelle jeweils eine Tangente $t_f$ an den Graphen von $f$ und eine Tangente $t_g$ an den Graphen von $g$ einzeichnen (siehe Abbildung). $t_f$ besitzt einen deutlich größeren Anstieg als $t_g.$

Grafik mit einer Funktion und Wasseroberfläche, die verschiedene Punkte und Linien zeigt.

An dieser Stelle $(x\approx 2,3)$ besitzt der Graph von $f$ also einen größeren Anstieg als der Graph von $g.$
Da $0\lt 2,3 \lt \frac{8}{3}$ ist, ist die Aussage also falsch.

1.4

1. Schritt: Eckpunkte des Rechtecks bestimmen

Der Abbildung lässt sich entnehmen, dass sich der linke untere Eckpunkt des Rechtecks gerade auf dem Punkt $S_u$ der unteren Spitze der Schwanzflosse befinden muss. Außerdem muss der obere rechte Eckpunkt des Rechtecks dem Punkt $Q$ entsprechen.
Die $x$ -Koordinaten von $S_u$ entsprechen den $x$ -Koordinaten des Schnittpunktes $S_o$ zwischen dem Graphen von $g$ und der Gerade $y = \frac{5}{4}$ . Dieser lässt sich mit der solve-Funktion des CAS bestimmen.

Dies liefert folgende Punkte mit gerundeten $x$ -Koordinaten:

$S_{o,1}\left(-1\mid \frac{5}{4} \right)$ und $S_{o,2}(1,38\mid \frac{5}{4})$
(alle weiteren Lösungen liegen zu weit rechts des Fischkopfes)

Aufgrund der Lage von $O$ und $Q$ liegt $S_{o,2}$ in der Fischmitte. Die $x$ -Koordinate von $S_u$ lautet also $-1.$

Die $y$ -Koordinate des Punktes $S_u$ lässt sich durch Einsetzen von $x = -1$ in $f$ bestimmen:

$f(-1) = \dfrac{1}{8} \cdot (-1)^3 = - \dfrac{1}{8}$

Die Koordinaten des unteren Eckpunktes des Rechtecks lauten also $S_u \left(-1 \mid -\frac{1}{8} \right).$
Die Koordinaten des oberen Eckpunktes des Rechtecks lauten $Q \left(\frac{8}{3} \mid \frac{64}{27}\right).$

2. Schritt: Seitenlängen des Rechtecks bestimmen

Da die Seiten des Rechtecks parallel zu den Achsen verlaufen sollen, entsprechen ihre Längen der Differenz der $y$ - bzw $x$ -Koordinaten der beiden zuvor berechneten Eckpunkte.

Länge des Rechtecks in $x$ -Richtung:

$\dfrac{8}{3} - (-1) = \dfrac{11}{3} \; [\text{dm}]$

Länge des Rechtecks in $y$ -Richtung:

$\dfrac{64}{27} - \dfrac{1}{8} \approx 2,5 \; [\text{dm}]$

1.5

Der Flächeninhalt setzt sich aus zwei Integralen zuammen.

Das erste Integral entspricht dem Flächeninhalt der Fläche, die von den Graphen von $f$ und $g$ unterhalb der Wasseroberfläche eingeschlossen werden. Die Integrationsgrenzen entsprechen den Schnittstellen $x_1$ $x_2$ von $g$ und $y$ .

Das zweite Integral entspricht dem Flächeninhalt der Fläche, die von $y$ und $f$ eingeschlossen wird. Die Integrationsgrenzen ergeben sich aus $x_2$ und der Schnittstelle von $f$ und $y$ .

Schritt 1: Bestimmung des ersten Integrals
Die Schnittpunkte von $g$ und $y$ wurden bereits in Aufgabe $1.4$ berechnet. Ihre $x$ -Koordinaten lauten $x_1 = -1$ und $x_2 \approx 1,38$

Somit ergibt sich $A_1= \displaystyle\int_{-1}^{1,38}g(x)- f(x)\;\mathrm dx.$

Schritt 2: Bestimmung des zweiten Integrals
Die untere Integrationsgrenze des zweiten Integrals ist $x_2$ . Die obere Integrationsgrenze, ist die x-Koordinate des Schnittpunktes von $f$ und $y$ , also $x_3 \approx 2,15.$ Damit folgt:

$A_2 = \displaystyle\int_{1,37}^{2,15}y(x)-f(x) \;\mathrm dx$

Schritt 3: Flächeninhalt berechnen
Mit dem CAS lassen sich die Integrale wie folgt berechnen.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$A_1= \displaystyle\int_{-1}^{1,37}f(x)- g(x)\;\mathrm dx \approx 0,96$

$A_2 = \displaystyle\int_{1,37}^{2,15}f(x)-y(x) \;\mathrm dx \approx 0,4$

Somit folgt für den Gesamtflächeninhalt
$A= \mid A_1 \mid + \mid A_2 \mid = 0,96 \, \text{dm} +0,4 \, \text{dm}$ $= 1,36 \approx 1,4 \, \text{dm}^2.$

1.6

Die Kopfspitze ist über der Wasseroberfläche, wenn die $y$ -Koordinate der Kopfspitze größer als $\frac{5}{4}$ ist.

$f_2(\dfrac{8}{2+2}) = \dfrac{1}{4} \cdot 2^3 = 2$

Da $2 \gt \frac{5}{4}$ , liegt die Kopfspitze über der Wasseroberfläche.

1.7

Die Schnittpunkte von den Graphen von $g$ und $f_k$ verlaufen entlang des Graphen von $g$ . Somit können sie nur bis zum Hochpunkt $Q$ von $g$ eine Kopfspitze beschreiben.

Nach Aufgabe $1.4$ liegt der Graph von $g$ für $x_1 \approx 1,38$ auf der Wasseroberfläche. Bei $x_2 = \frac{8}{3}$ befindet sich bei $g$ der Hochpunkt $Q$ , welcher überhalb der Wasseroberfläche liegt. Mit diesen beiden Werten lassen sich nun die Grenzwerte $k_1$ und $k_2$ bestimmen.

Da sich $f_k(x)$ und $g(x)$ schneiden, stimmen die $x$ - und $y$ -Koordinaten von $g$ mit $f_k(x)$ überein.
Nach Einsetzen der $x$ -Werte folgt:

$\begin{array}[t]{rll} f_k(1,38)&=& g(1,38) &\quad \scriptsize \\[5pt] \dfrac{1}{8} \cdot k_2 \cdot 1,38^3 &=& 1,25&\quad \scriptsize \mid\; \cdot \frac{8}{1,38^3} \\[5pt] k_2&\approx& 3,88 \end{array}$

$\begin{array}[t]{rll} f_k \left(\dfrac{8}{3} \right)&=&g \left( \dfrac{8}{3}\right) &\quad \scriptsize \\[5pt] \dfrac{1}{8} \cdot k_1 \cdot \left(\dfrac{8}{3} \right)^3 &=& 2,37&\quad \scriptsize \mid \; \cdot \frac{27}{64} \\[5pt] k_1&\approx& 1 \end{array}$

Somit kann $k$ die Werte $1 \lt k \leq 3,88$ annehmen.

1.8

Die Wahrscheinlichkeiten lassen sich in einer Vierfeldertafel darstellen. Hierbei steht $A$ für Anglerkleidung und $Z$ für Anglerzubehör.

Aus der Augabenstellung lässt sich folgendes ablesen: $P(A \cap Z) =0,1$ ; $P(\overline{A} \cap Z) =0,13$ und $P(\overline{A} \cap \overline{Z}) =0,19$ . Mit diesen Werten lässt sich die Vierfeldertafel vervollständigen:

	$A$	$\overline{A}$	Gesamt
$Z$	0,58	0,13	0,71
$\overline{Z}$	0,1	0,19	0,29
Gesamt	0,68	0,32	1

$P(E_1)= P(A)= 0,68$

$P(E_2)= P(Z)=0,71$

Wenn höchstens eins der beiden Ereignisse eintreten soll, muss mit der Gegenwahrscheinlichkeit gerechnet werden.
$P(E_3)$ $= 0,68 \cdot (1-0,71) + 0,71 \cdot (1-0,68)$ $\approx 0,4244 = 42,44 \; \%$

Die Ereignisse sind stochastisch unabhängig, wenn
$P(E_1) \cdot P(E_2) = P(E_1 \cap E_2)$
Mit $0,68 \cdot 0,71 =0,48 \neq 0,58$ sind die Ereignisse stochastisch abhängig.

1.9

Ereignis $E_1$ :
Sei $X$ die Anzahl der Kunden, die Anglerbekleidung kaufen. $X$ ist $B_{100; \; 0,68}$ -verteilt. Mit dem CAS folgt:

$P(E_1) = P(X\geq 75)= 1-P(X \leq 74)$ $\approx 0,0796.$

Ereignis $E_2$ :
Für den Erwartungswert gilt:
$E(x)= n \cdot p = 100 \cdot 0,68 =68$

Sei $X$ wie in Ergeinis $E_1$ definiert. Mit dem CAS folgt:

$P(E_2) = P(X \lt 68) =P(X \leq 67)$ $\approx 0,4523.$