Teil B2

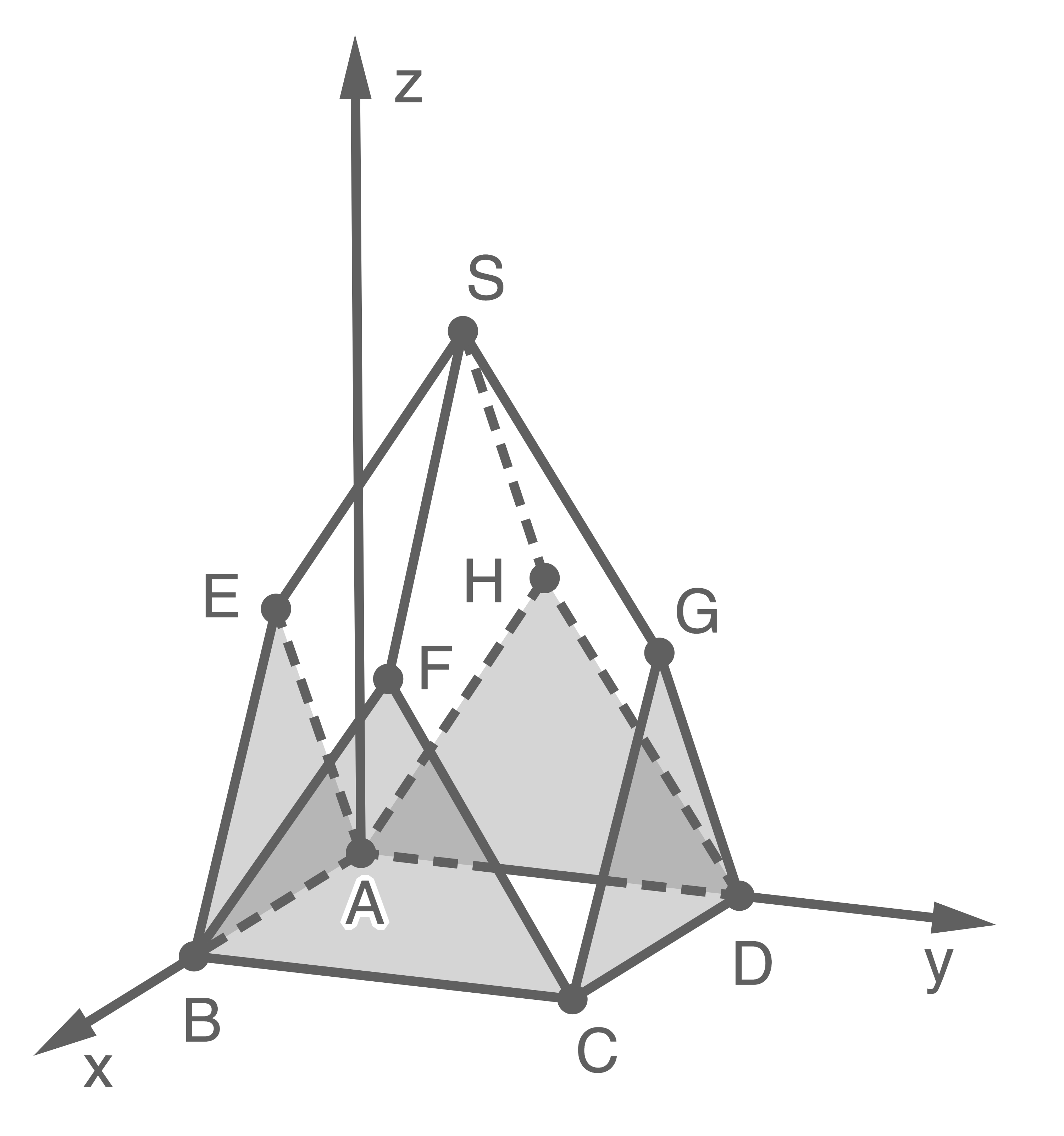
Die Abbildung zeigt modellhaft das Dach eines Kirchturms.

Die Eckpunkte der dreieckigen Giebelflächen und der viereckigen Dachflächen (grau markiert) werden durch die Punkte $A, B(8|0| 0), \quad C(8|8| 0), \quad D, \quad E(4|0| 6)$ , $F(8|4| 6), \quad G(4|8| 6), \quad H$ und $S(4|4| 12)$ dargestellt. Die vier Dachflächen haben die gleiche Form und die gleiche Größe.

Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Realität.

Die Materialstärken der Bauteile des Daches sollen im Folgenden vernachlässigt werden.

2.1

Die Ebene $L$ enthält die Punkte $C, F$ und $G$ .

Geben Sie eine Gleichung von $L$ in Parameterform an.

Zeigen Sie, dass auch $S$ in $L$ liegt.

(03 BE)

2.2

Weisen Sie nach, dass das Viereck $CGSF$ eine Raute ist.

(02 BE)

2.3

Gegeben sind drei Ebenen mit den folgenden Gleichungen:

$M_{1}: x=8$

$M_{2}: x-y=0$

$M_{3}: z=6$

Eine dieser Ebenen stellt eine Symmetrieebene des Daches dar.

Geben Sie diese Ebene an und beschreiben Sie ihre Lage.

Geben Sie eine Gleichung einer weiteren Symmetrieebene des Daches an.

(04 BE)

2.4

Berechnen Sie die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$ .

Ermitteln Sie den gesamten Flächeninhalt der Dachflächen.

(05 BE)

2.5

Zur Stabilisierung wird zwischen den durch $E$ und $G$ dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch $\overline{S F}$ dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, stimmt weder mit $S$ noch mit $F$ überein und wird im Modell mit $R$ bezeichnet.

Beschreiben Sie, wie man die Koordinaten von $R$ ermitteln könnte.

(04 BE)

Durch einen ebenen Zwischenboden, der im Modell die Punkte $E, F, G$ und $H$ enthält, ist ein pyramidenförmiger Dachraum im Kirchturm abgetrennt.

2.6

Ermitteln Sie das Volumen des pyramidenförmigen Dachraums.

(05 BE)

Betrachtet wird die Dachfläche, die im Modell die Punkte $E, B, F$ und $S$ enthält. Diese Punkte liegen in der Ebene mit der Gleichung $3 \cdot x-3 \cdot y+2 \cdot z=24$ .

2.7

Untersuchen Sie, ob die Größe des Neigungswinkels dieser Dachfläche gegenüber dem Zwischenboden größer als $60^{\circ}$ ist.

(03 BE)

2.8

Innerhalb des pyramidenförmigen Dachraums ist ein Laser zur Überwachung der Stabilität angebracht. Im Modell wird der Laser durch den Punkt $(4|4| k)$ mit $k \in \mathbb{R} ; 6\lt k\lt 12$ beschrieben und hat zur betrachteten Dachfläche den Abstand $\frac{8}{\sqrt{22}}$ .

Ermitteln Sie den Wert von $k$ .

(04 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Ebenengleichung aufstellen

Richtungsvektoren bestimmen:

$\begin{array}[t]{rll} \overrightarrow{CF}&=& \pmatrix{8\\4\\6}-\pmatrix{8\\8\\0} &=&\pmatrix{0\\-4\\6} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{CG}&=& \pmatrix{4\\8\\6}-\pmatrix{8\\8\\0} &=&\pmatrix{-4\\0\\6} \end{array}$

Ebenengleichung von $L$ in Parameterform:

$L: \overrightarrow{X}= \overrightarrow{C}+s\cdot \overrightarrow{CF} + t \cdot \overrightarrow{CG}$

Parameterform anzeigen

Punktprobe mit $S$

Rechenweg anzeigen

$\pmatrix{4\\4\\12}=\pmatrix{8-4t\\8-4s\\6s + 6t}$

Für $t=s=1$ ist dieses Gleichungssystem lösbar. Der Punkt $S$ liegt somit ebenso in der Ebene $L.$

2.2

$\begin{array}[t]{rll} \overrightarrow{GS}&=& \pmatrix{4\\4\\12}-\pmatrix{4\\8\\6} &=&\pmatrix{0\\-4\\6} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{FS}&=& \pmatrix{4\\4\\12}-\pmatrix{8\\4\\6} &=&\pmatrix{-4\\0\\6} \end{array}$

Aus $\overline {GS}=\overline{CF}$ und $\overline{FS}=\overline{CG}$ folgt die Parallelität der jeweils gegenüberliegenden Strecken.

Da zudem $|\overrightarrow{GS}|=|\overrightarrow{FS}|$ gilt, besitzen alle Seiten der Raute die gleiche Länge.

Das Viereck $CGSF$ erfüllt somit die Kriterien einer Raute.

2.3

$M_2$ stellt eine Symmetrieebene zum Dach dar.

Sie liegt parallel zur $z$ -Achse und schneidet die Grundfläche des Dachs vom Ursprung ausgehend diagonal. Die Symmetrieebene beinhaltet somit die Punkte $A$ , $C$ und $S$ .

Eine weitere Symmetrieebene stellt $M_4: x+y=8$ dar. Diese schneidet die Grundfläche ebenfalls diagonal, ist parallel zur $z$ -Achse und beinhaltet die Punkte $B$ , $D$ und $S$ .

2.4

Innenwinkel bestimmen

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\overrightarrow{GS}\circ \overrightarrow{FS}}{|\overrightarrow{GS}|\cdot |\overrightarrow{FS}|} &\\[5pt] \cos(\alpha)&=&\dfrac{\pmatrix{0\\-4\\6}\circ \pmatrix{-4\\0\\6}}{\left| \pmatrix{0\\-4\\6}\right|\cdot \left|\pmatrix{-4\\0\\6}\right|} &\\[5pt] \cos(\alpha)&=&\dfrac{36}{52} &\quad \scriptsize \mid\; \cos^{-1}\\[5pt] \alpha&\approx &46^{\circ} \end{array}$

Flächeninhalt berechnen

Flächeninhalt der Raute:

$\begin{array}[t]{rll} A_R&=&\dfrac{1}{2}\cdot |\overrightarrow{FG}|\cdot | \overrightarrow{CS}| & \\[5pt] &=&\dfrac{1}{2}\cdot \left|\pmatrix{-4\\4\\0}\right| \cdot \left| \pmatrix{-4\\-4\\12}\right| & \\[5pt] &=&\dfrac{1}{2}\cdot \sqrt{32}\cdot \sqrt{176} & \\[5pt] &\approx& 37,5 \; [\,\text {m}^2] \end{array}$

Inhalt der gesamten Dachfläche:

$A=4\cdot A_R=150\,\text{m}^2$

2.5

Die Stütze ist genau dann möglichst kurz, wenn sie orthogonal zu dem durch $\overline{S F}$ dargestellten Balken steht. Zunächst wird also der Mittelpunkt $T$ des Stahlträgers $\overline{E G}$ bestimmt.

Die Koordinaten des Mittelpunkts von $\overline{EG}$ lauten $T (4 \mid 4 \mid 6).$

Da der Punkt $R$ auf dem Balken liegen soll, ergeben sich die Koordinaten zu $\overrightarrow{OR}= \overrightarrow{OS} +\sigma \cdot \overrightarrow{SF}.$

Die Stütze ist orthogonal, wenn $\overline{TR}$ orthogonal zu $\overline{SF}$ ist.

Es gilt also:

$\begin{array}[t]{rll} \overrightarrow{TR} \circ \overrightarrow{SF}&=&0 \\[5pt] (\overrightarrow{OR}-\overrightarrow{OT}) \circ \overrightarrow{SF}&=&0 \\[5pt] (\overrightarrow{OS} +\sigma \cdot \overrightarrow{SF}-\overrightarrow{OT}) \circ \overrightarrow{SF}&=&0 \end{array}$

Jetzt kann $\sigma$ bestimmt werden und damit die Koordinaten von $R.$

2.6

1. Schritt: Seitenlänge $a$ der Grundfläche berechnen

$\begin{array}[t]{rll} a&=&|\overrightarrow{FG}| & \\[5pt] &=&\left| \pmatrix{4\\8\\6}-\pmatrix{8\\4\\6}\right| & \\[5pt] &=&\left| \pmatrix{-4\\4\\0}\right| & \\[5pt] &=&\sqrt{(-4)^2+4^2+0^2} & \\[5pt] &=&\sqrt{32} \end{array}$

2. Schritt: Volumen der Pyramide bestimmen

$V=\dfrac{1}{3}\cdot a^2\cdot h$

Die Höhe $h$ der Pyramide ergibt sich aus der Differenz der $z$ -Koordinaten von $S$ und $F$ :

$h=12-6=6$

$\begin{array}[t]{rll} V&=& \dfrac{1}{3}\cdot \sqrt{32}^2\cdot 6& \\[5pt] &=& 64 \,[\text{m}^3] \end{array}$

2.7

Ein Normalenvektor der gegebenen Ebene entspricht $\overrightarrow{n_1}=\pmatrix{3\\-3\\2}.$

Der Zwischenboden lässt sich ebenfalls als Ebene darstellen. Diese ist parallel zur $x-y-$ Ebene und besitzt somit entspricht $\overrightarrow{n_2}=\pmatrix{0\\0\\1}$ einem Normalenvektor.

Schnittwinkel der Ebenen berechnen:

Rechenweg anzeigen