Teil B1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet und ist symmetrisch bezüglich seines Wendepunkts
bezeichnet und ist symmetrisch bezüglich seines Wendepunkts 
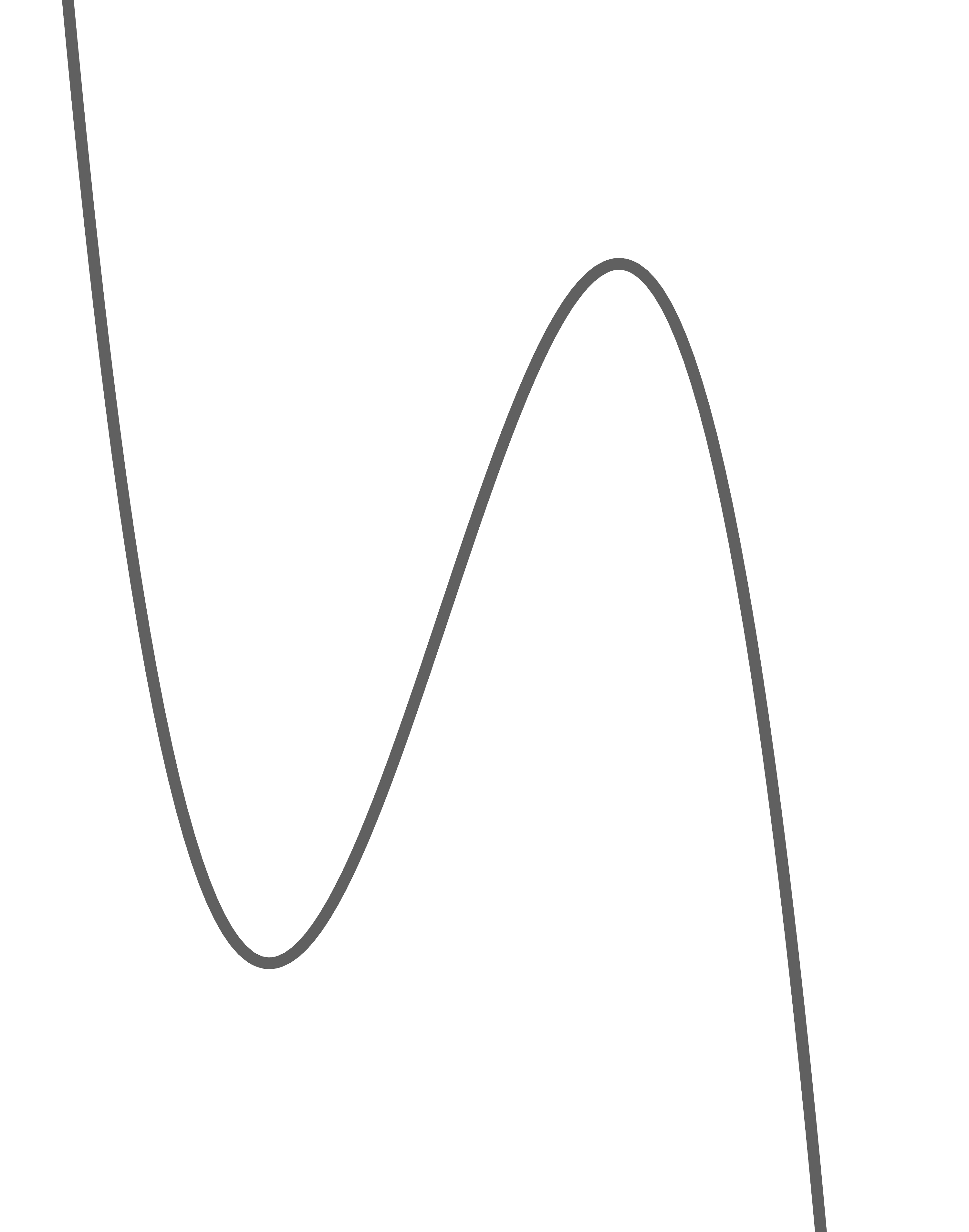 Die Gerade
Die Gerade  mit der Gleichung
mit der Gleichung  verläuft durch den Punkt
verläuft durch den Punkt  .
.
 aller Proben keimfrei. Die Entnahmen der Proben werden als unabhängig voneinander betrachtet.
aller Proben keimfrei. Die Entnahmen der Proben werden als unabhängig voneinander betrachtet.
1.1
Gib die Koordinaten der Schnittpunkte von  mit den Koordinatenachsen an.
mit den Koordinatenachsen an.
(2 BE)
1.2
Die Abbildung 1 soll  darstellen.
Ergänze in der Abbildung 1 die fehlenden Koordinatenachsen und skaliere diese passend.
darstellen.
Ergänze in der Abbildung 1 die fehlenden Koordinatenachsen und skaliere diese passend.
(2 BE)

Abbildung 1
1.3
Begründe, dass  keinen weiteren Wendepunkt haben kann.
Für die in
keinen weiteren Wendepunkt haben kann.
Für die in  definierte Funktion
definierte Funktion  gilt:
gilt:  Gib die Koordinaten des Wendepunkts des Graphen von
Gib die Koordinaten des Wendepunkts des Graphen von  an.
an.
(4 BE)
1.4
Die Gerade  die
die  -Achse und die Tangente im Schnittpunkt von
-Achse und die Tangente im Schnittpunkt von  mit der
mit der  -Achse für
-Achse für  schließen ein Dreieck ein.
Skizziere den Sachverhalt in der Abbildung 1.
Bestimme den Flächeninhalt des Dreiecks.
schließen ein Dreieck ein.
Skizziere den Sachverhalt in der Abbildung 1.
Bestimme den Flächeninhalt des Dreiecks.
(6 BE)
1.5
Die Gerade  schließt mit
schließt mit  zwei Flächenstücke ein.
Begründe ohne zu rechnen, dass diese zwei Flächenstücke den gleichen Inhalt haben.
Betrachtet werden alle Geraden mit positivem Anstieg, die durch
zwei Flächenstücke ein.
Begründe ohne zu rechnen, dass diese zwei Flächenstücke den gleichen Inhalt haben.
Betrachtet werden alle Geraden mit positivem Anstieg, die durch  verlaufen.
Bestimme diejenigen Anstiege, für welche die zugehörige Gerade mit
verlaufen.
Bestimme diejenigen Anstiege, für welche die zugehörige Gerade mit  Flächenstücke einschließt.
Flächenstücke einschließt.
(6 BE)
Die zeitliche Entwicklung der Größe der von Wasserpflanzen bedeckten Fläche eines Sees kann modellhaft durch die in  definierte Funktion
definierte Funktion  mit
mit  beschrieben werden.
Dabei ist
beschrieben werden.
Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Tagen und
die seit Beobachtungsbeginn vergangene Zeit in Tagen und  die Größe der von Wasserpflanzen bedeckten Fläche in Quadratmeter.
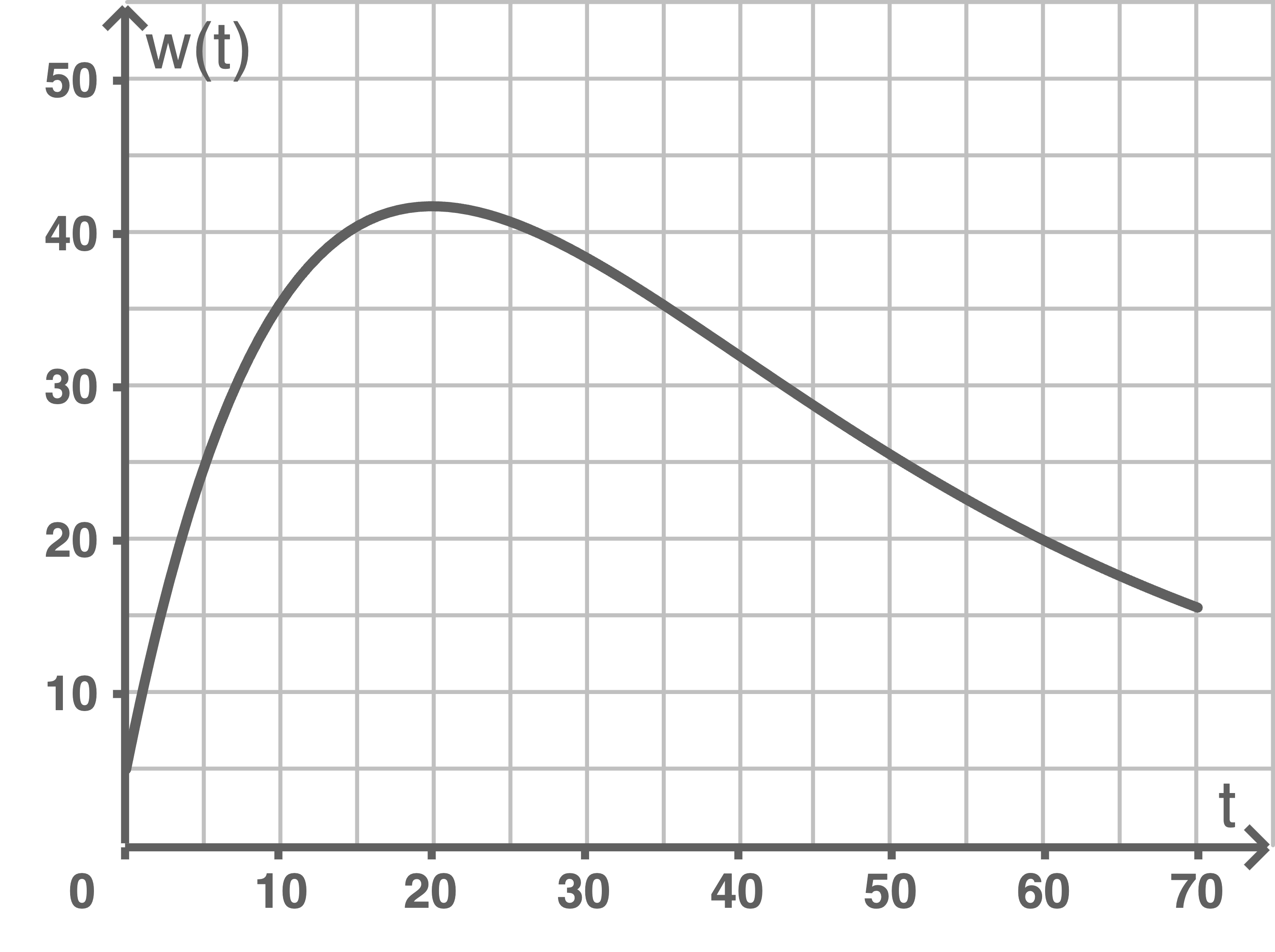
Die Abbildung 2 zeigt den Graphen der Funktion
die Größe der von Wasserpflanzen bedeckten Fläche in Quadratmeter.
Die Abbildung 2 zeigt den Graphen der Funktion  im Zeitraum
im Zeitraum 

Abbildung 2
1.6
Bestimme die Größe der bedeckten Fläche 10 Tage nach Beobachtungsbeginn.
Gib denjenigen Zeitpunkt an, zu dem diese Größe wieder erreicht wird.
(3 BE)
1.7
Untersuche, ob die Größe der bedeckten Fläche in den ersten 5 Tagen nach Beobachtungsbeginn mehr wächst als in den darauffolgenden 5 Tagen.
Ermittle denjenigen Zeitpunkt, zu dem die Größe der bedeckten Fläche am stärksten abnimmt.
(6 BE)
1.8
Die zeitliche Entwicklung der Größe der bedeckten Fläche soll ab dem 40. Tag nach Beobachtungsbeginn modellhaft durch eine lineare Funktion  beschrieben werden. Der Graph von
beschrieben werden. Der Graph von  geht in
geht in  ohne Knick in den Graphen von
ohne Knick in den Graphen von  über.
Ermittle den Zeitpunkt, zu dem entsprechend dieses Modells die Fläche des Sees frei von Wasserpflanzen ist.
über.
Ermittle den Zeitpunkt, zu dem entsprechend dieses Modells die Fläche des Sees frei von Wasserpflanzen ist.
Dem Wasser wird eine große Anzahl von Einzelproben entnommen und auf Keime untersucht. Erfahrungsgemäß sind
(4 BE)
1.9
An einem Tag werden an unterschiedlichen Stellen des Sees 150 Einzelproben entnommen.
Berechne die Wahrscheinlichkeit dafür, dass höchstens fünf dieser Einzelproben nicht keimfrei sind.
Gib ein Ereignis im Sachzusammenhang an, dessen Wahrscheinlichkeit sich mit dem Term  berechnen lässt.
berechnen lässt.
(4 BE)
1.10
Folgendes Verfahren wird zur Untersuchung von 10 Einzelproben genutzt:
Von jeder Einzelprobe wird ein Teil entnommen. Alle diese Teile werden zu einer Mischprobe zusammengeführt. Die Mischprobe wird untersucht. Ist sie keimfrei, so sind auch alle Einzelproben keimfrei und das Verfahren ist beendet. Ist sie nicht keimfrei, werden alle 10 Einzelproben einzeln untersucht.
Ermittle die Wahrscheinlichkeit dafür, dass die Mischprobe keimfrei ist.
Die Zufallsgröße  beschreibt die Anzahl der Untersuchungen bei diesem Verfahren.
Begründe, dass
beschreibt die Anzahl der Untersuchungen bei diesem Verfahren.
Begründe, dass  nur den Wert 1 oder den Wert 11 annehmen kann.
Gib die Wahrscheinlichkeitsverteilung und den Erwartungswert von
nur den Wert 1 oder den Wert 11 annehmen kann.
Gib die Wahrscheinlichkeitsverteilung und den Erwartungswert von  an.
an.
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Schnittpunkte mit der  -Achse
Für Punkte, die auf der
-Achse
Für Punkte, die auf der  -Achse liegen, gilt
-Achse liegen, gilt  Es muss also gelten:
Es muss also gelten:
![\(\begin{array}[t]{rll}
f(x)&=& 0& \\[5pt]
-x^3+3x^2&=& 0 & \\[5pt]
-x^2\cdot (x-3)&=& 0 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/baaaa44c1042392747cb9b8152739f2004496bbd2f52293c5a1a7d106ed282d1?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  und
und  Die Schnittpunkte mit der
Die Schnittpunkte mit der  -Achse besitzen somit die Koordinaten
-Achse besitzen somit die Koordinaten  und
und  Schnittpunkt mit der
Schnittpunkt mit der  -Achse
Für Punkte, die auf der
-Achse
Für Punkte, die auf der  -Achse liegen, gilt
-Achse liegen, gilt  Somit folgt:
Somit folgt:
![\(\begin{array}[t]{rll}
f(0)&=& -0^3+3\cdot 0^2 &\\[5pt]
&=& 0&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/db555b6944afd06d75527c510c22afca150e2cce561cf425549c34709133c5ed?color=5a5a5a) Der Schnittpunkt mit der
Der Schnittpunkt mit der  -Achse entspricht somit dem Schnittpunkt
-Achse entspricht somit dem Schnittpunkt 
1.2
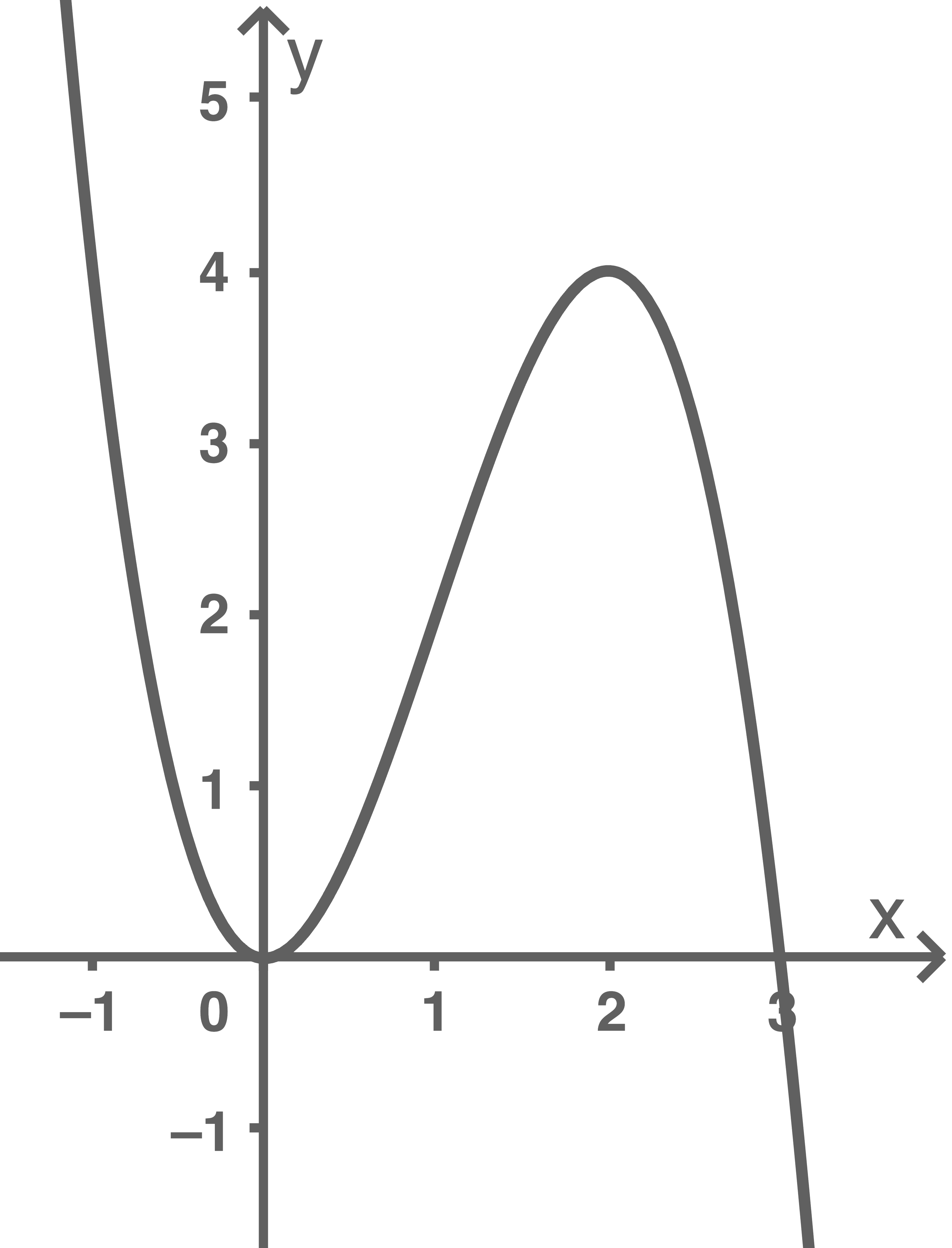
1.3
Wendepunkt begründen
Die Wendestellen entsprechen den Nullstellen der zweiten Ableitung.
Mit jeder Ableitung verliert eine Funktion einen Grad. Da die Funktion  den Grad 3 besitzt, folgt der Grad der zweiten Ableitungsfunktion
den Grad 3 besitzt, folgt der Grad der zweiten Ableitungsfunktion  mit 1.
Da der Grad einer Funktion der maximalen Anzahl ihrer Nullstellen entspricht, besitzt
mit 1.
Da der Grad einer Funktion der maximalen Anzahl ihrer Nullstellen entspricht, besitzt  folglich nur eine Nullstelle und
folglich nur eine Nullstelle und  damit nur eine Wendestelle.
damit nur eine Wendestelle.
 kann somit keinen weiteren Wendepunkt haben.
Koordinaten angeben
Die Funktion
kann somit keinen weiteren Wendepunkt haben.
Koordinaten angeben
Die Funktion  verschiebt den Graphen
verschiebt den Graphen  um eine Längeneinheit in negative
um eine Längeneinheit in negative  -Richtung und um zwei Einheiten in negative
-Richtung und um zwei Einheiten in negative  -Richtung.
Die Koordinaten des Wendepunkts
-Richtung.
Die Koordinaten des Wendepunkts  des Graphen von
des Graphen von  ergeben sich somit aus den Koordinaten des Wendepunkts
ergeben sich somit aus den Koordinaten des Wendepunkts  des Graphen von
des Graphen von  zu:
zu:

1.4
Sachverhalt skizzieren
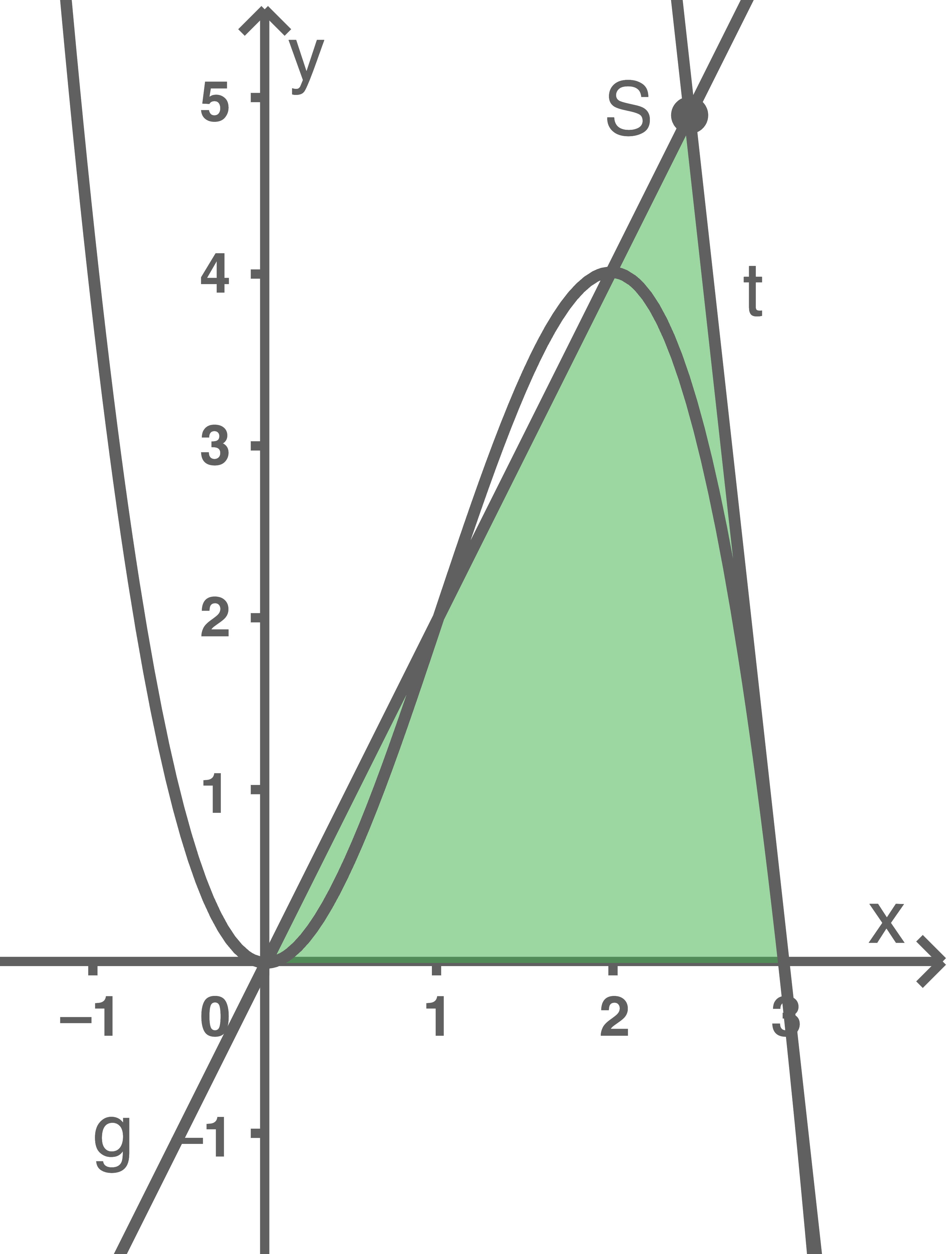 Flächeninhalt bestimmen
Formel für den Flächeninhalt eines Dreiecks:
Flächeninhalt bestimmen
Formel für den Flächeninhalt eines Dreiecks:
 Die Grundseite
Die Grundseite  liegt auf der
liegt auf der  -Achse und entspricht somit der Differenz der
-Achse und entspricht somit der Differenz der  -Koordinaten der Schnittpunkte von
-Koordinaten der Schnittpunkte von  und
und  mit der
mit der  -Achse.
Es gilt also:
-Achse.
Es gilt also:
![\(g=3-0=3 \; [\text{LE}]\)](https://mathjax.schullv.de/f6677f5e0b36d771f0425ff9e8f30e099557a98f7e57822ad37664c0960111b8?color=5a5a5a) Die Höhe des Dreiecks entspricht der
Die Höhe des Dreiecks entspricht der  -Koordinate des Schnittpunkts der Geraden
-Koordinate des Schnittpunkts der Geraden  mit der Tangente
mit der Tangente  Steigung der Tangente berechnen:
Steigung der Tangente berechnen:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/b4fd39865b721f228e32b2e63ba480f2667cfdce06bd4505eed9e7c197e796c1?color=5a5a5a) Einsetzen der Steigung
Einsetzen der Steigung  und der Koordinaten von
und der Koordinaten von  in die allgemeine Tangentengleichung liefert:
in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
t: \quad 0&=& -9\cdot 3 +c&\quad \scriptsize \mid\; +27 \\[5pt]
27&=& c
\end{array}\)](https://mathjax.schullv.de/b91353975bc627f961138f0275254aa501ab0b79ea3bd31c0330eba3cfdc2514?color=5a5a5a) Eine Tangentengleichung von
Eine Tangentengleichung von  ist somit gegeben durch
ist somit gegeben durch  Schnittstelle von
Schnittstelle von  und
und  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
-9x+27&=& 2x &\quad \scriptsize \mid\; +9x \\[5pt]
27&=& 11x &\quad \scriptsize \mid\; :11 \\[5pt]
2,45&\approx& x
\end{array}\)](https://mathjax.schullv.de/bc3a298edf3390c59332c17264b3a2d24364e73b095dfdc90073738727cd15e7?color=5a5a5a)
 -Koordinate durch Einsetzen in
-Koordinate durch Einsetzen in  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
g: \quad y&=& 2\cdot 2,45 & \\[5pt]
&=& 4,9
\end{array}\)](https://mathjax.schullv.de/38e01b17ad7a3bb18fde96e79956002b1378175eecead57155118f0bdcac7322?color=5a5a5a) Die Gerade
Die Gerade  schneidet die Tangente
schneidet die Tangente  somit im Punkt
somit im Punkt  Die Höhe des Dreiecks ist folglich gegeben durch
Die Höhe des Dreiecks ist folglich gegeben durch  Der Flächeninhalt des Dreiecks folgt also mit:
Der Flächeninhalt des Dreiecks folgt also mit:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot 3\cdot 4,9 & \\[5pt]
&=& 7,35 \; [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/ab4996d2b6573a4286fe8592e7f4b8278e5e6473476e6a94d234b4a4cccbbf0f?color=5a5a5a)

1.5
Flächeninhalte begründen
Die Funktion  hat den Wendepunkt
hat den Wendepunkt  durch welchen auch die Gerade
durch welchen auch die Gerade  verläuft. Der Graph von
verläuft. Der Graph von  ist symmetrisch bezüglich dieses Wendepunkts.
Aufgrund der symmetrischen Eigenschaften um den Wendepunkt sind die Flächen, die durch
ist symmetrisch bezüglich dieses Wendepunkts.
Aufgrund der symmetrischen Eigenschaften um den Wendepunkt sind die Flächen, die durch  und eine Gerade durch
und eine Gerade durch  eingeschlossen werden, auf beiden Seiten von
eingeschlossen werden, auf beiden Seiten von  identisch.
Anstiege bestimmen
identisch.
Anstiege bestimmen
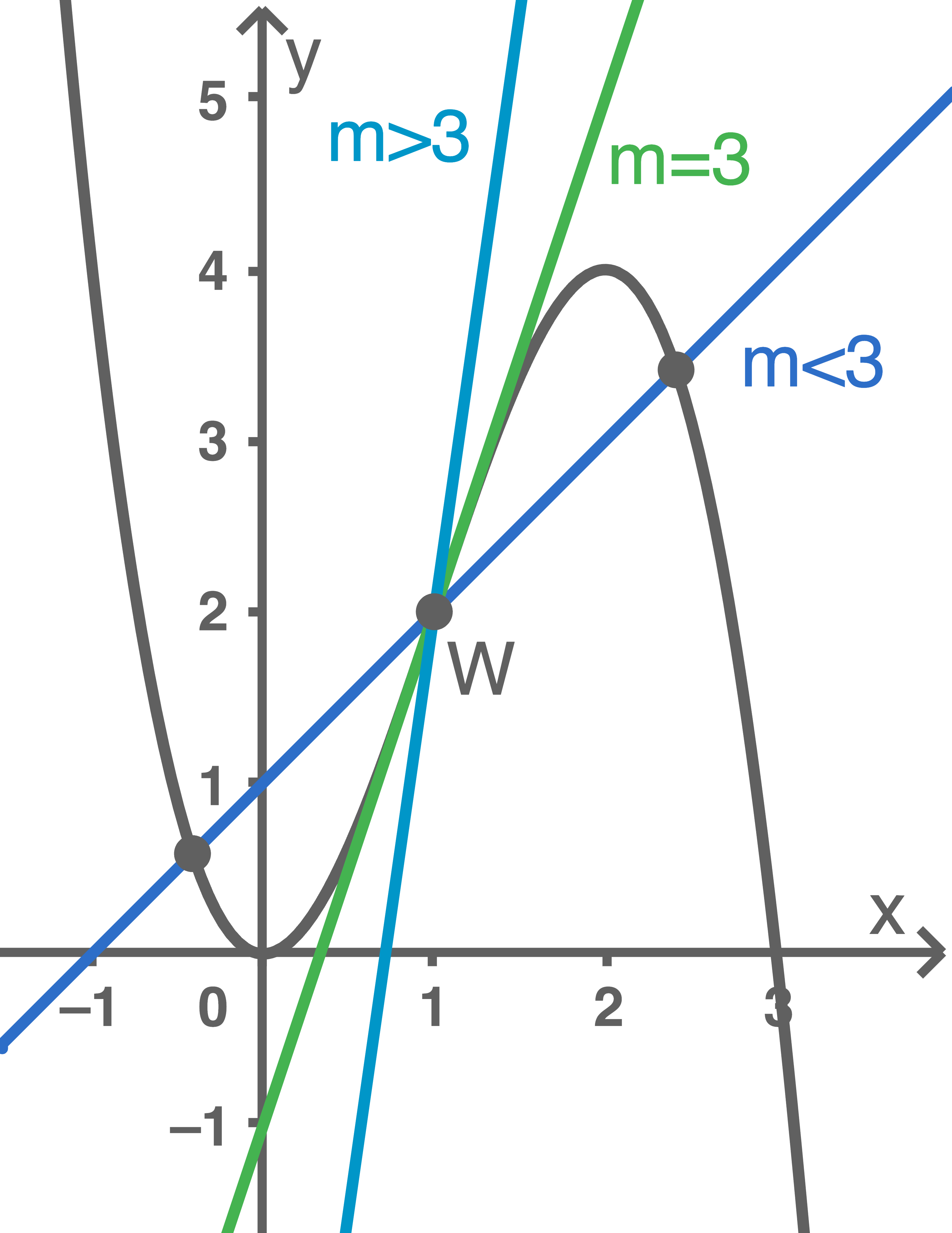 Die Gerade mit der Steigung
Die Gerade mit der Steigung  schneidet den Graphen
schneidet den Graphen  somit in genau einem Punkt, nämlich im Wendepunkt
somit in genau einem Punkt, nämlich im Wendepunkt  Für alle positiven Anstiege
Für alle positiven Anstiege  schließt die Gerade durch den Punkt
schließt die Gerade durch den Punkt  folglich Flächenstücke mit
folglich Flächenstücke mit  ein.
ein.
Eine Gerade durch  schließt genau dann Flächenstücke mit dem Graphen
schließt genau dann Flächenstücke mit dem Graphen  ein, wenn sie mit diesem 3 gemeinsame Punkte im Intervall hat.
Ab genau der Steigung von
ein, wenn sie mit diesem 3 gemeinsame Punkte im Intervall hat.
Ab genau der Steigung von  mit welcher die Gerade
mit welcher die Gerade  die Tangente an den Punkt
die Tangente an den Punkt  darstellt, schneidet die Gerade den Graphen
darstellt, schneidet die Gerade den Graphen  nur noch im Punkt
nur noch im Punkt  und schließt folglich keine Flächenstücke mehr ein.
Steigung von
und schließt folglich keine Flächenstücke mehr ein.
Steigung von  im Punkt
im Punkt  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/2938a1ba9d53f194dbe0d964e7cec551d520f19f9d2f08377f1f9632f9a71e71?color=5a5a5a)

Hilfsskizze
1.6
Größe bestimmen
![\(\begin{array}[t]{rll}
w(10)&=& 5\cdot 10\cdot \mathrm e^{-0,05\cdot 10}+5 & \\[5pt]
&\approx& 35,33 \;[\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/33f5f1bef4f34cc4cab06fd60a3efd49a713c4b2a7c5f5e2858c7712196e6067?color=5a5a5a) Zeitpunkt angeben
Zeitpunkt angeben
![\(\begin{array}[t]{rll}
w(t)&=& 35,33 & \\[5pt]
5\cdot t\cdot \mathrm e^{-0,05\cdot t}+5&=& 35,33 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/677c417b9c4e4d0b1f298938c05dfce28eae075e066da4fa154712d2de0c813c?color=5a5a5a) Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt  und
und  Während des 36. Tags nach Beobachtungsbeginn wird wieder eine Größe der bedeckten Fläche von
Während des 36. Tags nach Beobachtungsbeginn wird wieder eine Größe der bedeckten Fläche von  wie am 10. Tag erreicht.
wie am 10. Tag erreicht.
1.7
Wachstum untersuchen
Größe der Fläche zu Beobachtungsbeginn, nach 5 und nach 10 Tagen berechnen:
![\(\begin{array}[t]{rll}
w(0)&=& 5\cdot 0\cdot \mathrm e^{-0,05\cdot 0}+5 &\\[5pt]
&=& 5 \; [\text{m}^2]&\\[5pt]
w(5)&=& 5\cdot 5\cdot \mathrm e^{-0,05\cdot 5}+5 &\\[5pt]
&\approx& 24,47 \; [\text{m}^2] &\\[5pt]
w(10)&=& 5\cdot 10\cdot \mathrm e^{-0,05\cdot 10}+5&\\[5pt]
&\approx& 35,33 \; [\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/8360004dc1e2cef09d87c227be2ae82fa82c9b5135440722393e9336b67c0983?color=5a5a5a) In den ersten 5 Tagen nimmt die Größe der bedeckten Fläche um
In den ersten 5 Tagen nimmt die Größe der bedeckten Fläche um  Quadratmeter zu.
In den darauffolgenden 5 Tagen nimmt die Größe der bedeckten Fläche um
Quadratmeter zu.
In den darauffolgenden 5 Tagen nimmt die Größe der bedeckten Fläche um  Quadratmeter zu.
Die Größe der bedeckten Fläche wächst somit in den ersten 5 Tagen nach Beobachtungsbeginn mehr als in den darauffolgenden 5 Tagen.
Zeitpunkt ermitteln
Mit dem CAS ergeben sich die erste und zweite Ableitungsfunktion zu:
Quadratmeter zu.
Die Größe der bedeckten Fläche wächst somit in den ersten 5 Tagen nach Beobachtungsbeginn mehr als in den darauffolgenden 5 Tagen.
Zeitpunkt ermitteln
Mit dem CAS ergeben sich die erste und zweite Ableitungsfunktion zu:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/b8bcc90687eef23a663cec933c2333ec31098dde6b2567c8a8d606a634652357?color=5a5a5a) Notwendige Bedingung für Extremstellen der ersten Ableitung anwenden:
Notwendige Bedingung für Extremstellen der ersten Ableitung anwenden:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/bad30c08fdd501a6dd753d6128d8891abf669fd1d0774d9f6c292a5cb78a535e?color=5a5a5a) Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt  Überprüfen des Vorzeichenwechsels von
Überprüfen des Vorzeichenwechsels von  bei
bei 
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/334262cd6e8d17024b9c7b53fda4dc1bc3f3a541cae678d506301b29e92b5be0?color=5a5a5a) Da
Da  an der Stelle
an der Stelle  von negativ zu positiv wechselt, hat
von negativ zu positiv wechselt, hat  an dieser Stelle ein Minimum.
Alternativ kann das Minimum der Ableitungsfunktion auch graphisch mit dem CAS bestimmt werden.
Die Größe der von Wasserpflanzen bedeckten Fläche nimmt somit am 40. Tag nach Beobachtungsbeginn am stärksten ab.
an dieser Stelle ein Minimum.
Alternativ kann das Minimum der Ableitungsfunktion auch graphisch mit dem CAS bestimmt werden.
Die Größe der von Wasserpflanzen bedeckten Fläche nimmt somit am 40. Tag nach Beobachtungsbeginn am stärksten ab.
1.8
1.9
Wahrscheinlichkeit berechnen
Die Zufallsvariable  beschreibt die Anzahl der Einzelproben, die nicht keimfrei sind, und ist binomialverteilt mit
beschreibt die Anzahl der Einzelproben, die nicht keimfrei sind, und ist binomialverteilt mit  und
und  Mit dem binomcdf-Befehl des CAS folgt:
Mit dem binomcdf-Befehl des CAS folgt:
 Ereignis angeben
Von den 150 Einzelproben sind genau drei Proben nicht keimfrei.
Ereignis angeben
Von den 150 Einzelproben sind genau drei Proben nicht keimfrei.
1.10
Wahrscheinlichkeit berechnen
Die Mischprobe besteht aus 10 Einzelproben, welche jeweils mit einer Wahrscheinlichkeit von  keimfrei sind.
Die Wahrscheinlichkeit, dass die gesamte Mischprobe keimfrei ist, ergibt sich also zu:
keimfrei sind.
Die Wahrscheinlichkeit, dass die gesamte Mischprobe keimfrei ist, ergibt sich also zu:
 Begründung
Ist die Mischprobe keimfrei, so ist das Verfahren beendet, nachdem nur die Mischprobe untersucht wurde. In diesem Fall gibt es also genau eine Untersuchung.
Wenn die Mischprobe nicht keimfrei ist, werden zusätzlich zu der Mischprobe alle 10 Einzelproben einzeln untersucht, was insgesamt 11 Untersuchungen ergibt.
Wahrscheinlichkeitsverteilung ermitteln
Die Wahrscheinlichkeit dafür, dass eine einzelne Probe keimfrei ist, beträgt
Begründung
Ist die Mischprobe keimfrei, so ist das Verfahren beendet, nachdem nur die Mischprobe untersucht wurde. In diesem Fall gibt es also genau eine Untersuchung.
Wenn die Mischprobe nicht keimfrei ist, werden zusätzlich zu der Mischprobe alle 10 Einzelproben einzeln untersucht, was insgesamt 11 Untersuchungen ergibt.
Wahrscheinlichkeitsverteilung ermitteln
Die Wahrscheinlichkeit dafür, dass eine einzelne Probe keimfrei ist, beträgt  Da die Proben unabhängig sind, beträgt die Wahrscheinlichkeit, dass alle 10 Einzelproben keimfrei sind, somit
Da die Proben unabhängig sind, beträgt die Wahrscheinlichkeit, dass alle 10 Einzelproben keimfrei sind, somit  Die Wahrscheinlichkeit, dass die Mischprobe keimfrei ist, beträgt also
Die Wahrscheinlichkeit, dass die Mischprobe keimfrei ist, beträgt also  Die Wahrscheinlichkeit, dass die Mischprobe nicht keimfrei ist, also mindestens eine der Einzelproben nicht keimfrei ist, beträgt somit
Die Wahrscheinlichkeit, dass die Mischprobe nicht keimfrei ist, also mindestens eine der Einzelproben nicht keimfrei ist, beträgt somit  Die Wahrscheinlichkeitsverteilung von
Die Wahrscheinlichkeitsverteilung von  ist somit gegeben durch:
ist somit gegeben durch:
![\(\begin{array}[t]{rll}
E(X)&=& 1 \cdot P(X=1)+11 \cdot P(X=11) &\\[5pt]
&=& 1 \cdot 0,97^{10}+11 \cdot\left(1-0,97^{10}\right)&\\[5pt]
&=& 1 \cdot 0,737+11 \cdot 0,263 &\\[5pt]
&=& 0,737+2,893 &\\[5pt]
&=& 3,63
\end{array}\)](https://mathjax.schullv.de/57c498e71fe545cb9d2eff59bb388c115a4febfd51e83fb17ce725fa70232ba6?color=5a5a5a)