Teil A – Pflichtbereich
1
In den Teilaufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1
Die in  definierte Funktion
definierte Funktion  mit
mit  besitzt die Extremstelle:
besitzt die Extremstelle:
1.2
Der Graph einer ganzrationalen Funktion  ist symmetrisch zum Koordinatenursprung und hat den Hochpunkt
ist symmetrisch zum Koordinatenursprung und hat den Hochpunkt  Dann besitzt der Graph von
Dann besitzt der Graph von  ...
...
| im Punkt |
|
| im Punkt |
|
| im Punkt |
|
| im Punkt |
|
| keinen weiteren Extrempunkt. |
1.3
Für  gilt:
gilt: 
1.4
1.5
Welches der folgenden bestimmten Integrale hat den Wert Null?
(5 BE)
2
Gegeben sind die Punkte 
 und
und  wobei
wobei  eine reelle Zahl ist.
eine reelle Zahl ist.
2.1
Zeige, dass  für
für  auf der Geraden durch
auf der Geraden durch  und
und  liegt.
liegt.
(3 BE)
2.2
Ermittle denjenigen Wert von  für den das Dreieck
für den das Dreieck  im Punkt
im Punkt  rechtwinklig ist.
rechtwinklig ist.
(2 BE)
3
Die binomialverteilte Zufallsgröße  besitzt die Parameter
besitzt die Parameter  und
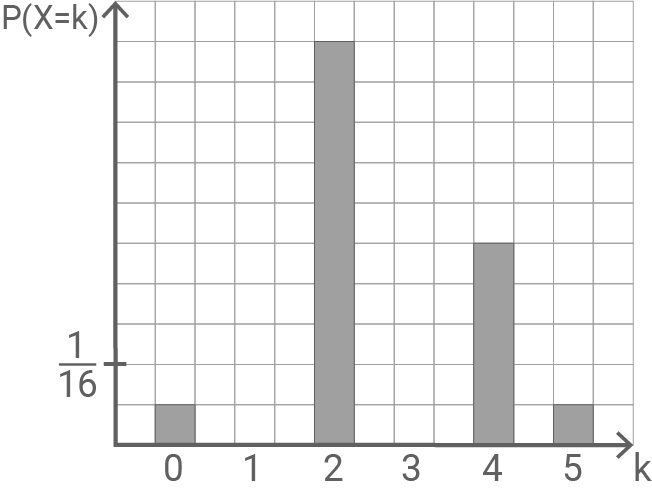
und  Die Abbildung zeigt die Wahrscheinlichkeitsverteilung von
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung von  bei der zwei Wahrscheinlichkeiten nicht dargestellt sind.
bei der zwei Wahrscheinlichkeiten nicht dargestellt sind.

3.1
Gib den Erwartungswert von  an.
Ermittle den Wert von
an.
Ermittle den Wert von 
(3 BE)
3.2
Vervollständige die Wahrscheinlichkeitsverteilung von  in der Abbildung.
Begründe die Eintragungen.
in der Abbildung.
Begründe die Eintragungen.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Lösungsweg:
Ableitung bilden:
 An der Extremstelle gilt:
An der Extremstelle gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/1ff23d5805980603bd5074bc6d61a06d6cdf814af99a1ba2d1c267f94cc10d87?color=5a5a5a)
1.2
| im Punkt |
|
| im Punkt |
|
| im Punkt |
|
| im Punkt |
|
| keinen weiteren Extrempunkt. |
Lösungsweg:
Symmetrie zum Koordinatenursprung bedeutet, dass der Graph der Funktion  punktsymmetrisch zum Punkt
punktsymmetrisch zum Punkt  ist und
ist und  gilt.
Da der Punkt
gilt.
Da der Punkt  diese Bedingung erfüllt, muss dieser auf dem Graphen liegen.
Aufgrund der Punktsymmetrie entspricht dieser Punkt dem Tiefpunkt des Graphen.
diese Bedingung erfüllt, muss dieser auf dem Graphen liegen.
Aufgrund der Punktsymmetrie entspricht dieser Punkt dem Tiefpunkt des Graphen.
1.3
Lösungsweg:
![\(\begin{array}[t]{rll}
\dfrac{a^3}{a^{-2}}&=& a^3\cdot a^{-(-2)}&\\[5pt]
&=& a^{3+2}&\\[5pt]
&=& a^5
\end{array}\)](https://mathjax.schullv.de/f8061d73ae90af73addae4d5ede99a6d91243f92d26b57f31b4b7eae6ed67363?color=5a5a5a)
1.4
Lösungsweg:
Es gilt:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to -\infty}2^x&=& \lim\limits_{x\to -\infty} \dfrac{1}{2^{-x}}& \\[5pt]
&=& \dfrac{1}{2^{\lim\limits_{x\to -\infty}-x}}& \\[5pt]
&=& \dfrac{1}{2^{\lim\limits_{x\to \infty}x}}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c9a335519b7b11f38a41339fbf9355ad585a24c1a4effa64d714c9181dc42c2b?color=5a5a5a) Da die Exponentialfunktion
Da die Exponentialfunktion  exponentiell ansteigt, wird der Nenner für große Werte von
exponentiell ansteigt, wird der Nenner für große Werte von  immer größer und der Bruch nähert sich folglich dem Wert null an.
immer größer und der Bruch nähert sich folglich dem Wert null an.
1.5
Lösungsweg:
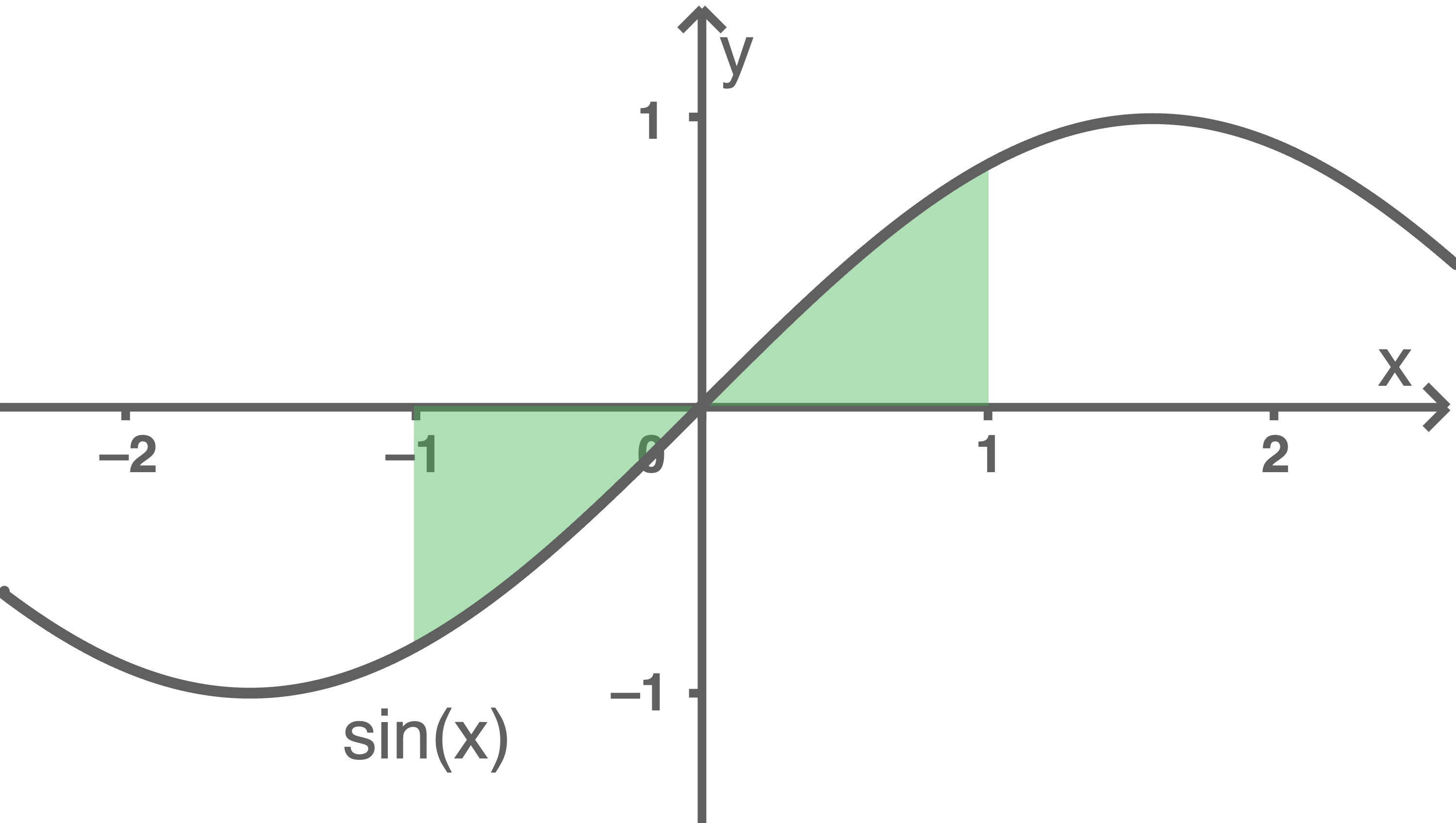 Da die Sinusfunktion durch den Ursprung verläuft und zu diesem punktsymmetrisch ist, gilt:
Da die Sinusfunktion durch den Ursprung verläuft und zu diesem punktsymmetrisch ist, gilt:  Da die Fläche unterhalb der
Da die Fläche unterhalb der  -Achse gleich groß wie die oberhalb ist, besitzt das gesamte Integral folglich den Wert null.
-Achse gleich groß wie die oberhalb ist, besitzt das gesamte Integral folglich den Wert null.

2.1
Geradengleichung der Geraden, die durch  und
und  verläuft, aufstellen:
verläuft, aufstellen:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OA}+t\cdot \overrightarrow{AB}&\\[5pt]
&=& \pmatrix{1\\0\\1}+t\cdot \pmatrix{3\\-4\\1}
\end{array}\)](https://mathjax.schullv.de/32c90a1d2880d5b46c89a5882002d81eca7d750bb159253c3b18cbcd95fb4c44?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  mit
mit  liefert:
liefert:
 Aus der zweiten Zeile folgt direkt
Aus der zweiten Zeile folgt direkt 
![\(\begin{array}[t]{rll}
\pmatrix{-2\\4\\0}&=& \pmatrix{1\\0\\1}-1\cdot \pmatrix{3\\-4\\1}& \\[5pt]
&=& \pmatrix{1-3\\0-(-4)\\1-1}& \\[5pt]
&=& \pmatrix{-2\\4\\0}
\end{array}\)](https://mathjax.schullv.de/847aaae186bda9b9bd071e2ffe2ef1eeca27e5044b41db2aca4c2db71fa5d904?color=5a5a5a) Somit liegt
Somit liegt  für
für  auf der Geraden durch
auf der Geraden durch  und
und 
2.2
Für einen rechten Winkel im Punkt  muss gelten:
muss gelten:
![\(\begin{array}[t]{rll}
\overrightarrow{AB}\circ \overrightarrow{AC}&=& 0 &\\[5pt]
\pmatrix{3\\-4\\1} \circ \pmatrix{-3\\4\\z-1}&=& 0 &\\[5pt]
3\cdot (-3)+(-4)\cdot 4+1\cdot (z-1)&=& 0 &\\[5pt]
-9-16+ z-1&=& 0 &\\[5pt]
-26+ z&=& 0 \quad \scriptsize \mid\, +26 \\[5pt]
z&=& 26
\end{array}\)](https://mathjax.schullv.de/fc10a293c19e188ace48e1c9f1dc65cedfd72c14ff07ec7f4c18fff32923f6a2?color=5a5a5a)
3.1
Erwartungswert angeben
Für den Erwartungswert  gilt:
gilt:
 Wert ermitteln
Ablesen der Werte von
Wert ermitteln
Ablesen der Werte von  und
und  aus der Abbildung ergibt:
aus der Abbildung ergibt:
![\(\begin{array}[t]{rll}
P(X\gt 3)&=& P(X=4)+P(X=5) & \\[5pt]
&=& \dfrac{5}{32}+\dfrac{1}{32} & \\[5pt]
&=& \dfrac{3}{16}
\end{array}\)](https://mathjax.schullv.de/3c11e44b2a952bd1be3509372d643f9d43015147635a052f9db2d2dbc2712cb1?color=5a5a5a)
3.2
Wahrscheinlichkeitsverteilung vervollständigen
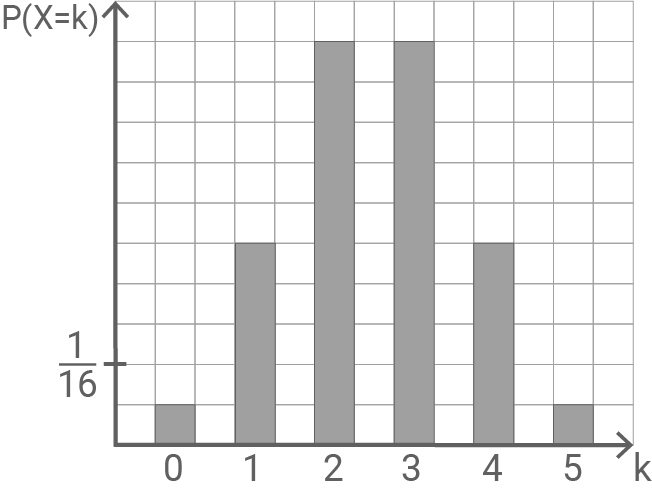 Eintragungen erklären
Für
Eintragungen erklären
Für  sind die Wahrscheinlichkeiten symmetrisch um den Erwartungswert verteilt.
Mit dem Erwartungswert
sind die Wahrscheinlichkeiten symmetrisch um den Erwartungswert verteilt.
Mit dem Erwartungswert  folgt also
folgt also 
 und
und 
