Teil B1

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\dfrac{3}{32} \cdot x^2-\dfrac{15}{4} \cdot x+\dfrac{75}{2}.$

1.1

Zeige, dass der Punkt $\left(22 \,\bigg \vert \, \dfrac{3}{8}\right)$ auf dem Graphen von $f$ liegt.

Gib eine Gleichung der Symmetrieachse des Graphen von $f$ an.

Gib das Verhalten von $f$ für $x \rightarrow-\infty$ und $x \rightarrow+\infty$ an.

Gib den Wertebereich von $f$ an.

(6 BE)

1.2

Die Tangente an den Graphen von $f$ im Punkt $(4 \mid f(4))$ schließt mit beiden Koordinatenachsen ein Dreieck ein.

Ermittle die Längen der Katheten dieses Dreiecks.

Beurteile folgende Aussage:

Es gibt zwei Tangenten an den Graphen von $f$ , deren Anstiege gleich sind.

(9 BE)

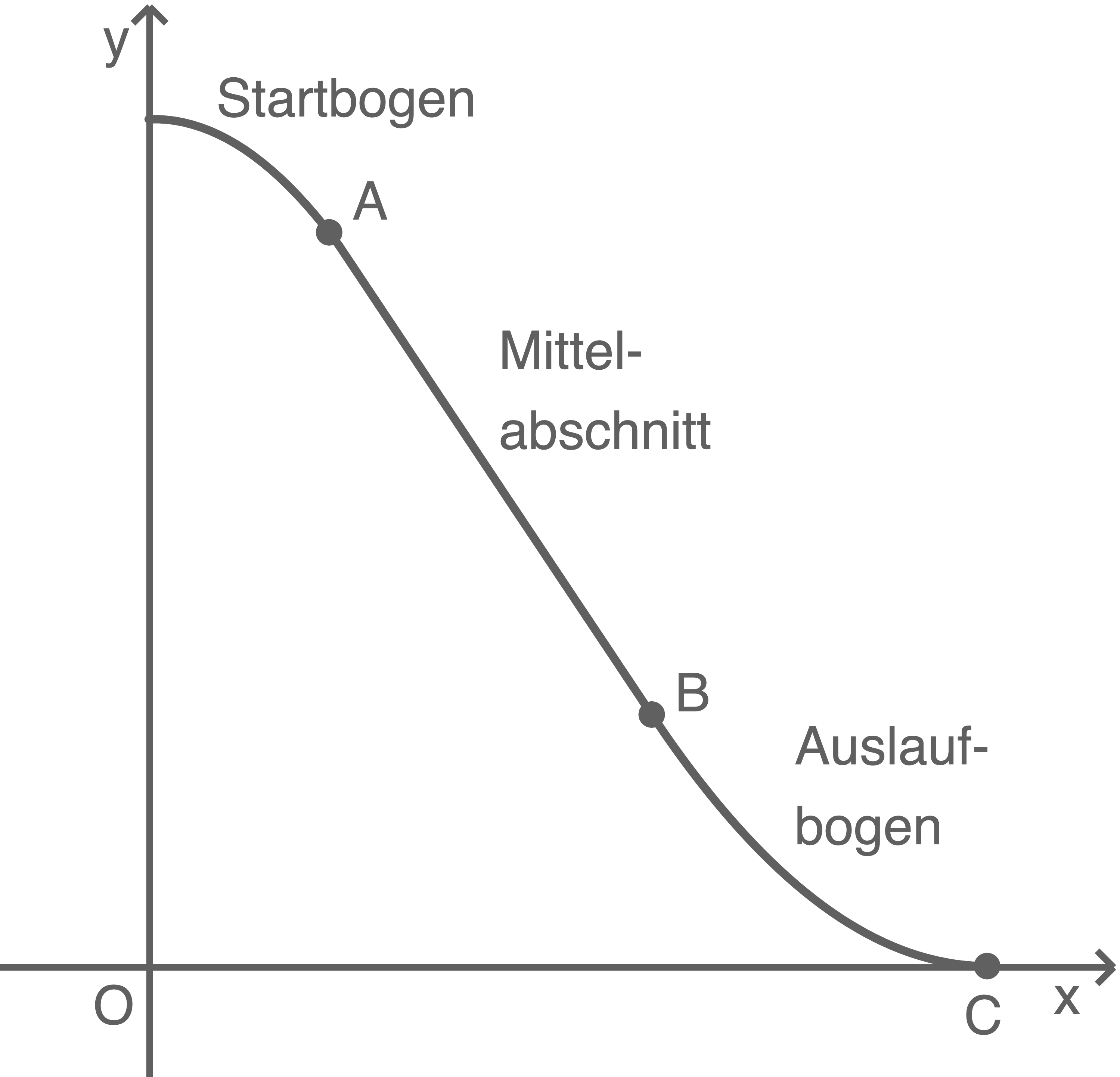
Die Abbildung 1 zeigt den Längsschnitt einer Wasserrutsche. Die Rutschbahn dieser Wasserrutsche ist aus einem Startbogen, einem Mittelabschnitt und einem Auslaufbogen zusammengesetzt.

Der Mittelabschnitt $\overline{A B}$ mit $A(4 \mid 18)$ liegt auf dem Graphen der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=-\dfrac{3}{2} \cdot x+24.$

Der Auslaufbogen zwischen den Punkten $B$ und $C(20 \mid 0)$ liegt auf dem Graphen der Funktion $f.$

Die $x$ -Achse beschreibt die Horizontale. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

Abbildung 1 (nicht maßstäblich)

1.3

Zeige, dass der Punkt $B$ die $x$ -Koordinate 12 hat.

Berechne die Größe des Neigungswinkels des Mittelabschnitts gegenüber der Horizontalen.

Eine Person benötigt 1,4 Sekunden, um den Mittelabschnitt zu durchrutschen.

Bestimme die Durchschnittsgeschwindigkeit der Person im Mittelabschnitt.

(6 BE)

Eine Seitenfläche der Wasserrutsche wird im Modell durch den Längsschnitt der Rutschbahn und beide Koordinatenachsen eingeschlossen.

1.4

Diese Seitenfläche ist bis zu einer Höhe von 18 Metern verkleidet.

Berechne den Inhalt der verkleideten Fläche.

(7 BE)

1.5

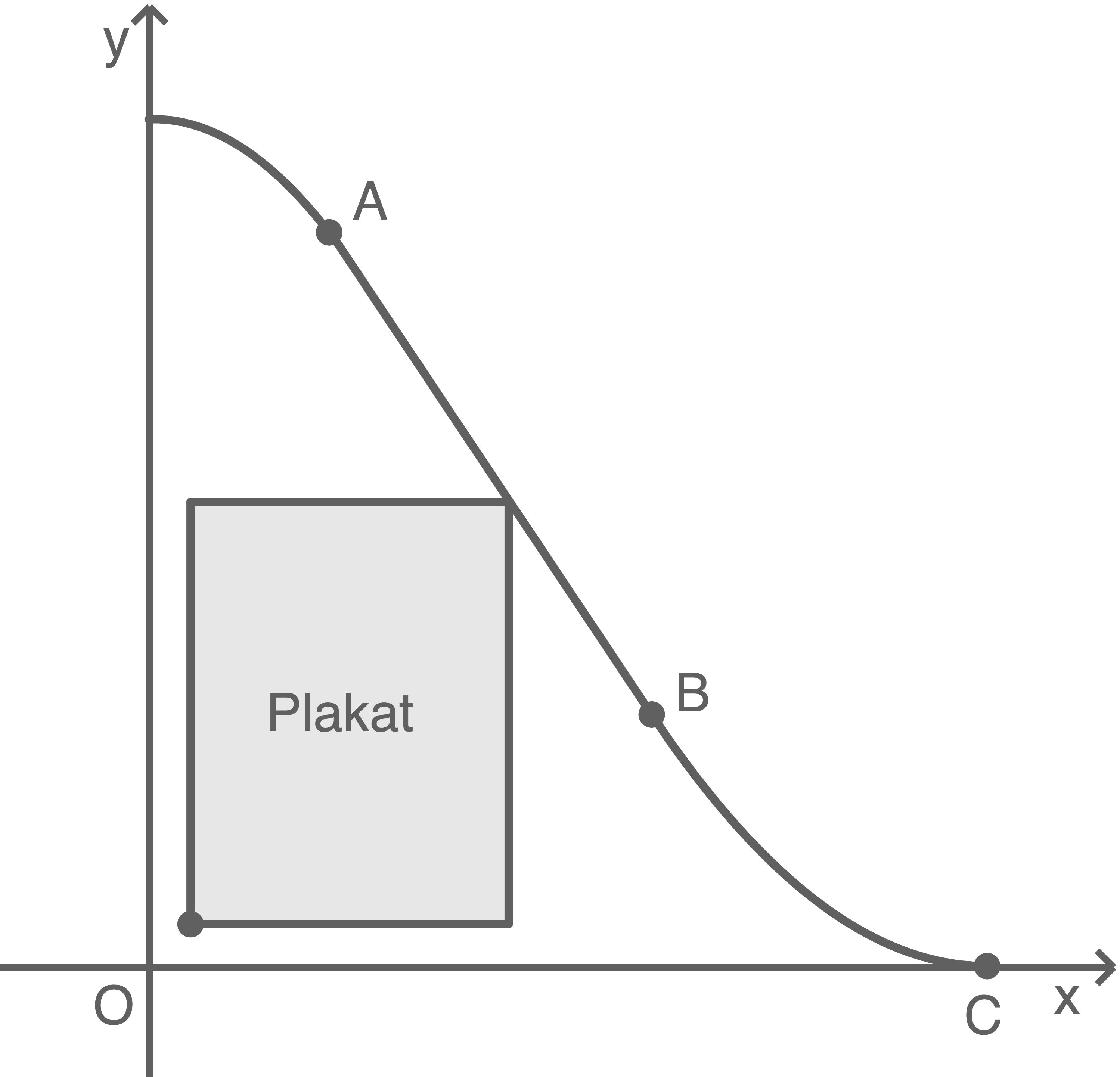
An dieser Seitenfläche wird ein rechteckiges Plakat angebracht. Die untere Kante des Plakats ist parallel zur Horizontalen. Ein Eckpunkt des Plakats ist $(1\mid1)$ (siehe Abbildung 2).

Für $u \in \mathbb{R}\; ; 4\lt u\lt12$ lässt sich der Flächeninhalt des Plakats durch die Funktion $p$ mit $p(u)=(u-1) \cdot(g(u)-1)$ berechnen.

Bestimme die Koordinaten der weiteren Eckpunkte des Plakats mit größtmöglichem Flächeninhalt.

(6 BE)

Sachsen Abi 2023 GK Wasserrutsche Plakat

Abbildung 2 (nicht maßstäblich)

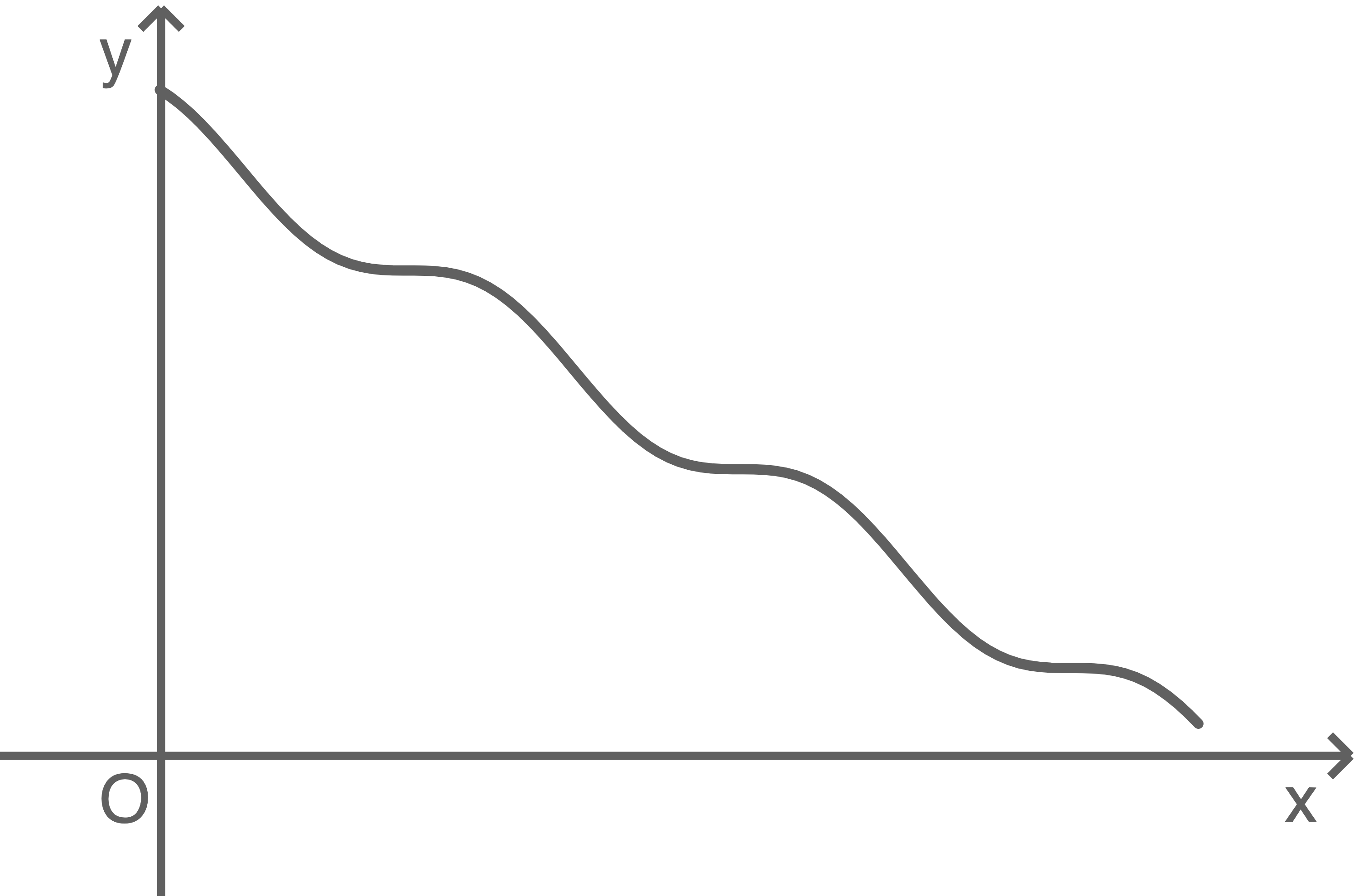
Die Abbildung 3 zeigt den vollständigen Längsschnitt einer anderen Wasserrutschbahn.

Ihr Verlauf kann mit Hilfe der in $\mathbb{R}$ definierten Funktion $h$ mit $h(x)=\dfrac{3}{5} \cdot \cos (x)-\dfrac{3}{5} \cdot x+12$ beschrieben werden.

Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

Die $x$ -Achse beschreibt die Wasseroberfläche. Die Rutschbahn endet 50 Zentimeter oberhalb der Wasseroberfläche.

Sachsen Abi 2023 GK Wasserrutsche Längsschnitt

Abbildung 3 (nicht maßstäblich)

1.6

Zeige, dass der Startpunkt der Rutschbahn 12,6 Meter oberhalb der Wasseroberfäche liegt.

Ermittle die horizontale Ausdehnung der Rutschbahn.

(3 BE)

1.7

Die Rutschbahn weist in mehreren Punkten ihre größte Neigung gegenüber der Horizontalen auf.

Bestimme diese Neigung in Prozent.

(4 BE)

1.8

Der Graph von $h$ enthält Punkte, in denen die Tangente an den Graphen parallel zur $x$ -Achse verläuft.

Weise nach, dass benachbarte Punkte mit dieser Eigenschaft jeweils den gleichen Abstand haben.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Lage des Punkts zeigen

$\begin{array}[t]{rll} f(22)&=& \dfrac{3}{32} \cdot 22^2-\dfrac{15}{4} \cdot 22+\dfrac{75}{2}& \\[5pt] &=& \dfrac{3}{8} \end{array}$

Somit liegt der Punkt $\left(22 \,\bigg \vert \,\dfrac{3}{8} \right)$ auf dem Graphen von $f.$

Gleichung angeben

Der Graph von $f$ entspricht einer Parabel. Diese ist symmetrisch zum Scheitelpunkt. Die Symmetrieachse verläuft folglich durch den Scheitelpunkt.

Für den Scheitelpunkt muss gelten:

$\(\begin{array}[t]{rll} f$

Die Gleichung der Symmetrieachse ist somit gegeben durch $x=20.$

Verhalten angeben

$\lim\limits_{x\to\pm\infty} f(x)=+\infty$

Wertebereich angeben

$\{y \mid y\in\mathbb{R}, y \geq 0 \}$

1.2

Längen berechnen

$\begin{array}[t]{rll} f(4)&=& \dfrac{3}{32} \cdot 4^2-\dfrac{15}{4} \cdot 4+\dfrac{75}{2}& \\[5pt] &=& 24 \end{array}$

$\(\begin{array}[t]{rll} f$

Einsetzen in die allgemeine Tangentengleichung liefert:

$\begin{array}[t]{rll} y&=& m\cdot x+c&\\[5pt] 24&=& -3\cdot 4+c&\quad \scriptsize \mid\; +12\\[5pt] 36&=& c \end{array}$

Die Schnittstelle mit der $y$ -Achse ist gegeben durch $c=36.$

Schnittstelle mit der $x$ -Achse berechnen:

$\begin{array}[t]{rll} -3\cdot x+36&=& 0 &\quad \scriptsize \mid\; -36 \\[5pt] -3\cdot x&=& -36&\quad \scriptsize \mid\; :(-3) \\[5pt] x &=& 12 \end{array}$

Die Längen der Katheten sind somit 12 und 36.

Aussage beurteilen

Die erste Ableitungsfunktion $\(f$ von $f$ gibt für jedes $x \in \mathbb{R}$ den Anstieg der Tangente an.

$\(f$ ist eineindeutig, weshalb die Aussage falsch ist.

1.3

$x$ -Koordinate nachweisen

$\begin{array}[t]{rll} g(x)&=& f(x)& \\[5pt] -\dfrac{3}{2}\cdot x+24&=& \dfrac{3}{32} \cdot x^2-\dfrac{15}{4} \cdot x+\dfrac{75}{2} \end{array}$

Mit dem solve-Befehl des CAS folgt $x=12.$

Neigungswinkel berechnen

Der Mittelabschnitt besitzt die Steigung $-\dfrac{3}{2}.$ Somit folgt:

$\begin{array}[t]{rll} \tan (\alpha)&=& \,\bigg \vert \,-\dfrac{3}{2}\,\bigg \vert \,&\quad \scriptsize \mid\; \tan^{-1} \\[5pt] \alpha&\approx& 56^{\circ} \end{array}$

Durchschnittsgeschwindigkeit bestimmen

Die $y$ -Koordinate von $B$ ergibt sich durch:

$g(12)=-\dfrac{3}{2}\cdot 12+24=6$

Somit ergibt sich die Durchschnittsgeschwindigkeit mit:

$\dfrac{\sqrt{(12-4)^2+(6-18)^2}}{1,4} \approx 10 \dfrac{\,\text{m}}{\,\text{s}}$

1.4

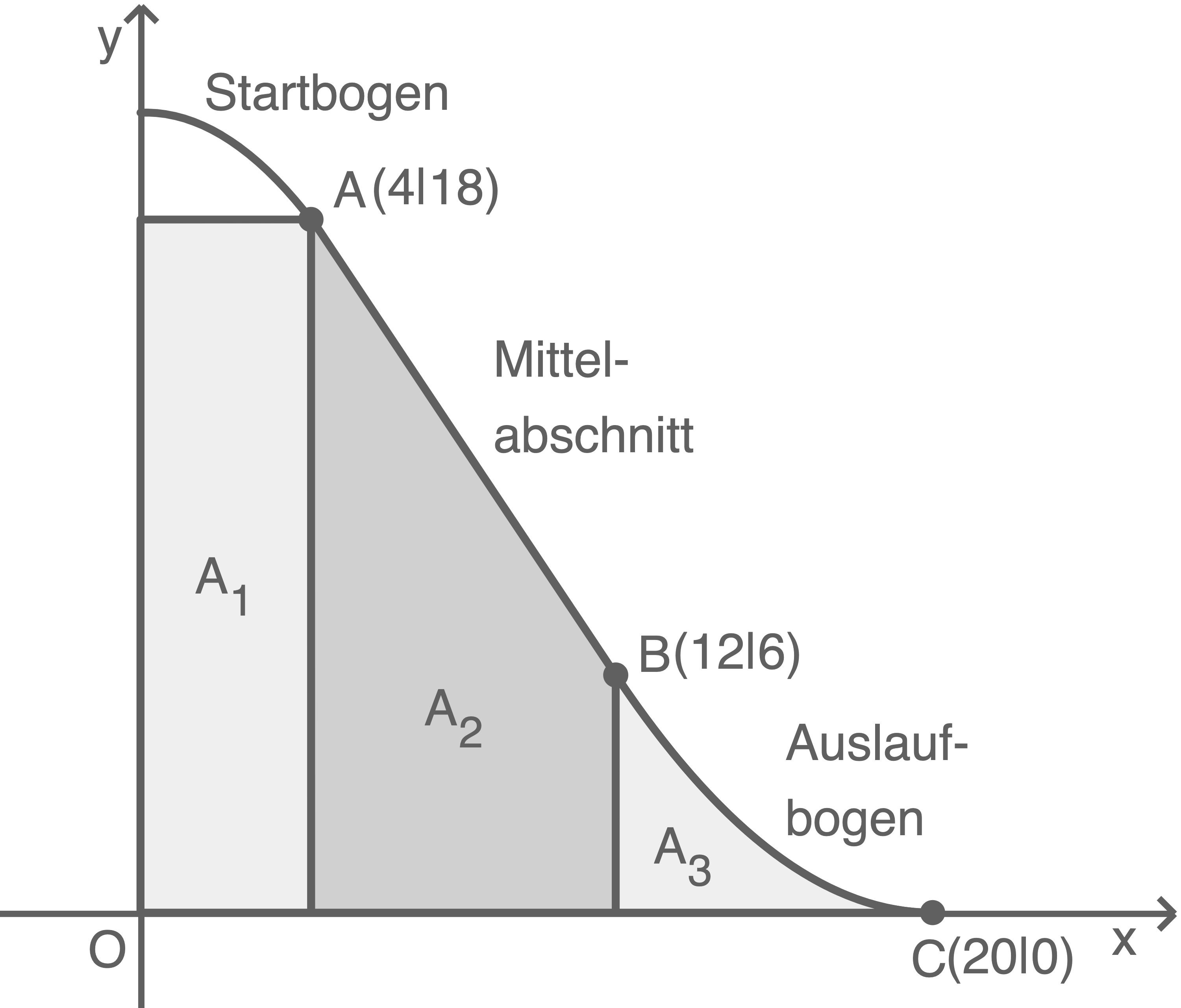
Die verkleidete Fläche setzt sich aus drei Teilen zusammen:

Rutsche Verkleidung Flaeche Sachsen Abi 2023

Hilfsskizze

$\begin{array}[t]{rll} A_1&=& 4\cdot 18&\\[5pt] &=& 72\; [\text{m}^2] \end{array}$

$\begin{array}[t]{rll} A_2&=& \dfrac{18+6}{2}\cdot 8 & \\[5pt] &=& 96\; [\text{m}^2] \end{array}$

$A_3=16 \; [\text{m}^2]$

Rechenweg anzeigen

Der gesamte Inhalt der verkleideten Fläche folgt also mit:

$\begin{array}[t]{rll} A&=& A_1+A_2+A_3 & \\[5pt] &=& 72\;\text{m}^2+96\;\text{m}^2+16\;\text{m}^2& \\[5pt] &=& 184 \; \text{m}^2 \end{array}$

1.5

Gesucht ist das Maximum der Funktion $p.$

$\begin{array}[t]{rll} p(u)&=& (u-1)\cdot (g(u)-1) & \\[5pt] &=& (u-1)\cdot \left(-\dfrac{3}{2}\cdot u+24-1\right) & \\[5pt] &=& -\dfrac{3}{2}\cdot u^2+23\cdot u+ \dfrac{3}{2}\cdot u-23 & \\[5pt] &=& -\dfrac{3}{2}\cdot u^2+ \dfrac{49}{2}\cdot u-23 \end{array}$

Notwendige Bedingung anwenden:

$\(\begin{array}[t]{rll} p$

Hinreichende Bedingung anwenden:

$\(p$

An der Stelle $x=\dfrac{49}{6}$ nimmt die Funktion $p$ somit ihr Maximum an.

$y$ -Koordinate bestimmen:

$\begin{array}[t]{rll} g\left(\dfrac{49}{6}\right)&=& -\dfrac{3}{2}\cdot \dfrac{49}{6}+24 & \\[5pt] &=& \dfrac{47}{4} \end{array}$

Die weiteren Eckpunkte des Plakats folgen also mit $\left(1 \,\bigg \vert \, \dfrac{47}{4}\right),$ $\left(\dfrac{49}{6} \,\bigg \vert \, 1\right)$ und $\left(\dfrac{49}{6} \,\bigg \vert \, \dfrac{47}{4}\right).$

1.6

Startpunkt prüfen

Für den Startpunkt gilt:

$\begin{array}[t]{rll} h(0)&=& \dfrac{3}{5} \cdot \cos (0)-\dfrac{3}{5} \cdot 0+12&\\[5pt] &=& 12,6 \; [\text{m}]&\\[5pt] \end{array}$

Horizontale Ausdehnung ermitteln

Da die Rutschbahn $0,5 \; \text{m}$ oberhalb der Wasseroberfläche endet, ergibt sich:

$\begin{array}[t]{rll} h(x)&=& 0,5 &\\[5pt] \dfrac{3}{5} \cdot \cos (x)-\dfrac{3}{5} \cdot x+12&=& 0,5 \end{array}$

Mit dem solve-Befehl des CAS folgt $x\approx 19,8.$

Die horizontale Ausdehnung beträgt somit ca. $19, 8 \text{m}.$

1.7

Die Steigung der Rutschbahn ist gegeben durch $\(h$

Die Graphen von $h(x)$ und $\(h$ können mit der graphischen Darstellung des GTR analysiert werden:

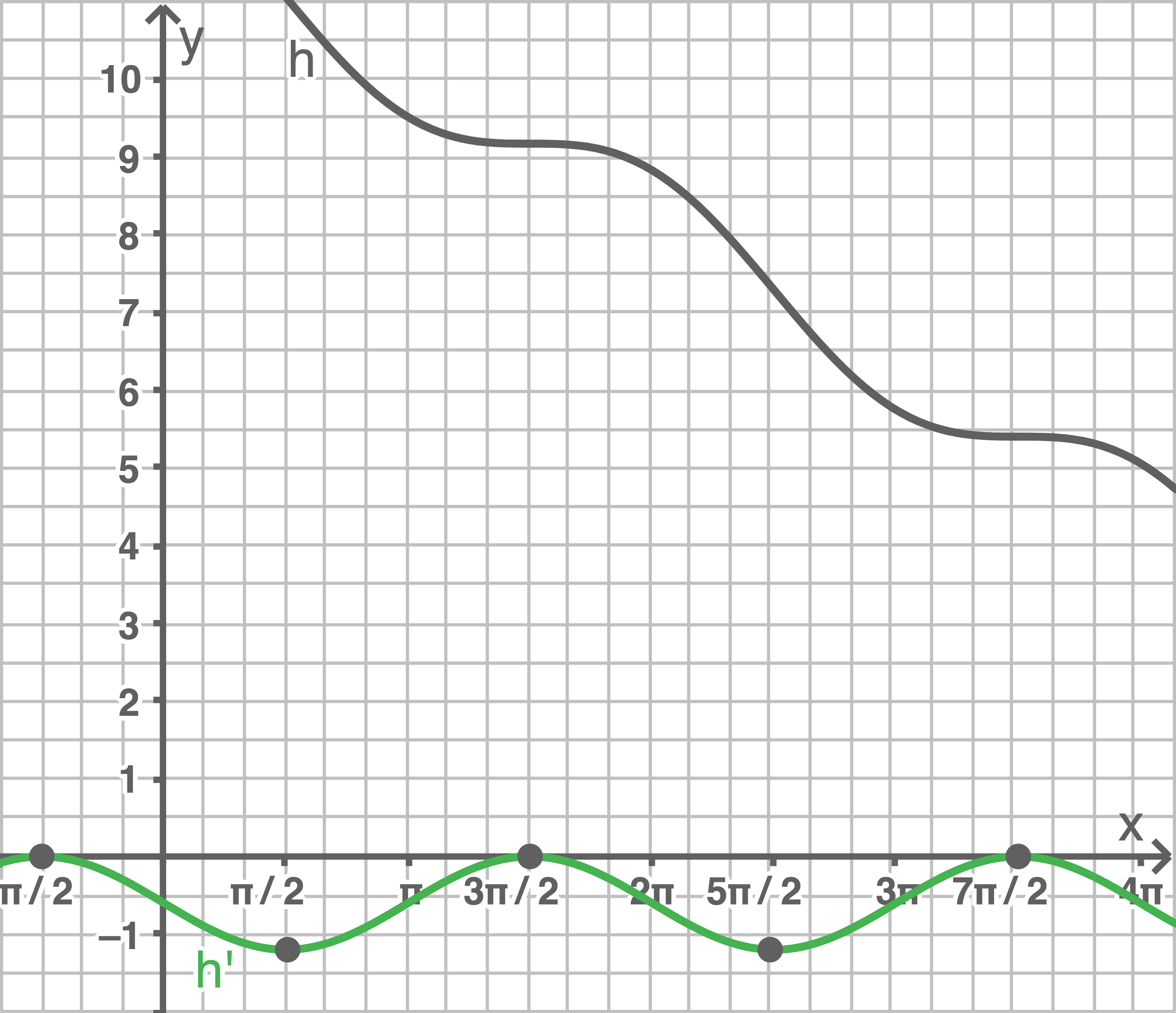Hilfsskizze GTR CAS Taschenrechner Sachsen Abi 2023

Es ist erkennbar, dass der Graph von $h$ die größte Neigung gegenüber der Horizontalen an den Stellen aufweist, an welchen der Graph von $\(h$ seine Minimalstellen annimmt.

Mit dem CAS ergibt sich beispielsweise $x=\dfrac{\pi}{2}$ als mögliche Minimalstelle.

Neigung bestimmen:

$\(\begin{array}[t]{rll} h$

Die größte Neigung beträgt somit $120\,\%.$

1.8

Es soll gelten:

$\(\begin{array}[t]{rll} h$

Eine Lösung der Gleichung ist $\dfrac{3}{2}\cdot\pi.$ Aufgrund der Symmetrie der Sinusfunktion folgen die $x$ -Koordinaten aller weiteren Punkte mit $\dfrac{3}{2}\cdot\pi+2\cdot \pi \cdot k$ und haben somit alle den gleichen Abstand von $2\cdot \pi$ zueinander.

$y$ -Koordinaten bestimmen:

$h\left(\dfrac{3}{2}\cdot\pi+2\cdot \pi \cdot k\right)=...$

Rechenweg anzeigen

Damit stimmen für benachbarte Punkte sowohl die Differenzen der $x$ -Koordinaten als auch die Differenzen der $y$ -Koordinaten und damit die Abstände überein.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?