Teil B1
Rasenroboter können Rasenflächen selbstständig mähen. Sie arbeiten mithilfe eines Begrenzungskabels. Das Begrenzungskabel muss vorab verlegt werden, um die zu mähende Rasenfläche einzugrenzen.
 Es gilt:
Es gilt: 


 und
und 
Im Punkt befindet sich die Ladestation des Rasenroboters.
befindet sich die Ladestation des Rasenroboters.
 .
.
Wenn das Hindernis erkannt wird, setzt der Rasenroboter entweder mit einer Wahrscheinlichkeit von seine Arbeit fort oder er bleibt stehen.
seine Arbeit fort oder er bleibt stehen.
Wenn das Hindernis nicht erkannt wird, setzt der Rasenroboter entweder seine Arbeit fort oder bleibt mit einer Wahrscheinlichkeit von stehen.
stehen.
Ein kartesisches Koordinatensystem mit dem Koordinatenursprung  (1 Längeneinheit entspricht 1 Meter) wird in eine Rasenfläche gelegt. Diese Rasenfläche liegt in der
(1 Längeneinheit entspricht 1 Meter) wird in eine Rasenfläche gelegt. Diese Rasenfläche liegt in der  -
- -Ebene.
-Ebene.
Der Verlauf des Begrenzungskabels wird zwischen den Punkten und
und  näherungsweise durch den Graphen der Funktion
näherungsweise durch den Graphen der Funktion  mit
mit

 sowie durch die Strecken
sowie durch die Strecken 


 und
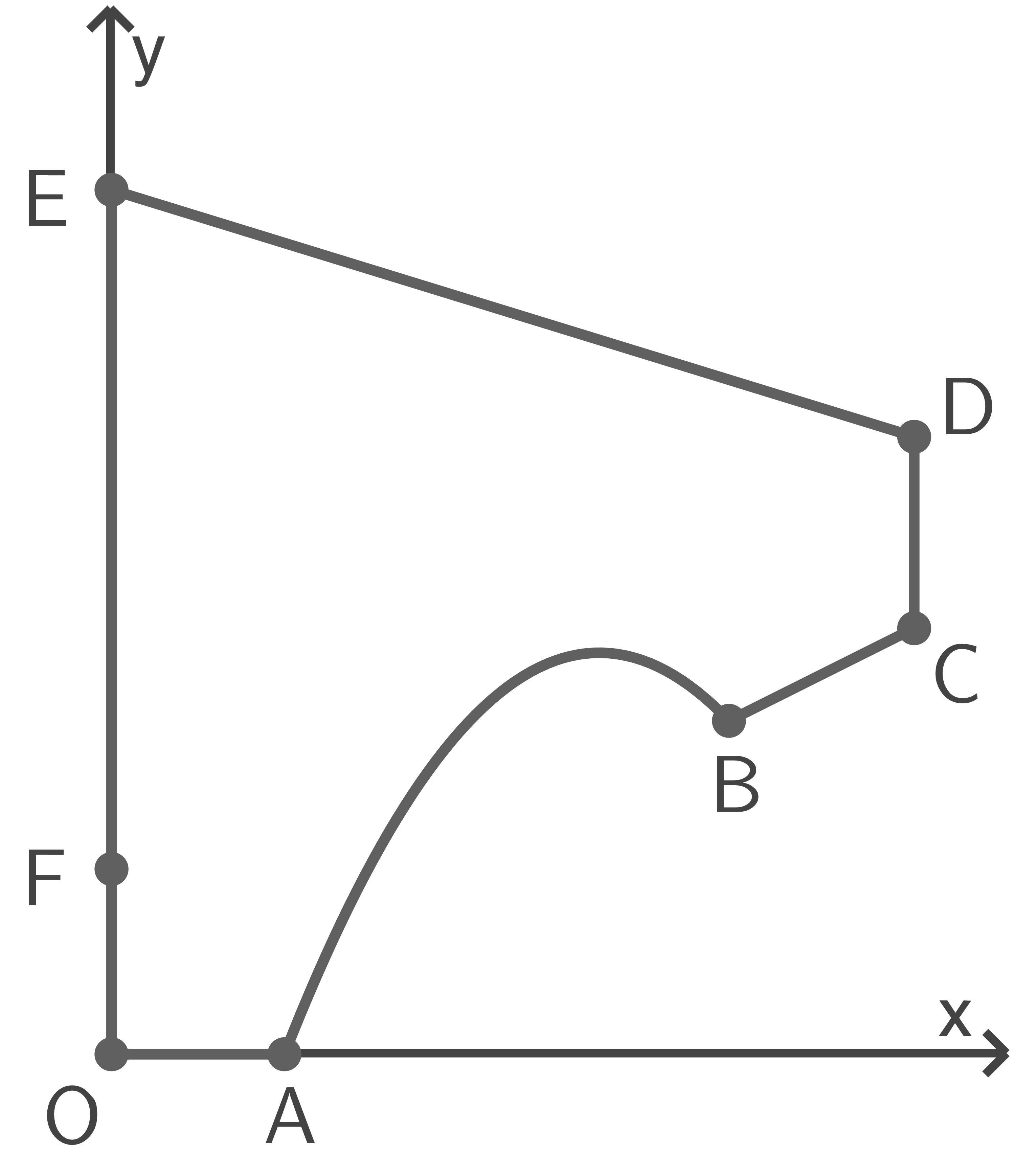
und  beschrieben (siehe Abbildung).
beschrieben (siehe Abbildung).
Der Verlauf des Begrenzungskabels wird zwischen den Punkten

Abbildung (nicht maßstäblich)
Im Punkt
1.1
Gib die Koordinaten des Maximumpuktes des Graphen von  an.
an.
Erreichbare BE-Anzahl: 02
1.2
Die Strecke  liegt auf einer Geraden
liegt auf einer Geraden  .
.
Weise nach, dass durch die Gleichung
durch die Gleichung  beschrieben werden kann.
beschrieben werden kann.
Die Tangente an den Graphen der Funktion im Punkt
im Punkt  verläuft parallel zu
verläuft parallel zu  .
.
Ermittle die -Koordinate von
-Koordinate von  .
.
Weise nach, dass
Die Tangente an den Graphen der Funktion
Ermittle die
Erreichbare BE-Anzahl: 05
1.3
Ein Rasenroboter kann unter optimalen Bedingungen in einer Minute eine Fläche von  mähen. Dieser Rasenroboter soll die durch das Begrenzungskabel eingeschlossene Rasenfläche vollständig mähen.
mähen. Dieser Rasenroboter soll die durch das Begrenzungskabel eingeschlossene Rasenfläche vollständig mähen.
Berechne die Zeit, die dieser Rasenroboter unter optimalen Bedingungen dafür benötigen würde.
Berechne die Zeit, die dieser Rasenroboter unter optimalen Bedingungen dafür benötigen würde.
Erreichbare BE-Anzahl: 05
1.4
Der Rasenroboter startet den Mähvorgang an der Ladestation im Punkt  . Er fährt geradlinig in Richtung des Punktes
. Er fährt geradlinig in Richtung des Punktes  , für den die Länge der Strecke
, für den die Länge der Strecke  minimal ist.
minimal ist.
Ermittle diese minimale Länge.
Ermittle diese minimale Länge.
Erreichbare BE-Anzahl: 03
1.5
Zum Auffinden der Ladestation wird für den Rasenroboter ein Suchkabel verlegt.
Das Suchkabel verläuft ab der Ladestation zunächst geradlinig und orthogonal zur Strecke
geradlinig und orthogonal zur Strecke  bis zu einem Punkt
bis zu einem Punkt  .
.
Der weitere Verlauf des Suchkabels wird im Intervall näherungsweise durch den Graphen einer ganzrationalen Funktion
näherungsweise durch den Graphen einer ganzrationalen Funktion  zweiten Grades beschrieben. Die Punkte
zweiten Grades beschrieben. Die Punkte 
 und
und  liegen auf dem Graphen von
liegen auf dem Graphen von 
Der Punkt hat, parallel zur
hat, parallel zur  -Achse gemessen, zu
-Achse gemessen, zu  die gleiche Entfernung wie zu
die gleiche Entfernung wie zu 
Weise nach, dass gilt:
Bestimme eine Gleichung von
Aus Sicherheitsgründen sollte der Rasenroboter reagieren, wenn er auf Hindernisse trifft. Die Sensoren des Rasenroboters erkennen ein Hidnernis mit einer Wahrscheinlichkeit von Das Suchkabel verläuft ab der Ladestation zunächst
Der weitere Verlauf des Suchkabels wird im Intervall
Der Punkt
Weise nach, dass gilt:
Bestimme eine Gleichung von
Erreichbare BE-Anzahl: 04
Wenn das Hindernis erkannt wird, setzt der Rasenroboter entweder mit einer Wahrscheinlichkeit von
Wenn das Hindernis nicht erkannt wird, setzt der Rasenroboter entweder seine Arbeit fort oder bleibt mit einer Wahrscheinlichkeit von
1.6
Der Rasenroboter trifft auf ein Hindernis.
Ermittle die Wahrscheinlichkeit dafür, dass der Rasenroboter nach dem Hindernis seine Arbeit fortsetzt.
Ermittle die Wahrscheinlichkeit dafür, dass der Rasenroboter nach dem Hindernis seine Arbeit fortsetzt.
Erreichbare BE-Anzahl: 03
1.7
Bestimme die Wahrscheinlichkeit für das folgende Ereignis:
Der Rasenroboter trifft auf vier Hindernisse, setzt bei den ersten drei Hindernissen seine Arbeit fort und bleibt beim vierten Hindernis stehen.
Erreichbare BE-Anzahl: 02
1.1
Mit dem CAS können die Koordinaten des Maximumpunkts wie folgt bestimmt werden:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrecher liefert
Casio Classpad II
Der Taschenrecher liefert 
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
1.2
Geradengleichung nachweisen
Die Steigung  der Geraden durch
der Geraden durch  und
und  kann über den Differenzenquotienten der Koordinaten von
kann über den Differenzenquotienten der Koordinaten von  und
und  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
m &=& \dfrac{y_C-y_B}{x_C-x_B} \\[5pt]
&=& \dfrac{6,9 - 5,4}{13,0- 10,0} \\[5pt]
&=& 0,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/37989ccd33d201c17204d51d24e3a1c496996b5e537dcc47ada23e3f94be6a7f?color=5a5a5a) Der zugehörige
Der zugehörige  -Achsenabschnitt kann durch Einsetzen von
-Achsenabschnitt kann durch Einsetzen von  bestimmt werden:
bestimmt werden:
![\(\begin{array}[t]{rll}
y &=& m\cdot x +b \quad \scriptsize \mid\; m =0,5 \\[5pt]
y &=& 0,5x +b \quad \scriptsize \mid\; B(10,0\mid 5,4) \\[5pt]
5,4 &=& 0,5 \cdot 10,0 + b \\[5pt]
5,4 &=& 5+b \quad \scriptsize \mid\; -5 \\[5pt]
0,4 &=& b\\
b &=& 0,4
\end{array}\)](https://mathjax.schullv.de/332b468ffefa0382d8f6225757a248d00139b07b6378bf806c48cecbc7f53a0a?color=5a5a5a) Die Gerade
Die Gerade  die durch
die durch  und
und  festgelegt wird, kann also durch die Gleichung
festgelegt wird, kann also durch die Gleichung  beschrieben werden.
beschrieben werden.
 -Koordinate ermitteln
Da die Tangente im Punkt
-Koordinate ermitteln
Da die Tangente im Punkt  parallel zur Geraden
parallel zur Geraden  verläuft, muss
verläuft, muss  gelten.
gelten.

 Die Gleichung
Die Gleichung  kann nun mit dem solve-Befehl des CAS gelöst werden. Es ergibt sich
kann nun mit dem solve-Befehl des CAS gelöst werden. Es ergibt sich 
1.3
1. Schritt: Flächeninhalt berechnen
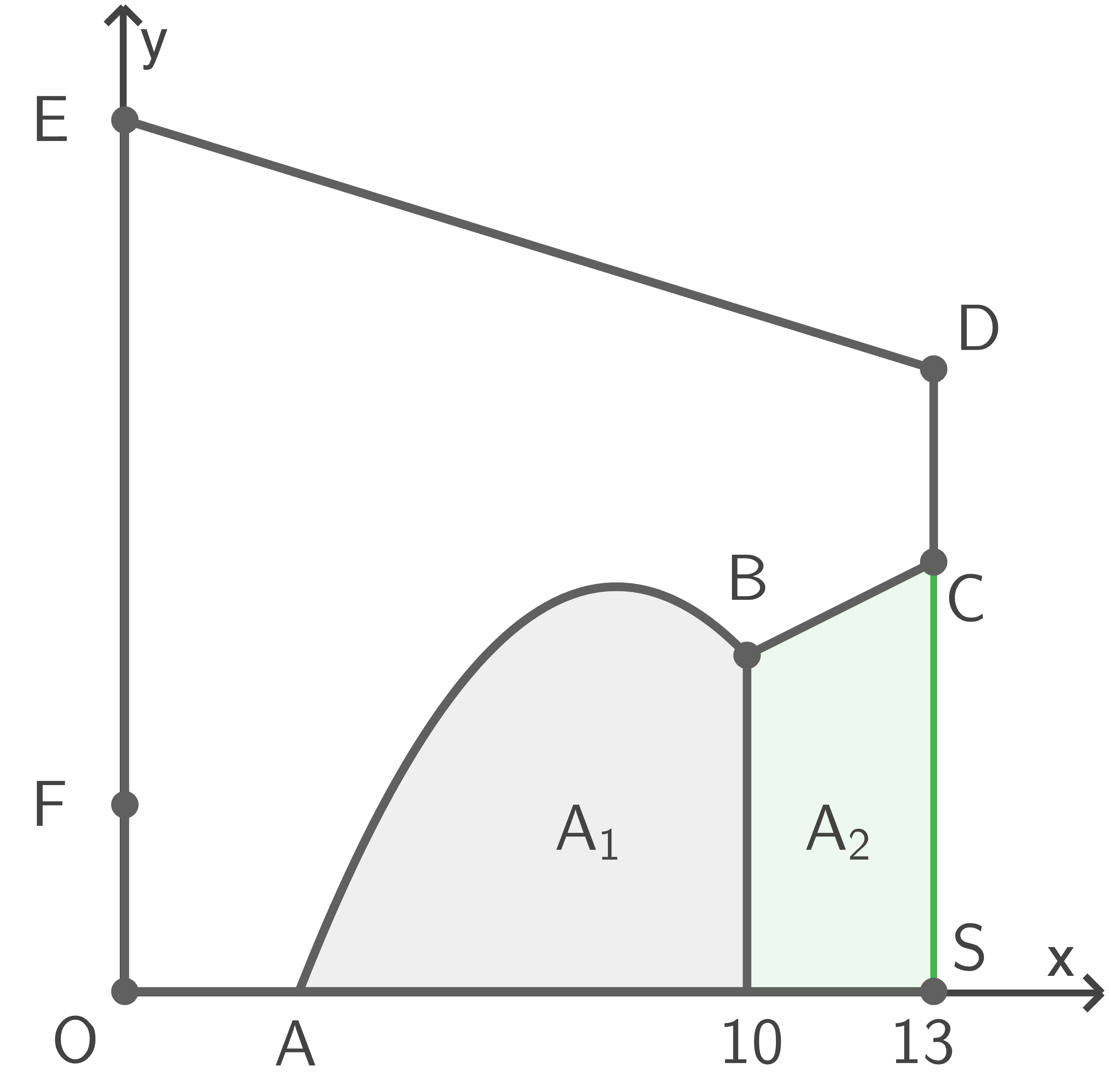 Der Flächeninhalt
Der Flächeninhalt  ist gegeben durch
ist gegeben durch 
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der CAS liefert
Casio Classpad II
Der CAS liefert ![\(A_1 \approx 34,992 \,[\text{m}^2]\)](https://mathjax.schullv.de/fd13dadb857e36a99e6aa2c183ea188fbddbcac3d191420654cafc610bc0cd12?color=5a5a5a) Der Flächeninhalt
Der Flächeninhalt  des Trapezes, das
des Trapezes, das  mit der
mit der  -Achse bildet, kann wie folgt berechnet werden:
-Achse bildet, kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
A_2 &=& \dfrac{1}{2}\cdot (y_c + y_b)\cdot \left(x_C-x_B \right) \\[5pt]
&=& \dfrac{1}{2}\cdot (6,9 + 5,4)\cdot (13,0 - 10,0) \\[5pt]
&=& 18,45\,[\text{m}^2] \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0a645bdf5582c8c318e173cf0fc952ed1f84314c6eb14dfbc8723b4a0230b0bb?color=5a5a5a) Für den Flächeninhalt
Für den Flächeninhalt  der begrenzten Fläche gilt insgesamt:
Der Rasenroboter muss also ca.
der begrenzten Fläche gilt insgesamt:
Der Rasenroboter muss also ca.  Rasenfläche mähen.
2. Schritt: Zeit berechnen
Der Rasenroboter kann unter optimalen Bedingungen
Rasenfläche mähen.
2. Schritt: Zeit berechnen
Der Rasenroboter kann unter optimalen Bedingungen  pro Minute mähen.
pro Minute mähen.
 Der Rasenroboter benötigt ca.
Der Rasenroboter benötigt ca.  Minuten zum Mähen der gesamten begrenzten Fläche.
Minuten zum Mähen der gesamten begrenzten Fläche.
Die Fläche lässt sich als Trapez auffassen, aus dem zwei Teilflächen mit den Flächeninhalten  und
und  herausgetrennt werden (siehe Skizze).
Es ergibt sich folgender Flächeninhalt
herausgetrennt werden (siehe Skizze).
Es ergibt sich folgender Flächeninhalt  für das Trapez
für das Trapez 
![\(\begin{array}[t]{rll}
A_T &=&\dfrac{1}{2}\cdot (\overline{OE} + \overline{SD})\cdot \overline{OS} \\
&=& \dfrac{1}{2}\cdot (y_E + y_D)\cdot x_D \\[5pt]
&=& \dfrac{1}{2}\cdot (14,0 + 10,0)\cdot 13,0 \\[5pt]
&=& 156,00\,[\text{m}^2] \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4a3f2509dc4cddd4a385ea9de249483e6e036cd7fd8dda080ad2d583a4d819e4?color=5a5a5a)

Skizze
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.4
1.5
Die beiden Punkte  und
und  die auf
die auf  bzw.
bzw.  liegen und den gleichen Abstand gemessen parallel zur
liegen und den gleichen Abstand gemessen parallel zur  -Achse zu
-Achse zu  haben, haben die gleiche
haben, haben die gleiche  -Koordinate wie
-Koordinate wie  also
also  1. Schritt: Koordinaten von
1. Schritt: Koordinaten von  bestimmen
Die Strecke
bestimmen
Die Strecke  liegt auf der Geraden
liegt auf der Geraden  Für die
Für die  -Koordinate von
-Koordinate von  gilt daher:
gilt daher:
![\(\begin{array}[t]{rll}
y_{P_2} &=& 0,5\cdot 10,4 + 0,4 \\[5pt]
&=& 5,6 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/38ddb04f810eafcaa4039b99bcd6a9d8b079fc56dc33ab730895a06eb5f409b2?color=5a5a5a)
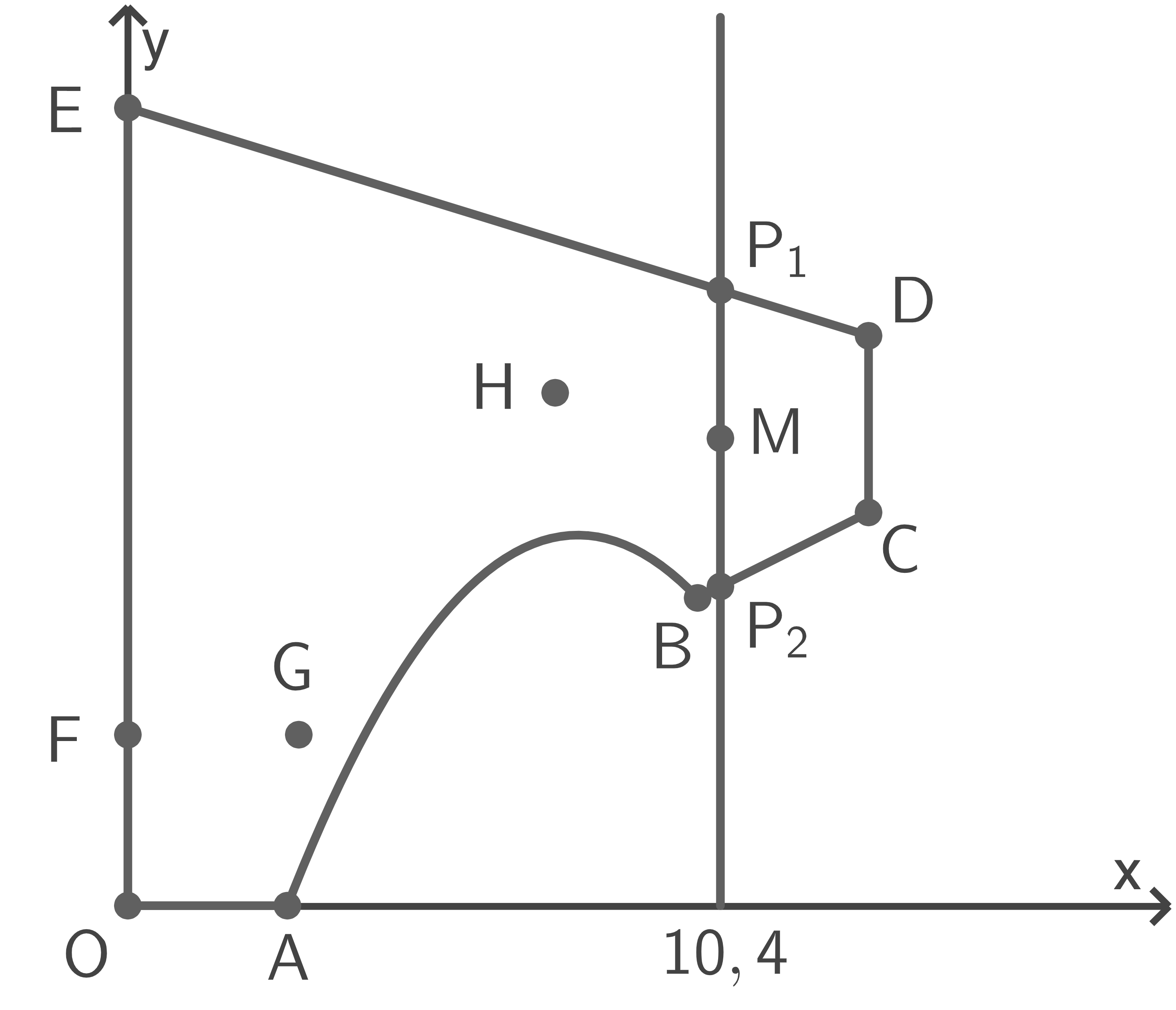
Skizze
menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

1.6
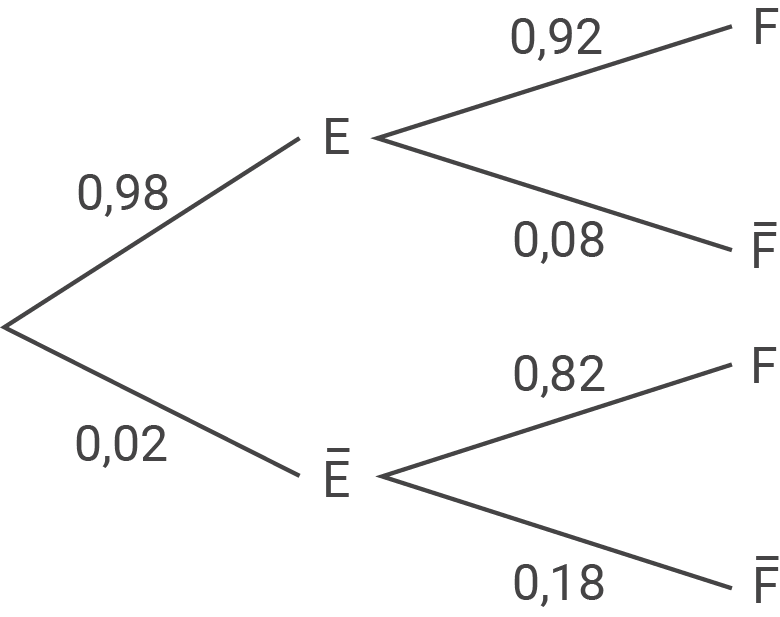
1.7
Trifft der Roboter auf ein Hindernis, dann setzt er seine Arbeit laut Aufgabe 1.6 mit einer Wahrscheinlichkeit von  fort. Mit der Pfadmultiplikationsregel gilt:
fort. Mit der Pfadmultiplikationsregel gilt:
 Die gesuchte Wahrscheinlichkeit beträgt ungefähr
Die gesuchte Wahrscheinlichkeit beträgt ungefähr 
Bildnachweise [nach oben]
© - SchulLV.