Teil B2
Vor einer Hauswand befindet sich ein rechteckiges Reklameschild, welches durch einen Scheinwerfer beleuchtet wird. Der Scheinwerfer lässt sich in einem kartesischen Koordinatensystem  entspricht
entspricht  modellhaft durch den Punkt
modellhaft durch den Punkt  beschreiben. Die Eckpunkte des Reklameschildes werden durch die Punkte
beschreiben. Die Eckpunkte des Reklameschildes werden durch die Punkte 

 und
und  dargestellt. Die
dargestellt. Die  -Ebene beschreibt den horizontalen Untergrund, auf dem das Haus steht. Die
-Ebene beschreibt den horizontalen Untergrund, auf dem das Haus steht. Die  -Ebene beschreibt die Ebene, in der die Hauswand liegt.
-Ebene beschreibt die Ebene, in der die Hauswand liegt.
 stellt den zu
stellt den zu  gehörenden Eckpunkt des Schattens dar, die Punkte
gehörenden Eckpunkt des Schattens dar, die Punkte  und
und  die zu
die zu  bzw.
bzw.  gehörenden Eckpunkte des Schattens.
gehörenden Eckpunkte des Schattens.
 aller Passanten dieses Reklameschild wahr. Von den Passanten, die dieses Reklameschild wahrnehmen, sind
aller Passanten dieses Reklameschild wahr. Von den Passanten, die dieses Reklameschild wahrnehmen, sind  männlich.
männlich.
2.1
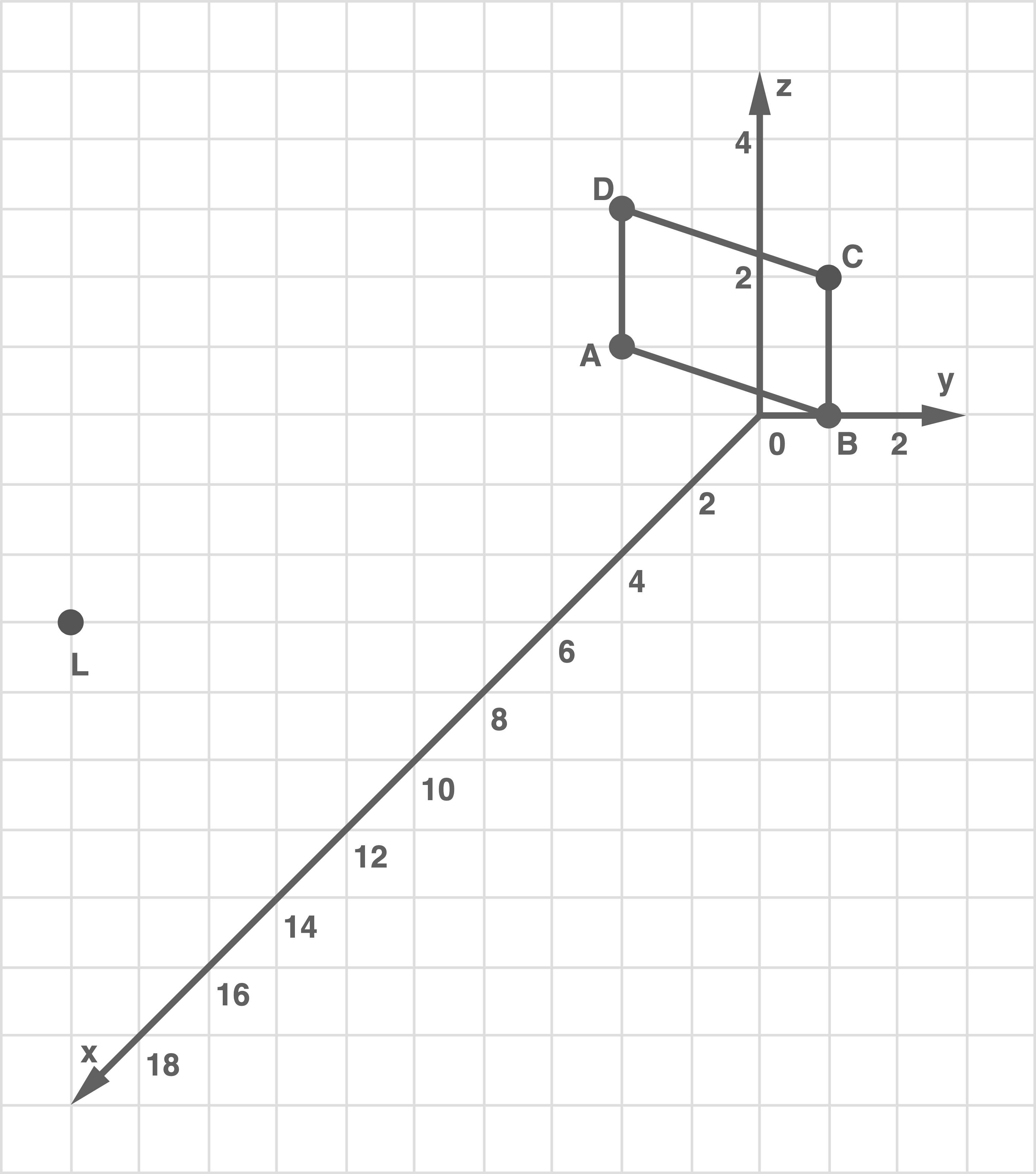
Stelle den Punkt  und das Rechteck
und das Rechteck  in einem kartesischen Koordinatensystem dar.
in einem kartesischen Koordinatensystem dar.
Auf der Hauswand ist der Schatten des Reklameschildes sichtbar. Der Punkt
(3 BE)
2.2
Weise nach, dass der vierte Eckpunkt des Schattens durch  dargestellt wird.
dargestellt wird.
(3 BE)
2.3
Zeige, dass das Viereck  ein Trapez ist.
ein Trapez ist.
Berechne den Flächeninhalt dieses Vierecks.
Berechne den Flächeninhalt dieses Vierecks.
(5 BE)
2.4
Der Scheinwerfer kann entlang einer senkrecht zum horizontalen Untergrund verlaufenden Stange in der Höhe vershcoben und modellhaft durch den Punkt  mit
mit  und
und  beschrieben werden.
beschrieben werden.
Betrachtet werden nur diejenigen Werte von für die der Schatten des Reklameschildes vollständig auf der Hauswand liegt.
für die der Schatten des Reklameschildes vollständig auf der Hauswand liegt.
Für jede der beiden Seiten des Schattens, die durch die linke und rechte Kante des Reklameschildes erzeugt werden, gilt folgende Aussage: „Die Länge der Seite bleibt bei Verschiebung des Scheinwerfers unverändert.“ Weise die Gültigkeit dieser Aussage für eine der beiden betrachteten Seiten des Schattens rechnerisch nach.
Erfahrungsgemäß nehmen Betrachtet werden nur diejenigen Werte von
Für jede der beiden Seiten des Schattens, die durch die linke und rechte Kante des Reklameschildes erzeugt werden, gilt folgende Aussage: „Die Länge der Seite bleibt bei Verschiebung des Scheinwerfers unverändert.“ Weise die Gültigkeit dieser Aussage für eine der beiden betrachteten Seiten des Schattens rechnerisch nach.
(4 BE)
2.5
Berechne die Wahrscheinlichkeit dafür, dass ein Passant dieses Reklameschild wahrnimmt und weiblich ist.
(2 BE)
2.6
Berechne die Wahrscheinlichkeit dafür, dass von  Passanten weniger als
Passanten weniger als  Passanten dieses Reklameschild wahrnehmen.
Passanten dieses Reklameschild wahrnehmen.
(2 BE)
2.7
Aufgrund einer besseren Verkehrsanbindung wird vermutet, dass der Anteil der Passanten, die dieses Reklameschild wahrnehmen, gestiegen ist.
In einem Test mit zufällig ausgewählten Passanten soll die Nullhypothese
„Der Anteil der Passanten, die dieses Reklameschild wahrnehmen, beträgt höchstens
zufällig ausgewählten Passanten soll die Nullhypothese
„Der Anteil der Passanten, die dieses Reklameschild wahrnehmen, beträgt höchstens  “
auf einem Signifikanzniveau von
“
auf einem Signifikanzniveau von  getestet werden.
getestet werden.
Bestimme die zugehörige Entscheidungsregel.
In einem Test mit
Bestimme die zugehörige Entscheidungsregel.
(3 BE)
2.1
2.2
Die Hauswand liegt laut Aufgabenstellung in der  -Ebene, welche durch die Gleichung
-Ebene, welche durch die Gleichung  beschrieben werden kann. Der Punkt
beschrieben werden kann. Der Punkt  muss als Schattenpunkt also auch in der
muss als Schattenpunkt also auch in der  -Ebene und gleichzeitig auf der Geraden
-Ebene und gleichzeitig auf der Geraden  liegen, die durch die Punkte
liegen, die durch die Punkte  und
und  verläuft.
verläuft.
Bestimme also den Schnittpunkt dieser Geraden mit der -Ebene.
1. Schritt: Geradengleichung bestimmen
Die Gerade durch die Punkte
-Ebene.
1. Schritt: Geradengleichung bestimmen
Die Gerade durch die Punkte  und
und  kann mit folgender Gleichung beschrieben werden:
kann mit folgender Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
g:\quad \overrightarrow{x}&=& \overrightarrow{OL} + r\cdot \overrightarrow{LB} \\[5pt]
&=& \pmatrix{12\\-4\\3} +r\cdot \pmatrix{-6\\8\\0} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ca6d2b6fdde0bafadda20771551407ea43034deae414aec6b30683b6d0509a7c?color=5a5a5a) 2. Schritt: Schnittpunkt bestimmen
Setze nun die Koordinaten der Gerade
2. Schritt: Schnittpunkt bestimmen
Setze nun die Koordinaten der Gerade  in die Ebenengleichung ein:
in die Ebenengleichung ein:
![\(\begin{array}[t]{rll}
x&=& 0 &\quad \scriptsize \mid\;x =12-6r \\[5pt]
12-6r &=& 0 &\quad \scriptsize \mid\; +6r \\[5pt]
12 &=& 6r &\quad \scriptsize \mid\; :6 \\[5pt]
2&=& r
\end{array}\)](https://mathjax.schullv.de/b4720c97a07a5f7227cdac8a836a785d362cbd70c33e64dd6a14c7015dd46eab?color=5a5a5a) Einsetzen in die Geradengleichung liefert:
Einsetzen in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OB](https://mathjax.schullv.de/ab54f513938b8bfa7a55e40c76b5791ddcdf25f5b6ab021d6f617808a5ab207f?color=5a5a5a) Die Koordinaten des vierten Eckpunkts
Die Koordinaten des vierten Eckpunkts  lauten also
lauten also 
Bestimme also den Schnittpunkt dieser Geraden mit der
2.3
Trapezform zeigen
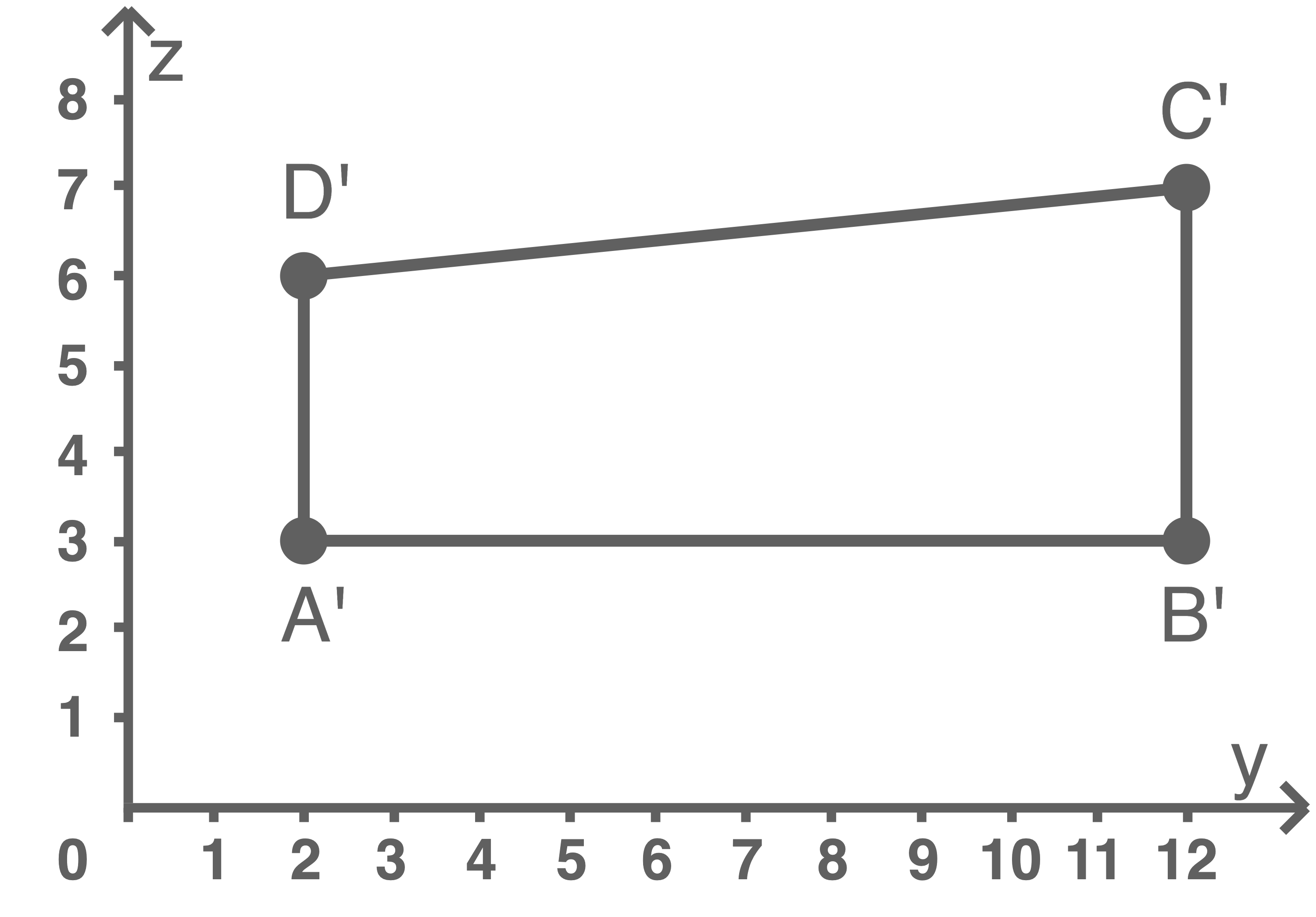 Es gilt also:
Es gilt also:  Die beiden Seiten
Die beiden Seiten  und
und  sind also parallel, wodurch es sich bei
sind also parallel, wodurch es sich bei  um ein Trapez handelt.
Flächeninhalt berechnen
Der Flächeninhalt eines Trapezes kaann mit der Formel
um ein Trapez handelt.
Flächeninhalt berechnen
Der Flächeninhalt eines Trapezes kaann mit der Formel  berechnet. Es gilt:
berechnet. Es gilt:

 Mithilfe der Skizze ist erkennbar, dass die Strecke
Mithilfe der Skizze ist erkennbar, dass die Strecke  die Höhe des Trapezes beschreibt.
die Höhe des Trapezes beschreibt.
 Insgesamt gilt:
Insgesamt gilt:  Der Flächeninhalt des Trapezes beträgt
Der Flächeninhalt des Trapezes beträgt 
Bei dem Viereck handelt es sich um ein Trapez, wenn es zwei gegenüberliegende Seiten gibt, die parallel sind. Zwei gegenüberliegende Seiten sind parallel, wenn die zugehörigen Verbindungsvektoren der jeweiligen Eckpunkte linear abhängig sind.
![\(\begin{array}[t]{rll}
\overrightarrow{A‘D‘}&=& \pmatrix{0\\0\\3} \\[5pt]
\overrightarrow{B‘C‘}&=& \pmatrix{0\\0\\4} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/91917186a74ee18edd6561f205913e869e42a3ad88fb5187b7c072de32321020?color=5a5a5a)

Skizze in der  -Ebene
-Ebene
2.4
Die Koordinaten der neuen Schattenpunkte  und
und  können analog zu Teil 2.2 als Schnittpunkte der
können analog zu Teil 2.2 als Schnittpunkte der  -Ebene mit den beiden Geraden durch die Punkte
-Ebene mit den beiden Geraden durch die Punkte  und
und  bzw.
bzw.  und
und  in Abhängigkeit von
in Abhängigkeit von  bestimmt werden.
1. Schritt: Geradengleichungen aufstellen
Die Gerade durch die beiden Punkte
bestimmt werden.
1. Schritt: Geradengleichungen aufstellen
Die Gerade durch die beiden Punkte  und
und  kann mit folgender Gleichung beschrieben werden:
kann mit folgender Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
j_h:\quad \overrightarrow{x}&=& \overrightarrow{OL_h} + t\cdot \overrightarrow{L_hB} \\[5pt]
&=& \pmatrix{12\\-4\\h} +t\cdot \pmatrix{-6\\8\\3-h} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4070115699e6310cb3e54aab0c9911496edff8d1746273f4093722bc68495fde?color=5a5a5a) Die Gerade durch die beiden Punkte
Die Gerade durch die beiden Punkte  und
und  kann analog mit folgender Gleichung beschrieben werden:
kann analog mit folgender Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
k_h:\quad \overrightarrow{x}&=& \overrightarrow{OL_h} + t\cdot \overrightarrow{L_hC} \\[5pt]
&=& \pmatrix{12\\-4\\h} +t\cdot \pmatrix{-6\\8\\5-h} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6ee68109144518a8960e78a5818a3c78c04b8d77d2274f5b7bfc45dcc8b93c12?color=5a5a5a) 2. Schritt: Koordinaten des Schattenpunkts
2. Schritt: Koordinaten des Schattenpunkts  bestimmen
Einsetzen der Koordinaten der Geraden
bestimmen
Einsetzen der Koordinaten der Geraden  in die Ebenengleichung
in die Ebenengleichung  der
der  -Ebene liefert:
-Ebene liefert:
![\(\begin{array}[t]{rll}
x&=& 0 &\quad \scriptsize \mid\;x = 12-6t \\[5pt]
12-6t&=& 0 &\quad \scriptsize \mid\;+6t \\[5pt]
12&=& 6t &\quad \scriptsize \mid\;:6 \\[5pt]
2&=& t
\end{array}\)](https://mathjax.schullv.de/de4cd7441da1306d185c4a1cc3c2255a78cbc13deb078c5bfa79b12b3dcd50a5?color=5a5a5a) Einsetzen in die Geradengleichung liefert:
Einsetzen in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OB‘_h}&=&\pmatrix{12\\-4\\h} +2\cdot \pmatrix{-6\\8\\3-h} \\[5pt]
&=& \pmatrix{0\\12\\6-h}
\end{array}\)](https://mathjax.schullv.de/0d1ebf7d49729e459a2d1402c44b394aff2a7c754dc0d1ff98ac39d57a90472d?color=5a5a5a) Die Koordinaten des neuen Schattenpunkts in Abhängigkeit von
Die Koordinaten des neuen Schattenpunkts in Abhängigkeit von  lauten also
lauten also  3. Schritt: Koordinaten des Schattenpunkts
3. Schritt: Koordinaten des Schattenpunkts  bestimmen
Einsetzen der Koordinaten der Geraden
bestimmen
Einsetzen der Koordinaten der Geraden  in die Ebenengleichung
in die Ebenengleichung  der
der  -Ebene liefert:
-Ebene liefert:
![\(\begin{array}[t]{rll}
x&=& 0 &\quad \scriptsize \mid\;x = 12-6t \\[5pt]
12-6t&=& 0 &\quad \scriptsize \mid\;+6t \\[5pt]
12&=& 6t &\quad \scriptsize \mid\;:6 \\[5pt]
2&=& t
\end{array}\)](https://mathjax.schullv.de/de4cd7441da1306d185c4a1cc3c2255a78cbc13deb078c5bfa79b12b3dcd50a5?color=5a5a5a) Einsetzen in die Geradengleichung liefert:
Einsetzen in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OC‘_h}&=&\pmatrix{12\\-4\\h} +2\cdot \pmatrix{-6\\8\\5-h} \\[5pt]
&=& \pmatrix{0\\12\\10-h}
\end{array}\)](https://mathjax.schullv.de/4cf995bee0579013302f48553fb98c99e29b068c0b3d1c6477d0d9801fea0598?color=5a5a5a) Die Koordinaten des neuen Schattenpunkts in Abhängigkeit von
Die Koordinaten des neuen Schattenpunkts in Abhängigkeit von  lauten also
lauten also  4. Schritt: Länge der Seite berechnen
Mit dem Vektorbetrag folgt für die Länge der Seite
4. Schritt: Länge der Seite berechnen
Mit dem Vektorbetrag folgt für die Länge der Seite 
![\(\begin{array}[t]{rll}
\left|\overrightarrow{B‘_hC‘_h} \right|&=& \left|\pmatrix{0\\0\\4} \right| \\[5pt]
&=& \sqrt{0^2+0^2+4^2} \\[5pt]
&=&4
\end{array}\)](https://mathjax.schullv.de/018e5adb961e25be98ffdc8cec368851782b2042b5e7f7d8f4c976a98bd13c17?color=5a5a5a) Die Länge der Seite
Die Länge der Seite  ist also unabhängig von
ist also unabhängig von  und beträgt
und beträgt  Die verändert sich mit der Verschiebung des Scheinwerfers also nicht.
Die verändert sich mit der Verschiebung des Scheinwerfers also nicht.
2.5
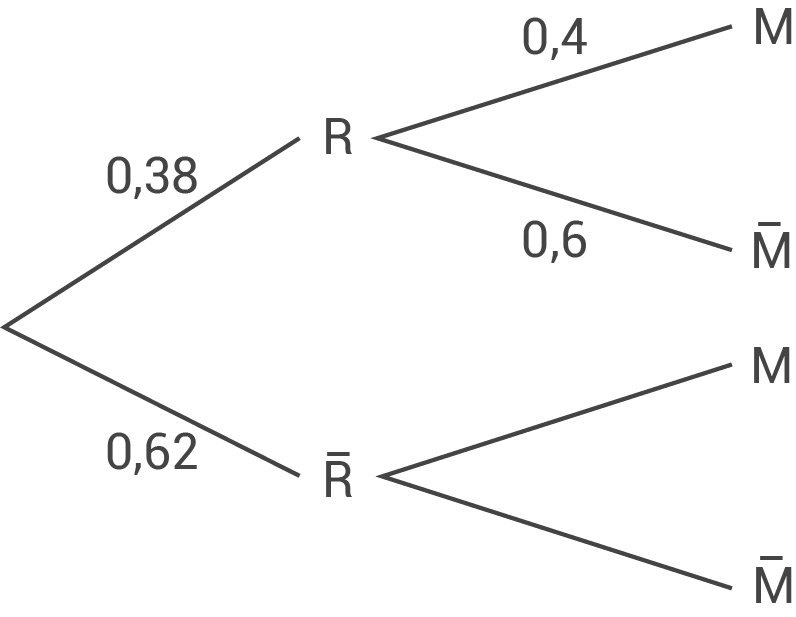
R: Passant nimmt Reklameschild wahr
M: Passant ist männlich Mit der Pfadmultiplikationsregel gilt: Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  nimmt ein Passant das Reklameschild wahr und ist weiblich.
nimmt ein Passant das Reklameschild wahr und ist weiblich.
M: Passant ist männlich Mit der Pfadmultiplikationsregel gilt:
2.6
Die Zufallsvariable  beschreibt die Anzahl der Passanten, die das Reklameschild wahrnehmen.
beschreibt die Anzahl der Passanten, die das Reklameschild wahrnehmen.  ist
ist  -verteilt.
-verteilt.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
![\(\begin{array}[t]{rll}
P(X\lt 100)&=& P(X\leq 99) \\[5pt]
&\approx& 0,7223 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f758d1636c86f12761e72f5ed70bb3d9553811c3478164c35827e458eac95693?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  befinden sich unter
befinden sich unter  Passanten weniger als
Passanten weniger als  die das Reklameschild wahrnehmen.
die das Reklameschild wahrnehmen.
menu  5
5  5
5  E: Binomial Cdf
E: Binomial Cdf
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  binomial CDf
binomial CDf
2.7
Die Zufallsvariable  beschreibt die Anzahl der Personen, die das Reklameschild wahrnehmen.
beschreibt die Anzahl der Personen, die das Reklameschild wahrnehmen.  ist
ist  -verteilt.
-verteilt.

 Mit einem Signifikanzniveau von
Mit einem Signifikanzniveau von  ist das kleinste
ist das kleinste  gesucht, für das Folgendes gilt:
gesucht, für das Folgendes gilt:
![\(\begin{array}[t]{rll}
P(X_p\geq k ) &\leq& 0,05 \\[5pt]
1-P(X_p\leq k-1)&\leq& 0,05 \quad \scriptsize \mid\;-1 \\[5pt]
-P(X_p\leq k-1)&\leq& -0,95 \quad \scriptsize \mid\;\cdot (-1) \\[5pt]
P(X_p\leq k-1)&\geq& 0,95
\end{array}\)](https://mathjax.schullv.de/d81a4275c34b546ccd780268c3b10418bc37cd60d5177c73844f7d521922142e?color=5a5a5a) Systematisches Ausprobieren mit dem CAS liefert:
Systematisches Ausprobieren mit dem CAS liefert:
![\(\begin{array}[t]{rll}
P(X_p\leq 50 ) &\approx& 0,8219 \\[5pt]
P(X_p\leq 60 ) &\approx& 0,9972 \\[5pt]
P(X_p\leq 55 ) &\approx& 0,9676 \\[5pt]
P(X_p\leq 54 ) &\approx& 0,9518 \\[5pt]
P(X_p\leq 53 ) &\approx& 0,9303 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0516f4843debb64d2894f4f2acf3f0d3d5e9dac1bcc49357685e1f1bfbdbfebc?color=5a5a5a) Es ist also
Es ist also  und damit
und damit 
Der Ablehnungsberreich der Nullhypothese ist damit gegeben durch Entscheidungsregel
Entscheidungsregel
Die Nullhypothese wird abgelehnt, wenn mindestens der
der  zufällig ausgewählten Personen das Reklameschild wahrnehmen. Ansonsten wird die Nullhypothese nicht abgelehnt.
zufällig ausgewählten Personen das Reklameschild wahrnehmen. Ansonsten wird die Nullhypothese nicht abgelehnt.
Bildnachweise [nach oben]
Der Ablehnungsberreich der Nullhypothese ist damit gegeben durch
Die Nullhypothese wird abgelehnt, wenn mindestens
© - SchulLV.