Teil B1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit 
Der Graph von wird mit
wird mit  bezeichnet.
bezeichnet.
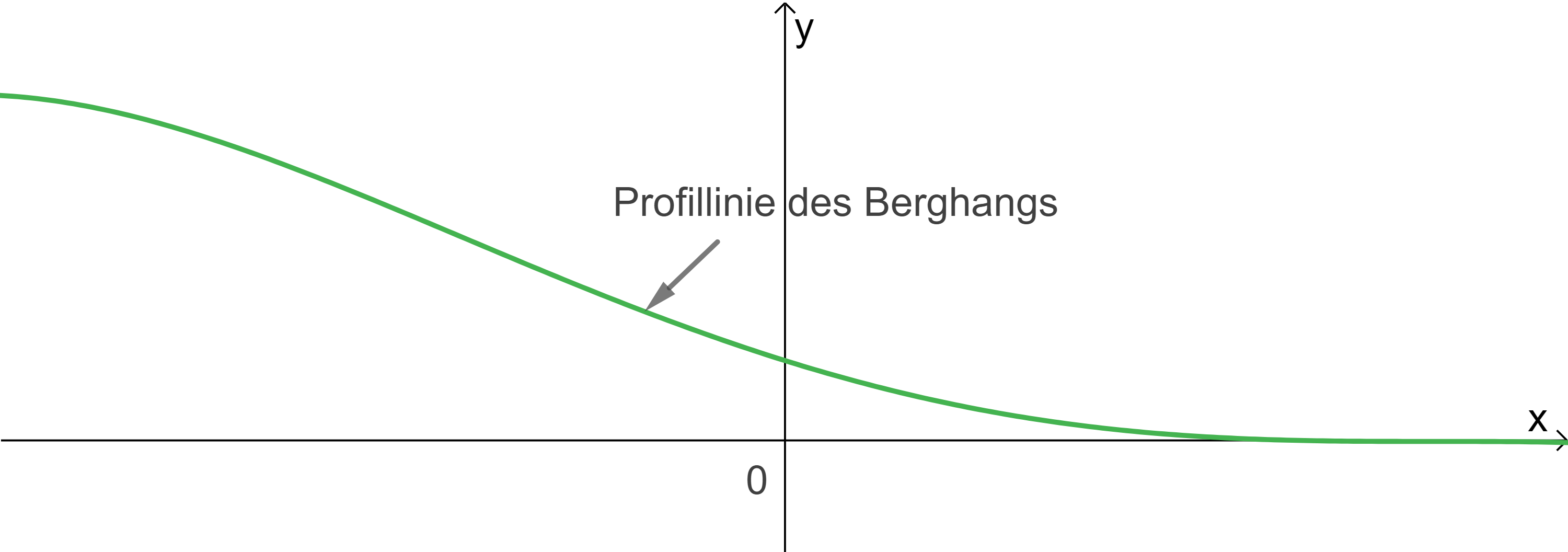
 modellhaft durch den Graphen der in
modellhaft durch den Graphen der in  definierten Funktion
definierten Funktion  mit
mit
 beschrieben werden (siehe Abbildung).
Es soll davon ausgegangen werden, dass der Hang in Querrichtung nicht geneigt ist. Im verwendeten Koordinatensystem beschreibt die x-Achse die Horizontale; eine Längeneinheit entspricht 100 Metern in der Wirklichkeit. Alle Höhen werden senkrecht zur Horizontalen gemessen.
beschrieben werden (siehe Abbildung).
Es soll davon ausgegangen werden, dass der Hang in Querrichtung nicht geneigt ist. Im verwendeten Koordinatensystem beschreibt die x-Achse die Horizontale; eine Längeneinheit entspricht 100 Metern in der Wirklichkeit. Alle Höhen werden senkrecht zur Horizontalen gemessen.
Der Graph von
1.1
Gib die Koordinaten des Schnittpunkts von  mit der y-Achse an.
mit der y-Achse an.
Zeige, dass an den Stellen
an den Stellen  und
und  gemeinsame Punkte mit der
gemeinsame Punkte mit der  -Achse besitzt.
-Achse besitzt.
 schließt mit der
schließt mit der  -Achse im Intervall
-Achse im Intervall  eine Fläche vollständig ein.
eine Fläche vollständig ein.
Bestimme den Inhalt dieser Fläche.
Ermittle, in welchem Verhältnis die -Achse diese Fläche teilt.
-Achse diese Fläche teilt.
Zeige, dass
Bestimme den Inhalt dieser Fläche.
Ermittle, in welchem Verhältnis die
(10 BE)
1.2
Die Funktion  lässt sich auch mit
lässt sich auch mit
 beschreiben.
Begründe ohne Rechnung, dass
beschreiben.
Begründe ohne Rechnung, dass  höchstens zwei Wendepunkte haben kann.
höchstens zwei Wendepunkte haben kann.
Bestimme den Schnittwinkel der Tangente an im Wendepunkt
im Wendepunkt  mit der x-Achse.
mit der x-Achse.
Bestimme den Schnittwinkel der Tangente an
(6 BE)
1.3
Für jeden reellen Wert von  mit
mit  legen die Punkte
legen die Punkte 
 und
und  ein Dreieck
ein Dreieck  fest.
fest.
Bestimme so, dass der Flächeninhalt des zugehörigen Dreiecks
so, dass der Flächeninhalt des zugehörigen Dreiecks  maximal ist.
maximal ist.
Im Längsschnitt eines Berghangs kann dessen Profillinie für Bestimme
(4 BE)
1.4
Der Hochpunkt des Graphen von  hat die x-Koordinate -5.
hat die x-Koordinate -5.
Bestimme die zugehörige y-Koordinate.
Zeige, dass der Höhenunterschied zwischen dem höchsten und tiefsten Punkt des Hangs etwa beträgt.
beträgt.
Ermittle das durchschnittliche Gefälle zwischen diesen beiden Punkten in Prozent.
Bestimme die zugehörige y-Koordinate.
Zeige, dass der Höhenunterschied zwischen dem höchsten und tiefsten Punkt des Hangs etwa
Ermittle das durchschnittliche Gefälle zwischen diesen beiden Punkten in Prozent.
(8 BE)
1.5
Der Hang wird als Skipiste genutzt. Der Tabelle kann der Zusammenhang zwischen dem Schwierigkeitsgrad von Skipisten und deren jeweiligen maximalen Gefälle entnommen werden:
Ermittle den Schwierigkeitsgrad der hier betrachteten Skipiste.
| Schwierigkeitsgrad | maximales Gefälle |
|---|---|
| leicht | bis 25 % |
| mittel | mehr als 25 % und bis 40 % |
| schwer | mehr als 40 % |
(3 BE)
1.6
Im Punkt  steht senkrecht zur Horizontalen ein
steht senkrecht zur Horizontalen ein  hoher Wegweiser.
hoher Wegweiser.
Im Punkt steht ein Wanderer mit einer Augenhöhe von
steht ein Wanderer mit einer Augenhöhe von 
Untersuche, ob der Wanderer den obersten Punkt des Wegweisers sehen kann.
Der Berghang befindet sich in einer Nationalparkregion, zu der auch ein Museum gehört.
Im Punkt
Untersuche, ob der Wanderer den obersten Punkt des Wegweisers sehen kann.
(4 BE)
1.7
Erfahrungsgemäß kommen 20 % der Besucher des Museums aus dem Ausland.
80 Besucher des Museums werden zufällig und unabhängig voneinander ausgewählt. Unter diesen 80 Besuchern befinden sich Besucher aus dem Ausland, deren Anzahl als binomialverteilt betrachtet wird.
Berechne die Wahrscheinlichkeiten der folgenden Ereignisse: Ereignis A: Höchstens 20 dieser Besucher kommen aus dem Ausland.
Ereignis B: Es kommen mehr Besucher aus dem Ausland, als zu erwarten sind.
80 Besucher des Museums werden zufällig und unabhängig voneinander ausgewählt. Unter diesen 80 Besuchern befinden sich Besucher aus dem Ausland, deren Anzahl als binomialverteilt betrachtet wird.
Berechne die Wahrscheinlichkeiten der folgenden Ereignisse: Ereignis A: Höchstens 20 dieser Besucher kommen aus dem Ausland.
Ereignis B: Es kommen mehr Besucher aus dem Ausland, als zu erwarten sind.
(5 BE)
1.8
Im Museum gibt es zwei Ausstellungen; eine Dauerausstellung und eine Sonderausstellung. Jeder Besucher des Museums besichtigt mindestens eine dieser beiden Ausstellungen. An einem Tag besichtigen 340 Besucher die Dauerausstellung und 250 Personen die Sonderausstellung. 143 Personen besichtigten beide Ausstellungen.
Bestimme die Gesamtanzahl der Besucher an diesem Tag.
Berechne für diesen Tag den Anteil der Besucher der Dauerausstellung, die auch die Sonderausstellung besichtigen.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Schnittpunkt mit der  -Achse
-Achse

 Der Graph
Der Graph  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  .
Gemeinsame Punkte mit der
.
Gemeinsame Punkte mit der  -Achse
Es gilt
-Achse
Es gilt  und
und  , sodass
, sodass  an den Stellen
an den Stellen  und
und  gemeinsame Punkte mit der
gemeinsame Punkte mit der  -Achse besitzt.
Flächeninhalt
-Achse besitzt.
Flächeninhalt
 Mit dem CAS folgt:
Mit dem CAS folgt:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrechner liefert
Casio Classpad II
Der Taschenrechner liefert 
 Flächenverhältnis
Für den Inhalt einer der beiden Teilflächen folgt mit dem CAS:
Flächenverhältnis
Für den Inhalt einer der beiden Teilflächen folgt mit dem CAS:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrechner liefert
Casio Classpad II
Der Taschenrechner liefert 
 Das Verhältnis beträgt:
Das Verhältnis beträgt: 
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.2
Begründung
Für Wendestellen von  muss das notwendige Kriterium
muss das notwendige Kriterium  erfüllt sein.
erfüllt sein.
 ist eine ganzrationale Funktion vierten Grades,
ist eine ganzrationale Funktion vierten Grades,  also eine ganzrationale Funktion zweiten Grades und kann damit höchstens zwei Nullstellen haben. Somit hat
also eine ganzrationale Funktion zweiten Grades und kann damit höchstens zwei Nullstellen haben. Somit hat  höchstens zwei Wendestellen.
Schnittwinkel
Für die Steigung von
höchstens zwei Wendestellen.
Schnittwinkel
Für die Steigung von  an der Stelle
an der Stelle  gilt:
gilt:
 Für den Schnittwinkel der zugehörigen Tangente mit der
Für den Schnittwinkel der zugehörigen Tangente mit der  -Achse folgt:
-Achse folgt:
![\(\begin{array}[t]{rll}
\tan(\alpha) &=& f](https://mathjax.schullv.de/ac077098e9908038c43fd96fc144d894a8db99f011c8f3b1df03b78365fdb7ab?color=5a5a5a) Der Schnittwinkel mit der
Der Schnittwinkel mit der  -Achse ist etwa
-Achse ist etwa  groß.
groß.
1.3
Das Dreieck  besitzt im Punkt
besitzt im Punkt  einen rechten Winkel. Der Flächeninhalt kann daher mit folgender Funktion beschrieben werden:
einen rechten Winkel. Der Flächeninhalt kann daher mit folgender Funktion beschrieben werden:
 Das Maximum von
Das Maximum von  und der zugehörige Wert für
und der zugehörige Wert für  lässt sich mit dem CAS bestimmen.
lässt sich mit dem CAS bestimmen.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrechner liefert den Wert
Casio Classpad II
Der Taschenrechner liefert den Wert  , für den das Dreieck
, für den das Dreieck  maximal wird.
maximal wird.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
1.4
1.5
Das maximale Gefälle entspricht dem Minimum von 
 TI nspire CAS
Mit dem fMin-Befehl erhältst du die Stelle
TI nspire CAS
Mit dem fMin-Befehl erhältst du die Stelle ![\(x\in[-5;4],\)](https://mathjax.schullv.de/04bdbf8336b01866cb5ddd0c93f5d69afc40f6c7bcd3ee8bc0d18015624a3594?color=5a5a5a) an der der Funktionswert von
an der der Funktionswert von  am kleinsten ist.
am kleinsten ist.

 Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
![\(\begin{array}[t]{lll}
h](https://mathjax.schullv.de/21ade2b06be88c9973644bc15e198e414b3e1c8cba7b18be595d93e3849fe7bf?color=5a5a5a)
 Casio Classpad II
Mit dem fMin-Befehl erhältst du den kleinsten Funktionswert von
Casio Classpad II
Mit dem fMin-Befehl erhältst du den kleinsten Funktionswert von  im angegebenen Intervall und die zugehörige Stelle
im angegebenen Intervall und die zugehörige Stelle  .
.

![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/ad907e3365ac6527558e02d2b8c80dfb0121e48b89278a1afa880fb8cb4d9066?color=5a5a5a) Das Gefälle am Minimum beträgt
Das Gefälle am Minimum beträgt  , sodass es sich um eine schwere Skipiste handelt.
, sodass es sich um eine schwere Skipiste handelt.
1.6
Der Wanderer kann den obersten Punkt des Wegweisers sehen, wenn die Gerade durch die beiden zugehörigen Punkte den Graphen nicht schneidet.

 Steigung der Geraden
Steigung der Geraden  durch die Punkte
durch die Punkte  und
und 

 Wegen
Wegen  folgt für die Geradengleichung:
folgt für die Geradengleichung:
 Die Schnittstellen von
Die Schnittstellen von  und
und  können mit dem CAS bestimmt werden.
Die Gerade
können mit dem CAS bestimmt werden.
Die Gerade  schneidet den Graphen von
schneidet den Graphen von  im Intervall
im Intervall  an den Stellen
an den Stellen  und
und  sodass der Wanderer den obersten Punkt des Wegweisers nicht sieht.
sodass der Wanderer den obersten Punkt des Wegweisers nicht sieht.
1.7
menu  5
5  5
5  E: Binomial Cdf
E: Binomial Cdf
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  binomial CDf
binomial CDf
1.8
Anzahl der Personen, die nur die Dauerausstellung besucht haben:  Anzahl der Personen, die nur die Sonderausstellung besucht haben:
Anzahl der Personen, die nur die Sonderausstellung besucht haben: 
 Die Gesamtanzahl der Besucher an diesem Tag beträgt
Die Gesamtanzahl der Besucher an diesem Tag beträgt  Anteil
Insgesamt haben
Anteil
Insgesamt haben  Besucher die Dauerausstellung besucht. Davon haben
Besucher die Dauerausstellung besucht. Davon haben  auch die Sonderausstellung besucht:
auch die Sonderausstellung besucht:
 Etwa
Etwa  der Besucher der Dauerausstellung besuchten auch die Sonderausstellung.
der Besucher der Dauerausstellung besuchten auch die Sonderausstellung.