Teil B2

Die Eckpunkte eines Holzkörpers werden durch
$A(0\mid0\mid0), B(10\mid0\mid0), C(10\mid10\mid0),$ $D(0\mid10\mid0)$ und $E(0\mid10\mid6)$ dargestellt (siehe Abbildung).
Die Punkte $B$ , $D$ und $E$ liegen im Modell in der Symmetrieebene des Körpers.
Eine Längeneinheit im verwendeten kartesischen Koordinatensystem entspricht einem Zentimeter in der Realität.

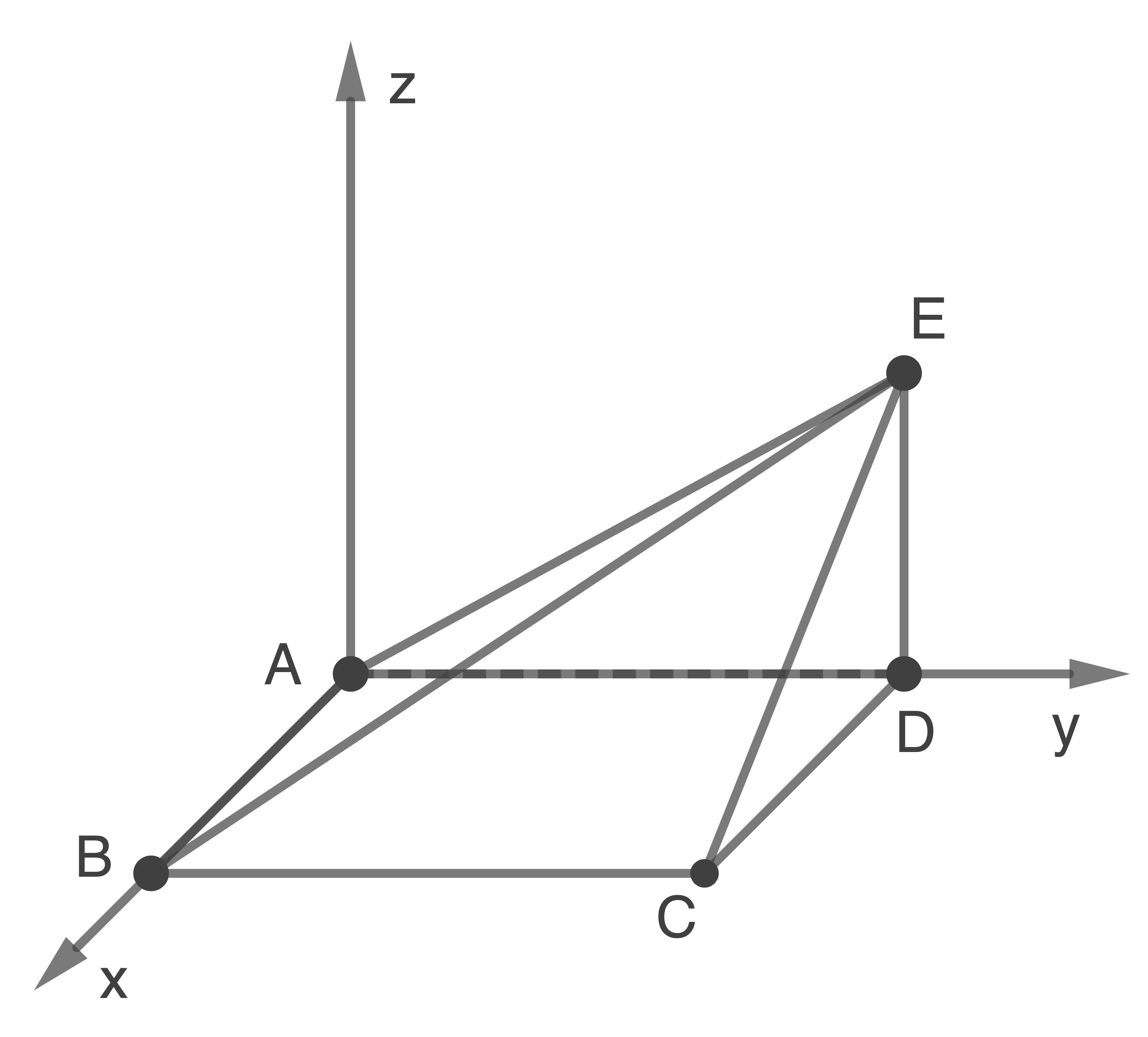
Grafik eines dreidimensionalen Koordinatensystems mit Punkten A, B, C, D und E.

Abbildung (nicht maßstäblich)

2.1

Gib an, ob die Pyramide $ABCDE$ gerade ist.
Begründe deine Angabe.

(3 BE)

2.2

Zeige, dass das Dreieck $BCE$ rechtwinklig ist.
Berechne den Inhalt der Oberfläche des Holzkörpers.

(5 BE)

2.3

Die quadratische Grundfläche des Holzkörpers schließt mit der Seitenfläche, die durch das Dreieck $BCE$ dargestellt wird, einen Winkel ein.
Berechne die Größe dieses Winkels.

(4 BE)

2.4

Der Holzkörper soll mit einer möglichst kurzen Linie versehen werden, die im Modell vom Punkt $A$ über die Kante $\overline{BE}$ zum Punkt $C$ verläuft.
Die Länge dieser Linie in Zentimetern kann folgendermaßen ermittelt werden:

$P(10-10\cdot t\mid10\cdot t\mid 6\cdot t)$

$\overrightarrow{PC} \circ \overrightarrow{PB} = 0 \Leftrightarrow t = \dfrac{25}{59}$

$0\leq\dfrac{25}{59}\leq1$

$2\cdot\begin{vmatrix}\overrightarrow{PC}\end{vmatrix}\approx15,2$

Erläutere dieses Vorgehen.

(4 BE)

2.5

Der Punkt $F ( 0\mid0 \mid 6)$ ergänzt die Pyramide $ABCDE$ zum Prisma $ABCDEF$ .
Ermittle, um wie viel Prozent das Volumen des Prismas $ABCDEF$ größer ist als das Volumen der Pyramide $ABCDE$ .

(4 BE)

Eine Firma produziert derartige Holzkörper.
Bei der Produktion der Holzkörper treten Materialfehler oder Beschichtungsfehler auf.

2.6

Die Wahrscheinlichkeit für einen Materialfehler beträgt 0,2. Ein Beschichtungsfehler tritt mit einer Wahrscheinlichkeit von 0, 15 auf. Die Wahrscheinlichkeit, dass keiner der beiden Fehler auftritt, beträgt 0,7.
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel oder in einem vollständig beschrifteten Baumdiagramm dar.
Bestimme die Wahrscheinlichkeit, dass ein zufällig ausgewählter Holzkörper genau einen der beiden Fehler aufweist.
Untersuche, ob die beiden Fehler stochastisch abhängig sind.

(8 BE)

2.7

In einer Kiste befinden sich 15 Holzkörper, von denen 10 Holzkörper fehlerfrei sind. Der Kiste werden drei Holzkörper zufällig und ohne Zurücklegen entnommen.
Berechne die Wahrscheinlichkeit, dass alle drei entnommenen Holzkörper fehlerfrei sind.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Eine Pyramide ist gerade, wenn alle Seitenkanten gleich lang sind. Für zwei Seitenkanten gilt beispielsweise:

Vollständigen Rechenweg anzeigen

$\mid \overrightarrow {BE} \mid=\sqrt {236}$

Vollständigen Rechenweg anzeigen

$\mid \overrightarrow {CE} \mid =\sqrt {136}$

Die Pyramide ist nicht gerade, da die beiden Seitenkanten $\overline{BE}$ und $\overline{CE}$ nicht gleich lang sind.

2.2

$\overrightarrow{CB}\circ\overrightarrow{CE}=\pmatrix{0\\-10\\0}\circ\pmatrix{-10\\0\\6}$ $=0\cdot(-10)+(-10)\cdot0+0\cdot6$ $=0$

Die Vektoren $\overrightarrow{CB}$ und $\overrightarrow{CE}$ stehen senkrecht zueinander, sodass das Dreieck $BCE$ rechtwinklig ist.

Oberflächeninhalt

Aufgrund der Symmetrie gilt $A_{BCE} = A_{EAB}$ und $A_{CDE}= A_{ADE}.$

Es gilt:

$\overrightarrow{DC}\circ \overrightarrow{DE}$ $= \pmatrix{10\\0\\0} \circ \pmatrix{0\\0\\6}$ $= 10\cdot 0 +0\cdot 0 + 0\cdot 6$ $=0$

Das Dreieck $CDE$ besitzt also einen rechten Winkel im Punkt $D.$ Die Grundfläche des Körpers ist quadratisch mit der Seitenlänge $10\,\text{cm}.$

Vollständigen Rechenweg anzeigen

$A_{BCE} = 5\cdot \sqrt{136}\,[\text{cm}^2]$

Vollständigen Rechenweg anzeigen

$A_{CDE} = 30 \,[\text{cm}^2]$

Insgesamt ergibt sich der Oberflächeninhalt des Holzkörpers wie folgt:

Vollständigen Rechenweg anzeigen

$O\approx 277\,\text{cm}^2$

Der Oberflächeninhalt des Holzkörpers beträgt ca. $277\,\text{cm}^2.$

2.3

Die Grundfläche liegt in der $xy$ -Ebene. Ein Normalenvektor der $xy$ -Ebene ist $\overrightarrow{n_{xy}} = \pmatrix{0\\0\\1}.$

Ein Normalenvektor der Seitenfläche ist gegeben durch $\overrightarrow{n}_L=\pmatrix{0\\10\\0}\times\pmatrix{-10\\0\\6}$ $=\pmatrix{3\\0\\5}.$

Mit der Formel für den Schnittwinkel zweier Ebenen folgt:

$\begin{array}[t]{rll} \cos \alpha &=& \dfrac{\left|\overrightarrow{n_{xy}}\circ \overrightarrow{n}_L \right|}{\left|\overrightarrow{n_{xy}}\right| \cdot \left|\overrightarrow{n_L}\right|} \\[5pt] \cos \alpha &=& \dfrac{\left| \pmatrix{0\\0\\1}\circ \pmatrix{3\\0\\5} \right|}{\left| \pmatrix{0\\0\\1}\right| \cdot \left|\pmatrix{3\\0\\5}\right|} \\[5pt] \cos \alpha &=& \dfrac{5}{ \sqrt{34}} \qquad \scriptsize \mid\; \cos^{-1}\\[5pt] \alpha &\approx& 31^{\circ} \end{array}$

Der Winkel, den die quadratische Grundfläche des Holzkörpers mit der Seitenfläche einschließt, die durch das Dreieck $BCE$ dargestellt wird, ist ca. $31^{\circ}$ groß.

2.4

Bezeichnet man im Modell denjenigen Punkt der gesuchten Linie, der auf $\overline{BE}$ liegt, mit $P,$ so ist die Länge der Linie aufgrund der Symmetrie des Körpers $2\cdot \left|\overrightarrow{PC} \right|.$
Da die Linie möglichst kurz sein soll, steht $\overline{PC}$ senkrecht zu $\overline{PB}.$
Damit der so bestimmte Punkt $P$ auch tatsächlich auf der Kante der Pyramide liegt, muss $0\leq t\leq 1$ erfüllt sein, andernfalls läge $P$ zwar auf der Geraden durch $B$ und $E,$ aber außerhalb der Pyramide.

2.5

Die Höhe der Pyramide und des Prismas ergibt sich aus der $z$ -Koordinate von $E.$

Volumen der Pyramide:

$\begin{array}[t]{rll} V_{\text {Py}}&=&\dfrac{1}{3}\cdot G\cdot h \\[5pt] &=& \dfrac{1}{3}\cdot 10^2\cdot 6 \\[5pt] &=& 200\,[\text{cm}^3] \\[5pt] \end{array}$

Volumen des Prismas: