Teil B1
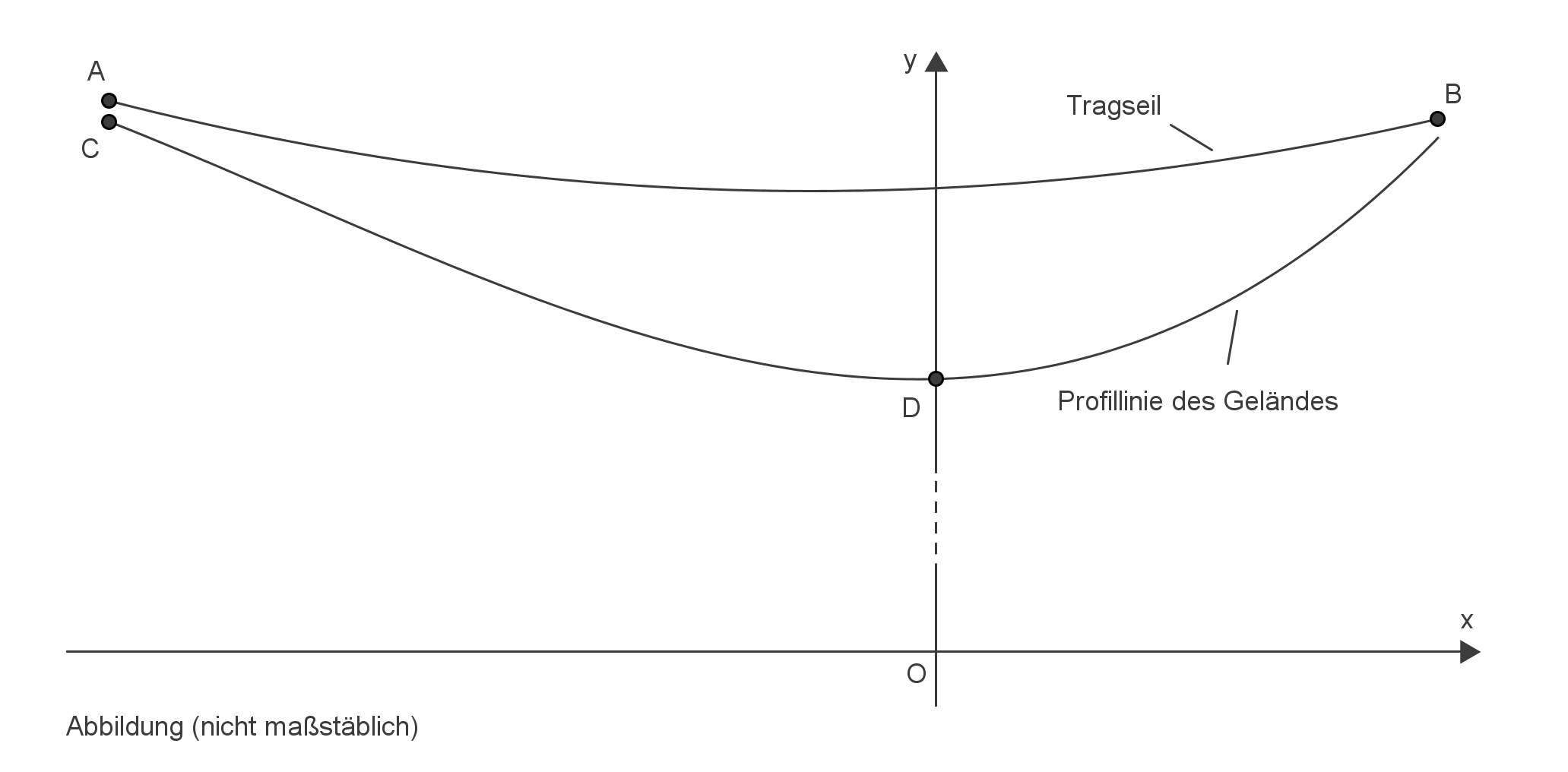
In einem Skigebiet wird eine Kabinenseilbahn betrieben. Der Verlauf des Tragseils der Kabinenseilbahn und die Profillinie des Geländes unterhalb der Kabinenseilbahn können in einem kartesischen Koordinatensystem ( Längeneinheit entspricht
Längeneinheit entspricht  ) dargestellt werden. Für die Höhe des Meeresspiegels gilt:
) dargestellt werden. Für die Höhe des Meeresspiegels gilt:  .
Das Tragseil verläuft zwischen zwei Befestigungspunkten. In der Abbildung werden der linke Befestigungspunkt mit
.
Das Tragseil verläuft zwischen zwei Befestigungspunkten. In der Abbildung werden der linke Befestigungspunkt mit  und der rechte Befestigungspunkt mit
und der rechte Befestigungspunkt mit  bezeichnet. Diese Punkte besitzen die Koordinaten
bezeichnet. Diese Punkte besitzen die Koordinaten  und
und  .
Der Verlauf des Tragseils kann durch den Graphen der Funktion
.
Der Verlauf des Tragseils kann durch den Graphen der Funktion  mit
mit
 beschrieben werden.
Der Verlauf der Profillinie des Geländes unterhalb der Kabinenseilbahn kann durch den Graphen der Funktion
beschrieben werden.
Der Verlauf der Profillinie des Geländes unterhalb der Kabinenseilbahn kann durch den Graphen der Funktion  mit
mit
 beschrieben werden.
beschrieben werden.
 und der Endpunkt mit
und der Endpunkt mit  bezeichnet.
Diese Punkte besitzen die Koordinaten
bezeichnet.
Diese Punkte besitzen die Koordinaten  und
und  .
.

1.1 Begründe, dass die  -Koordinate des Punktes
-Koordinate des Punktes  näherungsweise
näherungsweise  beträgt.
Zeige, dass der Höhenunterschied zwischen den beiden Befestigungspunkten des Tragseils etwa
beträgt.
Zeige, dass der Höhenunterschied zwischen den beiden Befestigungspunkten des Tragseils etwa  beträgt.
Gib die kleinste Höhe des Tragseils über dem Meeresspiegel an.
beträgt.
Gib die kleinste Höhe des Tragseils über dem Meeresspiegel an.
(4P)
1.2 Die Kabinen bewegen sich mit der Durchschnittsgeschwindigkeit  .
Berechne die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten des Tragseils.
Hinweis: Für die Länge
.
Berechne die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten des Tragseils.
Hinweis: Für die Länge  des Graphen einer Funktion
des Graphen einer Funktion  im Intervall
im Intervall  gilt:
gilt:
 .
.
(4P)
1.3 Jeder Punkt des Tragseils besitzt eine Höhe über der Profillinie des Geländes. Diese Höhen werden jeweils parallel zur  -Achse gemessen.
Ermittle den größten Wert dieser Höhen
Aus Sicherheitsgründen muss die Höhe jedes Punktes des Tragseils über der Profillinie des Geländes mindestens
-Achse gemessen.
Ermittle den größten Wert dieser Höhen
Aus Sicherheitsgründen muss die Höhe jedes Punktes des Tragseils über der Profillinie des Geländes mindestens  betragen.
betragen.
Zeige, dass diese Bedingung für die Befestigungspunkte und
und  erfüllt ist.
erfüllt ist.
Zeige, dass diese Bedingung für die Befestigungspunkte
(4P)
Entlang der Profillinie des Geländes verläuft eine Skipiste zwischen zwei Punkten. In der Abbildung werden der Anfangspunkt der Skipiste mit
1.4 Skipisten werden nach dem Schwierigkeitsgrad in blaue, rote und schwarze Skipisten unterteilt. Bei blauen Skipisten darf das maximale Gefälle höchstens  , bei roten Skipisten höchstens
, bei roten Skipisten höchstens  betragen. Schwarze Pisten besitzen ein maximales Gefälle von mehr als
betragen. Schwarze Pisten besitzen ein maximales Gefälle von mehr als  .
Bestimme den Schwierigkeitsgrad der Skipiste.
.
Bestimme den Schwierigkeitsgrad der Skipiste.
(3P)
1.5 Untersuche, ob die Profillinie des Geländes den Blick vom Endpunkt der Skipiste zum linken Befestigungspunkt des Tragseils behindert.
(2P)
1.6 Erfahrungsgemäß betreiben  der Wintertouristen des Skigebietes alpinen Skisport.
der Wintertouristen des Skigebietes alpinen Skisport.  der Wintertouristen des Skigebietes, die alpinen Skisport betreiben, nutzen auch diese Kabinenseilbahn.
der Wintertouristen des Skigebietes, die alpinen Skisport betreiben, nutzen auch diese Kabinenseilbahn.  der Wintertouristen des Skigebietes, welche keinen alpinen Skisport betreiben, nutzen ebenfalls diese Kabinenseilbahn.
Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Wintertourist des Skigebietes alpinen Skisport betreibt und diese Kabinenseilbahn nutzt.
Ermittle, wie viele von
der Wintertouristen des Skigebietes, welche keinen alpinen Skisport betreiben, nutzen ebenfalls diese Kabinenseilbahn.
Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Wintertourist des Skigebietes alpinen Skisport betreibt und diese Kabinenseilbahn nutzt.
Ermittle, wie viele von  Wintertouristen des Skigebietes diese Kabinenseilbahn erfahrungsgemäß nutzen werden.
Wintertouristen des Skigebietes diese Kabinenseilbahn erfahrungsgemäß nutzen werden.
(4P)
1.7 Für die Kabinenseilbahn können auch ermäßigte Tickets erworben werden.
Erfahrungsgemäß beträgt der Anteil der erworbenen ermäßigten Tickets .
Berechne die Wahrscheinlichkeit dafür, dass von
.
Berechne die Wahrscheinlichkeit dafür, dass von  erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Bestimme, wie viele Tickets mindestens erworben werden müssen, damit mit einer Wahrscheinlichkeit von mindestens
erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Bestimme, wie viele Tickets mindestens erworben werden müssen, damit mit einer Wahrscheinlichkeit von mindestens  mindestens ein ermäßigtes Ticket erworben wird.
mindestens ein ermäßigtes Ticket erworben wird.
Erfahrungsgemäß beträgt der Anteil der erworbenen ermäßigten Tickets
(4P)
1.
1.1

 -Koordinate des Punktes
-Koordinate des Punktes  berechnen
Der Punkt
berechnen
Der Punkt  ist der linke Befestigungspunkt des Tragseils und befindet sich somit auf der Funktion
ist der linke Befestigungspunkt des Tragseils und befindet sich somit auf der Funktion  . Setze also die
. Setze also die  -Koordinate des Punktes
-Koordinate des Punktes  in die Gleichung der Funktion
in die Gleichung der Funktion  ein, berechne also den Wert
ein, berechne also den Wert  .
.
 Die
Die  -Koordinate beträgt deshalb näherungsweise
-Koordinate beträgt deshalb näherungsweise  .
.
 Höhenunterschied berechnen
Der Höhenunterschied ist der Betrag der Differenz der
Höhenunterschied berechnen
Der Höhenunterschied ist der Betrag der Differenz der  -Koordinaten. Berechne also
-Koordinaten. Berechne also  . Dafür benötigst du die
. Dafür benötigst du die  -Koordinate des Punktes
-Koordinate des Punktes  , die du analog zur ersten Teilaufgabe berechnen kannst.
, die du analog zur ersten Teilaufgabe berechnen kannst.
 Damit kannst du nun den Höhenunterschied berechnen:
Damit kannst du nun den Höhenunterschied berechnen:
 Die Differenz der beiden
Die Differenz der beiden  -Werte beträgt ca.
-Werte beträgt ca.  .
.  Längeneinheit entspricht
Längeneinheit entspricht  Metern, somit ist die Höhendifferenz etwa
Metern, somit ist die Höhendifferenz etwa  .
.
 Kleinste Höhe des Tragseils bestimmen
Deine Aufgabe ist es die kleinste Höhe des Tragseils zu bestimmen. Die Höhe des Tragseils über dem Meeresspiegel wird durch die Funktion
Kleinste Höhe des Tragseils bestimmen
Deine Aufgabe ist es die kleinste Höhe des Tragseils zu bestimmen. Die Höhe des Tragseils über dem Meeresspiegel wird durch die Funktion  beschrieben. Die geringste Höhe des Tragseils ist somit der Minimalwert der Funktion
beschrieben. Die geringste Höhe des Tragseils ist somit der Minimalwert der Funktion  im Intervall
im Intervall ![\(\left[-9;5,8\right]\)](https://mathjax.schullv.de/f69b5f53aa35b041b4e10233b636c58cb0c8fa111474847c5420bbe3b9ad448a?color=5a5a5a) . Bestimme also den Minimalwert der Funktion
. Bestimme also den Minimalwert der Funktion  . Diesen kannst du mit deinem GTR berechnen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
. Diesen kannst du mit deinem GTR berechnen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
 und
und  ein.
ein.
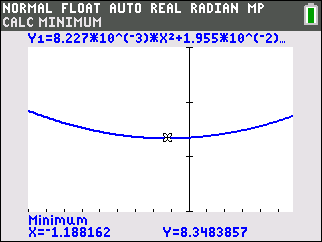 Die minimale Höhe des Tragseils ist somit ca.
Die minimale Höhe des Tragseils ist somit ca.  .
.
2nd  CALC (TRACE)
CALC (TRACE)  3:minimum
3:minimum
den Befehl zum Bestimmen des Minimums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen 
1.2
 Fahrzeit einer Kabine berechnen
Hier ist die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten gesucht. Dazu hast du die Durchschnittsgeschwindigkeit und einen Hinweis zur Berechnung der Länge des Graphen einer Funktion gegeben.
Fahrzeit einer Kabine berechnen
Hier ist die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten gesucht. Dazu hast du die Durchschnittsgeschwindigkeit und einen Hinweis zur Berechnung der Länge des Graphen einer Funktion gegeben.
Berechne zuerst die Länge des Tragseils, dann kannst du mit Hilfe der Durchschnittsgeschwindigkeit die Fahrzeit berechnen. 1. Schritt: Länge des Tragseils berechnen Der Verlauf des Tragseils wird durch die Funktion beschrieben, die Länge des Tragseils ist somit die Länge des Graphen der Funktion
beschrieben, die Länge des Tragseils ist somit die Länge des Graphen der Funktion  . Mit dem Hinweis kannst du die Länge
. Mit dem Hinweis kannst du die Länge  des Graphen von
des Graphen von  bestimmen. Die Länge
bestimmen. Die Länge  ist durch folgende Formel gegeben:
ist durch folgende Formel gegeben:
![\(\begin{array}[t]{rll}
l&=&\displaystyle\int_{-9}^{5,8}\left(\sqrt{1+\left(s‘(x)\right)^2}\right)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/8c1aee2b20b188447ca531695ec3aa4f0ec58b25083b86ab2cc4f80a5f3d1e54?color=5a5a5a) Definierst du dir die Funktion
Definierst du dir die Funktion  , so musst du das folgende Integral berechen:
, so musst du das folgende Integral berechen:
![\(\begin{array}[t]{rll}
l&=&\displaystyle\int_{-9}^{5,8}f(x)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/873b0a40705fb98740c3f2c18df609d7e39ac0eade9de0640ac94b7ef09afe31?color=5a5a5a) Berechne zuerst die erste Ableitung der Funktion
Berechne zuerst die erste Ableitung der Funktion  , um den Funktionsterm der Funktion
, um den Funktionsterm der Funktion  zu bestimmen:
zu bestimmen:
![\(\begin{array}[t]{rll}
s(x)&=&8,227 \cdot 10^{-3} \cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 8,360 \\[10pt]
s‘(x)&=&2 \cdot \left(8,227 \cdot 10^{-3} \cdot x \right)+ 1,955 \cdot 10^{-2} \\[5pt]
&=&16,454 \cdot 10^{-3} \cdot x + 1,955 \cdot 10^{-2} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/b36b3f3937d4d0659d0052eb0561bcaf5d3ae07f877397f0c25f71789c841e70?color=5a5a5a) Damit lautet die Funktionsgleichung von
Damit lautet die Funktionsgleichung von  folgendermaßen:
folgendermaßen:
 Das Integral kannst du nun mit deinem GTR berechnen. Wechsle dazu mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Das Integral kannst du nun mit deinem GTR berechnen. Wechsle dazu mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
 und die obere Grenze
und die obere Grenze  ein.
ein.
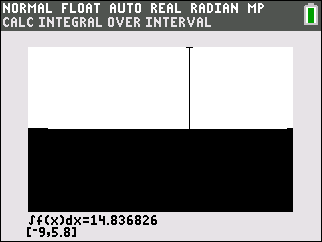 Das Tragseil hat somit ca. die Länge
Das Tragseil hat somit ca. die Länge  .
2. Schritt: Fahrzeit berechnen
Für Fahrzeit, Geschwindigkeit und Strecke gilt nun folgende Gleichung:
.
2. Schritt: Fahrzeit berechnen
Für Fahrzeit, Geschwindigkeit und Strecke gilt nun folgende Gleichung:
 Die zurückgelegte Strecke ist hier gerade die Länge
Die zurückgelegte Strecke ist hier gerade die Länge  , die Geschwindigkeit ist durch
, die Geschwindigkeit ist durch  gegeben. Nun kannst du die Gleichung nach der Fahrzeit umstellen und die Werte einsetzen:
gegeben. Nun kannst du die Gleichung nach der Fahrzeit umstellen und die Werte einsetzen:
![\(\begin{array}[t]{rll}
\text{Fahrzeit} \cdot \text{Geschwindigkeit}&=&\text{zurückgelegte Strecke} \quad \scriptsize \mid\; : \text{Geschwindigkeit}\\[5pt]
\text{Fahrzeit}&=& \dfrac{\text{zurückgelegte Strecke}}{ \text{Geschwindigkeit}} \\[5pt]
&=& \dfrac{1.483,7 \text{ m}}{7,5\,\dfrac{\text{m}}{\text{s}}}\\[5pt]
&\approx& 198 \text{ s}
\end{array}\)](https://mathjax.schullv.de/1f60000ede4d5985ad386c1a11e7161a7e73c9619be82aedadcf4a9e0ec7571f?color=5a5a5a) Damit ist die Fahrzeit einer Kabine zwischen den zwei Befestigungspunkten
Damit ist die Fahrzeit einer Kabine zwischen den zwei Befestigungspunkten  .
.
Berechne zuerst die Länge des Tragseils, dann kannst du mit Hilfe der Durchschnittsgeschwindigkeit die Fahrzeit berechnen. 1. Schritt: Länge des Tragseils berechnen Der Verlauf des Tragseils wird durch die Funktion
2nd  CALC (TRACE)
CALC (TRACE)  7:
7: 
den Befehl zum Bestimmen des Integrals aus und bestätige mit Enter. Gib anschließend die untere Grenze 
1.3
 Größte Höhe des Tragseils über der Profillinie bestimmen
Hier ist es deine Aufgabe die größte Höhe des Tragseils über der Profillinie zu bestimmen. Stelle dazu zuerst eine Funktion auf, die die Höhe des Tragseils über der Profillinie beschreibt, und berechne dann das Maximum dieser Funktion. Gehe also folgendermaßen vor:
Größte Höhe des Tragseils über der Profillinie bestimmen
Hier ist es deine Aufgabe die größte Höhe des Tragseils über der Profillinie zu bestimmen. Stelle dazu zuerst eine Funktion auf, die die Höhe des Tragseils über der Profillinie beschreibt, und berechne dann das Maximum dieser Funktion. Gehe also folgendermaßen vor:
 aufstellen
Die Höhe des Tragseils über der Profillinie ist gerade die Differenz der Höhe des Tragseils und der Höhe der Profillinie des Geländes. Die Höhe des Tragseils wird durch die Funktion
aufstellen
Die Höhe des Tragseils über der Profillinie ist gerade die Differenz der Höhe des Tragseils und der Höhe der Profillinie des Geländes. Die Höhe des Tragseils wird durch die Funktion  beschrieben, die Höhe der Profillinie des Geländes durch die Funktion
beschrieben, die Höhe der Profillinie des Geländes durch die Funktion  . Dementsprechend gilt für die Funktion
. Dementsprechend gilt für die Funktion  , die die Höhe des Tragseils über dem Gelände beschreibt:
, die die Höhe des Tragseils über dem Gelände beschreibt:
![\(\begin{array}[t]{rll}
d(x)&=& s(x) - g(x) \\[5pt]
&=& \left(8,227 \cdot 10^{-3} \cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 8,360\right) \\[5pt]
&&- \left(1,504 \cdot 10^{-3} \cdot x^3 + 3,125 \cdot 10^{-2} \cdot x^2 +7,300\right)\\[5pt]
&=& -1,504 \cdot 10^{-3} \cdot x^3 + \left(8,227 \cdot 10^{-3} - 3,125 \cdot 10^{-2} \right) \cdot x^2 \\[5pt]
&&+ 1,955 \cdot 10^{-2} \cdot x + \left(8,36-7,3\right) \\[5pt]
&=& -1,504 \cdot 10^{-3} \cdot x^3 - 2,302 \cdot 10^{-2}\cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 1,06
\end{array}\)](https://mathjax.schullv.de/f7b40c18fee63ed8ab9300772b9aca9c983410a42d1bc54d85835ef6a4bbd6e3?color=5a5a5a) 2. Schritt: Maximum der Funktion
2. Schritt: Maximum der Funktion  bestimmen
Nun musst du das Maximum der Funktion
bestimmen
Nun musst du das Maximum der Funktion  bestimmen. Dies kannst du mit deinem GTR.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
bestimmen. Dies kannst du mit deinem GTR.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Wähle dann unter
 und
und  ein.
ein.
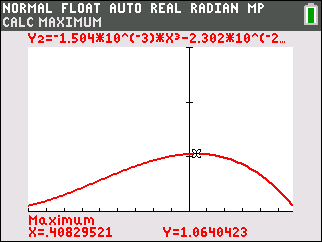 Die maximale Höhe des Tragseils über der Profillinie des Geländes ist somit ca.
Die maximale Höhe des Tragseils über der Profillinie des Geländes ist somit ca.  .
.
 Zeigen, dass Mindesthöhe erfüllt ist
Nun sollst du zeigen, dass die Höhe zwischen dem Tragseil und dem Gelände an den Befestigungspunkten mindestens
Zeigen, dass Mindesthöhe erfüllt ist
Nun sollst du zeigen, dass die Höhe zwischen dem Tragseil und dem Gelände an den Befestigungspunkten mindestens  ist. Berechne dazu die Höhen an den Stellen
ist. Berechne dazu die Höhen an den Stellen  und
und  mit der Funktion
mit der Funktion  und überprüfe die Bedingung.
und überprüfe die Bedingung.
 Befestigungspunkt
Befestigungspunkt  :
Berechne den Funktionswert
:
Berechne den Funktionswert  :
:
 Die Höhendifferenz beträgt an der Stelle
Die Höhendifferenz beträgt an der Stelle  ca.
ca.  und erfüllt somit die Bedingung.
und erfüllt somit die Bedingung.
 Befestigungspunkt
Befestigungspunkt  :
Berechne den Funktionswert
:
Berechne den Funktionswert  :
:
 Die Höhendifferenz beträgt an der Stelle
Die Höhendifferenz beträgt an der Stelle  ca.
ca.  und erfüllt somit die Bedingung.
und erfüllt somit die Bedingung.
- Stelle die Funktion
auf, die die Höhe des Tragseils über der Profillinie beschreibt.
- Berechne das Maximum der Funktion
im Intervall
.
2nd  CALC (TRACE)
CALC (TRACE)  4:maximum
4:maximum
den Befehl zum Bestimmen des Maximums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen 
1.4
 Schwierigkeitsgrad der Skipiste bestimmen
Hier sollst du den Schwierigkeitsgrad der beschriebenen Skipiste bestimmen. Eine Skipiste wird nach ihrem maximalen Gefälle bewertet. Berechne also das maximale Gefälle der Skipiste.
Schwierigkeitsgrad der Skipiste bestimmen
Hier sollst du den Schwierigkeitsgrad der beschriebenen Skipiste bestimmen. Eine Skipiste wird nach ihrem maximalen Gefälle bewertet. Berechne also das maximale Gefälle der Skipiste.
Die Skipiste wird durch die Funktion auf dem Intervall
auf dem Intervall ![\(\left[-9;0\right]\)](https://mathjax.schullv.de/cbbf6c098e50c918532c32a5e832d2cc3b2655a1b8208066b1695f2b76e3003c?color=5a5a5a) beschrieben. Das Gefälle der Skipiste ist dementsprechend die Steigung der Funktion
beschrieben. Das Gefälle der Skipiste ist dementsprechend die Steigung der Funktion  , die durch die erste Ableitung
, die durch die erste Ableitung  beschrieben wird. Um das maximale Gefälle zu bestimmen, musst du somit die betragsmäßig größte negative Steigung der Funktion
beschrieben wird. Um das maximale Gefälle zu bestimmen, musst du somit die betragsmäßig größte negative Steigung der Funktion  , also das Minimum der Funktion
, also das Minimum der Funktion  auf dem Intervall
auf dem Intervall ![\(\left[-9;0\right]\)](https://mathjax.schullv.de/cbbf6c098e50c918532c32a5e832d2cc3b2655a1b8208066b1695f2b76e3003c?color=5a5a5a) bestimmen. Hast du dieses gegeben, so kannst du die Schwierigkeit der Skipiste bewerten.
Gehe also folgendermaßen vor:
bestimmen. Hast du dieses gegeben, so kannst du die Schwierigkeit der Skipiste bewerten.
Gehe also folgendermaßen vor:
 bestimmen
Leite hierzu die Funktion
bestimmen
Leite hierzu die Funktion  ab:
ab:
![\(\begin{array}[t]{rll}
g(x)&=&1,504 \cdot 10^{-3} \cdot x^3 + 3,125 \cdot 10^{-2}\cdot x^2 + 7,3 \\[10pt]
g‘(x)&=&3 \cdot \left(1,504 \cdot 10^{-3} \cdot x^2\right) + 2 \cdot \left(3,125 \cdot 10^{-2}\cdot x\right) \\[5pt]
&=&4,512 \cdot 10^{-3} \cdot x^2 + 6,25 \cdot 10^{-2}\cdot x
\end{array}\)](https://mathjax.schullv.de/f963b98de49e4b375ed406be2c5a22d5f94b1e2bcb77660ced328af428eebf07?color=5a5a5a) 2. Schritt: Minimum von
2. Schritt: Minimum von  bestimmen
Bestimme nun den Minimalwert der Funktion
bestimmen
Bestimme nun den Minimalwert der Funktion  . Dies kannst du mit deinem GTR wie bereits in 1.1. Du erhältst:
. Dies kannst du mit deinem GTR wie bereits in 1.1. Du erhältst:
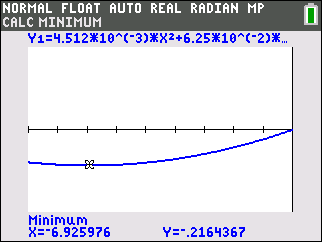 Der Minimalwert der Funktion
Der Minimalwert der Funktion  ist somit ca.
ist somit ca.  . Das maximale Gefälle der Skipiste ist somit ca.
. Das maximale Gefälle der Skipiste ist somit ca.  .
3. Schritt: Schwierigkeitsgrad der Skipiste bestimmen
Das Gefälle der Skipiste beträgt
.
3. Schritt: Schwierigkeitsgrad der Skipiste bestimmen
Das Gefälle der Skipiste beträgt  . Es gilt:
. Es gilt:  . Somit handelt es sich bei der Skipiste um eine blaue Piste.
. Somit handelt es sich bei der Skipiste um eine blaue Piste.
Die Skipiste wird durch die Funktion
- Bestimme die erste Ableitung
.
- Bestimme das Minimum von
.
- Bestimme den Schwierigkeitsgrad der Skipiste.

1.5
 Untersuchen, ob die Profillinie den Blick behindert
Deine Aufgabe ist es zu untersuchen ob die Profillinie des Geländes den Blick vom Endpunkt
Untersuchen, ob die Profillinie den Blick behindert
Deine Aufgabe ist es zu untersuchen ob die Profillinie des Geländes den Blick vom Endpunkt  der Skipiste zum linken Befestigungspunkt
der Skipiste zum linken Befestigungspunkt  des Tragseils behindert. Den Blick vom Punkt
des Tragseils behindert. Den Blick vom Punkt  zum Punkt
zum Punkt  kannst du mit der Gerade
kannst du mit der Gerade  durch die Punkte
durch die Punkte  und
und  beschreiben. Der Blick wird nun von der Profillinie behindert, wenn sich die Gerade
beschreiben. Der Blick wird nun von der Profillinie behindert, wenn sich die Gerade  und die Funktion
und die Funktion  im Intervall
im Intervall  , also dem Bereich zwischen den Punkten
, also dem Bereich zwischen den Punkten  und
und  , schneiden.
Gehe also folgendermaßen vor:
, schneiden.
Gehe also folgendermaßen vor:
 bestimmen
Die allgemeine Form einer Gerade lautet:
bestimmen
Die allgemeine Form einer Gerade lautet:  . Setze also die beiden gegebenen Punkte
. Setze also die beiden gegebenen Punkte  und
und  ein und du erhältst ein lineares Gleichungssystem. Berechne dazu zuerst die
ein und du erhältst ein lineares Gleichungssystem. Berechne dazu zuerst die  -Koordinate des Punktes
-Koordinate des Punktes  :
:
 Damit erhältst du folgendes LGS:
Damit erhältst du folgendes LGS:
 Es gilt somit
Es gilt somit  und
und  . Die Gerade
. Die Gerade  ist damit durch folgende Geradengleichung gegeben:
ist damit durch folgende Geradengleichung gegeben:
 2. Schritt:
2. Schritt:  und
und  auf Schnittpunke überprüfen
Überprüfe nun mit deinem GTR, ob die Funktion
auf Schnittpunke überprüfen
Überprüfe nun mit deinem GTR, ob die Funktion  und die Gerade
und die Gerade  einen Schnittpunkt im Intervall
einen Schnittpunkt im Intervall  besitzen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort die Funktionsterme von
besitzen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort die Funktionsterme von  und
und  . Hast du diese dort gespeichert, dann lass dir die zugehörigen Graphen über GRAPH anzeigen.
Wähle dann unter
. Hast du diese dort gespeichert, dann lass dir die zugehörigen Graphen über GRAPH anzeigen.
Wähle dann unter
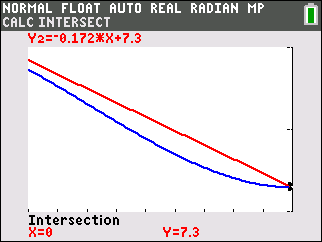 Der einzige Schnittpunkt ist
Der einzige Schnittpunkt ist  und somit außerhalb des Intervalls
und somit außerhalb des Intervalls  . Insgesamt existieren somit keine Schnittstellen im Intervall
. Insgesamt existieren somit keine Schnittstellen im Intervall  und damit ist der Blick nicht behindert.
und damit ist der Blick nicht behindert.
- Bestimme die Gerade
durch die Punkte
und
.
- Überprüfe, ob die Gerade
und die Funktion
sich im Intervall
schneiden.
2nd  CALC (TRACE)
CALC (TRACE)  5:intersect
5:intersect
den Befehl zum Bestimmen der Schnittpunkte aus und bestätige mit Enter.

1.6
 Wahrscheinlichkeit für Seilbahnnutzung bestimmen
Zuerst sollst du die Wahrscheinlichkeit berechnen, dass ein zufällig ausgewählter Wintertourist des Skigebiets alpinen Skisport betreibt und diese Kabinenseilbahn benutzt, also die Wahrscheinlichkeit:
Wahrscheinlichkeit für Seilbahnnutzung bestimmen
Zuerst sollst du die Wahrscheinlichkeit berechnen, dass ein zufällig ausgewählter Wintertourist des Skigebiets alpinen Skisport betreibt und diese Kabinenseilbahn benutzt, also die Wahrscheinlichkeit:
 .
Dir ist zum einen gegeben, dass
.
Dir ist zum einen gegeben, dass  der Wintertouristen alpinen Skisport betreiben, zum anderen ist dir gegeben, dass
der Wintertouristen alpinen Skisport betreiben, zum anderen ist dir gegeben, dass  der Touristen, die alpinen Skisport betreiben, die Seilbahn benutzen:
der Touristen, die alpinen Skisport betreiben, die Seilbahn benutzen:
 ,
,
 .
Nun kannst du mit der Pfadmultiplikationsregel die gesuchte Wahrscheinlichkeit berechnen:
.
Nun kannst du mit der Pfadmultiplikationsregel die gesuchte Wahrscheinlichkeit berechnen:
![\(\begin{array}{rll}
P\left(\text{„Seilbahnnutzung und Skisport“}\right) &=& P\left(\text{„Skisport“}\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„Skisport“}\right) \\[5pt]
&=& 0,72 \cdot 0,95 = 0,684 =68,4\,\%
\end{array}\)](https://mathjax.schullv.de/0398a98f2760384fa4db038e9284c12e3b16272e9e3d06481841dccfdd58fab2?color=5a5a5a) Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Wintertourist alpinen Skisport betreibt und die Seilbahn benutzt, liegt bei
Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Wintertourist alpinen Skisport betreibt und die Seilbahn benutzt, liegt bei  .
.
 Erwartete Seilbahnnutzer bestimmen
Hier ist nach der Anzahl Touristen gefragt, die unter
Erwartete Seilbahnnutzer bestimmen
Hier ist nach der Anzahl Touristen gefragt, die unter  Wintertouristen erfahrungsgemäß die Seilbahn benutzen. Berechne dazu mit den dir gegebenen Wahrscheinlichkeiten die Wahrscheinlichkeit, dass ein zufällig ausgewählter Tourist die Seilbahn benutzt. Damit kannst du dann die erwarteten Besucher ausrechnen. Es ist also zuerst nach folgender Wahrscheinlichkeit gesucht:
Wintertouristen erfahrungsgemäß die Seilbahn benutzen. Berechne dazu mit den dir gegebenen Wahrscheinlichkeiten die Wahrscheinlichkeit, dass ein zufällig ausgewählter Tourist die Seilbahn benutzt. Damit kannst du dann die erwarteten Besucher ausrechnen. Es ist also zuerst nach folgender Wahrscheinlichkeit gesucht:
 .
Diese ist dir nicht direkt gegeben und du musst sie mit Hilfe der angegebenen Wahrscheinlichkeiten berechnen. Dir sind jeweils die Wahrscheinlichkeiten gegeben, dass ein Tourist der Skisport betreibt oder kein Skisport betreibt mit der Seilbahn fährt. Da die Touristen entweder Skisport betreiben oder nicht, kannst du mit den jeweils bedingten Wahrscheinlichkeiten die Wahrscheinlichkeit der Seilbahnnutzung bestimmen:
.
Diese ist dir nicht direkt gegeben und du musst sie mit Hilfe der angegebenen Wahrscheinlichkeiten berechnen. Dir sind jeweils die Wahrscheinlichkeiten gegeben, dass ein Tourist der Skisport betreibt oder kein Skisport betreibt mit der Seilbahn fährt. Da die Touristen entweder Skisport betreiben oder nicht, kannst du mit den jeweils bedingten Wahrscheinlichkeiten die Wahrscheinlichkeit der Seilbahnnutzung bestimmen:
![\(\begin{array}{rll}
&&P\left(\text{„Seilbahnnutzung“}\right)\\[5pt]
&=&P\left(\text{„Seilbahnnutzung und Skisport“}\right) + P\left(\text{„Seilbahnnutzung und kein Skisport“}\right)
\end{array}\)](https://mathjax.schullv.de/b91d69e348b54bcec76cb3e7f23a5f8e3a3641943d9f63d5470468424703702c?color=5a5a5a) Die erste Wahrscheinlichkeit hast du bereits berechnet. Die zweite kannst du genauso mit der Pfadmultiplikationsregel und dem Gegenereignis bestimmen:
Die erste Wahrscheinlichkeit hast du bereits berechnet. Die zweite kannst du genauso mit der Pfadmultiplikationsregel und dem Gegenereignis bestimmen:
![\(\begin{array}{rll}
&&P\left(\text{„Seilbahnnutzung und kein Skisport“}\right) \\[5pt]
&=& P\left(\text{„kein Skisport“}\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„kein Skisport“}\right) \\[5pt]
&=& \left(1- P\left(\text{„Skisport“}\right)\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„kein Skisport“}\right) \\[5pt]
&=& \left(1- 0,72\right) \cdot 0,50 = 0,28 \cdot 0,5 = 0,14 =14\,\%
\end{array}\)](https://mathjax.schullv.de/8403b2f4185d62ac0dc24ab388c120a55ab67040bdf4b59b12e353babef5b9a3?color=5a5a5a) Also gilt für die Wahrscheinlichkeit der Seilbahnnutzung:
Also gilt für die Wahrscheinlichkeit der Seilbahnnutzung:
 Multipliziere diese Wahrscheinlichkeit mit
Multipliziere diese Wahrscheinlichkeit mit  , um die erwartete Anzahl an Seilbahnnutzern zu bestimmen:
, um die erwartete Anzahl an Seilbahnnutzern zu bestimmen:
 Damit benutzen erfahrungsgemäß
Damit benutzen erfahrungsgemäß  von
von  Wintertouristen die Kabinenseilbahn.
Wintertouristen die Kabinenseilbahn.
1.7
 Wahrscheinlichkeit für Tickets bestimmen
Berechne hier die Wahrscheinlichkeit, dass von
Wahrscheinlichkeit für Tickets bestimmen
Berechne hier die Wahrscheinlichkeit, dass von  erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Definiere die Zufallsvariable
erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Definiere die Zufallsvariable  , die die Anzahl an erworbenen ermäßigten Tickets unter
, die die Anzahl an erworbenen ermäßigten Tickets unter  erworbenen Tickets beschreibt. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „ermäßigt“ und „nicht ermäßigt“ gibt und mit einem Anteil von
erworbenen Tickets beschreibt. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „ermäßigt“ und „nicht ermäßigt“ gibt und mit einem Anteil von  ermäßigte Tickets erworben werden. Es gilt dementsprechend
ermäßigte Tickets erworben werden. Es gilt dementsprechend  .
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
.
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
 .
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Verwende dazu den binomcdf-Befehl deines GTR. Diesen findest du unter
.
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Verwende dazu den binomcdf-Befehl deines GTR. Diesen findest du unter
 ,
,  und
und  eingeben.
eingeben.
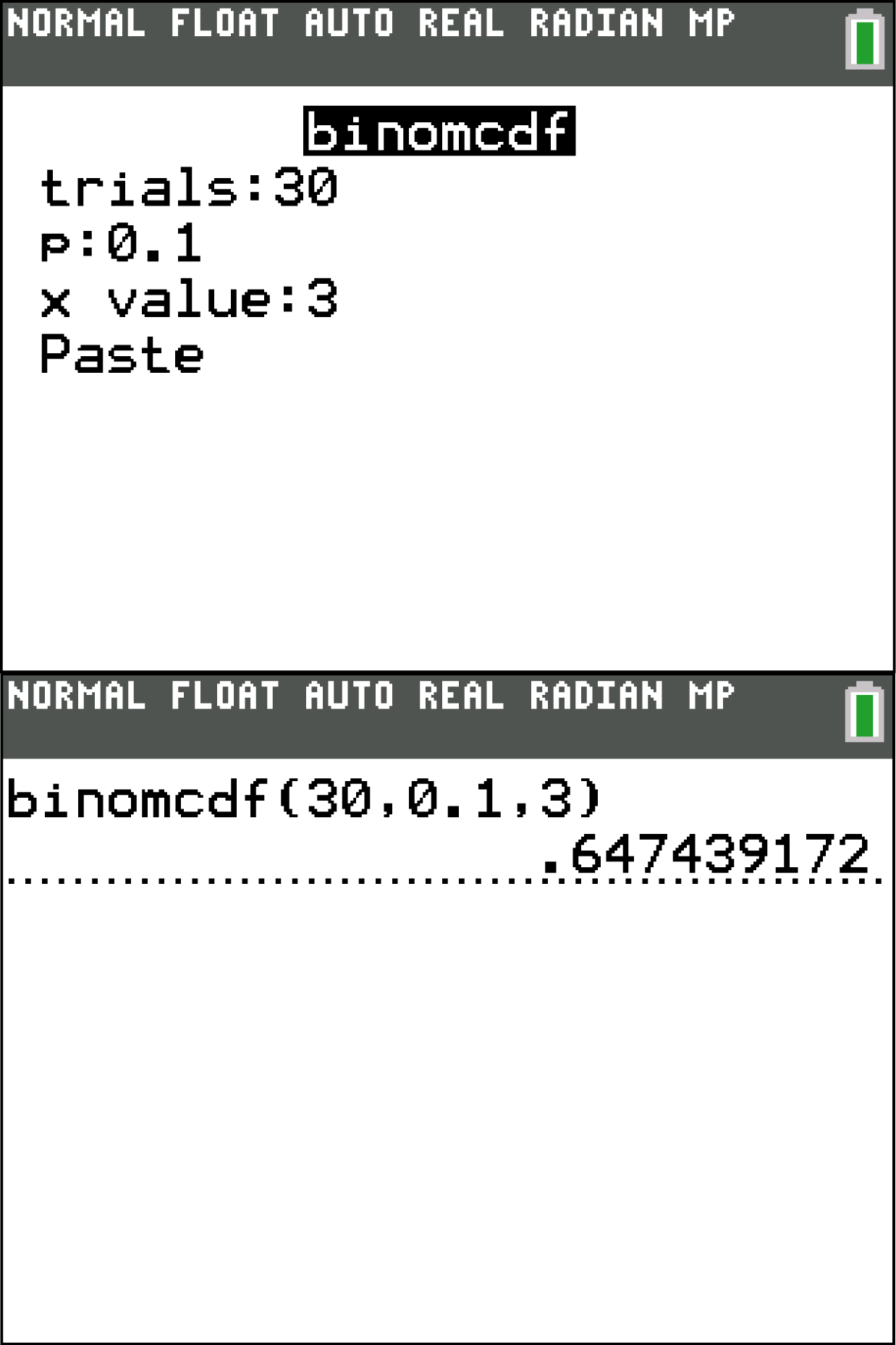 Du erhältst dann das Ergebnis
Du erhältst dann das Ergebnis  . Für die gesuchte Wahrscheinlichkeit gilt somit:
. Für die gesuchte Wahrscheinlichkeit gilt somit:
 .
Die Wahrscheinlichkeit, dass von
.
Die Wahrscheinlichkeit, dass von  erworbenen Tickets mehr als drei Tickets ermäßigt sind, liegt bei ca.
erworbenen Tickets mehr als drei Tickets ermäßigt sind, liegt bei ca.  .
.
 Mindestanzahl an Tickets bestimmen
Betrachte hier wieder die Zufallsvariable
Mindestanzahl an Tickets bestimmen
Betrachte hier wieder die Zufallsvariable  , die die Anzahl an erworbenen ermäßigten Tickets unter der gesuchten Anzahl von
, die die Anzahl an erworbenen ermäßigten Tickets unter der gesuchten Anzahl von  erworbenen Tickets beschreibt.
erworbenen Tickets beschreibt.  ist binomialverteilt mit
ist binomialverteilt mit  . Die Bedingung an
. Die Bedingung an  lautet hier nun:
lautet hier nun:
 Diese Bedingung können wir nun in eine Bedingung an
Diese Bedingung können wir nun in eine Bedingung an  umformen und die Mindestanzahl an Tickets bestimmen:
umformen und die Mindestanzahl an Tickets bestimmen:
![\(\begin{array}[t]{rll}
P\left(X \geq 1\right) &\geq& 0,98 \\[5pt]
1- P\left(X \lt 1\right) &\geq& 0,98 \\[5pt]
1- P\left(X =0 \right) &\geq& 0,98 &\quad \mid\; -1\\[5pt]
- P\left(X =0 \right) &\geq& -0,02 &\quad \mid\; \cdot (-1)\\[5pt]
P\left(X =0 \right) &\leq& 0,02\\[5pt]
\binom{n}{0} \cdot \left(0,1\right)^0 \cdot \left(0,9\right)^n &\leq& 0,02\\[5pt]
\left(0,9\right)^n &\leq& 0,02&\quad \mid\; ln\\[5pt]
\ln\left(\left(0,9\right)^n\right) &\leq& \ln\left(0,02\right)\\[5pt]
n \cdot \ln\left(0,9\right) &\leq& \ln\left(0,02\right)&\quad\mid\; :\ln\left(0,9\right)\, \left(\lt 0\right)\\[5pt]
n &\geq& \dfrac{\ln\left(0,02\right)}{\ln\left(0,9\right)}\\[5pt]
&\approx& 37,13
\end{array}\)](https://mathjax.schullv.de/36a77c25c731ac8f006b5f76ece230bae46ac8d8487a907411f17537186e058f?color=5a5a5a) Da
Da  nur ganze Zahlen annehmen kann, ist die Mindestanzahl
nur ganze Zahlen annehmen kann, ist die Mindestanzahl  . Es müssen somit
. Es müssen somit  Tickets erworben werden, sodass mit einer Wahrscheinlichkeit von mindestens
Tickets erworben werden, sodass mit einer Wahrscheinlichkeit von mindestens  mindestens ein ermäßigtes Ticket erworben wird.
mindestens ein ermäßigtes Ticket erworben wird.
2ND  VARS(DISTR)
VARS(DISTR)  B: binomcdf
B: binomcdf
Du musst dann die entsprechenden Parameter 
1.
1.1

 -Koordinate des Punktes
-Koordinate des Punktes  berechnen
Der Punkt
berechnen
Der Punkt  ist der linke Befestigungspunkt des Tragseils und befindet sich somit auf der Funktion
ist der linke Befestigungspunkt des Tragseils und befindet sich somit auf der Funktion  . Setze also die
. Setze also die  -Koordinate des Punktes
-Koordinate des Punktes  in die Gleichung der Funktion
in die Gleichung der Funktion  ein, berechne also den Wert
ein, berechne also den Wert  .
.
 Die
Die  -Koordinate beträgt deshalb näherungsweise
-Koordinate beträgt deshalb näherungsweise  .
.
 Höhenunterschied berechnen
Der Höhenunterschied ist der Betrag der Differenz der
Höhenunterschied berechnen
Der Höhenunterschied ist der Betrag der Differenz der  -Koordinaten. Berechne also
-Koordinaten. Berechne also  . Dafür benötigst du die
. Dafür benötigst du die  -Koordinate des Punktes
-Koordinate des Punktes  , die du analog zur ersten Teilaufgabe berechnen kannst.
, die du analog zur ersten Teilaufgabe berechnen kannst.
 Damit kannst du nun den Höhenunterschied berechnen:
Damit kannst du nun den Höhenunterschied berechnen:
 Die Differenz der beiden
Die Differenz der beiden  -Werte beträgt ca.
-Werte beträgt ca.  .
.  Längeneinheit entspricht
Längeneinheit entspricht  Metern, somit ist die Höhendifferenz etwa
Metern, somit ist die Höhendifferenz etwa  .
.
 Kleinste Höhe des Tragseils bestimmen
Deine Aufgabe ist es die kleinste Höhe des Tragseils zu bestimmen. Die Höhe des Tragseils über dem Meeresspiegel wird durch die Funktion
Kleinste Höhe des Tragseils bestimmen
Deine Aufgabe ist es die kleinste Höhe des Tragseils zu bestimmen. Die Höhe des Tragseils über dem Meeresspiegel wird durch die Funktion  beschrieben. Die geringste Höhe des Tragseils ist somit der Minimalwert der Funktion
beschrieben. Die geringste Höhe des Tragseils ist somit der Minimalwert der Funktion  im Intervall
im Intervall ![\(\left[-9;5,8\right]\)](https://mathjax.schullv.de/f69b5f53aa35b041b4e10233b636c58cb0c8fa111474847c5420bbe3b9ad448a?color=5a5a5a) . Bestimme also den Minimalwert der Funktion
. Bestimme also den Minimalwert der Funktion  . Diesen kannst du mit deinem GTR berechnen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
. Diesen kannst du mit deinem GTR berechnen.
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
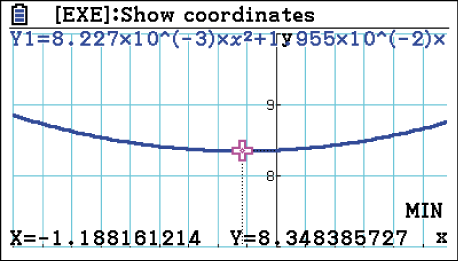 Die minimale Höhe des Tragseils ist somit ca.
Die minimale Höhe des Tragseils ist somit ca.  .
.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F3 (MIN)
F3 (MIN)
den Befehl zum Bestimmen des Minimums aus.

1.2
 Fahrzeit einer Kabine berechnen
Hier ist die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten gesucht. Dazu hast du die Durchschnittsgeschwindigkeit und einen Hinweis zur Berechnung der Länge des Graphen einer Funktion gegeben.
Fahrzeit einer Kabine berechnen
Hier ist die Fahrzeit einer Kabine zwischen den beiden Befestigungspunkten gesucht. Dazu hast du die Durchschnittsgeschwindigkeit und einen Hinweis zur Berechnung der Länge des Graphen einer Funktion gegeben.
Berechne zuerst die Länge des Tragseils, dann kannst du mit Hilfe der Durchschnittsgeschwindigkeit die Fahrzeit berechnen. 1. Schritt: Länge des Tragseils berechnen Der Verlauf des Tragseils wird durch die Funktion beschrieben, die Länge des Tragseils ist somit die Länge des Graphen der Funktion
beschrieben, die Länge des Tragseils ist somit die Länge des Graphen der Funktion  . Mit dem Hinweis kannst du die Länge
. Mit dem Hinweis kannst du die Länge  des Graphen von
des Graphen von  bestimmen. Die Länge
bestimmen. Die Länge  ist durch folgende Formel gegeben:
ist durch folgende Formel gegeben:
![\(\begin{array}[t]{rll}
l&=&\displaystyle\int_{-9}^{5,8}\left(\sqrt{1+\left(s‘(x)\right)^2}\right)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/8c1aee2b20b188447ca531695ec3aa4f0ec58b25083b86ab2cc4f80a5f3d1e54?color=5a5a5a) Definierst du dir die Funktion
Definierst du dir die Funktion  , so musst du das folgende Integral berechen:
, so musst du das folgende Integral berechen:
![\(\begin{array}[t]{rll}
l&=&\displaystyle\int_{-9}^{5,8}f(x)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/873b0a40705fb98740c3f2c18df609d7e39ac0eade9de0640ac94b7ef09afe31?color=5a5a5a) Berechne zuerst die erste Ableitung der Funktion
Berechne zuerst die erste Ableitung der Funktion  , um den Funktionsterm der Funktion
, um den Funktionsterm der Funktion  zu bestimmen:
zu bestimmen:
![\(\begin{array}[t]{rll}
s(x)&=&8,227 \cdot 10^{-3} \cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 8,360 \\[10pt]
s‘(x)&=&2 \cdot \left(8,227 \cdot 10^{-3} \cdot x \right)+ 1,955 \cdot 10^{-2} \\[5pt]
&=&16,454 \cdot 10^{-3} \cdot x + 1,955 \cdot 10^{-2} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/b36b3f3937d4d0659d0052eb0561bcaf5d3ae07f877397f0c25f71789c841e70?color=5a5a5a) Damit lautet die Funktionsgleichung von
Damit lautet die Funktionsgleichung von  folgendermaßen:
folgendermaßen:
 Das Integral kannst du nun mit deinem GTR berechnen. Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Das Integral kannst du nun mit deinem GTR berechnen. Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[-9;5,8\right]\)](https://mathjax.schullv.de/f69b5f53aa35b041b4e10233b636c58cb0c8fa111474847c5420bbe3b9ad448a?color=5a5a5a) .
.
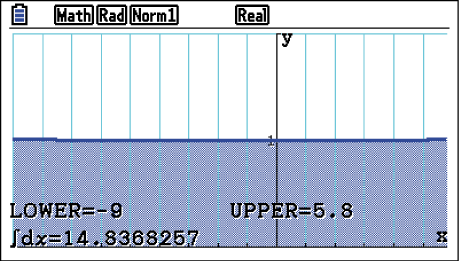 Das Tragseil hat somit ca. die Länge
Das Tragseil hat somit ca. die Länge  .
2. Schritt: Fahrzeit berechnen
Für Fahrzeit, Geschwindigkeit und Strecke gilt nun folgende Gleichung:
.
2. Schritt: Fahrzeit berechnen
Für Fahrzeit, Geschwindigkeit und Strecke gilt nun folgende Gleichung:
 Die zurückgelegte Strecke ist hier gerade die Länge
Die zurückgelegte Strecke ist hier gerade die Länge  , die Geschwindigkeit ist durch
, die Geschwindigkeit ist durch  gegeben. Nun kannst du die Gleichung nach der Fahrzeit umstellen und die Werte einsetzen:
gegeben. Nun kannst du die Gleichung nach der Fahrzeit umstellen und die Werte einsetzen:
![\(\begin{array}[t]{rll}
\text{Fahrzeit} \cdot \text{Geschwindigkeit}&=&\text{zurückgelegte Strecke} \quad \scriptsize \mid\; : \text{Geschwindigkeit}\\[5pt]
\text{Fahrzeit}&=& \dfrac{\text{zurückgelegte Strecke}}{ \text{Geschwindigkeit}} \\[5pt]
&=& \dfrac{1.483,7 \text{ m}}{7,5\,\dfrac{\text{m}}{\text{s}}}\\[5pt]
&\approx& 198 \text{ s}
\end{array}\)](https://mathjax.schullv.de/1f60000ede4d5985ad386c1a11e7161a7e73c9619be82aedadcf4a9e0ec7571f?color=5a5a5a) Damit ist die Fahrzeit einer Kabine zwischen den zwei Befestigungspunkten
Damit ist die Fahrzeit einer Kabine zwischen den zwei Befestigungspunkten  .
.
Berechne zuerst die Länge des Tragseils, dann kannst du mit Hilfe der Durchschnittsgeschwindigkeit die Fahrzeit berechnen. 1. Schritt: Länge des Tragseils berechnen Der Verlauf des Tragseils wird durch die Funktion
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F6
F6  F3 (
F3 ( dx)
dx)  F1 (
F1 ( dx)
dx)
das Integral über 
1.3
 Größte Höhe des Tragseils über der Profillinie bestimmen
Hier ist es deine Aufgabe die größte Höhe des Tragseils über der Profillinie zu bestimmen. Stelle dazu zuerst eine Funktion auf, die die Höhe des Tragseils über der Profillinie beschreibt, und berechne dann das Maximum dieser Funktion. Gehe also folgendermaßen vor:
Größte Höhe des Tragseils über der Profillinie bestimmen
Hier ist es deine Aufgabe die größte Höhe des Tragseils über der Profillinie zu bestimmen. Stelle dazu zuerst eine Funktion auf, die die Höhe des Tragseils über der Profillinie beschreibt, und berechne dann das Maximum dieser Funktion. Gehe also folgendermaßen vor:
 aufstellen
Die Höhe des Tragseils über der Profillinie ist gerade die Differenz der Höhe des Tragseils und der Höhe der Profillinie des Geländes. Die Höhe des Tragseils wird durch die Funktion
aufstellen
Die Höhe des Tragseils über der Profillinie ist gerade die Differenz der Höhe des Tragseils und der Höhe der Profillinie des Geländes. Die Höhe des Tragseils wird durch die Funktion  beschrieben, die Höhe der Profillinie des Geländes durch die Funktion
beschrieben, die Höhe der Profillinie des Geländes durch die Funktion  . Dementsprechend gilt für die Funktion
. Dementsprechend gilt für die Funktion  , die die Höhe des Tragseils über dem Gelände beschreibt:
, die die Höhe des Tragseils über dem Gelände beschreibt:
![\(\begin{array}[t]{rll}
d(x)&=& s(x) - g(x) \\[5pt]
&=& \left(8,227 \cdot 10^{-3} \cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 8,360\right) \\[5pt]
&&- \left(1,504 \cdot 10^{-3} \cdot x^3 + 3,125 \cdot 10^{-2} \cdot x^2 +7,300\right)\\[5pt]
&=& -1,504 \cdot 10^{-3} \cdot x^3 + \left(8,227 \cdot 10^{-3} - 3,125 \cdot 10^{-2} \right) \cdot x^2 \\[5pt]
&&+ 1,955 \cdot 10^{-2} \cdot x + \left(8,36-7,3\right) \\[5pt]
&=& -1,504 \cdot 10^{-3} \cdot x^3 - 2,302 \cdot 10^{-2}\cdot x^2 + 1,955 \cdot 10^{-2} \cdot x + 1,06
\end{array}\)](https://mathjax.schullv.de/f7b40c18fee63ed8ab9300772b9aca9c983410a42d1bc54d85835ef6a4bbd6e3?color=5a5a5a) 2. Schritt: Maximum der Funktion
2. Schritt: Maximum der Funktion  bestimmen
Nun musst du das Maximum der Funktion
bestimmen
Nun musst du das Maximum der Funktion  bestimmen. Dies kannst du mit deinem GTR.
Wechsle mit deinem GTR in das Graph-Menü und speichere dort den Funktionsterm von
bestimmen. Dies kannst du mit deinem GTR.
Wechsle mit deinem GTR in das Graph-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
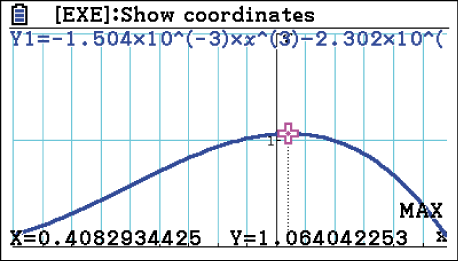 Die maximale Höhe des Tragseils über der Profillinie des Geländes ist somit ca.
Die maximale Höhe des Tragseils über der Profillinie des Geländes ist somit ca.  .
.
 Zeigen, dass Mindesthöhe erfüllt ist
Nun sollst du zeigen, dass die Höhe zwischen dem Tragseil und dem Gelände an den Befestigungspunkten mindestens
Zeigen, dass Mindesthöhe erfüllt ist
Nun sollst du zeigen, dass die Höhe zwischen dem Tragseil und dem Gelände an den Befestigungspunkten mindestens  ist. Berechne dazu die Höhen an den Stellen
ist. Berechne dazu die Höhen an den Stellen  und
und  mit der Funktion
mit der Funktion  und überprüfe die Bedingung.
und überprüfe die Bedingung.
 Befestigungspunkt
Befestigungspunkt  :
Berechne den Funktionswert
:
Berechne den Funktionswert  :
:
 Die Höhendifferenz beträgt an der Stelle
Die Höhendifferenz beträgt an der Stelle  ca.
ca.  und erfüllt somit die Bedingung.
und erfüllt somit die Bedingung.
 Befestigungspunkt
Befestigungspunkt  :
Berechne den Funktionswert
:
Berechne den Funktionswert  :
:
 Die Höhendifferenz beträgt an der Stelle
Die Höhendifferenz beträgt an der Stelle  ca.
ca.  und erfüllt somit die Bedingung.
und erfüllt somit die Bedingung.
- Stelle die Funktion
auf, die die Höhe des Tragseils über der Profillinie beschreibt.
- Berechne das Maximum der Funktion
im Intervall
.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F2 (MAX)
F2 (MAX)
den Befehl zum Bestimmen des Maximums aus.

1.4
 Schwierigkeitsgrad der Skipiste bestimmen
Hier sollst du den Schwierigkeitsgrad der beschriebenen Skipiste bestimmen. Eine Skipiste wird nach ihrem maximalen Gefälle bewertet. Berechne also das maximale Gefälle der Skipiste.
Schwierigkeitsgrad der Skipiste bestimmen
Hier sollst du den Schwierigkeitsgrad der beschriebenen Skipiste bestimmen. Eine Skipiste wird nach ihrem maximalen Gefälle bewertet. Berechne also das maximale Gefälle der Skipiste.
Die Skipiste wird durch die Funktion auf dem Intervall
auf dem Intervall ![\(\left[-9;0\right]\)](https://mathjax.schullv.de/cbbf6c098e50c918532c32a5e832d2cc3b2655a1b8208066b1695f2b76e3003c?color=5a5a5a) beschrieben. Das Gefälle der Skipiste ist dementsprechend die Steigung der Funktion
beschrieben. Das Gefälle der Skipiste ist dementsprechend die Steigung der Funktion  , die durch die erste Ableitung
, die durch die erste Ableitung  beschrieben wird. Um das maximale Gefälle zu bestimmen, musst du somit die betragsmäßig größte negative Steigung der Funktion
beschrieben wird. Um das maximale Gefälle zu bestimmen, musst du somit die betragsmäßig größte negative Steigung der Funktion  , also das Minimum der Funktion
, also das Minimum der Funktion  auf dem Intervall
auf dem Intervall ![\(\left[-9;0\right]\)](https://mathjax.schullv.de/cbbf6c098e50c918532c32a5e832d2cc3b2655a1b8208066b1695f2b76e3003c?color=5a5a5a) bestimmen. Hast du dieses gegeben, so kannst du die Schwierigkeit der Skipiste bewerten.
Gehe also folgendermaßen vor:
bestimmen. Hast du dieses gegeben, so kannst du die Schwierigkeit der Skipiste bewerten.
Gehe also folgendermaßen vor:
 bestimmen
Leite hierzu die Funktion
bestimmen
Leite hierzu die Funktion  ab:
ab:
![\(\begin{array}[t]{rll}
g(x)&=&1,504 \cdot 10^{-3} \cdot x^3 + 3,125 \cdot 10^{-2}\cdot x^2 + 7,3 \\[10pt]
g‘(x)&=&3 \cdot \left(1,504 \cdot 10^{-3} \cdot x^2\right) + 2 \cdot \left(3,125 \cdot 10^{-2}\cdot x\right) \\[5pt]
&=&4,512 \cdot 10^{-3} \cdot x^2 + 6,25 \cdot 10^{-2}\cdot x
\end{array}\)](https://mathjax.schullv.de/f963b98de49e4b375ed406be2c5a22d5f94b1e2bcb77660ced328af428eebf07?color=5a5a5a) 2. Schritt: Minimum von
2. Schritt: Minimum von  bestimmen
Bestimme nun den Minimalwert der Funktion
bestimmen
Bestimme nun den Minimalwert der Funktion  . Dies kannst du mit deinem GTR wie bereits in 1.1. Du erhältst:
. Dies kannst du mit deinem GTR wie bereits in 1.1. Du erhältst:
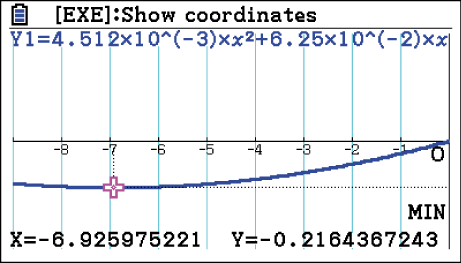 Der Minimalwert der Funktion
Der Minimalwert der Funktion  ist somit ca.
ist somit ca.  . Das maximale Gefälle der Skipiste ist somit ca.
. Das maximale Gefälle der Skipiste ist somit ca.  .
3. Schritt: Schwierigkeitsgrad der Skipiste bestimmen
Das Gefälle der Skipiste beträgt
.
3. Schritt: Schwierigkeitsgrad der Skipiste bestimmen
Das Gefälle der Skipiste beträgt  . Es gilt:
. Es gilt:  . Somit handelt es sich bei der Skipiste um eine blaue Piste.
. Somit handelt es sich bei der Skipiste um eine blaue Piste.
Die Skipiste wird durch die Funktion
- Bestimme die erste Ableitung
.
- Bestimme das Minimum von
.
- Bestimme den Schwierigkeitsgrad der Skipiste.

1.5
 Untersuchen, ob die Profillinie den Blick behindert
Deine Aufgabe ist es zu untersuchen ob die Profillinie des Geländes den Blick vom Endpunkt
Untersuchen, ob die Profillinie den Blick behindert
Deine Aufgabe ist es zu untersuchen ob die Profillinie des Geländes den Blick vom Endpunkt  der Skipiste zum linken Befestigungspunkt
der Skipiste zum linken Befestigungspunkt  des Tragseils behindert. Den Blick vom Punkt
des Tragseils behindert. Den Blick vom Punkt  zum Punkt
zum Punkt  kannst du mit der Gerade
kannst du mit der Gerade  durch die Punkte
durch die Punkte  und
und  beschreiben. Der Blick wird nun von der Profillinie behindert, wenn sich die Gerade
beschreiben. Der Blick wird nun von der Profillinie behindert, wenn sich die Gerade  und die Funktion
und die Funktion  im Intervall
im Intervall  , also dem Bereich zwischen den Punkten
, also dem Bereich zwischen den Punkten  und
und  , schneiden.
Gehe also folgendermaßen vor:
, schneiden.
Gehe also folgendermaßen vor:
 bestimmen
Die allgemeine Form einer Gerade lautet:
bestimmen
Die allgemeine Form einer Gerade lautet:  . Setze also die beiden gegebenen Punkte
. Setze also die beiden gegebenen Punkte  und
und  ein und du erhältst ein lineares Gleichungssystem. Berechne dazu zuerst die
ein und du erhältst ein lineares Gleichungssystem. Berechne dazu zuerst die  -Koordinate des Punktes
-Koordinate des Punktes  :
:
 Damit erhältst du folgendes LGS:
Damit erhältst du folgendes LGS:
 Es gilt somit
Es gilt somit  und
und  . Die Gerade
. Die Gerade  ist damit durch folgende Geradengleichung gegeben:
ist damit durch folgende Geradengleichung gegeben:
 2. Schritt:
2. Schritt:  und
und  auf Schnittpunke überprüfen
Überprüfe nun mit deinem GTR, ob die Funktion
auf Schnittpunke überprüfen
Überprüfe nun mit deinem GTR, ob die Funktion  und die Gerade
und die Gerade  einen Schnittpunkt im Intervall
einen Schnittpunkt im Intervall  besitzen.
Wechsle mit deinem GTR in das Graph-Menü und speichere dort die Funktionsterme von
besitzen.
Wechsle mit deinem GTR in das Graph-Menü und speichere dort die Funktionsterme von  und
und  . Hast du diese dort gespeichert, gib unter
. Hast du diese dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir die zugehörigen Graphen über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir die zugehörigen Graphen über DRAW anzeigen.
Wähle dann unter
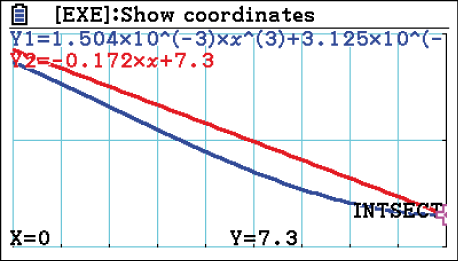 Der einzige Schnittpunkt ist
Der einzige Schnittpunkt ist  und somit außerhalb des Intervalls
und somit außerhalb des Intervalls  . Insgesamt existieren somit keine Schnittstellen im Intervall
. Insgesamt existieren somit keine Schnittstellen im Intervall  und damit ist der Blick nicht behindert.
und damit ist der Blick nicht behindert.
- Bestimme die Gerade
durch die Punkte
und
.
- Überprüfe, ob die Gerade
und die Funktion
sich im Intervall
schneiden.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F5 (INTSECT)
F5 (INTSECT)
den Befehl zum Bestimmen der Schnittpunkte aus.

1.6
 Wahrscheinlichkeit für Seilbahnnutzung bestimmen
Zuerst sollst du die Wahrscheinlichkeit berechnen, dass ein zufällig ausgewählter Wintertourist des Skigebiets alpinen Skisport betreibt und diese Kabinenseilbahn benutzt, also die Wahrscheinlichkeit:
Wahrscheinlichkeit für Seilbahnnutzung bestimmen
Zuerst sollst du die Wahrscheinlichkeit berechnen, dass ein zufällig ausgewählter Wintertourist des Skigebiets alpinen Skisport betreibt und diese Kabinenseilbahn benutzt, also die Wahrscheinlichkeit:
 .
Dir ist zum einen gegeben, dass
.
Dir ist zum einen gegeben, dass  der Wintertouristen alpinen Skisport betreiben, zum anderen ist dir gegeben, dass
der Wintertouristen alpinen Skisport betreiben, zum anderen ist dir gegeben, dass  der Touristen, die alpinen Skisport betreiben, die Seilbahn benutzen:
der Touristen, die alpinen Skisport betreiben, die Seilbahn benutzen:
 ,
,
 .
Nun kannst du mit der Pfadmultiplikationsregel die gesuchte Wahrscheinlichkeit berechnen:
.
Nun kannst du mit der Pfadmultiplikationsregel die gesuchte Wahrscheinlichkeit berechnen:
![\(\begin{array}{rll}
P\left(\text{„Seilbahnnutzung und Skisport“}\right) &=& P\left(\text{„Skisport“}\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„Skisport“}\right) \\[5pt]
&=& 0,72 \cdot 0,95 = 0,684 =68,4\,\%
\end{array}\)](https://mathjax.schullv.de/0398a98f2760384fa4db038e9284c12e3b16272e9e3d06481841dccfdd58fab2?color=5a5a5a) Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Wintertourist alpinen Skisport betreibt und die Seilbahn benutzt, liegt bei
Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Wintertourist alpinen Skisport betreibt und die Seilbahn benutzt, liegt bei  .
.
 Erwartete Seilbahnnutzer bestimmen
Hier ist nach der Anzahl Touristen gefragt, die unter
Erwartete Seilbahnnutzer bestimmen
Hier ist nach der Anzahl Touristen gefragt, die unter  Wintertouristen erfahrungsgemäß die Seilbahn benutzen. Berechne dazu mit den dir gegebenen Wahrscheinlichkeiten die Wahrscheinlichkeit, dass ein zufällig ausgewählter Tourist die Seilbahn benutzt. Damit kannst du dann die erwarteten Besucher ausrechnen. Es ist also zuerst nach folgender Wahrscheinlichkeit gesucht:
Wintertouristen erfahrungsgemäß die Seilbahn benutzen. Berechne dazu mit den dir gegebenen Wahrscheinlichkeiten die Wahrscheinlichkeit, dass ein zufällig ausgewählter Tourist die Seilbahn benutzt. Damit kannst du dann die erwarteten Besucher ausrechnen. Es ist also zuerst nach folgender Wahrscheinlichkeit gesucht:
 .
Diese ist dir nicht direkt gegeben und du musst sie mit Hilfe der angegebenen Wahrscheinlichkeiten berechnen. Dir sind jeweils die Wahrscheinlichkeiten gegeben, dass ein Tourist der Skisport betreibt oder kein Skisport betreibt mit der Seilbahn fährt. Da die Touristen entweder Skisport betreiben oder nicht, kannst du mit den jeweils bedingten Wahrscheinlichkeiten die Wahrscheinlichkeit der Seilbahnnutzung bestimmen:
.
Diese ist dir nicht direkt gegeben und du musst sie mit Hilfe der angegebenen Wahrscheinlichkeiten berechnen. Dir sind jeweils die Wahrscheinlichkeiten gegeben, dass ein Tourist der Skisport betreibt oder kein Skisport betreibt mit der Seilbahn fährt. Da die Touristen entweder Skisport betreiben oder nicht, kannst du mit den jeweils bedingten Wahrscheinlichkeiten die Wahrscheinlichkeit der Seilbahnnutzung bestimmen:
![\(\begin{array}{rll}
&&P\left(\text{„Seilbahnnutzung“}\right)\\[5pt]
&=&P\left(\text{„Seilbahnnutzung und Skisport“}\right) + P\left(\text{„Seilbahnnutzung und kein Skisport“}\right)
\end{array}\)](https://mathjax.schullv.de/b91d69e348b54bcec76cb3e7f23a5f8e3a3641943d9f63d5470468424703702c?color=5a5a5a) Die erste Wahrscheinlichkeit hast du bereits berechnet. Die zweite kannst du genauso mit der Pfadmultiplikationsregel und dem Gegenereignis bestimmen:
Die erste Wahrscheinlichkeit hast du bereits berechnet. Die zweite kannst du genauso mit der Pfadmultiplikationsregel und dem Gegenereignis bestimmen:
![\(\begin{array}{rll}
&&P\left(\text{„Seilbahnnutzung und kein Skisport“}\right) \\[5pt]
&=& P\left(\text{„kein Skisport“}\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„kein Skisport“}\right) \\[5pt]
&=& \left(1- P\left(\text{„Skisport“}\right)\right) \cdot P\left(\text{„Seilbahnnutzung“} \mid \text{„kein Skisport“}\right) \\[5pt]
&=& \left(1- 0,72\right) \cdot 0,50 = 0,28 \cdot 0,5 = 0,14 =14\,\%
\end{array}\)](https://mathjax.schullv.de/8403b2f4185d62ac0dc24ab388c120a55ab67040bdf4b59b12e353babef5b9a3?color=5a5a5a) Also gilt für die Wahrscheinlichkeit der Seilbahnnutzung:
Also gilt für die Wahrscheinlichkeit der Seilbahnnutzung:
 Multipliziere diese Wahrscheinlichkeit mit
Multipliziere diese Wahrscheinlichkeit mit  , um die erwartete Anzahl an Seilbahnnutzern zu bestimmen:
, um die erwartete Anzahl an Seilbahnnutzern zu bestimmen:
 Damit benutzen erfahrungsgemäß
Damit benutzen erfahrungsgemäß  von
von  Wintertouristen die Kabinenseilbahn.
Wintertouristen die Kabinenseilbahn.
1.7
 Wahrscheinlichkeit für Tickets bestimmen
Berechne hier die Wahrscheinlichkeit, dass von
Wahrscheinlichkeit für Tickets bestimmen
Berechne hier die Wahrscheinlichkeit, dass von  erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Definiere die Zufallsvariable
erworbenen Tickets mehr als drei Tickets ermäßigt sind.
Definiere die Zufallsvariable  , die die Anzahl an erworbenen ermäßigten Tickets unter
, die die Anzahl an erworbenen ermäßigten Tickets unter  erworbenen Tickets beschreibt. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „ermäßigt“ und „nicht ermäßigt“ gibt und mit einem Anteil von
erworbenen Tickets beschreibt. Diese Zufallsvariable ist binomialverteilt, da es nur die Möglichkeiten „ermäßigt“ und „nicht ermäßigt“ gibt und mit einem Anteil von  ermäßigte Tickets erworben werden. Es gilt dementsprechend
ermäßigte Tickets erworben werden. Es gilt dementsprechend  .
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
.
Die gesuchte Wahrscheinlichkeit kannst du nun formulieren als
 .
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Du kannst den binomcdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
.
Wahrscheinlichkeiten dieser Form kannst du mit deinem GTR berechnen. Du kannst den binomcdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
 ,
,  und
und  eingeben:
eingeben:
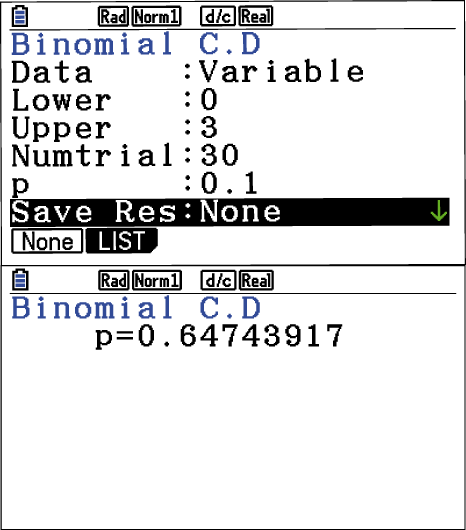 Du erhältst dann das Ergebnis
Du erhältst dann das Ergebnis  . Für die gesuchte Wahrscheinlichkeit gilt somit:
. Für die gesuchte Wahrscheinlichkeit gilt somit:
 .
Die Wahrscheinlichkeit, dass von
.
Die Wahrscheinlichkeit, dass von  erworbenen Tickets mehr als drei Tickets ermäßigt sind, liegt bei ca.
erworbenen Tickets mehr als drei Tickets ermäßigt sind, liegt bei ca.  .
.
 Mindestanzahl an Tickets bestimmen
Betrachte hier wieder die Zufallsvariable
Mindestanzahl an Tickets bestimmen
Betrachte hier wieder die Zufallsvariable  , die die Anzahl an erworbenen ermäßigten Tickets unter der gesuchten Anzahl von
, die die Anzahl an erworbenen ermäßigten Tickets unter der gesuchten Anzahl von  erworbenen Tickets beschreibt.
erworbenen Tickets beschreibt.  ist binomialverteilt mit
ist binomialverteilt mit  . Die Bedingung an
. Die Bedingung an  lautet hier nun:
lautet hier nun:
 Diese Bedingung können wir nun in eine Bedingung an
Diese Bedingung können wir nun in eine Bedingung an  umformen und die Mindestanzahl an Tickets bestimmen:
umformen und die Mindestanzahl an Tickets bestimmen:
![\(\begin{array}[t]{rll}
P\left(X \geq 1\right) &\geq& 0,98 \\[5pt]
1- P\left(X \lt 1\right) &\geq& 0,98 \\[5pt]
1- P\left(X =0 \right) &\geq& 0,98 &\quad \mid\; -1\\[5pt]
- P\left(X =0 \right) &\geq& -0,02 &\quad \mid\; \cdot (-1)\\[5pt]
P\left(X =0 \right) &\leq& 0,02\\[5pt]
\binom{n}{0} \cdot \left(0,1\right)^0 \cdot \left(0,9\right)^n &\leq& 0,02\\[5pt]
\left(0,9\right)^n &\leq& 0,02&\quad \mid\; ln\\[5pt]
\ln\left(\left(0,9\right)^n\right) &\leq& \ln\left(0,02\right)\\[5pt]
n \cdot \ln\left(0,9\right) &\leq& \ln\left(0,02\right)&\quad\mid\; :\ln\left(0,9\right)\, \left(\lt 0\right)\\[5pt]
n &\geq& \dfrac{\ln\left(0,02\right)}{\ln\left(0,9\right)}\\[5pt]
&\approx& 37,13
\end{array}\)](https://mathjax.schullv.de/36a77c25c731ac8f006b5f76ece230bae46ac8d8487a907411f17537186e058f?color=5a5a5a) Da
Da  nur ganze Zahlen annehmen kann, ist die Mindestanzahl
nur ganze Zahlen annehmen kann, ist die Mindestanzahl  . Es müssen somit
. Es müssen somit  Tickets erworben werden, sodass mit einer Wahrscheinlichkeit von mindestens
Tickets erworben werden, sodass mit einer Wahrscheinlichkeit von mindestens  mindestens ein ermäßigtes Ticket erworben wird.
mindestens ein ermäßigtes Ticket erworben wird.
F5: DIST  F5: BINOMIAL
F5: BINOMIAL  F2: Bcd
F2: Bcd  F2: Var
F2: Var
Du musst dann die entsprechenden Parameter 