Wahlbereich

Aufgabe W1

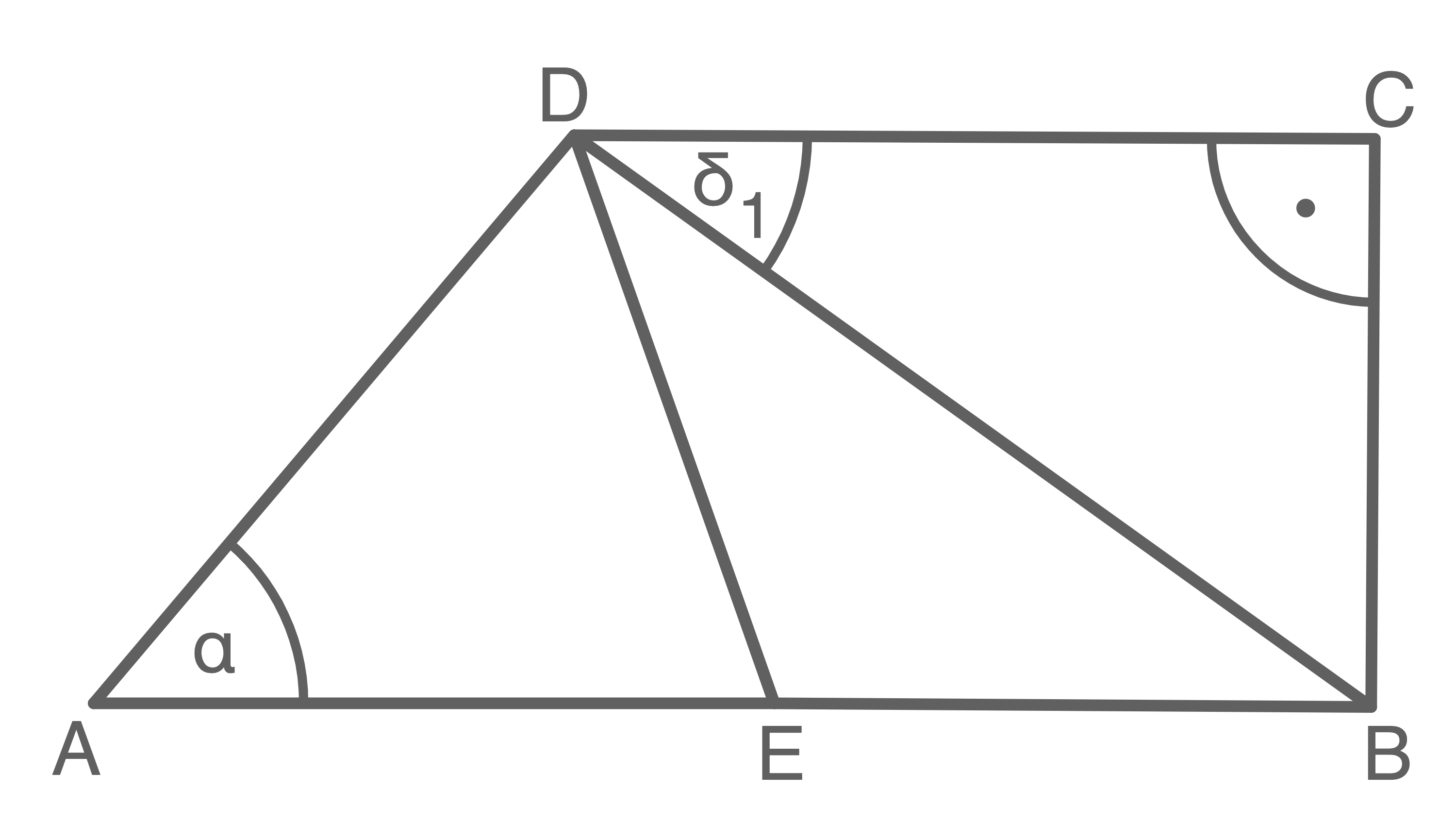
Geometrische Darstellung eines Dreiecks und Rechtecks mit beschrifteten Winkeln.

Im Trapez $ABCD$ gilt:

$\overline{AD}=8,4\,\text{cm}$

$\overline{AE}=7,8\,\text{cm}$

$\quad \alpha=50,0^{\circ}$

$\overline{BE}=\overline{DE}$

Berechne den Winkel $\delta_1$ .
Berechne den Flächeninhalt des Dreiecks $EBD$ .

5,5 P

Von einem rechteckigen Blatt Papier wird entlang der gestrichelten Linie ein Stück abgeschnitten und an einer anderen Stelle angelegt (siehe Skizze).

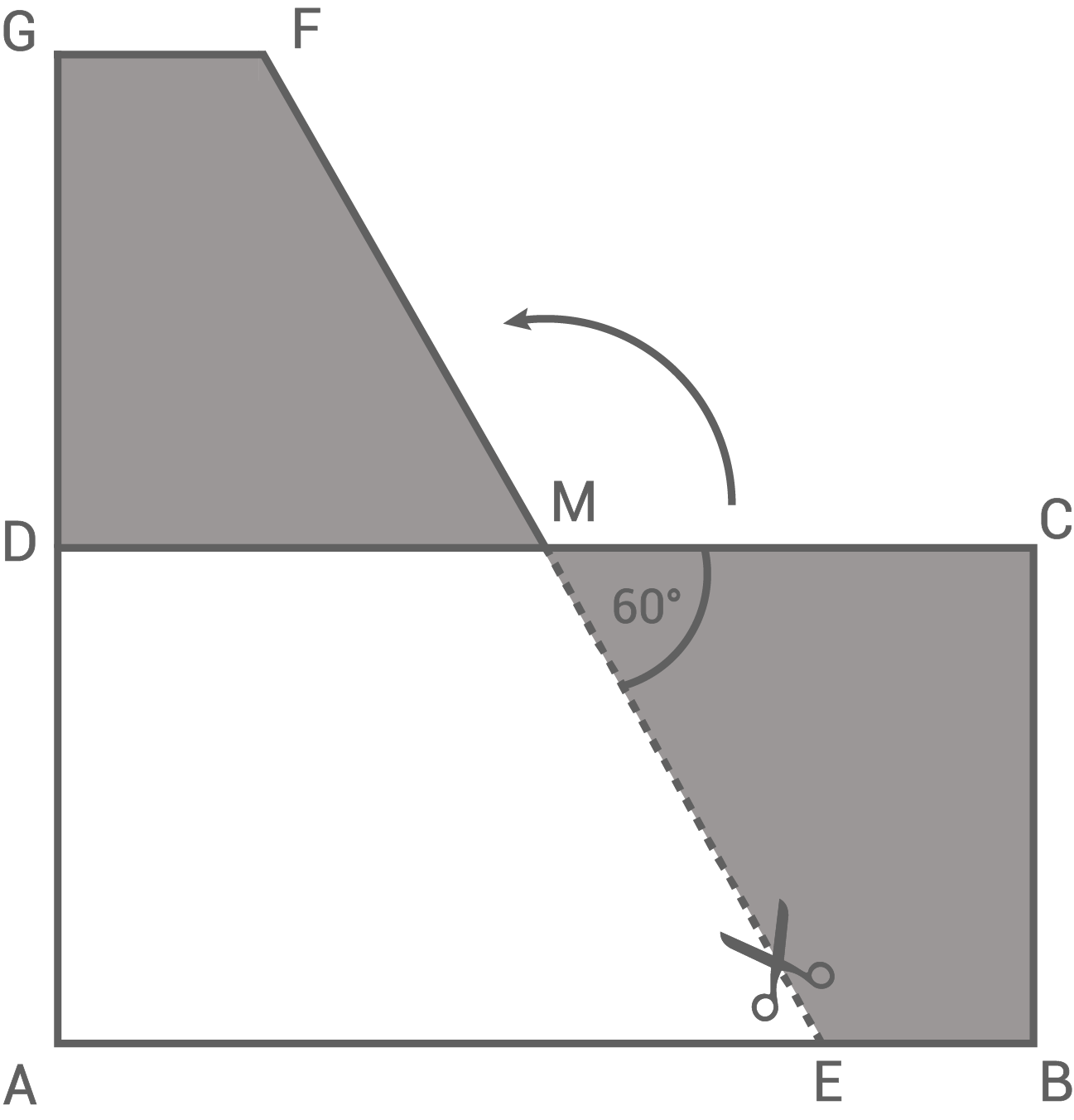Diagramm eines geometrischen Problems mit einem Winkel von 60° und einer gestrichelten Linie.

Es gilt:
$\overline{AB}=6\mathrm{e}$
$\overline{BC}=3\mathrm{e}$
$M$ ist Mittelpunkt von $\overline{CD}.$

Bea behauptet:
„Das Viereck $AEFG$ hat den gleichen Umfang wie das Rechteck $ABCD$ “.

Hat Bea recht?
Begründe deine Aussage rechnerisch oder durch Argumentation.

4,5 P

Aufgabe W2

Gegeben sind zwei Dreiviertelkreise.

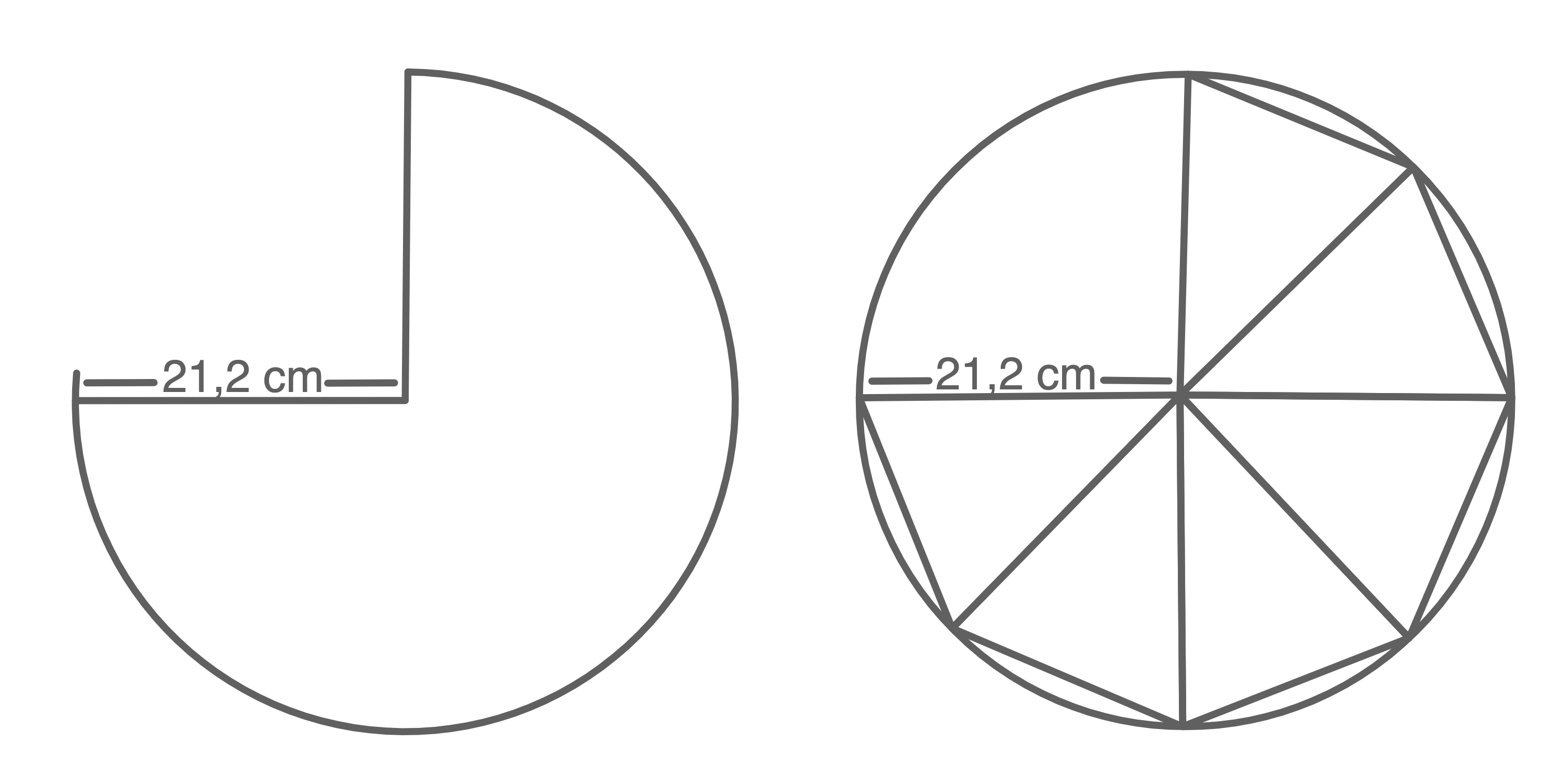Zwei geometrische Formen mit einer Seitenlänge von 21,2 cm: ein Viertelkreis und ein Kreis mit unterteilten Segmenten.

Aus ihnen werden der Mantel eines Kegels und der Mantel einer regelmäßigen sechsseitigen Pyramide gefertigt.

Berechne die Differenz der beiden Körperhöhen.

5,5 P

Ein zusammengesetzter Körper besteht aus einem gleichschenkligen Dreiecksprisma und einem halben Kegel (siehe Skizze).

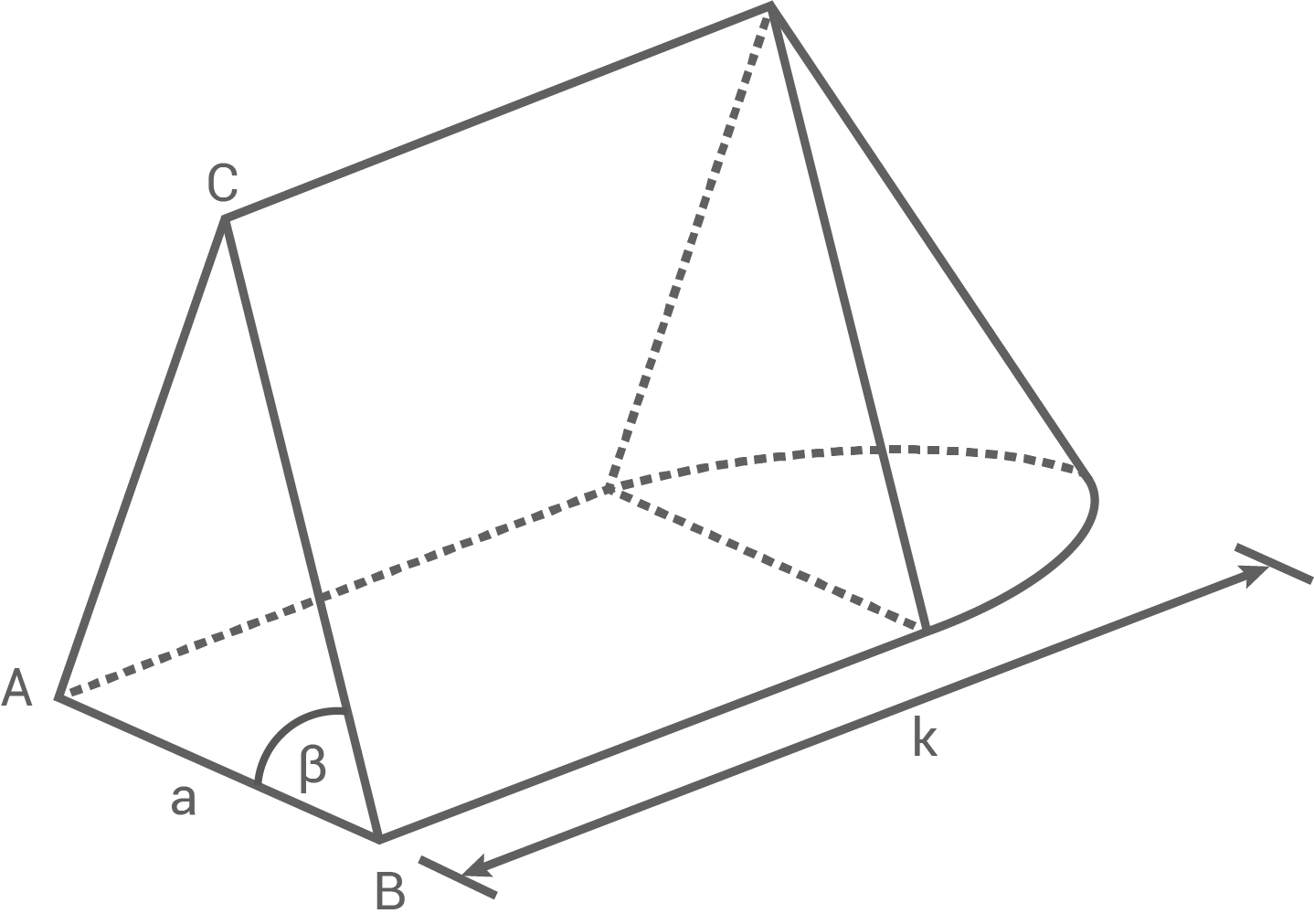Diagramm eines geometrischen Körpers mit Linien und Winkeln, beschriftet mit Buchstaben und Symbolen.

Es gilt:
$\begin{array}[t]{rll} \overline{AC}&=& \overline{BC}\\[5pt] \overline{AB}&=& 11,4 \,\text{cm} \\[5pt] \beta&=& 62,0 ^{\circ} \\[5pt] V_{\,\text{ges}}&=& 1 \,280 \,\text{cm}^3 \\[5pt] \end{array}$
(Volumen des zusammengesetzten Körpers)

Berechne die Gesamtlänge $k$ des zusammengesetzten Körpers.

4,5 P

Aufgabe W3

Zu einer verschobenen nach oben geöffneten Normalparabel $p$ gehört die unvollständig ausgefüllte Wertetabelle.

$x$	0	1	2	3	4	5
$y$	11	6			3

Gib die Gleichung der Parabel $p$ an.

Vervollständige die Wertetabelle.

Eine Gerade $g$ hat die Steigung $m=-1$ und geht durch den Punkt $P(-2,5\mid 6)$ .
Weise rechnerisch nach, dass $p$ und $g$ keine gemeinsamen Punkte haben.

Eine Gerade $h$ verläuft parallel zur Geraden $g$ und geht durch den Scheitelpunkt von $p$ .
Berechne die Koordinaten des Schnittpunktes $R$ der Geraden $h$ mit der $x$ -Achse.

5,5 P

Eine Parabel $p_1$ der Form $y=ax^2+c$ mit dem Scheitelpunkt $S_1(0\mid 4,5)$ schneidet die $x$ -Achse in den Punkten $N_1(-3\mid 0)$ und $N_2(3\mid 0)$ .

Eine nach oben geöffnete Normalparabel $p_2$ hat den Scheitelpunkt $S_2(3\mid 1,5)$ .

Die beiden Parabeln haben einen gemeinsamen Punkt $T$ .
Berechne die Koordinaten von $T$ .

Die Punkte $N_1$ , $N_2$ und $T$ bilden ein Dreieck.
Berechne den Flächeninhalt des Dreiecks $N_1N_2T$ .

Der Punkt $T$ bewegt sich auf der Parabel $p_1$ oberhalb der $x$ -Achse.
Für welche Lage von $T$ wird der Flächeninhalt des Dreiecks $N_1N_2T$ am größten?
Begründe deine Aussage rechnerisch oder durch Argumentation.

4,5 P

Aufgabe W4

In einem Kartenstapel liegen zwölf Karten. Die Verteilung ist in der Tabelle dargestellt.

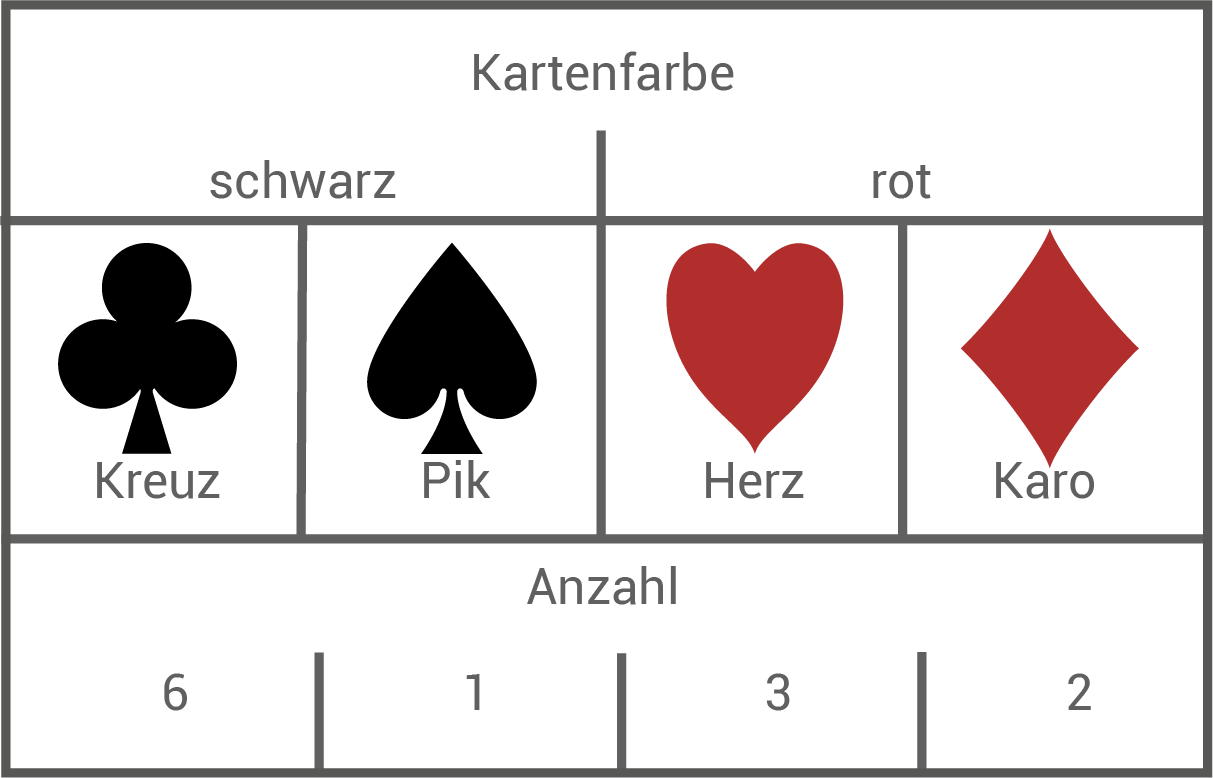Tabelle mit Kartensymbolen und deren Häufigkeit in schwarz und rot.

Die Karten werden gemischt und verdeckt auf den Tisch gelegt. Zwei Karten werden gleichzeitig gezogen.

Wie groß ist die Wahrscheinlichkeit, eine rote und eine schwarze Karte zu erhalten?

Die zwölf Karten werden für ein Glücksspiel eingesetzt. Es sollen ebenfalls zwei Karten gleichzeitig gezogen werden.

Dazu wird nebenstehender Gewinnplan geprüft.

Ergebnisse	Gewinn
zweimal Karo	$10,00\,€$
zweimal Herz	$5,00\,€$
sonstige	kein Gewinn
Einsatz pro Spiel: $1,00\,€$

Berechne den Erwartungswert.

Sophia macht den Vorschlag, den Gewinn für „zweimal Karo“ auf $20,00\,€$ hochzusetzen und alles andere zu belassen.
Der Betreiber des Glücksspiels protestiert und behauptet, er würde dann Verlust machen.

Hat der Betreiber recht? Begründe durch Rechnung.

5,5 P

David und Tim messen sich im Kugelstoßen. Beim Stoß von David verlässt die Kugel seine Hand in einer Höhe von $2,20\,\text{m}$ (siehe Skizze).

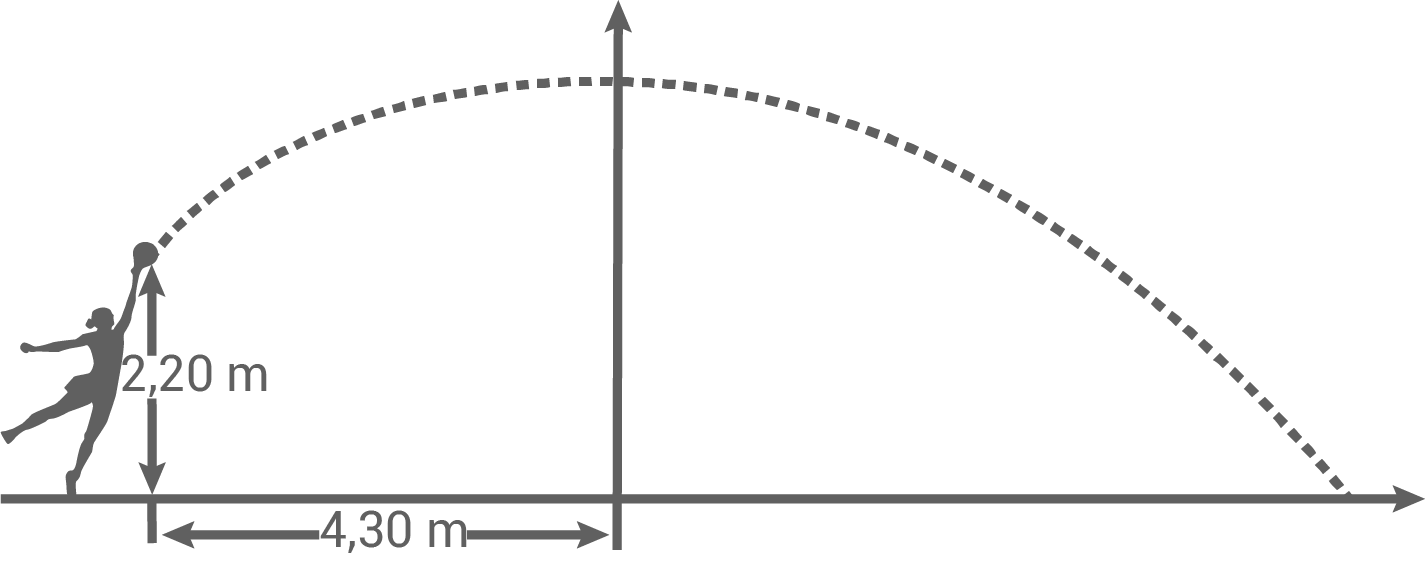Diagramm einer Wurfbewegung mit Höhen- und Distanzangaben.

Nach einer horizontalen Entfernung von $4,30\,\text{m}$ hat die Kugel ihre maximale Höhe von $3,90\,\text{m}$ erreicht.
Die Flugbahn der Kugel lässt sich annähernd durch eine Parabel mit der Funktionsgleichung $y=ax^2+c$ beschreiben.

Welche Weite hat David erzielt?

Tim stößt die Kugel ebenfalls aus dem Stoßkreis. Die Kugel verlässt seine Hand in einer Höhe von $1,90\,\text{m}$ .

Die Parabelgleichung für diesen Stoß lautet: $y=-\dfrac{1}{10}x^2+3,5$ .

Vergleiche die beiden Kugelstoßweiten.

4,5 P

Lösung W1

Größe des Winkels $\boldsymbol{\delta_1}$ berechnen

1. Schritt: Länge der Strecke $\boldsymbol{\overline{DR}}$ berechnen

$\begin{array}[t]{rll} \sin(\alpha)&=&\dfrac{\overline{DR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt] \overline{DR} &=& \sin(\alpha)\cdot \overline{AD} &\quad \scriptsize \\[5pt] \overline{DR} &=& \sin(50^{\circ}) \cdot 8,4 \,\text{cm} &\quad \scriptsize \\[5pt] \overline{DR} &=& \underline{ 6,43 \,\text{cm}} \end{array}$

2. Schritt: Länge der Strecke $\boldsymbol{\overline{AR}}$ berechnen

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\overline{AR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt] \overline{AR} &=& \cos(\alpha) \cdot \overline{AD} &\quad \scriptsize \\[5pt] \overline{AR} &=& \cos(50^{\circ}) \cdot 8,4\,\text{cm} &\quad \scriptsize \\[5pt] \overline{AR} &= & \underline{ 5,40\,\text{cm}} \end{array}$

3. Schritt: Länge der Strecke $\boldsymbol{\overline{ER}}$ berechnen

$\begin{array}[t]{rll} \overline{ER}&=&\overline{AE}-\overline{AR} &\quad \scriptsize \\[5pt] \overline{ER}&=& 7,8\,\text{cm}- 5,40\,\text{cm} &\quad \scriptsize \\[5pt] \overline{ER}&=& \underline{ 2,40 \,\text{cm}} \end{array}$

4. Schritt: Größe des Winkels $\boldsymbol{\beta}$ berechnen

$\begin{array}[t]{rll} \tan(\beta)&=&\dfrac{\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt] \tan(\beta)&=&\dfrac{2,4\,\text{cm}}{6,43\,\text{cm} } \quad \scriptsize \mid\; \tan^{-1}\\[5pt] \beta&=& \underline{ 20,5^{\circ}} \end{array}$

5. Schritt: Länge der Strecke $\boldsymbol{\overline{DE}}$ berechnen

$\begin{array}[t]{rll} \sin(\beta)&=& \dfrac{\overline{ER}}{\overline{DE}}\quad \scriptsize \mid\; \cdot \overline{DE} \\[5pt] \sin(\beta)\cdot \overline{DE}&=& \overline{ER}\quad \scriptsize \mid\; : \sin(\beta) \\[5pt] \overline{DE}&=&\dfrac{\overline{ER}}{\sin(\beta)} &\quad \scriptsize \\[5pt] \overline{DE}&=&\dfrac{2,4\,\text{cm}}{\sin(20,5^{\circ} )} &\quad \scriptsize \\[5pt] \overline{DE}&=& \underline{ 6,85\,\text{cm}} \end{array}$

6. Schritt: Größe des Winkels $\boldsymbol{\delta_2}$ berechnen

$\begin{array}[t]{rll} \tan(\delta_2)&=&\dfrac{\overline{BR}}{\overline{DR}} &\quad \scriptsize \\[5pt] \tan(\delta_2)&=&\dfrac{\overline{BE}+\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt] \tan(\delta_2)&=& \dfrac{6,85\,\text{cm}+2,4\,\text{cm}}{6,43\,\text{cm}}\quad \scriptsize \mid\; \tan^{-1}\\[5pt] \delta_2&=& \underline{ 55,2^{\circ}} \end{array}$

7. Schritt: Größe des Winkels $\boldsymbol{\delta_1}$ berechnen

$\begin{array}[t]{rll} \delta_1&=&90^{\circ}-\delta_2 &\quad \scriptsize \\[5pt] &=&90^{\circ}- 55,2^{\circ} &\quad \scriptsize \\[5pt] \delta_1 &=& \underline{\underline{ 34,8^{\circ}}} \end{array}$

Flächeninhalt des Dreiecks $\boldsymbol{EBD}$ berechnen

wahlbereich trapez dreieck flaecheninhalt

$\begin{array}[t]{rll} A_{\,\text{EBD}}&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt] &=&\dfrac{1}{2}\cdot \overline{EB}\cdot \overline{DR} &\quad \scriptsize \\[5pt] &=&\dfrac{1}{2}\cdot 6,86 \,\text{cm}\cdot 6,43 \,\text{cm} &\quad \scriptsize \\[5pt] A_{EBD}&=& \underline{\underline{ 22,1 \,\text{cm}^2}} \end{array}$

Beas Aussage prüfen

$\begin{array}[t]{rll} u_{\,\text{Rechteck}}&=& 2\cdot 6e+2\cdot 3e &\quad \scriptsize \\[5pt] u_{\,\text{Rechteck}}&=& 18e \end{array}$

$U_{AEFG}=\overline{AG}+\overline{FG}+\overline{AE}+\overline{EF}$

1. Schritt: Länge der Strecke $\boldsymbol{\overline{AG}}$ berechnen

$\begin{array}[t]{rll} \overline{AG}&=& 2\cdot \overline{BC}&\quad \scriptsize \\[5pt] &=& 2\cdot 3e &\quad \scriptsize \\[5pt] \overline{AG}&=& \underline{ 6e} \end{array}$

2. Schritt: Länge der Strecke $\boldsymbol{\overline{FG}}$ berechnen

$\begin{array}[t]{rll} \overline{BE}&=&\dfrac{\overline{CM}}{2} &\quad \scriptsize \\[5pt] &=&\dfrac{3e}{2} &\quad \scriptsize \\[5pt] \overline{BE}&=& \underline{ 1,5e }=\overline{FG} \end{array}$

3. Schritt: Länge der Strecke $\boldsymbol{\overline{AE}}$ berechnen

$\begin{array}[t]{rll} \overline{AE}&=&\overline{AB}-\overline{BE} &\quad \scriptsize \\[5pt] &=& 6e-1,5e &\quad \scriptsize \\[5pt] \overline{AE}&=&\underline{ 4,5e} \end{array}$

4. Schritt: Länge der Strecke $\boldsymbol{\overline{EF}}$ berechnen

$\begin{array}[t]{rll} \cos(30^{\circ})&=&\dfrac{\overline{MR}}{\overline{EM}} \quad \scriptsize \mid\; \cdot \overline{EM} \\[5pt] \cos(30^{\circ}) \cdot \overline{EM}&=& \overline{MR}\quad \scriptsize \mid\; :\cos(30^{\circ})\\[5pt] \overline{EM}&=&\dfrac{\overline{MR}}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt] \overline{EM}&=&\dfrac{3e}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt] \overline{EM}&=& 2\cdot \sqrt{3}e \end{array}$

$\begin{array}[t]{rll} \overline{EF}&=& 2 \cdot \overline{EM} &\quad \scriptsize \\[5pt] &=& 2 \cdot 2\cdot \sqrt{3}e &\quad \scriptsize \\[5pt] \overline{EF}&=& \underline{ 4\sqrt{3}e} \end{array}$

5. Schritt: Umfang des Vierecks $\boldsymbol{AEFG}$ berechnen

$\begin{array}[t]{rll} u_{AEFG}&=& \overline{AG}+\overline{FG}+\overline{AE}+\overline{EF} \quad \scriptsize \\[5pt] &=& 6e+1,5e+4,5e+4\cdot \sqrt{3}e \\[5pt] u_{AEFG}&=& \underline{ 18,93e} \end{array}$

Beas Aussage ist nicht richtig, da $18,93e\gt 18e$ gilt.

Lösung W2

Höhe des Kegels berechnen

1. Schritt: Radius der Grundfläche berechnen

Umfang Dreiviertelkreis:

$\begin{array}[t]{rll} U_{\,\text{Dr}}&=& \dfrac{3}{4}\cdot 2\cdot \pi \cdot r_K &\quad \scriptsize \\[5pt] &=& \dfrac{3}{4}\cdot 2\cdot \pi \cdot 21,2\,\text{cm} &\quad \scriptsize \\[5pt] U_{\,\text{Dr}}&=& \dfrac{159}{5}\cdot \pi \,\text{cm} \end{array}$

Umfang Dreiviertelkreis = Umfang Grundfläche

Umfang Grundfläche

$\begin{array}[t]{rll} U_G&=&2\cdot \pi \cdot r_K \quad \scriptsize \mid\; : 2\pi \\[5pt] r_K&=&\dfrac{U_G}{2\pi} \quad \scriptsize \mid\; U_G=\dfrac{159}{5}\cdot \pi \,\text{cm} \\[5pt] r_K&=& \dfrac{\dfrac{159}{5}\cdot \pi \,\text{cm} }{2\pi} &\quad \scriptsize \\[5pt] r_K&=& \underline{ 15,9\,\text{cm}} \end{array}$

2. Schritt: Höhe des Kegels berechnen

Rechenweg anzeigen

$h_K=\underline{ 14\,\text{cm}}$

Höhe der Pyramide berechnen

wahlbereich pyramide dreieck seitenlaenge

1. Schritt: Seitenlänge der Grundfläche berechnen

Größe des Winkels $\gamma$ berechnen

Die Winkelsumme eines Dreiviertelkreis wird in sechs regelmäßige Dreiecke aufgeteilt. Für $\gamma$ gilt also:

$\begin{array}[t]{rll} \gamma&=&\dfrac{360^{\circ} \cdot \dfrac{3}{4}}{6} &\quad \scriptsize \\[5pt] \gamma&=&\dfrac{270^{\circ}}{6} \\[5pt] \gamma&=& 45^{\circ} \end{array}$

Länge von $a$ berechnen

$\begin{array}[t]{rll} \sin\left(\dfrac{\gamma}{2}\right)&=& \dfrac{\dfrac{a}{2}}{s_P}\quad \scriptsize \mid\;\cdot s_P \\[5pt] \dfrac{a}{2}&=&\sin\left(\dfrac{\gamma}{2}\right) \cdot s_P &\quad \scriptsize \\[5pt] \dfrac{a}{2}&=&\sin(22,5^{\circ})\cdot 21,2\,\text{cm} \quad \scriptsize \mid\; \cdot 2\\[5pt] a&=& \underline{ 16,2\,\text{cm}} \end{array}$

2. Schritt: Höhe der Pyramide berechnen

Vogelsicht der Pyramide:

wahlbereich sechseck pyramide seitenlaenge

Querschnitt der Pyramide:

Rechenweg anzeigen

$h_P=\underline{ 13,7\,\text{cm}}$

Differenz D der Körperhöhen berechnen

$\begin{array}[t]{rll} d&=& h_K-h_P &\quad \scriptsize \\[5pt] &=& 14\,\text{cm}-13,7\,\text{cm} &\quad \scriptsize \\[5pt] d&=& \underline{\underline{ 0,3\,\text{cm}}} \end{array}$

Kegelvolumen berechnen

Volumenformel für einen halben Kegel: $V_K=\dfrac{\dfrac{1}{3}\cdot \pi \cdot r^2\cdot h}{2}$

1. Schritt: Kegelradius berechnen

$\begin{array}[t]{rll} \overline{BM}&=&\dfrac{\overline{AB}}{2} &\quad \scriptsize \\[5pt] \overline{BM}&=& \dfrac{11,4\,\text{cm}}{2}&\quad \scriptsize \\[5pt] \overline{BM} &=& \underline{ 5,70\,\text{cm}} = r \end{array}$

2. Schritt: Kegelhöhe berechnen

$\begin{array}[t]{rll} \tan(\beta)&=&\dfrac{h}{\overline{BM}} \quad \scriptsize \mid\; \cdot \overline{BM} \\[5pt] h&=&\tan(\beta)\cdot \overline{BM} &\quad \scriptsize \\[5pt] h&=&\tan(62^{\circ})\cdot 5,7\,\text{cm} &\quad \scriptsize \\[5pt] h &= & \underline{ 10,72 \,\text{cm}} \end{array}$

3. Schritt: Volumen des halben Kegels berechnen

$\begin{array}[t]{rll} V_K&=&\dfrac{\dfrac{1}{3}\cdot \pi \cdot r^2\cdot h}{2} &\quad \scriptsize \\[5pt] &=& \dfrac{\dfrac{1}{3}\cdot \pi \cdot (5,7\,\text{cm})^2\cdot 10,72\,\text{cm} }{2} &\quad \scriptsize \\[5pt] V_K&=&\underline{ 182,37 \,\text{cm}^3} \end{array}$

Differenz der bekannten Volumina berechnen

$\begin{array}[t]{rll} V_P&=&V_{\,\text{Ges}}-V_K &\quad \scriptsize \\[5pt] &=& 1280\,\text{cm}^3-182,37\,\text{cm}^3&\quad \scriptsize \\[5pt] V_P&=& \underline{ 1\,097,63 \,\text{cm}^3} \end{array}$

Volumen des Dreiecksprismas berechnen

$V_P=G\cdot l$

1. Schritt: Grundfläche $\boldsymbol{G}$ berechnen

$\begin{array}[t]{rll} G&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt] &=&\dfrac{1}{2}\cdot \overline{AB}\cdot h &\quad \scriptsize \\[5pt] &=&\dfrac{1}{2}\cdot 11,4\,\text{cm}\cdot 10,72\,\text{cm} &\quad \scriptsize \\[5pt] G&=&\underline{ 61,10\,\text{cm}^3} \end{array}$

2. Schritt: Länge des Dreiecksprismas berechnen

$\begin{array}[t]{rll} V_P&=&G\cdot l_P \quad \scriptsize \mid\; :G \\[5pt] l_P&=&\dfrac{V_P}{G} &\quad \scriptsize \\[5pt] l_P&=& \dfrac{1097,63\,\text{cm}^3}{61,1\,\text{cm}^2}&\quad \scriptsize \\[5pt] l_P&= & \underline{ 17,96\,\text{cm}} \end{array}$

Gesamtlänge des Körpers berechnen

$\begin{array}[t]{rll} l_{\,\text{Ges}}&=& l_K+l_P&\quad \scriptsize \\[5pt] &=& r_K+l_P&\quad \scriptsize \\[5pt] &=& 5,7\,\text{cm}+17,96\,\text{cm}&\quad \scriptsize \\[5pt] l_{\,\text{Ges}}&=& \underline{\underline{ 23,7\,\text{cm}}} \end{array}$

Lösung W3

Parabelgleichung $\boldsymbol{p}$ angeben

Scheitelpunktform einer verschobenen und nach oben geöffneten Normalparabel:

$y=(x-b)^2+c$

Mit dem Einsetzungsverfahren können die Werte berechnet werden:

1. Schritt: Zwei Punkte einsetzen

1) $(0\mid 11)$

$11=(-b)^2+c$

2) $(1\mid 6)$

$6=(1-b)^2+c$

2. Schritt: 1) nach $\boldsymbol{c}$ auflösen

$\begin{array}[t]{rll} 11&=& (-b)^2+c&\quad \scriptsize \mid\; -b^2\\[5pt] c&=& \underline{ 11-b^2} \end{array}$

3. Schritt: $\boldsymbol{c}$ in 2) einsetzen, um $\boldsymbol{b}$ zu berechnen

Rechenweg anzeigen

$\underline{ b=3}$

4. Schritt: $\boldsymbol{b}$ in 1) einsetzen, um $\boldsymbol{c}$ zu berechnen

$\begin{array}[t]{rll} 11&=&b^2+c \quad \scriptsize \mid\; b=3 \\[5pt] 11&=&3^2+c \quad \scriptsize \mid\; -9 \\[5pt] c&=&\underline{ 2} \end{array}$

Die Parabelgleichung $p$ lautet also $\underline{\underline{ p:y=(x-3)^2+2}}$

Wertetabelle vervollständigen

Durch Einsetzen der $x$ -Werte in die Parabelgleichung ergibt sich:

$x$	0	1	2	3	4	5
$y$	11	6	3	2	3	6

Nachweisen, dass keine gemeinsamen Punkte vorliegen

1. Schritt: Geradengleichung $\boldsymbol{g}$ aufstellen

Durch Einsetzen der Informationen in die allgemeine Geradengleichung $y=mx+c$ ergibt sich:

$\begin{array}[t]{rll} 6&=&(-1)\cdot (-2,5)+c &\quad \scriptsize \mid\; -2,5\\[5pt] c&=& \underline{ 3,5} \end{array}$

Die Geradengleichung $g$ lautet also $y=-x+3,5$

2. Schritt: $\boldsymbol{g}$ und $\boldsymbol{p}$ gleichsetzen

Rechenweg anzeigen

$x_{1,2}=\dfrac{5}{2}\pm \sqrt{-\frac{5}{4}}$

Da die Diskriminante $D\lt 0$ ist, gibt es keine Lösung und $g$ und $p$ haben keine gemeinsamen Punkte.

Koordinaten des Schnittpunkts berechnen

1. Schritt: Geradengleichung $\boldsymbol{h}$ aufstellen

Der Scheitelpunkt der Parabel $p: y=(x-3)^2+2$ ist $S (3\mid 2).$

Die Steigung $m$ ist gleich zu $g,$ also $-1.$

Durch Einsetzen in die allgemeine Geradengleichung ergibt sich:

$\begin{array}[t]{rll} y&=&m\cdot x +c &\quad \scriptsize\mid\; m=-1 ;\,S (3\mid 2) \\[5pt] 2&=&(-1)\cdot 3 +c &\quad \scriptsize \mid\;+3 \\[5pt] c&=&5 \end{array}$

Die Geradengleichung $h$ lautet also: $\underline{ h:y=-x+5}$

2. Schritt: Schnittpunkt mit $\boldsymbol{x}$ -Achse berechnen

Der Schnittpunkt mit der $x$ -Achse entspricht der Nullstelle der Gerade. Sie wird also mit 0 gleichgesetzt:

$\begin{array}[t]{rll} -x+5&=& 0& \quad \scriptsize \mid\;-5 \\[5pt] - x&=& -5& \quad \scriptsize \mid\;:(-1)\\[5pt] x&=& 5 \end{array}$

Der Schnittpunkt $R$ hat also die Koordinaten $\underline{\underline{ (5\mid 0)}}.$

Koordinaten von Punkt $\boldsymbol{T}$ berechnen

1. Schritt: Parabelgleichung $\boldsymbol{p_1}$ aufstellen

Durch den Scheitelpunkt $S_1 (0\mid 4,5)$ gilt, dass die Parabel um $4,5 \,\text{LE}$ nach oben verschoben ist, also $c=4,5.$

Die Punktprobe mit $N_2(3\mid 0)$ zeigt:

$\begin{array}[t]{rll} y&=&a\cdot x^2+c \quad \scriptsize \mid\; c=4,5 ; N_2(3\mid 0) \\[5pt] 0&=&a\cdot 3^2+4,5 \quad \scriptsize \mid\;-4,5 \\[5pt] -4,5&=& 9\cdot a \quad \scriptsize \mid\;:9 \\[5pt] a&=&-\dfrac{1}{2} \end{array}$

Die Parabelgleichung $p_1$ lautet also $\underline{ p_1:y=-\dfrac{1}{2}x^2+4,5}.$

2. Schritt: Parabelgleichung $\boldsymbol{p_2}$ aufstellen

Bei einer Normalparabel gilt $a=1.$

Mit dem Scheitelpunkt $S_2(3\mid 1,5)$ lässt sich die Scheitelpunktform aufstellen:

$\begin{array}[t]{rll} y&=&a\cdot (x-b)^2+c \quad \scriptsize a=1 ; S_2(3\mid1,5) \\[5pt] y&=&1\cdot(x-3)^2+1,5 \end{array}$

Die Parabelgleichung $p_2$ lautet also $\underline{ p_2:y=(x-3)^2+1,5}.$

3. Schritt: Schnittpunkt $\boldsymbol{T}$ berechnen

Rechenweg anzeigen

$x=2$

$x$ in eine Parabelgleichung einsetzen, um $y$ zu berechnen:

$\begin{array}[t]{rll} y&=&(x-3)^2+1,5 \quad \scriptsize \mid\; x=2 \\[5pt] &=&(2-3)^2+1,5 &\quad \scriptsize \\[5pt] &=& 1+1,5 &\quad \scriptsize \\[5pt] y&=& 2,5 \end{array}$

Die Koordinaten des gemeinsamen Punkts $T$ sind also $\underline{\underline{ T(2\mid 2,5)}}.$

Flächeninhalt des Dreiecks berechnen

$\begin{array}[t]{rll} A_{\,\text{Dreieck}}&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt] A_{N_1N_2T}&=& \dfrac{1}{2}\cdot \overline{N_1N_2}\cdot h&\quad \scriptsize \\[5pt] A_{N_1N_2T}&=& \dfrac{1}{2}\cdot 6\,\text{LE} \cdot 2,5\,\text{LE}&\quad \scriptsize \\[5pt] A_{N_1N_2T}&=& \underline{\underline{ 7,5 \,\text{FE}}} \end{array}$

wahlbereich koordinatensystem dreieck flaecheninhalt

Der Flächeninhalt des Dreiecks $N_1N_2T$ beträgt $7,5\,\text{FE}.$

Maximalen Flächeninhalt begründen

Da sich $T$ nur auf $p_1$ oberhalb der $x$ -Achse bewegt und die $y$ -Koordinate von $T$ die Höhe $h$ des Dreiecks beschreibt, wird diese im Scheitelpunkt von $p_1$ maximal sein. Das heißt: $T_{\,\text{neu}}=(0\mid4,5).$

Lösung W4

Wahrscheinlichkeit berechnen

$\begin{array}[t]{rll} P(s\,\text{und}\; r)&=& \dfrac{7}{12}\cdot \dfrac{5}{11}+\dfrac{5}{12}\cdot \dfrac{7}{11}&\quad \scriptsize \\[5pt] &=& 0,53 \\[5pt] P(s\,\text{und}\; r) &=& \underline{\underline{ 53\,\%}} \end{array}$

Erwartungswert berechnen

Ergebnisse	Gewinn	Wahrscheinlichkeit
zweimal Karo	$10\,€$	$\dfrac{2}{12}\cdot \dfrac{1}{11}=\dfrac{1}{66}$
zweimal Herz	$5\,€$	$\dfrac{3}{12}\cdot \dfrac{2}{11}=\dfrac{1}{22}$
sonstige	kein Gewinn	$1-\dfrac{1}{66}-\dfrac{1}{22}= \dfrac{31}{33}$

Rechenweg anzeigen

$E= \underline{\underline{ -0,62\,€}}$

Der Spieler macht auf Dauer also Verlust.

Behauptung prüfen

Der Gewinn von „zweimal Karo“ wird von 10€ auf 20€ erhöht.

Rechenweg anzeigen

$E_{\,\text{neu}}=-0,47\,€$

Die Behauptung des Betreibers ist nicht richtig. Er macht weiterhin Gewinn aber weniger als zuvor.

Davids Stoßweite berechnen

1. Schritt: Parabelgleichung aufstellen

Rechenweg anzeigen

$a -0,09$

Die Parabelgleichung von Davids Kugelstoß lautet also $\underline{ y=-0,09\cdot x^2+3,9}.$

2. Schritt: Nullstellen berechnen

$\begin{array}[t]{rll} 0&=& -0,09\cdot x^2+3,9 \quad \scriptsize \mid\; -3,9\\[5pt] -3,9&=&-0,09\cdot x^2 \quad \scriptsize \mid\; :(-0,09) \\[5pt] \dfrac{3,9}{0,09}&=& x^2\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] x&=& \underline{ \pm 6,58} \end{array}$

3. Schritt: Davids Stoßweite $\boldsymbol{W_D}$ berechnen

$\begin{array}[t]{rll} W_D&=& 6,58\,\text{m}- (-4,30\,\text{m}) &\quad \scriptsize \\[5pt] &=& \underline{ \underline{ 10,9\,\text{m}}} \end{array}$

Tims Stoßweite berechnen

1. Schritt: Koordinaten des Abstoßpunkts berechnen

$\begin{array}[t]{rll} y&=& -\dfrac{1}{10}\cdot x^2+3,5 \quad \scriptsize \mid\; (x\mid 1,90)\\[5pt] 1,90&=& -\dfrac{1}{10}\cdot x^2+3,5\quad \scriptsize \mid\; -3,5\\[5pt] -1,60&=& -\dfrac{1}{10}\cdot x^2\quad \scriptsize \mid\; :(-\dfrac{1}{10}) \\[5pt] 16&=& x^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt] x&=& \pm 4 \end{array}$

Da der Abstoß links neben der $y$ -Achse erfolgt ist, sind die Koordinaten $\underline{ (-4\mid 1,90)}.$

2. Schritt: Nullstellen berechnen

$\begin{array}[t]{rll} 0&=& -\dfrac{1}{10}\cdot x^2+3,5 \quad \scriptsize \mid\;-3,5 \\[5pt] -3,5&=& -\dfrac{1}{10}\cdot x^2 \quad \scriptsize \mid\; :(-\dfrac{1}{10})\\[5pt] 35&=& x^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt] x&=& \underline{ \pm 5,92} \end{array}$

3. Schritt: Tims Stoßweite $\boldsymbol{W_T}$ berechnen

$\begin{array}[t]{rll} W_T&=& 5,92\,\text{m} - (-4\,\text{m}) &\quad \scriptsize \\[5pt] &=& \underline{\underline{ 9,9\,\text{m}}} \end{array}$

Stoßweiten vergleichen

$\begin{array}[t]{rll} W&=& 10,9\,\text{m} -9,9\,\text{m} &\quad \scriptsize \\[5pt] &=& \underline{ 1\,\text{m}} \end{array}$

David hat seine Kugel also $1\,\text{m}$ weiter als Tim gestoßen.