Pflichtbereich
Aufgabe P1
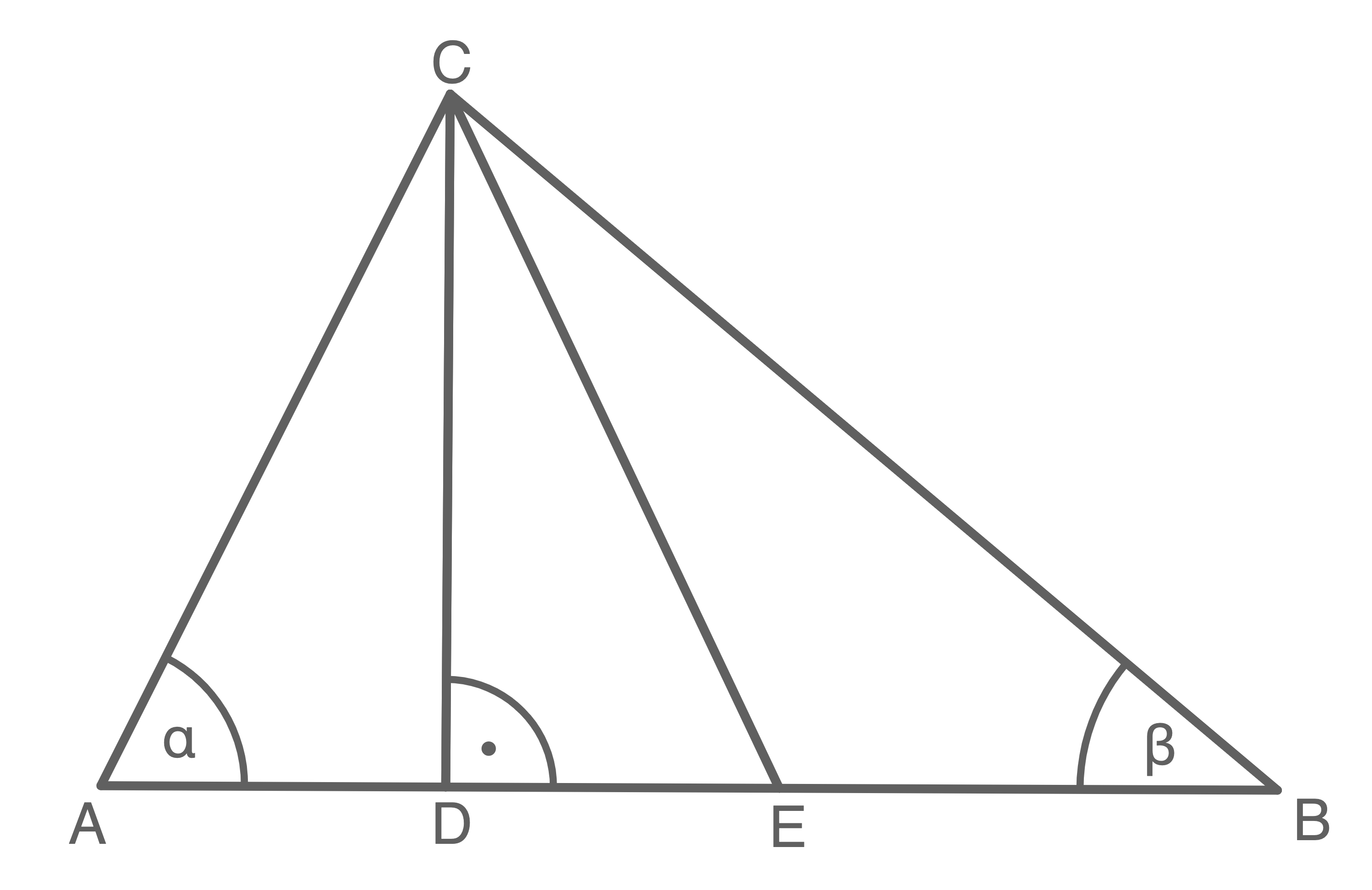
Berechne den Umfang des Dreiecks
4 P
Aufgabe P2
Das Viereck  ist ein Quadrat.
ist ein Quadrat.
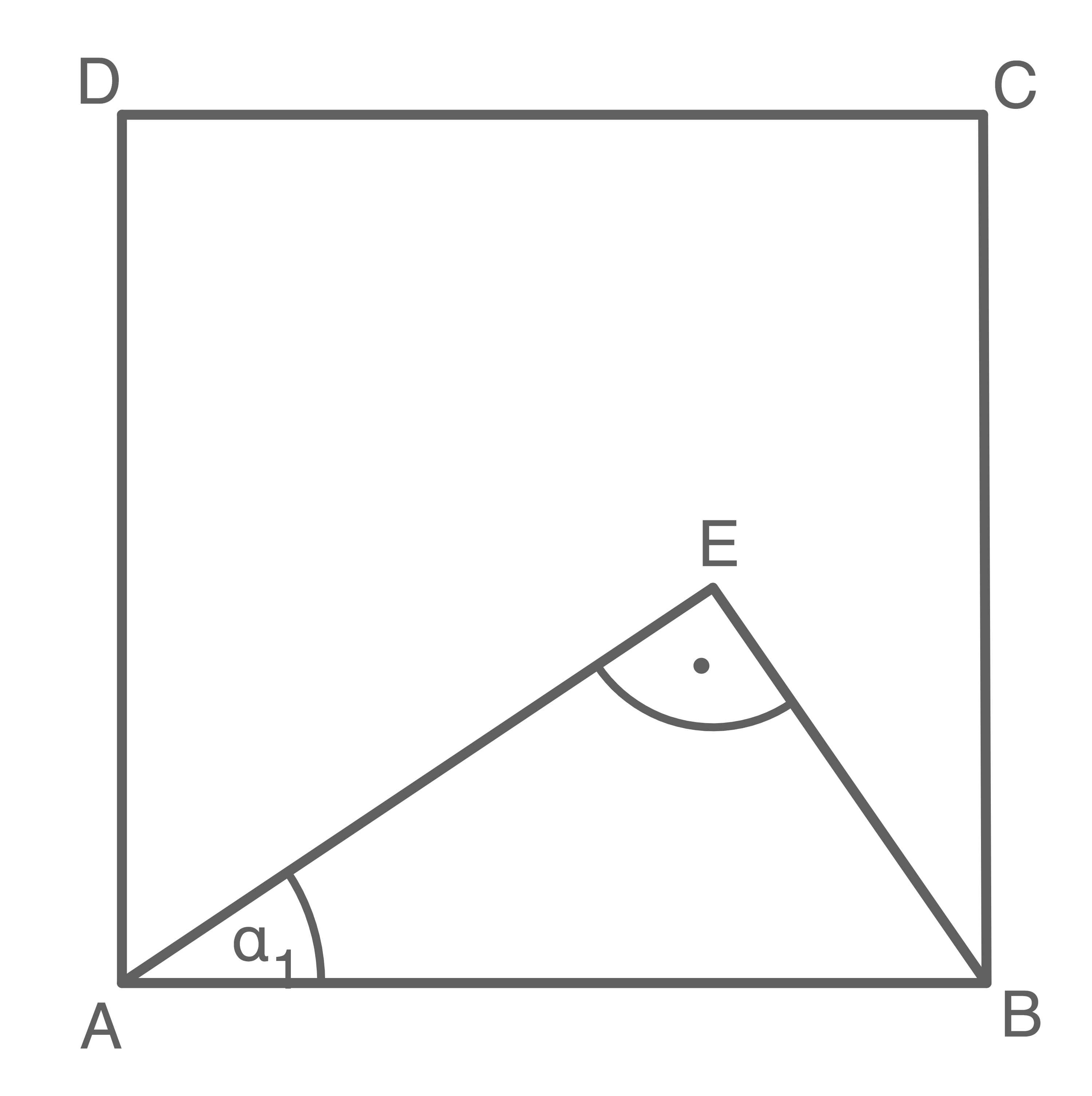 Es gilt:
Es gilt:


Berechne die Länge von .
.

Berechne die Länge von
4 P
Aufgabe P3
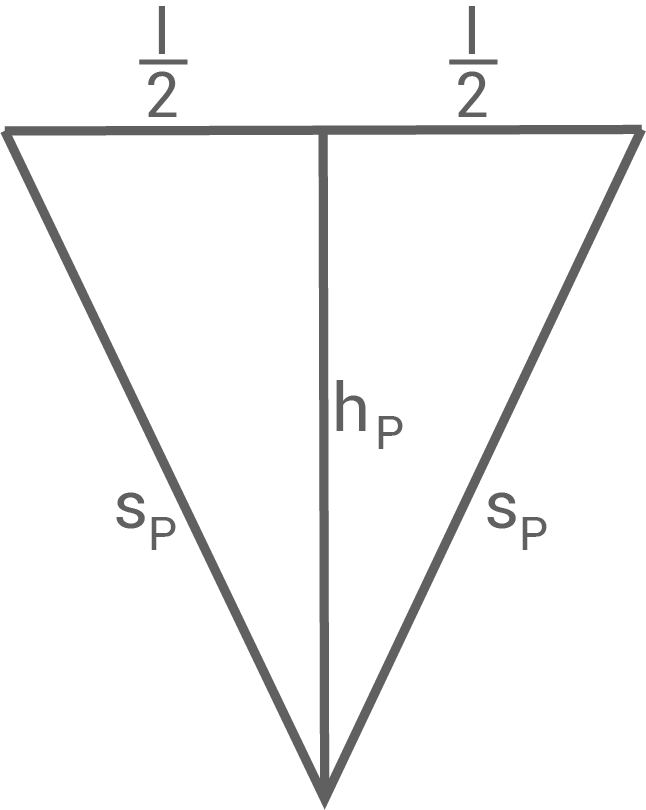
Ein Kegel ist teilweise mit Wasser gefüllt. Dabei nimmt das Wasser die Hälfte des Kegelvolumens ein.
Dieses Wasser soll vollständig in eine quadratische Pyramide umgefüllt werden.
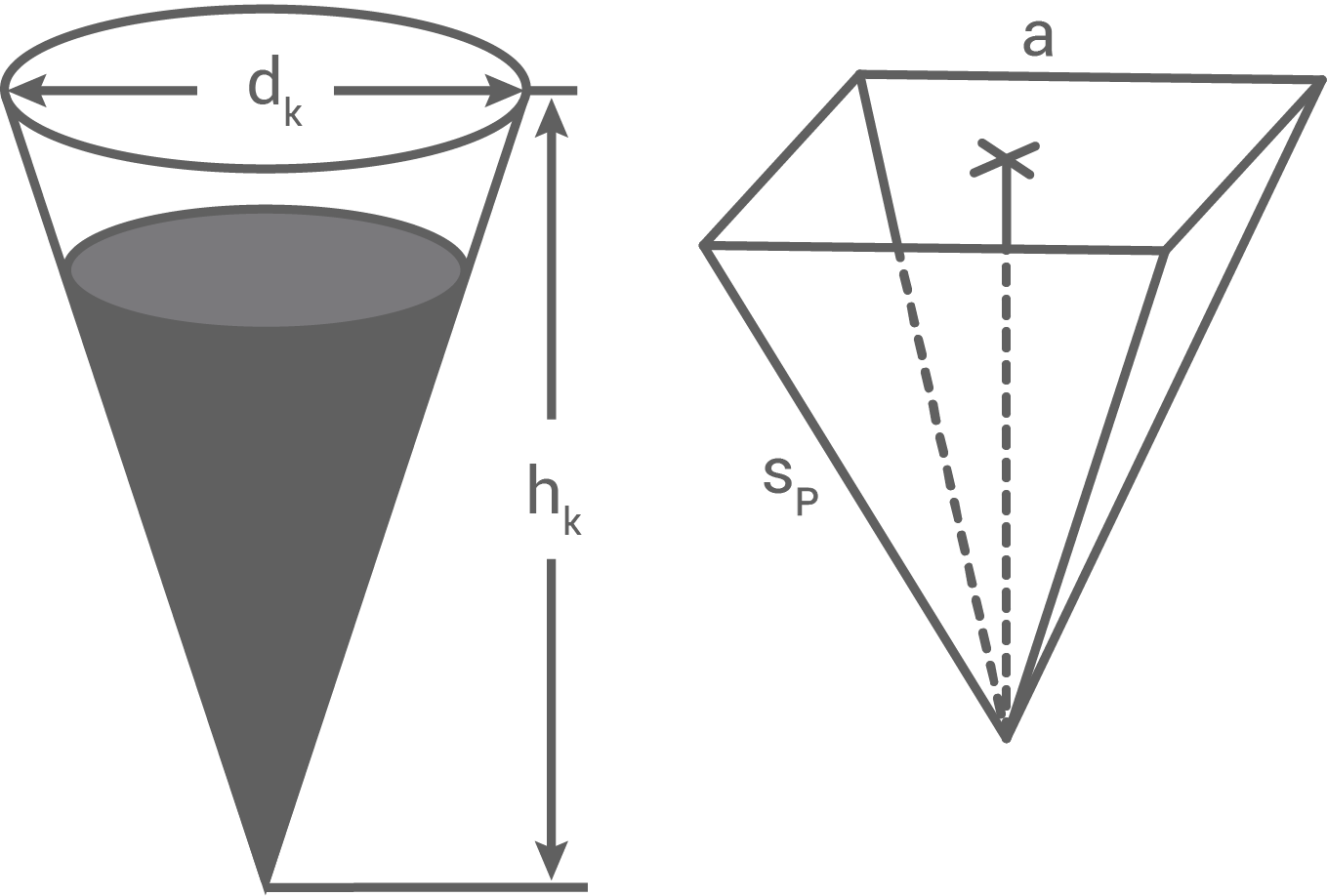 Es gilt:
Es gilt:




Läuft das Wasser über?
Überprüfe durch Rechnung.
Dieses Wasser soll vollständig in eine quadratische Pyramide umgefüllt werden.

Läuft das Wasser über?
Überprüfe durch Rechnung.
3,5 P
Aufgabe P4
In einem Behälter liegen 20 Kugeln. Sie sind rot, blau und grün gefärbt.
Es werden zwei Kugeln gleichzeitig gezogen.
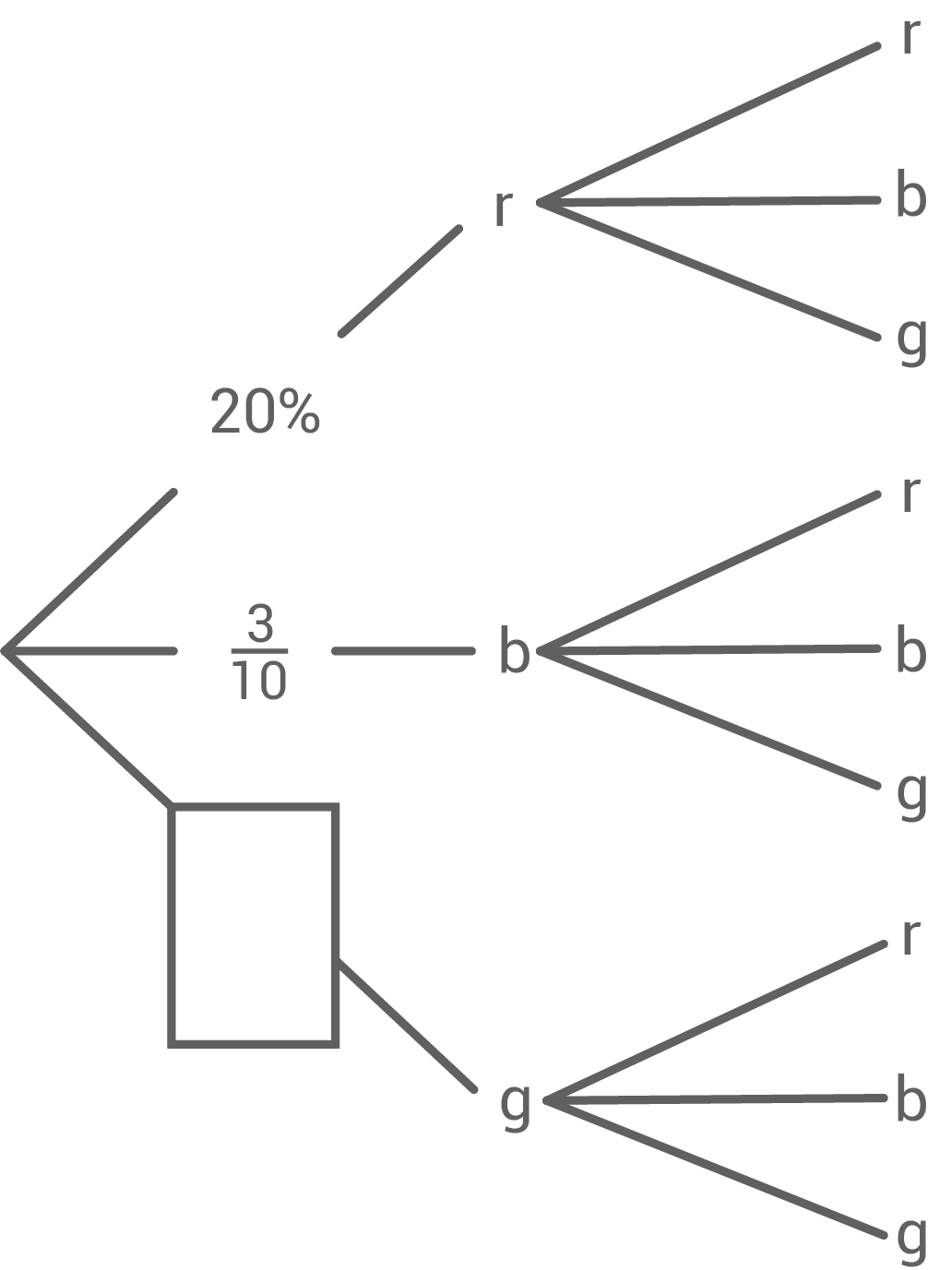 Im Baumdiagramm fehlt eine Wahrscheinlichkeitsangabe.
Im Baumdiagramm fehlt eine Wahrscheinlichkeitsangabe.
Ergänze diese. Wie groß ist die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen? In einem anderen Behälter liegen von jeder Farbe doppelt so viele Kugeln, also insgesamt 40 Kugeln.
Es werden ebenfalls zwei Kugeln gleichzeitig gezogen. Uli sagt: „Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, ist gleich.“
Hat Uli recht?
Begründe durch Rechnung.
Es werden zwei Kugeln gleichzeitig gezogen.

Ergänze diese. Wie groß ist die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen? In einem anderen Behälter liegen von jeder Farbe doppelt so viele Kugeln, also insgesamt 40 Kugeln.
Es werden ebenfalls zwei Kugeln gleichzeitig gezogen. Uli sagt: „Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, ist gleich.“
Hat Uli recht?
Begründe durch Rechnung.
4 P
Aufgabe P5
Das Schaubild zeigt die Ausschnitte von vier Parabeln.
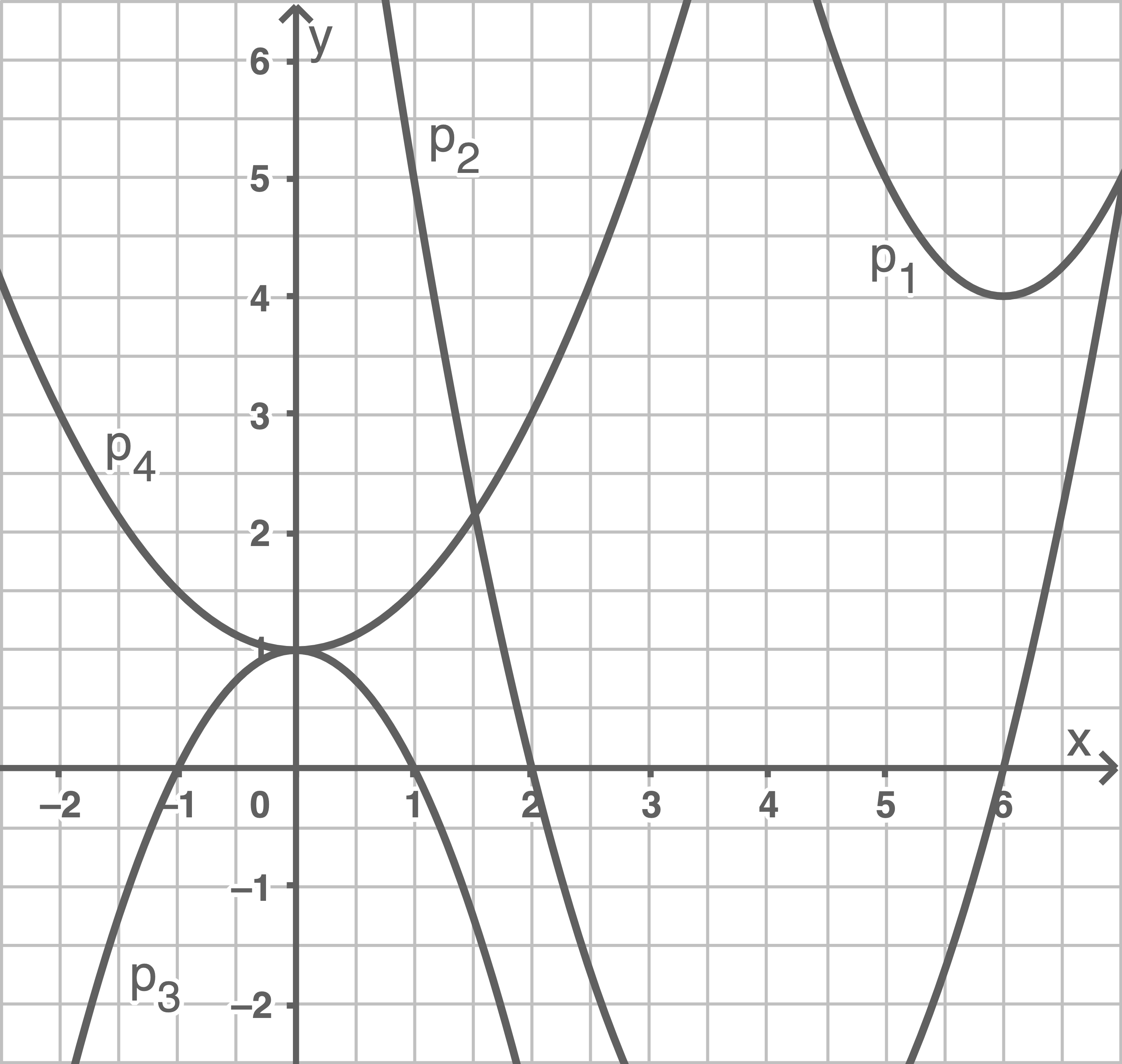
Welcher Graph gehört zur angegebenen Wertetabelle?
Begründe deine Entscheidung.
Berechne die Koordinaten des Schnittpunktes der beiden verschobenen Normalparabeln
der beiden verschobenen Normalparabeln  und
und  .
Wie heißt die Gleichung der Parabel
.
Wie heißt die Gleichung der Parabel  ?
?
Entnimm dazu erforderliche Werte dem Schaubild.

| 0 | 1 | 2 | 3 | |
| 1 | 0 | -3 | 8 |
Begründe deine Entscheidung.
Berechne die Koordinaten des Schnittpunktes
Entnimm dazu erforderliche Werte dem Schaubild.
4 P
Aufgabe P6
Löse das Gleichungssystem:
| (1) | |
| (2) |
3 P
Aufgabe P7
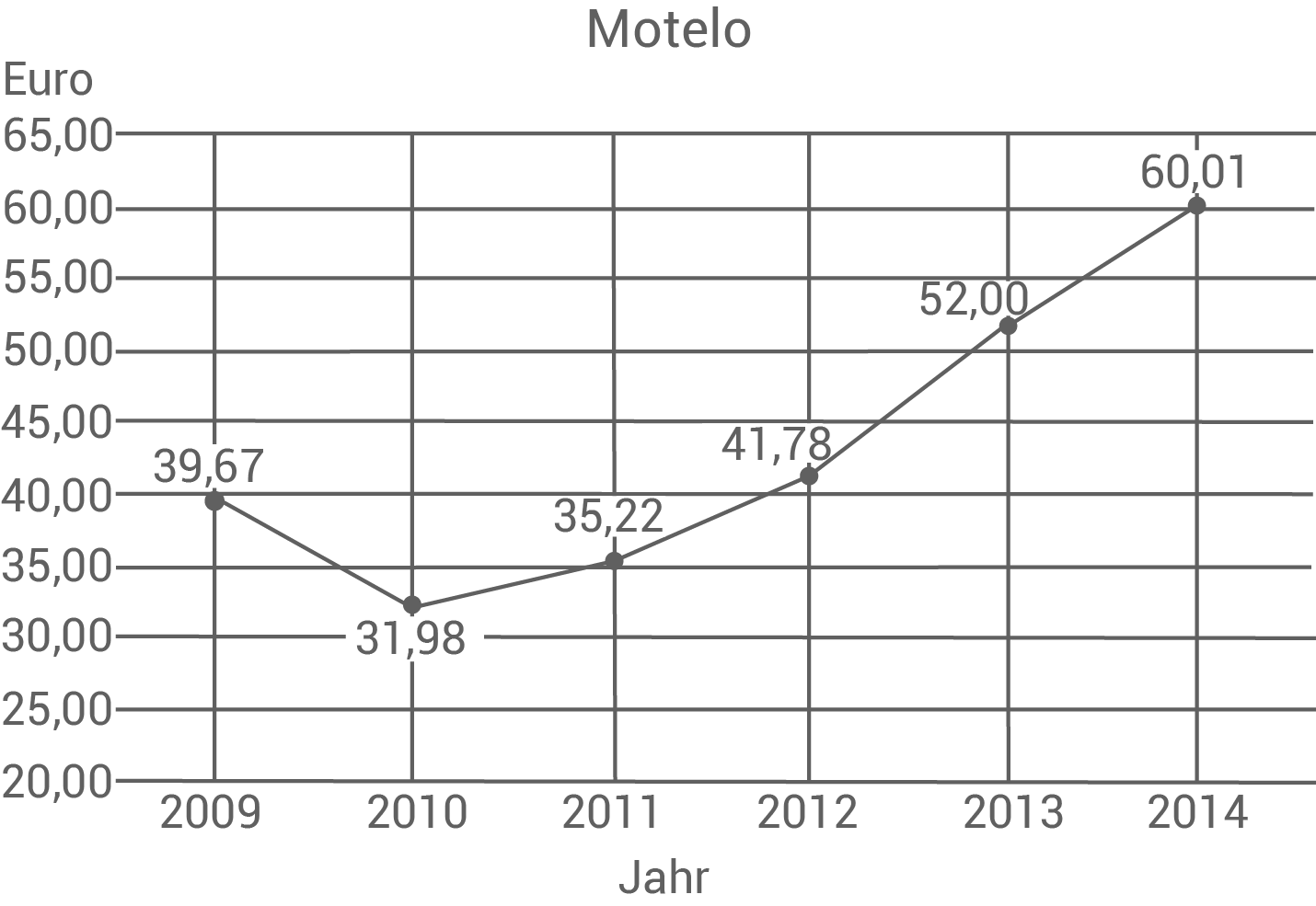
Das Diagramm zeigt den Wert der Aktie „Motelo“ jeweils am Jahresende.
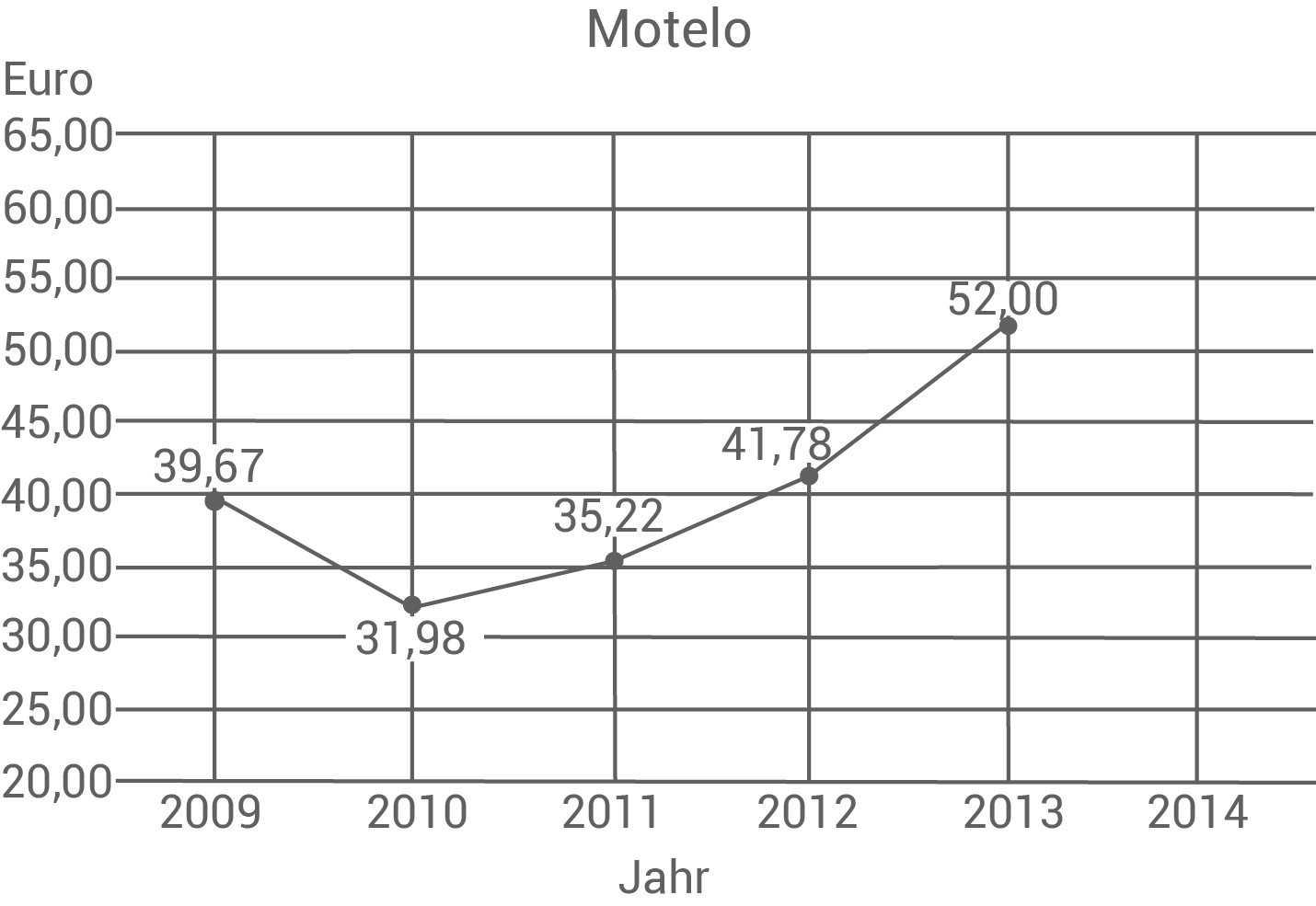 Um wie viel Prozent ist der Wert der Aktie von 2010 bis 2013 insgesamt angestiegen?
Um wie viel Prozent ist der Wert der Aktie von 2010 bis 2013 insgesamt angestiegen?
Am Ende des Jahres 2014 lag der Wert der Aktie % über dem Wert am Ende des Jahres 2013.
% über dem Wert am Ende des Jahres 2013.
Zeichne im Diagramm den Jahresendwert von 2014 ein. Welchen jährlich gleichbleibenden Zinssatz hätte eine Bank bieten müssen, um von 2009 bis 2013 den gleichen Wertzuwachs zu erzielen?

Am Ende des Jahres 2014 lag der Wert der Aktie
Zeichne im Diagramm den Jahresendwert von 2014 ein. Welchen jährlich gleichbleibenden Zinssatz hätte eine Bank bieten müssen, um von 2009 bis 2013 den gleichen Wertzuwachs zu erzielen?
3,5 P
Aufgabe P8
Die Klassen 10a und 10b machen einen gemeinsamen Ausflug und spielen Minigolf.
Beim Minigolf zählt jeder Schlag als Punkt.
Hat der Ball nach sechs Punkten das Ziel nicht erreicht, ist ein Zusatzpunkt anzurechnen.
Die Höchstpunktzahl an einer Bahn beträgt also sieben Punkte.
Die Diagramme und die Boxplots zeigen die Ergebnisse der beiden Klassen nach der ersten Bahn.
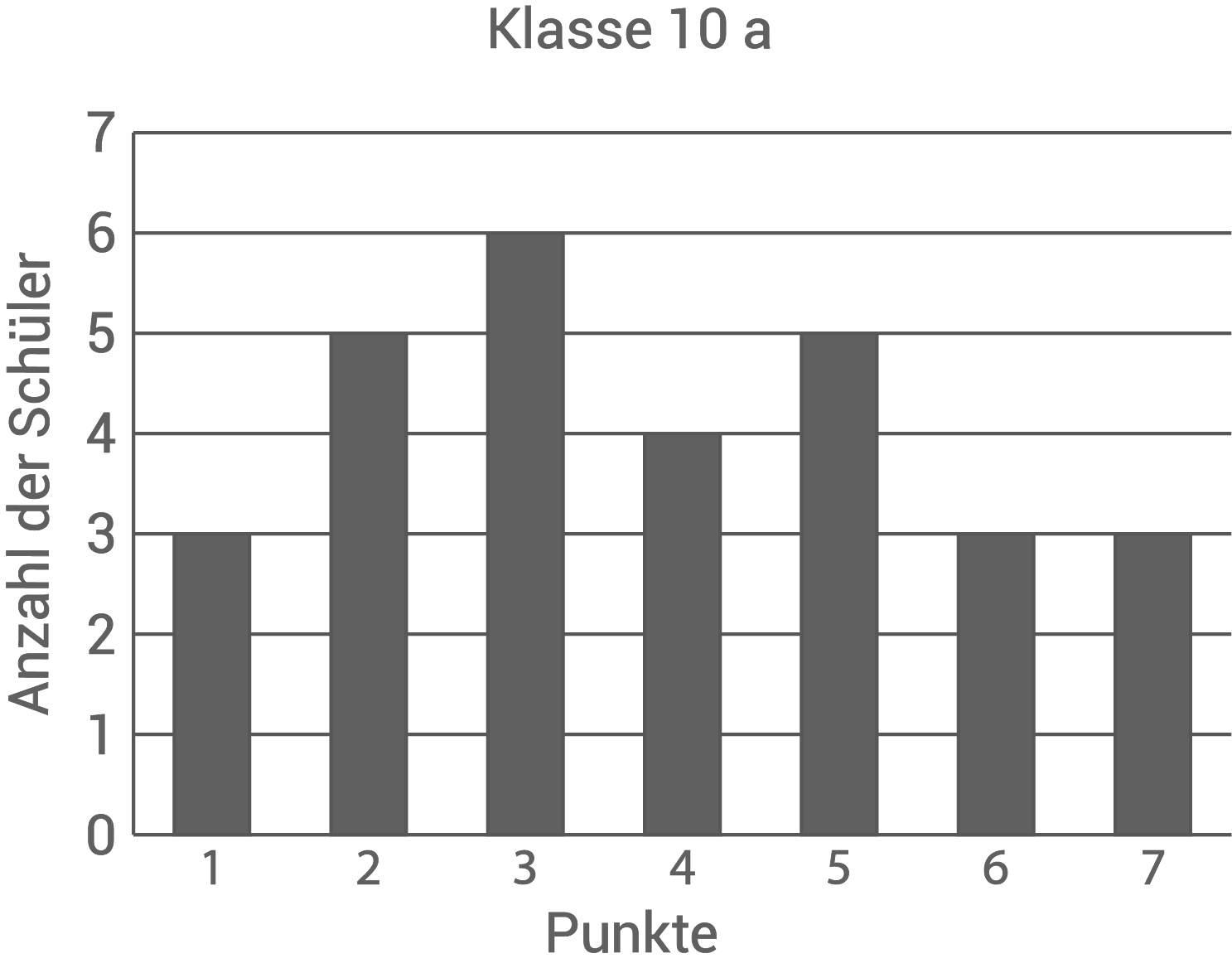
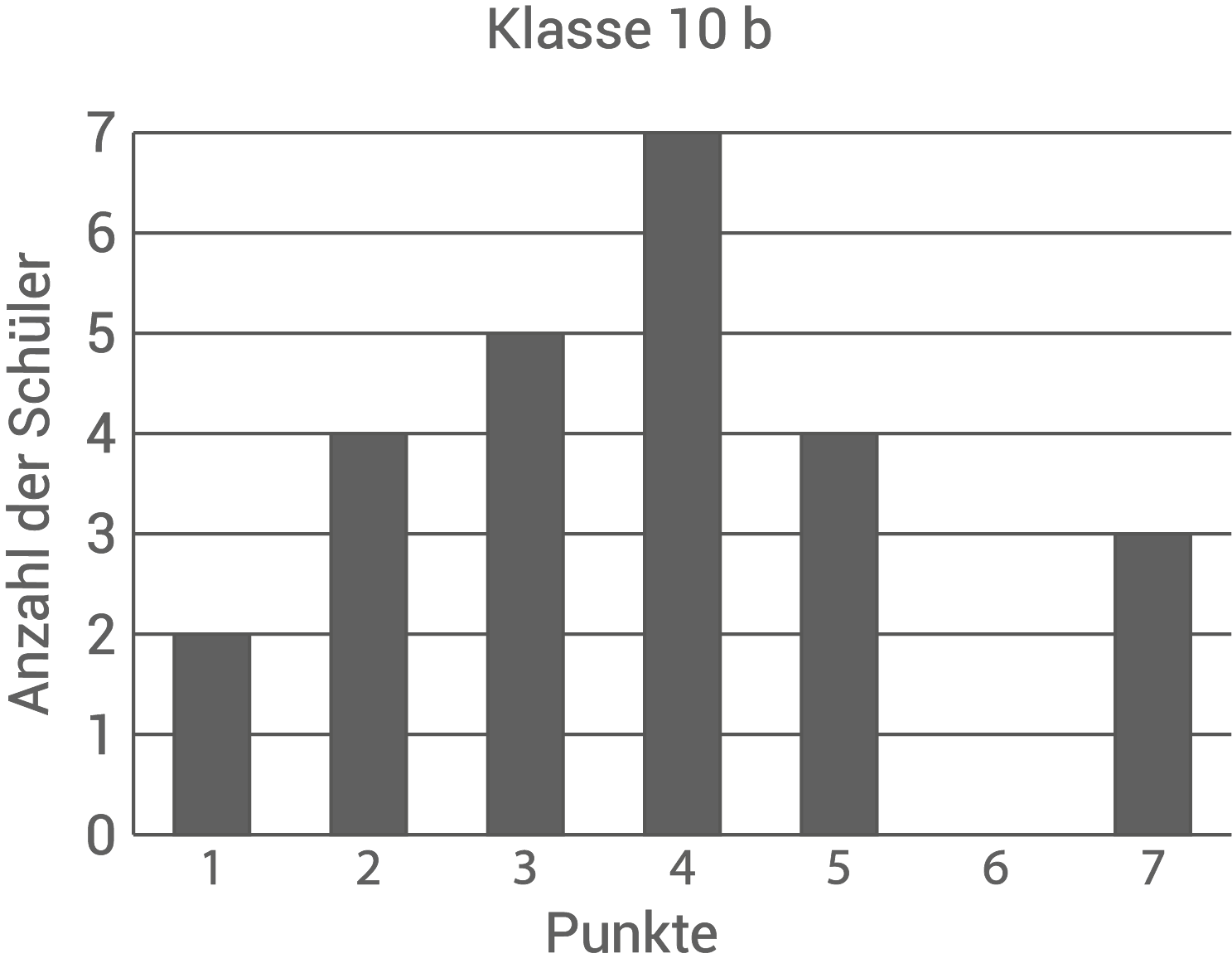
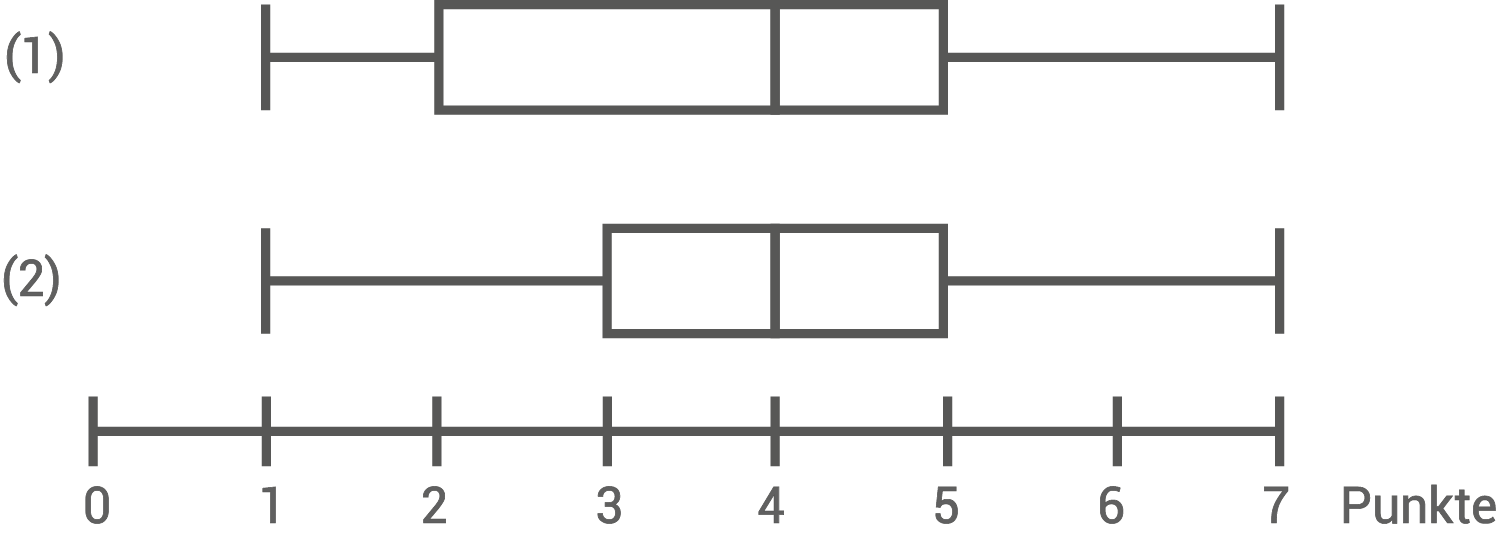 Zu welcher Klasse gehört der jeweilige Boxplot? Begründe.
Zu welcher Klasse gehört der jeweilige Boxplot? Begründe.
Wie viel Prozent der Schüler der Klasse 10a haben fünf oder mehr Punkte?
Überprüfe folgende Aussage:
„Die durchschnittliche Punktzahl der Klasse 10b beträgt genau vier Punkte.“
Beim Minigolf zählt jeder Schlag als Punkt.
Hat der Ball nach sechs Punkten das Ziel nicht erreicht, ist ein Zusatzpunkt anzurechnen.
Die Höchstpunktzahl an einer Bahn beträgt also sieben Punkte.
Die Diagramme und die Boxplots zeigen die Ergebnisse der beiden Klassen nach der ersten Bahn.



Wie viel Prozent der Schüler der Klasse 10a haben fünf oder mehr Punkte?
Überprüfe folgende Aussage:
„Die durchschnittliche Punktzahl der Klasse 10b beträgt genau vier Punkte.“
4 P
Lösung 1
1. Schritt: Länge der StreckeLösung 2
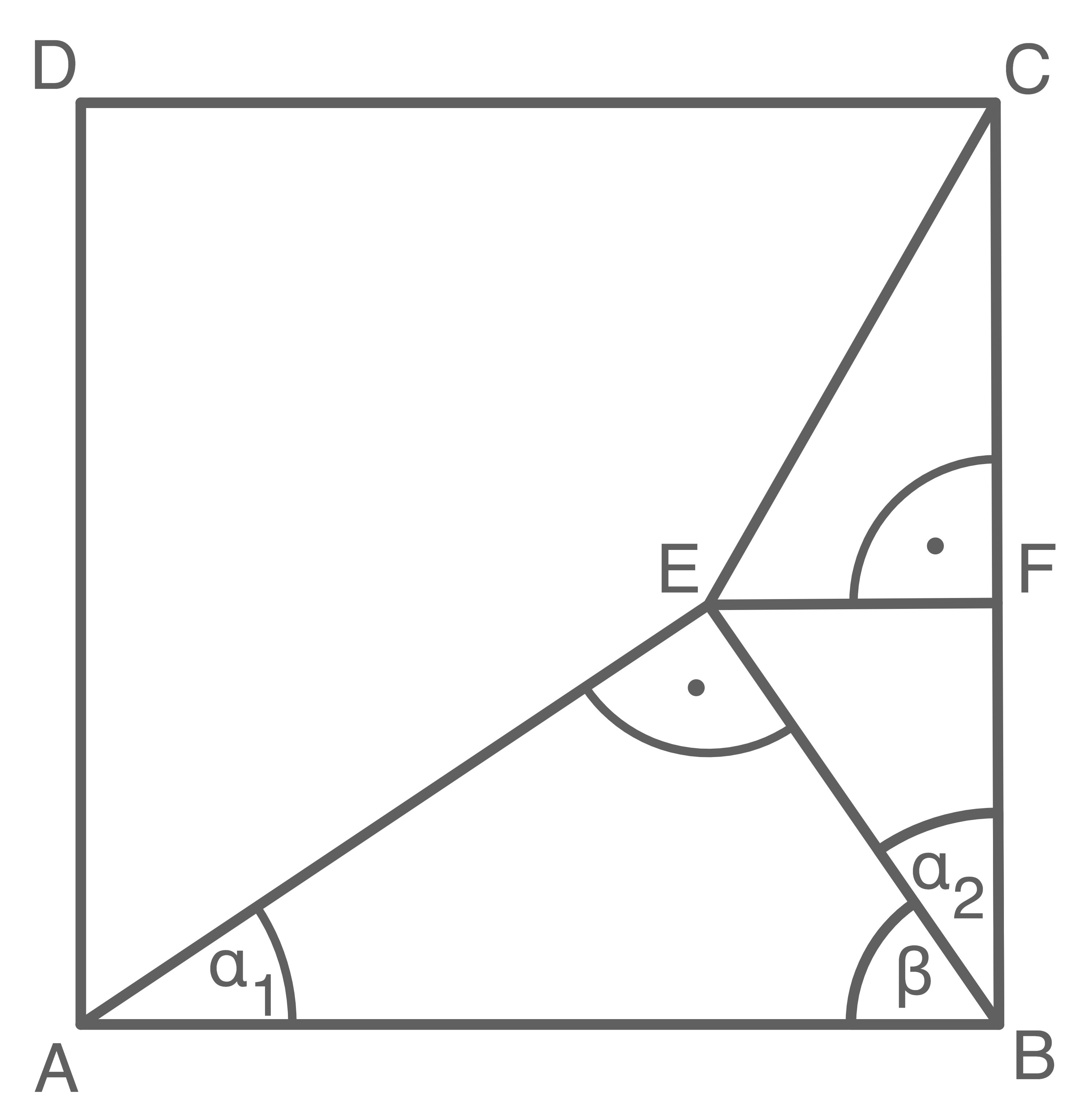
Lösung 3
Volumen der Pyramide berechnen 1. Schritt: Länge der Diagonale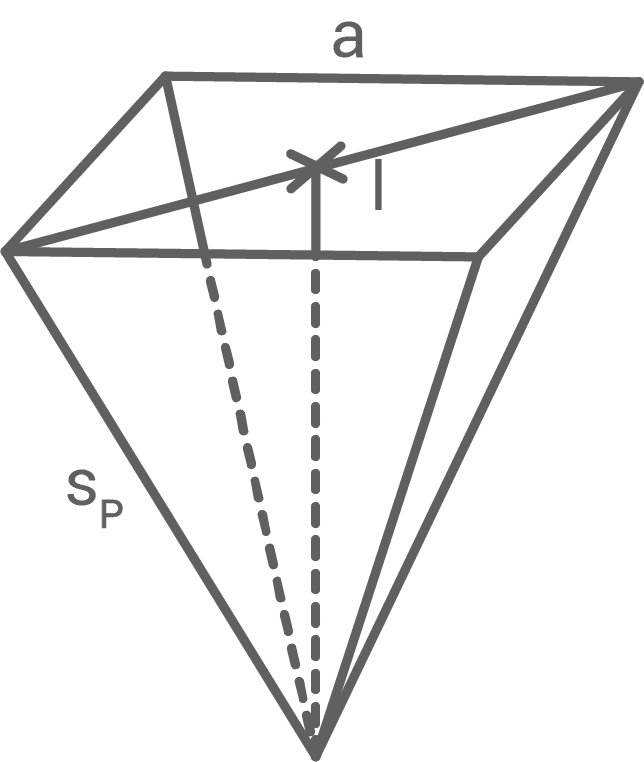
Lösung 4
Fehlende Angabe ergänzen 1. Schritt: Anzahl rote und blaue Kugeln berechnenEs gilt also: Da nach der Ziehung der ersten grünen Kugel nur noch 19 Kugeln im Behälter sind, liegt die Wahrscheinlichkeit für die zweite grüne Kugel bei
Die Wahrscheinlichkeit für die erste grüne Kugel liegt noch immer bei
Lösung 5
Welcher Graph gehört zur angegebenen Wertetabelle? Durch die Punktprobe können die verschiedenen Werte geprüft werden:- Punkt
: Da nur die Parabeln
und
durch diesen Punkt verlaufen, können die anderen beiden Parabeln ausgeschlossen werden.
- Punkt
: Nur Parabel
verläuft durch diesen Punkt. Die gegebene Wertetabelle gehört also zur Parabel
.
Es gilt also:
Lösung 6
1. Schritt: Gleichung (1) nachLösung 7
Um wie viel Prozent ist der Wert der Aktie von 2010 bis 2013 insgesamt angestiegen? 1. Schritt: Wertveränderung