Pflichtbereich
Aufgabe P1
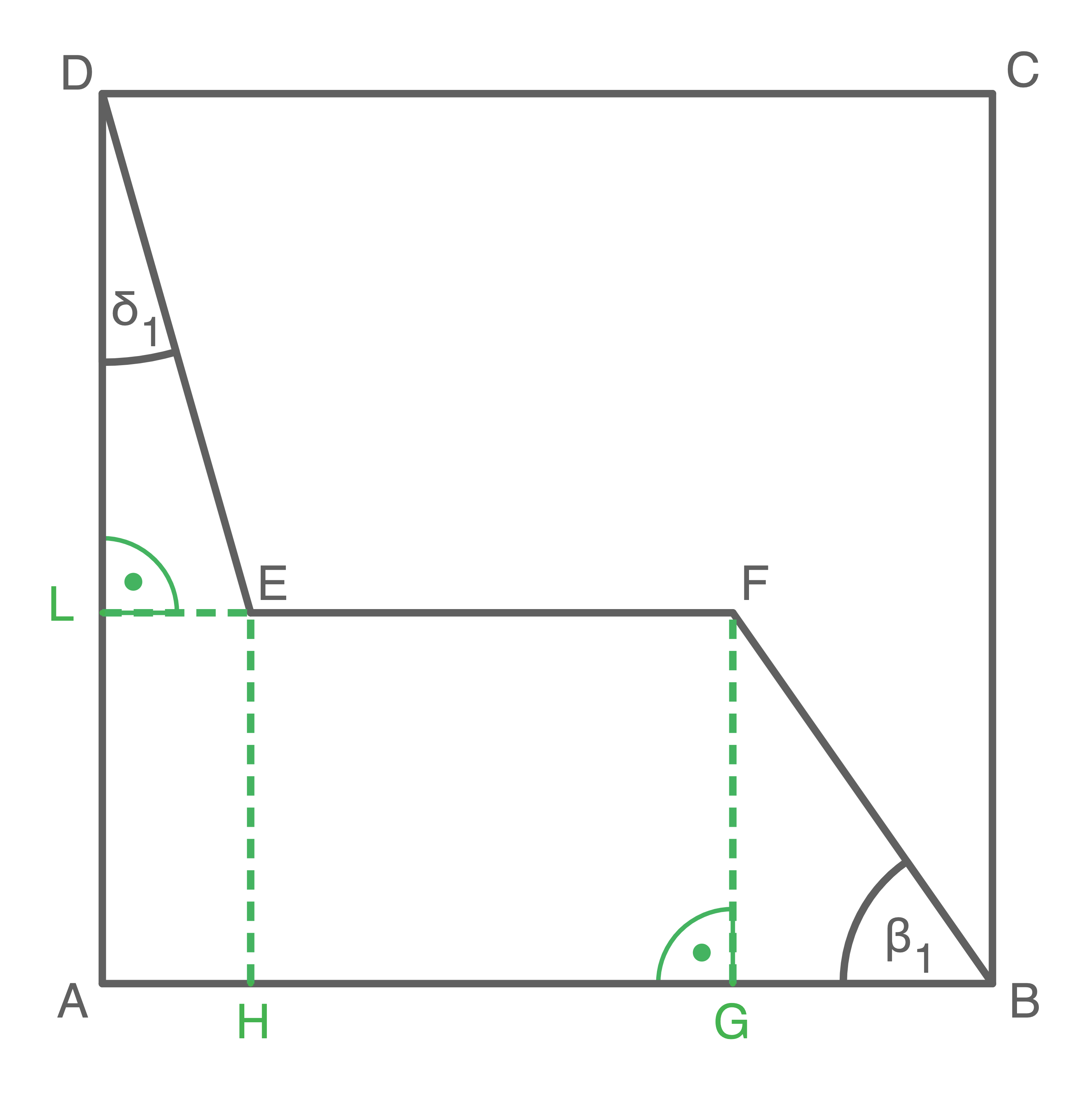
lm Quadrat  Iiegt der Streckenzug
Iiegt der Streckenzug 
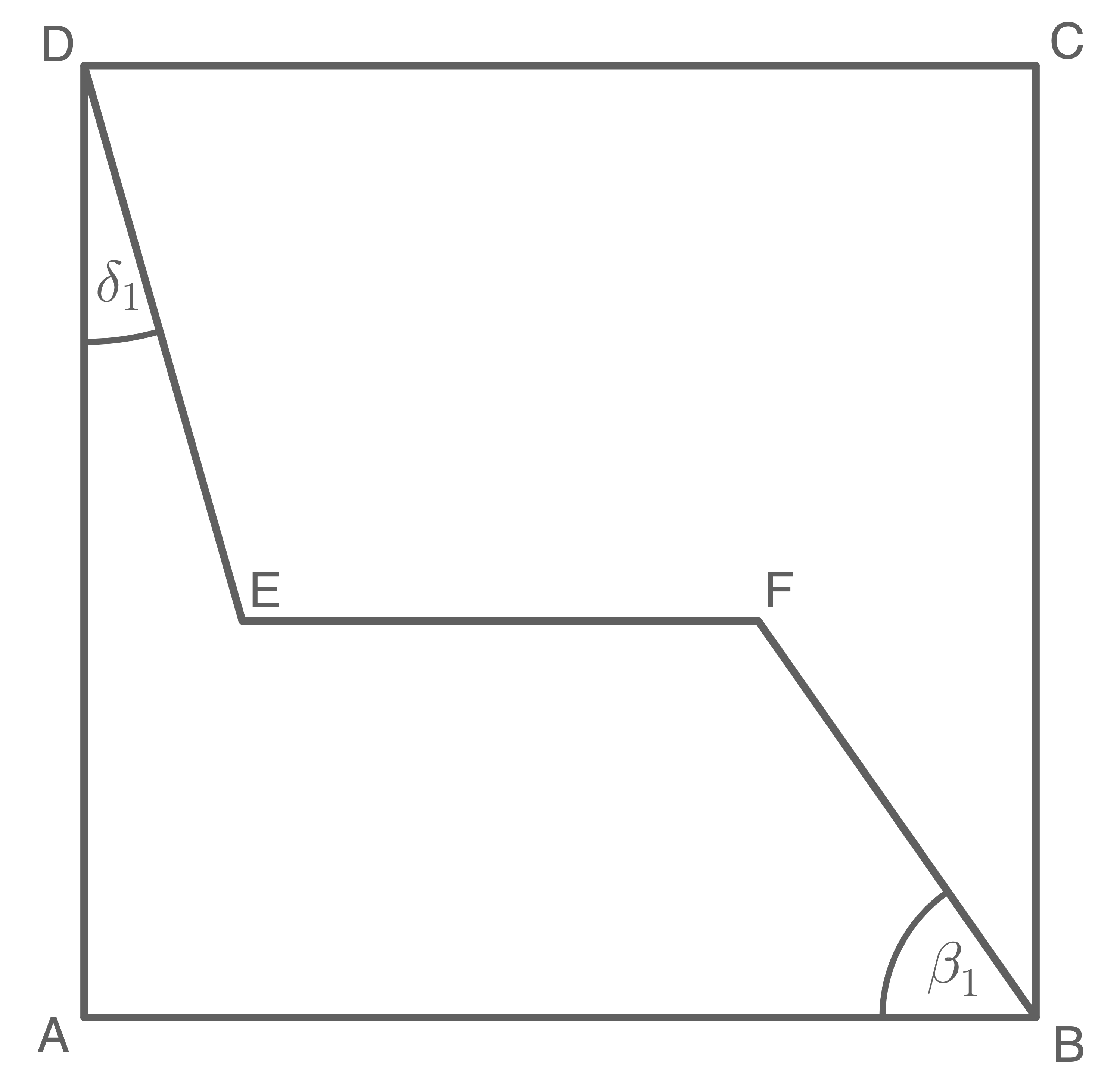 Es gilt:
Es gilt:




 verläuft parallel zu
verläuft parallel zu  Berechne den Winkel
Berechne den Winkel 

(4 P)
Aufgabe P2
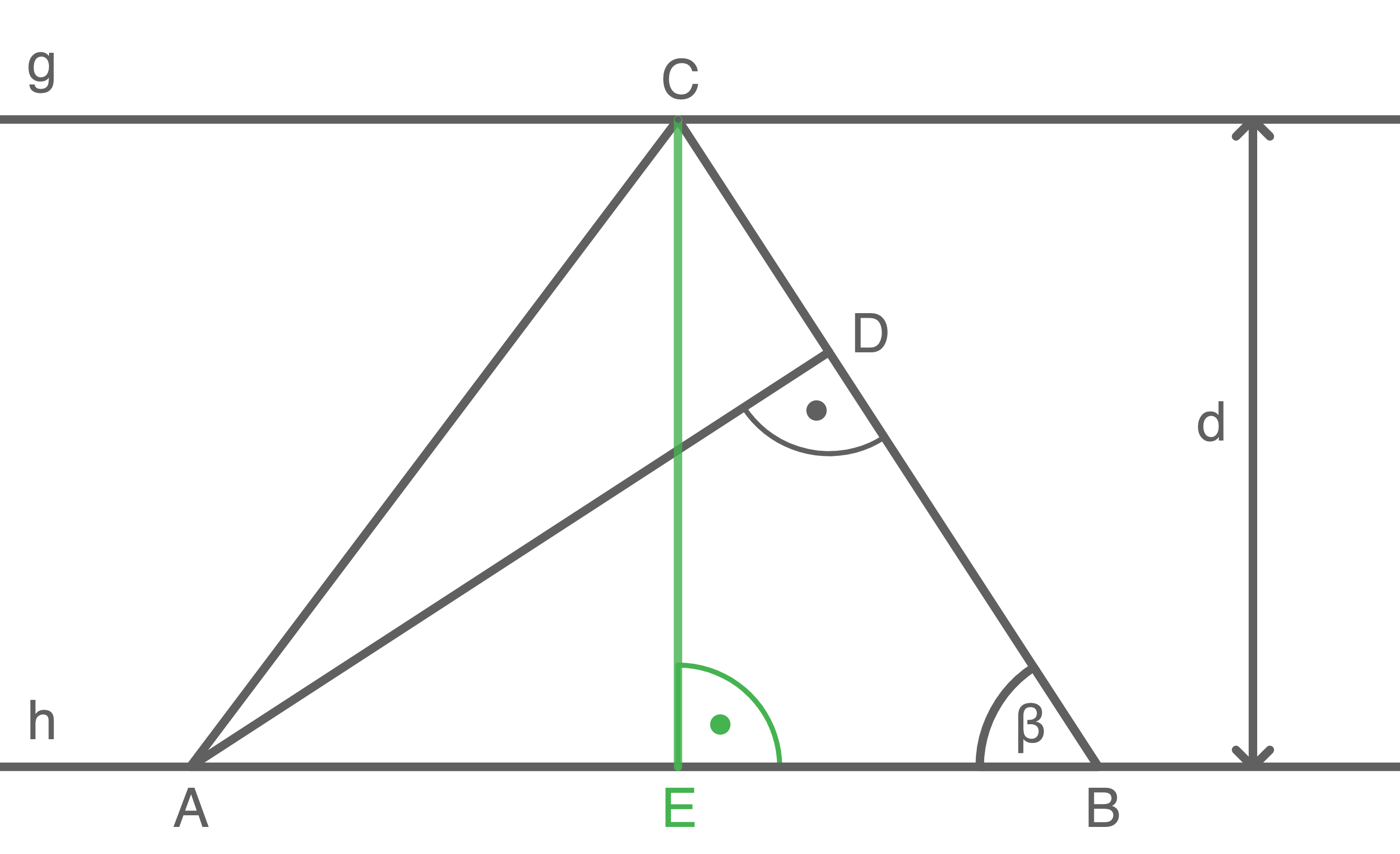
Die Eckpunkte des Dreiecks  liegen auf den Parallelen
liegen auf den Parallelen  und
und 
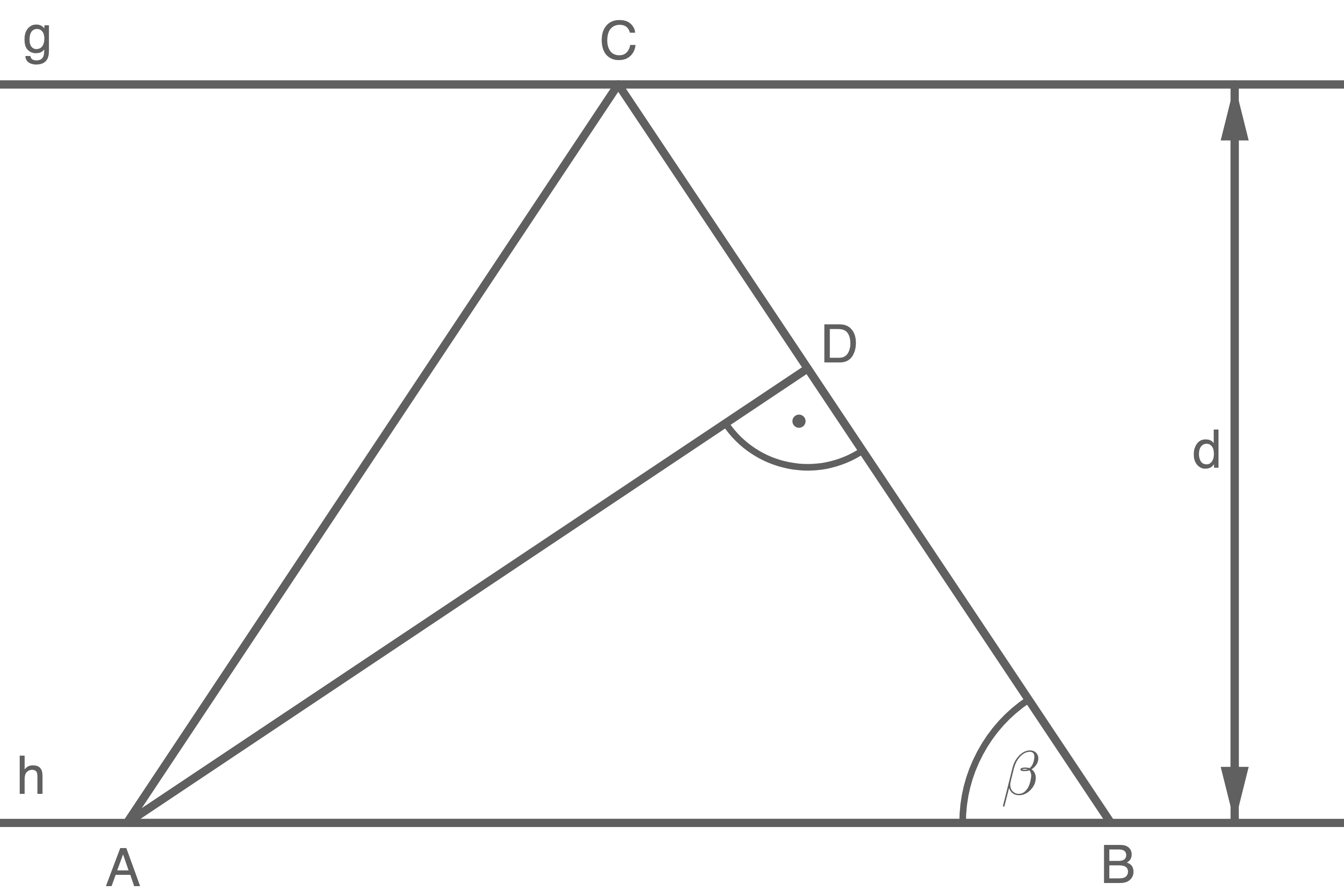 Es gilt:
Es gilt:


 Berechne den Umfang des Dreiecks
Berechne den Umfang des Dreiecks 

(4,5 P)
Aufgabe P3
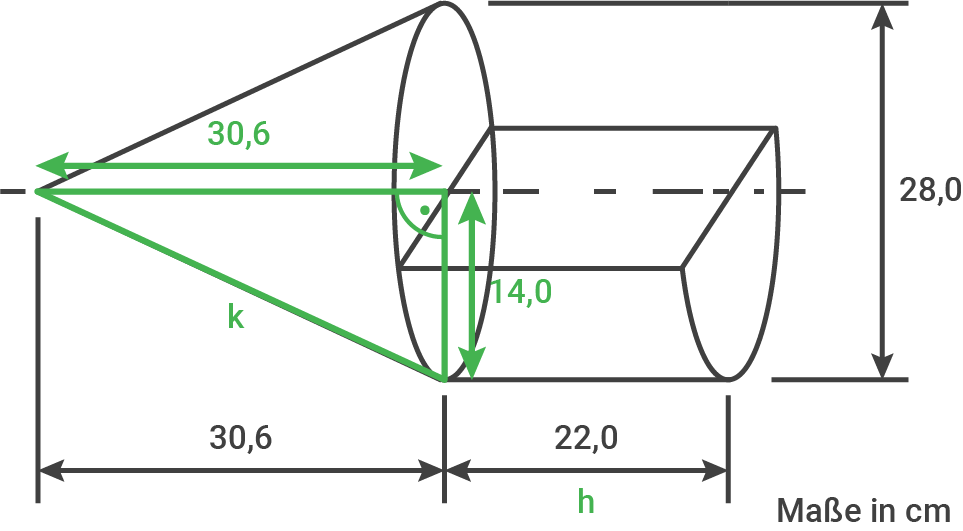
Ein Werkstück besteht aus einem Kegel und einem halben Zylinder.
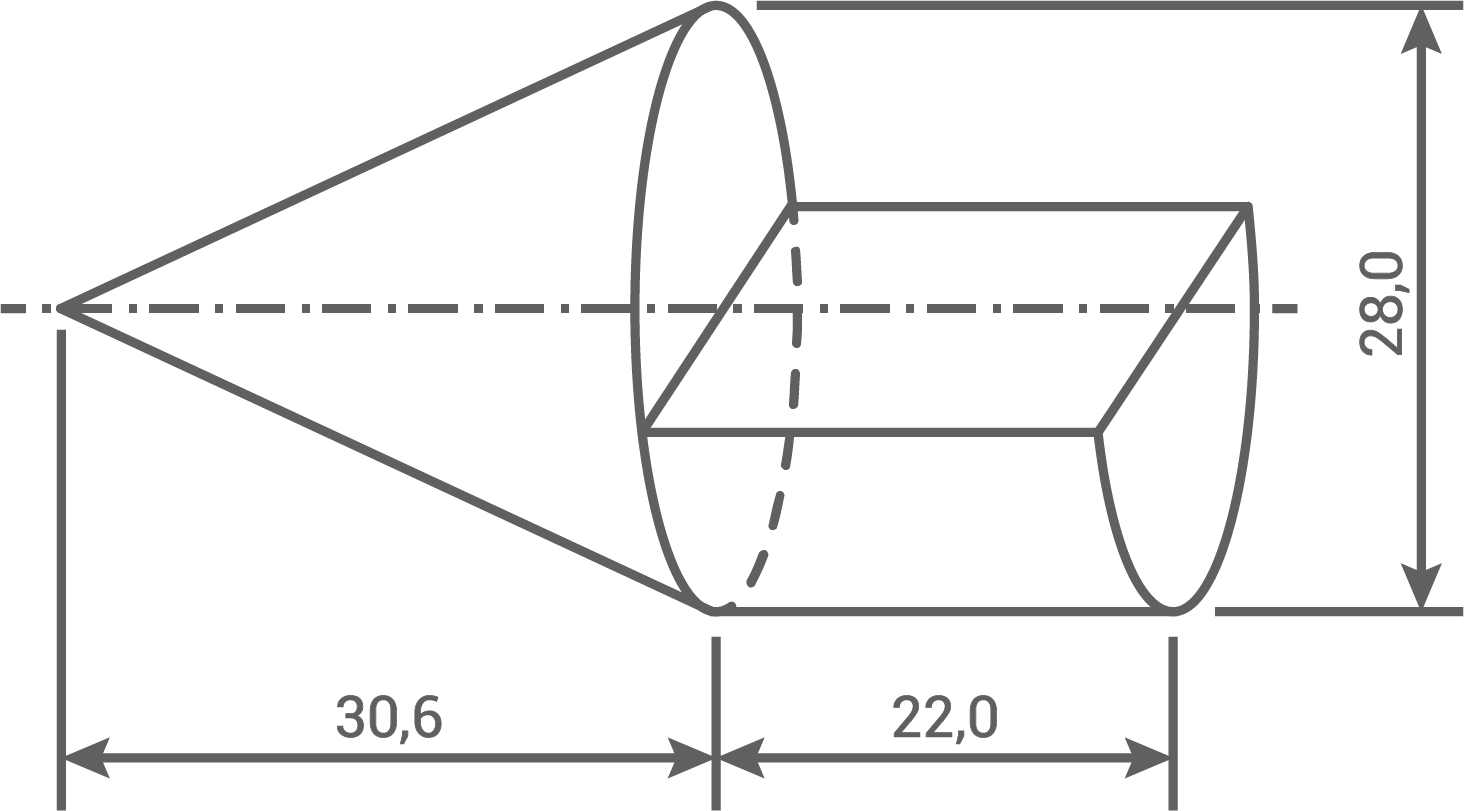 Berechne den Oberflächeninhalt des Werkstücks.
Berechne den Oberflächeninhalt des Werkstücks.

(Maße in cm)
(3,5 P)
Aufgabe P4
Löse die Gleichung:


(3,5 P)
Aufgabe P5
Gegeben sind fünf Funktionsgleichungen und drei Graphen.
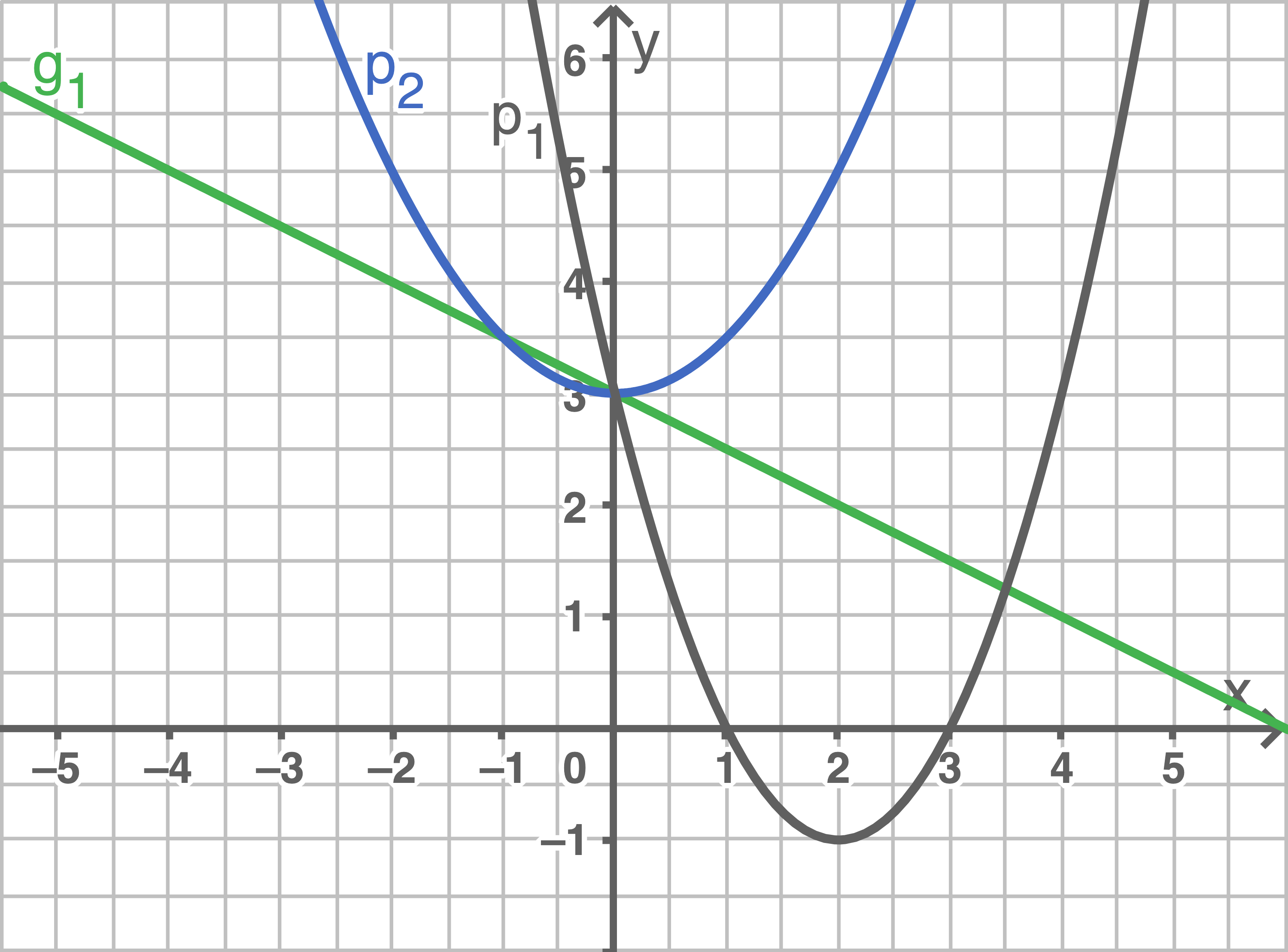 Ordne jedem Graphen die zugehörige Funktionsgleichung zu.
Ordne jedem Graphen die zugehörige Funktionsgleichung zu.
Begründe deine Entscheidung. Zeichne die beiden fehlenden Graphen in das Koordinatensystem ein.
(1)  (2)
(2)  (3)
(3)  (4)
(4)  (5)
(5) 

Begründe deine Entscheidung. Zeichne die beiden fehlenden Graphen in das Koordinatensystem ein.
(4 P)
Aufgabe P6
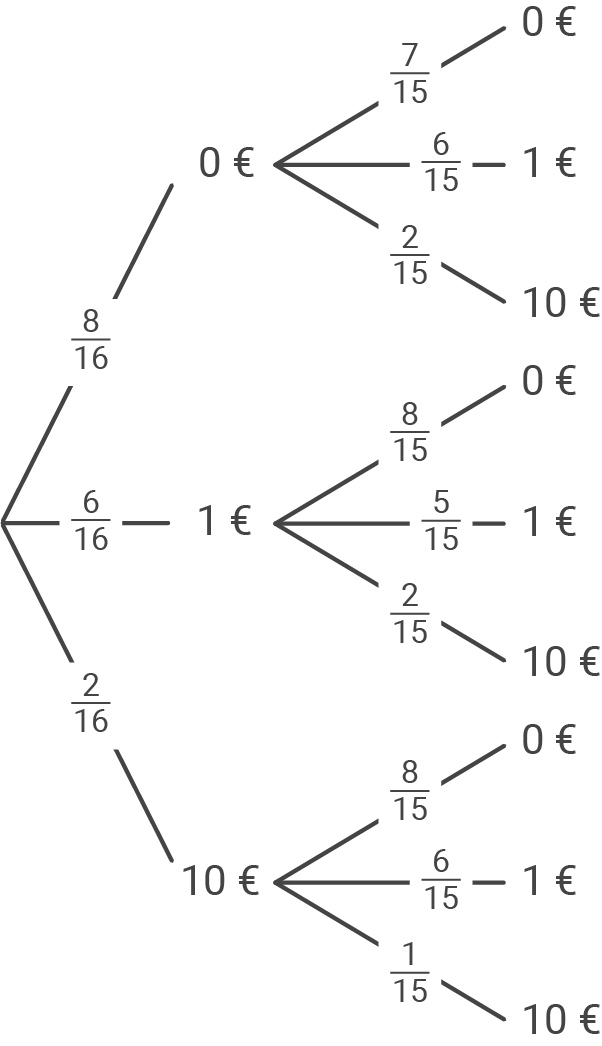
Ben, Laura und Emma besitzen jeweils ein Rubbel-Los. Auf jedem Los befinden sich 16 gleich große Felder.
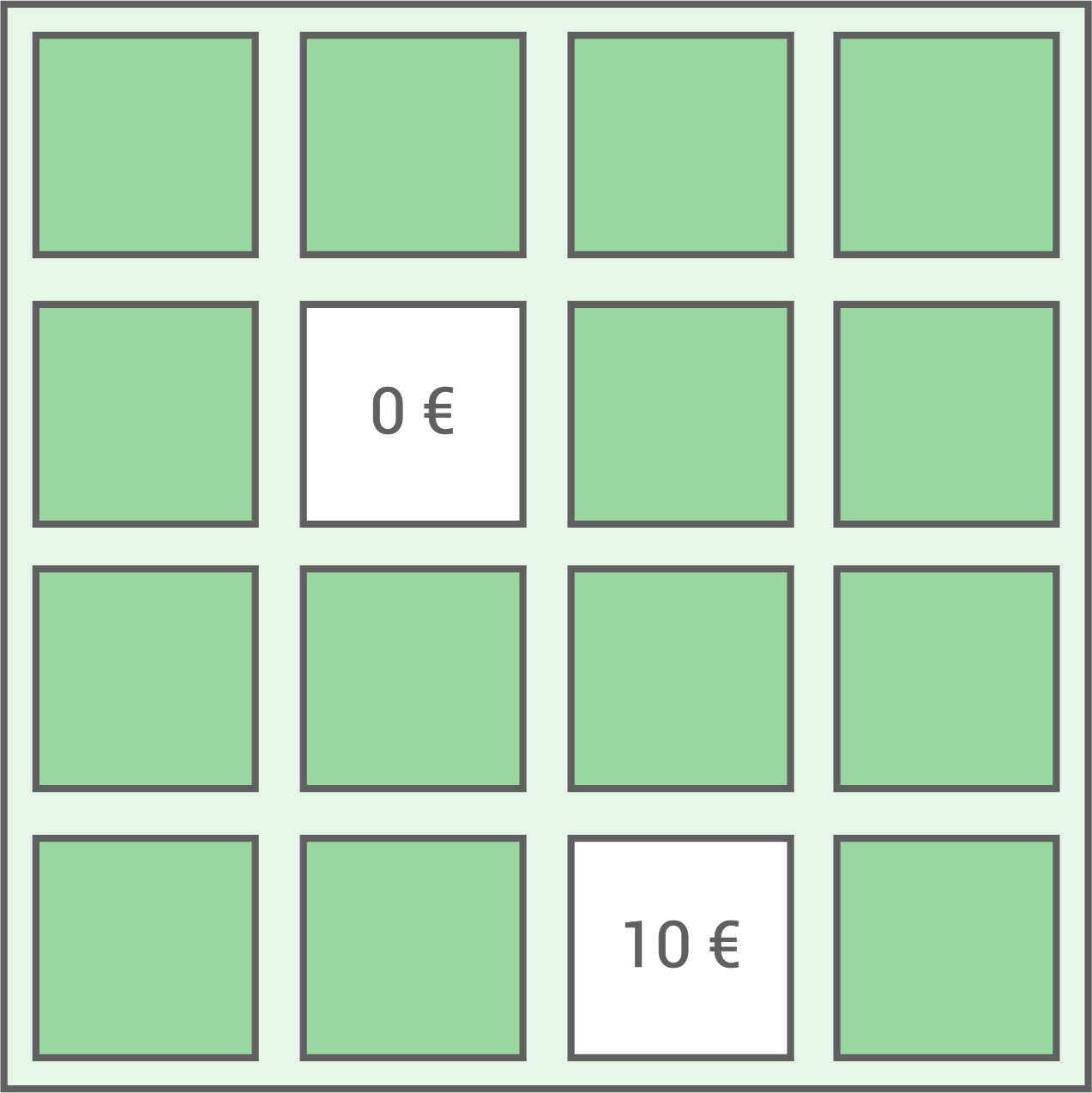 Nur zwei der 16 Felder werden freigerubbelt. Die beiden Beträge, die dadurch sichtbar werden, werden addiert und ergeben den Gewinn. Auf acht Feldern steht der Betrag
Nur zwei der 16 Felder werden freigerubbelt. Die beiden Beträge, die dadurch sichtbar werden, werden addiert und ergeben den Gewinn. Auf acht Feldern steht der Betrag  auf sechs Feldern steht der Betrag
auf sechs Feldern steht der Betrag  und auf zwei Feldern der Betrag
und auf zwei Feldern der Betrag 

- Ben hat auf seinem Los zwei Felder freigerubbelt (siehe Abbildung).
Berechne die Wahrscheinlichkeit für das Ereignis "Gewinn".
- Laura überlegt sich, wie groß die Wahrscheinlichkeit ist, den Hauptgewinn von
zu erhalten.
Berechne die Wahrscheinlichkeit. - Emma möchte mehr als
gewinnen.
Berechne diese Wahrscheinlichkeit.
(4 P)
Aufgabe P7
Die Diagramme zeigen den Verbrauch von Getränkeverpackungen.
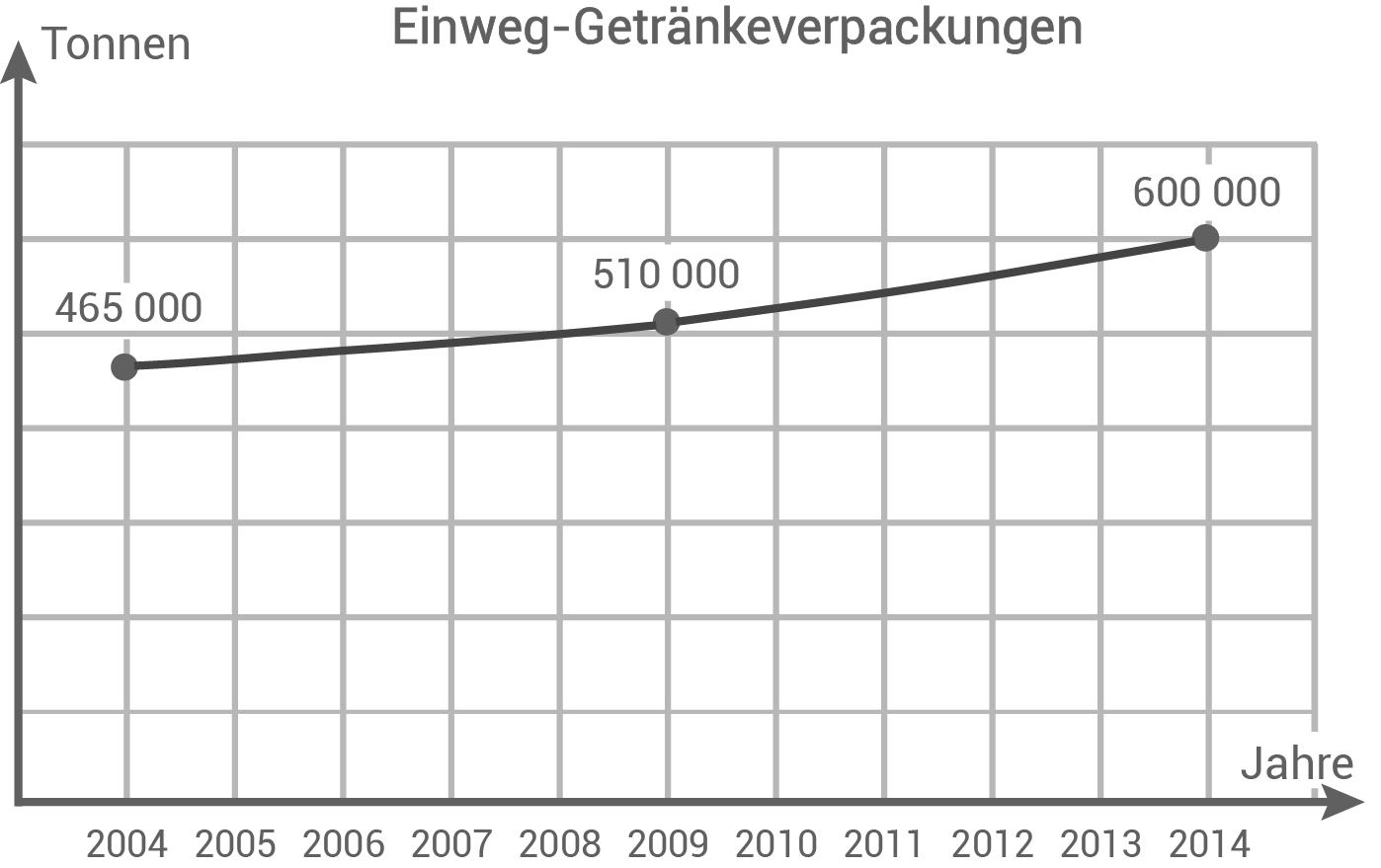
 Um wie viel Prozent ist der Verbrauch der Einweg-Getränkeverpackungen von 2004 bis 2014 insgesamt gestiegen?
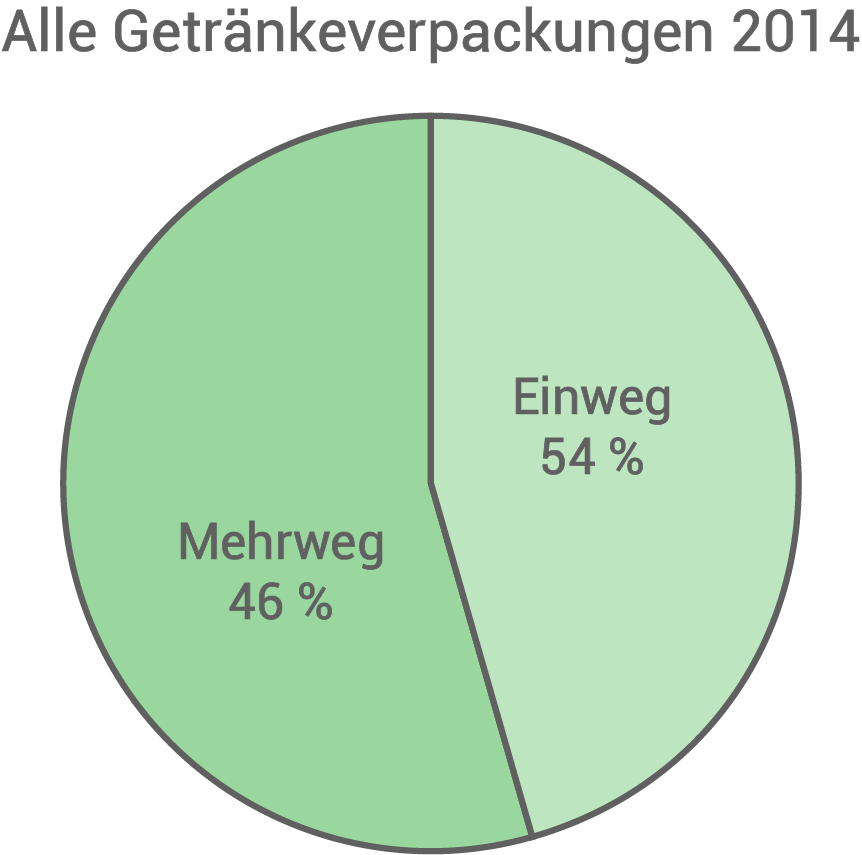
Wie viele Tonnen Getränkeverpackungen (Einweg und Mehrweg) wurden im Jahr 2014 insgesamt verbraucht?
Der Verbrauch von Einweg-Getränkeverpackungen soll in den zehn Jahren von 2014 bis 2024 jährlich um jeweils
Um wie viel Prozent ist der Verbrauch der Einweg-Getränkeverpackungen von 2004 bis 2014 insgesamt gestiegen?
Wie viele Tonnen Getränkeverpackungen (Einweg und Mehrweg) wurden im Jahr 2014 insgesamt verbraucht?
Der Verbrauch von Einweg-Getränkeverpackungen soll in den zehn Jahren von 2014 bis 2024 jährlich um jeweils  gegenüber dem Vorjahr sinken.
gegenüber dem Vorjahr sinken.
Wie viele Tonnen Einweg-Getränkeverpackungen wären es dann im Jahr 2024?


Wie viele Tonnen Einweg-Getränkeverpackungen wären es dann im Jahr 2024?
(3 P)
Aufgabe P8
lm Rahmen einer Untersuchung wurden die Wartezeiten beim Anruf zweier Hotlines notiert.
Das Diagramm zeigt die Wartezeiten von 41 Anrufern der Hotline QUICK-TEL.
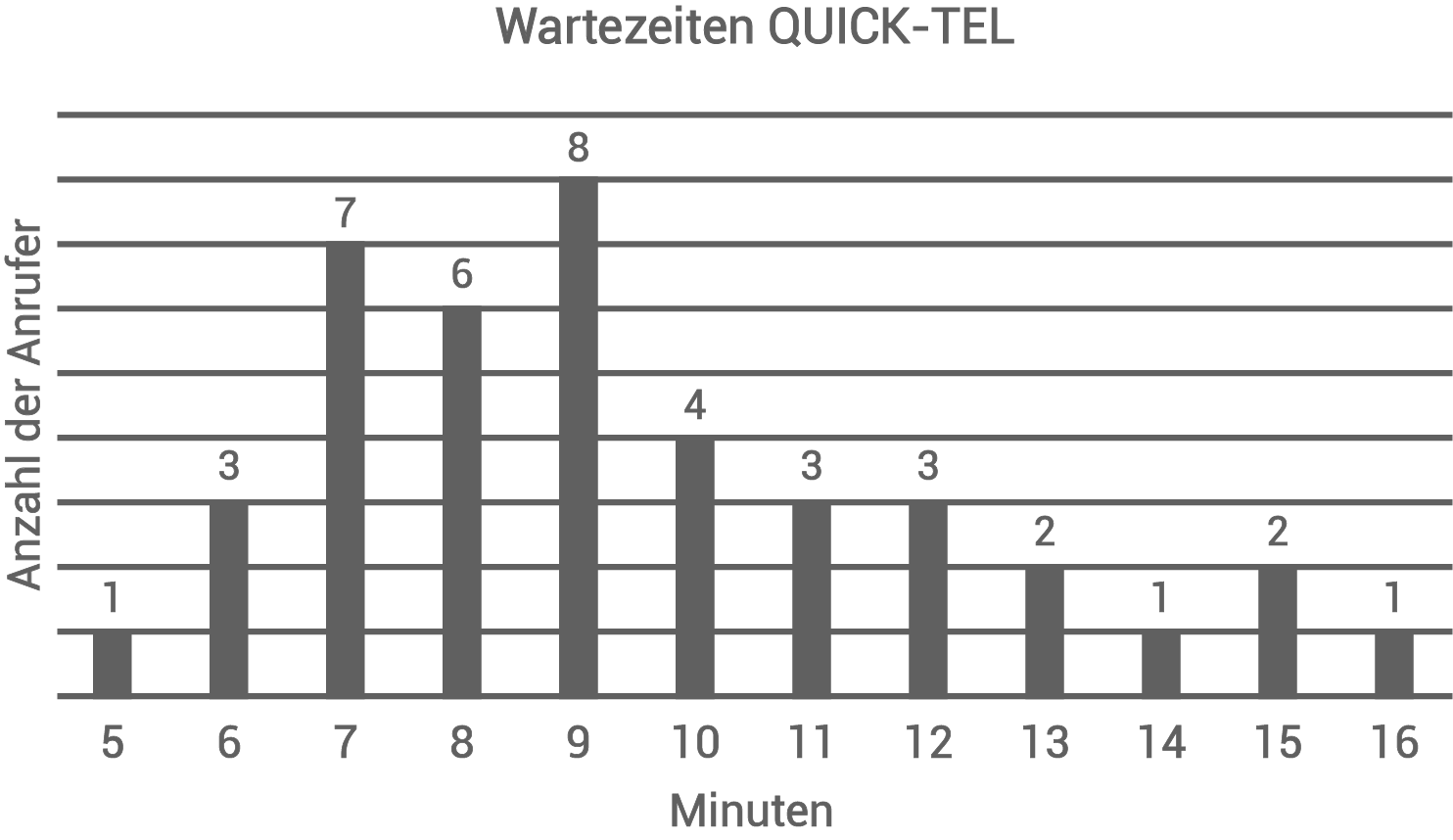 Welcher der beiden Boxplots stellt die Verteilung der Wartezeiten aus dem Diagramm dar?
Welcher der beiden Boxplots stellt die Verteilung der Wartezeiten aus dem Diagramm dar?
Begründe mit Hilfe der Kennwerte.
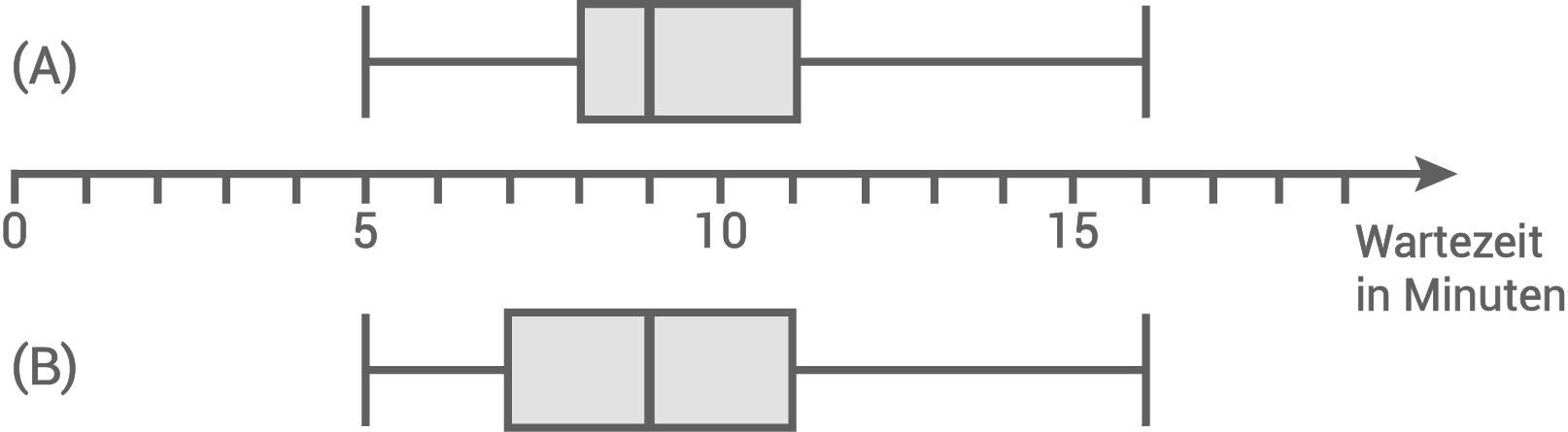 Der andere Boxplot zeigt die Verteilung der Wartezeiten der Hotline FAST-PHONE.
Der andere Boxplot zeigt die Verteilung der Wartezeiten der Hotline FAST-PHONE.
Hier wurden ebenfalls 41 Wartezeiten erfasst. ln der Strichliste fehlen die Werte für 8, 9 und 11 Minuten.
Ergänze diese drei Felder mit möglichen Werten.
Das Diagramm zeigt die Wartezeiten von 41 Anrufern der Hotline QUICK-TEL.

Begründe mit Hilfe der Kennwerte.

Hier wurden ebenfalls 41 Wartezeiten erfasst. ln der Strichliste fehlen die Werte für 8, 9 und 11 Minuten.
Ergänze diese drei Felder mit möglichen Werten.
| Minuten | Anzahl der Anrufer |
|---|---|
| 5 |  |
| 6 |  |
| 7 |  |
| 8 | |
| 9 | |
| 10 |  |
| 11 | |
| 12 |  |
| 13 |  |
| 14 |  |
| 15 |  |
| 16 |  |
(3,5 P)
Lösung P1
Lösung P2
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{\overline{AD}}{\overline{AB}}\quad \scriptsize \\[5pt]
\sin(57^{\circ})&=& \dfrac{\overline{AD}}{9,4\,\text{cm}}\quad \scriptsize \mid\; \cdot\,9,4\,\text{cm} \\[5pt]
\sin(57^{\circ})\cdot\,9,4\,\text{cm} &=& \overline{AD} \\[5pt]
\overline{AD} &=& \sin(57^{\circ})\cdot\,9,4\,\text{cm} \\[5pt]
\overline{AD} &=& \underline{ 7,88\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/a32a7a5edfdf7a32c1036e272a06e23572222de7466dcd7602e4c013d855eaf7?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{\overline{CE}}{\overline{CB}}\\[5pt]
\sin(57^{\circ})&=&\dfrac{6,7\,\text{cm}}{\overline{CB}} \qquad \scriptsize \mid\; \cdot\,\overline{CB} \\[5pt]
\sin(57^{\circ})\cdot \overline{CB}&=&6,7\,\text{cm} \qquad \scriptsize \mid\; : \sin(57^{\circ})\\[5pt]
\overline{CB}&=&\dfrac{6,7\,\text{cm}}{\sin(57^{\circ})} \\[5pt]
\overline{CB}&=&\underline{ 7,99\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/4b9818851f6a3b93e891b6292b1ae5740a78274e6a7fe10a6defeb5c3689a99b?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{DB}}{\overline{AB}} \quad \scriptsize \\[5pt]
\cos(57^{\circ})&=&\dfrac{\overline{DB}}{9,4\,\text{cm}} \quad \scriptsize \mid\;\cdot 9,4\,\text{cm} \\[5pt]
\cos(57^{\circ})\cdot9,4\,\text{cm} &=& \overline{DB} \\[5pt]
\overline{DB} &=& \cos(57^{\circ})\cdot9,4\,\text{cm} \\[5pt]
\overline{DB}&=&\underline{ 5,12\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/28fc0f76fe53acb6782d0e253c1abbbd32a7b1e8ea1913ccf75cb460bab7dfa5?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}&=& \overline{CB}-\overline{DB}&\quad \scriptsize \\[5pt]
&=& 7,99\,\text{cm}-5,12\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 2,87\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/2be525c9026ef2eaab25137ce6addcc5a702f7401e962863b1bc514f36ccc985?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2&=&\overline{AD}^2+\overline{CD}^2 \\[5pt]
\overline{AC}^2&=&(7,88\,\text{cm})^2+(2,87\,\text{cm})^2 \; \scriptsize \mid\;\sqrt{\,} \\[5pt]
\overline{AC}&=&\sqrt{(7,88\,\text{cm})^2+(2,87\,\text{cm})^2} \\[5pt]
\overline{AC}&= & \underline{ 8,39\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/6df06376851b80b16c736121dfa4465506a9f55f858a9a07d2abfe5a8594fa27?color=5a5a5a) Umfang berechnen
Umfang berechnen
![\(\begin{array}[t]{rll}
u&=& \overline{AD}+\overline{CD}+\overline{AC}\\[5pt]
&=&7,88\,\text{cm}\,+2,87\,\text{cm}+8,39\,\text{cm}\\[5pt]
&=&19,14\,\text{cm}\\[5pt]
u&=&\underline{\underline{ 19,1\,\text{cm} }}
\end{array}\)](https://mathjax.schullv.de/ed054cf3b0ea79196db4a53fc23aae7d2774a4a1e9dec6fb054b0145c50c921d?color=5a5a5a)

Lösung P3
Radius des Kegels berechnen
 Kantenlänge des Kegelmantels berechnen
Kantenlänge des Kegelmantels berechnen
![\(\begin{array}[t]{rll}
k^2&=&(30,6\,\text{cm})^2+(14,0\,\text{cm})^2\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
k&=&\sqrt{(30,6\,\text{cm})^2+(14,0\,\text{cm})^2} \\[5pt]
k&=&\underline{ 33,65\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/1ba9ae324cd392080a11c8123282e8172c4837d41468890db04e879ff168a25f?color=5a5a5a) Oberflächeninhalt berechnen
Oberflächeninhalt berechnen

Lösung P4
Lösung P5
Graphen zuordnen

 kein passender Graph
Die Funktionsgleichung beschreibt eine Gerade mit positiver Steigung
kein passender Graph
Die Funktionsgleichung beschreibt eine Gerade mit positiver Steigung  und dem
und dem  -Achsenabschnitt
-Achsenabschnitt  Da es keine steigende Gerade gibt, kann die Funktionsgleichung keinem Graphen zugeordnet werden. Der Graph muss neu eingezeichnet werden.
Da es keine steigende Gerade gibt, kann die Funktionsgleichung keinem Graphen zugeordnet werden. Der Graph muss neu eingezeichnet werden.

 kein passender Graph
Umformung mit quadratischer Ergänzung:
kein passender Graph
Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2+4x+3 \\[5pt]
y&=&x^2+2\cdot 2x+3 \\[5pt]
y &=&x^2+2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x+2)^2-1
\end{array}\)](https://mathjax.schullv.de/cd7edf9aaee45253702a437acf573f94ba901d2a698e64beff792f1fe0b4ed44?color=5a5a5a) Der zugehörige Graph besitzt den Scheitelpunkt
Der zugehörige Graph besitzt den Scheitelpunkt  Da es keinen Graphen mit diesem Scheitelpunkt gibt, muss der Graph dieser Funktion neu eingezeichnet werden.
Da es keinen Graphen mit diesem Scheitelpunkt gibt, muss der Graph dieser Funktion neu eingezeichnet werden.


 Die Funktionsgleichung beschreibt eine Parabel, die durch ihren
Die Funktionsgleichung beschreibt eine Parabel, die durch ihren  -Achsenabschnitt um
-Achsenabschnitt um  Einheiten nach oben verschoben ist, mit dem Faktor
Einheiten nach oben verschoben ist, mit dem Faktor  gestaucht wurde und den Scheitelpunkt
gestaucht wurde und den Scheitelpunkt  besitzt.
Diese Eigenschaften treffen auf den Graphen
besitzt.
Diese Eigenschaften treffen auf den Graphen  zu.
zu.


 Umformung mit quadratischer Ergänzung:
Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2-4x+3 \\[5pt]
y &=&x^2-2\cdot 2x+3 \\[5pt]
y &=&x^2-2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x-2)^2-1
\end{array}\)](https://mathjax.schullv.de/7c8c733974479bbec3284f43dcd2fcca8e11ea714bd696f72d4ed55254f31312?color=5a5a5a) Der Graph besitzt den Scheitelpunkt
Der Graph besitzt den Scheitelpunkt  .
Deshalb kann die Funktionsgleichung dem Graphen
.
Deshalb kann die Funktionsgleichung dem Graphen  zugeordnet werden.
zugeordnet werden.


 Die Funktionsgleichung beschreibt eine Gerade mit negativer Steigung
Die Funktionsgleichung beschreibt eine Gerade mit negativer Steigung  und mit dem
und mit dem  -Achsenabschnitt
-Achsenabschnitt  .
Dies trifft auf den Graphen
.
Dies trifft auf den Graphen  zu.
Fehlende Graphen einzeichnen
zu.
Fehlende Graphen einzeichnen
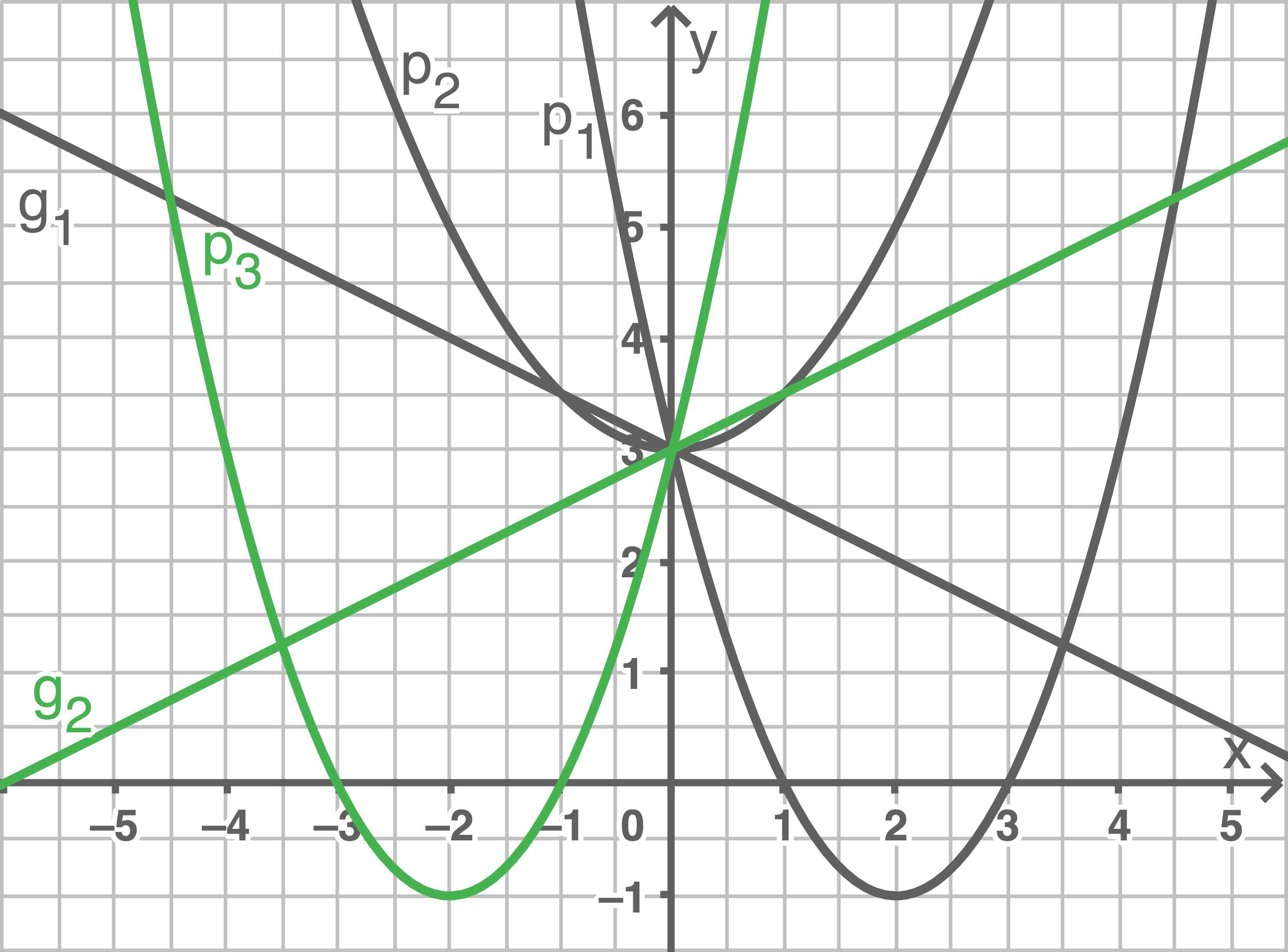
(1)
(2)
(3)
(4)
(5)

Lösung P6
Lösung P7
Um wie viel Prozent ist der Verbrauch der Einweg-Getränkeverpackungen von 2004 bis 2014 insgesamt gestiegen?
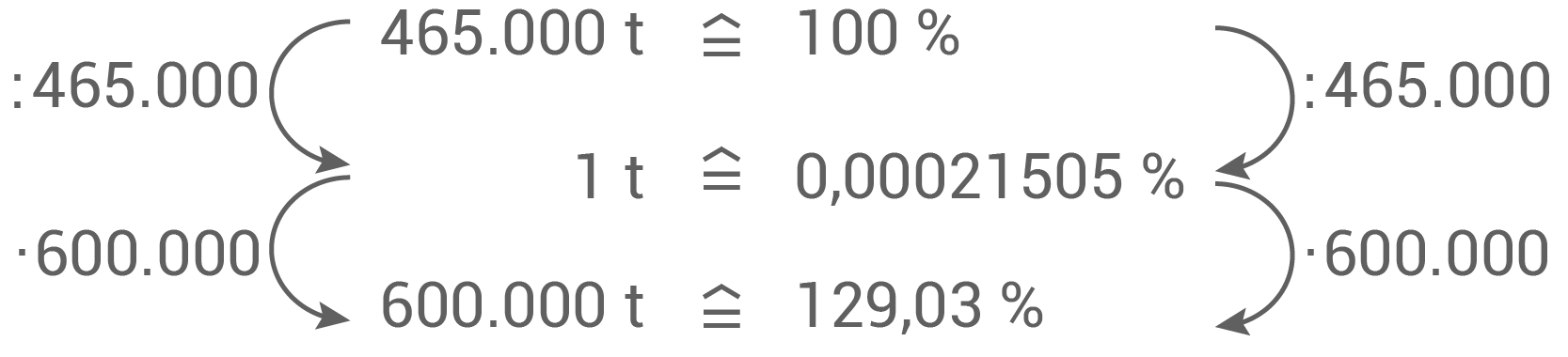

 Der Verbrauch der Einweg-Getränkeverpackungen ist also um 29 % gestiegen.
Wie viele Tonnen Getränkeverpackungen wurden 2014 insgesamt verbraucht?
Der Verbrauch der Einweg-Getränkeverpackungen ist also um 29 % gestiegen.
Wie viele Tonnen Getränkeverpackungen wurden 2014 insgesamt verbraucht?
 Im Jahr 2014 wurden insgesamt
Im Jahr 2014 wurden insgesamt  Getränkeverpackungen verbraucht.
Wie viele Tonnen Einweg-Getränkeverpackungen wären es dann im Jahr 2024?
Getränkeverpackungen verbraucht.
Wie viele Tonnen Einweg-Getränkeverpackungen wären es dann im Jahr 2024?
![\(\begin{array}[t]{rll}
G_{2024}&=& G_{2014} \cdot q^n \\[5pt]
&=& 600.000\,\text{t} \cdot (1-0,05)^{10} \\[5pt]
&=& 600.000\,\text{t} \cdot 0,95^{10} \\[5pt]
&=& \underline{\underline{ 359.242,2\,\text{t}}}
\end{array}\)](https://mathjax.schullv.de/6047d7b1d363bdabce51e885cc02eb5f73a93f31558a0cfcd663a7257d4e9775?color=5a5a5a) Im Jahr 2024 wären es also 359.242,2 t Einweg-Getränkeverpackungen.
Im Jahr 2024 wären es also 359.242,2 t Einweg-Getränkeverpackungen.
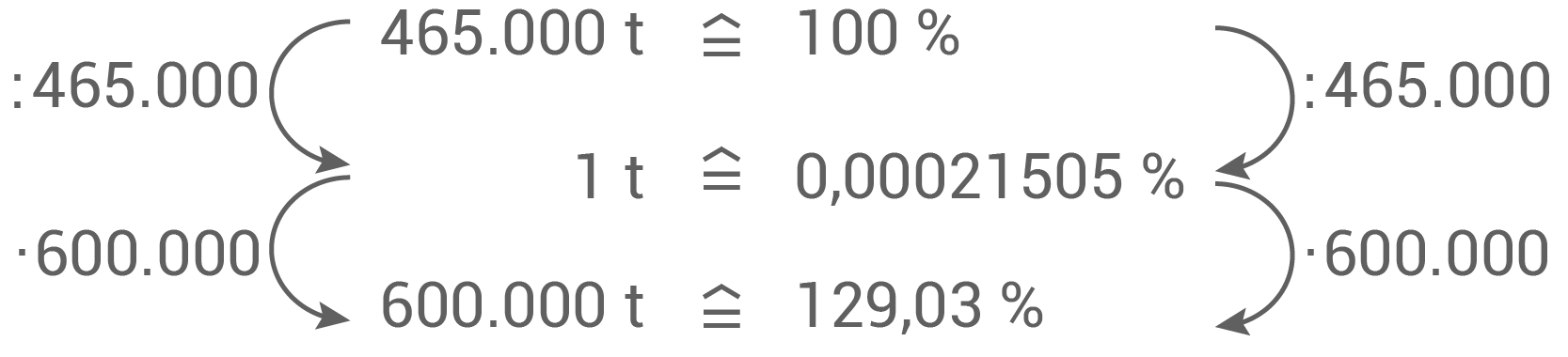

Lösung P8
Welcher der beiden Boxplots stellt die Verteilung der Wartezeiten aus dem Diagramm dar?
Die beiden Boxplots unterscheiden sich nur im unteren Quartil.

 Anhand des Diagrammes sieht man, dass die Anruferzahl von 11 nach 7 min erreicht ist.
Dies entspricht
Anhand des Diagrammes sieht man, dass die Anruferzahl von 11 nach 7 min erreicht ist.
Dies entspricht  Tabelle ergänzen
1. Schritt: Anzahl fehlender Striche berechnen
Tabelle ergänzen
1. Schritt: Anzahl fehlender Striche berechnen

 2. Schritt: Kennwerte ermitteln
2. Schritt: Kennwerte ermitteln


Die Anruferzahl von 11 ist nach 8 min erreicht (= unteres Quartil).

Die Anruferzahl von 21 ist nach 9 min erreicht (= Zentralwert).

Die Anruferzahl von 31 ist nach 11 min erreicht (= oberes Quartil).
Hinweis: Dies ist nur eine mögliche Lösung, es gibt noch weitere. Wichtig ist, dass die Kennwerte des Boxplots korrekt erfüllt sind.
Die Anruferzahl von 11 ist nach 8 min erreicht (= unteres Quartil).
Die Anruferzahl von 21 ist nach 9 min erreicht (= Zentralwert).
Die Anruferzahl von 31 ist nach 11 min erreicht (= oberes Quartil).
| Minuten | Anzahl der Anrufer |
|---|---|
| 5 |  |
| 6 |  |
| 7 |  |
| 8 |  |
| 9 |   |
| 10 |  |
| 11 |   |
| 12 |  |
| 13 |  |
| 14 |  |
| 15 |  |
| 16 |  |