Wahlteil B
Aufgabe 1
a)
Gegeben ist das Trapez  für das gilt:
für das gilt:
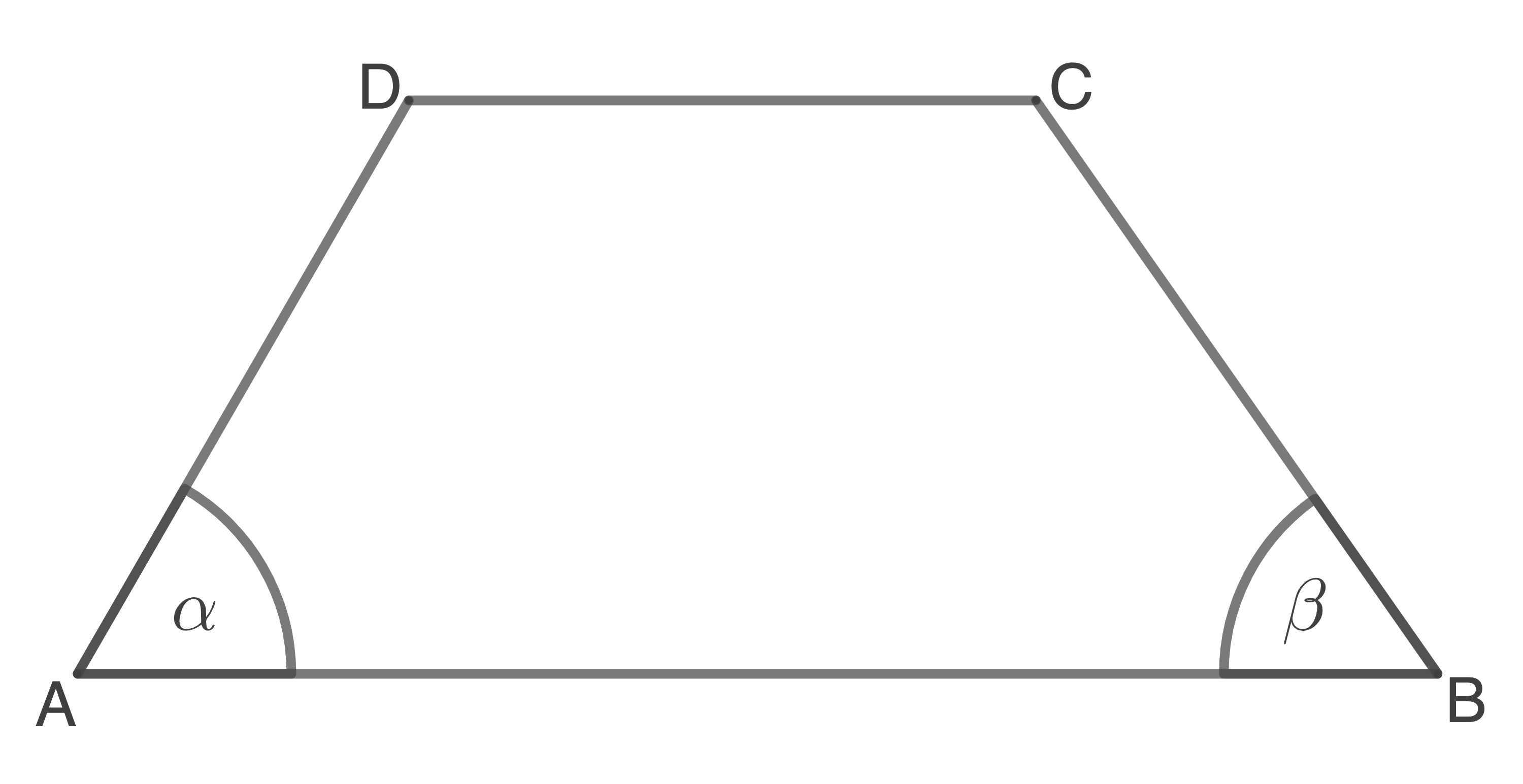


(Skizze nicht maßstäblich)
(5 P)
b)
Die Funktionsgleichung einer Parabel  lautet
lautet  Eine weitere Parabel
Eine weitere Parabel  ist gegeben mit
ist gegeben mit  Durch die beiden Scheitelpunkte der Parabeln
Durch die beiden Scheitelpunkte der Parabeln  und
und  verläuft eine Gerade
verläuft eine Gerade  .
.
- Bestimme die Gleichung dieser Geraden
.
- Bestimme die Gleichung der zur Geraden
senkrechten Gerade
durch den Punkt
und gib deren Schnittpunkt mit der
-Achse an.
(5 P)
Aufgabe 2
a)
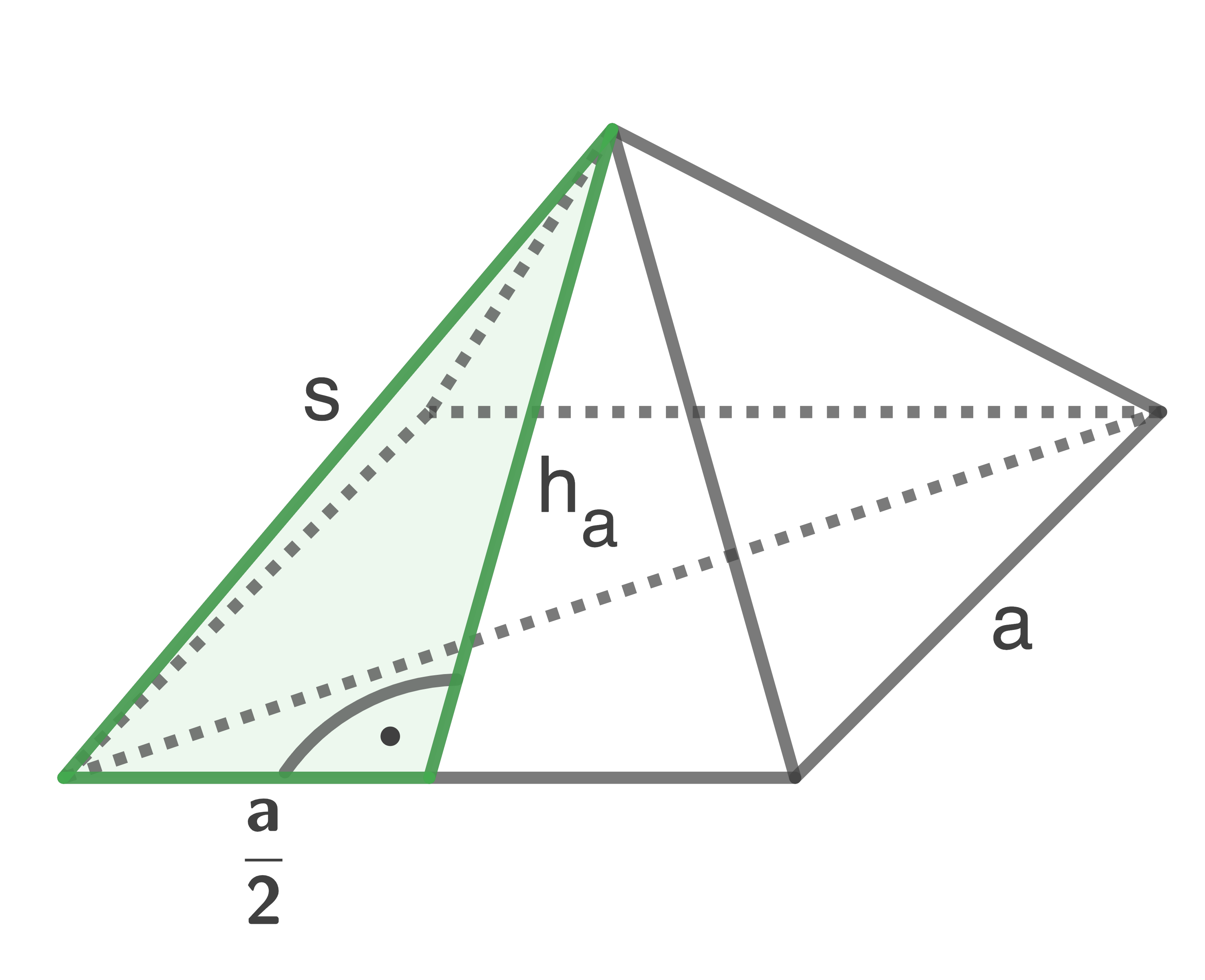
Die Abbildung zeigt einen zusammengesetzten Körper, der aus einem Quader mit aufgesetzter Pyramide besteht.
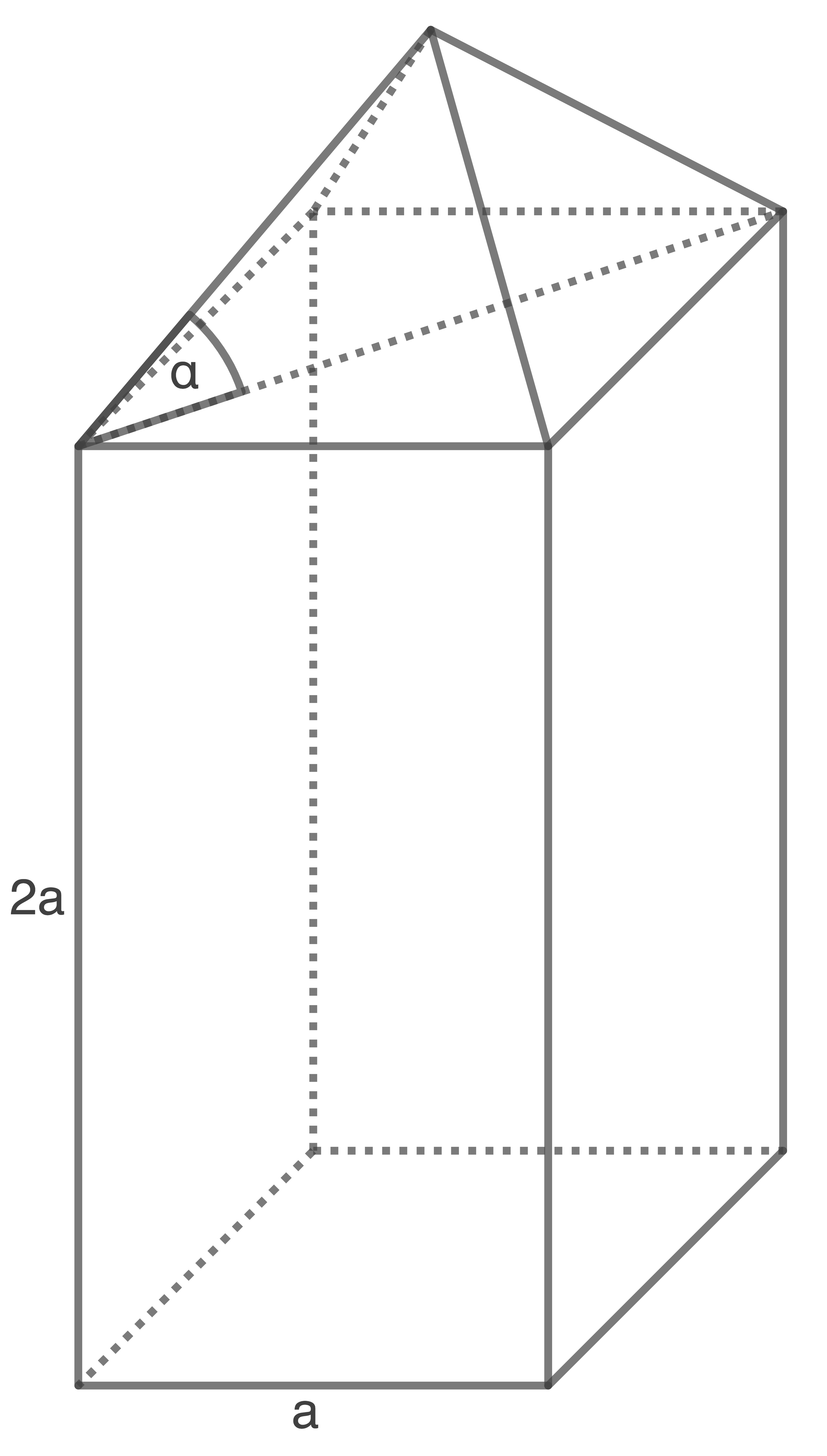 Es gilt:
Es gilt:


(Skizze nicht maßstäblich)
(5,5 P)
b)
Eine Umfrage über die Höhe des Taschengeldes in der Klasse 6a ergab folgende Strichliste:
| Betrag in € | Anzahl Schüler*innen |
|---|---|
| 14,00 | |
| 14,50 | |
| 16,00 | |
| 17,00 | |
| 18,00 | |
| 18,50 | |
| 19,00 | |
| 22,00 | |
| 24,00 |
- Berechne das arithmetische Mittel sowie den Zentralwert (Median).
- Stelle die Verteilung der Werte in einem Boxplot dar.
- Um wie viel Prozent weicht dieser Wert vom Zentralwert aus der Befragung der Klasse 6a ab?
(4,5 P)
Aufgabe 3
a)
Eine Parabel  ist gegeben durch die Gleichung
ist gegeben durch die Gleichung  Außerdem ist die Gerade
Außerdem ist die Gerade  mit der Gleichung
mit der Gleichung  gegeben.
gegeben.
Eine zweite Gerade verläuft parallel zu
verläuft parallel zu  und durch den Scheitelpunkt der Parabel
und durch den Scheitelpunkt der Parabel 
Eine zweite Gerade
- Gib die Gleichung der Parabel
in Scheitelpunktform an.
- Berechne die Koordinaten des Schnittpunkts der Geraden
mit der
-Achse.
(5 P)
b)
Ein Glücksrad besteht aus sechs gleich großen Abschnitten. Diese sind beschriftet mit den Buchstaben A, B, B, B, C und C. Das Glücksrad wird zweimal gedreht.
| Ereignis | Gewinn |
|---|---|
| zweimal B | 6,00 € |
| ein A und ein C | 4,50 € |
| Sonstiges | 0 € |
| Einsatz pro Spiel: 3,00 € | |
- Mit welcher Wahrscheinlichkeit erhält man zweimal den Buchstaben C?
- Das Glücksrad soll für ein Glücksspiel verwendet werden. Berechne für den angegebenen Gewinnplan den Erwartungswert.
- Wie groß müsste der Gewinn für "zweimal B" sein, damit das Spiel fair ist, während die anderen Gewinnbeiträge gleich bleiben?
(5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
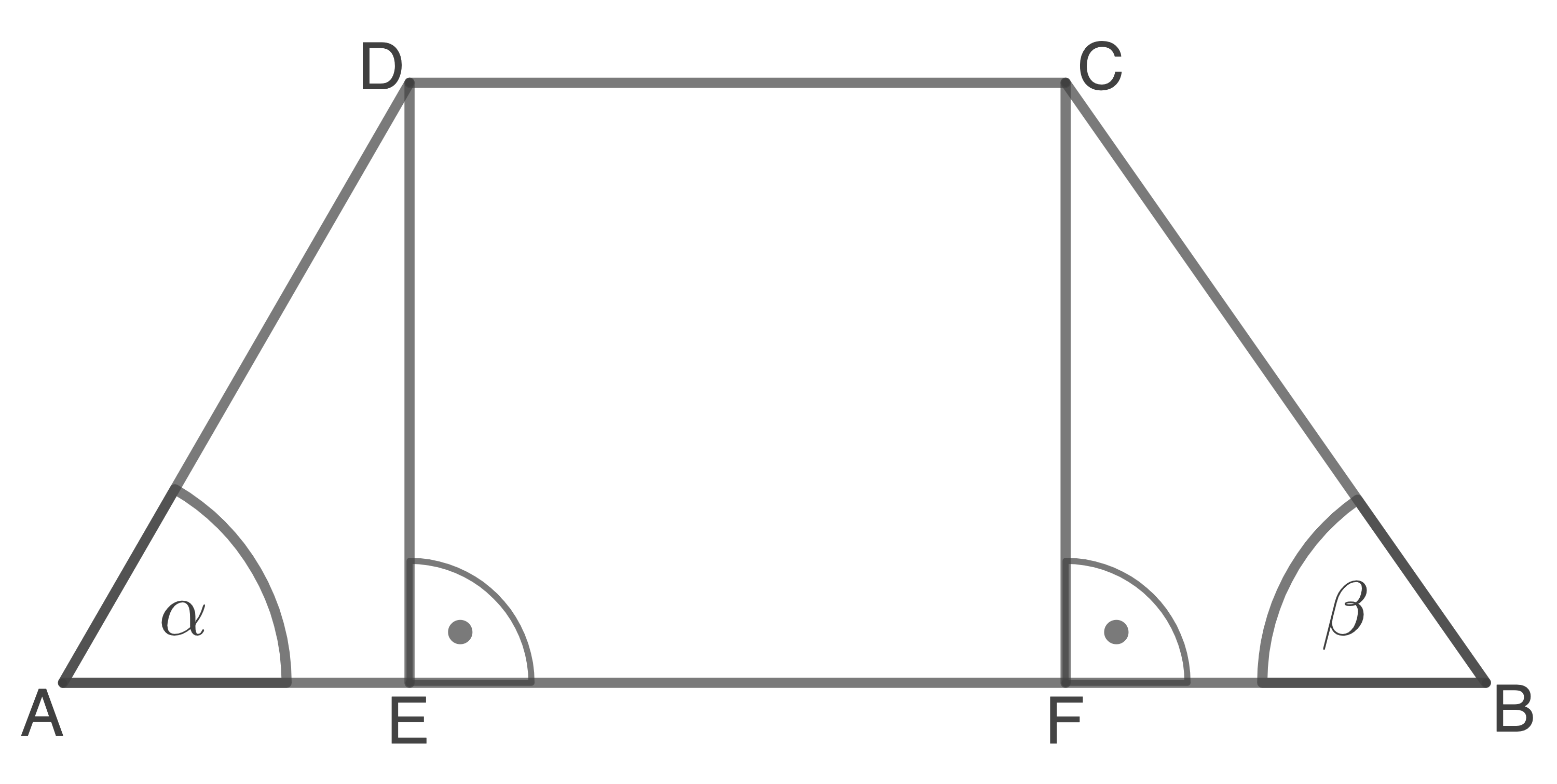
b)
Gleichung von  bestimmen
Scheitelpunkt von
bestimmen
Scheitelpunkt von  bestimmen
bestimmen
 erhält man durch Ablesen
Scheitelpunkt von
erhält man durch Ablesen
Scheitelpunkt von  berechnen
Umformen der Funktionsgleichung mithilfe der quadratischen Ergänzung:
berechnen
Umformen der Funktionsgleichung mithilfe der quadratischen Ergänzung:
![\(\begin{array}[t]{rll}
y&=& x^2-4x+6 &\quad \scriptsize \\[5pt]
y &=& x^2-2\cdot 2x+(-2)^2+6-(-2)^2&\quad \scriptsize \\[5pt]
y &=& (x-2)^2+2
\end{array}\)](https://mathjax.schullv.de/6165fe0a62b6ae142733dccccfa97497e08e8bc80c46f36b000ac1767b39e78f?color=5a5a5a)

 und
und  in die allgemeine Geradengleichung einsetzen und ein lineares Gleichungssystem erstellen
Allgemeine Geradengleichung:
in die allgemeine Geradengleichung einsetzen und ein lineares Gleichungssystem erstellen
Allgemeine Geradengleichung: 

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
2&=&2\cdot (-3)+c \\[5pt]
2&=&-6+c &\quad \scriptsize \mid\;+6 \\[5pt]
c&=& 8
\end{array}\)](https://mathjax.schullv.de/d4f85e3768ad2d0b26c3741ffaae7b17440275e46d7d376d0eacde69fa002e9f?color=5a5a5a) Die Geradengleichung lautet also
Die Geradengleichung lautet also  Gleichung von
Gleichung von  bestimmen
Steigung der Gerade bestimmen
bestimmen
Steigung der Gerade bestimmen


 bestimmen
bestimmen
![\(\begin{array}[t]{rll}
y&=&\dfrac{1}{3}x+c &\quad \scriptsize \mid\; P(1\mid 1)\\[5pt]
1&=&\dfrac{1}{3}\cdot 1+c \\[5pt]
1&=&\dfrac{1}{3}+c &\quad \scriptsize \mid\;-\dfrac{1}{3}\\[5pt]
c&=&\dfrac{2}{3}
\end{array}\)](https://mathjax.schullv.de/f3427c80e492768394e08d7eb8827a956c816a68af926a67077088352309d6fd?color=5a5a5a) Die Geradengleichung lautet also
Die Geradengleichung lautet also  Schnittpunkt mit
Schnittpunkt mit  -Achse angeben
-Achse angeben
![\(\begin{array}[t]{rll}
\dfrac{1}{3}x+\dfrac{2}{3}&=&0 &\quad \scriptsize \mid\;-\dfrac{2}{3} \\[5pt]
\dfrac{1}{3}x&=&-\dfrac{2}{3}&\quad \scriptsize \mid\;\cdot 3 \\[5pt]
x&=&-2
\end{array}\)](https://mathjax.schullv.de/f18e353258a33408b3a4c3371b15ee627fb71032e62a14b0bb4063b248587551?color=5a5a5a) Daraus folgt der Schnittpunkt
Daraus folgt der Schnittpunkt 
Lösung 2
a)
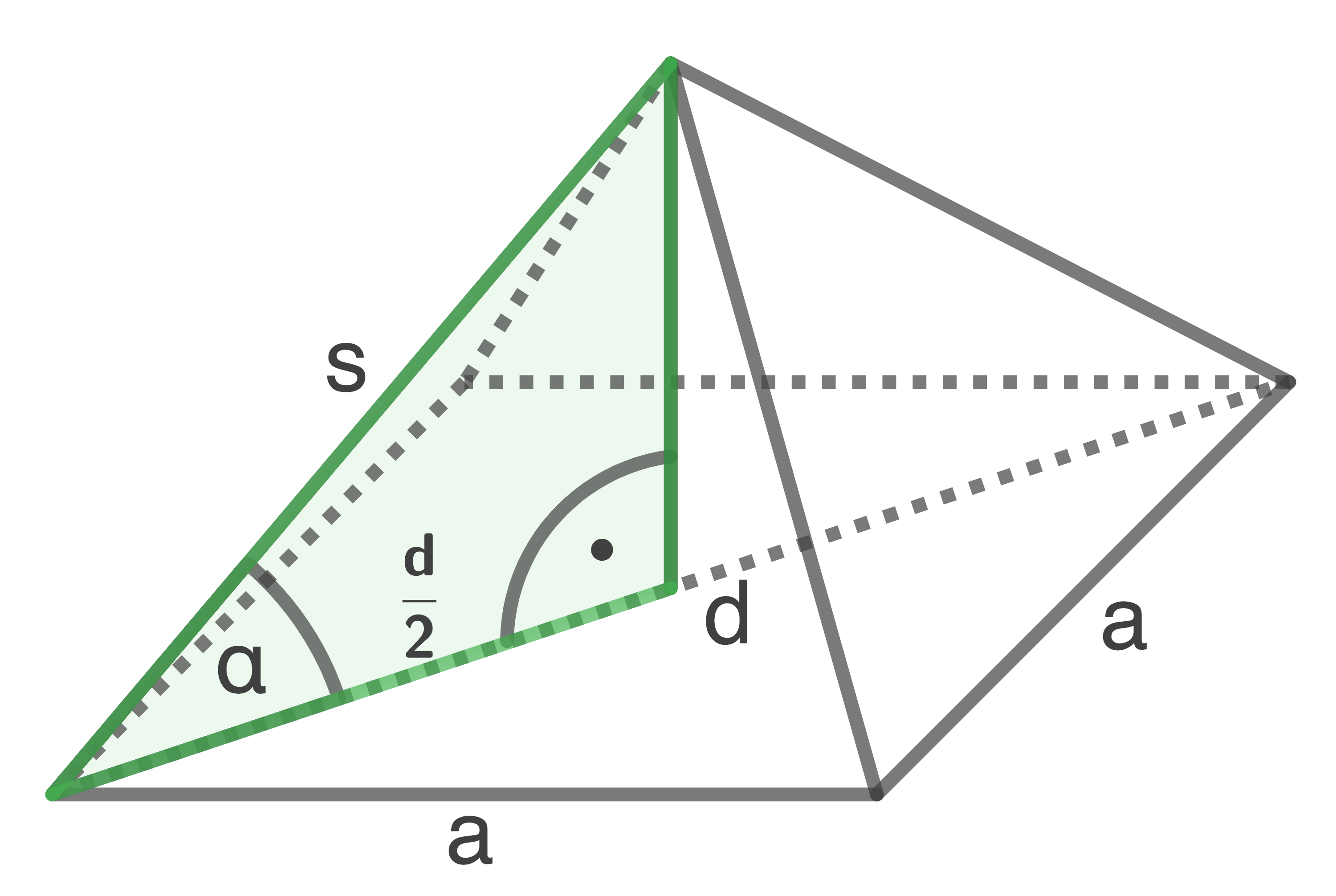
b)
Arithmetisches Mittel berechnen
![\(\begin{array}[t]{rll}
&1\cdot 14,00\,€+2\cdot 14,50\,€+ 1\cdot 17,00\,€& \\[5pt]
&+1\cdot 18,00\,€+2\cdot 18,50\,€+3\cdot 19,00\,€& \\[5pt]
&+2\cdot 22,00\,€+1\cdot 24,00\,€& \\[5pt]
&=240\,€&
\end{array}\)](https://mathjax.schullv.de/f72b7fb6b51a1d5089f97cff3fdbe5270111b799217eca111824966d99c18c16?color=5a5a5a) Somit gilt für das arithmetische Mittel:
Somit gilt für das arithmetische Mittel:  Zentralwert (Median) berechnen
Zentralwert (Median) berechnen
 Verteilung der Werte in einem Boxplot darstellen
Kennwerte ermitteln
Damit ergibt sich folgender Boxplot:
Verteilung der Werte in einem Boxplot darstellen
Kennwerte ermitteln
Damit ergibt sich folgender Boxplot:
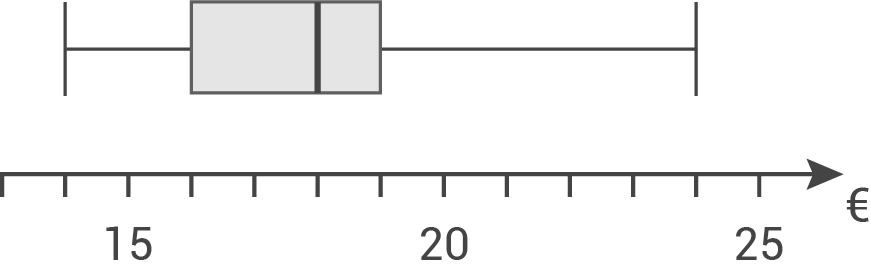 Um wie viel Prozent weicht dieser Wert vom Zentralwert aus der Befragung der Klasse 6a ab?
Um wie viel Prozent weicht dieser Wert vom Zentralwert aus der Befragung der Klasse 6a ab?




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 18,25\,€\\[5pt]
6,35\,\% & \mathrel{\widehat{=}}& 1\,€\\[5pt]
86,30\,\% & \mathrel{\widehat{=}}& 15,75\,€
\end{array}\)](https://mathjax.schullv.de/a17050d2cd813d25370d5400e5a8cbb6f4c2b6080664af8ac51fe524c229b27c?color=5a5a5a)



 Der Zentralwert der Klasse 6b weicht um
Der Zentralwert der Klasse 6b weicht um  vom Zentralwert der Klasse 6a ab.
vom Zentralwert der Klasse 6a ab.
| Rangplatz | Betrag in € |
|---|---|
| 1 | 14,00 |
| 2 | 14,50 |
| 3 | 14,50 |
| 4 | 16,00 |
| 5 | 16,00 |
| 6 | 16,00 |
| 7 | 17,00 |
| 8 | 18,00 |
| 9 | 18,50 |
| 10 | 18,50 |
| 11 | 19,00 |
| 12 | 19,00 |
| 13 | 19,00 |
| 14 | 22,00 |
| 15 | 22,00 |
| 16 | 24,00 |

Lösung 3
a)
Scheitelpunktform mit der quadratischen Ergänzung angeben
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10 &\quad \scriptsize \\[5pt]
y &=& x^2-2\cdot 3x+ 10\quad \scriptsize \mid\; \\[5pt]
y &=& x^2 -2\cdot 3x+3^2-3^2+10&\quad \scriptsize \\[5pt]
y &=& (x-3)^2-3^2+10&\quad \scriptsize \\[5pt]
y &=& (x-3)^2-9+10 &\quad \scriptsize \\[5pt]
y &=&(x-3)^2+1 &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a1fd209e13b0a780ed7b4797f4b6f2b6c9311495ffcb61ef1b12303cf5855ada?color=5a5a5a) Also gilt
Also gilt  Koordinaten des Schnittpunkts berechnen
Scheitelpunkt der Parabel
Koordinaten des Schnittpunkts berechnen
Scheitelpunkt der Parabel  bestimmen
bestimmen
 (kann mithilfe der Scheitelpunktform abgelesen werden)
Parabel
(kann mithilfe der Scheitelpunktform abgelesen werden)
Parabel  berechnen
berechnen
 Koordinaten des Schnittpunkts berechnen
Wenn der Schnittpunkt mit der
Koordinaten des Schnittpunkts berechnen
Wenn der Schnittpunkt mit der  -Achse berechnet werden soll, gilt:
-Achse berechnet werden soll, gilt: 
![\(\begin{array}[t]{rll}
y&=& -4x+13 &\quad \scriptsize \\[5pt]
0&=& -4x+13 &\quad \scriptsize \mid\; -13 \\[5pt]
-13&=& -4x &\quad \scriptsize \mid\; : (-4)\\[5pt]
x&=& 3,25
\end{array}\)](https://mathjax.schullv.de/869f48f927342dcee8dd3822120d6cb08617119cce8607c1ab88df36bd10ce3e?color=5a5a5a)

- Allgemeine Geradengleichung:
- Da die Geraden
und
parallel sind, gilt für den Steigungsfaktor:
- Also gilt für
b)
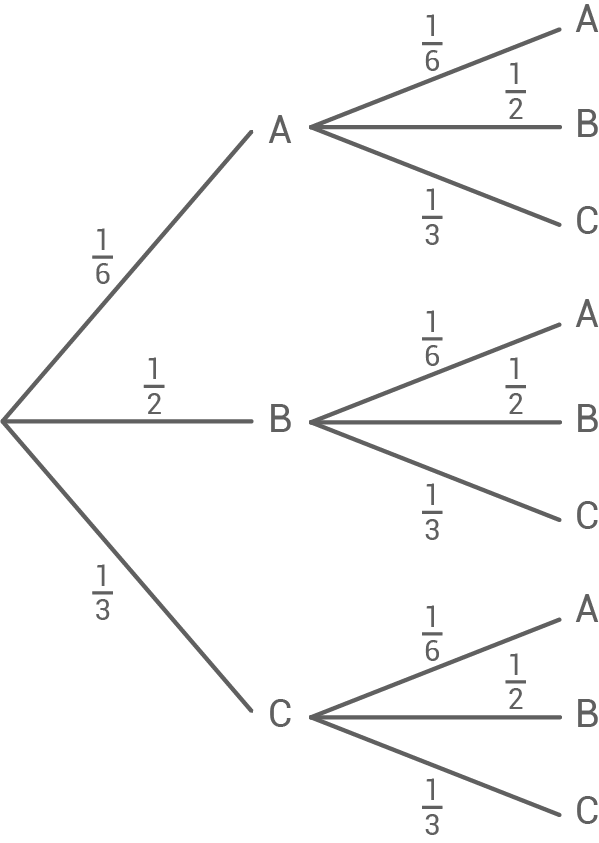
| Ereignis | Gewinn | Wahrscheinlichkeit |
|---|---|---|
| zweimal B | 6,00 € | |
| ein A und ein C | 4,50 € | |
| Sonstiges | 0 € |