Wahlbereich
Aufgabe W 1
a)
Das Fünfeck  besteht aus dem gleichseitigen Dreieck
besteht aus dem gleichseitigen Dreieck  den beiden gleichschenkligen Dreiecken
den beiden gleichschenkligen Dreiecken  und
und  sowie dem Drachenviereck
sowie dem Drachenviereck 
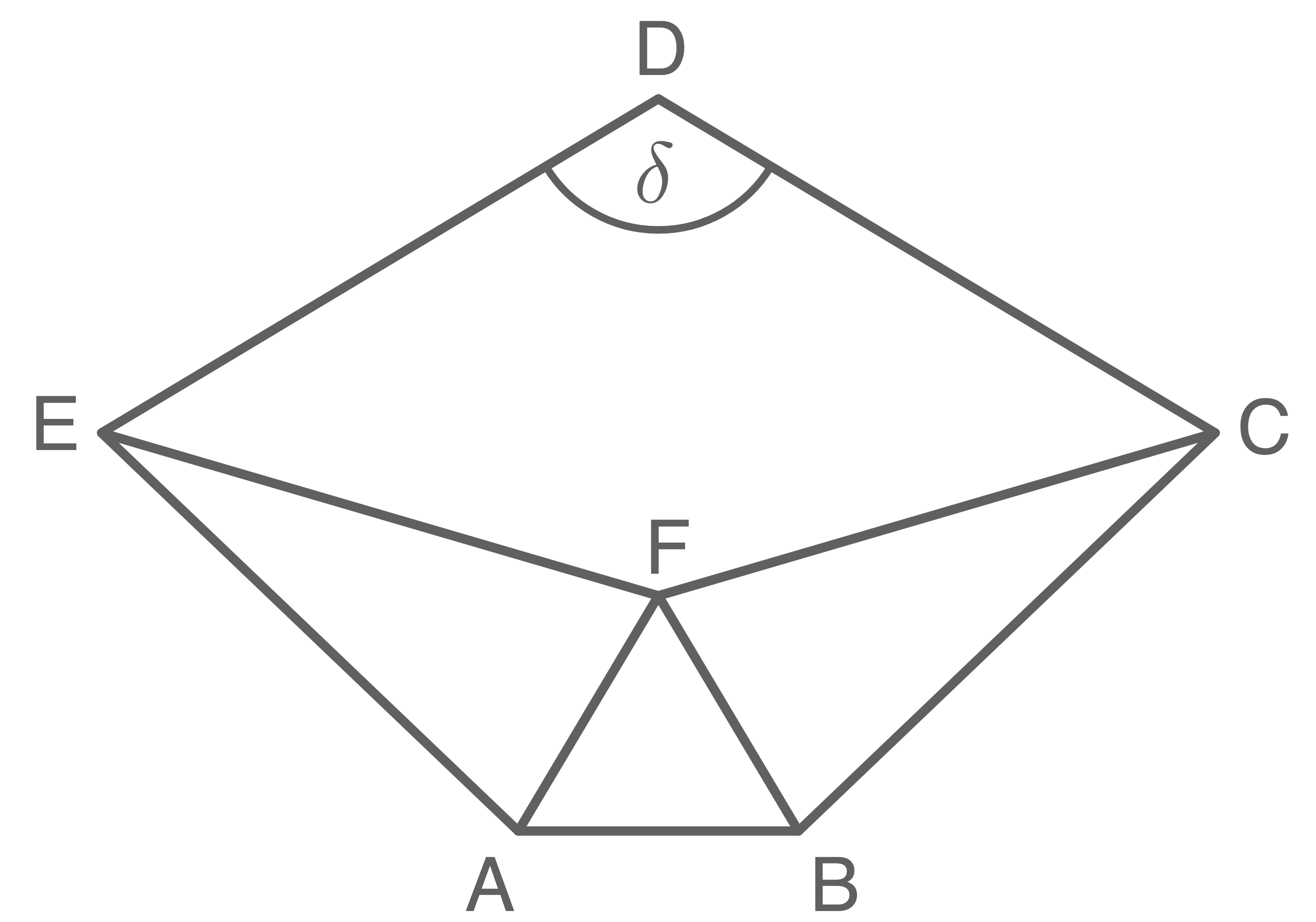 Es gilt:
Es gilt:
 zur Strecke
zur Strecke 

5,5 P
b)
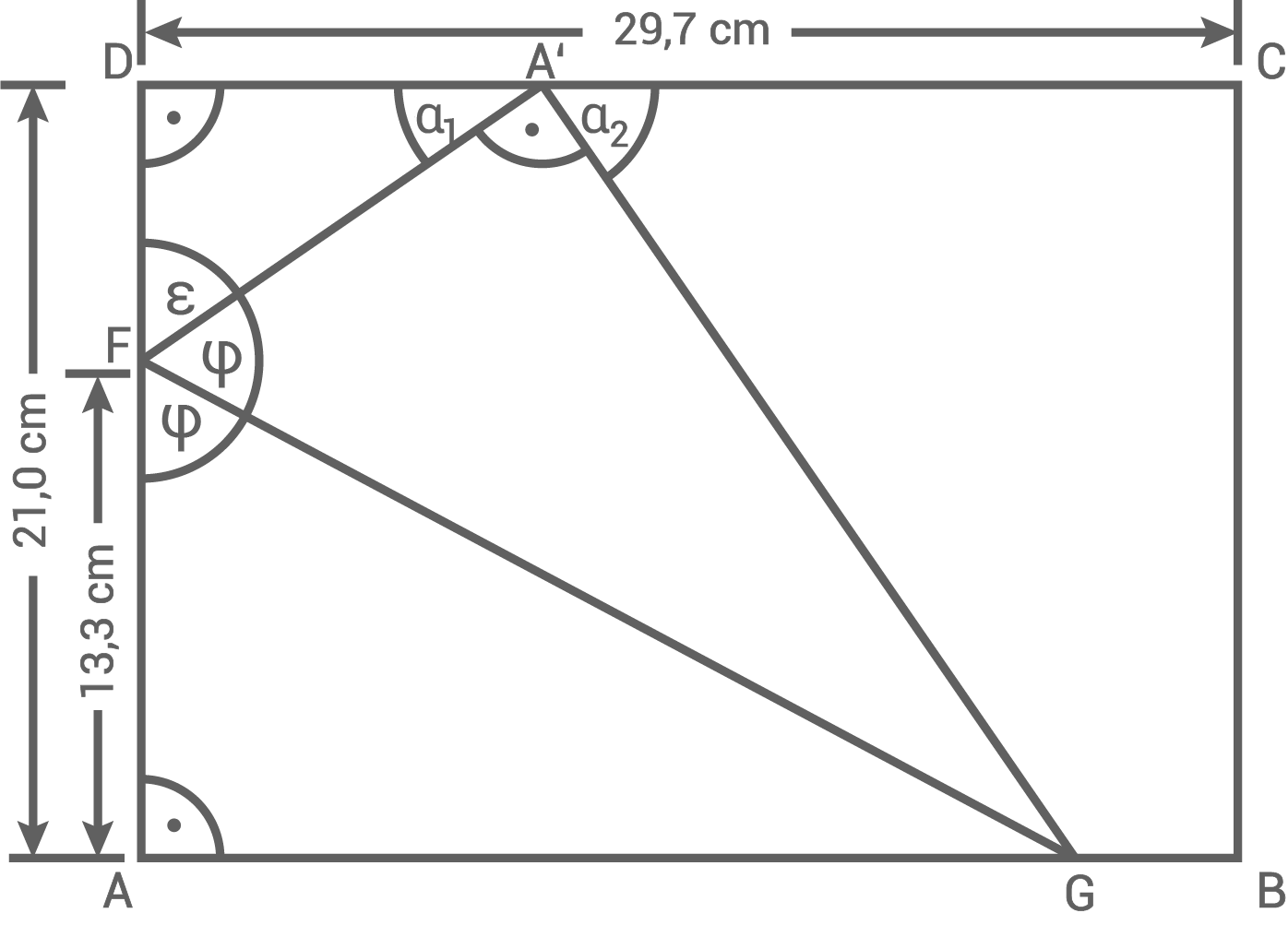
Ein DIN-A4-Blatt mit den Eckpunkten  ,
, 
 und
und  wird entlang von
wird entlang von  gefaltet. Dadurch entsteht der Punkt
gefaltet. Dadurch entsteht der Punkt  auf
auf 
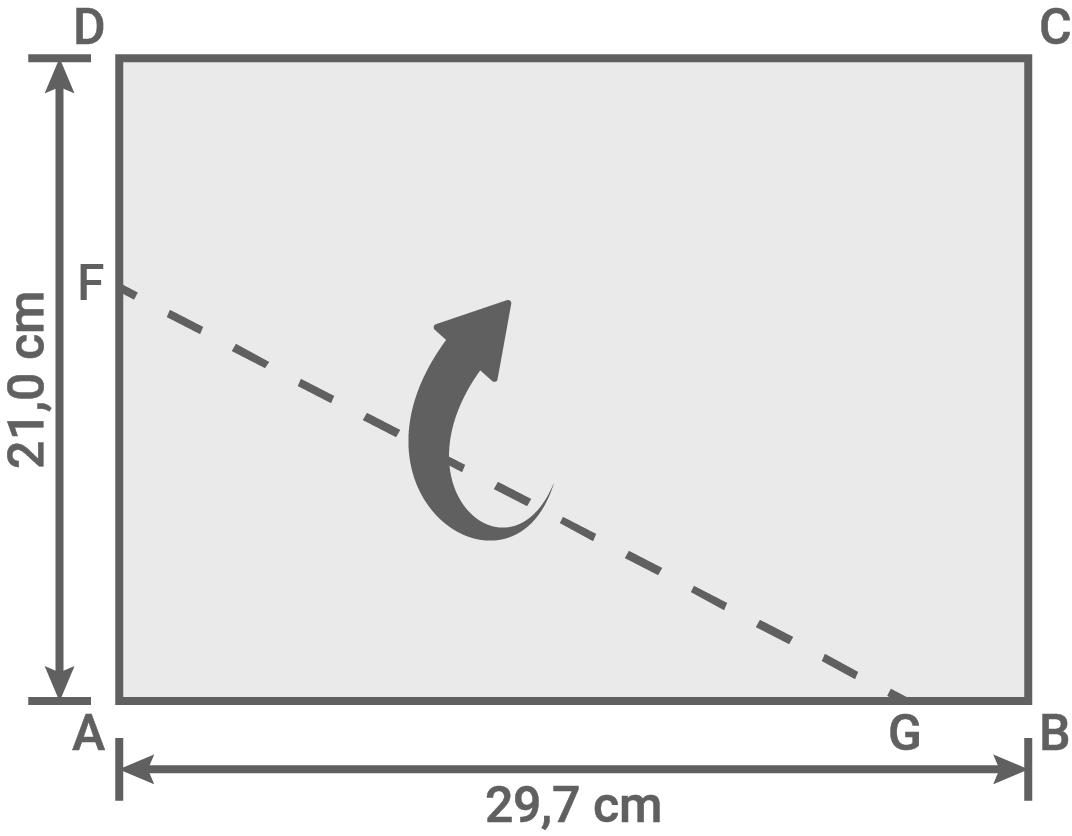
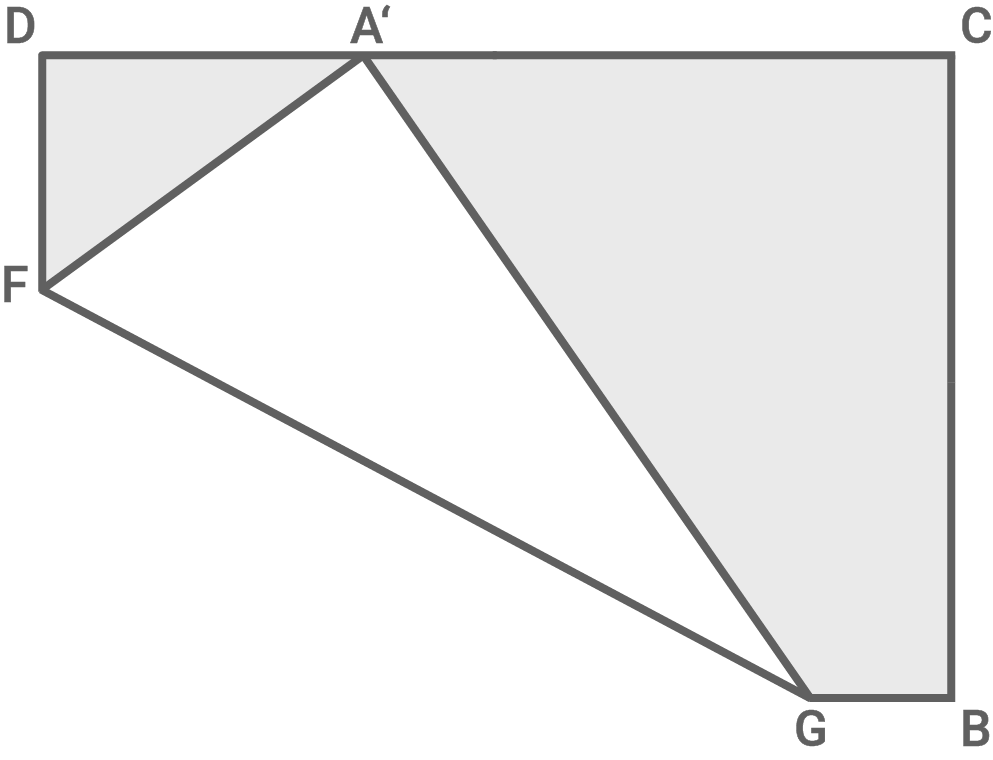 Es gilt:
Es gilt:
 Berechne den Flächeninhalt des Vierecks
Berechne den Flächeninhalt des Vierecks 


4,5 P
Aufgabe W 2
a)
In einer regelmäßigen fünfseitigen Pyramide liegt das gleichschenklige Dreieck 
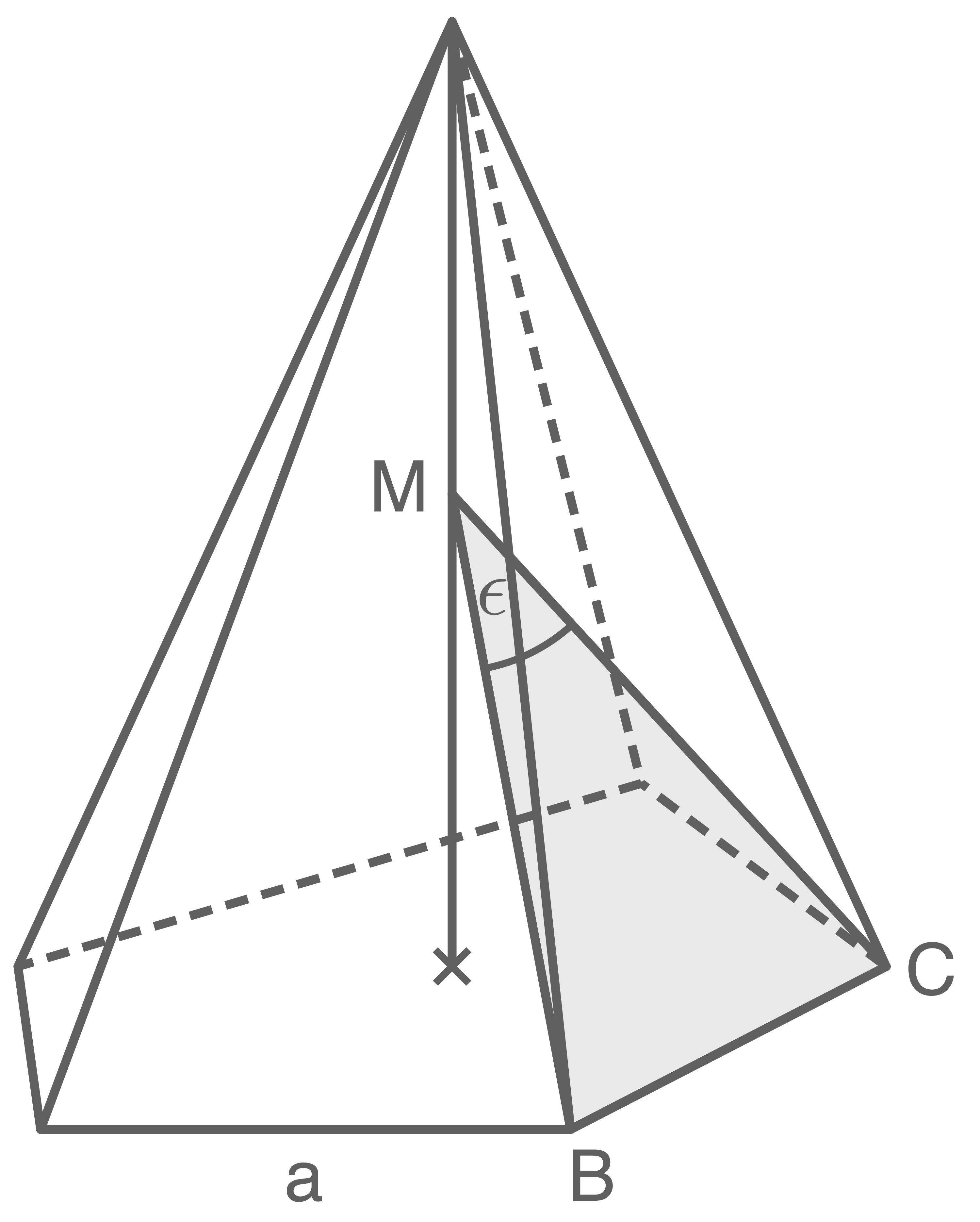 Es gilt:
Es gilt:
Der Punkt bewegt sich auf der Höhe der Pyramide.
bewegt sich auf der Höhe der Pyramide.
Dadurch entsteht das Dreieck Berechne den minimalen und den maximalen Flächeninhalt, den das Dreieck
Berechne den minimalen und den maximalen Flächeninhalt, den das Dreieck  annehmen kann.
annehmen kann.

halbiert die Höhe der Pyramide.
Der Punkt
Dadurch entsteht das Dreieck
5,5 P
b)
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel (siehe Achsenschnitt).
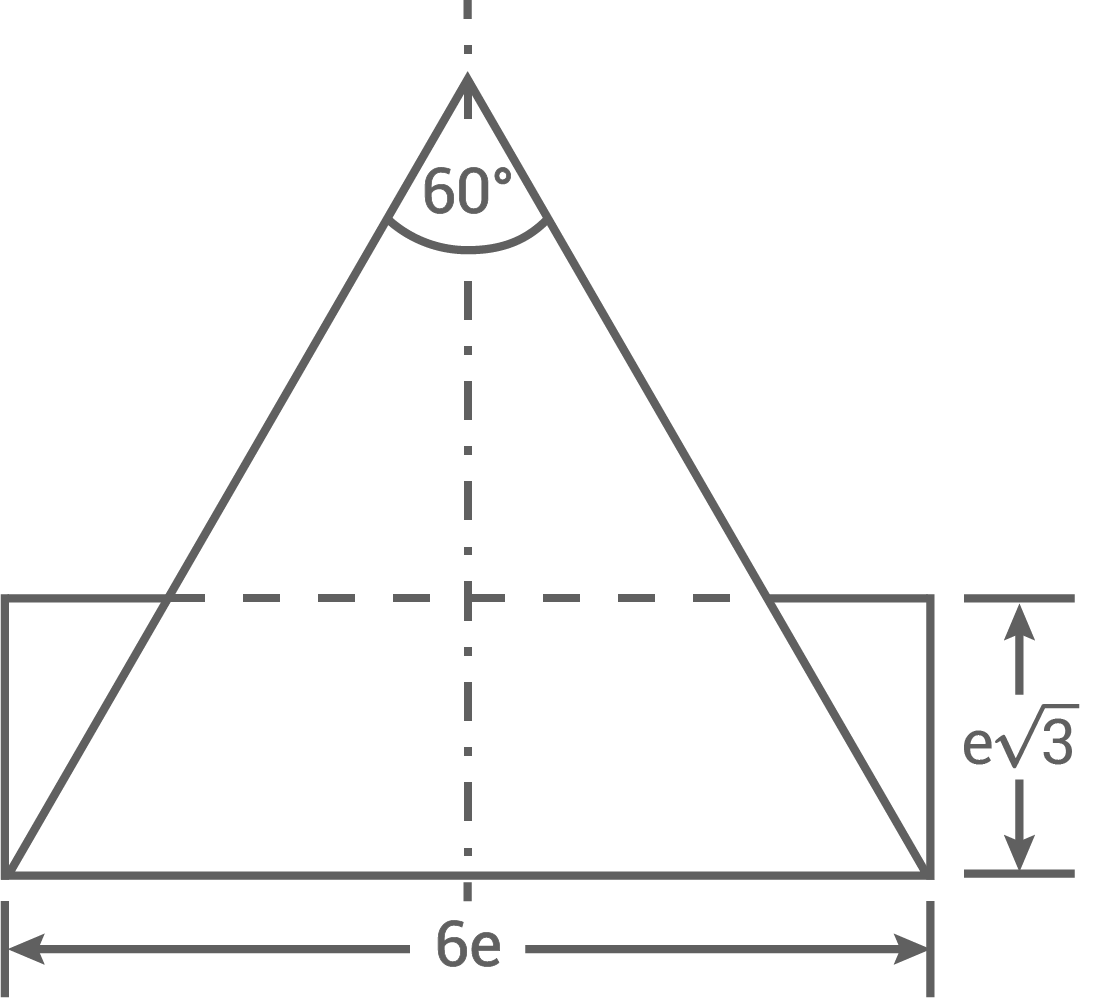 Zeige, dass für das Volumen des zusammengesetzten Körpers gilt:
Zeige, dass für das Volumen des zusammengesetzten Körpers gilt:



4,5 P
Aufgabe W 3
a)
Die nach oben geöffnete Normalparabel  hat den Scheitelpunkt
hat den Scheitelpunkt  Die nach unten geöffnete Normalparabel
Die nach unten geöffnete Normalparabel  hat mit der
hat mit der  -Achse die Schnittpunkte
-Achse die Schnittpunkte  und
und  .
.
Berechne die Koordinaten des gemeinsamen Punktes der beiden Parabeln.
Die Gerade
der beiden Parabeln.
Die Gerade  mit der Steigung
mit der Steigung  schneidet beide Parabeln ebenfalls im Punkt
schneidet beide Parabeln ebenfalls im Punkt  .
.
Berechne die Gleichung von .
.
Berechne die Winkel, unter denen sich die Gerade und die
und die  -Achse schneiden.
Gib die Gleichung einer Parabel
-Achse schneiden.
Gib die Gleichung einer Parabel  an, die weder mit
an, die weder mit  noch mit
noch mit  einen gemeinsamen Punkt hat.
einen gemeinsamen Punkt hat.
Berechne die Koordinaten des gemeinsamen Punktes
Berechne die Gleichung von
Berechne die Winkel, unter denen sich die Gerade
5,5 P
b)
Eine Parabel  mit der Gleichung
mit der Gleichung  hat den Scheitelpunkt
hat den Scheitelpunkt 
Eine zweite Parabel hat die Gleichung
hat die Gleichung 
Der Punkt ist einer der beiden Schnittpunkte von
ist einer der beiden Schnittpunkte von  und
und  Berechne die Koordinaten des zweiten Schnittpunkts
Berechne die Koordinaten des zweiten Schnittpunkts  der beiden Parabeln.
Zeige rechnerisch, dass die Punkte
der beiden Parabeln.
Zeige rechnerisch, dass die Punkte  und
und  auf einer Geraden liegen.
auf einer Geraden liegen.
Eine zweite Parabel
Der Punkt
4,5 P
Aufgabe W 4
a)
Beim Würfelspiel „Augensumme 4 gewinnt“ wird gleichzeitig mit zwei Spielwürfeln geworfen. Die Augenzahlen werden addiert (Augensumme).
Dieses Spiel soll als Glücksspiel eingesetzt werden. Dazu wird nebenstehender Gewinnplan verwendet.
Berechne den Erwartungswert.
Der Betreiber bekommt die Vorgabe, das Glücksspiel zu verändern. Er soll auf einem der beiden Spielwürfel die Vier, die Fünf und die Sechs entweder durch drei Einsen oder durch drei Dreien ersetzen.
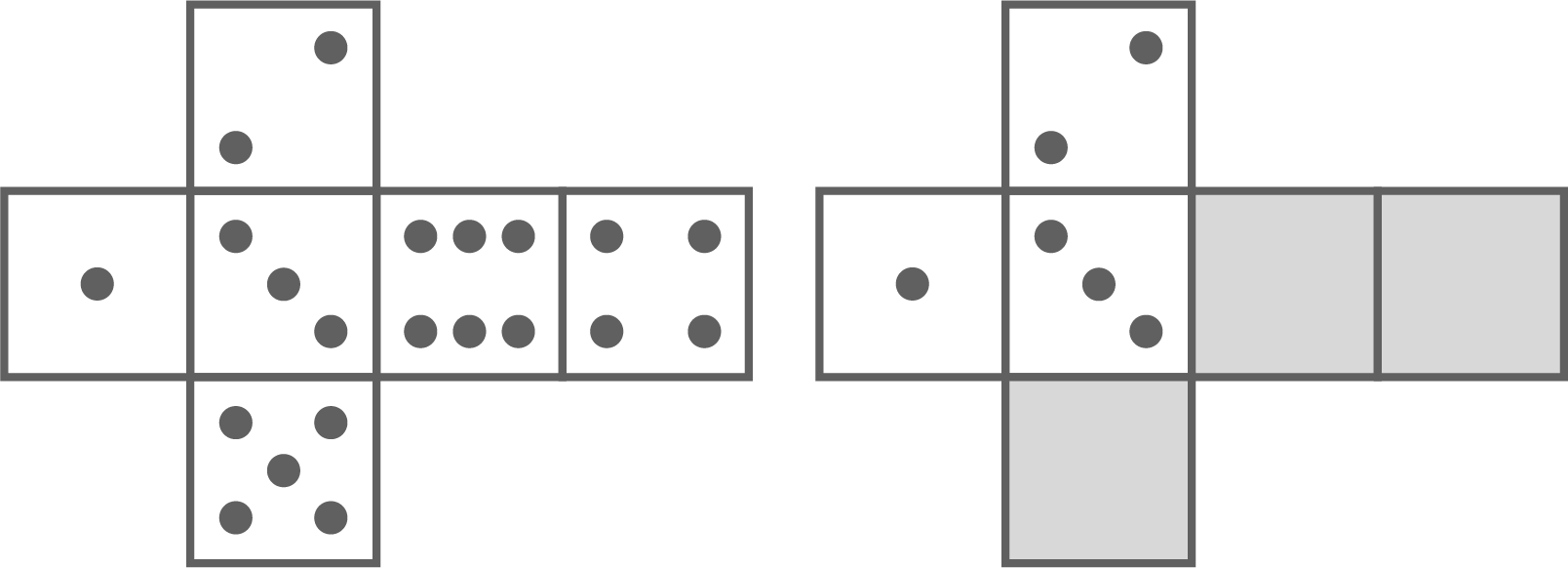 Wofür sollte sich der Betreiber entscheiden?
Wofür sollte sich der Betreiber entscheiden?
Begründe deine Entscheidung durch Rechnung oder Argumentation.
Dieses Spiel soll als Glücksspiel eingesetzt werden. Dazu wird nebenstehender Gewinnplan verwendet.
| Ereignisse | Gewinn |
|---|---|
| „Augensumme gleich 4“ | |
| „Augensumme kleiner 4“ | |
| „Augensumme größer 4“ | kein Gewinn |
| Einsatz pro Spiel: |
|

Begründe deine Entscheidung durch Rechnung oder Argumentation.
6 P
b)
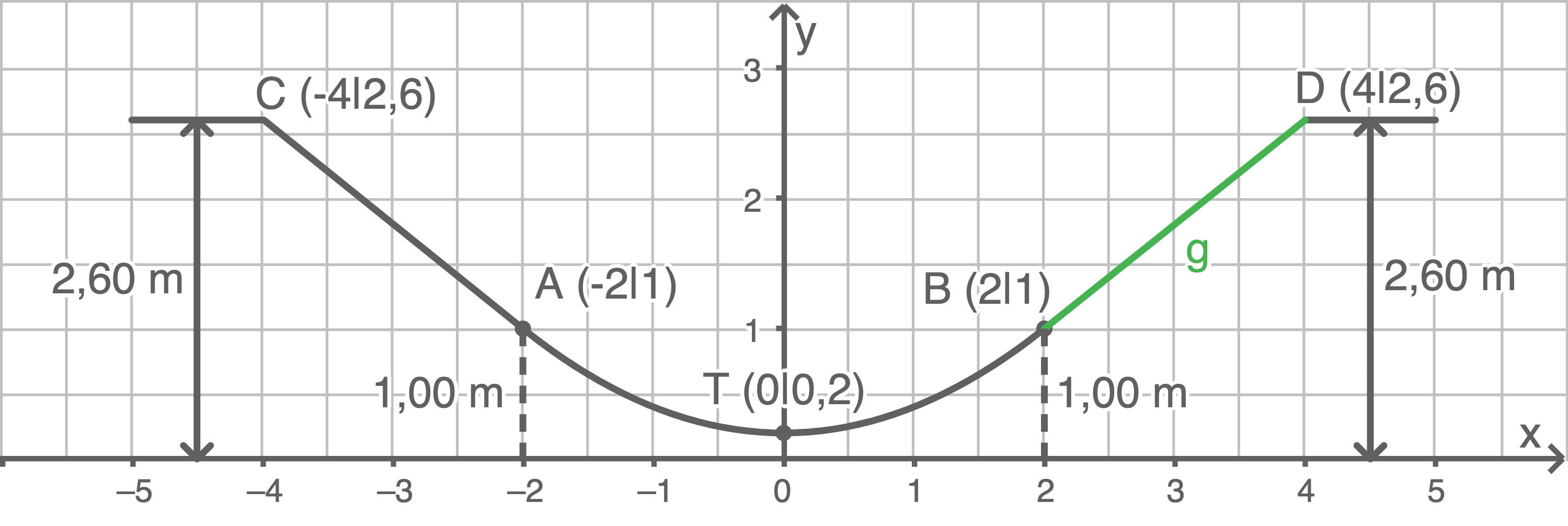
Im Querschnitt einer Skater-Rampe sieht man die beiden geraden Teilstücke  und
und  sowie das parabelförmige Teilstück
sowie das parabelförmige Teilstück 
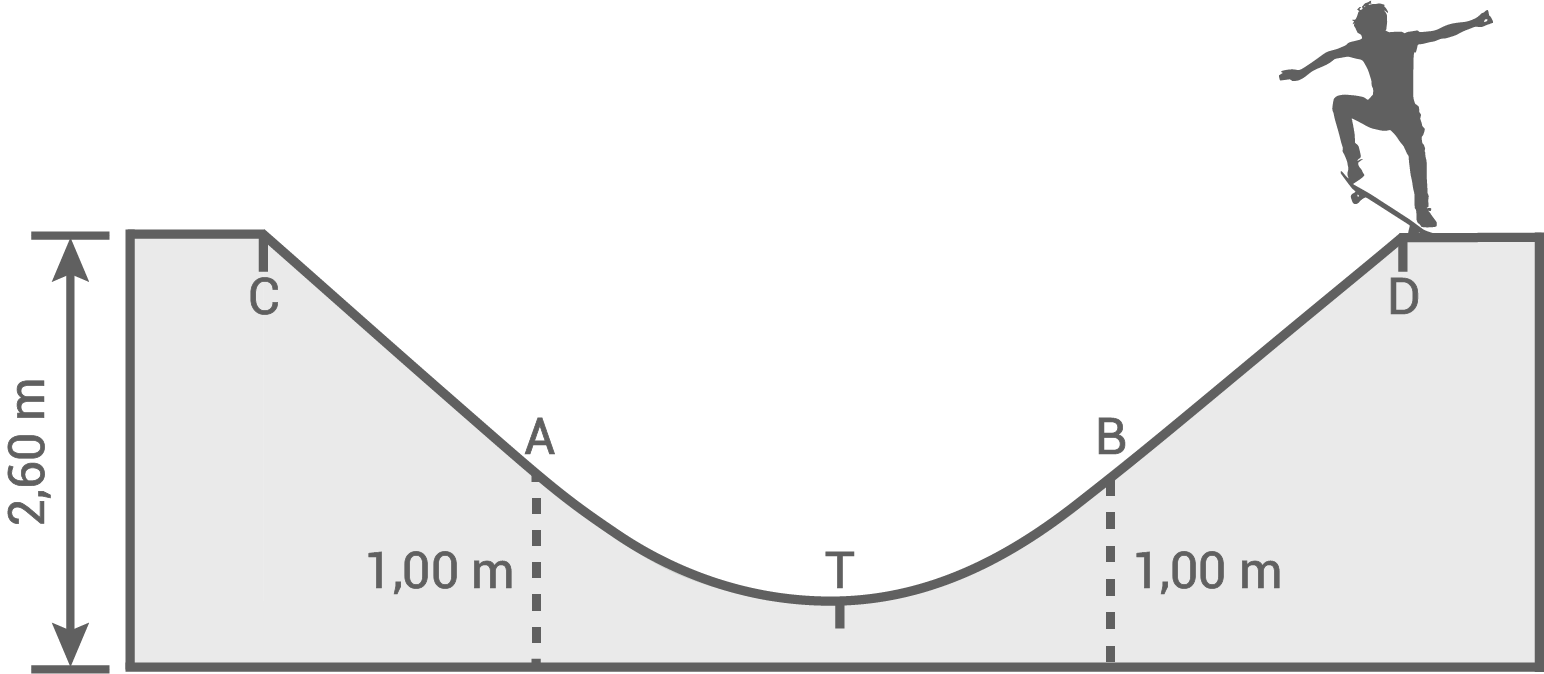 Die beiden Punkte
Die beiden Punkte  und
und  liegen auf gleicher Höhe und sind
liegen auf gleicher Höhe und sind  voneinander entfernt.
voneinander entfernt.
Der tiefste Punkt der Skater-Rampe liegt
der Skater-Rampe liegt  über dem Boden.
Bestimme eine mögliche Funktionsgleichung für das parabelförmige Teilstück
über dem Boden.
Bestimme eine mögliche Funktionsgleichung für das parabelförmige Teilstück  Die beiden Punkte
Die beiden Punkte  und
und  liegen ebenfalls auf gleicher Höhe und sind
liegen ebenfalls auf gleicher Höhe und sind  voneinander entfernt.
Bestimme eine mögliche Funktionsgleichung für die Gerade, auf der das gerade Teilstück
voneinander entfernt.
Bestimme eine mögliche Funktionsgleichung für die Gerade, auf der das gerade Teilstück  liegt.
liegt.

(Skizze nicht maßstabsgetreu)
Der tiefste Punkt
4 P
Lösung W 1
a)
1. Schritt: Länge der Strecke  berechnen
berechnen
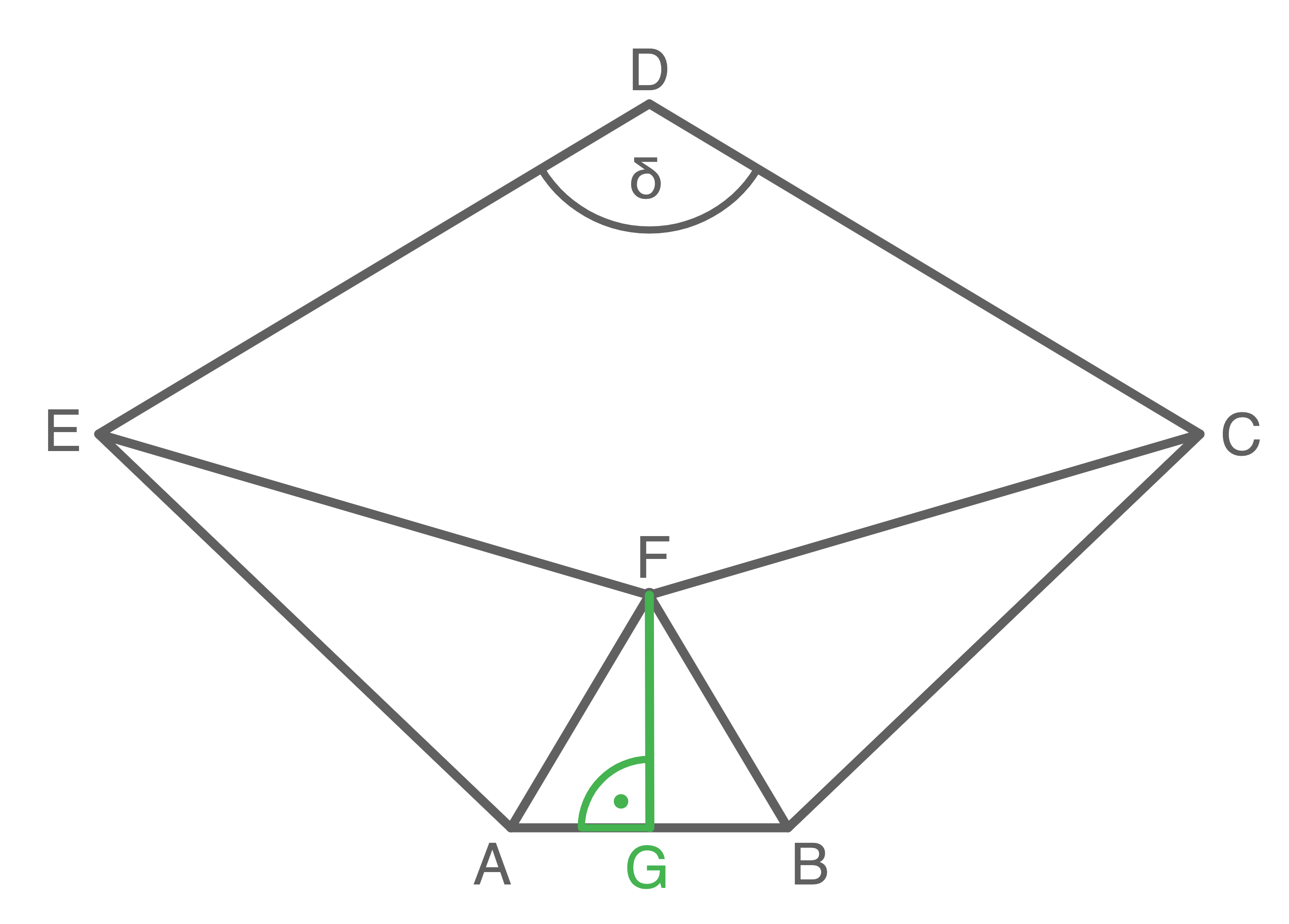 Satz des Pythagoras anwenden
Satz des Pythagoras anwenden
![\(\begin{array}[t]{rll}
\overline{AF}^2&=& \overline{AG}^2+\overline{FG}^2\quad \scriptsize \mid\;-\overline{AG}^2 \\[5pt]
\overline{FG}^2&=&\overline{AF}^2-\overline{AG}^2\\[5pt]
\overline{FG}^2&=&(3,4\,\text{cm})^2-(1,7\,\text{cm})^2\quad \scriptsize \mid\; \sqrt{\,\,\,} \\[5pt]
\overline{FG}&=& \sqrt{(3,4\,\text{cm})^2-(1,7\,\text{cm})^2}\\[5pt]
\overline{FG}&=& \underline{ 2,94\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/87e6120b7190b1b40d9577506acfdd47e32b2508a324fca0cfa76ce3443ccf56?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
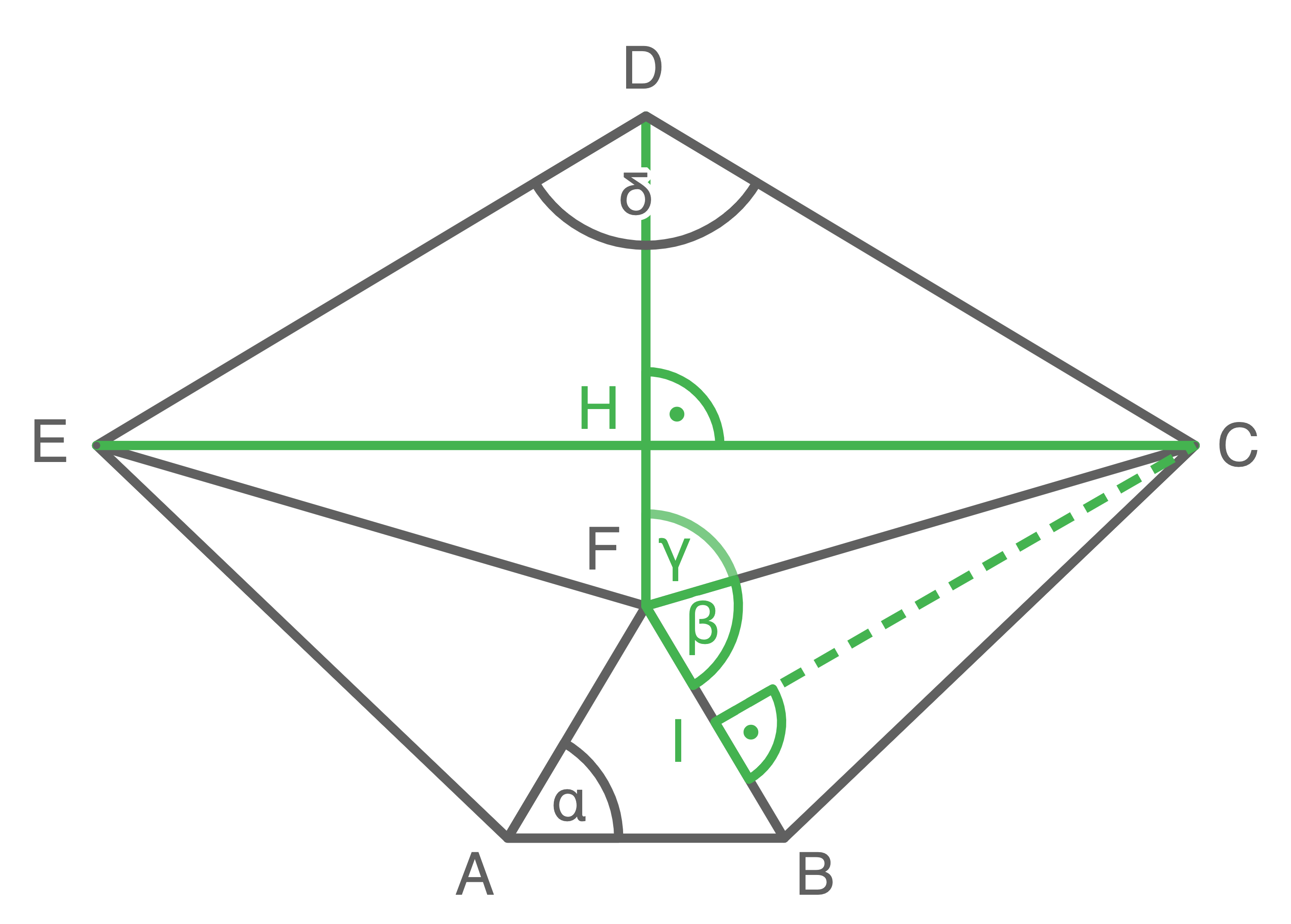 Größe des Winkels
Größe des Winkels  berechnen
Da das Dreieck
berechnen
Da das Dreieck  gleichschenklig ist, gilt
gleichschenklig ist, gilt 
![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{FI}}{\overline{CF}} &\quad \\[5pt]
\cos(\beta)&=&\dfrac{1,7\,\text{cm} }{7,0\,\text{cm} } \\[5pt]
\beta&=&\underline{ 75,94^{\circ}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/de67ce1b76d4327f746a41d0dd29517648895853a9bfafd0ae963ee1a5c0d3fa?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=&180^{\circ}-\beta-\dfrac{\alpha}{2} \\[5pt]
\gamma&=&180^{\circ}-75,94^{\circ}-\dfrac{60^{\circ}}{2} \\[5pt]
\gamma&=&\underline{ 74,06^{\circ}}
\end{array}\)](https://mathjax.schullv.de/4181315cf5edbbdfd4956520a4f5ab002b5f475c97559859aa9f2826478ace31?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\gamma)&=&\dfrac{\overline{HF}}{\overline{CF}} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{HF}&=&\overline{CF}\cdot \cos(\gamma) \\[5pt]
\overline{HF}&=&7,0\,\text{cm}\cdot \cos(74,06^{\circ}) \\[5pt]
\overline{HF}&=&\underline{ 1,92\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/8db02f0d87cd45c689719dc60f3a8be45e4b6870b6d44bece549ea30b24d0b8d?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma)&=&\dfrac{\overline{CH}}{CF} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{CH}&=&\overline{CF}\cdot \sin(\gamma) \\[5pt]
\overline{CH}&=&7,0\,\text{cm}\cdot \sin(74,06^{\circ}) \\[5pt]
\overline{CH}&=&\underline{ 6,73\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7b9a3cddf7b716c276bb1781c596c67b2ec89b456ba6bfe64a1e87792f354721?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\delta}{2}\right)&=&\dfrac{\overline{CH}}{\overline{DH}} &\quad \scriptsize \mid\;\cdot \overline{DH} \\[5pt]
\overline{DH}\cdot \tan\left(\dfrac{\delta}{2}\right) &=& \overline{CH}&\quad\scriptsize \mid\;:\tan\left(\dfrac{\delta}{2}\right) \\[5pt]
\overline{DH}&=&\dfrac{\overline{CH}}{\tan\left(\dfrac{\delta}{2}\right)} \\[5pt]
\overline{DH}&=&\dfrac{6,73\,\text{cm}}{\tan(59^{\circ})} \\[5pt]
\overline{DH}&=&\underline{ 4,04\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/c49c22667f04cca3450464288390dd93e849472a19b22adcfaa5678bc82fcea3?color=5a5a5a) 3. Schritt: Abstand des Punktes
3. Schritt: Abstand des Punktes  zur Strecke
zur Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DG}&=&\overline{DH}+\overline{HF}+\overline{FG} & \\[5pt]
\overline{DG}&=&4,04\,\text{cm}+1,92\,\text{cm}+2,94\,\text{cm} \\[5pt]
\overline{DG}&=&\underline{\underline{ 8,9\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/249199456a9a8cc30ec1111d7ee985dccd0a5037a45caef03fe4f3392c347bca?color=5a5a5a)


b)
Lösung W 2
a)
Berechnung der Höhe der Pyramide
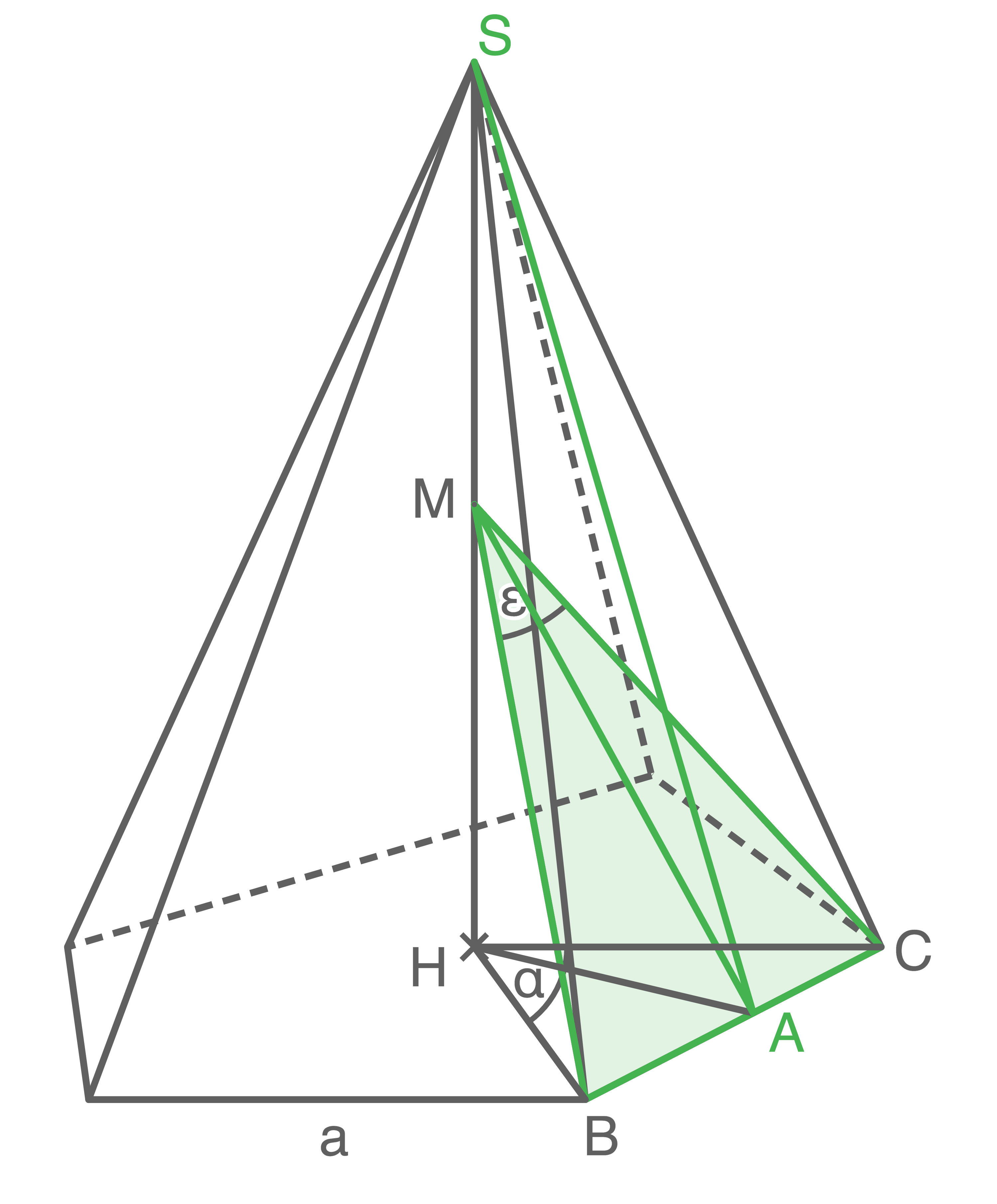 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\epsilon}{2}\right)&=&\dfrac{\overline{AM}}{\overline{BM}} &\quad \scriptsize \mid\;\cdot\overline{BM} \\[5pt]
\overline{AM}&=&\overline{BM}\cdot \cos\left(\dfrac{\epsilon}{2}\right) \\[5pt]
\overline{AM}&=&8,0 \,\text{cm}\cdot \cos\left(\dfrac{48^{\circ}}{2}\right)\\[5pt]
\overline{AM}&=&\underline{ 7,31 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/73e7149ff137337f0d06da8c2ab99bcce885803227c96921f0a7efd8bfdae7ca?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\left(\dfrac{\epsilon}{2}\right)&=&\dfrac{\overline{AB}}{BM} &\quad \scriptsize \mid\;\cdot\overline{BM} \\[5pt]
\overline{AB}&=&\overline{BM}\cdot \sin\left(\dfrac{\epsilon}{2}\right) \\[5pt]
\overline{AB}&=&8,0 \,\text{cm} \cdot \sin\left(\dfrac{48^{\circ}}{2}\right) \\[5pt]
\overline{AB}&=&\underline{ 3,25 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ba83353a7feaa02979f5269c5a94ff60eca9318ee9309fe3275dd9715c732964?color=5a5a5a) 3. Schritt: Größe des Mittelpunktswinkels
3. Schritt: Größe des Mittelpunktswinkels  berechnen
berechnen
 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\alpha}{2}\right)&=&\dfrac{\overline{AB}}{AH} &\quad \scriptsize \mid\;\cdot\overline{AH} \\[5pt]
\overline{AH}\cdot \tan\left(\dfrac{\alpha}{2}\right) &=&\overline{AB}&\quad \scriptsize \mid\;: \tan\left(\dfrac{\alpha}{2}\right) \\[5pt]
\overline{AH}&=&\dfrac{\overline{AB}}{\tan\left(\dfrac{\alpha}{2}\right)} \\[5pt]
\overline{AH}&=&\dfrac{3,25 \,\text{cm}}{\tan\left(\dfrac{72^{\circ}}{2}\right)} \\[5pt]
\overline{AH}&=&\underline{ 4,47 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/af8950ee06be72f9509a085cd1b4009fe31023e045d4370c222989566acff181?color=5a5a5a) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AM}^2&=&\overline{MH}^2+\overline{AH}^2 \quad \scriptsize \mid\;-\overline{AH}^2 \\[5pt]
\overline{MH}^2&=&\overline{AM}^2-\overline{AH}^2 \quad \scriptsize \mid\;\sqrt{\,\,\,}\\[5pt]
\overline{MH}&=& \sqrt{(7,31\,\text{cm})^2-(4,47\,\text{cm})^2}\\[5pt]
\overline{MH}&=&\underline{ 5,78\,\text{cm} }\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bfbb05a78313b169b45670906db180100ef7fe838a150c51e17c3e3331b30de1?color=5a5a5a) 6. Schritt: Höhe der Pyramide berechnen
6. Schritt: Höhe der Pyramide berechnen
![\(\begin{array}[t]{rll}
\overline{SH}&=&2\cdot \overline{MH} & \\[5pt]
&=& 2\cdot 5,78\,\text{cm} \\[5pt]
&=& 11,56\,\text{cm} \\[5pt]
\overline{SH}&=&\underline{\underline{ 11,6\,\text{cm}}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cca1fc4ce816f4b32039e484c723941288444e5a25624f9c2b782dc2db17bae4?color=5a5a5a) Berechnung des minimalen Flächeninhalts
Berechnung des minimalen Flächeninhalts
![\(\begin{array}[t]{rll}
A_{\,\text{min}}&=&\dfrac{1}{2}\cdot \overline{BC}\cdot \overline{AM](https://mathjax.schullv.de/19ee3d26fca41873b30e02adf2d6bfff2d20e9ba9e8671ca12e7af4b8c56ba3e?color=5a5a5a) Berechnung des maximalen Flächeninhalts
Länge der Strecke
Berechnung des maximalen Flächeninhalts
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AS}^2&=&\overline{SH}^2+\overline{AH}^2 & \\[5pt]
\overline{AS}^2&=&(11,6\,\text{cm})^2+(4,47\,\text{cm})^2 &\quad \scriptsize \mid\;\sqrt{\quad} \\[5pt]
\overline{AS}&=& \sqrt{(11,6\,\text{cm})^2+(4,47\,\text{cm})^2} \\[5pt]
\overline{AS}&=&\underline{ 12,43\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2cc28c461894bb663f645fac185a98ee21ba7b18a752d2c8791dde2dc37a8db2?color=5a5a5a) Somit gilt:
Somit gilt:
![\(\begin{array}[t]{rll}
A_{\,\text{max}}&=&\dfrac{1}{2}\cdot \overline{BC}\cdot \overline{AS} & \\[5pt]
&=&\dfrac{1}{2}\cdot (2\cdot \overline{AB})\cdot \overline{AS} & \\[5pt]
&=&\dfrac{1}{2}\cdot (2\cdot 3,25\,\text{cm}) \cdot 12,43\,\text{cm} \\[5pt]
A_{\,\text{max}}&=&\underline{\underline{ 40,4\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/1a92cf3991e21c6614f446a85deaa28ea9fe94cfe87b4dac18d24bf8e96feb2c?color=5a5a5a)

b)
.png)
Lösung W 3
a)
Koordinaten des gemeinsamen Punktes  berechnen
1. Schritt: Funktionsgleichung von
berechnen
1. Schritt: Funktionsgleichung von  berechnen
berechnen
![\(\begin{array}[t]{rll}
p_1:& y&=&(x-d)^2+e &\quad \scriptsize \mid\; S_1(2\mid2) \\[5pt]
&&=&(x-2)^2+2 \\[5pt]
&&=&x^2-4x+4+2 \\[5pt]
p_1: &y&=&x^2-4x+6
\end{array}\)](https://mathjax.schullv.de/9315ce6130a9d7b7332db2de13d2672741672bc5bbdf5bc3ef8620333d49f3b9?color=5a5a5a) 2. Schritt: Funktionsgleichung von
2. Schritt: Funktionsgleichung von  berechnen
berechnen
 und
und  in die allgemeine Funktionsgleichung
in die allgemeine Funktionsgleichung  eingesetzt, ergibt ein LGS:
eingesetzt, ergibt ein LGS:

 in
in  eingesetzt, ergibt:
eingesetzt, ergibt:
![\(\begin{array}[t]{rll}
&0&=& -4+2b+4 \\[5pt]
&2b&=& 0& \scriptsize \mid\;:2 \\[5pt]
&b&=& 0
\end{array}\)](https://mathjax.schullv.de/8e31cd8e0d8eb6a4948f0c79db25e0b286c9e67b6527868eb0abbca4dad826b8?color=5a5a5a) Daraus folgt:
Daraus folgt:  3. Schritt: Koordinaten des gemeinsamen Punktes
3. Schritt: Koordinaten des gemeinsamen Punktes  berechnen
berechnen
![\(\begin{array}[t]{rll}
p_1&=&p_2 & \\[5pt]
x^2-4x+6&=&-x^2+4 &\quad \scriptsize \mid\;+x^2 \quad \scriptsize \mid\;-4 \\[5pt]
2x ^2-4x+2&=&0 &\quad \scriptsize \mid\;:2 \\[5pt]
x^2-2x+1&=&0
\end{array}\)](https://mathjax.schullv.de/41ab9a292a9bfb7abbc417ea84ed581906d1a5fa8fd19c8c0e633f647b291fb4?color=5a5a5a) Weiter mit der
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{-2}{2}\pm \sqrt{\left(\dfrac{-2}{2}\right)^2-1} \\[5pt]
x_{1/2}&=&1\pm \sqrt{1-1} \\[5pt]
x_{1/2}&=&1\pm \sqrt{0} \\[5pt]
x&=&1+0=1
\end{array}\)](https://mathjax.schullv.de/34080111411c8ed93629bdf27c3eaa549816458248621d217e87859aa4a65230?color=5a5a5a)
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&-1^2+4 \\[5pt]
y&=&3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/98094f85898c7d9310e1468719f4f9b0884a7a791008266366be40c271c9ab8c?color=5a5a5a) Somit gilt:
Somit gilt:  Gleichung von
Gleichung von  berechnen
Die allgemeine Geradengleichung lautet:
berechnen
Die allgemeine Geradengleichung lautet:  Aus
Aus  folgt:
folgt: 
 eingesetzt, ergibt:
eingesetzt, ergibt:
![\(\begin{array}[t]{rll}
y&=&2x+c_{g} \\[5pt]
3&=&2\cdot 1+c_{g} \\[5pt]
3&=&2+c_{g} &\quad \scriptsize \mid\;-2 \\[5pt]
c_{g}&=&1 &\quad \scriptsize \mid\;-2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0b023e1979f7d5b0492dabe7ba95d13b8d2d560730da31a335643f150dd40fd6?color=5a5a5a) Somit gilt:
Somit gilt:  Winkel berechnen, unter denen sich die Gerade
Winkel berechnen, unter denen sich die Gerade  und die
und die  -Achse schneiden
-Achse schneiden
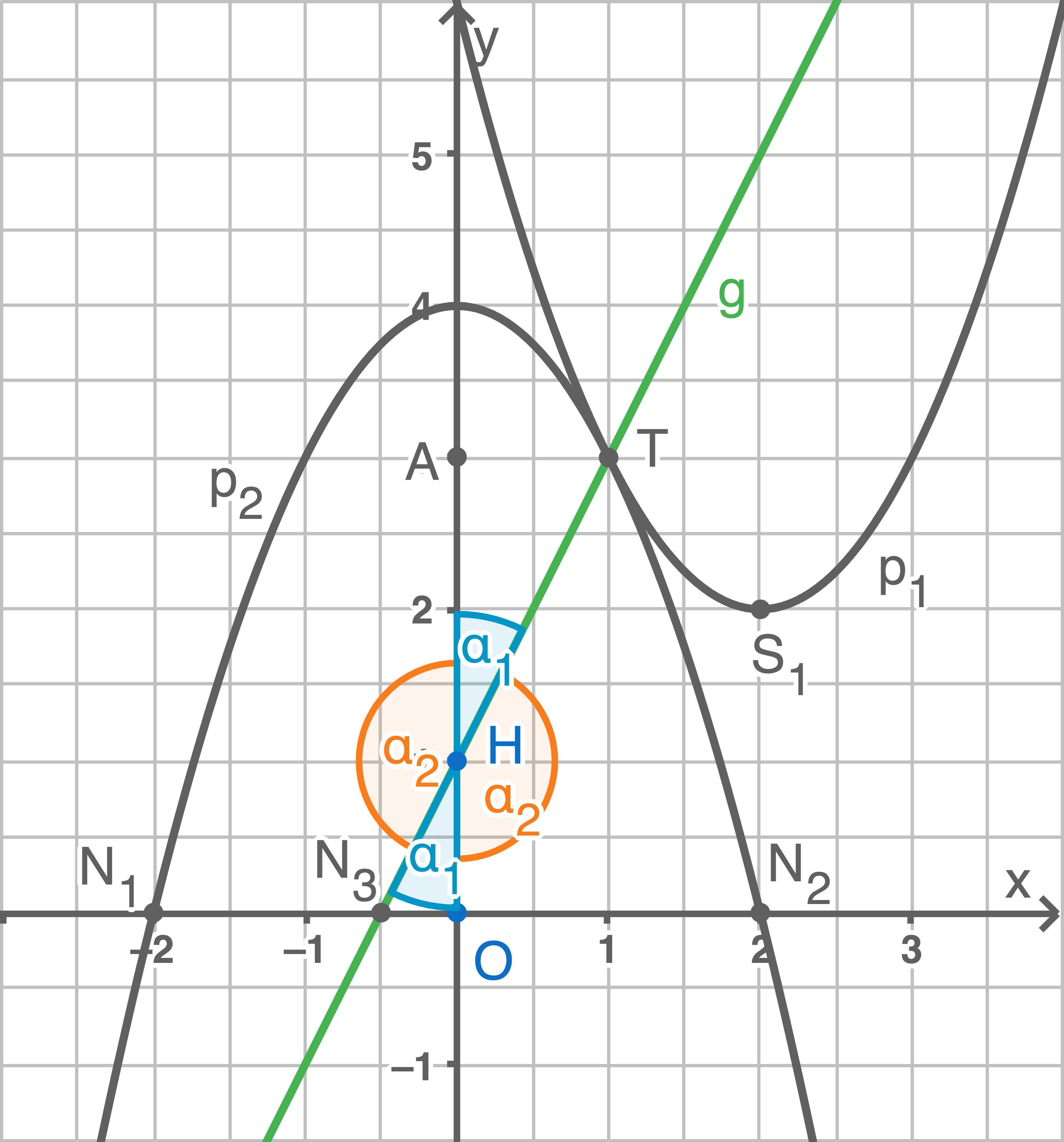 Es gibt vier Winkel:
Es gibt vier Winkel:
 berechnen
berechnen
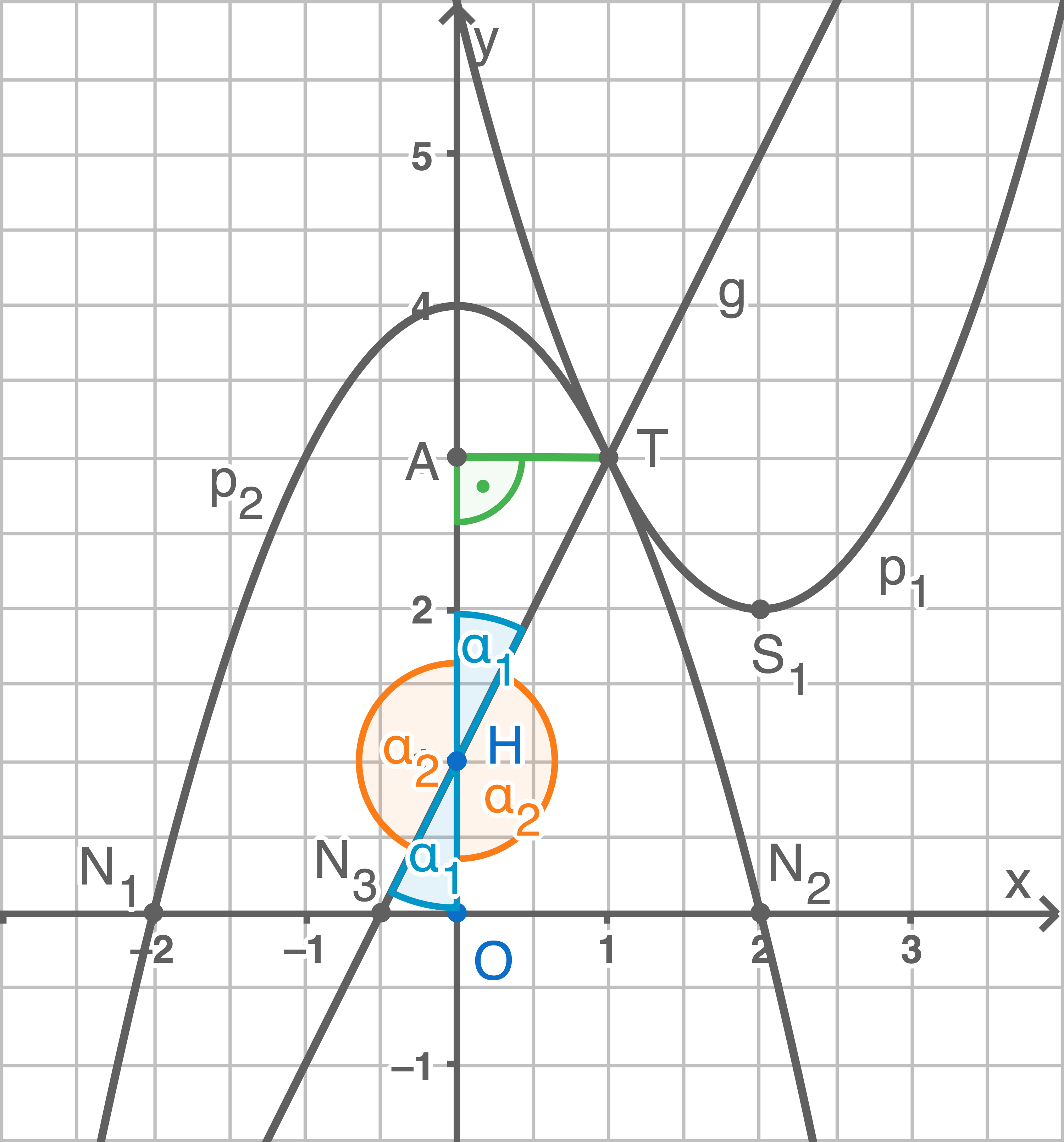
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=&\dfrac{\overline{TA}}{\overline{AH}} & \\[5pt]
\tan(\alpha_1)&=&\dfrac{1}{2} \\[5pt]
\alpha_1&=& 26,57^{\circ}\\[5pt]
\alpha_1&=&\underline{\underline{ 26,6^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/4729f6aba03a24c0865c5aa40bdaec1063b9c28e841c535dd2d3a29c0a0ba9ef?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\alpha_2&=&180^{\circ} -\alpha_1\\[5pt]
&=&180^{\circ} -26,57^{\circ} \\[5pt]
&=& 153,43^{\circ} \\[5pt]
\alpha_2&=&\underline{\underline{ 153,4^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/be2c5848e06c73cae412b88ad2f1bc1a30c9b737045a756769a5cad99570b988?color=5a5a5a) Gleichung einer Parabel
Gleichung einer Parabel  angeben, die weder mit
angeben, die weder mit  noch mit
noch mit  einen gemeinsamen Punkt hat
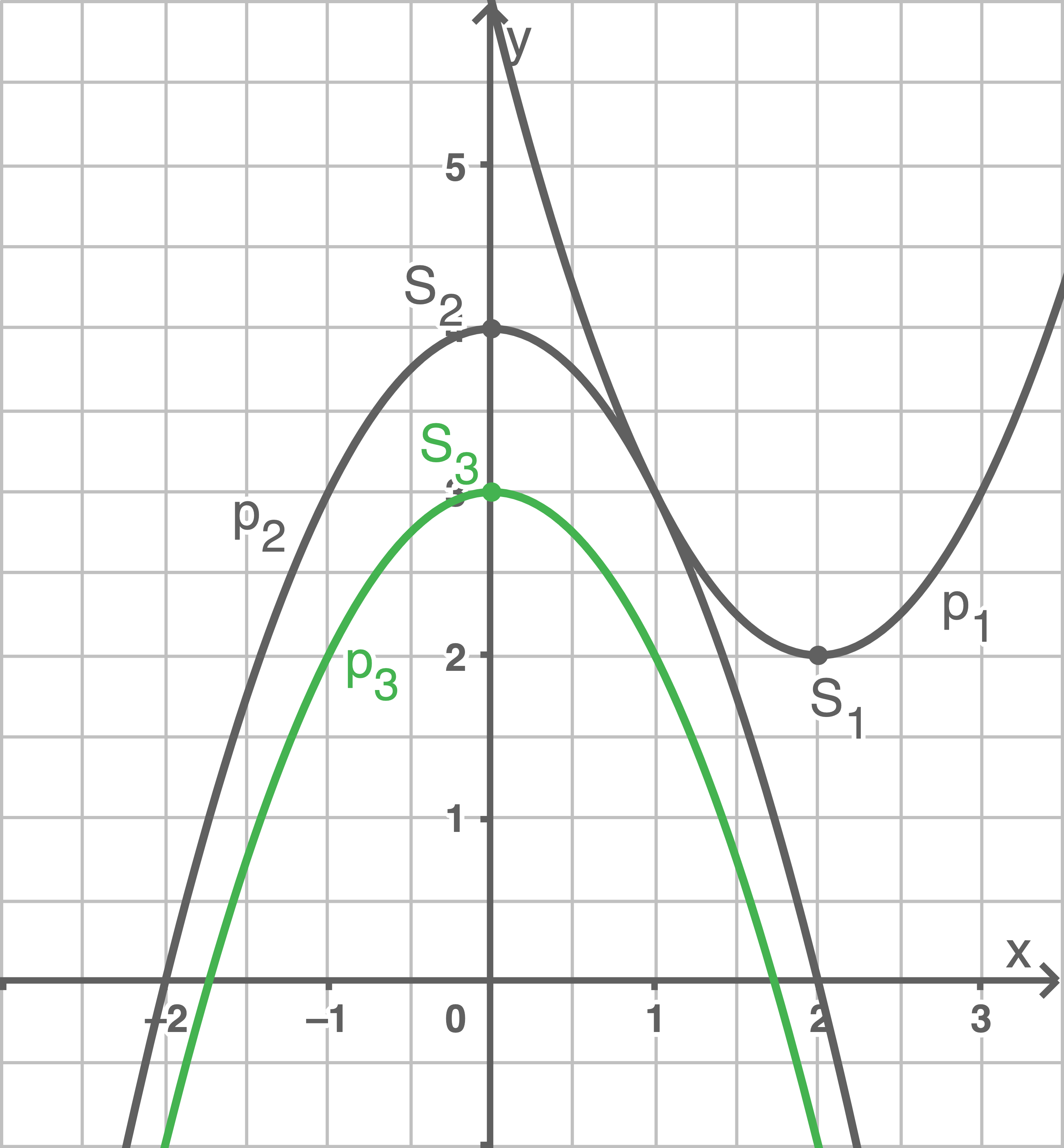
Lösungsvorschlag am Besipiel der Parabel
einen gemeinsamen Punkt hat
Lösungsvorschlag am Besipiel der Parabel  , die „innerhalb“ von
, die „innerhalb“ von  eingebettet ist:
Scheitelpunkt
eingebettet ist:
Scheitelpunkt 


 Skizze zur Veranschaulichung
Skizze zur Veranschaulichung

| Scheitelwinkel zu
| Scheitelwinkel zu

- Liegt unterhalb von
auf der
-Achse
- Scheitelpunkt
mit
- Form der Gleichung:
- Nach unten geöffnet
- Also gilt:
- Gleich gestreckt oder gestreckter als
- Also gilt:
- Aus
und
folgt:

b)
Koordinaten des zweiten Schnittpunkts  berechnen
1. Schritt: Funktionsgleichung von
berechnen
1. Schritt: Funktionsgleichung von  ermitteln
Es gilt:
ermitteln
Es gilt:
 Somit gilt für den Vorfaktor
Somit gilt für den Vorfaktor 
![\(\begin{array}[t]{rll}
y&=&ax^2+c &\quad \scriptsize \mid\;-\,c \\[5pt]
ax^2&=&y-c &\quad \scriptsize \mid\;:x^2 \\[5pt]
a&=&\dfrac{y-c}{x^2} &\quad \scriptsize \mid\; c=6, \, B(2|4)\\[5pt]
a&=&\dfrac{4-6}{2^2} \\[5pt]
a&=&\dfrac{-2}{4} \\[5pt]
a&=&-0,5 \\[10pt]
\underline{ p_1:y=-0,5x^2+6 }\\[5pt]
\end{array}\)](https://mathjax.schullv.de/4306e678049f07dd66f1e7b766434384bfc1c8be328ac821da506d0c16141bf6?color=5a5a5a) 2. Schritt: Funktionsgleichung von
2. Schritt: Funktionsgleichung von  ermitteln
ermitteln
![\(\begin{array}[t]{rll}
y&=&x^2+3x+q &\quad \scriptsize \mid\;B(2\mid 4) \\[5pt]
4&=&2^2+3\cdot 2+q \\[5pt]
4&=&4+6+q \\[5pt]
4&=&10+q &\quad \scriptsize \mid\;-10 \\[5pt]
q&=&-6 \\[10pt]
\underline{ p_2:y=x^2+3x-6}
\end{array}\)](https://mathjax.schullv.de/acb6662a890e5fc046b0dc1ca5f866055ee3558b9c996e3cae439661631d721c?color=5a5a5a) 3. Schritt: Koordinaten des zweiten Schnittpunkts
3. Schritt: Koordinaten des zweiten Schnittpunkts  berechnen
berechnen
![\(\begin{array}[t]{rll}
p_1&=&p_2 \\[5pt]
-0,5x^2+6&=&x^2+3x-6 & \scriptsize \mid\;+0,5x^2\\[5pt]
6&=&1,5x^2+3x-6 & \scriptsize \mid\;-6 \\[5pt]
0&=&1,5x^2+3x-12 &\scriptsize \mid\;:1,5 \\[5pt]
0&=&x^2+2x-8 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b5156823de02ab048d31d04ca16353dc151467b221e57216ec194477f5aca008?color=5a5a5a) Weiter mit der
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{2}{2}\pm \sqrt{\left(\dfrac{2}{2}\right)^2-(-8)} \\[5pt]
x_{1/2}&=&-1\pm \sqrt{1+8} \\[5pt]
x_{1/2}&=&-1\pm \sqrt{9} \\[5pt]
x_1&=&-1+3=2 \\[5pt]
x_2&=&-1-3=-4 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6af6bf6b579afd8d16a661c0cf6ac123a4385035afb104a488523700705eb33d?color=5a5a5a)
 ist die
ist die  -Koordinate des bekannten Schnittpunkts
-Koordinate des bekannten Schnittpunkts  Deswegen wird
Deswegen wird  in
in  eingesetzt:
eingesetzt:
![\(\begin{array}[t]{rll}
y&=&-0,5x^2+6 & \\[5pt]
y&=&-0,5\cdot (-4)^2 +6 \\[5pt]
y&=&-8+6 \\[5pt]
y&=&-2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/149ff1322f303a632db8d8ba451675cc2ed85aa472937b89ee47ecc936ee9e69?color=5a5a5a) Somit gilt:
Somit gilt:  Rechnerisch zeigen, dass
Rechnerisch zeigen, dass  ,
,  und
und  auf einer Geraden liegen
1. Schritt: Funktionsgleichung der Geraden
auf einer Geraden liegen
1. Schritt: Funktionsgleichung der Geraden  ermitteln, die von den Punkten
ermitteln, die von den Punkten  und
und  festgelegt wird
festgelegt wird
 2. Schritt: Zeigen, dass
2. Schritt: Zeigen, dass  auch auf der Gerade
auch auf der Gerade  liegt
liegt
![\(\begin{array}[t]{rll}
y&=&x+2 &\quad \scriptsize \mid\;C(0\mid 2)\, \,\text{einsetzen} \\[5pt]
2&=&0+2 \\[5pt]
2&=&2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/70460ef52629e54bd29777749a0f680881f4868521909599d53187509ea6984c?color=5a5a5a) Damit ist gezeigt, dass die Punkte
Damit ist gezeigt, dass die Punkte  und
und  auf einer Geraden liegen.
auf einer Geraden liegen.
- Scheitelpunkt
- Allgemeine Geradengleichung:
- Für den Steigungsfaktor
gilt:
- Also gilt für
Lösung W 4
a)
Erwartungswert berechnen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{3}{36}+2\,€\cdot \dfrac{3}{36}+0\,€\cdot \dfrac{30}{36}-1\,€\\[5pt]
&=&\dfrac{12}{36}\,€+\dfrac{6}{36}\,€-1\,€\\[5pt]
&=& \dfrac{1}{2}\,€-1\,€\\[5pt]
&=& -\dfrac{1}{2}\,€\\[5pt]
E &=& \underline{\underline{ -0,50\,€}}
\end{array}\)](https://mathjax.schullv.de/1aaebe9aecb5661dee4a64b7a8703ae5c78eaad1924f3ceabaf9526c3963e288?color=5a5a5a) Wofür sollte sich der Betreiber entscheiden?
Version 1: Würfel mit drei Einsen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
Wofür sollte sich der Betreiber entscheiden?
Version 1: Würfel mit drei Einsen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
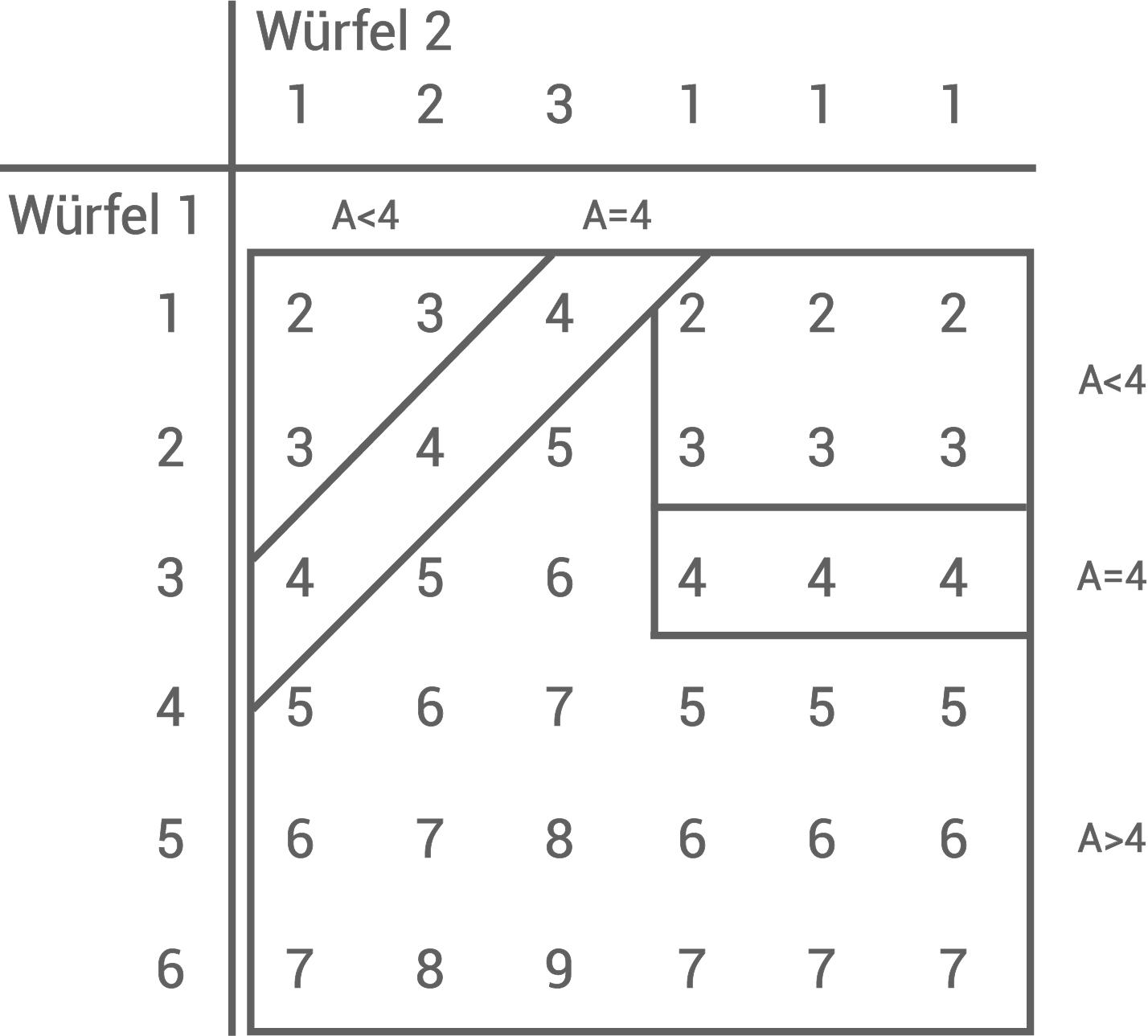 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{6}{36}+2\,€\cdot \dfrac{9}{36}+0\,€\cdot \dfrac{21}{36}-1\,€\\[5pt]
&=&\dfrac{24}{36}\,€+\dfrac{18}{36}\,€-1\,€\\[5pt]
E&=& \underline{ 0,17\,€}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/047a430c022f5a78989ad03777c00d845e607bf25d0c844291d18d1261c66eee?color=5a5a5a) Version 2: Würfel mit drei Dreien
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
Version 2: Würfel mit drei Dreien
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{6}{36}+2\,€\cdot \dfrac{3}{36}+0\,€\cdot \dfrac{27}{36}-1\,€\\[5pt]
&=&\dfrac{24}{36}\,€+\dfrac{6}{36}\,€-1\,€\\[5pt]
E&=& \underline{ -0,17\,€}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/03d2a7c98049b6add614589853e4a891877fdf37f602fc1d65136f4d0af71654?color=5a5a5a) Da der zu erwartende Gewinn für die Teilnehmer bei Version 2: Würfel mit drei Dreien kleiner als bei Version 1: Würfel mit drei Einsen ist, macht es für den Betreiber mehr Sinn, sich für den Würfel mit drei Dreien zu entscheiden.
Da der zu erwartende Gewinn für die Teilnehmer bei Version 2: Würfel mit drei Dreien kleiner als bei Version 1: Würfel mit drei Einsen ist, macht es für den Betreiber mehr Sinn, sich für den Würfel mit drei Dreien zu entscheiden.
Denn damit kann der Betreiber mit einem durchschnittlichen Gewinn von pro Spiel rechnen.
pro Spiel rechnen.



Denn damit kann der Betreiber mit einem durchschnittlichen Gewinn von
b)
Eine mögliche Funktionsgleichung für das parabelförmige Teilstück bestimmen
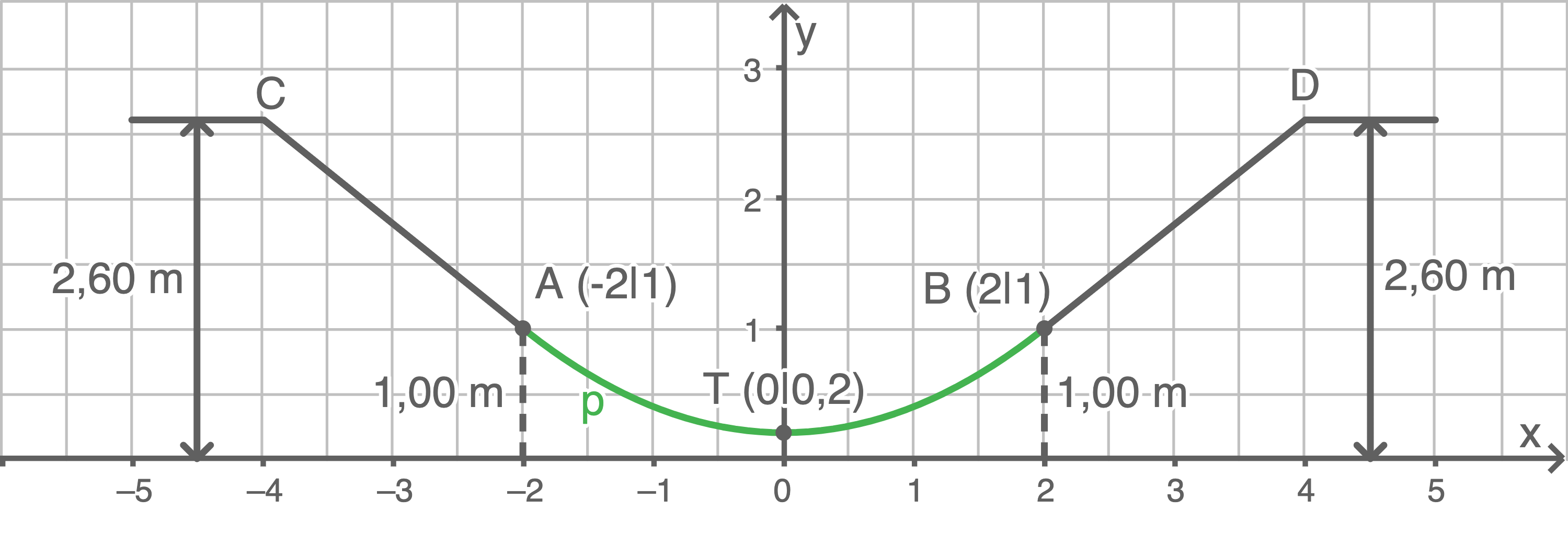 Es gilt:
Es gilt:
 Somit gilt für den Vorfaktor
Somit gilt für den Vorfaktor 
![\(\begin{array}[t]{rll}
y&=&ax^2+c &\quad \scriptsize \mid\;-\,c \\[5pt]
ax^2&=&y-c &\quad \scriptsize \mid\;:x^2 \\[5pt]
a&=&\dfrac{y-c}{x^2} &\quad \scriptsize \mid\; c=0,2, \, B(2|1)\\[5pt]
a&=&\dfrac{1-0,2}{2^2} \\[5pt]
a&=&\dfrac{0,8}{4} \\[5pt]
a&=&0,2 \\[10pt]
\end{array}\)](https://mathjax.schullv.de/bc4938917352a4eaa4ae014817ca19c270bf485e46d819473cc3cd3702691c3f?color=5a5a5a) Damit folgt
Damit folgt  Eine mögliche Funktionsgleichung für die Gerade bestimmen
Eine mögliche Funktionsgleichung für die Gerade bestimmen


- Allgemeine Funktionsgleichung:
- Scheitelpunkt

- Allgemeine Funktionsgleichung:
- Für den Steigungsfaktor
gilt:
- Also gilt für