Wahlbereich
Aufgabe W1
a)
Das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck  haben die Seite
haben die Seite  gemeinsam.
gemeinsam.
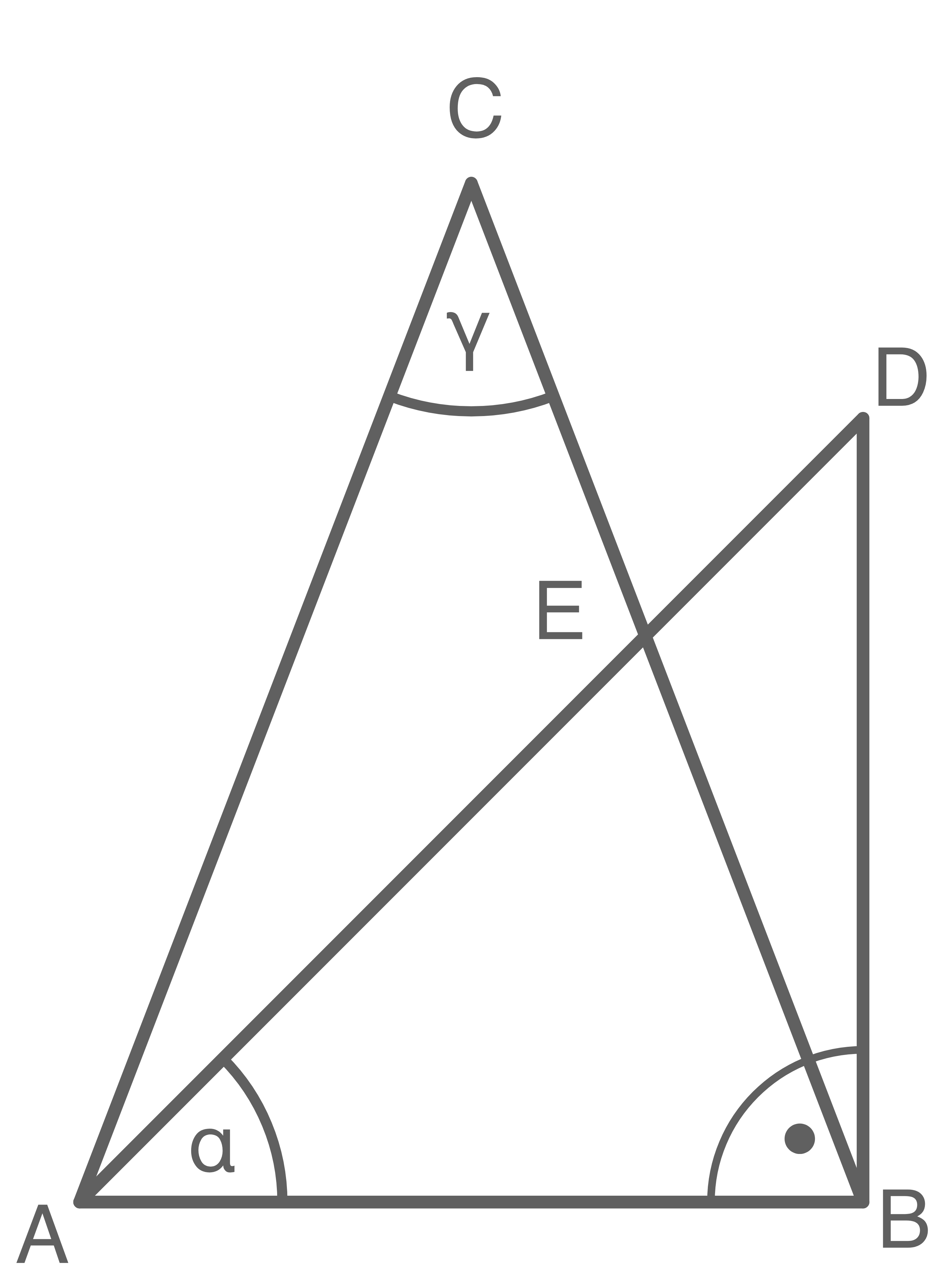 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BD}&=&7,2 \text{ cm} & \\[5pt]
\overline{DE}&=&3,0 \text{ cm} & \\[5pt]
\alpha&=&42,0^{\circ} & \\[5pt]
\overline{AC}&=&\overline{BC}
\end{array}\)](https://mathjax.schullv.de/173beec24dfb84acf70b77bc0c5969496211bc9cf7a25a3bb4404c07f6ac96fa?color=5a5a5a) Berechne den Abstand des Punktes
Berechne den Abstand des Punktes  von
von  sowie den Winkel
sowie den Winkel  .
.

5,5 P
b)
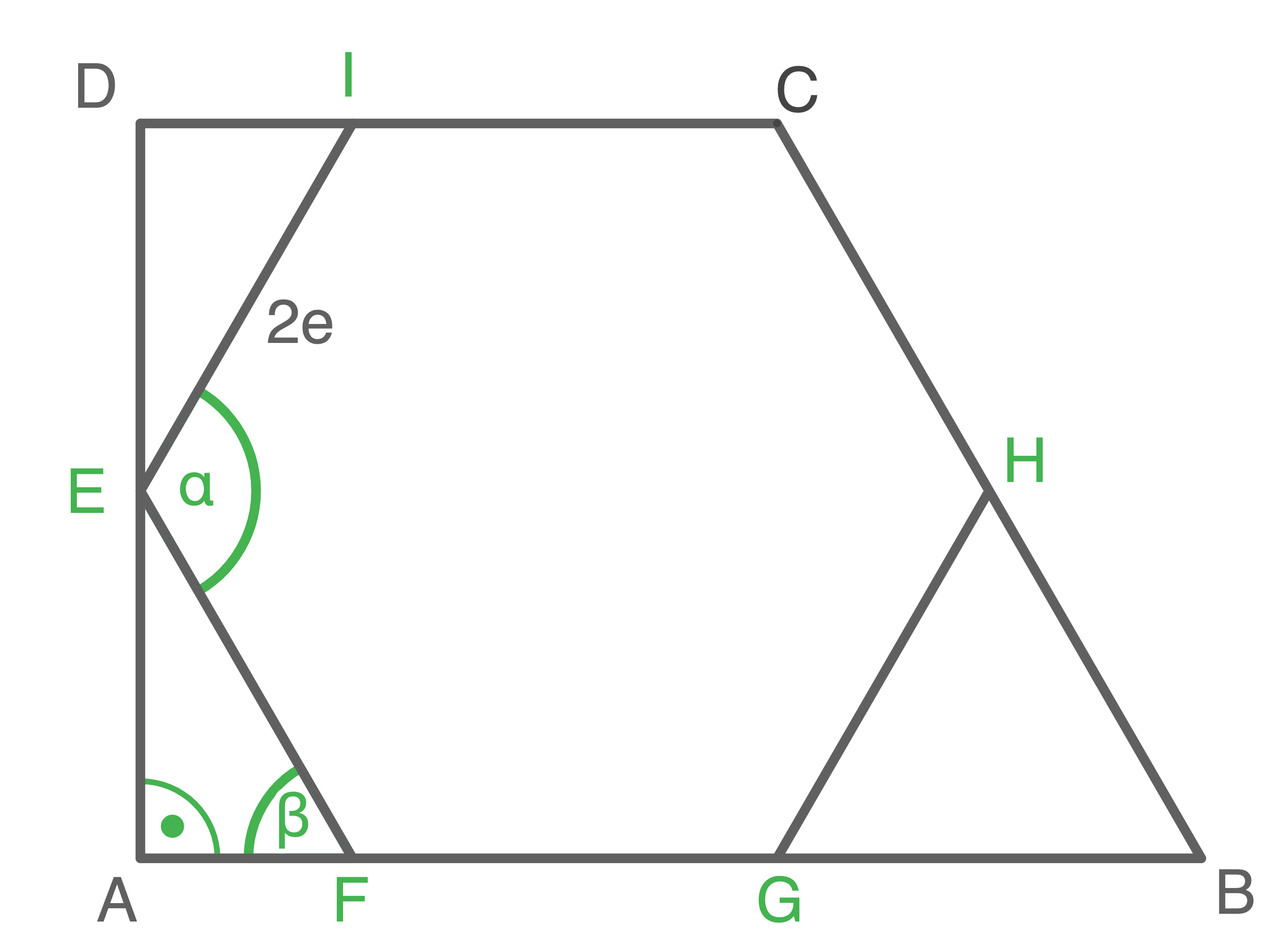
Gegeben sind ein rechtwinkliges Trapez  und ein regelmäßiges Sechseck.
und ein regelmäßiges Sechseck.
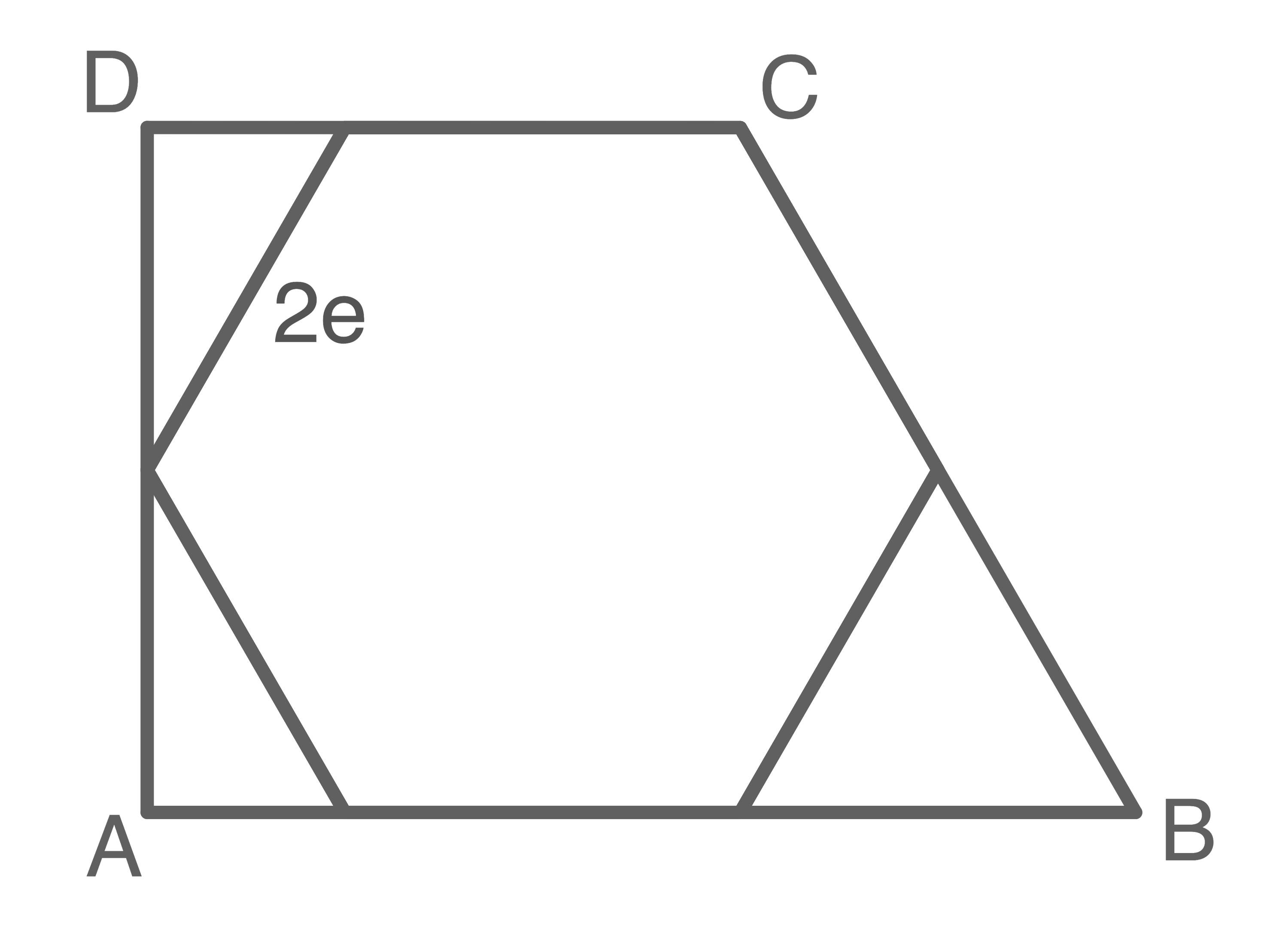 Die Eckpunkte des Sechsecks liegen auf den Seiten des Trapezes.
Zeige ohne Verwendung gerundeter Werte, dass für den Flächeninhalt des Trapezes
Die Eckpunkte des Sechsecks liegen auf den Seiten des Trapezes.
Zeige ohne Verwendung gerundeter Werte, dass für den Flächeninhalt des Trapezes  gilt:
gilt:
 Gib die Länge der Diagonale
Gib die Länge der Diagonale  ohne Verwendung gerundeter Werte an.
ohne Verwendung gerundeter Werte an.

4,5 P
Aufgabe W2
a)
Für einen Zylinder gilt:
![\(\begin{array}[t]{rll}
r&=&3,5 \text{ cm} \\[5pt]
h&=&12,0 \text{ cm}
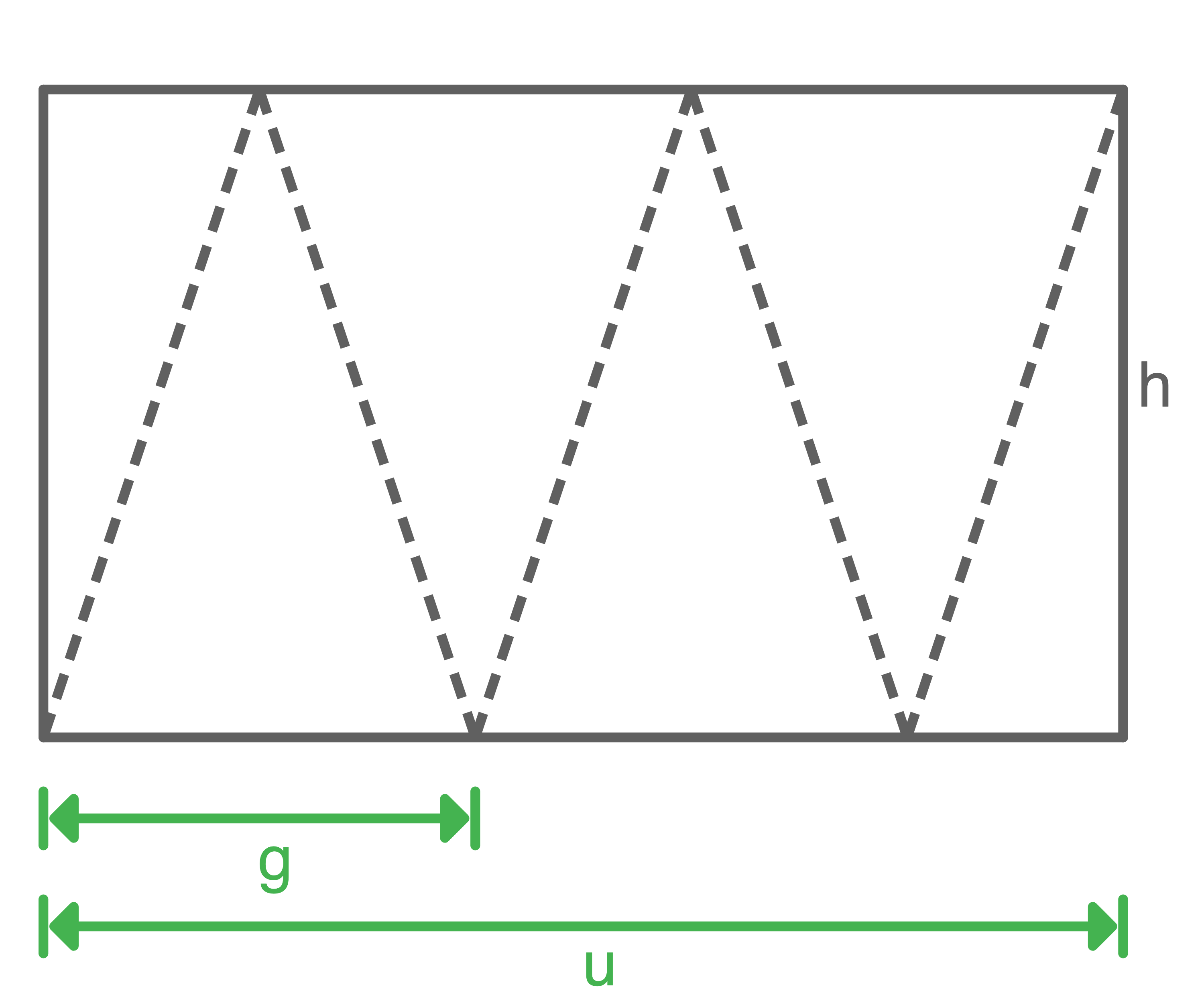
\end{array}\)](https://mathjax.schullv.de/2c534d08b688773bd3b31d717264990557acd6e3a5ca8eee5aea091d8ff3540b?color=5a5a5a) Die Mantelfläche des Zylinders wird abgerollt.
Die Mantelfläche des Zylinders wird abgerollt.
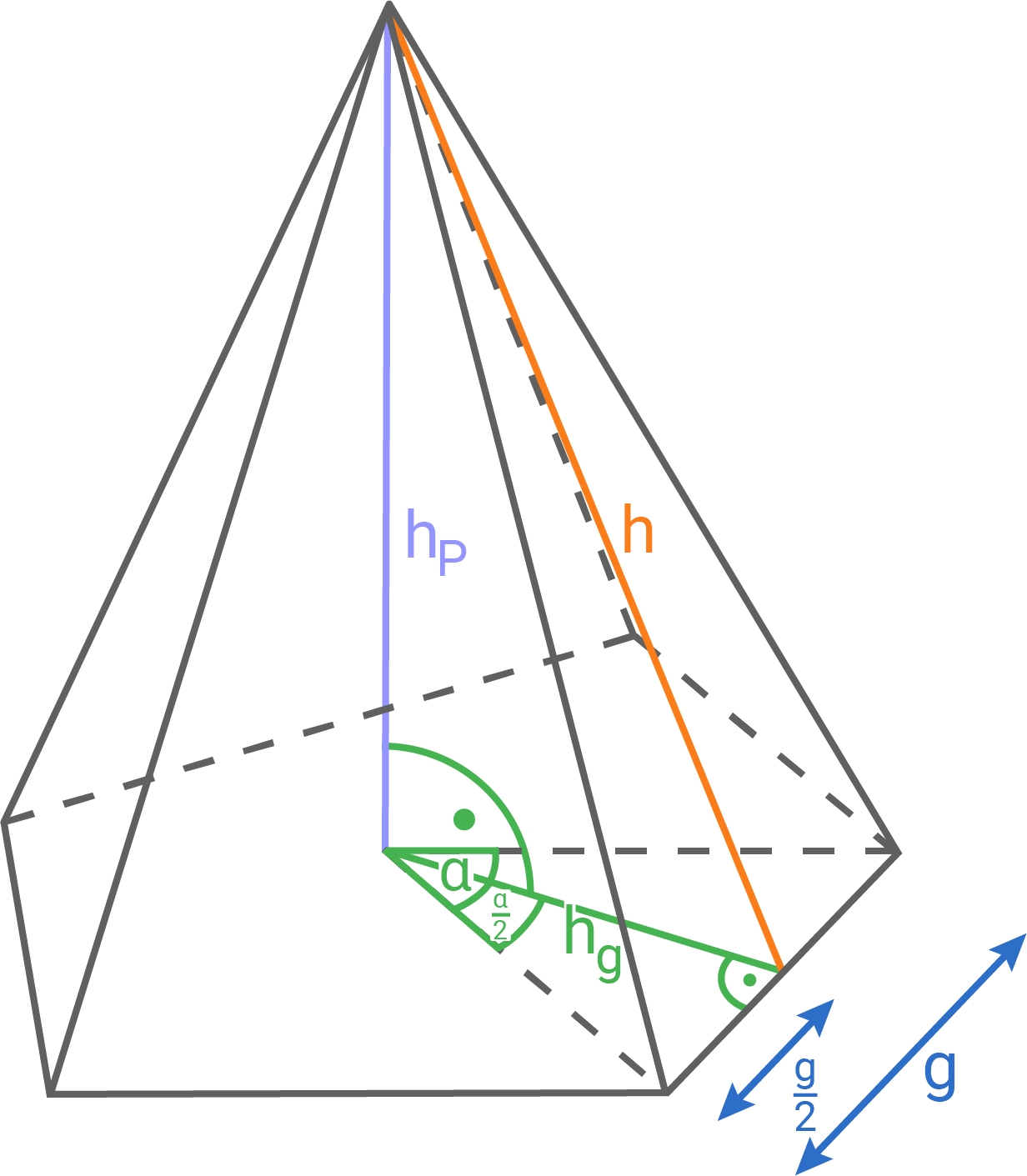
).png) Mit den Einzelteilen dieses Rechtecks wird die Mantelfläche einer regelmäßigen fünfseitigen Pyramide vollständig beklebt.
Berechne das Volumen dieser Pyramide.
Mit den Einzelteilen dieses Rechtecks wird die Mantelfläche einer regelmäßigen fünfseitigen Pyramide vollständig beklebt.
Berechne das Volumen dieser Pyramide.
).png)
5 P
b)
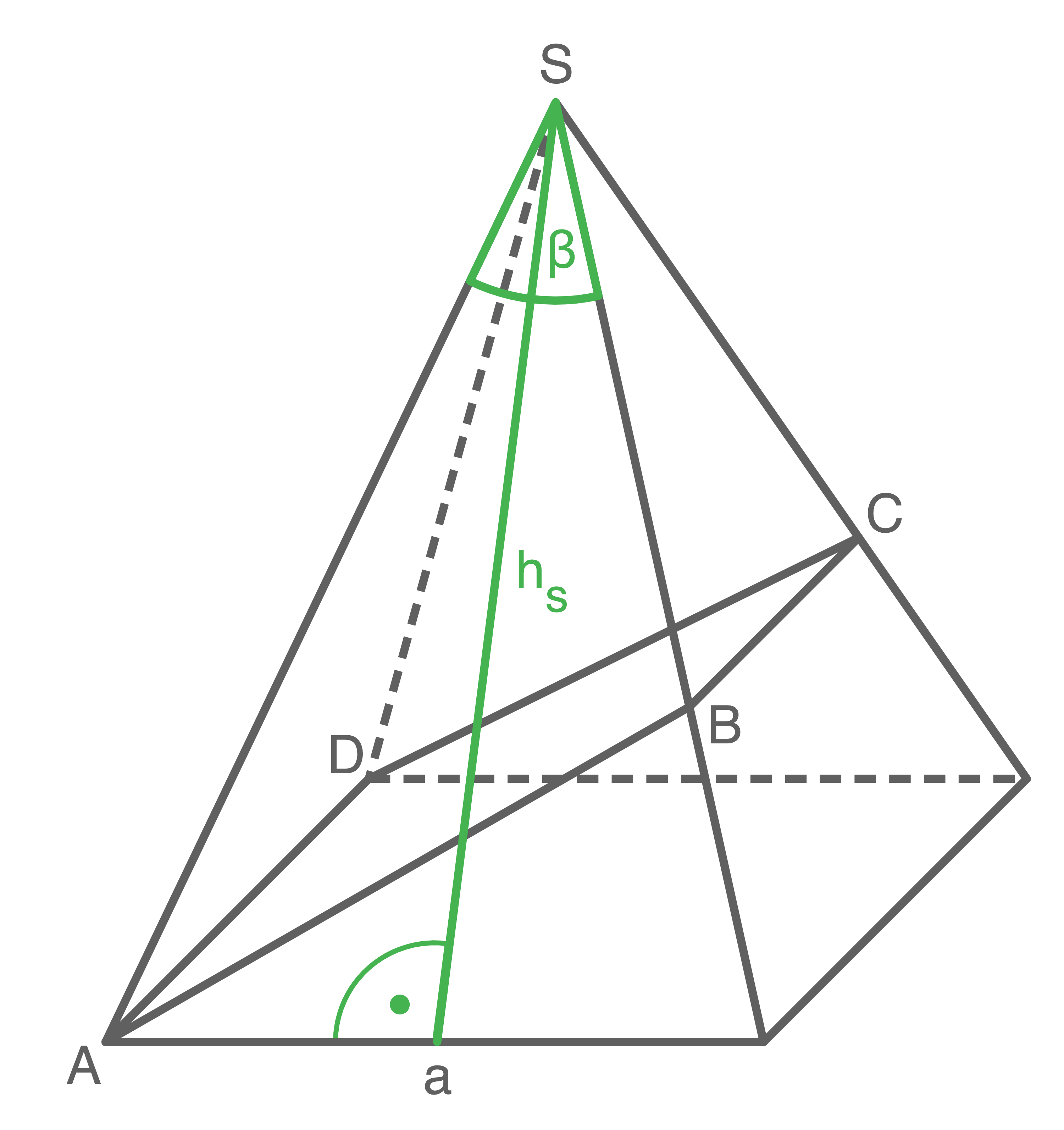
Die Eckpunkte des gleichschenkligen Trapezes  liegen auf den Kanten bzw. Eckpunkten einer quadratischen Pyramide.
liegen auf den Kanten bzw. Eckpunkten einer quadratischen Pyramide.
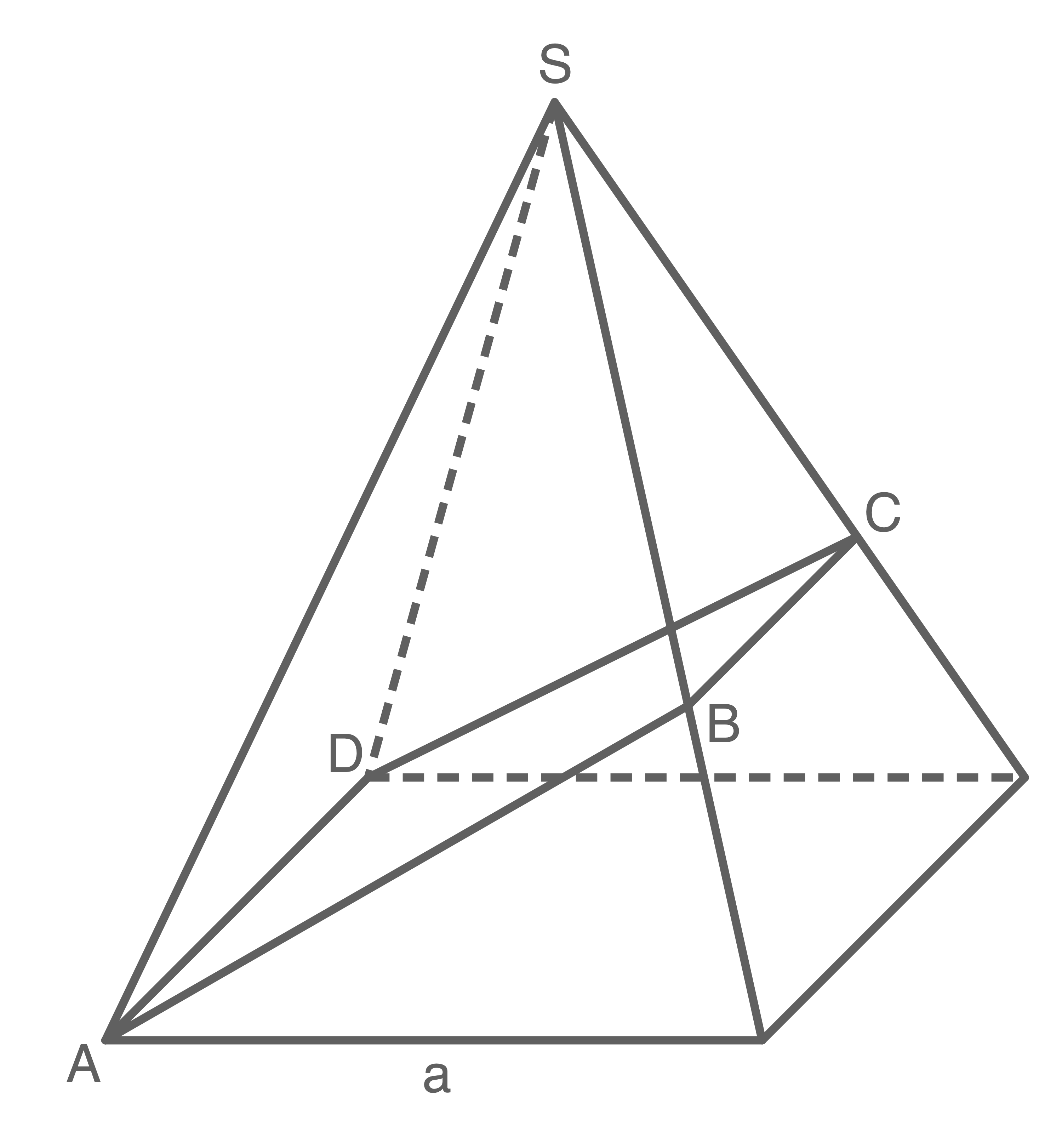 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
O_{Pyr}&=&357 \text{ cm}^2 \\[5pt]
a&=&10,0 \text{ cm} \\[5pt]
\overline{AB}&=&\overline{BS}
\end{array}\)](https://mathjax.schullv.de/56d299627bc9a11e1fc26a2ec4417351d9def064c6aa852d07869165be0357c5?color=5a5a5a) Berechne den Umfang des Trapezes
Berechne den Umfang des Trapezes 

5 P
Aufgabe W3
a)
Begründe deine Entscheidung. Vervollständige die Funktionsgleichungen von
Berechne die Funktionsgleichung von
5 P
b)
Die Parabel  mit
mit  und die nach oben geöffnete Normalparabel
und die nach oben geöffnete Normalparabel  mit dem Scheitel
mit dem Scheitel  haben einen gemeinsamen Punkt
haben einen gemeinsamen Punkt  .
.
Die Gerade geht durch den Ursprung
geht durch den Ursprung  und den Punkt
und den Punkt  .
.
Bestimme die Funktionsgleichung der Geraden Die Schnittpunkte der Parabel
Die Schnittpunkte der Parabel  mit der
mit der  -Achse und der Punkt
-Achse und der Punkt  bilden ein Dreieck.
bilden ein Dreieck.
Bestimme den Flächeninhalt dieses Dreiecks. Bastian behauptet:
„Die Gerade halbiert den Flächeninhalt des Dreiecks.“
halbiert den Flächeninhalt des Dreiecks.“
Hat Bastian recht?
Begründe deine Antwort durch Rechnung oder Argumentation.
Die Gerade
Bestimme die Funktionsgleichung der Geraden
Bestimme den Flächeninhalt dieses Dreiecks. Bastian behauptet:
„Die Gerade
Hat Bastian recht?
Begründe deine Antwort durch Rechnung oder Argumentation.
5 P
Aufgabe W4
a)
Bei einer Wohltätigkeitsveranstaltung wird ein Glücksrad eingesetzt.
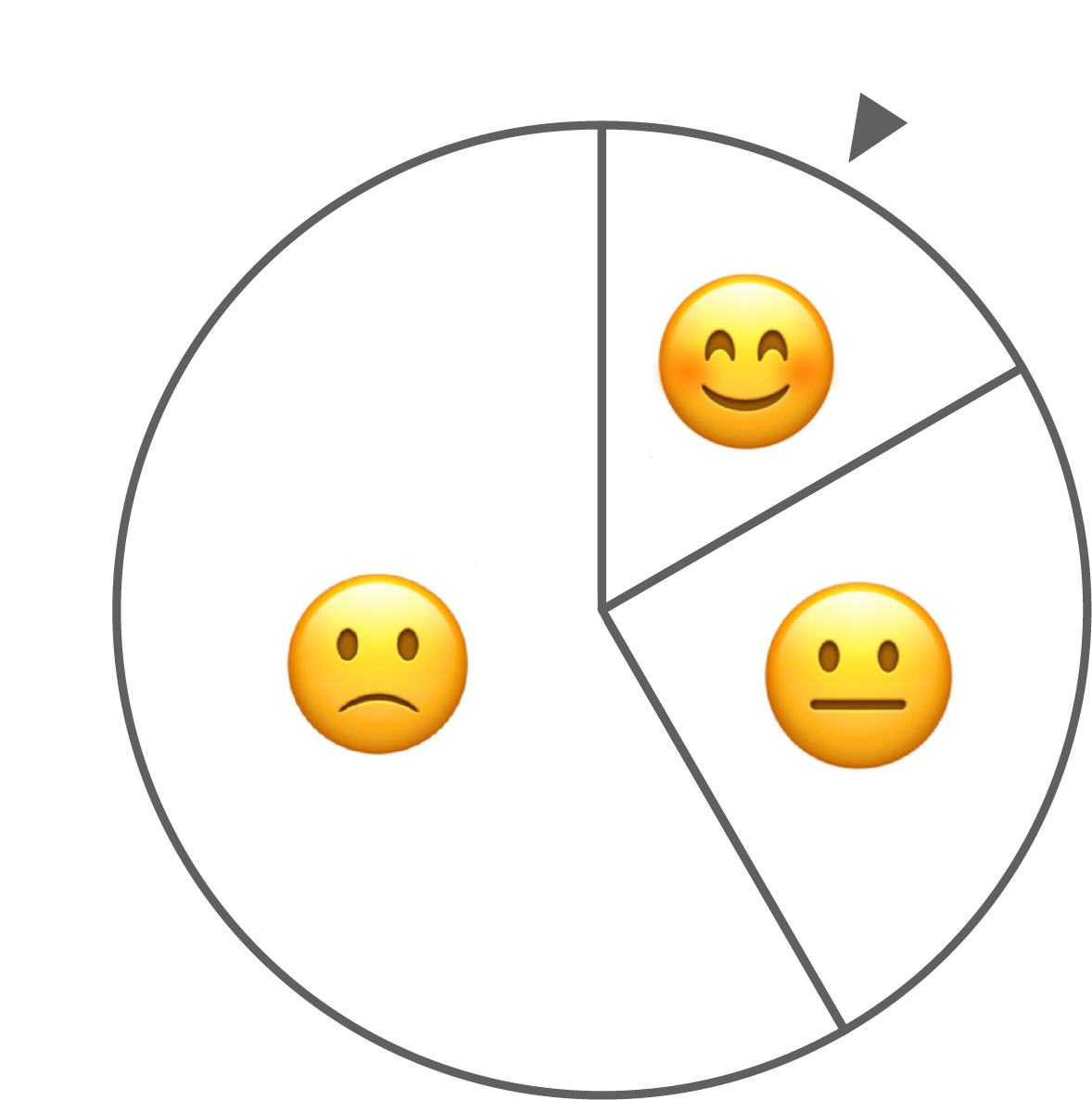 Die Mittelpunktswinkel betragen
Die Mittelpunktswinkel betragen  .
.
Das Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊 ? Das Glücksrad wird für ein Glücksspiel verwendet.
Berechne den Erwartungswert unter Berücksichtigung des untenstehenden Gewinnplans.
Der Gewinnplan soll so verändert werden, dass das Spiel fair wird.
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ sein, wenn alles andere unverändert bleibt?

Das Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊 ? Das Glücksrad wird für ein Glücksspiel verwendet.
Berechne den Erwartungswert unter Berücksichtigung des untenstehenden Gewinnplans.
| Ereignisse | Gewinn |
|---|---|
| zweimal 😊 | 4,00€ |
| zweimal 😐 | 2,00€ |
| sonstige | kein Gewinn |
| Einsatz pro Spiel: 0,50€ |
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ sein, wenn alles andere unverändert bleibt?
5,5 P
b)
Die Lupu-Brücke überspannt den Fluss Huangpu in Shanghai.
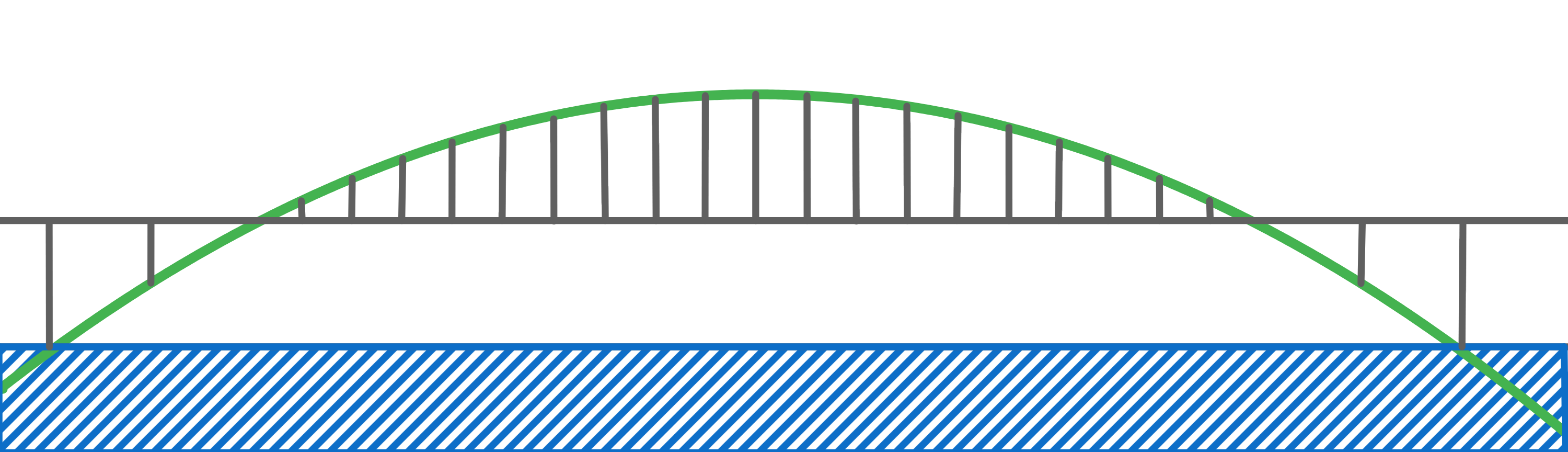 Sie ist die zweitlängste Bogenbrücke der Welt und hat annähernd die Form einer Parabel.
Sie ist die zweitlängste Bogenbrücke der Welt und hat annähernd die Form einer Parabel.
Sie kann mit der Funktionsgleichung beschrieben werden.
Die Bogenbrücke hat auf Höhe der Wasseroberfläche eine Weite von 550 m.
beschrieben werden.
Die Bogenbrücke hat auf Höhe der Wasseroberfläche eine Weite von 550 m.
Die Fahrbahn befindet sich 50 m über der Wasseroberfläche.
Das ist die Hälfte der maximalen Höhe der Brücke. Bestimme eine mögliche Funktionsgleichung für den Brückenbogen. Berechne die Länge der Fahrbahn innerhalb des Brückenbogens.

Sie kann mit der Funktionsgleichung
Die Fahrbahn befindet sich 50 m über der Wasseroberfläche.
Das ist die Hälfte der maximalen Höhe der Brücke. Bestimme eine mögliche Funktionsgleichung für den Brückenbogen. Berechne die Länge der Fahrbahn innerhalb des Brückenbogens.
4,5 P
Lösung W1
a)
Abstand von  zu
zu  berechnen
berechnen
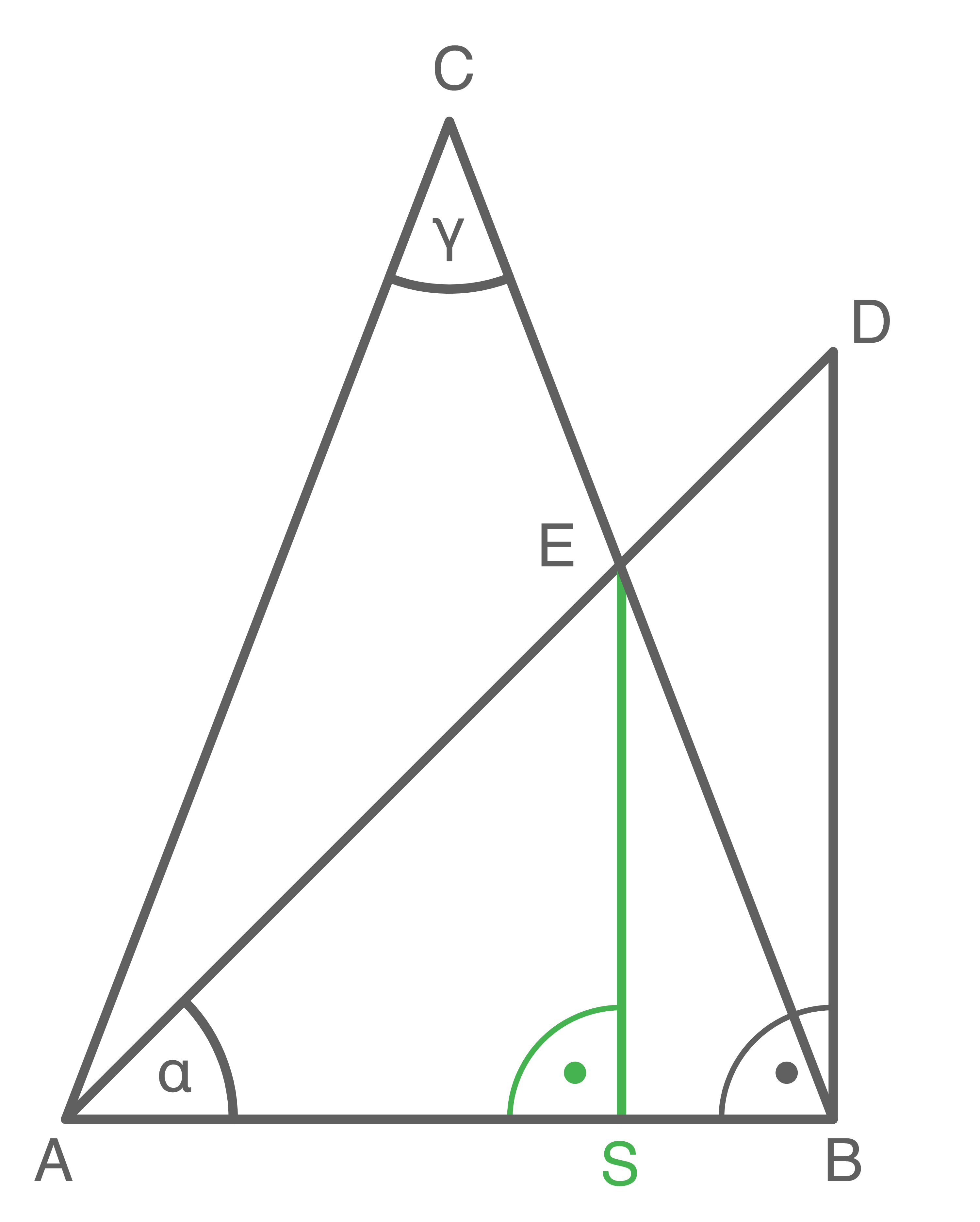 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BD}}{\overline{AD}} \\[5pt]
\sin(42,0^{\circ})&=& \dfrac{7,2 \,\text{cm}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt]
\sin(42,0^{\circ})\cdot \overline{AD}&=& 7,2 \,\text{cm} \quad \scriptsize \mid\; : \sin(42,0^{\circ}) \\[5pt]
\overline{AD}&=& \dfrac{7,2 \,\text{cm}}{\sin(42,0^{\circ})} \\[5pt]
\overline{AD}&=& \underline{10, 76 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/661948f8774e92cf4bf7fa2b32eead09ad2937ccd27d3bcea1c342fecc87dd6e?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AD}-\overline{DE} \\[5pt]
&=& 10,76 \,\text{cm} - 3,0 \,\text{cm} \\[5pt]
&=& \underline{7,76 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/dce5af3145091ba9b110ed52ba11d265f8d161c87bb3e22724a7eb26eeac5d80?color=5a5a5a) 3. Schritt: Abstand bestimmen
Größe des Winkels
3. Schritt: Abstand bestimmen
Größe des Winkels  berechnen
berechnen
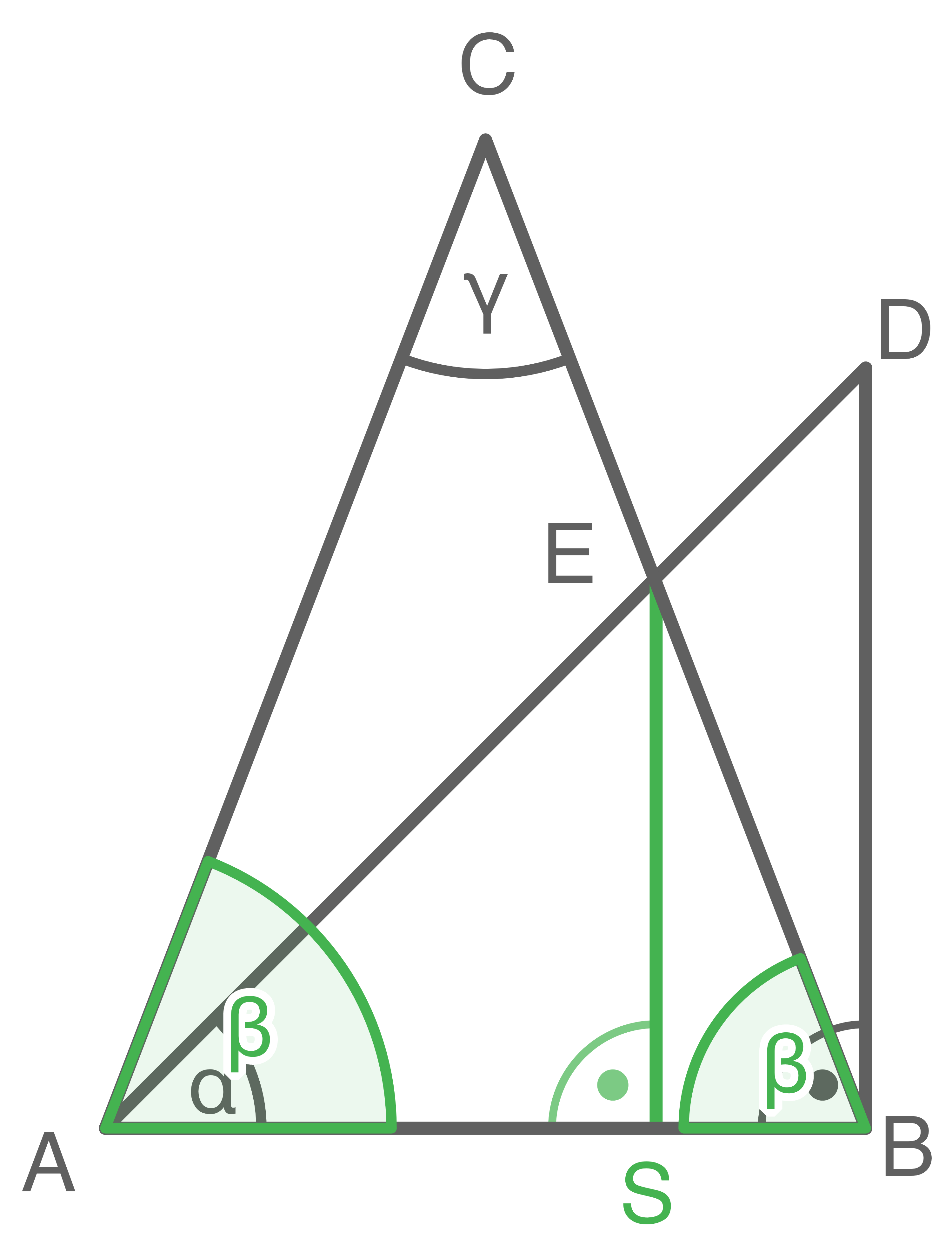 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{\overline{BD}}{\overline{AB}} \\[5pt]
\tan(42,0^{\circ})&=& \dfrac{7,2\,\text{cm}}{\overline{AB}} \quad \scriptsize \mid\; \cdot \overline{AB} \\[5pt]
\tan(42,0^{\circ})\cdot \overline{AB} &=& 7,2\,\text{cm} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{AB}&=& \dfrac{7,2 \,\text{cm}}{\tan(42,0^{\circ})} \\[5pt]
\overline{AB}&=& 8,00 \,\text{cm} \\[5pt]
\overline{AB}&=& \underline{8\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/69c4174b0183bca04e80f7edf6ed62c17f5de24899fdd748e851f35fa055e3e8?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
3. Schritt: Länge der Strecke
bestimmen
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BS}&=& \overline{AB} - \overline{AS} \\[5pt]
&=& 8 \,\text{cm} - 5,77 \,\text{cm} \\[5pt]
&=& \underline{2,23 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/d5b351aff2815f26b297353b725af0c828da674f5a530b53160679cabcac8a6a?color=5a5a5a) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan (\beta)&=&\dfrac{\overline{ES}}{\overline{BS}} \\[5pt]
\tan (\beta)&=&\dfrac{5,19\text{ cm}}{2,23 \,\text{cm} } &\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\beta&=& \underline{66,75^{\circ}}
\end{array}\)](https://mathjax.schullv.de/8d3fa08a5b7a68213960f2756ffe16afcbb4f3b10d7f87998424472a1db4b2ba?color=5a5a5a) 5. Schritt: Größe des Winkels
5. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=& 180^{\circ}-2\cdot \beta \\[5pt]
&=& 180^{\circ}-2\cdot 66,75^{\circ} \\[5pt]
&=& \underline{\underline{ 46,5^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/5c2cb8e02eebe1ead9b561d8cef36348a09f9266065da608338c902833945696?color=5a5a5a)


b)
Somit sind alle Innenwinkel von
Lösung W2
a)
b)
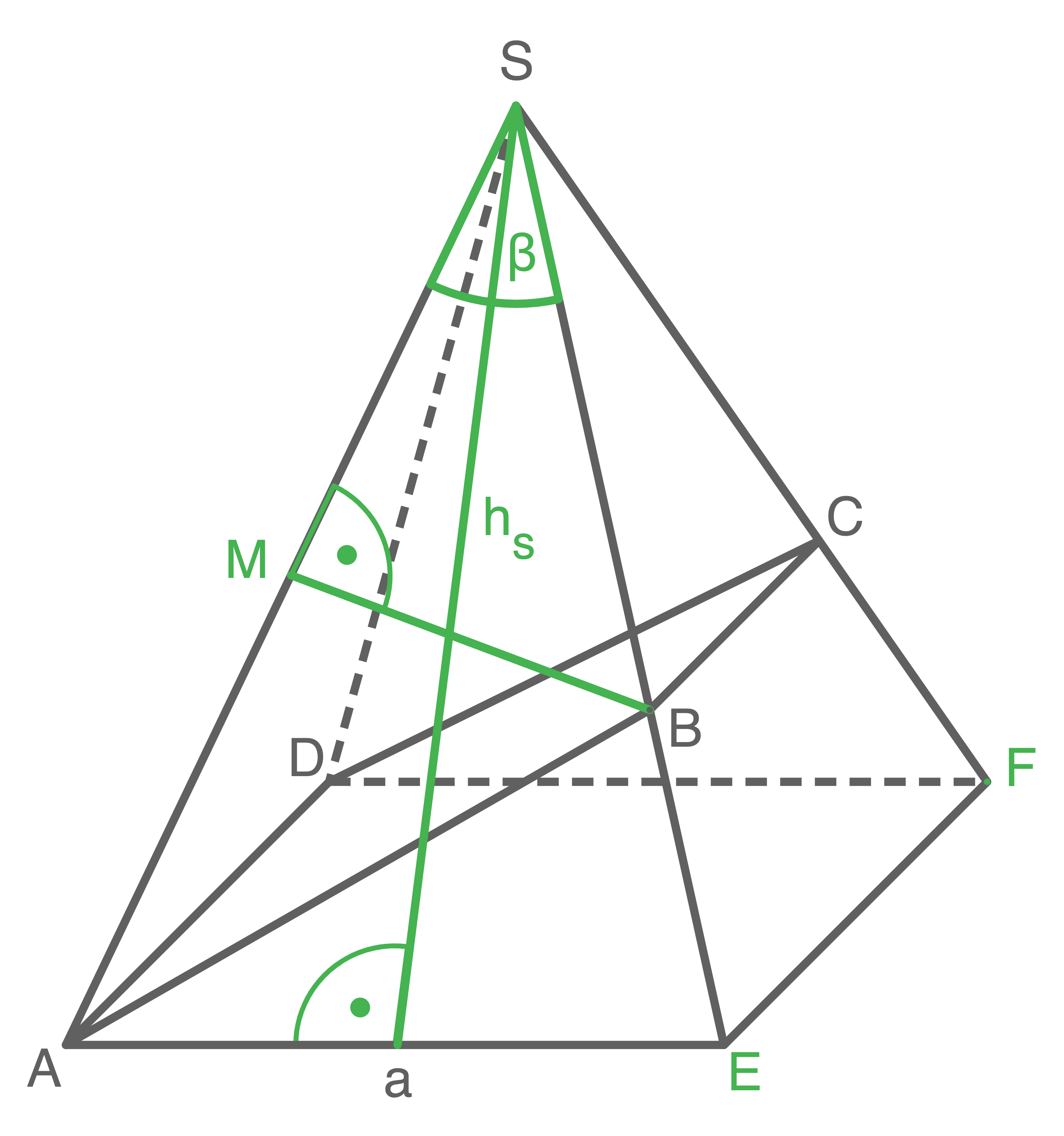
Lösung W3
a)
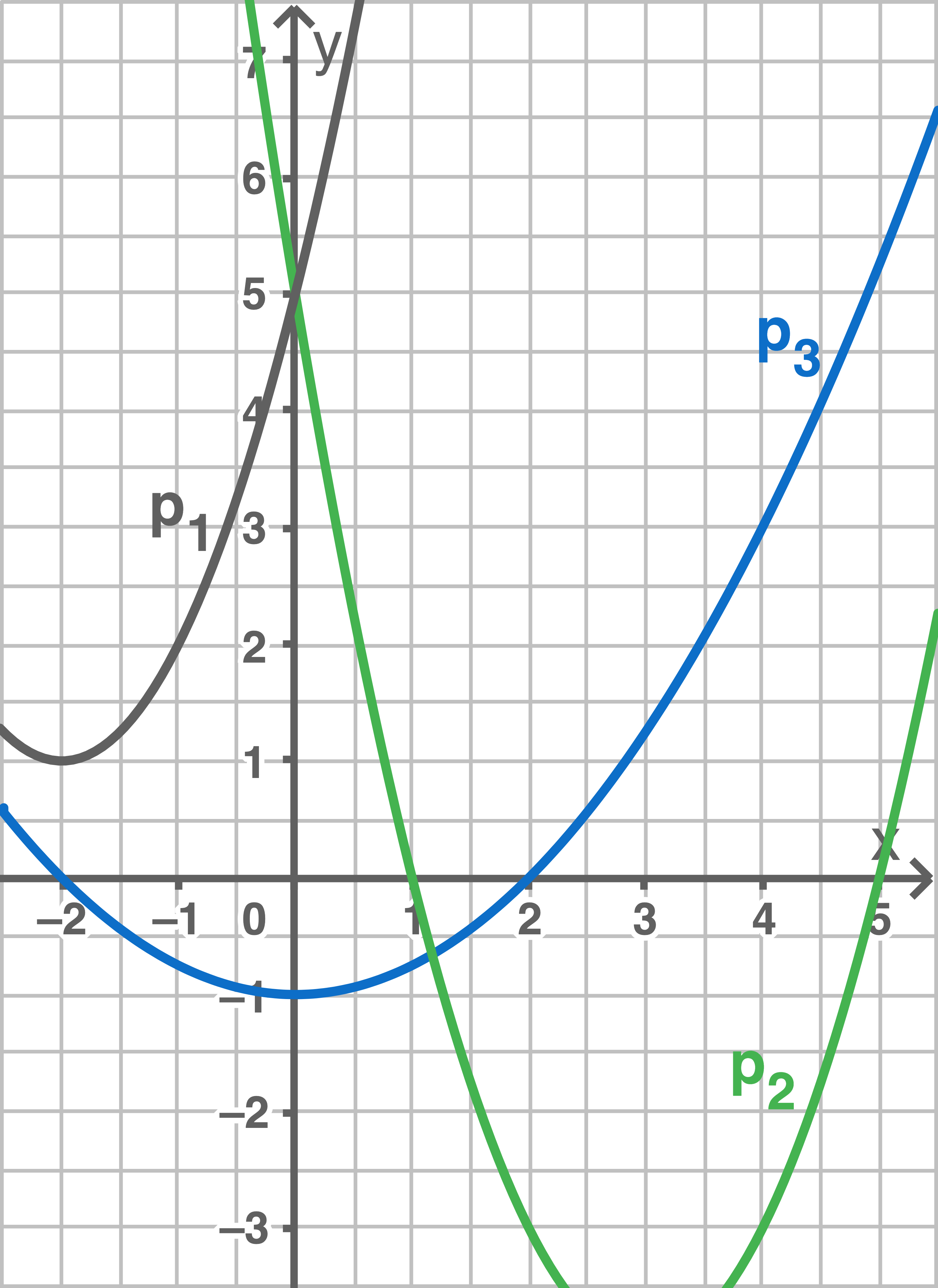
Welcher Graph gehört zu welcher Funktionsgleichung?
Gleichung 
Da der Graph im Vergleich zu einer Normalparabel entlang der
im Vergleich zu einer Normalparabel entlang der  -Achse gestaucht ist, kann er nur zur Gleichung
-Achse gestaucht ist, kann er nur zur Gleichung  gehören. Die Parabel wird durch den Parameter
gehören. Die Parabel wird durch den Parameter  gestaucht.
Gleichung
gestaucht.
Gleichung 
Gleichung mit quadratischer Ergänzung in die Scheitelpunktform bringen:![\(\begin{array}[t]{rll}
y&=& x^2-6x+5 \\[5pt]
&=& x^2-2\cdot 3x+5 \\[5pt]
&=& x^2-2\cdot 3x+3^2-3^2+5 \\[5pt]
y&=&(x-3)^2-4
\end{array}\)](https://mathjax.schullv.de/ca06f3207654c1a18809610d2fc5c8b243843340e39cdcd1a02846872421a61e?color=5a5a5a)
 Da
Da  bereits Gleichung (A) zugeordnet ist und der Scheitelpunkt von
bereits Gleichung (A) zugeordnet ist und der Scheitelpunkt von  nicht den Koordinaten von
nicht den Koordinaten von  entspricht, muss
entspricht, muss  zu Gleichung
zu Gleichung  gehören.
Gleichung
gehören.
Gleichung 
Da als einziger Graph übrig bleibt, kann dieser per Ausschlussverfahren der Gleichung
als einziger Graph übrig bleibt, kann dieser per Ausschlussverfahren der Gleichung  zugeordnet werden.
Funktionsgleichung von
zugeordnet werden.
Funktionsgleichung von  vervollständigen
Einen Punkt des Graphen ablesen und in die Gleichung
vervollständigen
Einen Punkt des Graphen ablesen und in die Gleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& ax^2-1 \quad \scriptsize (2\mid 0)\\[5pt]
0&=& a\cdot 2^2-1 \\[5pt]
0&=& 4a-1 \quad \scriptsize \mid\; +1 \\[5pt]
1&=& 4a \quad \scriptsize \mid\; :4 \\[5pt]
\dfrac{1}{4}&=& a \\[5pt]
a&=&\underline{ \dfrac{1}{4}}
\end{array}\)](https://mathjax.schullv.de/2198385a664363b29165e32dbaae189fae801c251e78297ffac325b58620852c?color=5a5a5a)
 Funktionsgleichung von
Funktionsgleichung von  vervollständigen
Gleichung mit quadratischer Ergänzung in die Scheitelpunktform bringen:
vervollständigen
Gleichung mit quadratischer Ergänzung in die Scheitelpunktform bringen:
![\(\begin{array}[t]{rll}
y &=& x^2+4x+q \\[5pt]
&=& x^2+2\cdot 2x+q \\[5pt]
&=& x^2+2\cdot 2x + 2^2-2^2+q\\[5pt]
y&=&\underline{ (x+2)^2-4+q}
\end{array}\)](https://mathjax.schullv.de/bd55c1f637c40007d6d320d550056d6cc74392a46515581cb97f88546df8b1ef?color=5a5a5a)
 Aus dem Schaubild von
Aus dem Schaubild von  lässt sich der Scheitelpunkt
lässt sich der Scheitelpunkt  ablesen.
ablesen.
![\(\begin{array}[t]{rll}
-4+q&=& 1 \quad \scriptsize \mid\; +4 \\[5pt]
q&=&\underline{ 5}
\end{array}\)](https://mathjax.schullv.de/9760c8bcbbd2d051dab95f41852054a1f2beac42c5e5c1bf803473ee5c723c02?color=5a5a5a)
 Funktionsgleichung von
Funktionsgleichung von  berechnen
Die Gerade
berechnen
Die Gerade  geht durch die Scheitelpunkte
geht durch die Scheitelpunkte  und
und  und wird durch die Gleichung
und wird durch die Gleichung  bestimmt.
bestimmt.
 einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-1&=& m\cdot 0 +b \\[5pt]
b&=& -1
\end{array}\)](https://mathjax.schullv.de/437b2c007f7d89ac3f18f5210fa4fe89444360d085609b394b48b84365621f21?color=5a5a5a)
 und
und  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-4&=& m\cdot 3-1 &\quad \scriptsize \mid\; +1 \\[5pt]
-3&=& 3m &\quad \scriptsize \mid\; :3 \\[5pt]
-1&=& m \\[5pt]
m&=& -1
\end{array}\)](https://mathjax.schullv.de/258e38edd566ee58512d9c39b19445439f00e1d7eea51250a6137914cc00f8c8?color=5a5a5a)
 Rechnerisch nachweisen, dass der Scheitelpunkt
Rechnerisch nachweisen, dass der Scheitelpunkt  auf
auf  liegt
liegt
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
1&=&-(-2)-1 \\[5pt]
1&=&1
\end{array}\)](https://mathjax.schullv.de/3b8b86a5ffb816bb3b8bef07442b8c2d5f9a6d7a715531727d9249dd5b528894?color=5a5a5a) Der Scheitelpunkt
Der Scheitelpunkt  von
von  liegt somit auf
liegt somit auf 
Da der Graph
Gleichung mit quadratischer Ergänzung in die Scheitelpunktform bringen:
Da
b)
1. Schritt: Gleichung der Parabel  bestimmen
Durch die Angabe des Scheitelpunkts von
bestimmen
Durch die Angabe des Scheitelpunkts von  lässt sich die Scheitelpunktform bestimmen:
lässt sich die Scheitelpunktform bestimmen:
![\(\begin{array}[t]{rll}
p_2:\; y&=&(x-1,5)^2-3,25 \\[5pt]
&=& x^2-3x+2,25-3,25 \\[5pt]
&=& x^2-3x-1
\end{array}\)](https://mathjax.schullv.de/b155acaae8ae3f9d7aa01413d8595228c7c857da97840112dd9c4b43eb05d96c?color=5a5a5a)
 2. Schritt: Koordinaten des Punkts
2. Schritt: Koordinaten des Punkts  berechnen
berechnen
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&\dfrac{1}{4}\cdot2^2-4 \\[5pt]
&=& -3
\end{array}\)](https://mathjax.schullv.de/6948f58f0875a2f59d719381fa40f298a97f7320e3d108a880108ce0134c318d?color=5a5a5a)
 3. Schritt: Funktionsgleichung der Geraden
3. Schritt: Funktionsgleichung der Geraden  bestimmen
bestimmen
 verläuft durch den Ursprung
verläuft durch den Ursprung  sowie
sowie  und ist durch die Gleichung
und ist durch die Gleichung  definiert.
Koordinaten von
definiert.
Koordinaten von  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
h:\; y&=& m\cdot x+b \\[5pt]
0&=& m\cdot 0+b \\[5pt]
0&=& b \\[5pt]
b &=& 0
\end{array}\)](https://mathjax.schullv.de/2a0f5f7325bb4ef816b14ebe16f42611a4bb474af17db34b8cee1c565efab745?color=5a5a5a)
 und
und  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
h:\; y&=& m\cdot x+b \\[5pt]
-3&=& m\cdot 2+0 \\[5pt]
-3&=& 2m &\scriptsize \mid \; :2 \\[5pt]
-\dfrac{3}{2} &=& m \\[5pt]
m &=& -\dfrac{3}{2}
\end{array}\)](https://mathjax.schullv.de/560e7cc1eff8b3b1d1eb50377f9e153812477332d313aafae603886f39434794?color=5a5a5a)
 Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  bestimmen
1. Schritt: Eckpunkte
bestimmen
1. Schritt: Eckpunkte  und
und  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\dfrac{1}{4}x^2-4 &=& 0 \quad \scriptsize \mid\; +4\\[5pt]
\dfrac{1}{4}x^2 &=& 4 \quad \scriptsize \mid\; \cdot 4\\[5pt]
x^2&=& 16 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x&=&\underline{ \pm 4}
\end{array}\)](https://mathjax.schullv.de/51d4ffa7dade28a5cb2af0a8923010d80c2d5b549de07fee9ef2db13fe98e8f8?color=5a5a5a) Die Eckpunkte des Dreiecks
Die Eckpunkte des Dreiecks  sind
sind 
 und
und 
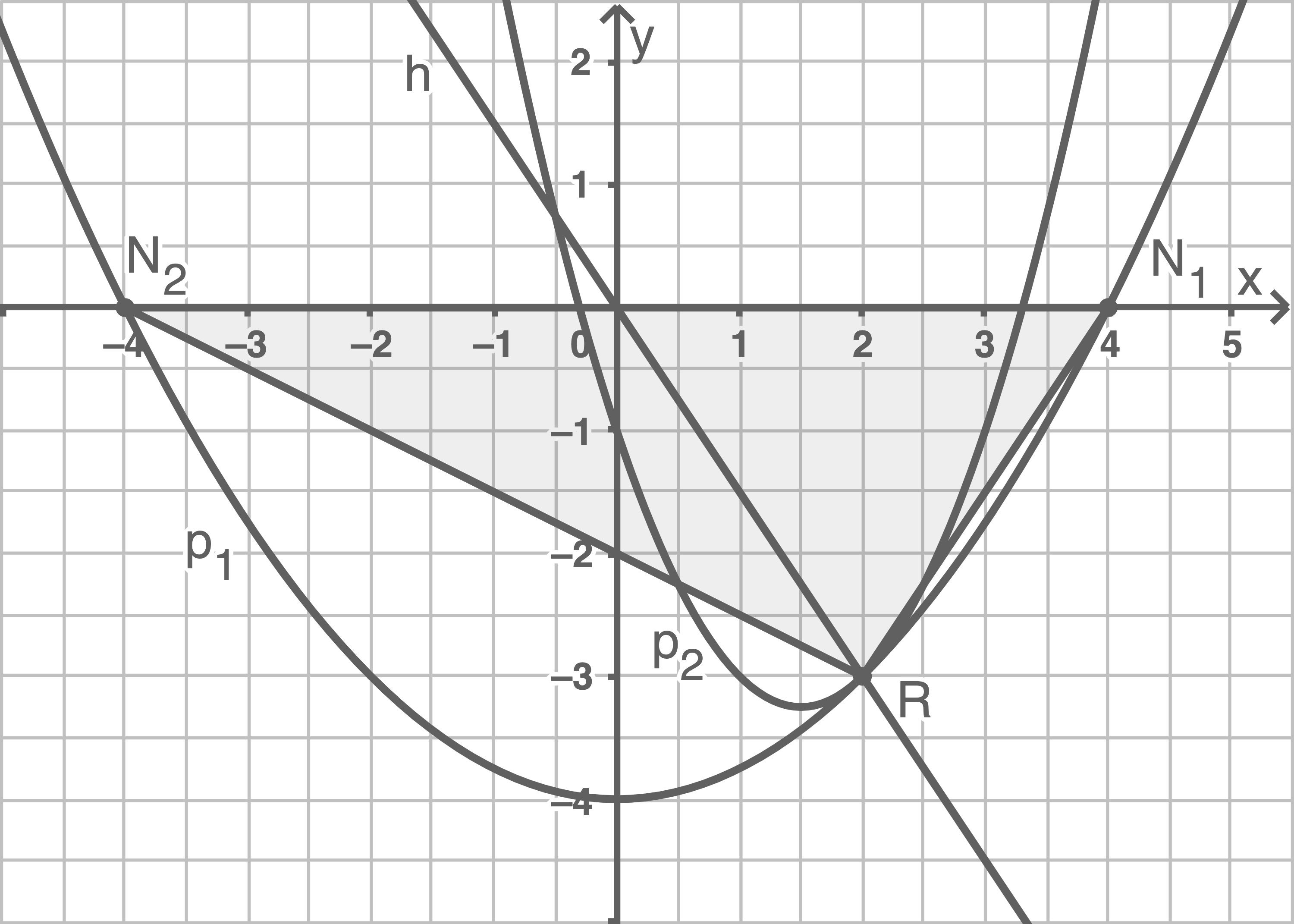 2. Schritt: Flächeninhalt bestimmen
2. Schritt: Flächeninhalt bestimmen
 kann als Grundseite des Dreiecks gewählt werden.
kann als Grundseite des Dreiecks gewählt werden.
Da und
und  auf der
auf der  -Achse liegen, gilt:
-Achse liegen, gilt:
 Die zugehörige Höhe
Die zugehörige Höhe  entspricht dem Abstand von
entspricht dem Abstand von  zur
zur  -Achse, also dem Betrag von
-Achse, also dem Betrag von 

![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot g\cdot h \\[5pt]
&=&\dfrac{1}{2}\cdot 8\,\text{LE}\cdot 3\,\text{LE}\\[5pt]
&=& \underline{\underline{ 12 \,\text{FE}}}
\end{array}\)](https://mathjax.schullv.de/0a1ab4114ecc8f90e241773fc073b73f86bc42ef3bfb2f4e631707298d2036be?color=5a5a5a) Der Flächeninhalt des Dreiecks
Der Flächeninhalt des Dreiecks  enstpricht
enstpricht  Bastians Aussage prüfen
Bastians Aussage prüfen
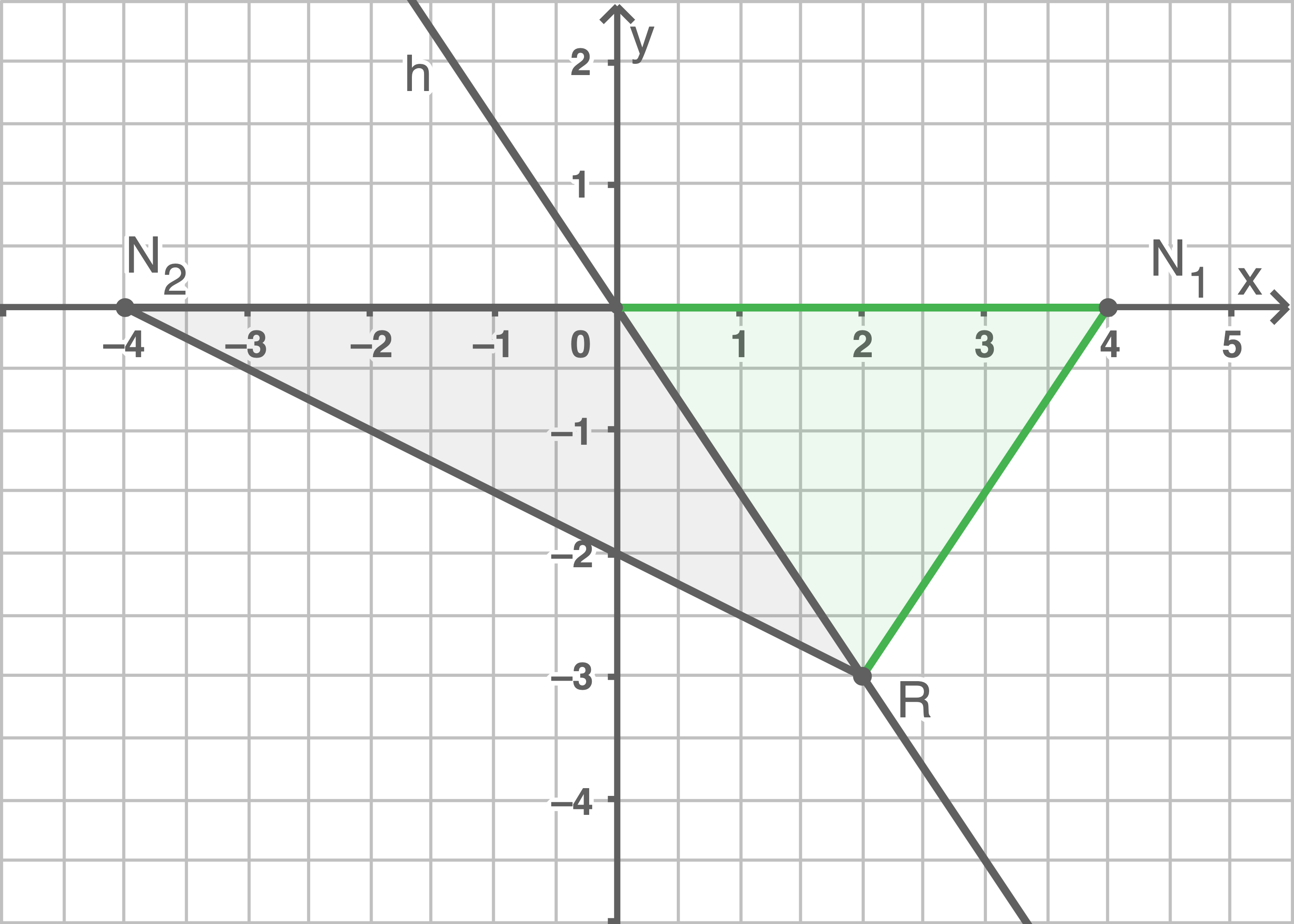 Rechnerische Begründung
Um Bastians Aussage zu prüfen, muss der Flächeninhalt eines der Teildreiecke berechnet werden.
Rechnerische Begründung
Um Bastians Aussage zu prüfen, muss der Flächeninhalt eines der Teildreiecke berechnet werden.
 geht durch den Ursprung
geht durch den Ursprung  und den Punkt
und den Punkt 
Somit gilt für die Grundseite des Teildreiecks
 Die Höhe
Die Höhe  bleibt gleich.
bleibt gleich.
![\(\begin{array}[t]{rll}
A_{N_1UR}&=& \dfrac{1}{2}\cdot 4\,\text{LE}\cdot 3\,\text{LE}&\quad \scriptsize \\[5pt]
&=& 6 \,\text{FE}
\end{array}\)](https://mathjax.schullv.de/cb2276cf25e6361dcaa38cc6b709492ec8648c39676df089f61129e9dcc5f703?color=5a5a5a) Der Flächeninhalt des Teildreiecks
Der Flächeninhalt des Teildreiecks  enstpricht genau der Hälfte des Flächeninhaltes des Dreiecks
enstpricht genau der Hälfte des Flächeninhaltes des Dreiecks 
Somit ist Bastians Behauptung richtig. Argumentative Begründung Die Höhe beider Teildreiecke entspricht weiterhin dem Abstand von zur
zur  -Achse. Diese bleibt für beide Teildreiecke also unverändert.
-Achse. Diese bleibt für beide Teildreiecke also unverändert.
Die Gerade verläuft durch den Ursprung und halbiert damit die Grundseite des Dreiecks
verläuft durch den Ursprung und halbiert damit die Grundseite des Dreiecks 
Dadurch, dass die Höhe gleich bleibt und die Grundseite halbiert wird, wird insgesamt auch der Flächeninhalt halbiert.
Bastian hat also recht.

Da

Somit gilt für die Grundseite des Teildreiecks
Somit ist Bastians Behauptung richtig. Argumentative Begründung Die Höhe beider Teildreiecke entspricht weiterhin dem Abstand von
Die Gerade
Dadurch, dass die Höhe gleich bleibt und die Grundseite halbiert wird, wird insgesamt auch der Flächeninhalt halbiert.
Bastian hat also recht.
Lösung W4
a)
Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊?
1. Schritt: Anteile der Felder berechnen
😊:  😐:
😐:  🙁:
🙁:  2. Schritt: Wahrscheinlichkeit berechnen
2. Schritt: Wahrscheinlichkeit berechnen
 Berechnung des Erwartungswerts
Berechnung des Erwartungswerts
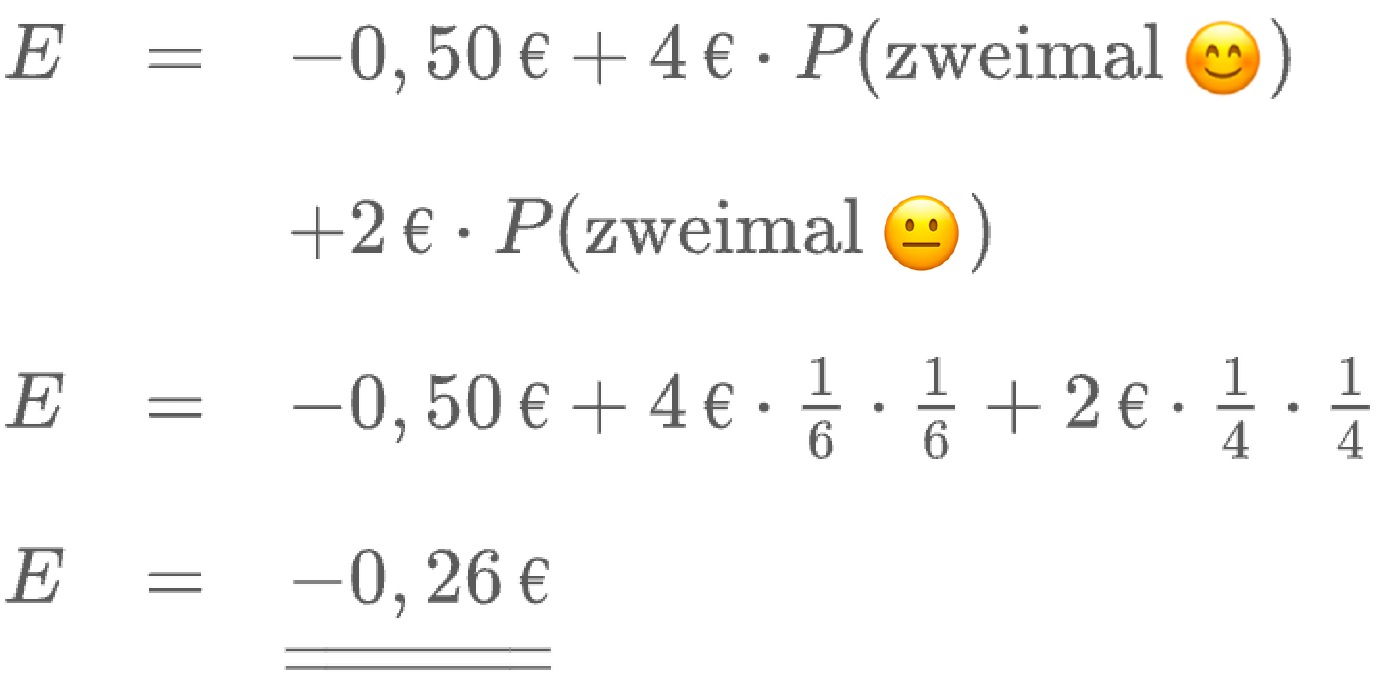 Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ bei einem fairen Spiel sein, wenn alles andere unverändert bleibt?
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ bei einem fairen Spiel sein, wenn alles andere unverändert bleibt?
 neuer Gewinn bei „ zweimal 😊 “
neuer Gewinn bei „ zweimal 😊 “
 Für ein faires Spiel muss der Gewinn für „ zweimal 😊 “ 13,50 € betragen, wenn alles andere unverändert bleiben soll.
Für ein faires Spiel muss der Gewinn für „ zweimal 😊 “ 13,50 € betragen, wenn alles andere unverändert bleiben soll.

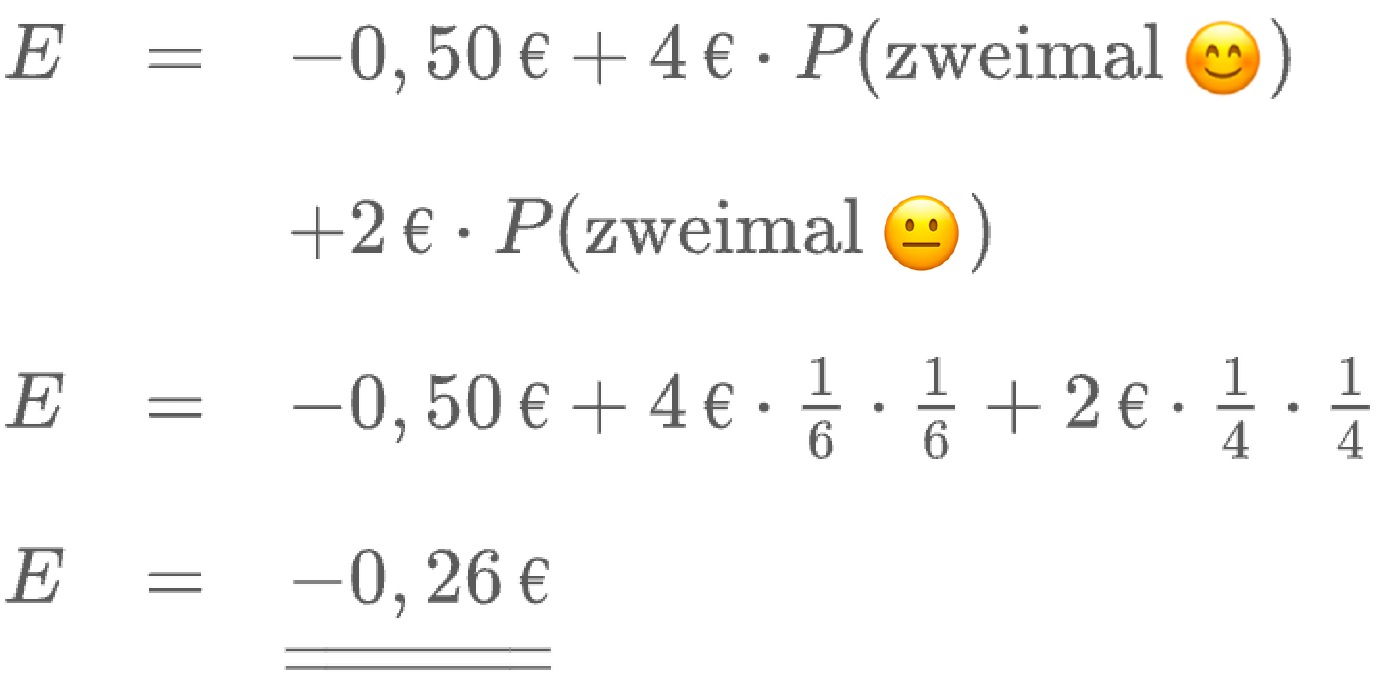

b)
Eine mögliche Funktionsgleichung für den Brückenbogen bestimmen
1. Schritt: Gegebene Punkte einzeichnen
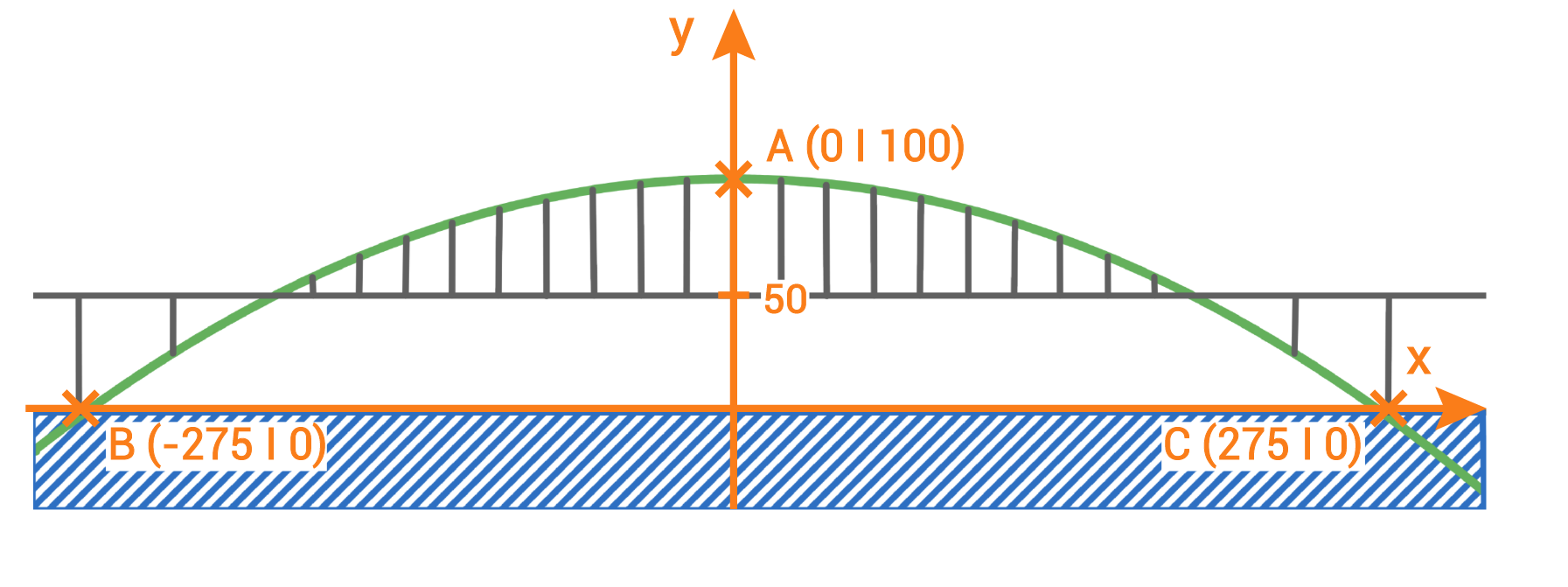 2. Schritt: Funktionsgleichung bestimmen
Wegen
2. Schritt: Funktionsgleichung bestimmen
Wegen  gilt
gilt 
 und
und  einsetzen in
einsetzen in 
![\(\begin{array}[t]{rll}
y &=& ax^2 + c \\[5pt]
0&=& a\cdot 275^2+100 \quad \scriptsize \mid\; -a\cdot 275^2 \\[5pt]
-275^2\cdot a &=& 100 \quad \scriptsize \mid\; : (-275^2) \\[5pt]
a&=& \underline{ -\dfrac{4}{3025}}
\end{array}\)](https://mathjax.schullv.de/8ba7040cb95b48604c257b7ee7f1e1a7e358221c44ddcaf4690d667ca257f70f?color=5a5a5a) Eine mögliche Funktionsgleichung für den Brückenbogen lautet also:
Eine mögliche Funktionsgleichung für den Brückenbogen lautet also:
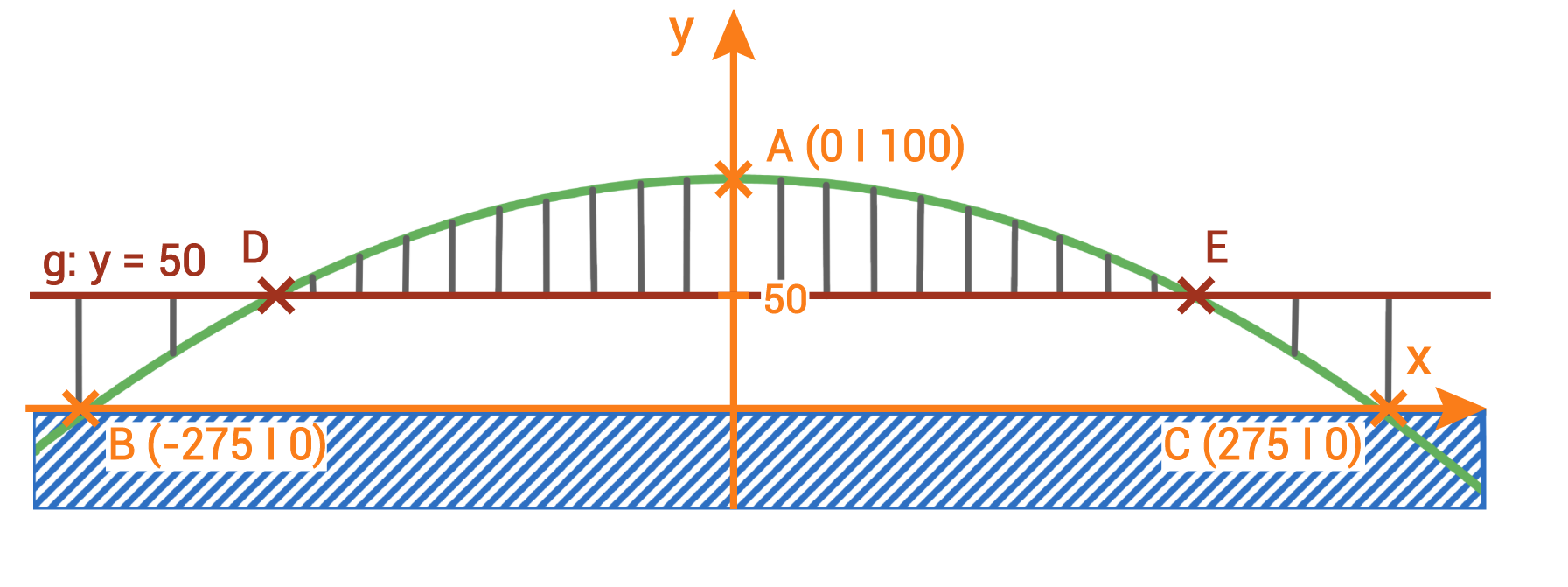
 Länge der Fahrbahn innerhalb des Brückenbogens berechnen
Der Verlauf der Fahrbahn kann durch die Gerade mit der Gleichung
Länge der Fahrbahn innerhalb des Brückenbogens berechnen
Der Verlauf der Fahrbahn kann durch die Gerade mit der Gleichung  beschrieben werden.
beschrieben werden.
![\(\begin{array}[t]{rll}
50&=&-\frac{4}{3025}x^2+100 &\quad \scriptsize \mid\; +\frac{4}{3025}x^2 ;-50 \\[5pt]
\frac{4}{3025}x^2&=& 50 &\quad \scriptsize \mid\; \cdot \frac{3025}{4} \\[5pt]
x^2&=& \frac{75625}{2} &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
x_{1/2}&=& \underline{ \pm 194,45}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/3f588d45b0ec284f4255e9fb0247dbe326e2d0ee1f04c8d626baa3b8a26f6431?color=5a5a5a) Damit gilt für die Länger der Fahrbahn
Damit gilt für die Länger der Fahrbahn  :
:
![\(\begin{array}[t]{rll}
l&=& |x_1|+|x_2| \\[5pt]
&=& |194,45|+|-194,45| \\[5pt]
&=& \underline{\underline{ 388,9\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/b3b80f98daf2093dd17b195e523080f77fa5724cc866132490f6981dbeab5676?color=5a5a5a) Somit beträgt die Länge der Fahrbahn
Somit beträgt die Länge der Fahrbahn 
- Die
-Achse kann auf Höhe der Wasseroberfläche eingezeichnet werden.
- Die
-Achse verläuft durch den höchsten Punkt der Parabel.
- Der höchste Punkt der Brücke liegt
über der Wasseroberfläche. Er kann mit
beschrieben werden.
- Die Brücke ist
lang. Die beiden Schnittpunkte der Parabel mit der
-Achse haben also die
-Koordinaten

