Wahlbereich

Aufgabe W1

Gegeben ist das Dreieck $ABC.$

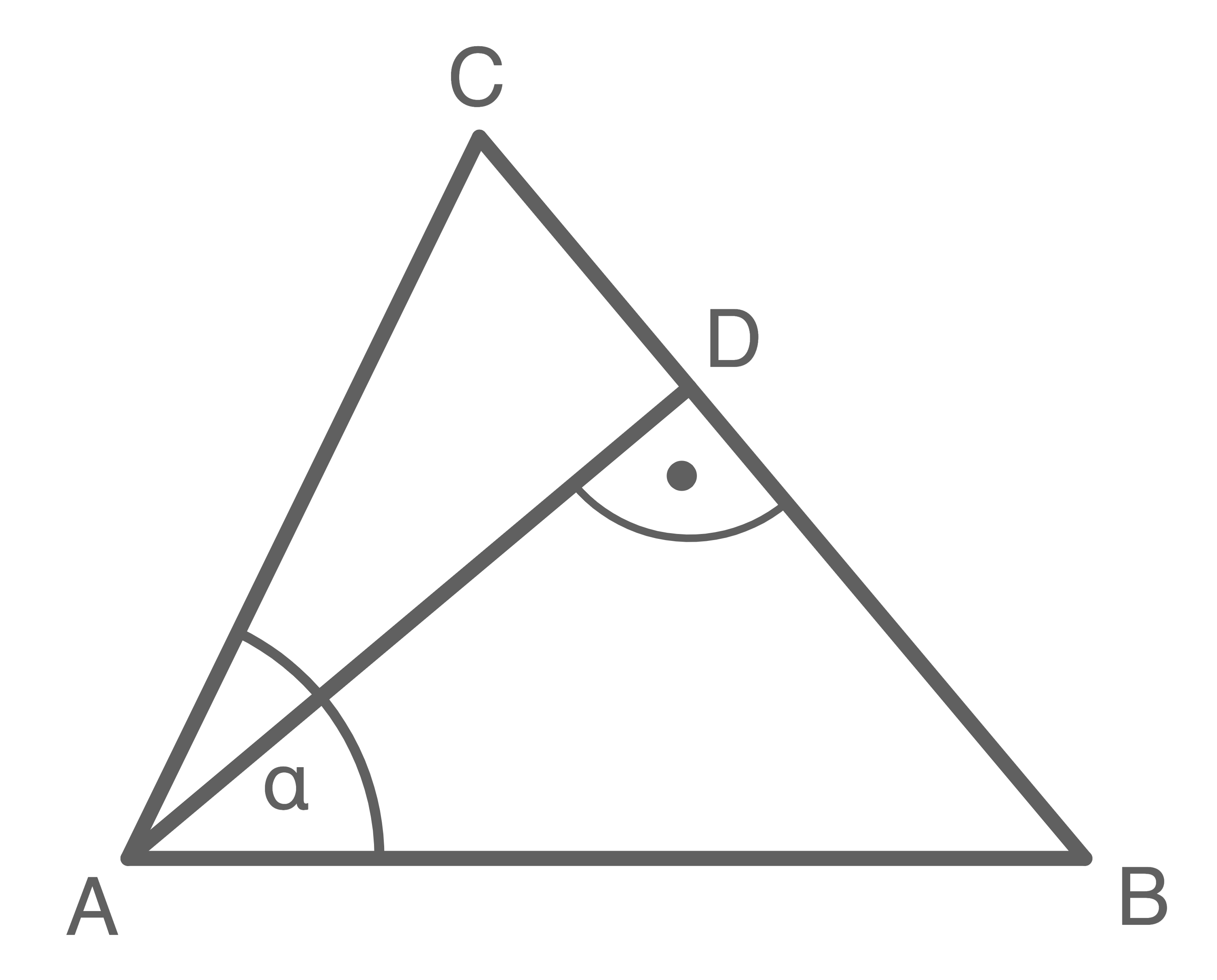Geometrische Darstellung eines Dreiecks mit Punkten und einem Winkel.

Es gilt:

$\overline{AB} = 12,0\,\text{cm}$
$\overline{BC} = 11,6\,\text{cm}$
$A_{ABC} = 54,0\,\text{cm}^2$

Berechne den Winkel $\alpha$ sowie den Abstand des Punktes $D$ zur Strecke $\overline{AB}.$

5,5 P

Im rechtwinkligen Dreieck $ABC$ liegt das gleichseitige Dreieck $DBC.$

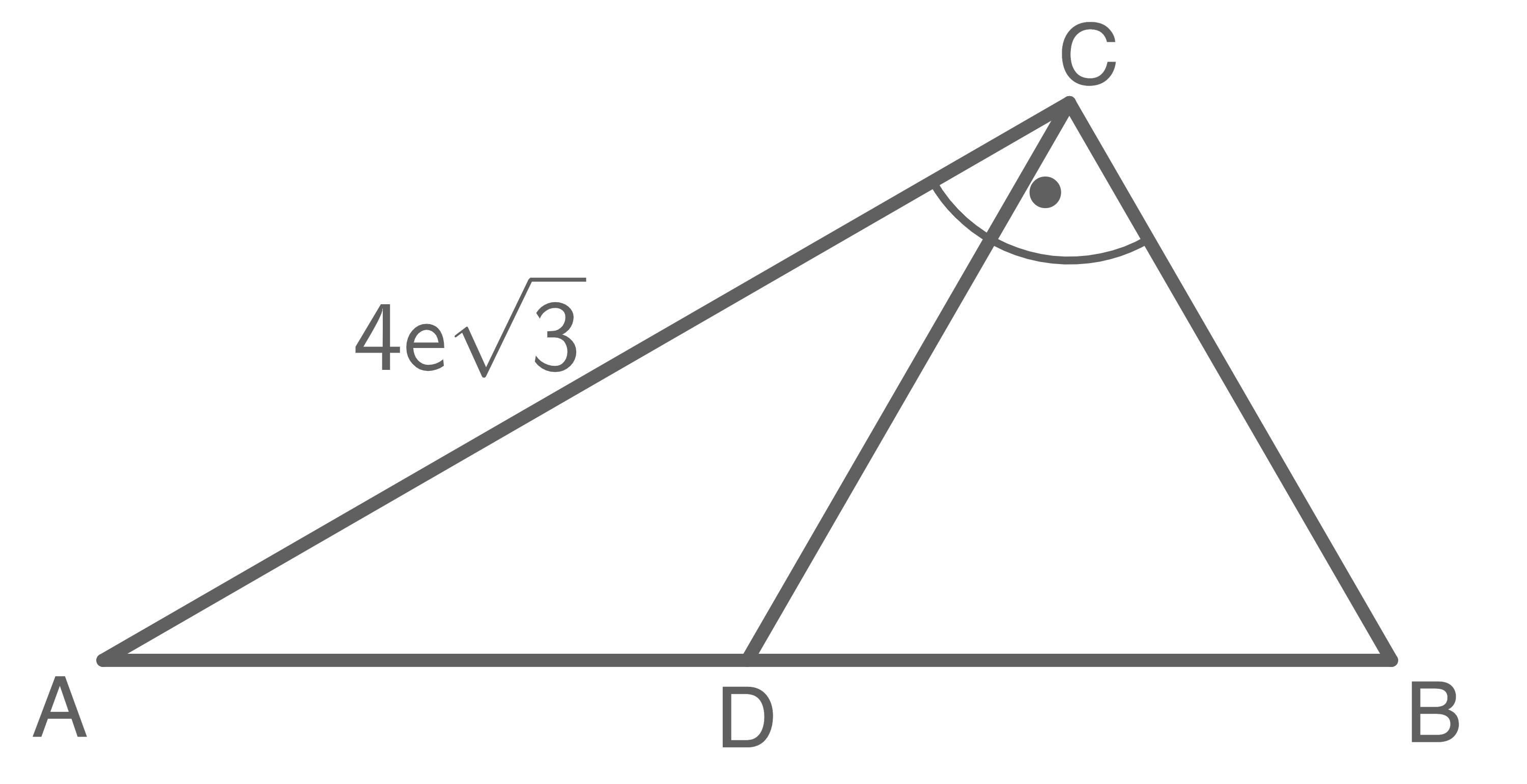
Geometrische Darstellung eines Dreiecks mit Beschriftungen und einer Markierung für einen Winkel.

Zeige ohne Verwendung gerundeter Werte, dass die beiden Dreiecke $ADC$ und $DBC$ flächengleich sind.
Der Flächeninhalt des Dreiecks $ABC$ soll $200\,\text{cm}^2$ betragen. Für welchen Wert von $e$ trifft dies zu?

4,5 P

Aufgabe W2

Grafische Darstellung eines Kegels mit Schnittfläche und Winkelmaß.

Ein massiver Kegel hat folgende Maße:

$V_{\text{Kegel}} = 500\,\text{cm}^3$
$d_{\text{Kegel}} = 13,0\,\text{cm}$

Dieser Kegel wird so bearbeitet, dass eine regelmäßige achtseitige Pyramide gleicher Höhe entsteht. Ein Manteldreieck ist bereits sichtbar. Berechne das Volumen der entstehenden Pyramide.

5 P

Aus einem quadratischen Blatt Papier wird das Netz einer quadratischen Pyramide hergestellt.

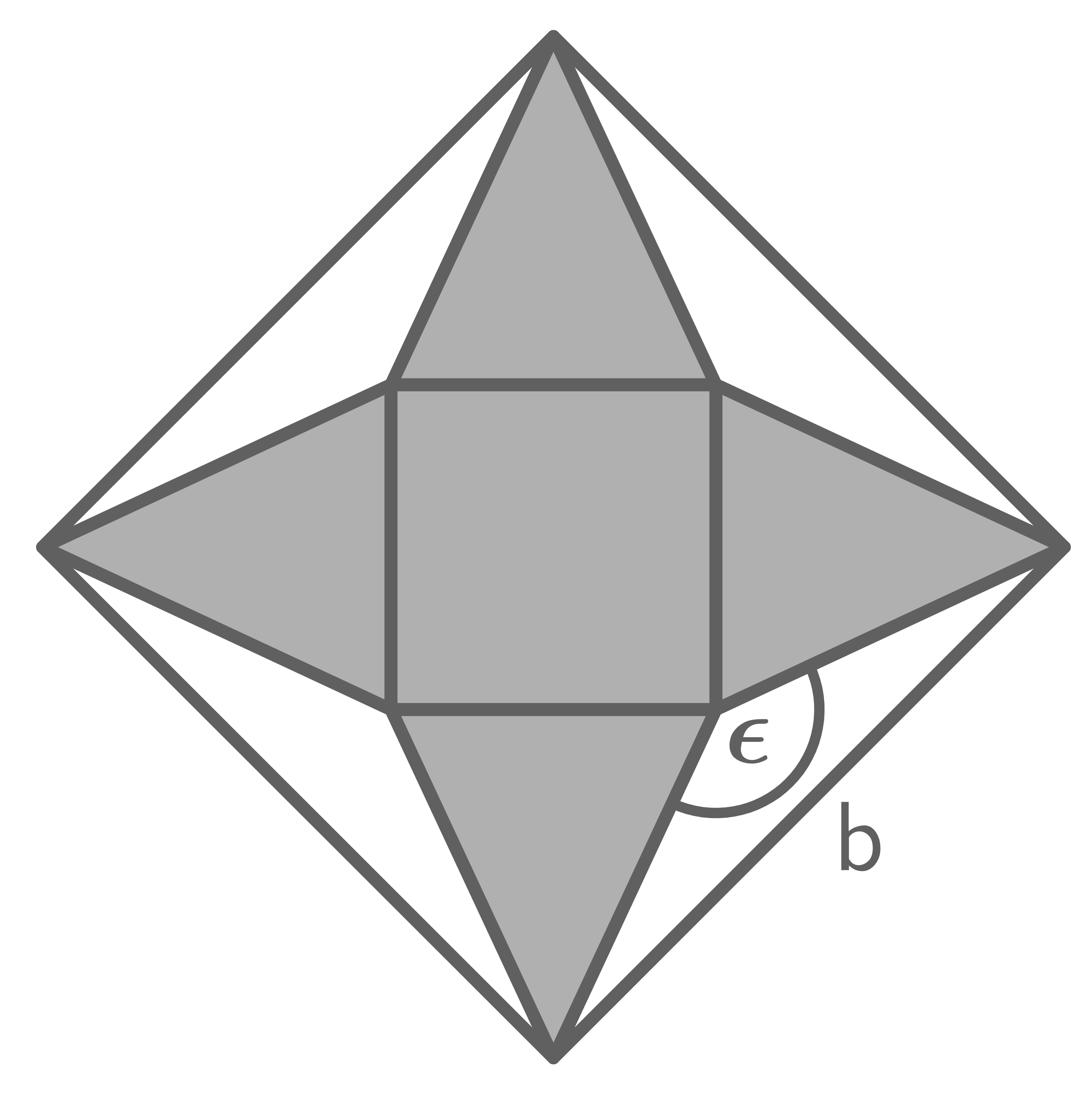Grafische Darstellung eines geometrischen Körpers mit beschrifteten Seiten und Winkeln.

Es gilt:

$b= 20,0\,\text{cm}$
$\epsilon = 140,0^{\circ}$

Berechne die Höhe der quadratischen Pyramide.

5 P

Aufgabe W3

Das Schaubild zeigt Ausschnitte einer verschobenen Normalparabel $p_1$ und einer Geraden $g.$

Grafik mit zwei Funktionen, einer Parabel und einer Geraden, dargestellt im Koordinatensystem.

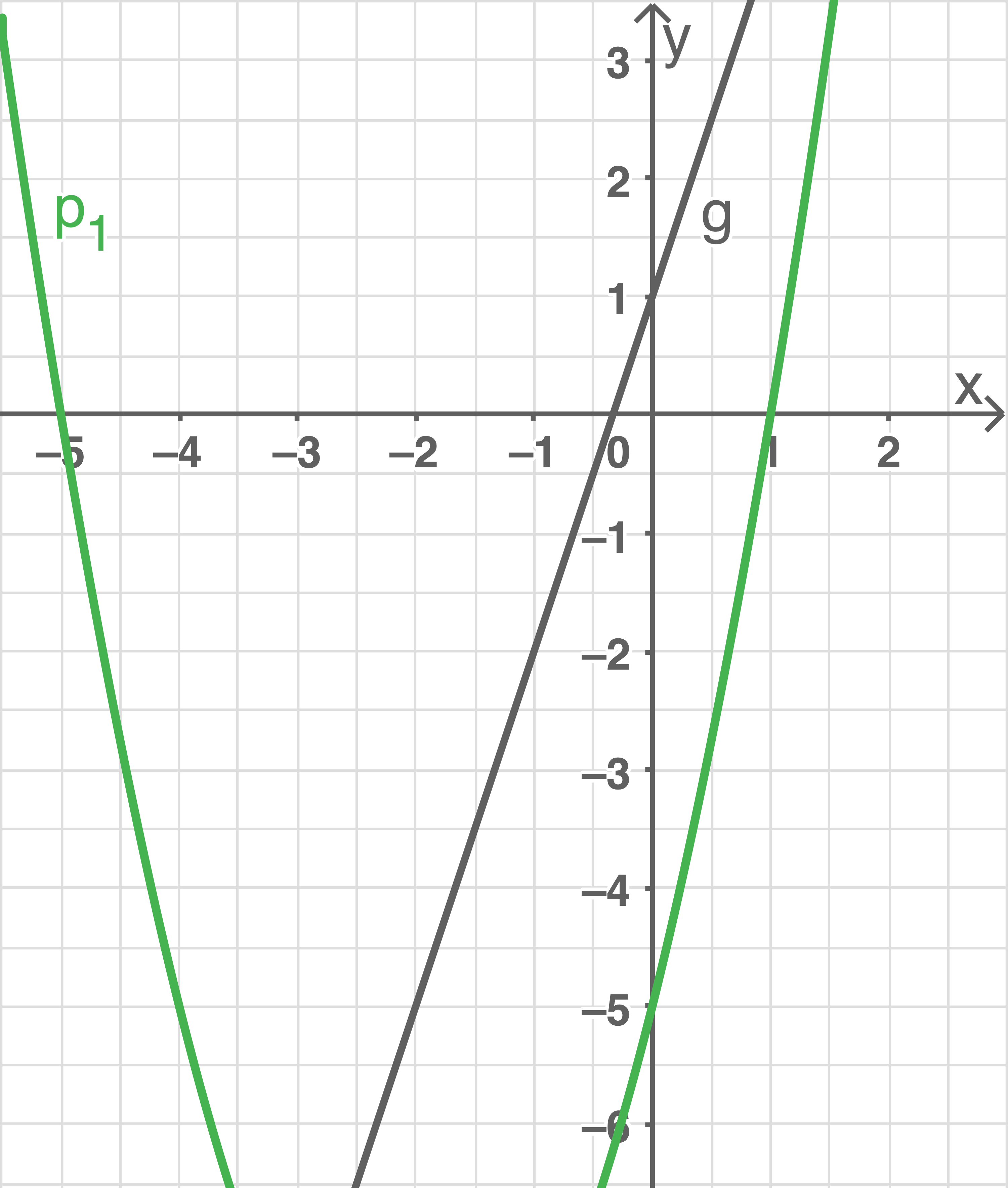
Bestimme die Funktionsgleichungen der Parabel $p_1$ und der Geraden $g.$
Die verschobene, nach oben geöffnete Normalparabel $p_2$ hat den Scheitelpunkt $S_2(5\mid -2).$
Prüfe rechnerisch, ob der Schnittpunkt $Q$ der beiden Parabeln auf der Geraden $g$ liegt.
Die Gerade $h$ verläuft durch die beiden Scheitelpunkte $S_1$ und $S_2.$
Berechne die Funktionsgleichung der Geraden $h.$

5,5 P

Die Parabel $p$ der Form $y= ax^2+c$ hat den Scheitel $S(0\mid -4,5).$ Sie geht durch den Punkt $P(-3\mid 0).$
Die Gerade $g$ mit der Steigung $m=1,5$ geht durch den Punkt $R(0\mid 0,5).$ Sie schneidet die Parabel $p$ in den Punkten $A$ und $C.$
Die Punkte $A$ und $C$ sind Eckpunkte des Rechtecks $ABCD.$ Zudem sind die Punkte $A$ und $C$ Anfangs- und Endpunkt einer Diagonalen dieses Rechtecks.
Die Seiten des Rechtecks verlaufen parallel zur $x$ - bzw. $y$ -Achse.
Berechne den Flächeninhalt des Rechtecks.

4,5 P

Aufgabe W4

Im Technikunterricht wurde für ein Schulfest ein Zufallsgerät gebaut, bei dem sich zwei Walzen unabhängig voneinander drehen. Die Walzen sind mit Symbolen beklebt. Auf jeder Walze sind vier Zitronen, zwei Glocken und eine Sieben abgebildet.

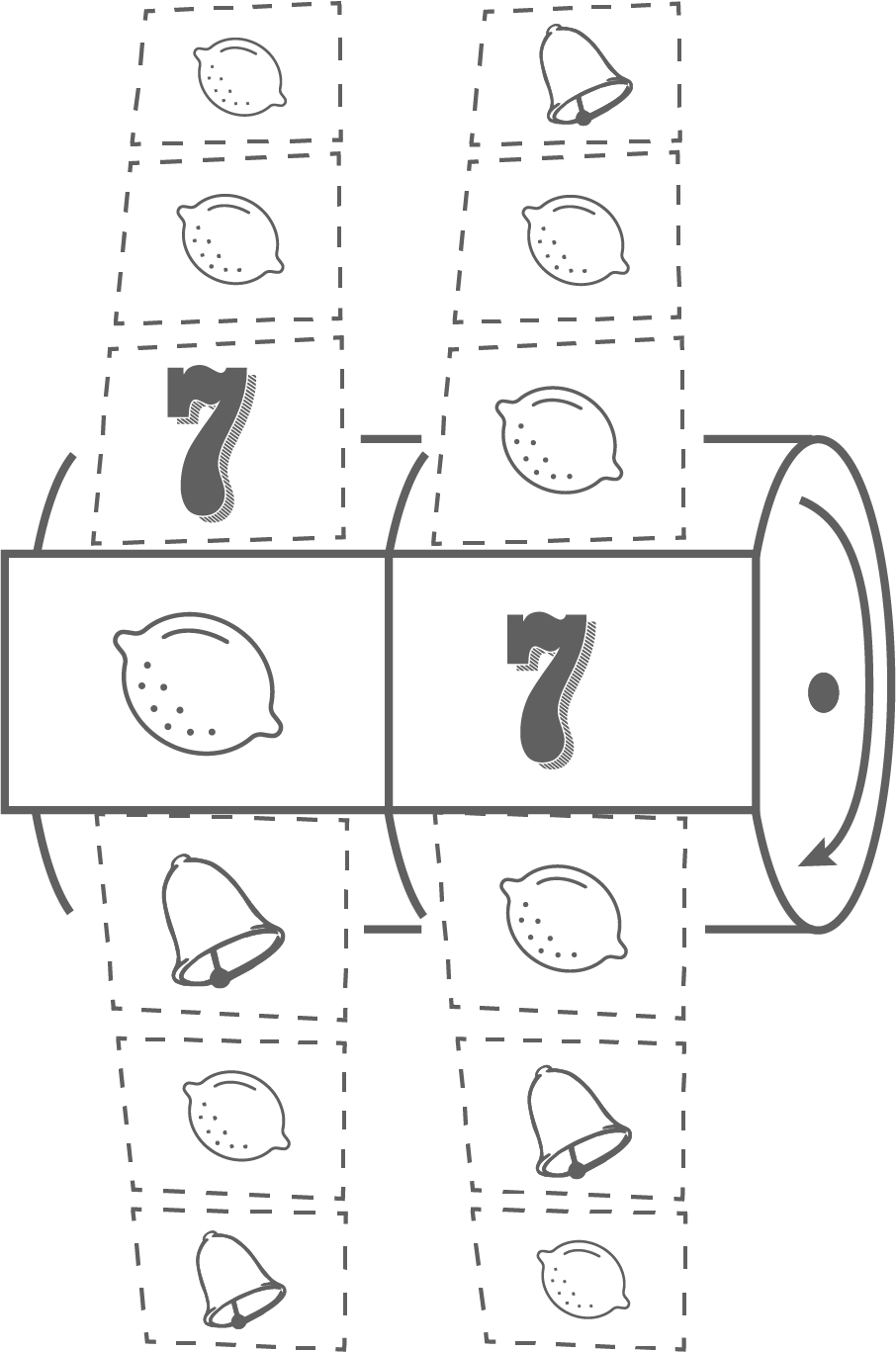Wahlbereich Stochastik Zufallsgerät Glocke

Wenn sie stehen bleiben, erkennt man im Sichtfenster zwei Symbole nebeneinander.

Wie groß ist die Wahrscheinlichkeit für das Ereignis "zweimal Glocke"?

Ereignis	Gewinn
zweimal Glocke	$4,00\,€$
zweimal Sieben	$10,00\,€$
sonstige	kein Gewinn
Einsatz pro Spiel: $1,00\,€$

Das Zufallsgerät wird für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.

Berechne den Erwartungswert. Was bedeutet das für den Spieler?

Der Einsatz soll auf $1,20\,€$ erhöht werden. Der Gewinn für "zweimal Glocke" sowie der Erwartungswert bleiben gleich.

Merle behauptet: "Der Gewinn für ‚zweimal Sieben‘ beträgt dann etwa 20€."

Hat Merle recht? Begründe rechnerisch.

5,5 P

Ein Golfspieler schlägt seinen Golfball ab. Die Flugbahn des Golfballes ist annähernd parabelförmig.

(Skizze nicht maßstäblich)

In einer horizontalen Entfernung von 95 m zum Abschlag erreicht der Ball seine maximale Flughöhe von 25 m über dem Boden.

Gib eine Gleichung der zugehörigen Parabel an.

Ein 15 m hoher Baum steht in 45 m Entfernung vom Abschlag. In welchem Abstand überfliegt der Ball die Baumspitze?

Das Loch befindet sich auf einer 2 m höher gelegenen Ebene in 180 m horizontaler Entfernung vom Abschlag.

In welcher Entfernung vom Loch trifft der Ball auf der höher gelegenen Ebene auf?

4,5 P

Lösung W1

Hilfsskizze

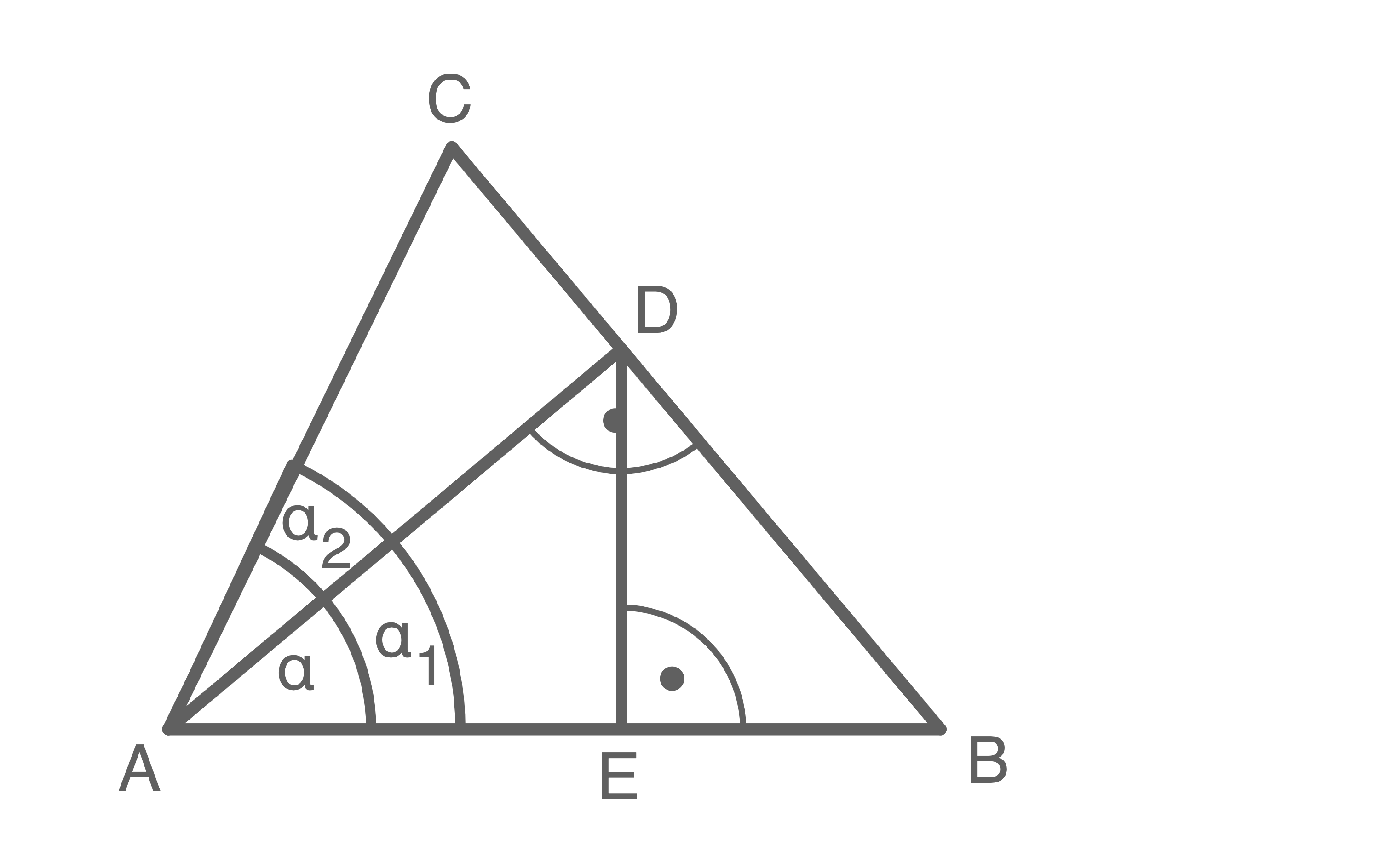Winkel $\alpha$ berechnen

1. Schritt: Länge der Strecke $\overline{AD}$ berechnen

Die Strecke $\overline{AD}$ ist die Höhe des Dreiecks $ABC$ zur Grundseite $\overline{BC}.$

$\begin{array}[t]{rll} A&=& \dfrac{1}{2} \cdot g \cdot h \\[5pt] A_{ABC}&=& \dfrac{1}{2} \cdot \overline{BC} \cdot \overline{AD}\\[5pt] 54\,\text{cm}^2 &=& \dfrac{1}{2} \cdot 11,6\,\text{cm} \cdot \overline{AD} \\[5pt] 54\,\text{cm}^2 &=& 5,8\,\text{cm} \cdot \overline{AD} \quad\scriptsize \mid\; :5,8\,\text{cm} \\[5pt] \overline{AD} &=& \underline{ 9,31 \,\text{cm}} \\[5pt] \end{array}$

2. Schritt: Winkel $\alpha_1$ berechnen

$\begin{array}[t]{rll} \cos(\alpha_1)&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} &\quad \scriptsize \\[5pt] \cos(\alpha_1) &=& \dfrac{\overline{AD}}{\overline{AB}} &\quad \scriptsize \\[5pt] \cos(\alpha_1) &=& \dfrac{9,31\,\text{cm}}{12,0\,\text{cm}} \quad \scriptsize \mid\;\cos^{-1} \\[5pt] \alpha_1&=& \underline{ 39,12^{\circ}} \end{array}$

3. Schritt: Länge der Strecke $\overline{BD}$ berechnen

Rechenweg anzeigen

$\overline{BD} = \underline{ 7,57 \,\text{cm}}$

4. Schritt: Länge der Strecke $\overline{CD}$ berechnen

$\begin{array}[t]{rll} \overline{CD} &=& \overline{BC} - \overline{BD} &\quad \scriptsize \\[5pt] &=& 11,6 \,\text{cm} - 7,57 \,\text{cm} &\quad \scriptsize \\[5pt] \overline{CD} &=& \underline{ 4,03 \,\text{cm}} &\quad \scriptsize \\[5pt] \end{array}$

5. Schritt: Winkel $\alpha_2$ berechnen

$\begin{array}[t]{rll} \tan(\alpha_2)&=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} &\quad \scriptsize \\[5pt] \tan(\alpha_2) &=& \dfrac{\overline{CD}}{\overline{AD}} &\quad \scriptsize \\[5pt] \tan(\alpha_2) &=& \dfrac{4,03\,\text{cm}}{9,31\,\text{cm}} \quad \scriptsize \mid\;\tan^{-1} \\[5pt] \alpha_2&=& \underline{ 23,41^{\circ}} \end{array}$

6. Schritt: Winkel $\alpha$ berechnen

$\begin{array}[t]{rll} \alpha &=& \alpha_1 + \alpha_2 &\quad \scriptsize \\[5pt] &=& 39,12^{\circ} + 23,41^{\circ} &\quad \scriptsize \\[5pt] &=& 62,53^{\circ} \\[5pt] \alpha&=&\underline{\underline{ 62,5^{\circ}}} \end{array}$

Länge der Strecke $\boldsymbol{\overline{DE}}$ berechnen

$\begin{array}[t]{rll} \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} &=& \sin(\alpha_1)&\quad \scriptsize \\[5pt] \end{array}$

$\begin{array}[t]{rll} \dfrac{\overline{DE}}{\overline{AD}} &=& \sin(\alpha_1)\quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt] \overline{DE} &=& \sin(\alpha_1)\cdot \overline{AD} &\quad \scriptsize\\[5pt] &=& \sin(39,12^{\circ}) \cdot 9,31\,\text{cm} &\quad \scriptsize \\[5pt] &=& 5,87\,\text{cm} \\[5pt] \overline{DE} &=& \underline{\underline{ 5,9\,\text{cm}}} &\quad \scriptsize \\[5pt] \end{array}$

Nachweis, dass die Dreiecke flächengleich sind

1. Schritt: Flächeninhalt des Dreiecks $DBC$ berechnen

Länge von $\overline{BC}$ berechnen

$\begin{array}[t]{rll} \tan(\beta)&=&\dfrac{\overline{AC}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt] \tan(\beta)\cdot \overline{BC}&=&\overline{AC}\quad \scriptsize \mid\;:\tan(\beta)\\[5pt] \overline{BC}&=&\dfrac{\overline{AC}}{\tan(\beta)}\quad \scriptsize \mid\;:\tan(\beta) \end{array}$

Da das Dreieck $DBC$ gleichseitig ist, gilt: $\beta=60^\circ$

$\overline{BC}=\dfrac{4e\sqrt{3}}{\tan(60^\circ)}$ $=\dfrac{4e\sqrt{3}}{\sqrt{3}}=4e$

Flächeninhalt $A_{DBC}$ berechnen

$\begin{array}[t]{rll} A_{DBC}&=&\dfrac{\overline{BC}^2}{4}\sqrt{3}\\[5pt] &=&\dfrac{(4e)^2}{4}\sqrt{3}\\[5pt] &=&\dfrac{16e^2}{4}\sqrt{3}\\[5pt] A_{DBC}&=&\underline{ 4e^2\sqrt{3}}\\[5pt] \end{array}$

2. Schritt: Flächeninhalt des Dreiecks $ADC$ berechnen

Flächeninhalt $A_{ABC}$ berechnen

$\begin{array}[t]{rll} A_{ABC}&=&\dfrac{1}{2}\cdot\overline{BC}\cdot \overline{AC}\\[5pt] &=&\dfrac{1}{2}\cdot4e\cdot 4e\sqrt{3}\\[5pt] A_{ABC}&=&8e^2\sqrt{3}\\[5pt] \end{array}$

Flächeninhalt $A_{ADC}$ berechnen

$\begin{array}[t]{rll} A_{ADC}&=&A_{ABC}-A_{DBC}\\[5pt] &=&8e^2\sqrt{3}-4e^2\sqrt{3}\\[5pt] A_{ADC}&=&\underline{ 4e^2\sqrt{3}} \end{array}$

Damit ist gezeigt, dass beide Dreiecke flächengleich sind.

Wert von $e$ berechnen

Der Flächeninhalt des Dreiecks $ABC$ lautet (s.o.) $A_{ABC}=8e^2\sqrt{3}.$

$\begin{array}[t]{rll} A_{ABC}&=& 200 \\[5pt] 8e^2\sqrt{3}&=& 200 \quad \scriptsize \mid\;:(8\sqrt{3}) \\[5pt] e^2&=&\dfrac{25}{\sqrt{3}}\\[5pt] &=&\dfrac{25\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}}\\[5pt] e^2&=&\dfrac{25\cdot \sqrt{3}}{3}\\[5pt] e_1&=&5\sqrt{\dfrac{\sqrt{3}}{3}} \\[5pt] e_2&=&-5\sqrt{\dfrac{\sqrt{3}}{3}} \end{array}$

$e_2$ ist negativ und scheidet somit als Ergebnis aus.

Für $\underline{\underline{ e=5\sqrt{\dfrac{\sqrt{3}}{3}}\,\text{cm}}}$ beträgt der Flächeninhalt $A_{ABC}=200\,\text{cm}^2.$

Lösung W2

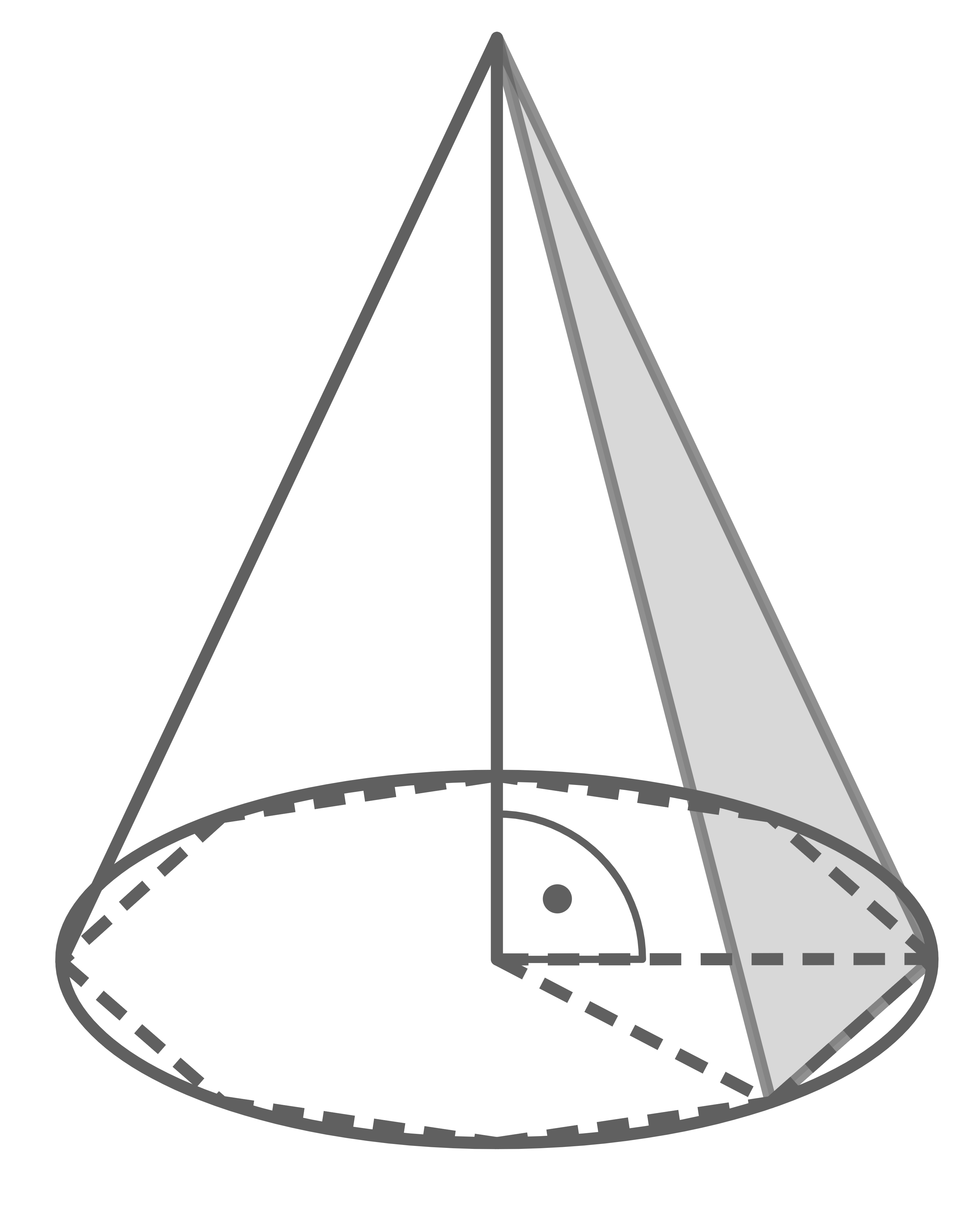
Um das Volumen berechnen zu können, werden folgende Größen benötigt:

Flächeninhalt der Pyramidengrundfläche, also des regelmäßigen Achtecks.
Die Höhe der Pyramide.

Die Grundfläche lässt sich in acht gleichschenklige, identische Dreiecke aufteilen. Betrachtet wird einzig das grüne in der Skizze stellvertretende Dreieck.

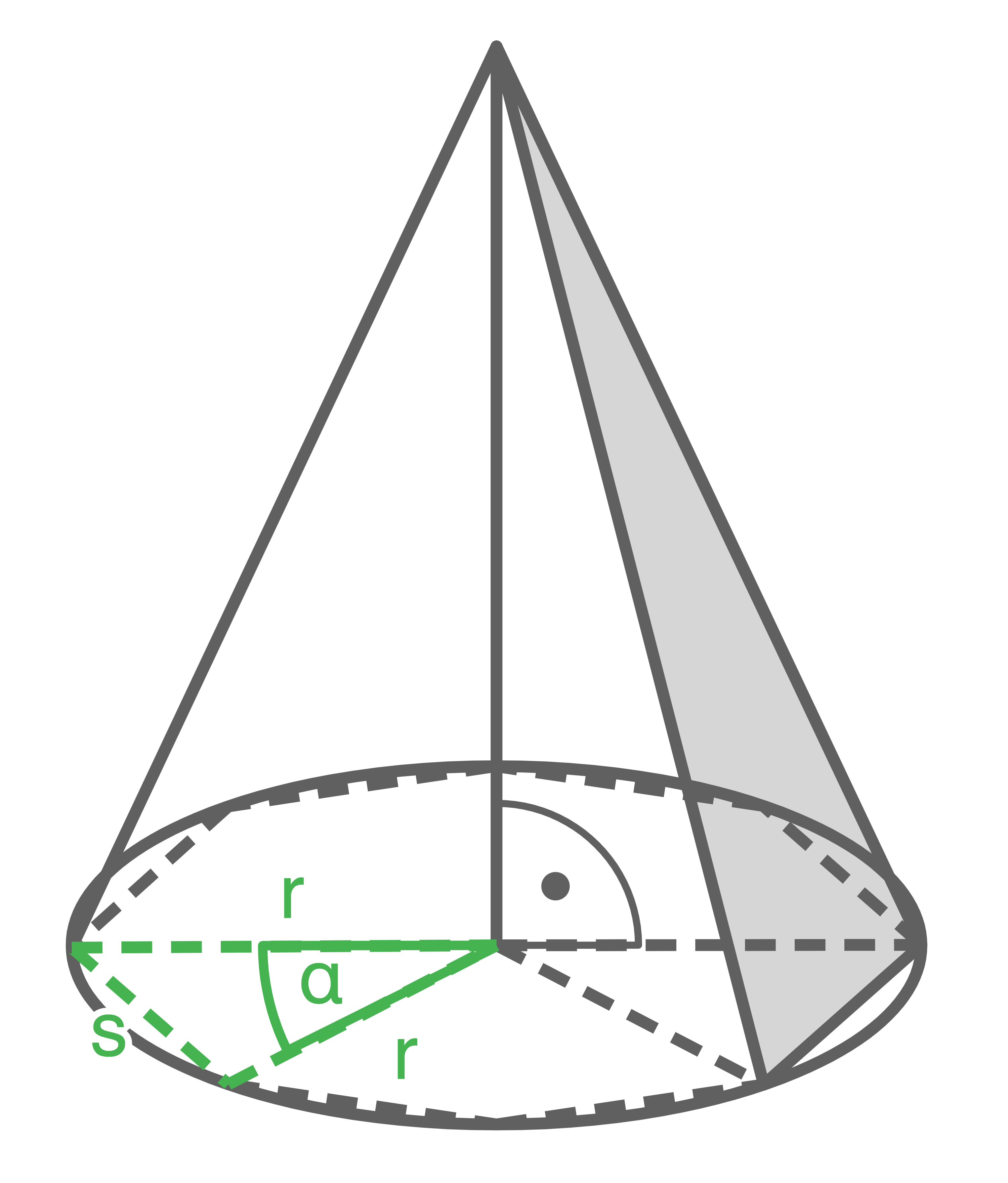
wahlbereich kegel volumen dreieck winkel strecke

1. Schritt: Schenkellänge $\boldsymbol{r}$ bestimmen

Die Schenkel dieses Dreiecks reichen vom Kreismittelpunkt bis zur Kreislinie und haben daher die Länge des Kreisradius:

$r= \dfrac{d_{\text{Kegel}}}{2}$ $=\dfrac{13,0\,\text{cm}}{2} =\underline{ 6,5\,\text{cm}}.$

2. Schritt: Innenwinkel $\boldsymbol{\alpha}$ berechnen

Die Innenwinkel der acht Dreiecke, die am Kreismittelpunkt liegen, bilden gemeinsam $360^{\circ}.$

$\alpha = 360^{\circ}:8 = \underline{ 45^{\circ}}$

3. Schritt: Pyramidenhöhe über Kegelhöhe berechnen

$\begin{array}[t]{rll} V_{\,\text{Kegel}}&=&\dfrac{1}{3}\pi\cdot r^2\cdot h_{\,\text{Ke}} \quad \scriptsize \mid\; \cdot 3 \\[5pt] V_{\,\text{Kegel}}\cdot 3 &=& \pi r^2 \cdot h_{\,\text{Ke}}\quad \scriptsize \mid\; :(\pi r^2) \\[5pt] \dfrac{3\cdot V_{\,\text{Kegel}}}{\pi r^2} &=& h_{\,\text{Ke}}&\quad \scriptsize \\[5pt] \dfrac{3\cdot 500\,\text{cm}^3}{\pi \cdot (6,5\,\text{cm}) ^2} &=& h_{\,\text{Ke}} &\quad \scriptsize \\[5pt] h_{Ke} &= & \underline{ 11,30\,\text{cm} } \end{array}$

4. Schritt: Pyramidenvolumen berechnen

Rechenweg anzeigen

$V=450\,\text{cm}^3$

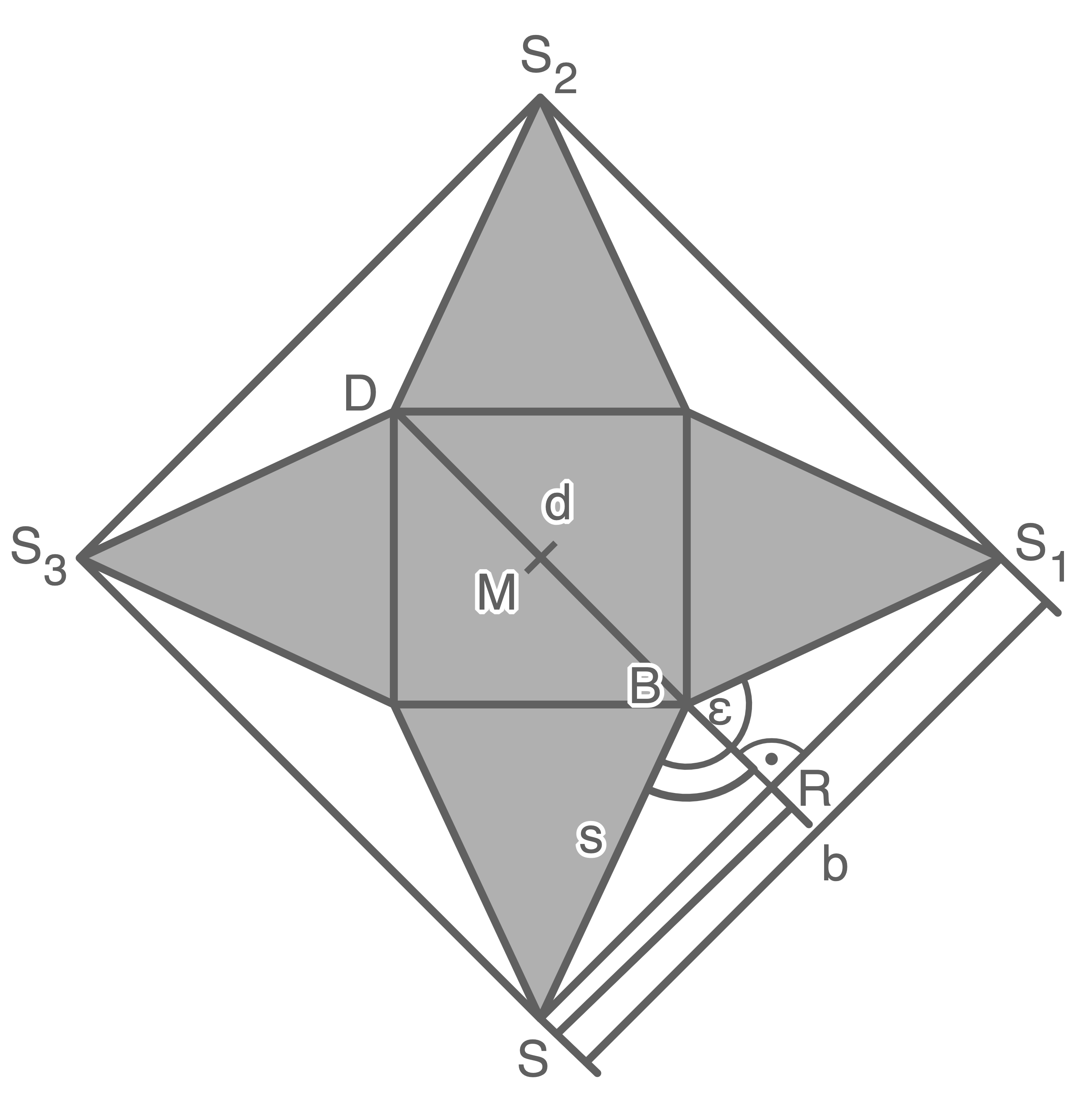
wahlbereich quadratisches blatt pyramidennetz

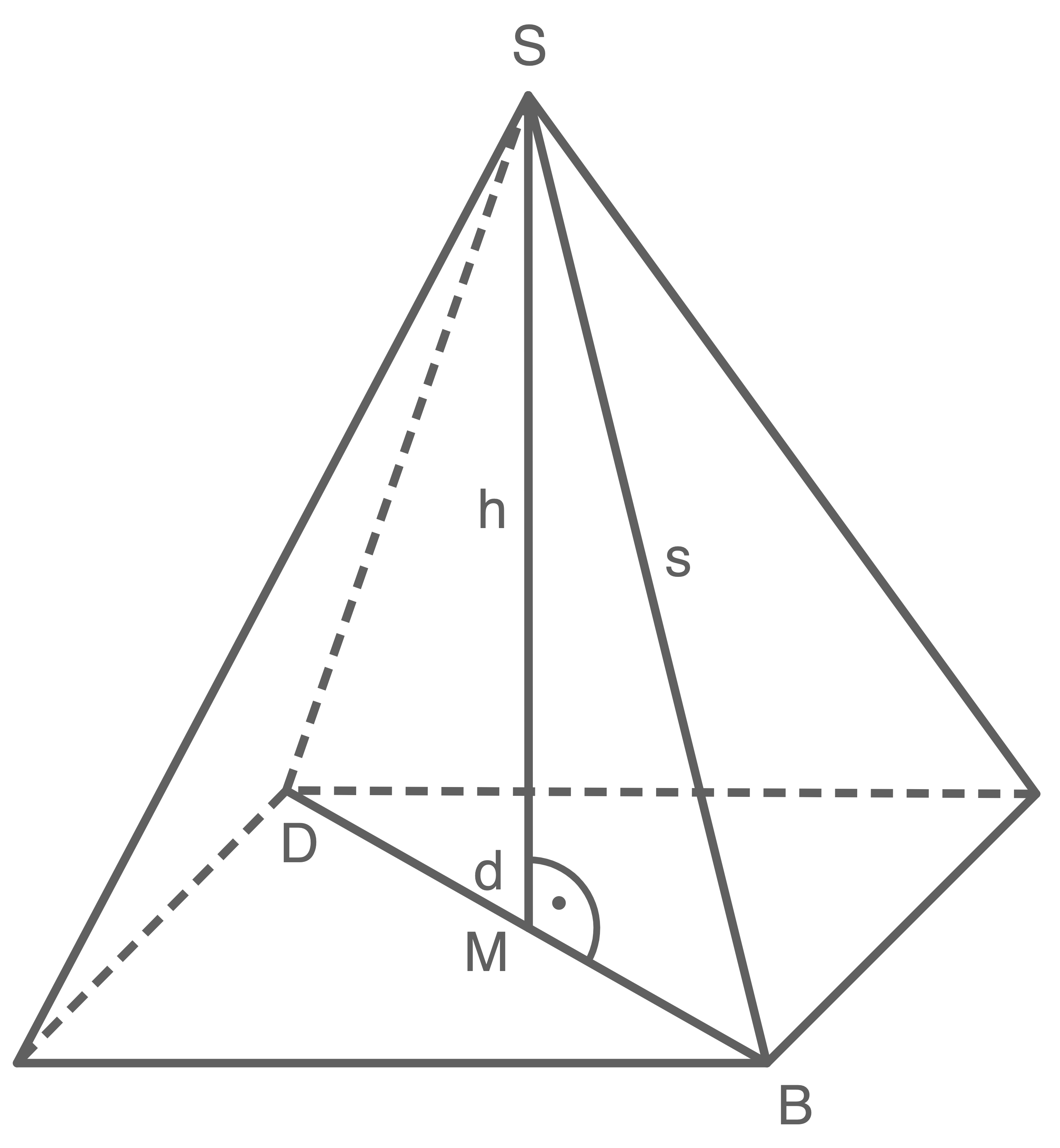
wahlbereich pyramide strecken winkel mittelpunkt

1. Schritt: Länge der Seitenkante s berechnen

Verhältnis im Dreieck $BSR:$

$\begin{array}[t]{rll} \sin\left(\dfrac{\epsilon}{2}\right)&=& \dfrac{\frac{b}{2}}{s} \quad \scriptsize \mid\; \cdot s\\[5pt] s \cdot \sin\left(\dfrac{\epsilon}{2}\right) &=& \dfrac{b}{2} \quad \scriptsize \mid\; :\sin\left(\dfrac{\epsilon}{2}\right) \\[5pt] s &=& \dfrac{b}{2 \cdot \sin\left(\frac{\epsilon}{2}\right)} \quad \scriptsize \mid\; \frac{\epsilon}{2}=\frac{140^{\circ}}{2}= 70^{\circ} \\[5pt] s &=&\dfrac{20}{2\cdot \sin(70^{\circ} )} &\quad \scriptsize \\[5pt] s&=& \underline{ 10,64\,\text{cm}} \end{array}$

2. Schritt: Länge der Strecke $\boldsymbol{\overline{RB}}$ berechnen

Verhältnis im Dreieck $BSR:$

$\begin{array}[t]{rll} \tan\left(\dfrac{\epsilon}{2}\right)&=&\dfrac{\frac{b}{2}}{\overline{RB}} \quad \scriptsize \mid\; \cdot \overline{RB} \\[5pt] \overline{RB}\cdot \tan\left(\dfrac{\epsilon}{2}\right) &=& \dfrac{b}{2} \quad \scriptsize \mid\; : \tan\left(\dfrac{\epsilon}{2}\right) \\[5pt] \overline{RB} &=& \dfrac{b}{2\cdot \tan\left(\frac{\epsilon}{2}\right)} \\[5pt] \overline{RB} &=& \dfrac{20}{2\cdot \tan(70^{\circ} )} \\[5pt] \overline{RB} &=& \underline{ 3,64 \,\text{cm}} \end{array}$

3. Schritt: Länge der Strecke $\boldsymbol{\dfrac{d}{2}}$ berechnen

$\overline{MR}=\dfrac{b}{2}=10\,\text{cm}$

$\begin{array}[t]{rll} \dfrac{d}{2} &=& \overline{MR}-\overline{RB}&\quad \scriptsize \\[5pt] \dfrac{d}{2} &=& 10-3,64 &\quad \scriptsize \\[5pt] \dfrac{d}{2}&=& \underline{ 6,36 \,\text{cm}} \end{array}$

4. Schritt: Länge der Pyramidenhöhe h berechnen

$\begin{array}[t]{rll} h^2+\left(\dfrac{d}{2}\right)^2&=& s^2 \quad \scriptsize \mid\; - \left(\dfrac{d}{2}\right)^2 \\[5pt] h^2 &=& s^2- \left(\dfrac{d}{2}\right)^2 &\quad \scriptsize \\[5pt] h^2 &=& 10,64^2 - 6,36^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt] h &=& \sqrt{10,64^2 - 6,36^2 } \\[5pt] h &= & \underline{\underline{ 8,5 \,\text{cm}}} \end{array}$

Lösung W3

Funktionsgleichung der Parabel $p_1$ ermitteln

Da $p_1$ eine verschobene Normalparabel ist, hat ihre Funktionsgleichung folgende Form:

$p_1: y= (x-x_S)^2 +y_S$

Dabei sind $(x_S\mid y_S)$ die Koordinaten des Scheitelpunkts.
Die Abbildung zeigt, dass $p_1$ die $x$ -Achse in den Punkten $P_1(-5\mid 0)$ und $P_2(1\mid 0)$ schneidet.
Wegen der Symmetrie, muss die $x$ -Koordinate des Scheitelpunkts genau mittig dazwischen liegen, also ist $x_S= -2.$

$y_s$ durch Einsetzen berechnen:

$\begin{array}[t]{rll} p_1: y&=& (x-(-2))^2 +y_S \quad \scriptsize \mid\; P_2(1\mid 0) \\[5pt] 0 &=& (1+2)^2 +y_S \\[5pt] 0&=& 9 +y_S \quad \scriptsize \mid\;-9 \\[5pt] -9&=& y_S \end{array}$

Eine Funktionsgleichung von $p_1$ lautet also:

$\underline{\underline{ p_1:y= (x+2)^2 -9}}$

Funktionsgleichung der Gerade $g$ bestimmen

Ein Steigungsdreieck in der Abbildung zeigt, dass die Gerade $g$ die Steigung $m=3$ hat und die $y-$ Achse im Punkt $(0\mid 1)$ schneidet.
Daher lautet die Geradengleichung:

$\underline{\underline{ g:y= 3x+1}}$

Lage des Schnittpunkts prüfen

1. Schritt: Funktionsgleichung von $\boldsymbol{p_2}$ aufstellen

Mit der Scheitelpunktform ergibt sich:

$\underline{ p_2:y= (x-5)^2-2}$

2. Schritt: Schnittpunkt berechnen

$p_1(x)= p_2(x)$

Rechenweg anzeigen

$x=2$

Die beiden Parabeln schneiden sich an der Stelle $x=2.$
Einsetzen in eine der beiden Funktionsgleichungen, z.B. in $p_1:$

$\begin{array}[t]{rll} y&=& (2+2)^2 -9 \\[5pt] &=& 16 -9 \\[5pt] &=& 7 \end{array}$

Der Schnittpunkt hat also die Koordinaten $\underline{ Q(2\mid 7)}.$

3. Schritt: Einsetzen in die Gerade $g$

$\begin{array}[t]{rll} y&=& 3\cdot 2+1 \\[5pt] &=& 7 \end{array}$

Die Gerade $g$ verläuft also ebenfalls durch den Punkt $Q(2\mid 7).$ Der Schnittpunkt $Q$ der beiden Parabeln liegt also auf der Geraden $g.$

Funktionsgleichung der Geraden $h$ berechnen

Die beiden Scheitelpunkte sind $S_1(-2\mid -9)$ und $S_2(5\mid -2).$

1. Schritt: Steigung berechnen

Mit dem Differenzquotient ergibt sich:

$\begin{array}[t]{rll} m_h &=& \dfrac{y_2 - y_1}{ x_2-x_1} \\[5pt] &=& \dfrac{-2-(-9)}{5-(-2)} \\[5pt] &=& \dfrac{7}{7}\\[5pt] m_h&=& 1 \end{array}$

2. Schritt: $\boldsymbol{y}$ -Achsenabschnitt berechnen

Durch eine Punktprobe kannst du nun den $y$ -Achsenabschnitt $c$ berechnen:

$\begin{array}[t]{rll} y&=& m\cdot x + c \\[5pt] y&=& 1\cdot x + c&\quad \scriptsize \mid\; S_1(-2\mid -9) \\[5pt] -9&=& 1\cdot (-2) + c &\quad \scriptsize \mid\; +2\\[5pt] -7 &=& c \end{array}$

Eine Funktionsgleichung von $h$ ist also

$\underline{\underline{ h:y = x-7}}$

1. Schritt: Funktionsgleichung der Parabel bestimmen

Die Punktprobe in $S$ zeigt:

$\begin{array}[t]{rll} y &=& a\cdot x^2 +c& \\[5pt] -4,5 &=& a\cdot 0^2 +c \\[5pt] -4,5 &=& c \end{array}$

Mit einer Punktprobe von $P(-3\mid 0)$ kann $a$ berechnet werden:

$\begin{array}[t]{rll} p:y &=& ax^2 +c \quad \scriptsize \mid\;c = -4,5 \\[5pt] p:y&=& ax^2 -4,5 \quad \scriptsize \mid\; P(-3\mid 0)\\[5pt] 0&=& a\cdot (-3)^2 -4,5 \quad \scriptsize \mid\;+4,5 \\[5pt] 4,5 &=& 9a \quad \scriptsize \mid\; :9\\[5pt] 0,5 &=& a \end{array}$

Eine Gleichung der Parabel $p$ lautet also $\underline{ y= 0,5x^2-4,5}.$

2. Schritt: Geradengleichung angeben

Mit den Informationen aus der Aufgabe kann eine Geradengleichung aufgestellt werden:

$\underline{ g: y = 1,5x +0,5}$

3. Schritt: Schnittpunkte von $p$ mit $g$ berechnen

$p(x)= g(x)$

Rechenweg anzeigen

$\begin{array}[t]{rll} x_1&=& -2,5\\[5pt] x_2&=& 5 \end{array}$

Einsetzen in die Geradengleichung liefert die zugehörigen $y$ -Koordinaten.

$\begin{array}[t]{rll} y_1 &=& 1,5\cdot (-2) +0,5 \\[5pt] &=& -2,5 \\[10pt] y_2 &=& 1,5\cdot 5 +0,5 \\[5pt] &=& 8 \end{array}$

Die Punkte $A$ und $C$ haben also die Koordinaten $\underline{ A(-2\mid -2,5)}$ und $\underline{ C(5\mid 8)}.$

4. Schritt: Flächeninhalt berechnen

Da die Seiten des Rechtecks parallel zur $x$ - bzw. $y$ -Achse verlaufen, ergeben sich die Seitenlängen aus den Differenzen der $y$ - und $x$ -Koordinaten von $A$ und $C.$

$\begin{array}[t]{rll} a&=& y_C -y_A \\[5pt] &=& 8-(-2,5) \\[5pt] &=& 10,5 \\[10pt] b&=& x_C-x_A \\[5pt] &=& 5-(-2) \\[5pt] &=&7 \end{array}$

Der Flächeninhalt ergibt sich daher wie folgt:

$\begin{array}[t]{rll} A &=& a\cdot b \\[5pt] &=& 10,5\cdot 7 \\[5pt] &=& 73,5 \end{array}$

Der Flächeninhalt des Rechtecks beträgt ca. $\underline{\underline{ 73,5\,\text{FE}}}.$

Lösung W4

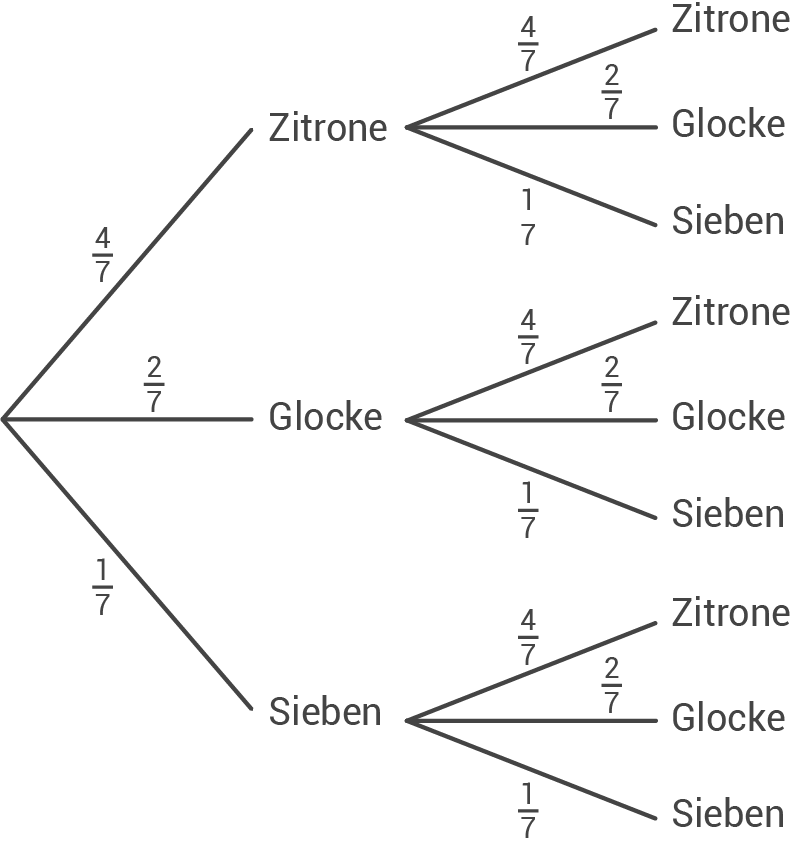
wahlbereich baumdiagramm wahrscheinlichkeit

$\begin{array}[t]{rll} P(\text{Zweimal Glocke})&=& \dfrac{2}{7} \cdot \dfrac{2}{7} \\[5pt] &=& \dfrac{4}{49} \\[5pt] &= & 0,082 \\[5pt] P(\text{Zweimal Glocke})&=&\underline{\underline{ 8,2\,\%}} \\[5pt] \end{array}$

Erwartungswert berechnen

Ereignis	Gewinn	Wahrscheinlichkeit
zweimal Glocke	4 €	$\dfrac{4}{49}$
zweimal Sieben	10 €	$\dfrac{1}{7}\cdot \dfrac{1}{7}=\dfrac{1}{49}$
sonstige	0 €	$1-\dfrac{4}{49}-\dfrac{1}{49}=\dfrac{44}{49}$

Rechenweg anzeigen

$E(G)\approx -0,47\,€$

Der Spieler macht auf lange Zeit ungefähr $0,47\,€$ Verlust pro Spiel.

Neuen Gewinn überprüfen

Neue Informationen:

$E= -0,47\,€$ als Erwartungswert
Gewinn ("zweimal Sieben") als Unbekannte $x$
Alle anderen Werte bleiben gleich

Rechenweg anzeigen

$x= 19,77\,€$

Merle hat recht, da der neue Gewinn nur wenig von 20 € abweicht.

Gleichung der zugehörigen Parabel angeben

Da die Koordinaten $S(95\mid 25)$ die höchste Flughöhe des Balls beschreiben, bilden sie den Scheitelpunkt.
Mithilfe der Scheitelpunktform hat die Parabel $p$ dann folgende vorläufige Gleichung:

$p:y= a\cdot(x-95)^2 +25$

Der Parameter $a$ kann nun mit Hilfe einer Punktprobe so bestimmmt werden, dass der Abschlagspunkt, also der Koordinatenursprung $(0\mid 0)$ auf der Parabel liegt.

$\begin{array}[t]{rll} p:y &=& a\cdot (x-95)^2 +25 \quad \scriptsize \mid\; (0\mid 0) \\[5pt] 0&=& a\cdot (0-95)^2 +25 \\[5pt] 0&=& a\cdot 9025 +25 \quad \scriptsize \mid\;-25 \\[5pt] -25 &=& a\cdot 9025 \quad \scriptsize \mid\;:9025 \\[5pt] -\dfrac{1}{361}&=& a \end{array}$

Eine Gleichung der zugehörigen Parabel lautet also $\underline{\underline{ p:y= -\dfrac{1}{361} \cdot (x-95)^2 +25}}.$

In welchem Abstand überfliegt der Ball die Baumspitze?

Die Flughöhe des Balles an der Stelle des Baumes wird durch $p$ an der Stelle 45 beschrieben:

$\begin{array}[t]{rll} y&=& -\dfrac{1}{361} \cdot (45-95)^2 +25 \\[5pt] &=& 18,07 \\[5pt] y&=& 18,1 \end{array}$

Über dem Baum befindet sich der Ball also in einer Höhe von $18,1\,\text{m}$ über dem Erdboden. Da der Baum $15\,\text{m}$ hoch ist, überfliegt er die Baumspitze mit einem Abstand von ca. $\underline{\underline{ 3,1\,\text{m}}}.$

In welcher Entfernung vom Loch trifft der Ball auf der höher gelegenen Ebene auf?

Rechenweg anzeigen

$x = 95 \pm \sqrt{8303}$

Für die beiden Stellen ergibt sich also:

$\begin{array}[t]{rll} x_1&=& 95-\sqrt{8303} \\[5pt] &=& 3,88 \\[5pt] x1&=& 3,9 \\[10pt] x_2&=& 95+\sqrt{8303} \\[5pt] &=& 186,12 \\[5pt] x_2&=& 186,1 \end{array}$

$x_1$ beschreibt den ersten Punkt nach dem Abschlag, an dem der Ball eine Höhe von 2 m erreicht hat.
$x_2$ ist für diese Aufgabe relevant und gibt den gesuchten Auftreffpunkt an.
Das Loch befindet sich an der Stelle $x=$ 180. Der Ball trifft also in einer Entfernung von ca. $\underline{\underline{ 6,1 \,\text{m}}}$ zum Loch auf der höher gelegenen Ebene auf.