Wahlteil B
Aufgabe 1
a)
Das gleichschenklige Dreieck  und das rechtwinklige Trapez
und das rechtwinklige Trapez  überdecken sich teilweise.
überdecken sich teilweise.
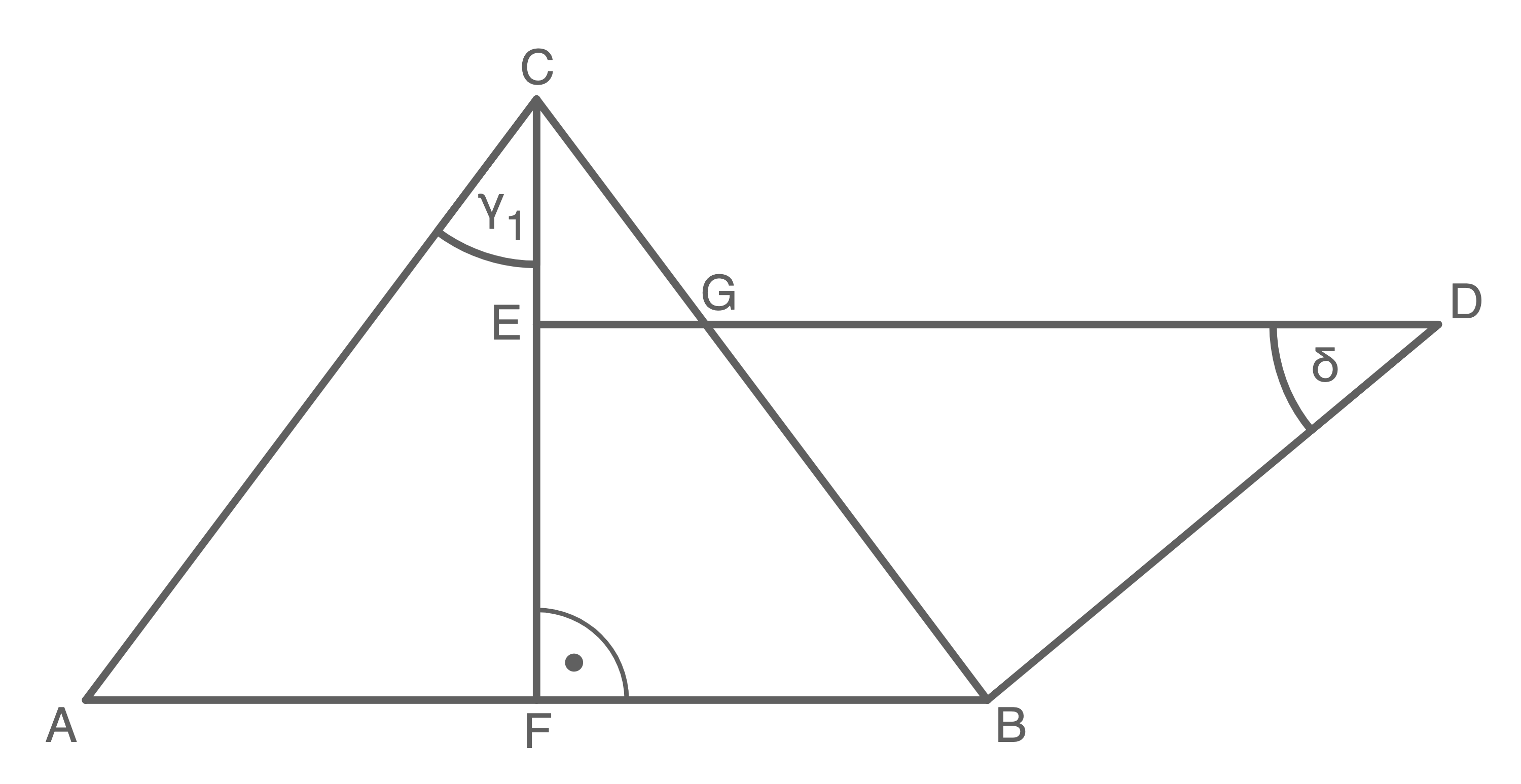 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AC}&=&11,4\,\text{cm}\\
\overline{BD}&=&8,2\,\text{cm}\\
\gamma_1&=&37,6^\circ\\
\delta&=&39,2^\circ\\
\overline{AC}&=&\overline{BC}
\end{array}\)](https://mathjax.schullv.de/39ae3fd492617cfa9f183792abbf261def5e0f40331d608caca90085004f111b?color=5a5a5a) Berechne den Flächeninhalt des Vierecks
Berechne den Flächeninhalt des Vierecks 

(5 P)
b)
Eine nach oben geöffnete verschobene Normalparabel  mit der Form
mit der Form  geht durch den Punkt
geht durch den Punkt  .
.
 geht auch durch den Punkt
geht auch durch den Punkt  .
.
Sie schneidet die -Achse im Punkt
-Achse im Punkt  .
.
 und
und  bilden das Dreieck ABC.
bilden das Dreieck ABC.
 geht durch den Punkt
geht durch den Punkt  und hat die Steigung
und hat die Steigung  .
.
 halbiert den Flächeninhalt des Dreiecks
halbiert den Flächeninhalt des Dreiecks  "
"
- Berechne die Funktionsgleichung der Parabel
Sie schneidet die
- Bestimme die Koordinaten der Punkte
und
- Berechne den Flächeninhalt des Dreiecks
- Gib die Funktionsgleichung von
an.
- Überprüfe diese Aussage und begründe deine Antwort durch Rechnung oder Argumentation.
(5 P)
Aufgabe 2
a)
Zu einer verschobenen nach oben geöffneten Normalparabel  gehört die unvollständige Wertetabelle.
gehört die unvollständige Wertetabelle.
 hat die Funktionsgleichung
hat die Funktionsgleichung  und geht durch den Punkt
und geht durch den Punkt  .
.
- Bestimme die Funktionsgleichung von
- Vervollständige die Wertetabelle.
- Berechne die Funktionsgleichung von
- Zeige rechnerisch, dass
keinen Schnittpunkt mit
hat.
- Gib die Funktionsgleichung einer verschobenen nach oben geöffneten Normalparabel
an, die keinen Schnittpunkt mit
und
hat.
(5 P)
b)
Aus einem Kegel wird eine regelmäßige fünfseitige Pyramide herausgearbeitet (siehe Abbildung).
Die Eckpunkte der Grundfläche der fünfseitigen Pyramide liegen auf der Kreislinie der Grundfläche des Kegels.
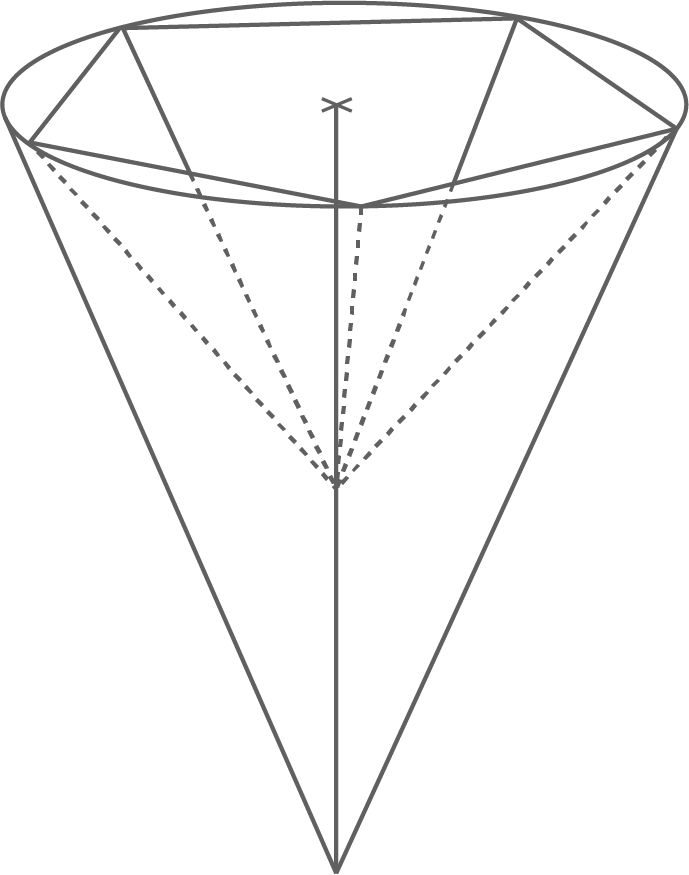 Es gilt:
Es gilt:
 (Grundkante der Pyramide)
(Grundkante der Pyramide)
 (Körperhöhe des Kegels)
(Körperhöhe des Kegels)
 (Körperhöhe der Pyramide)
(Körperhöhe der Pyramide)
Um wie viele unterscheiden sich die Inhalte der Mantelflächen des Kegels und der Pyramide?
unterscheiden sich die Inhalte der Mantelflächen des Kegels und der Pyramide?
Die Eckpunkte der Grundfläche der fünfseitigen Pyramide liegen auf der Kreislinie der Grundfläche des Kegels.

Um wie viele
(5 P)
Aufgabe 3
a)
Die Klasse 10a verkauft Rubbellose.
Auf jedem Los befinden sich zwei Streifen.
Jeder Streifen enthält die folgenden Ziffern:
 Die Ziffern sind in zufälliger Reihenfolge angeordnet. Der linke Streifen zeigt die Zehnerziffern, der rechte die Einerziffern.
Die Ziffern sind in zufälliger Reihenfolge angeordnet. Der linke Streifen zeigt die Zehnerziffern, der rechte die Einerziffern.
 Auf jedem Streifen wird genau ein Feld freigerubbelt, wodurch eine zweistellige Zahl entsteht.
Auf jedem Streifen wird genau ein Feld freigerubbelt, wodurch eine zweistellige Zahl entsteht.
Die obenstehende Abbildung zeigt die Zahl
 durch eine
durch eine  zu ersetzen.
zu ersetzen.
Auf jedem Los befinden sich zwei Streifen.
Jeder Streifen enthält die folgenden Ziffern:


Die obenstehende Abbildung zeigt die Zahl
- Wie groß ist die Wahrscheinlichkeit, eine Zahl zu erhalten, die größer als
ist?
| Ereignis | Gewinn |
|---|---|
| Zahl größer als |
|
| Zahl |
|
| restliche Möglichkeiten | kein Gewinn |
| Einsatz: |
|
- Berechne den Erwartungswert.
- Erhöht sich dadurch der Gewinn für die Klasse?
Begründe deine Entscheidung durch Rechnung.
(5 P)
b)
Die Abbildung zeigt den Sprung eines Frosches, der annähernd die Form einer Parabel mit der Gleichung  hat.
hat.
Die maximale Höhe des Sprungs ist . Die Sprungweite beträgt
. Die Sprungweite beträgt  .
.

 nach dem Absprung befindet sich ein Schilfrohr, das
nach dem Absprung befindet sich ein Schilfrohr, das  aus dem Wasser ragt.
aus dem Wasser ragt.
 dargestellt werden.
dargestellt werden.
Die maximale Höhe des Sprungs ist

- Gib eine mögliche Gleichung der zugehörigen Parabel an.
- In welchem Abstand springt der Frosch darüber?
- Welcher der beiden Frösche springt weiter?
Berechne die Differenz der Sprungweiten.
(5 P)
Aufgabe 4
a)
Das Schaubild zeigt Ausschnitte der Parabel  und der Geraden
und der Geraden 
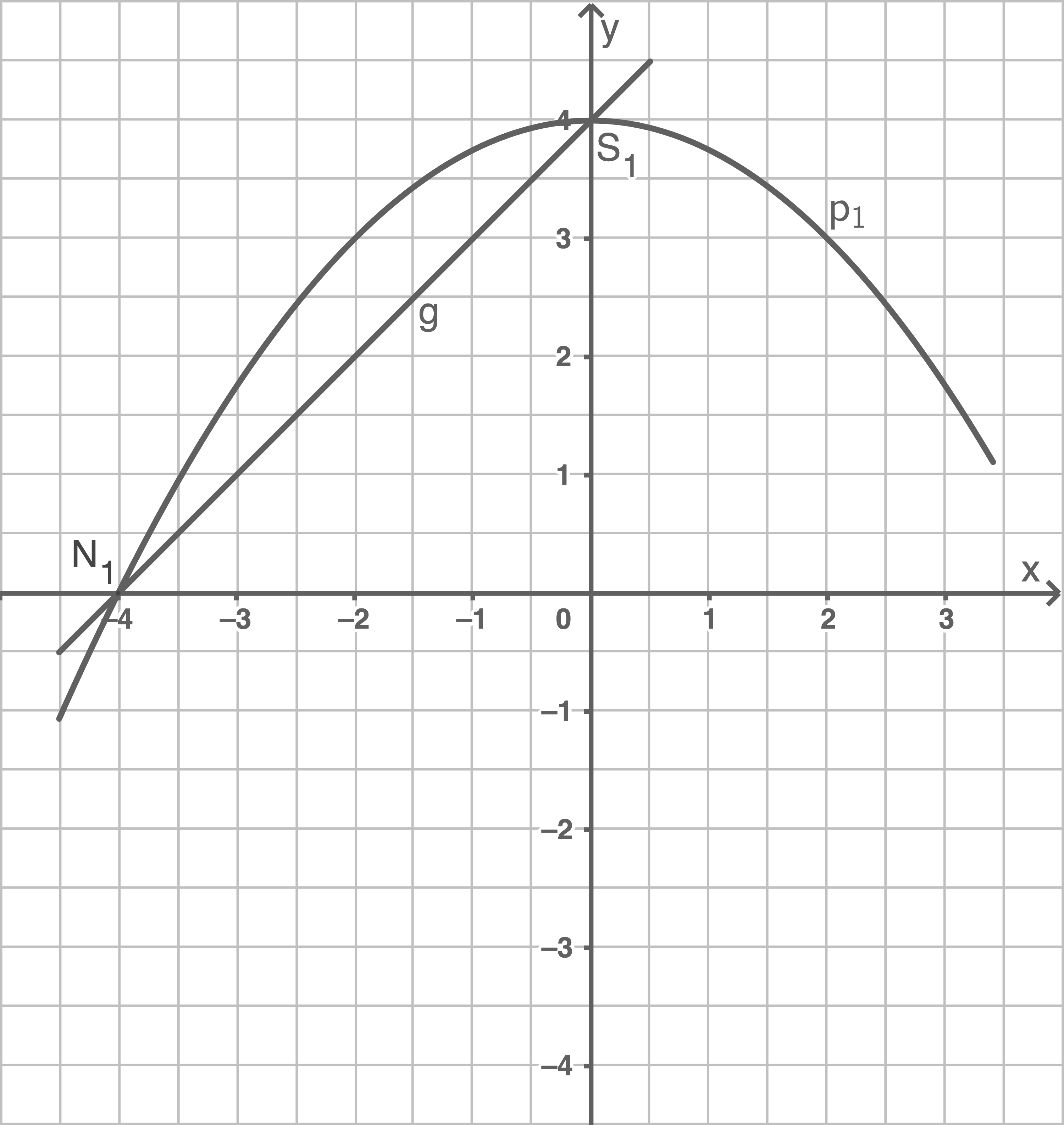
 schneidet die
schneidet die  -Achse in den Punkten
-Achse in den Punkten  und
und  .
.
 hat die Funktionsgleichung
hat die Funktionsgleichung  .
.
 bildet mit
bildet mit  und
und  das Dreieck
das Dreieck  . Ebenso bildet
. Ebenso bildet  mit
mit  und
und  das Dreieck
das Dreieck  .
.

- Bestimme die Funktionsgleichungen von
und
.
Entnimm dazu geeignete Werte aus dem Schaubild.
- Gib die Koordinaten von
an.
- Berechne die Koordinaten des Scheitelpunktes
von
- Um wie viele Flächeneinheiten (FE) unterscheiden sich die Flächeninhalte dieser beiden Dreiecke?
(5 P)
b)
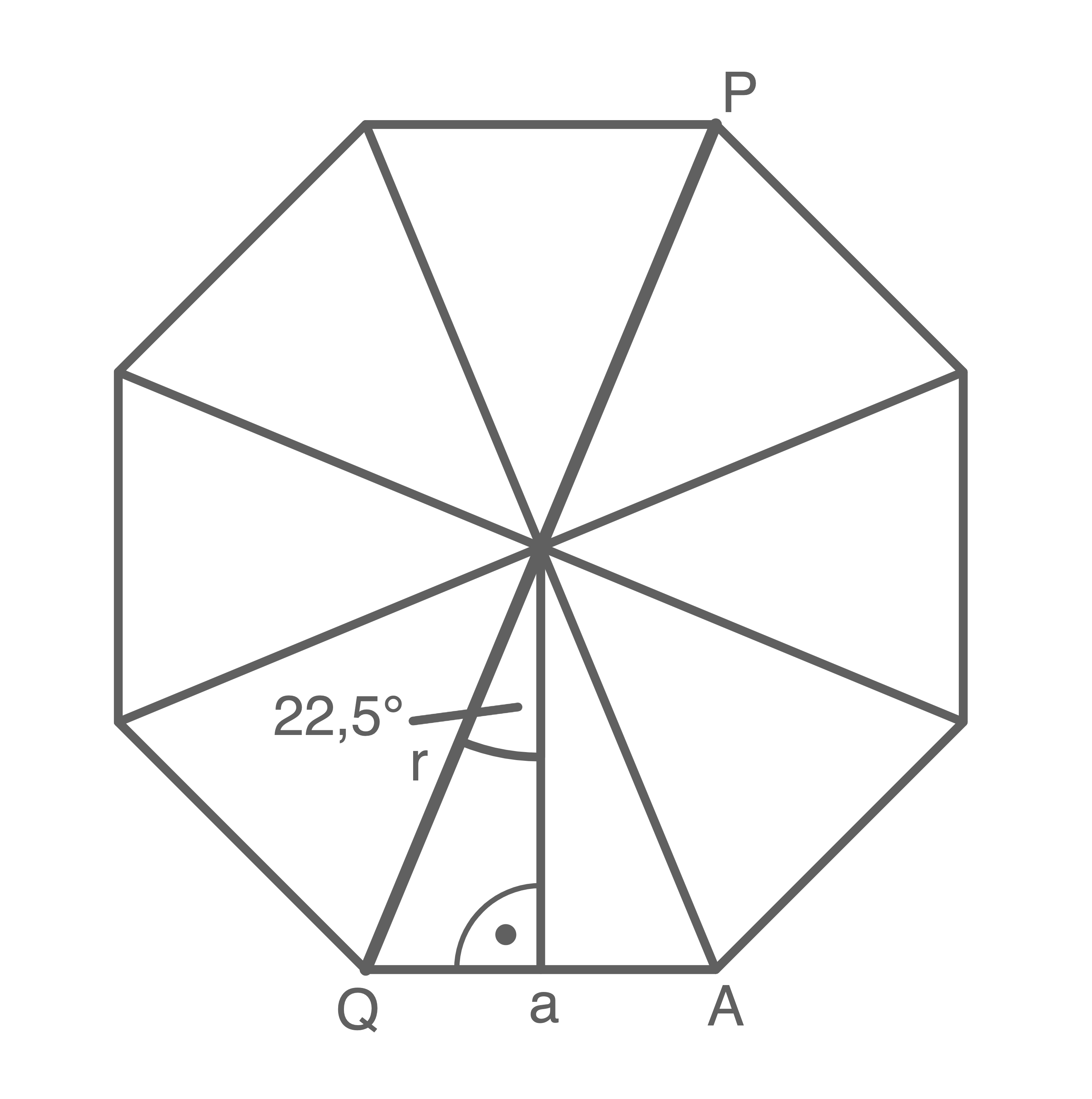
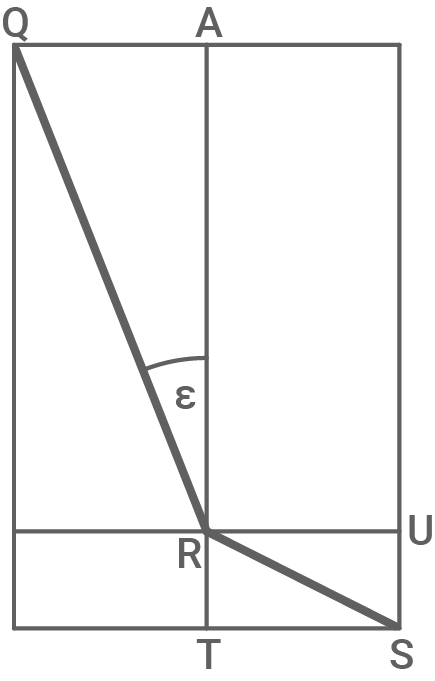
Auf einem regelmäßigen achtseitigen Prisma liegt der Streckenzug  mit der Länge
mit der Länge 
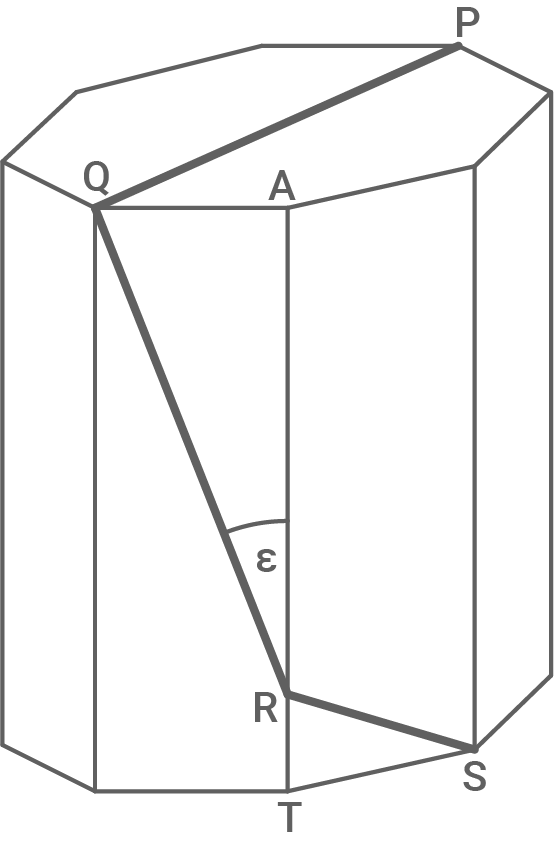 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AR}&=&14,2\,\text{cm}\\
\varepsilon&=&23,0^\circ
\end{array}\)](https://mathjax.schullv.de/86bace01aeef13653cea60bb3f7cc0d884d7030b051c516697fe275db44c6592?color=5a5a5a) Berechne die Höhe des achtseitigen Prismas.
Berechne die Höhe des achtseitigen Prismas.

(5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Hilfsskizze:
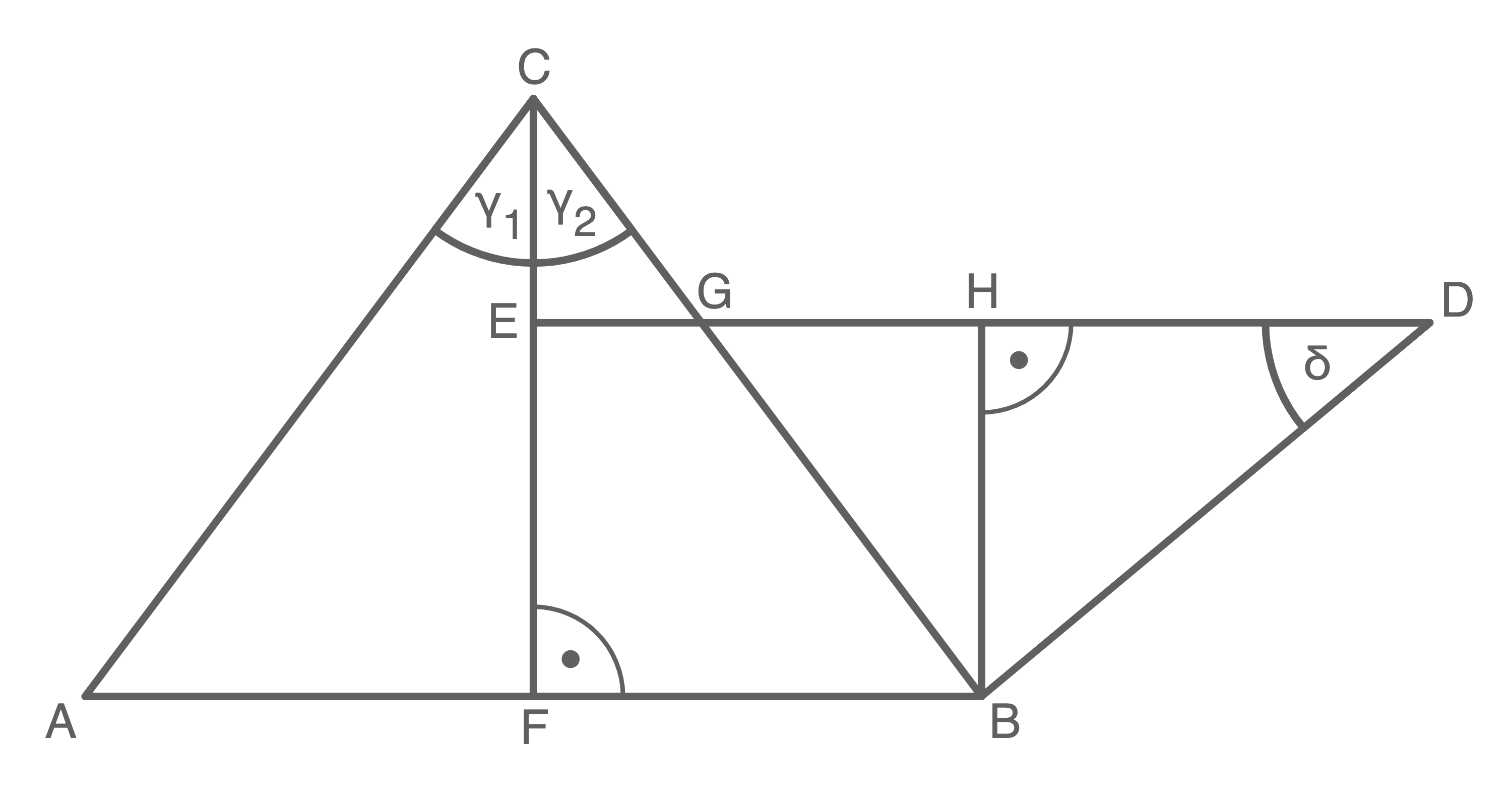 1. Schritt: Länge von
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\gamma_1&=&\dfrac{\overline{AF}}{\overline{AC}} \quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\sin\gamma_1\cdot \overline{AC}&=&\overline{AF}\\[5pt]
\overline{AF}&=&\sin\gamma_1\cdot \overline{AC}\\[5pt]
&=&\sin 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{AF}&=&\underline{6,96\,\text{cm}}=\overline{BF}
\end{array}\)](https://mathjax.schullv.de/dcc53dafe9a49d40e4ab0d2a03e1550f3dd1c585d4161498121ee1d24f6cf467?color=5a5a5a) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\delta&=&\dfrac{\overline{BH}}{\overline{BD}} \quad \scriptsize \mid\;\cdot \overline{BD} \\[5pt]
\sin\delta\cdot \overline{BD}&=&\overline{BH}\\[5pt]
\overline{BH}&=&\sin\delta\cdot \overline{BD}\\[5pt]
&=&\sin 39,2^\circ\cdot 8,2\,\text{cm}\\[5pt]
\overline{BH}&=&\underline{5,18\,\text{cm}}=\overline{EF}
\end{array}\)](https://mathjax.schullv.de/1c6dcf442e1d9de3af8ace8871ace8642933b403aa17ec1e943f7d3049a708f4?color=5a5a5a) 3. Schritt: Länge von
3. Schritt: Länge von  berechnen
3.1. Schritt: Länge von
berechnen
3.1. Schritt: Länge von  berechnen
Es gilt:
berechnen
Es gilt:  und
und 
![\(\begin{array}[t]{rll}
\cos\gamma_2&=&\dfrac{\overline{CF}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt]
\cos\gamma_2\cdot \overline{BC}&=&\overline{CF}\\[5pt]
\overline{CF}&=&\cos\gamma_2\cdot \overline{BC}\\[5pt]
&=&\cos 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{CF}&=&9,03\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/771528dbb41d53ab9d7f9d27d8a9b18dd7bd8a3192f6c9996b8869480c70a644?color=5a5a5a) 3.2. Schritt: Länge von
3.2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CE}&=&\overline{CF}-\overline{EF}\\[5pt]
\overline{CE}&=&9,03\,\text{cm}-5,18\,\text{cm}\\[5pt]
\overline{CE}&=&3,85\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ffafff46286d42bf65ff3f60794966f7fb29fb8f068cbd5203540ea45c50a1a5?color=5a5a5a) 3.3. Schritt: Länge von
3.3. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\gamma_2&=&\dfrac{\overline{EG}}{\overline{CE}} \quad \scriptsize \mid\;\cdot \overline{CE} \\[5pt]
\tan\gamma_2\cdot \overline{CE}&=&\overline{EG}\\[5pt]
\overline{EG}&=&\tan\gamma_2\cdot \overline{CE}\\[5pt]
&=&\tan37,6^\circ\cdot 3,85\,\text{cm}\\[5pt]
\overline{EG}&=&\underline{2,96\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/89d479436556b14e7543658774fdae6307c33e1bd5bb0685e2a22ffc0f3d4c8b?color=5a5a5a) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{\overline{BF}+\overline{EG}}{2}\cdot\overline{EF}\\[5pt]
&=&\dfrac{6,96\,\text{cm}+2,96\,\text{cm}}{2}\cdot 5,18\,\text{cm}\\[5pt]
A&=&\underline{\underline{25,7\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/ebb137dcaeb9d20e4dc05e839fd31af90119e2c7ce6ebecd6a76b801e0459d26?color=5a5a5a)

b)
Funktionsgleichung berechnen
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
1^2+b\cdot 1-2&=& 1 \\[5pt]
-1+b&=& 1 \quad \scriptsize \mid\;+1 \\[5pt]
b&=& 2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e62a998ca83513d4f2c59dfabf3727424e90dc1be8f08357cd0e2c2e8f1bb9c4?color=5a5a5a)
 Koordinaten bestimmen
Koordinaten bestimmen



 Flächeninhalt berechnen
Flächeninhalt berechnen


 Funktionsgleichung angeben
Funktionsgleichung angeben

 in
in 
 also
also 
 Aussage überprüfen
Julius hat Recht.
Mögliche Begründungen:
rechnerisch:
Schnittpunkt der Geraden
Aussage überprüfen
Julius hat Recht.
Mögliche Begründungen:
rechnerisch:
Schnittpunkt der Geraden  mit der Geraden durch
mit der Geraden durch  und
und 
![\(\begin{array}[t]{rll}
-3x-2&=&1 &\quad \scriptsize \mid\;+2 \\[5pt]
-3x&=&3&\quad \scriptsize \mid\;:3 \\[5pt]
x&=&-1
\end{array}\)](https://mathjax.schullv.de/63d5694e14522afd67c765087a5d8aa6ee559922f86b5307386df41a8a34ec2d?color=5a5a5a)
 Flächeninhalte der Teildreiecke vergleichen:
Flächeninhalte der Teildreiecke vergleichen:
 argumentativ:
Die Gerade
argumentativ:
Die Gerade  schneidet die Gerade
schneidet die Gerade  (durch
(durch  und
und  ) im Punkt
) im Punkt  Dieser Punkt liegt genau zwischen
Dieser Punkt liegt genau zwischen  und
und  Da die Gerade zudem durch den Punkt
Da die Gerade zudem durch den Punkt  verläuft, halbiert sie also das Dreieck.
verläuft, halbiert sie also das Dreieck.
Lösung 2
a)
Funktionsgleichung von  bestimmen
bestimmen
 Punkt
Punkt  in
in  einsetzen:
einsetzen:
 also
also  Punkt
Punkt  und
und  in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
1&=&4^2+b\cdot 4+1 \\[5pt]
1&=&17+4b &\quad \scriptsize \mid\;-17 \\[5pt]
-16&=&4b &\quad \scriptsize \mid\;:4 \\[5pt]
-4&=&b
\end{array}\)](https://mathjax.schullv.de/81695b9b55d6a2e7e66383ebe6282150c6f657b0e7e89782d4857b8785834cb1?color=5a5a5a)
 Wertetabelle vervollständigen
Wertetabelle vervollständigen
Funktionsgleichung von  bestimmen
bestimmen
 einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-5&=&m\cdot 3-2 \quad \scriptsize \mid\;+2 \\[5pt]
-3&=&m\cdot 3 \quad \scriptsize \mid\;:3\\[5pt]
-1&=&m
\end{array}\)](https://mathjax.schullv.de/e1edc3d917b90afb4424a0c87f1244c05f5a253fd0a6b533efa8ed3451bd49e2?color=5a5a5a)
 Rechnerisch zeigen, dass kein Schnittpunkt vorliegt
Gleichsetzen:
Rechnerisch zeigen, dass kein Schnittpunkt vorliegt
Gleichsetzen:
![\(\begin{array}[t]{rll}
x^2-4x+1&=&-x-2 \quad \scriptsize \mid\;+x+2 \\[5pt]
x^2-3x+3&=&0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/795bbe38adefbeeafef62de71fdfc496f58f1dab48d73eed78dd28f5594af06d?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-3}{2} \pm \sqrt{\left(\dfrac{-3}{2}\right)^2-3} \\[5pt]
x_{1,2}&=& \dfrac{3}{2} \pm \sqrt{-\dfrac{3}{4}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9b9582fe6ac970fad5ce9a8578cef0c62a089a27356803c2e5825a3ff75b5c73?color=5a5a5a) Für die Diskriminante gilt
Für die Diskriminante gilt  also gibt es keine Lösung.
Funktionsgleichung angeben
also gibt es keine Lösung.
Funktionsgleichung angeben
 in Scheitelpunktform:
in Scheitelpunktform:



 Der Scheitelpunkt der verschobenen Normalparabel
Der Scheitelpunkt der verschobenen Normalparabel  muss oberhalb dem Scheitelpunkt von
muss oberhalb dem Scheitelpunkt von  liegen. Liegt dieser oberhalb der
liegen. Liegt dieser oberhalb der  -Achse, so kann
-Achse, so kann  auch nicht die Gerade
auch nicht die Gerade  schneiden.
Mögliche Funktionsgleichung:
schneiden.
Mögliche Funktionsgleichung:
 mit
mit 
b)
1. Schritt: Radius  des Kegels berechnen
des Kegels berechnen
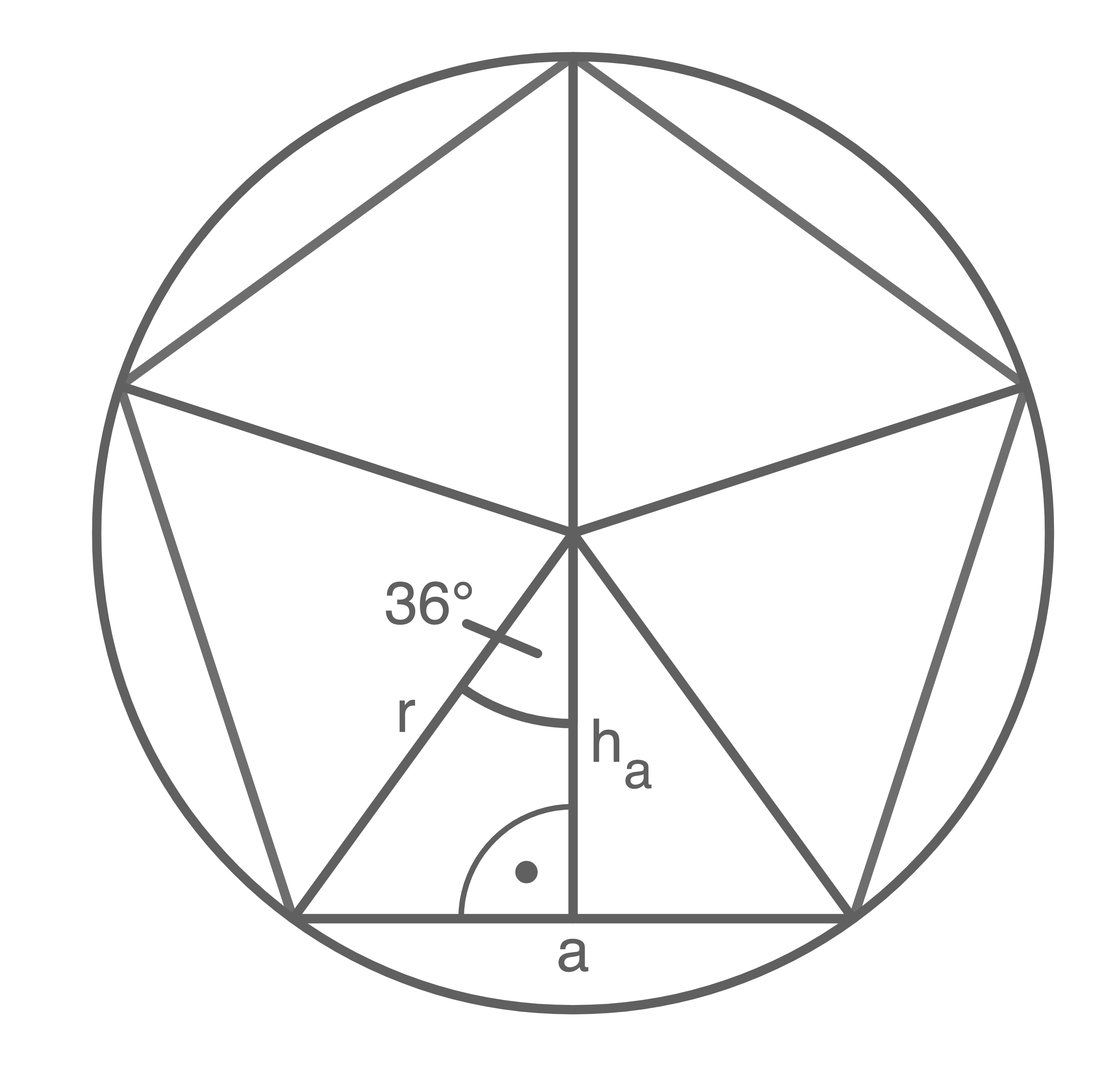
![\(\begin{array}[t]{rll}
\sin 36^\circ&=&\dfrac{\frac{a}{2}}{r} \quad \scriptsize \mid\;\cdot r \\[5pt]
\sin 36^\circ\cdot r&=&\dfrac{a}{2} \quad \scriptsize \mid\;: \sin 36^\circ \\[5pt]
r&=&\dfrac{a}{2\cdot \sin 36^\circ} \\[5pt]
&=&\dfrac{8,6\,\text{cm}}{2\cdot \sin 36^\circ} \\[5pt]
r&=&\underline{7,32\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/23c47a9369826e2f9fcc2618cf6e734a03aad40f04e2964a1c6c4a87fbb7c687?color=5a5a5a) 2. Schritt: Höhe
2. Schritt: Höhe  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_a^2&=&r^2-\left(\frac{a}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
h_a&=&\sqrt{r^2-\left(\frac{a}{2}\right)^2} \\[5pt]
&=&\sqrt{(7,32\,\text{cm})^2-\left(\frac{8,6\,\text{cm}}{2}\right)^2} \\[5pt]
h_a&=&\underline{5,92\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/2f576e8b459f8f947915b4340c9d8ca30b8a28559677d8fdb32549859d171bee?color=5a5a5a) 3. Schritt: Höhe
3. Schritt: Höhe  berechnen
berechnen
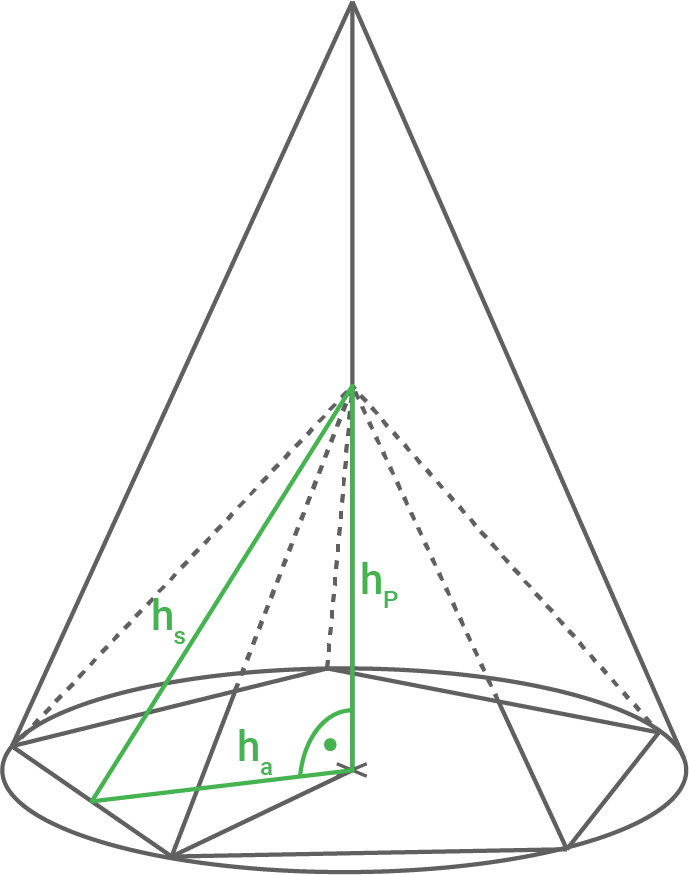
![\(\begin{array}[t]{rll}
h_s^2&=&h_P^2+h_a^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h_s&=&\sqrt{h_P^2+h_a^2}\\[5pt]
&=&\sqrt{(7,6\,\text{cm})^2+(5,92\,\text{cm})^2}\\[5pt]
h_s&=&\underline{9,63\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/6a7fefd1853a73ed49879650653ba175b5514e8a9dc1c5e935d430c532e13ed2?color=5a5a5a) 4. Schritt: Länge von
4. Schritt: Länge von  berechnen
berechnen
 ist die Mantellinie des Kegels.
ist die Mantellinie des Kegels.
![\(\begin{array}[t]{rll}
s_K^2&=&r^2+h_K^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
s_K&=&\sqrt{r^2+h_K^2}\\[5pt]
&=&\sqrt{(7,32\,\text{cm})^2+(15,2\,\text{cm})^2}\\[5pt]
s_K&=&\underline{16,87\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/94e1b268642319f9b594c579920f062656ef713e1709737c7e88ed80e4dbfb43?color=5a5a5a) 5. Schritt: Mantelflächeninhalt der Pyramide berechnen
5. Schritt: Mantelflächeninhalt der Pyramide berechnen
![\(\begin{array}[t]{rll}
M_P&=&5\cdot A_\text{Seitenfläche} \\[5pt]
&=&5\cdot \dfrac{a\cdot h_s}{2} \\[5pt]
&=&5\cdot \dfrac{8,6\,\text{cm}\cdot 9,63\,\text{cm}}{2}\\[5pt]
M_P&=&\underline{207,05\,\text{cm}^2}
\end{array}\)](https://mathjax.schullv.de/c0b9e2370e33b1a6c60c5fcd72cff7e17ed179fa3feaf50e56d93655d33f4c96?color=5a5a5a) 6. Schritt: Mantelflächeninhalt des Kegels berechnen
6. Schritt: Mantelflächeninhalt des Kegels berechnen
![\(\begin{array}[t]{rll}
M_K&=&\pi\cdot r\cdot s_K \\[5pt]
&=&\pi\cdot 7,32\,\text{cm}\cdot 16,87\,\text{cm}\\[5pt]
M_K&=&\underline{387,95\,\text{cm}^2}
\end{array}\)](https://mathjax.schullv.de/97e2519e62c939c79691ce72a35867e6a0ddde1e621a5dfe3fd2663a62c8fa5e?color=5a5a5a) 7. Schritt: Differenz der Mantelflächeninhalte berechnen
7. Schritt: Differenz der Mantelflächeninhalte berechnen
![\(\begin{array}[t]{rll}
M_\text{Differenz}&=&M_K-M_P\\[5pt]
&=&387,95\,\text{cm}^2-207,05\,\text{cm}^2\\[5pt]
M_\text{Differenz}&=&\underline{\underline{180,9\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/ea3ebcdbc196b4dc98123f2423e5795a1b177e93831ecb26e0cca277c69e23d9?color=5a5a5a)


Lösung 3
a)
Wahrscheinlichkeit berechnen



 bzw.
bzw.  Erwartungswert berechnen
Erwartungswert berechnen

 Entscheidung treffen und begründen
Ja, der Gewinn erhöht sich dadurch auf lange Sicht.
Entscheidung treffen und begründen
Ja, der Gewinn erhöht sich dadurch auf lange Sicht.


b)
Gleichung der zugehörigen Parabel angeben

 da der Scheitelpunkt bei
da der Scheitelpunkt bei  die
die  -Koordinate
-Koordinate  hat.
hat.
 , denn von Absprung bis Landung sind es
, denn von Absprung bis Landung sind es 

 in
in 
![\(\begin{array}[t]{rll}
0&=&a\cdot 110^2+139 &\quad \scriptsize \mid\;-139 \\[5pt]
-139&=&12100a&\quad \scriptsize \mid\;:12100 \\[5pt]
-0,011&=&a\\[5pt]
a&=&-0,011
\end{array}\)](https://mathjax.schullv.de/e9fe73f154dfcf69719aba7dd4baac31ade2f3dcef1d3a18f756e8acbf21fc6e?color=5a5a5a)
 Abstand berechnen
Die Parabel hat an der Stelle
Abstand berechnen
Die Parabel hat an der Stelle  den
den  -Wert
-Wert 
 Beurteilen, welcher Frosch weiter springt und Differenz berechnen
Beurteilen, welcher Frosch weiter springt und Differenz berechnen
![\(\begin{array}[t]{rll}
-\dfrac{3}{200}x^2+165&=&0 \quad \scriptsize \mid\;-165 \\[5pt]
-\dfrac{3}{200}x^2&=&-165 \quad \scriptsize \mid\;:(-\dfrac{3}{200})\\[5pt]
x^2&=& 165\cdot \dfrac{200}{3}\\[5pt]
x_1&=& 104,9\\[5pt]
x_2&=& -104,9
\end{array}\)](https://mathjax.schullv.de/b3441cda9829135a8cdfc106e7ff3b773f4af34b59deca78442526f4cbf612d5?color=5a5a5a) Frosch 2 springt also
Frosch 2 springt also ![\(104,9\cdot 2=209,8\,\left[\text{cm}\right]\)](https://mathjax.schullv.de/96a1239f36b2ed7607f63baf2c2d738c9d12fc6e061e5bdff9241a5d1cced5d6?color=5a5a5a) weit.
Frosch 1 springt demnach ca.
weit.
Frosch 1 springt demnach ca.  weiter.
weiter.
Lösung 4
a)
Funktionsgleichung von  bestimmen
bestimmen

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
0&=& a\cdot (-4)^2+4 \\[5pt]
0&=& 16a+4 &\quad \scriptsize \mid\; -4\\[5pt]
-4&=& 16a &\quad \scriptsize \mid\; :16\\[5pt]
-\dfrac{1}{4}&=& a\\[5pt]
a&=& -\dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/9f903f99ed88e4c1a291f04b9cca4c51346c10b5f924997af22be998f2a30044?color=5a5a5a)
 Funktionsgleichung von
Funktionsgleichung von  bestimmen
bestimmen

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
0&=& m\cdot (-4)+4 &\quad \scriptsize \mid\; -4\\[5pt]
-4&=& -4m &\quad \scriptsize \mid\; :(-4)\\[5pt]
1 &=& m \\[5pt]
m&=& 1\\[5pt]
\end{array}\)](https://mathjax.schullv.de/30c33f05bc6baf6f6f825af672839d3dd36bcdb7b66756e9bb2d65c503830bcc?color=5a5a5a)
 Koordinaten angeben
Koordinaten angeben
![\(\begin{array}[t]{rll}
-\dfrac{1}{4}x^2+4&=& 0 &\quad \scriptsize \mid\;-4 \\[5pt]
-\dfrac{1}{4}x^2&=& -4 &\quad \scriptsize \mid\;:\left(-\dfrac{1}{4}\right) \\[5pt]
x^2&=& 16\\[5pt]
x_1&=& -4\\[5pt]
x_2&=& 4
\end{array}\)](https://mathjax.schullv.de/30f20b59c4c5cb52149ea087aab88ba12effb3c305ff9567493af33637ca0074?color=5a5a5a)
 Koordinaten des Scheitelpunkts berechnen
Koordinaten des Scheitelpunkts berechnen



 Flächeneinheiten angeben
Flächeneinheiten angeben

 Unterschied:
Unterschied: 
b)