Pflichtbereich
Aufgabe P1
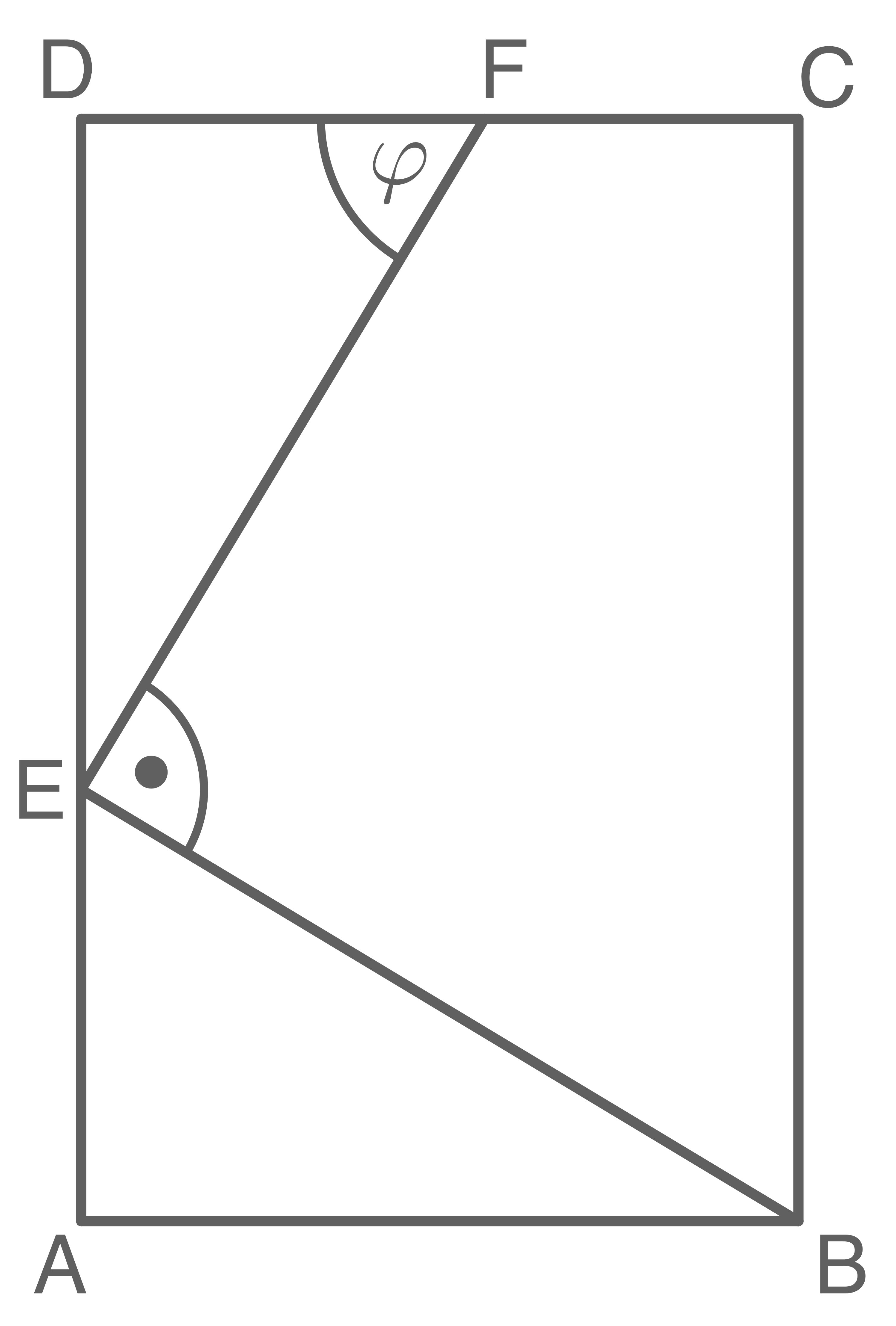
4,5 P
Aufgabe P2
Das Dreieck  und das Rechteck
und das Rechteck  überdecken sich teilweise.
überdecken sich teilweise.
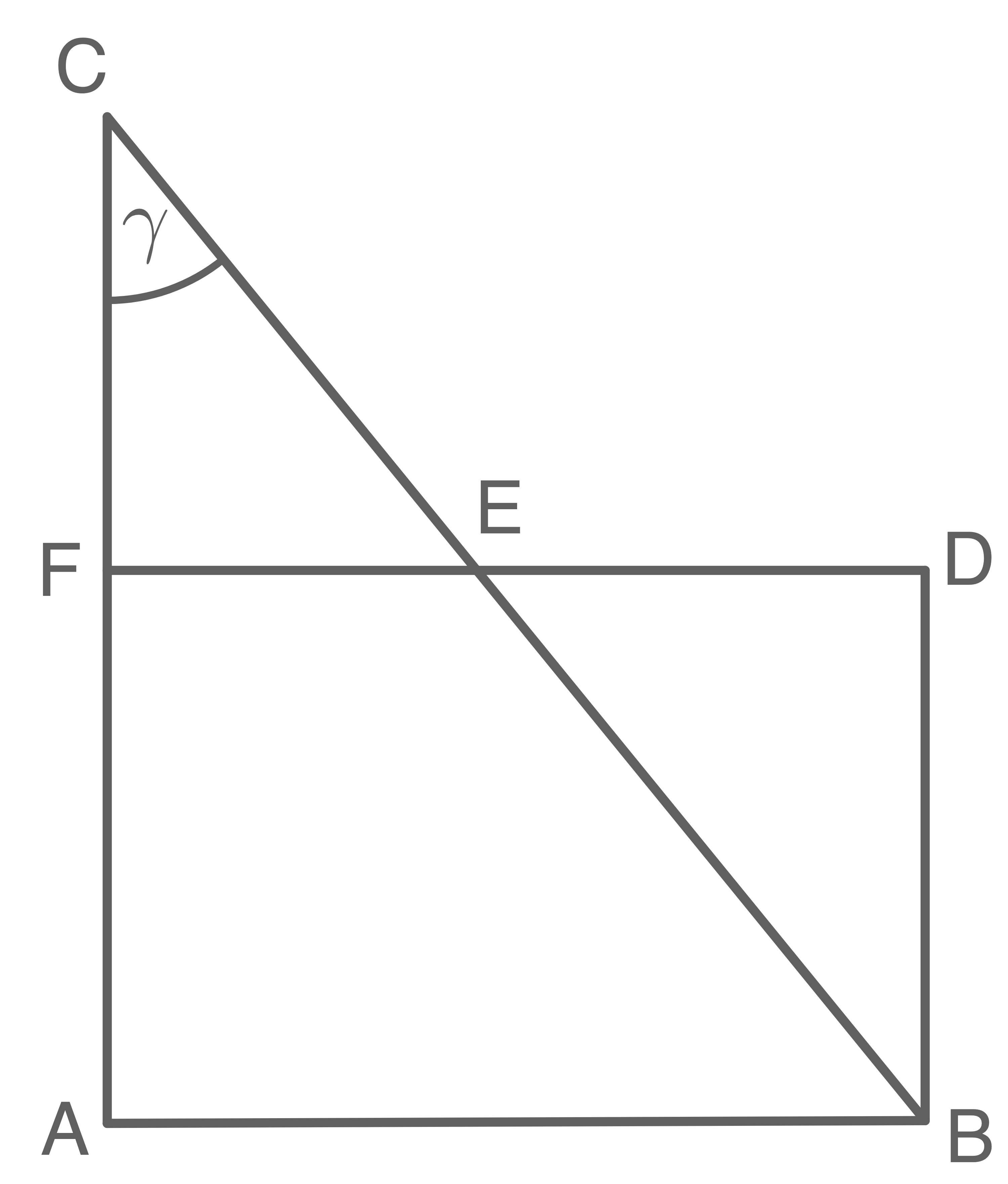 Es gilt:
Es gilt:


4 P
Aufgabe P3
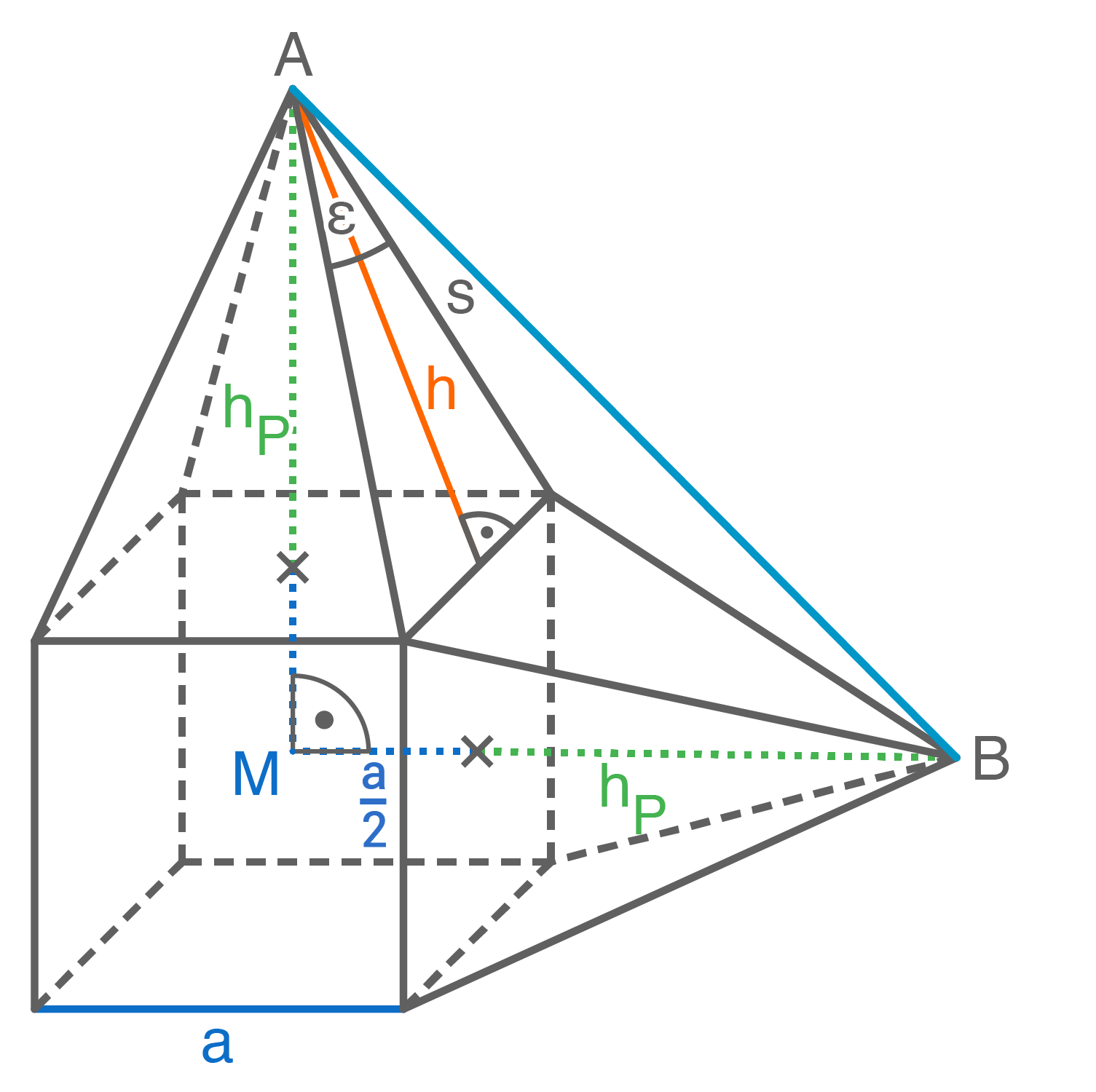
Ein zusammengesetzter Körper besteht aus einem Würfel und zwei quadratischen Pyramiden.
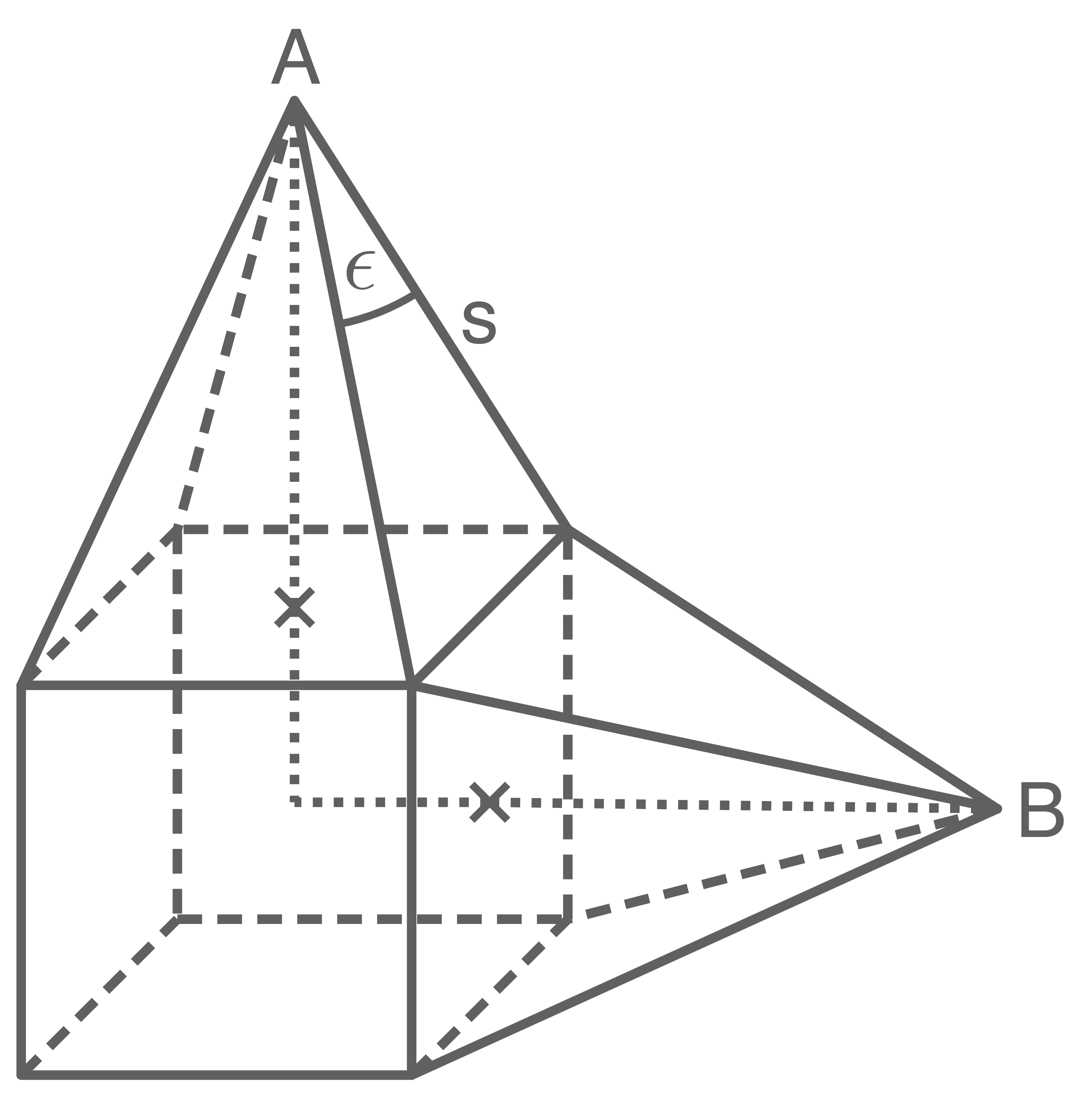 Die Pyramiden haben die gleiche Höhe.
Die Pyramiden haben die gleiche Höhe.
Es gilt: und
und  voneinander entfernt?
voneinander entfernt?

Es gilt:
4 P
Aufgabe P4
In Deutschland boomt der Verkauf von E-Bikes.
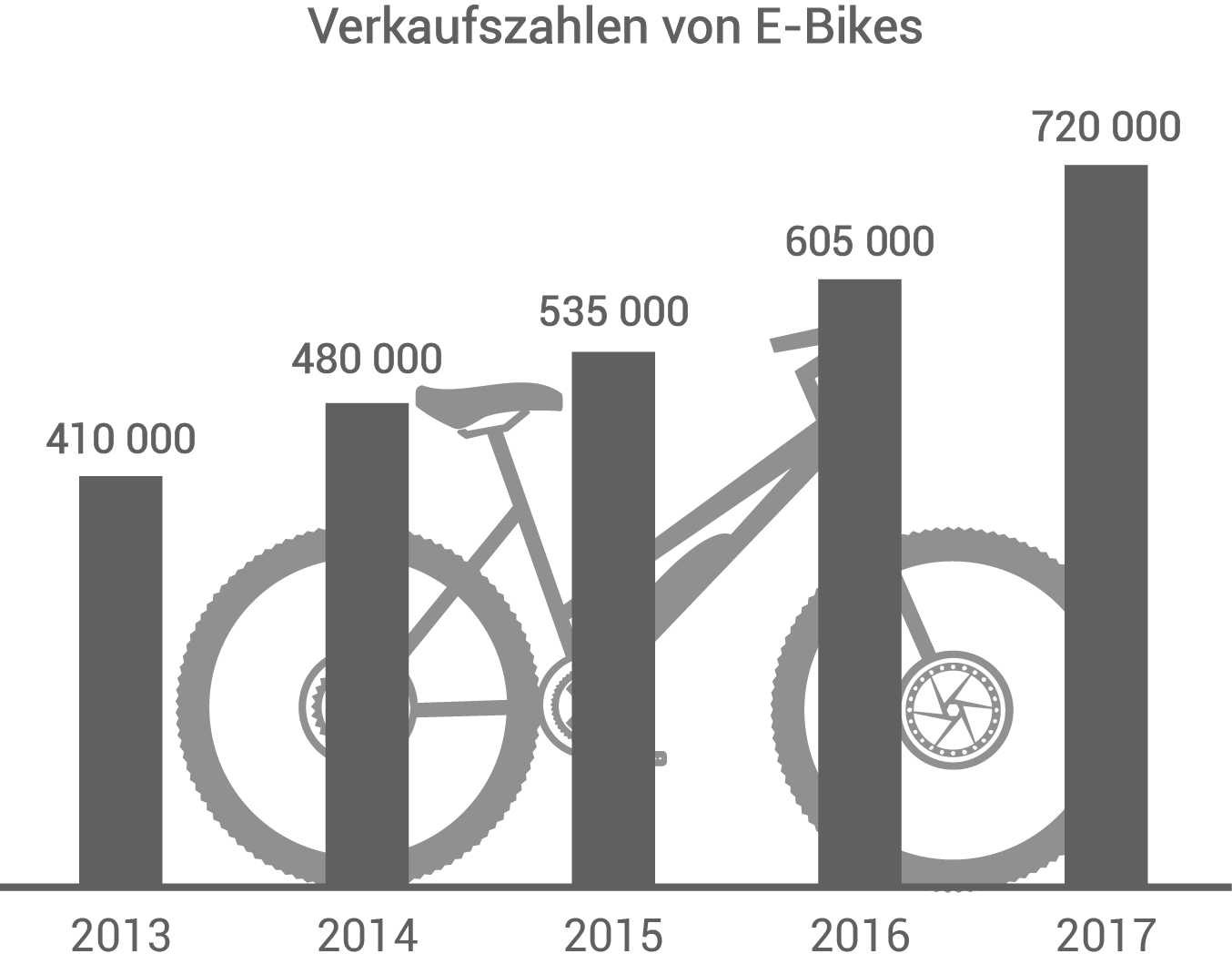
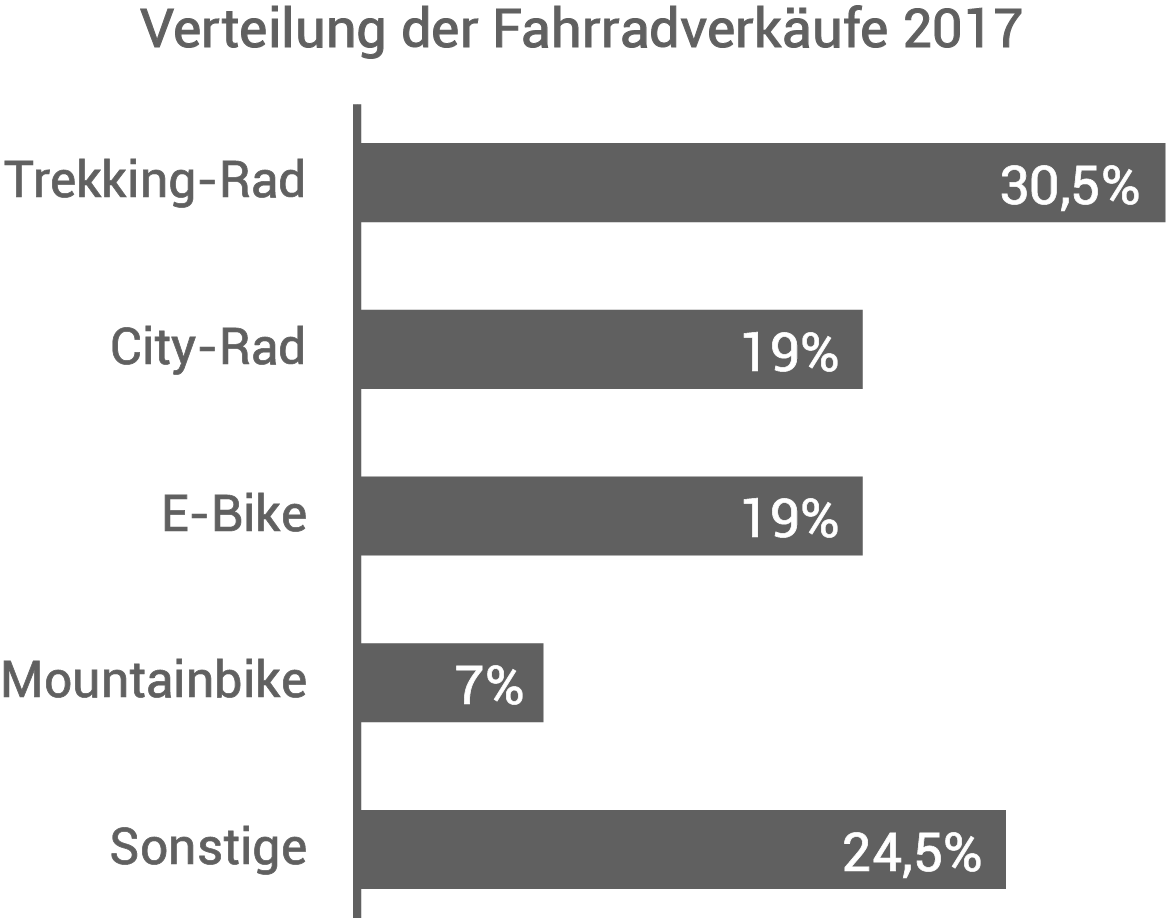 Um wie viel Prozent ist der Verkauf von E-Bikes von 2013 bis 2017 insgesamt angestiegen?
Berechne die Anzahl aller Fahrräder, die im Jahr 2017 verkauft wurden.
In einer Fachzeitschrift war zu lesen, dass 22 % der im Jahr 2017 verkauften Mountainbikes eine Vollfederung hatten. Wie viele Mountainbikes hatten eine Vollfederung?
Um wie viel Prozent ist der Verkauf von E-Bikes von 2013 bis 2017 insgesamt angestiegen?
Berechne die Anzahl aller Fahrräder, die im Jahr 2017 verkauft wurden.
In einer Fachzeitschrift war zu lesen, dass 22 % der im Jahr 2017 verkauften Mountainbikes eine Vollfederung hatten. Wie viele Mountainbikes hatten eine Vollfederung?


3 P
Aufgabe P5
Löse das Gleichungssystem:

3,5 P
Aufgabe P6
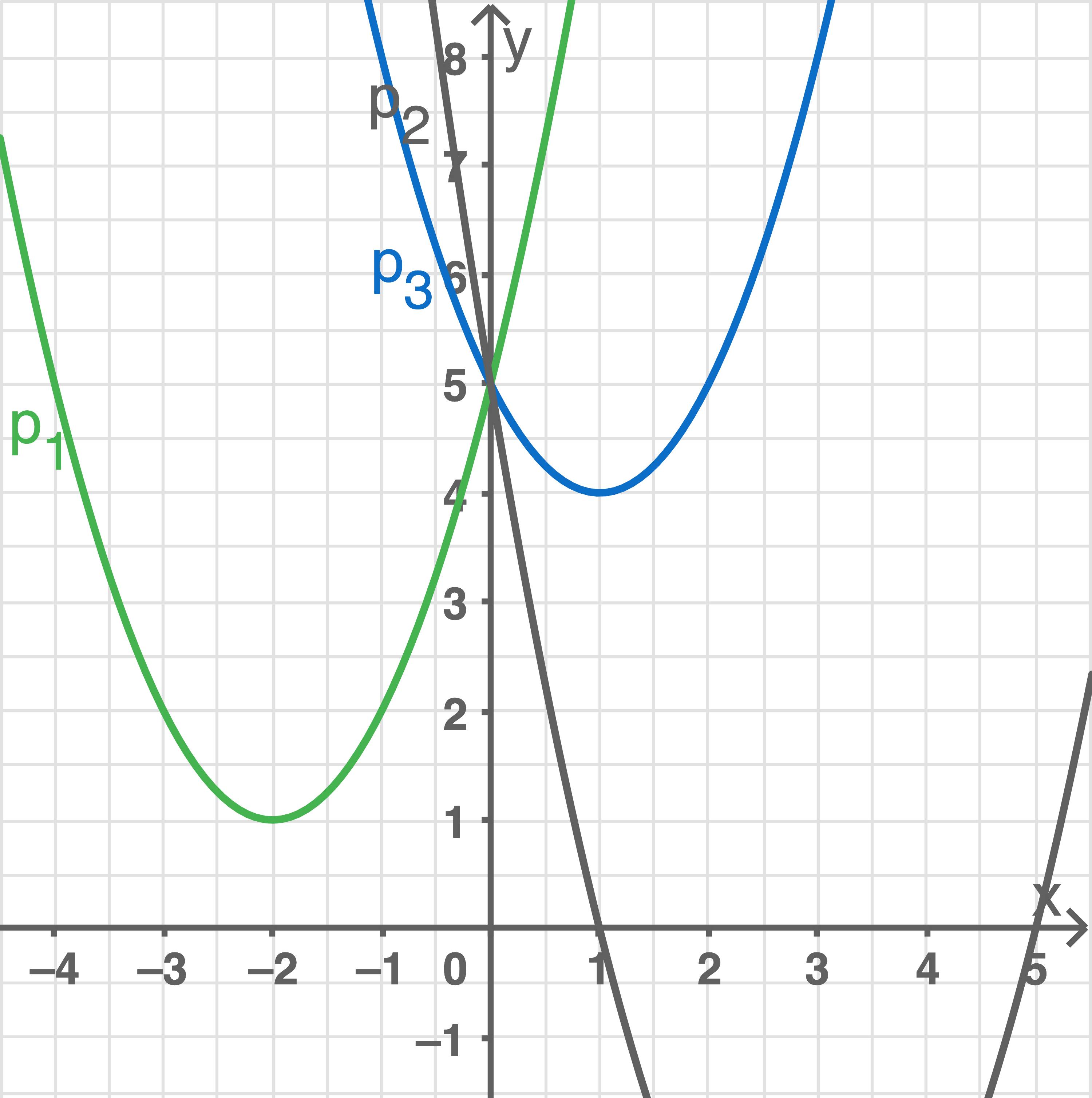
Gegeben sind eine Wertetabelle, die Graphen von zwei verschobenen Normalparabeln und drei Funktionsgleichungen.

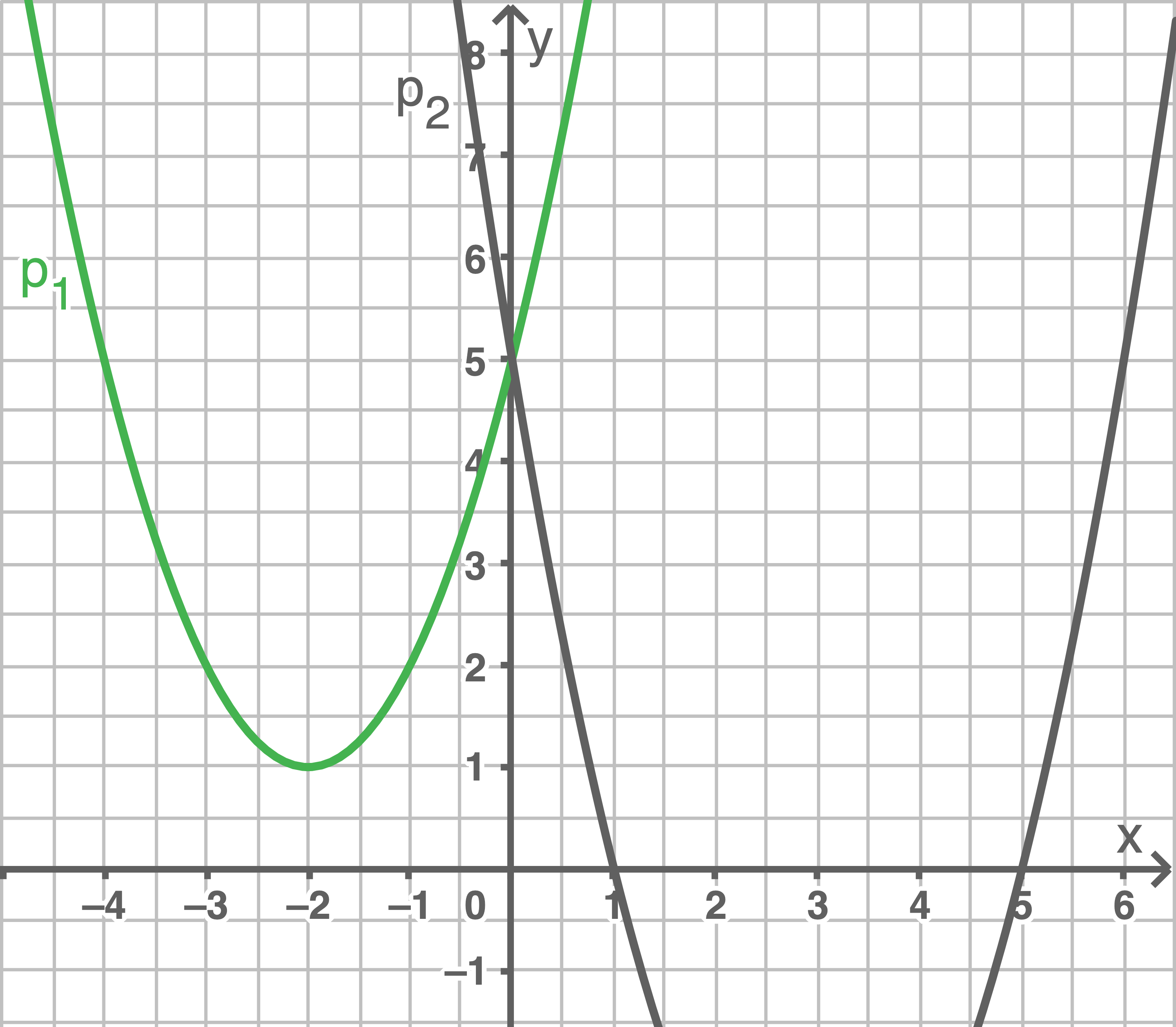 Zur Wertetabelle gehören einer der beiden Graphen sowie eine der drei Funktionsgleichungen.
Ordne der Wertetabelle ihren Graphen und ihre Funktionsgleichung zu. Begünde deine Entscheidung.
Im Schaubild fehlt der Graph
Zur Wertetabelle gehören einer der beiden Graphen sowie eine der drei Funktionsgleichungen.
Ordne der Wertetabelle ihren Graphen und ihre Funktionsgleichung zu. Begünde deine Entscheidung.
Im Schaubild fehlt der Graph  der dritten Parabel. Zeichne den fehlenden Graphen
der dritten Parabel. Zeichne den fehlenden Graphen  in das Koordinatensystem ein.
in das Koordinatensystem ein.

4 P
Aufgabe P7
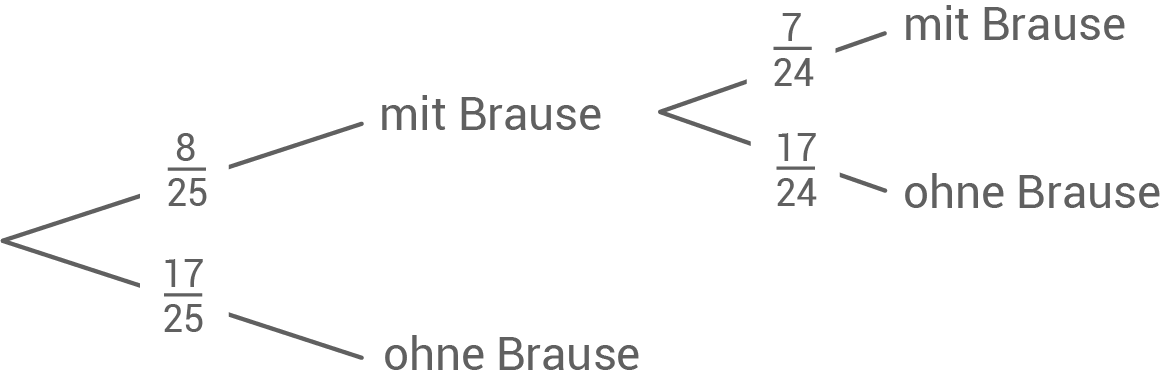
In einem Kaugummiautomaten befinden sich 10 rote, 9 weiße und 6 grüne Kaugummis.
Betätigt man den Drehgriff, erhält man einen Kaugummi. Luisa dreht zweimal. Mit welcher Wahrscheinlichkeit erhält sie
Betätigt man den Drehgriff, erhält man einen Kaugummi. Luisa dreht zweimal. Mit welcher Wahrscheinlichkeit erhält sie
- zuerst einen roten, dann einen weißen Kaugummi?
- keinen grünen Kaugummi?
3,5 P
Aufgabe P8
Die beiden Ranglisten zeigen die monatlichen Vergütungen von zwei Berufsgruppen im ersten Ausbildungsjahr.
17 Jugendliche machen eine Ausbildung in einem technischen Beruf und 13 Jugendliche in einem kaufmännischen Beruf.
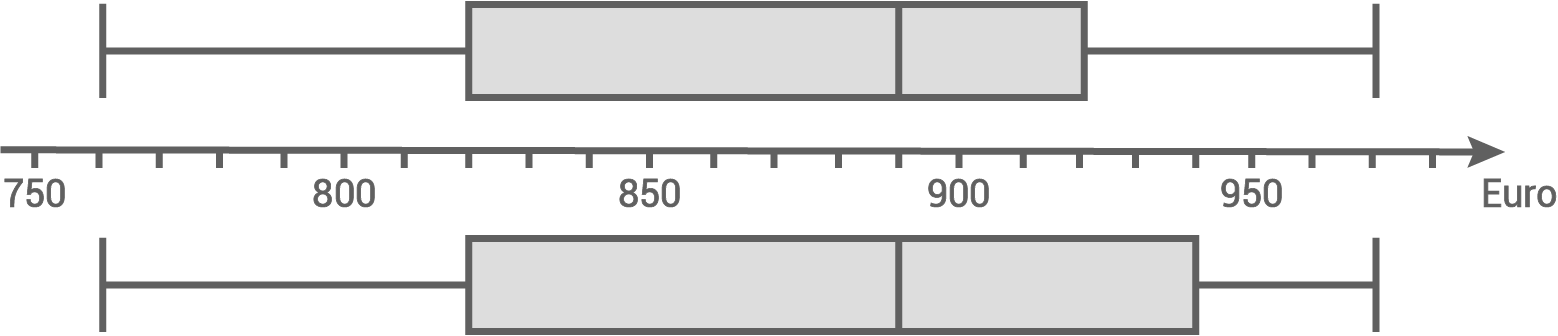
 Zu welcher Rangliste gehört der dargestellte Boxplot? Begründe.
Zeichne den Boxplot der anderen Berufsgruppe ein.
Vier Jugendliche, die eine kaufmännische Ausbildung machen, wurden nachträglich befragt.
Zu welcher Rangliste gehört der dargestellte Boxplot? Begründe.
Zeichne den Boxplot der anderen Berufsgruppe ein.
Vier Jugendliche, die eine kaufmännische Ausbildung machen, wurden nachträglich befragt.
Sie verdienen monatlich ,
,  ,
,  und
und  .
.
Wie verändert sich der zugehörige Boxplot, wenn diese Werte hinzukommen? Begründe.
17 Jugendliche machen eine Ausbildung in einem technischen Beruf und 13 Jugendliche in einem kaufmännischen Beruf.
| Ausbildungsvergütung in technischen Berufen (in Euro) |
|---|
| 760 |
| 780 |
| 800 |
| 820 |
| 820 |
| 840 |
| 840 |
| 860 |
| 890 |
| 910 |
| 910 |
| 920 |
| 920 |
| 920 |
| 950 |
| 960 |
| 970 |
| Ausbildungsvergütung in kaufmännischen Berufen (in Euro) |
|---|
| 760 |
| 770 |
| 820 |
| 820 |
| 840 |
| 880 |
| 890 |
| 910 |
| 920 |
| 940 |
| 940 |
| 950 |
| 970 |

Sie verdienen monatlich
Wie verändert sich der zugehörige Boxplot, wenn diese Werte hinzukommen? Begründe.
3,5 P
Lösung P1
1. Schritt: Länge der Strecke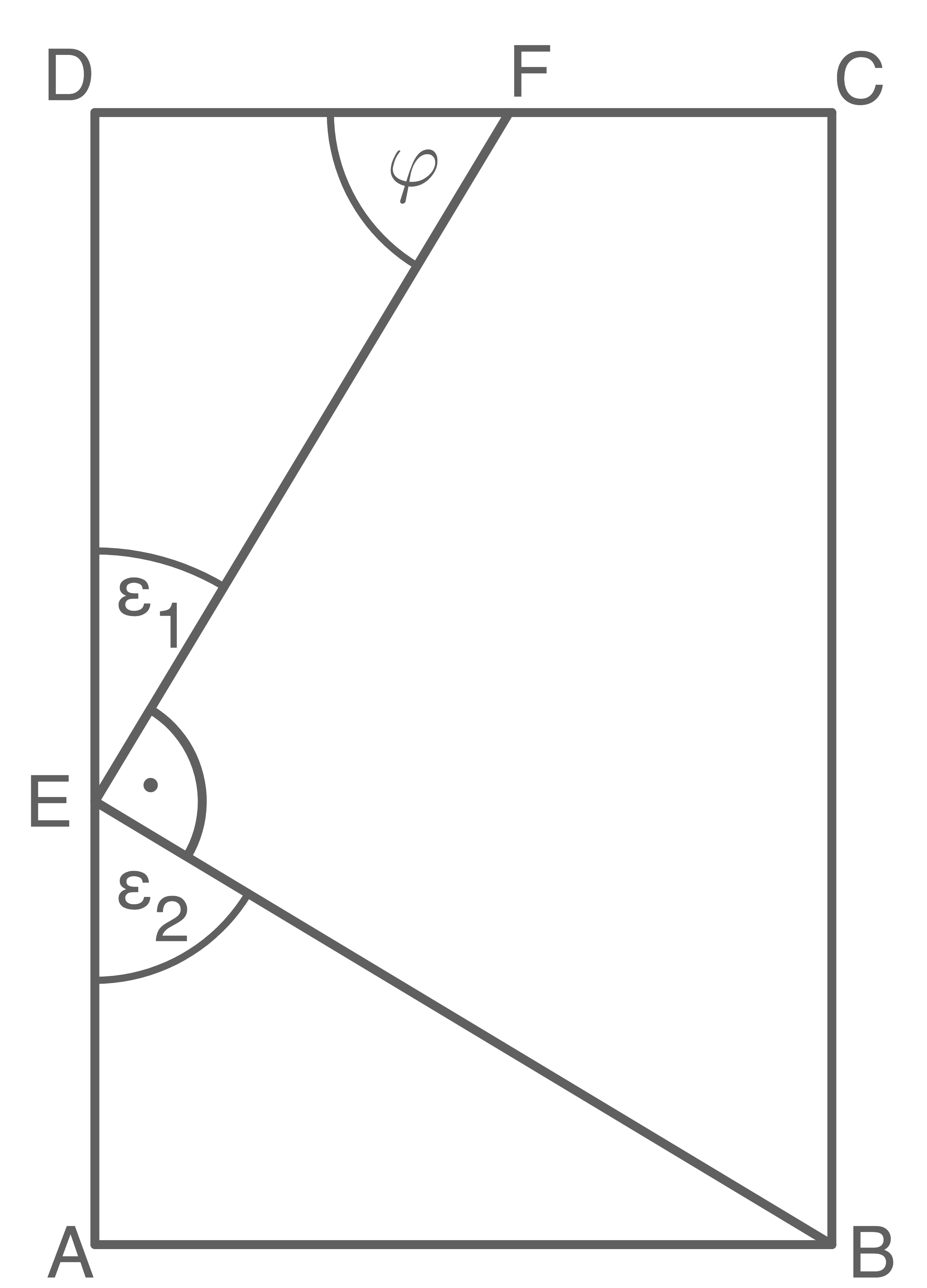
Lösung P2
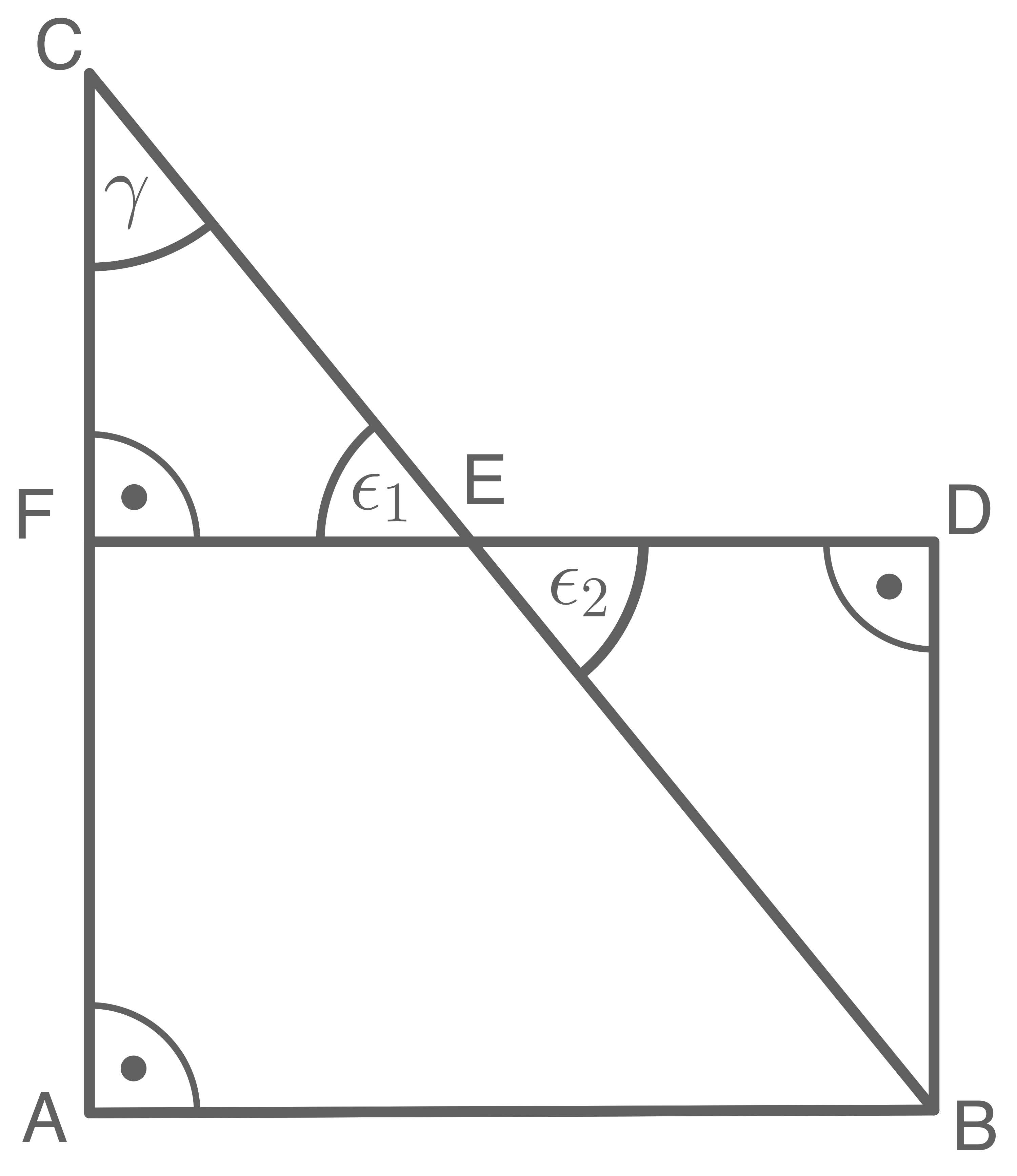
Lösung P3
Berechnung des Oberflächeninhalts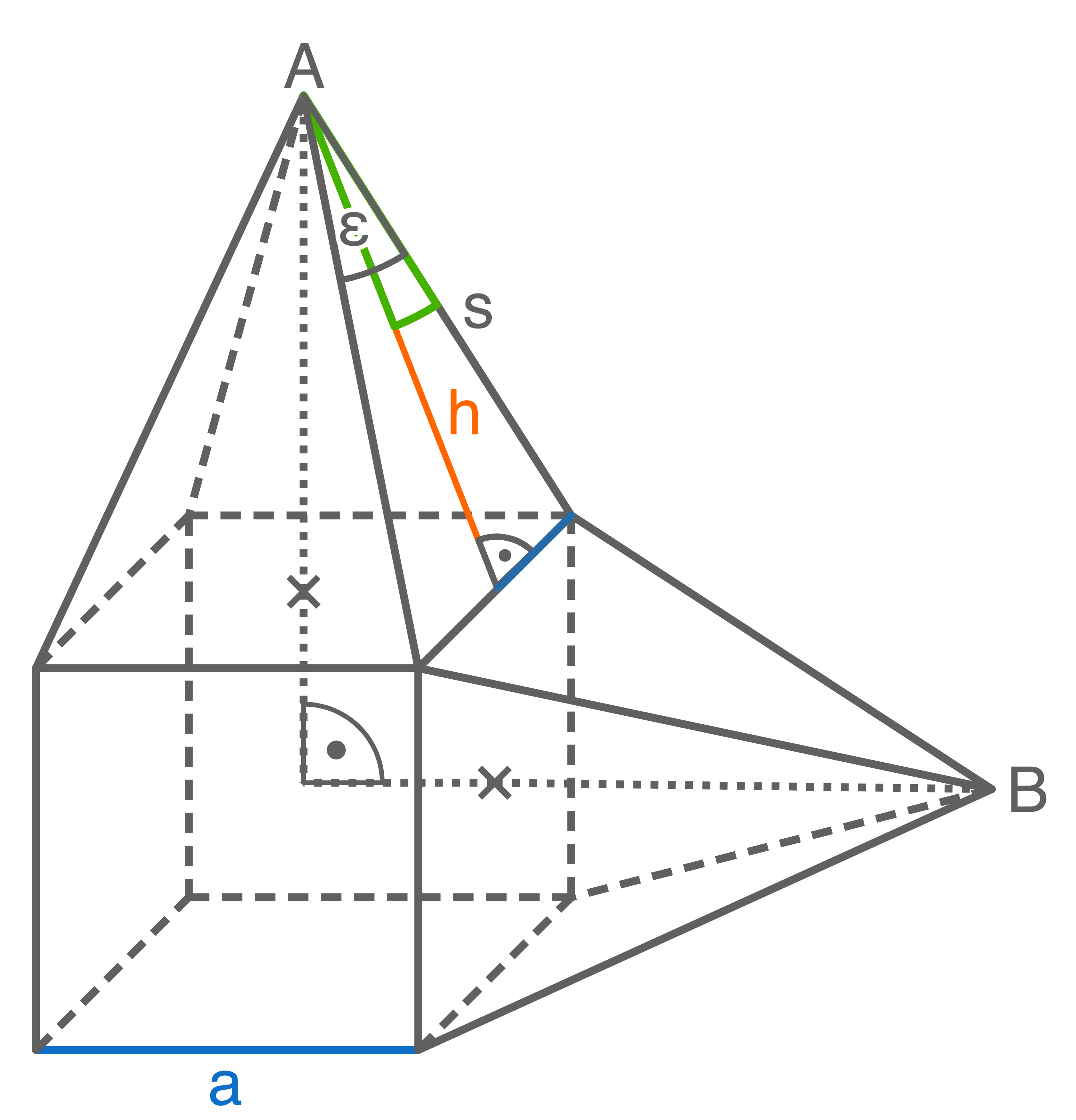
Lösung P4
Um wie viel Prozent ist der Verkauf von E-Bikes von 2013 bis 2017 angestiegen?Lösung P5
1. Schritt:Lösung P6
Wertetabelle, Graph und Funktionsgleichung zuordnen In der Wertetabelle ist das WertepaarDie Funktionsgleichung
- Verschobene Normalparabel
- Nach oben geöffnet
- Scheitelpunkt
Lösung P7
Mit welcher Wahrscheinlichkeit erhält sie zuerst einen roten, dann einen weißen Kaugummi?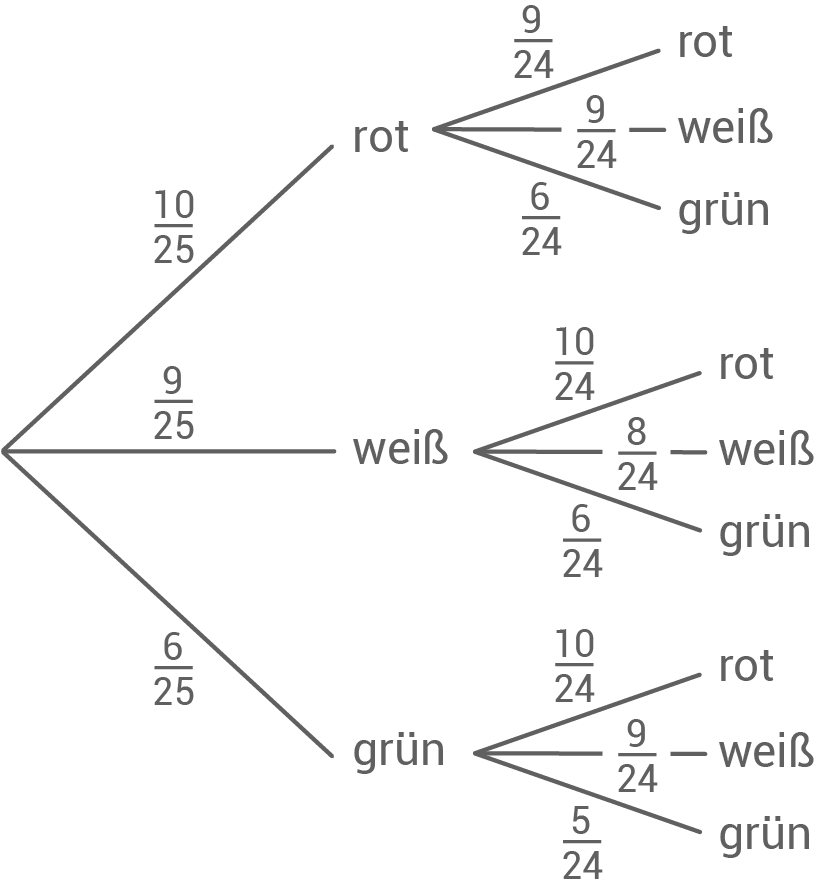
Lösung P8
Zu welcher Rangliste gehört der dargestellte Boxplot?
Betrachtung der oberen Quartile:
Boxplot für die kaufmännischen Berufe einzeichnen
1. Schritt: Kennwerte ermitteln
 Wie verändert sich der Boxplot?
1. Schritt: Rangliste um die vier Werte ergänzen
Wie verändert sich der Boxplot?
1. Schritt: Rangliste um die vier Werte ergänzen
2. Schritt: Kennwerte für die ergänzte Rangliste ermitteln
- Boxplot:
- Kaufmännische Berufe:
- Technische Berufe:

| Ausbildungsvergütung in kaufmännischen Berufen (in Euro) |
|---|
| 760 |
| 770 |
| 800 |
| 820 |
| 820 |
| 840 |
| 850 |
| 880 |
| 890 |
| 900 |
| 910 |
| 920 |
| 940 |
| 940 |
| 950 |
| 950 |
| 970 |