Pflichtteil A2
Aufgabe 1
Die Figur besteht aus den Dreiecken  und
und 
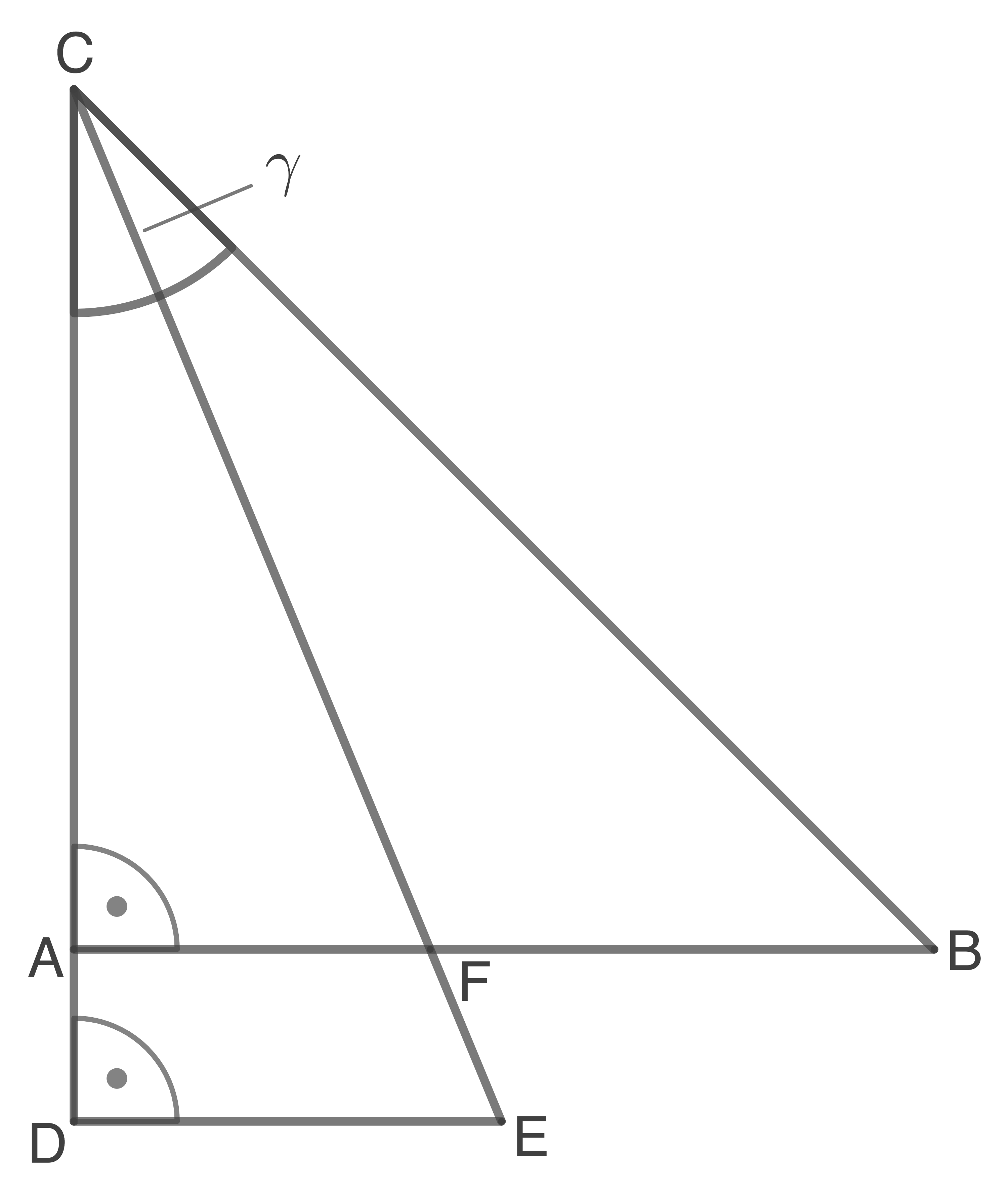 (Skizze nicht maßstäblich)
Davon sind gegeben:
(Skizze nicht maßstäblich)
Davon sind gegeben:



 ist die Winkelhalbierende von
ist die Winkelhalbierende von  Berechne die Streckenlänge
Berechne die Streckenlänge 
 (Skizze nicht maßstäblich)
(Skizze nicht maßstäblich)
(4 P)
Aufgabe 2
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel.
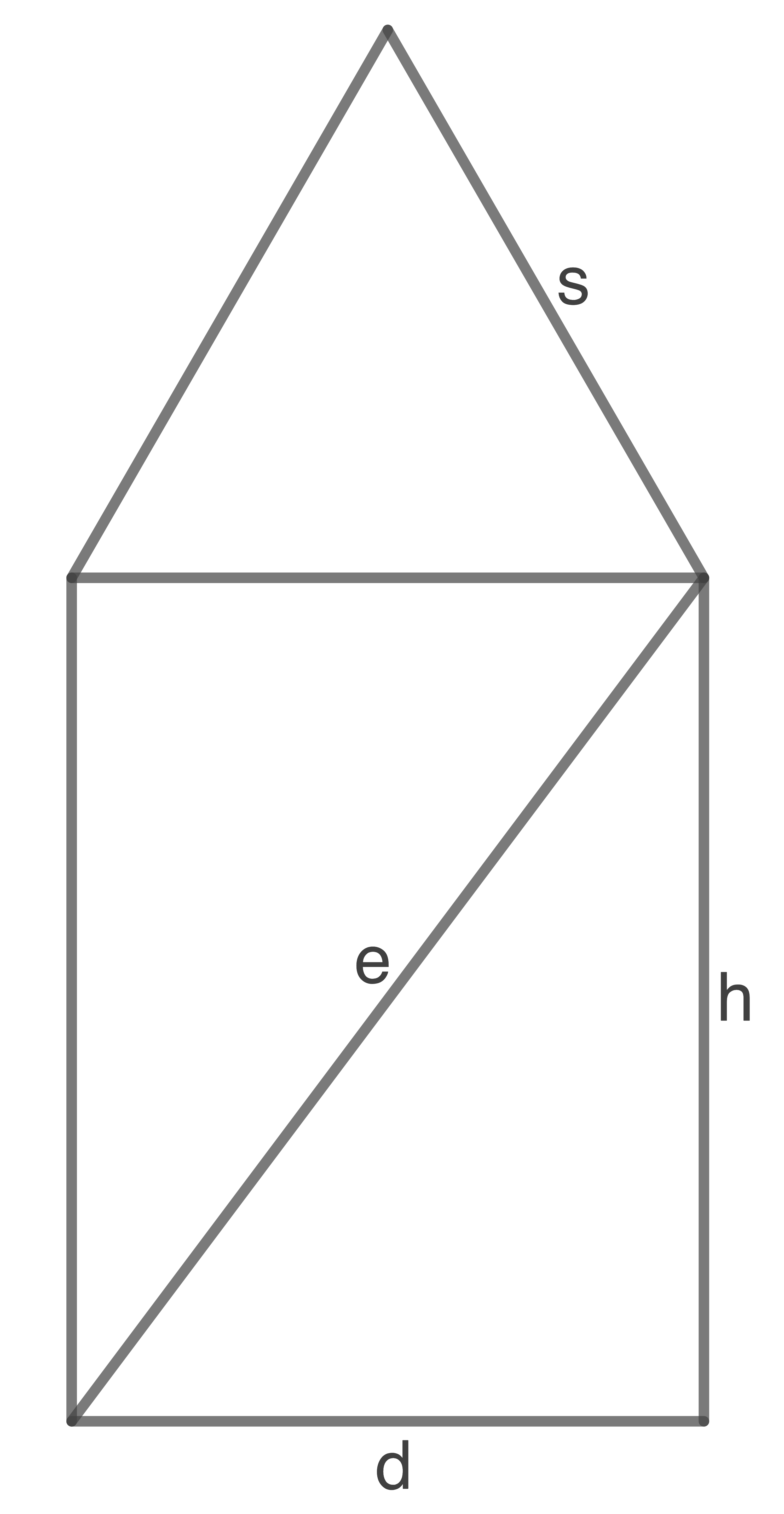 (Querschnitt des Körpers, Skizze nicht maßstäblich)
Es gilt:
(Querschnitt des Körpers, Skizze nicht maßstäblich)
Es gilt:
 (Grundfläche des Kegels)
(Grundfläche des Kegels)
 Der Durchmesser
Der Durchmesser  entspricht der Seitenkante
entspricht der Seitenkante  des Kegels.
Berechne die Oberfläche des zusammengesetzten Körpers
des Kegels.
Berechne die Oberfläche des zusammengesetzten Körpers
 (Querschnitt des Körpers, Skizze nicht maßstäblich)
(Querschnitt des Körpers, Skizze nicht maßstäblich)
(4 P)
Aufgabe 3
Eine Parabel  ist mit der Funktionsgleichung
ist mit der Funktionsgleichung  gegeben.
Bestimme den Scheitelpunkt und zeichne die Parabel in ein Koordinatensystem.
Die beiden Schnittpunkte der Parabel mit der
gegeben.
Bestimme den Scheitelpunkt und zeichne die Parabel in ein Koordinatensystem.
Die beiden Schnittpunkte der Parabel mit der  -Achse und der Scheitelpunkt bilden ein Dreieck.
Berechne den Umfang des Dreiecks.
-Achse und der Scheitelpunkt bilden ein Dreieck.
Berechne den Umfang des Dreiecks.
(3 P)
Aufgabe 4
Der Kauf eines Elektroautos wird durch den Bund mit einem Zuschuss von 10.000 € gefördert.
Emilias Familie hat sich für ein Auto eines großen Herstellers entschieden, das mit der Standardausstattung 39.990 € kostet.
Das Auto kann online bestellt werden. Bei einer Bestellung bis Ende des Monats erhält Emilias Familie 3 % Rabatt.
Emilias Familie hat sich für ein Auto eines großen Herstellers entschieden, das mit der Standardausstattung 39.990 € kostet.
Das Auto kann online bestellt werden. Bei einer Bestellung bis Ende des Monats erhält Emilias Familie 3 % Rabatt.

a)
Was kostet das Auto, wenn der Rabatt wahrgenommen wird?
b)
Ein anderer Online-Händler gibt einen Rabatt von 4 %. Der Kaufpreis beträgt nach Abzug des Rabatts und des Zuschusses vom Bund noch 29.871 €.
Berechne den ursprünglichen Verkaufspreis vor Rabatt und Zuschuss.
(3 P)
Aufgabe 5
Auf einem Jahrmarkt gibt es eine Lostrommel. In dieser befinden sich 4 Lose für die Hauptgewinne, 10 Lose für Trostpreise und 10 Nieten. Mia zieht ohne hinzuschauen zwei Lose.
a)
Mit welcher Wahrscheinlichkeit zieht sie genau zwei Hauptgewinne?
b)
Mit welcher Wahrscheinlichkeit erhält sie mindestens einen Hauptgewinn?
(3 P)
Aufgabe 6
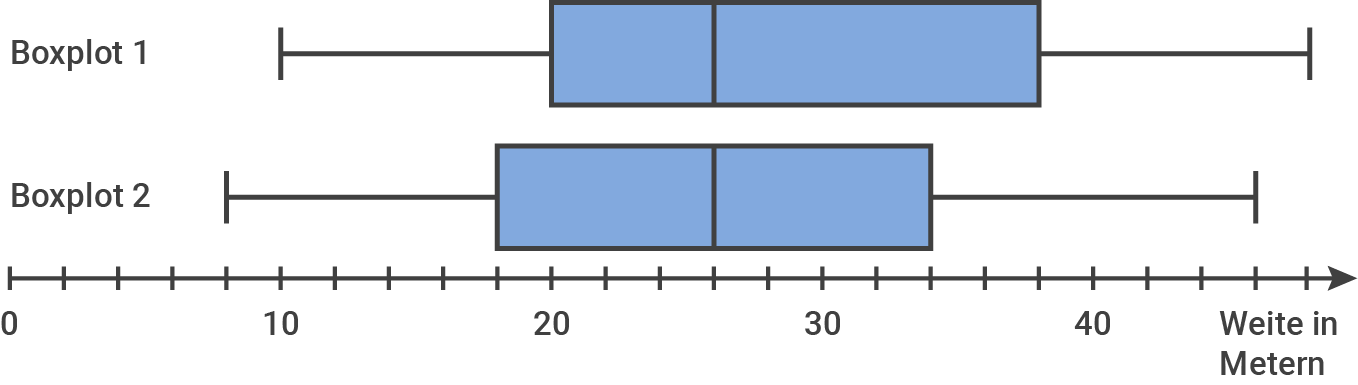
Die Schüler*innen der Klassen 10b und 10c werfen im Sportunterricht mit einem Ball. Die Wurfweiten werden in ganzen Metern erfasst. Die Verteilungen der Wurfweiten der 17 Schüler*innen der Klasse 10b und der 19 Schüler*innen der Klasse 10c sind in den folgenden Boxplots dargestellt.
| Rangplatz | Kl. 10b |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | 18 |
| 6 | 22 |
| 7 | 25 |
| 8 | 26 |
| 9 | 26 |
| 10 | 28 |
| 11 | 32 |
| 12 | 34 |
| 13 | 34 |
| 14 | |
| 15 | |
| 16 | |
| 17 |
| Rangplatz | Kl. 10c |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | 16 |
| 5 | 20 |
| 6 | 21 |
| 7 | 24 |
| 8 | 25 |
| 9 | 25 |
| 10 | 26 |
| 11 | 31 |
| 12 | 32 |
| 13 | 32 |
| 14 | 38 |
| 15 | 38 |
| 16 | |
| 17 | |
| 18 | |
| 19 |
a)
Ordne die Boxplots den Ranglisten der Klasse 10b und 10c zu. Begründe deine Entscheidung.
b)
Ergänze die Ranglisten mit möglichen Werten.
c)
Würde sich der Boxplot der Klasse 10c ändern, wenn Schüler*in Nr. 14 einen Meter weiter geworfen hätte?
(3 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
1. Schritt: Länge der StreckeLösung 2
1. Schritt: Mantelflächeninhalt des Kegels berechnen RadiusLösung 3
Scheitelpunkt mit der quadratischen Ergänzung bestimmen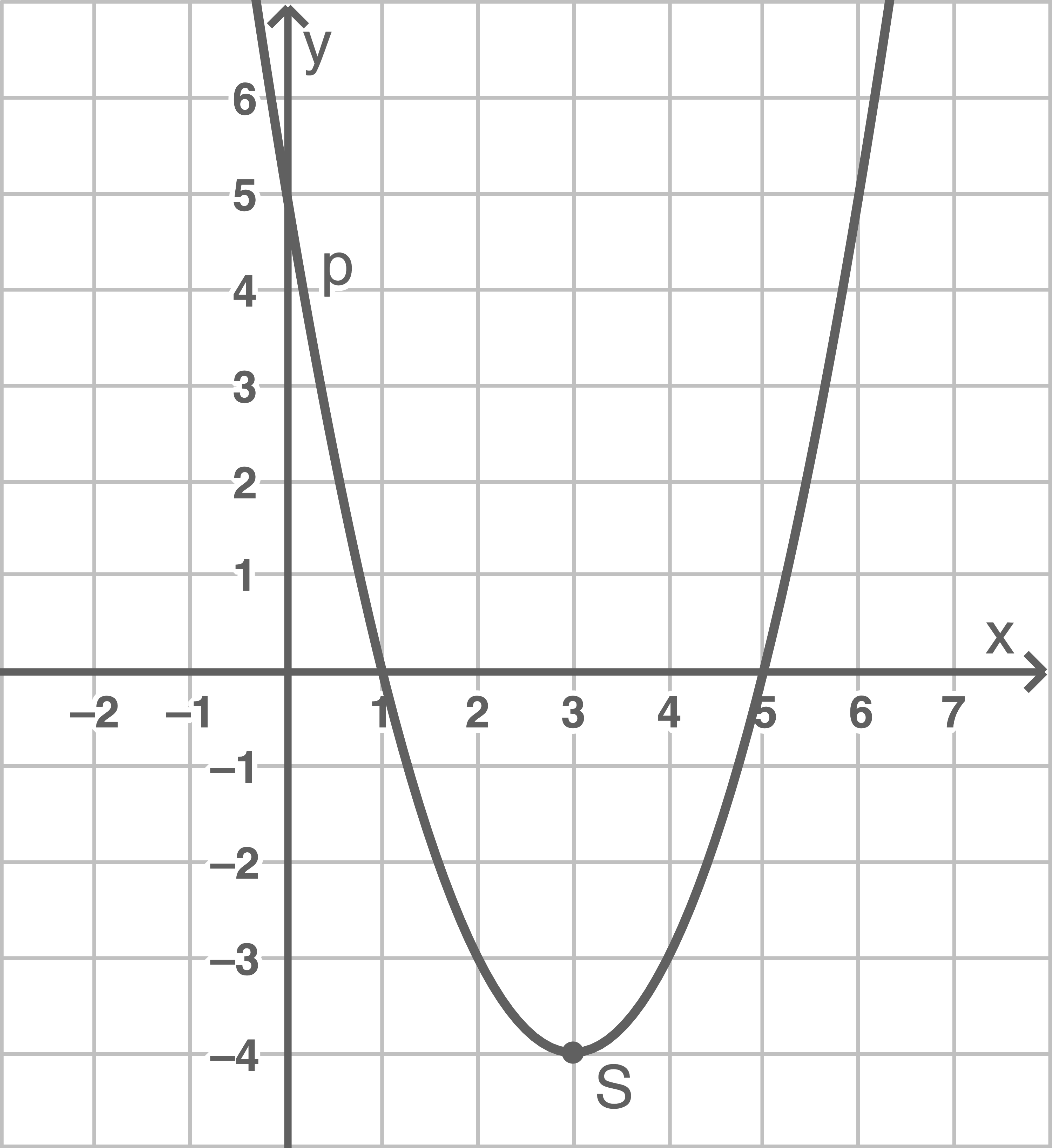
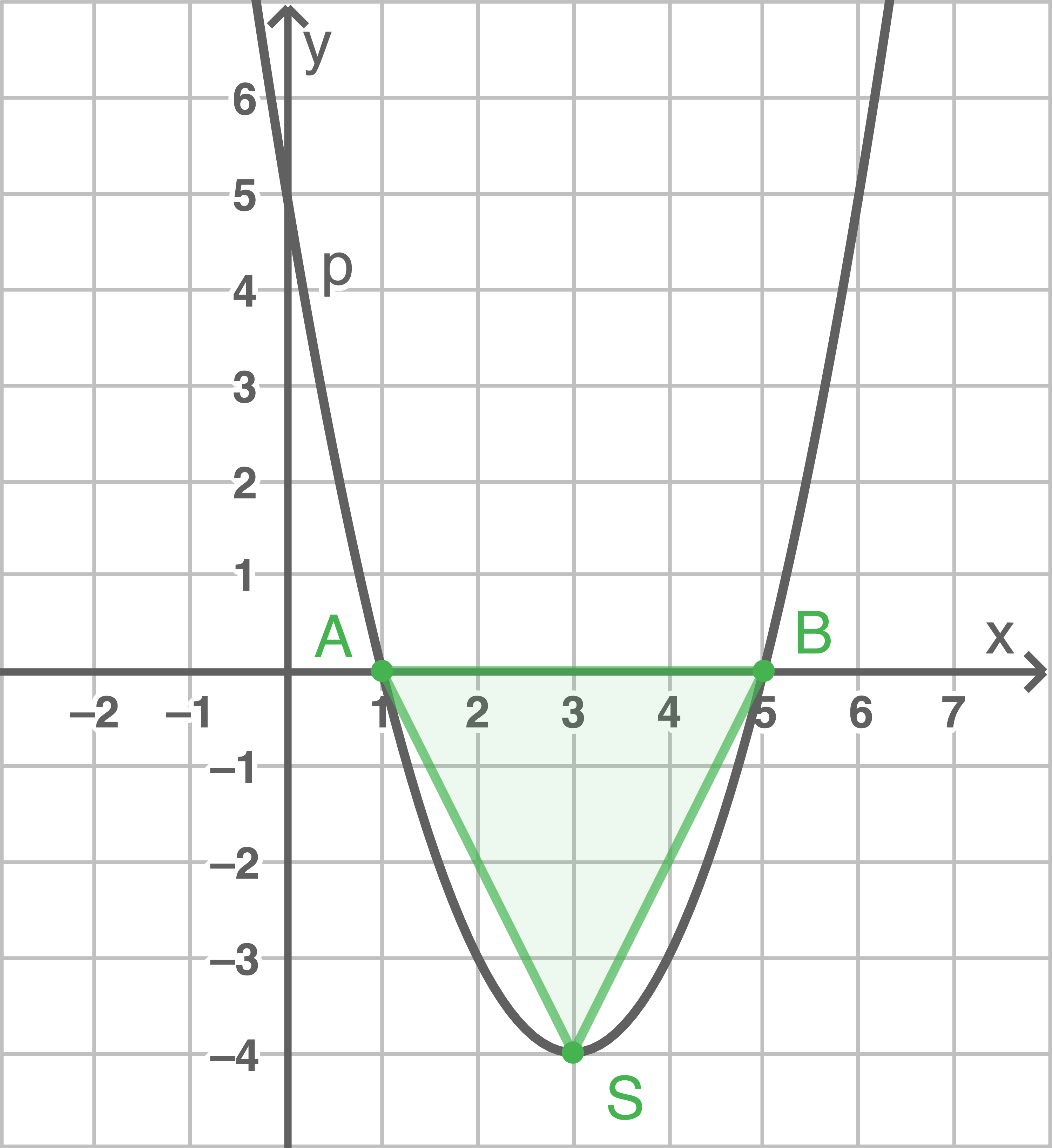
Lösung 4
a)
1. Schritt: Rabatt verrechnen
 2. Schritt: Zuschuss abziehen
2. Schritt: Zuschuss abziehen


b)
1. Schritt: Zuschuss addieren
 2. Schritt: Rabatt herausrechnen
2. Schritt: Rabatt herausrechnen




![\(\begin{array}{rcl}
96\,\%&\mathrel{\widehat{=}}&39\,871\,€\\[5pt]
1\,\%&\mathrel{\widehat{=}}&415,32\,€\\[5pt]
100\,\%&\mathrel{\widehat{=}}&41\,532\,€
\end{array}\)](https://mathjax.schullv.de/c86922c6fe9ad2e3f95d80980079141bdebd01dee851cbe6a15f3248e01a419b?color=5a5a5a)



 Der ursprüngliche Verkaufspreis liegt bei
Der ursprüngliche Verkaufspreis liegt bei 
Lösung 5
a)
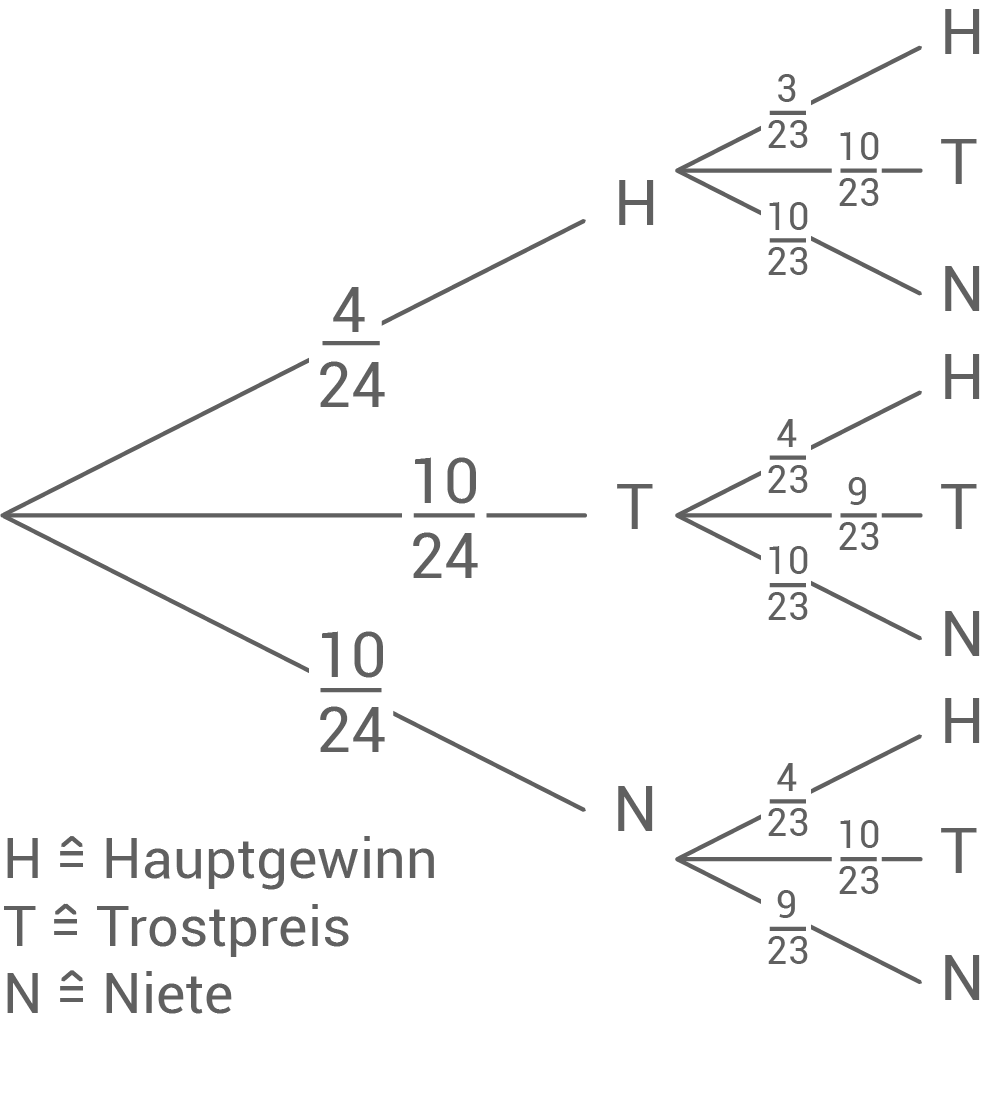
b)
Das Gegenereignis von „mindestens ein Hauptgewinn“ ist „kein Hauptgewinn“:
![\(\begin{array}[t]{rll}
P(\text{mind. 1x H})&=& 1-P(\text{kein H}) \\[5pt]
&=& 1-\dfrac{20}{24}\cdot \dfrac{19}{23}&\quad \scriptsize \\[5pt]
&=& 0,3116\\[5pt]
&=& \underline{\underline{ 31,16\,\%}}
\end{array}\)](https://mathjax.schullv.de/a09bf9ef4a7a17e5df6e4dcd5cddf2ba1cf150667e0e34eab371389028615ba7?color=5a5a5a)
Lösung 6
a)
Boxplot 1: Klasse 10c
Boxplot 2: Klasse 10b Begründung über Betrachtung der unteren Quartile
Boxplot 2: Klasse 10b Begründung über Betrachtung der unteren Quartile
- Klasse 10b:
Zur Rangliste der 10b passt also Boxlot 2. - Klasse 10c:
Zur Rangliste der 10c passt also Boxlot 1.
b)
Kennwerte für die Rangliste der Klasse 10b ermitteln
Kennwerte für die Rangliste der Klasse 10c ermitteln
(muss noch in die Rangliste eingetragen werden)
(bereits in der Rangliste eingetragen)
(bereits in der Rangliste eingetragen)
(bereits in der Rangliste eingetragen)
(muss noch in die Rangliste eingetragen werden)
- Die Werte
sind belieblig wählbar.
| Rangplatz | Kl. 10b |
|---|---|
| 1 | 8 |
| 2 | 10 |
| 3 | 11 |
| 4 | 16 |
| 5 | 18 |
| 6 | 22 |
| 7 | 25 |
| 8 | 26 |
| 9 | 26 |
| 10 | 28 |
| 11 | 32 |
| 12 | 34 |
| 13 | 34 |
| 14 | 40 |
| 15 | 40 |
| 16 | 44 |
| 17 | 46 |
(muss noch in die Rangliste eingetragen werden)
(bereits in der Rangliste eingetragen)
(bereits in der Rangliste eingetragen)
(bereits in der Rangliste eingetragen)
(muss noch in die Rangliste eingetragen werden)
- Die Werte
sind belieblig wählbar.
| Rangplatz | Kl. 10c |
|---|---|
| 1 | 10 |
| 2 | 11 |
| 3 | 14 |
| 4 | 16 |
| 5 | 20 |
| 6 | 21 |
| 7 | 24 |
| 8 | 25 |
| 9 | 25 |
| 10 | 26 |
| 11 | 31 |
| 12 | 32 |
| 13 | 32 |
| 14 | 38 |
| 15 | 38 |
| 16 | 39 |
| 17 | 42 |
| 18 | 42 |
| 19 | 48 |
c)
Ja, denn dann tauschen Schüler*in Nr.14 und Schüler*in Nr.15 die Plätze. Dadurch ändert sich der Werte  und damit das obere Quartil.
und damit das obere Quartil.