Pflichtbereich
Aufgabe P1
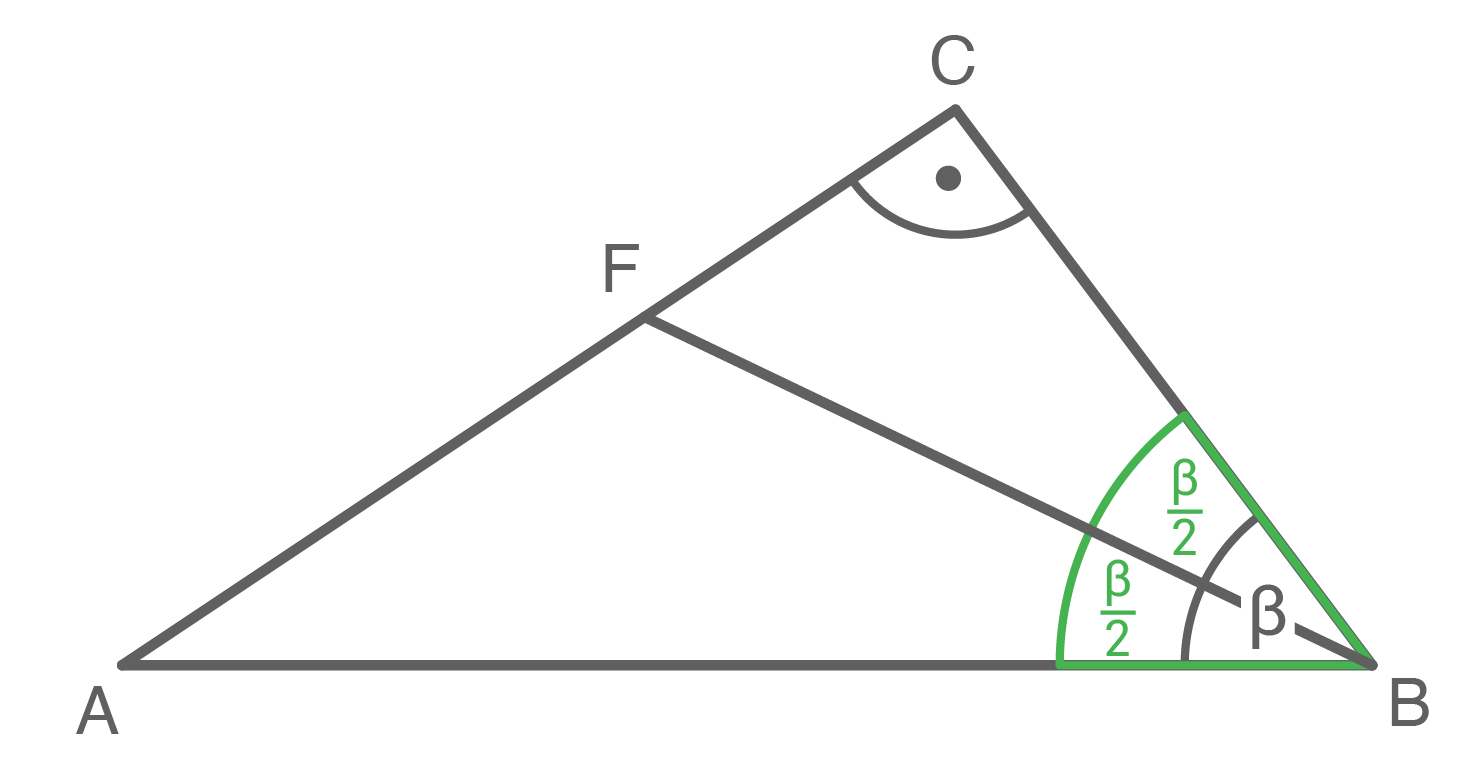
Gegeben ist das rechtwinklige Dreieck  .
.
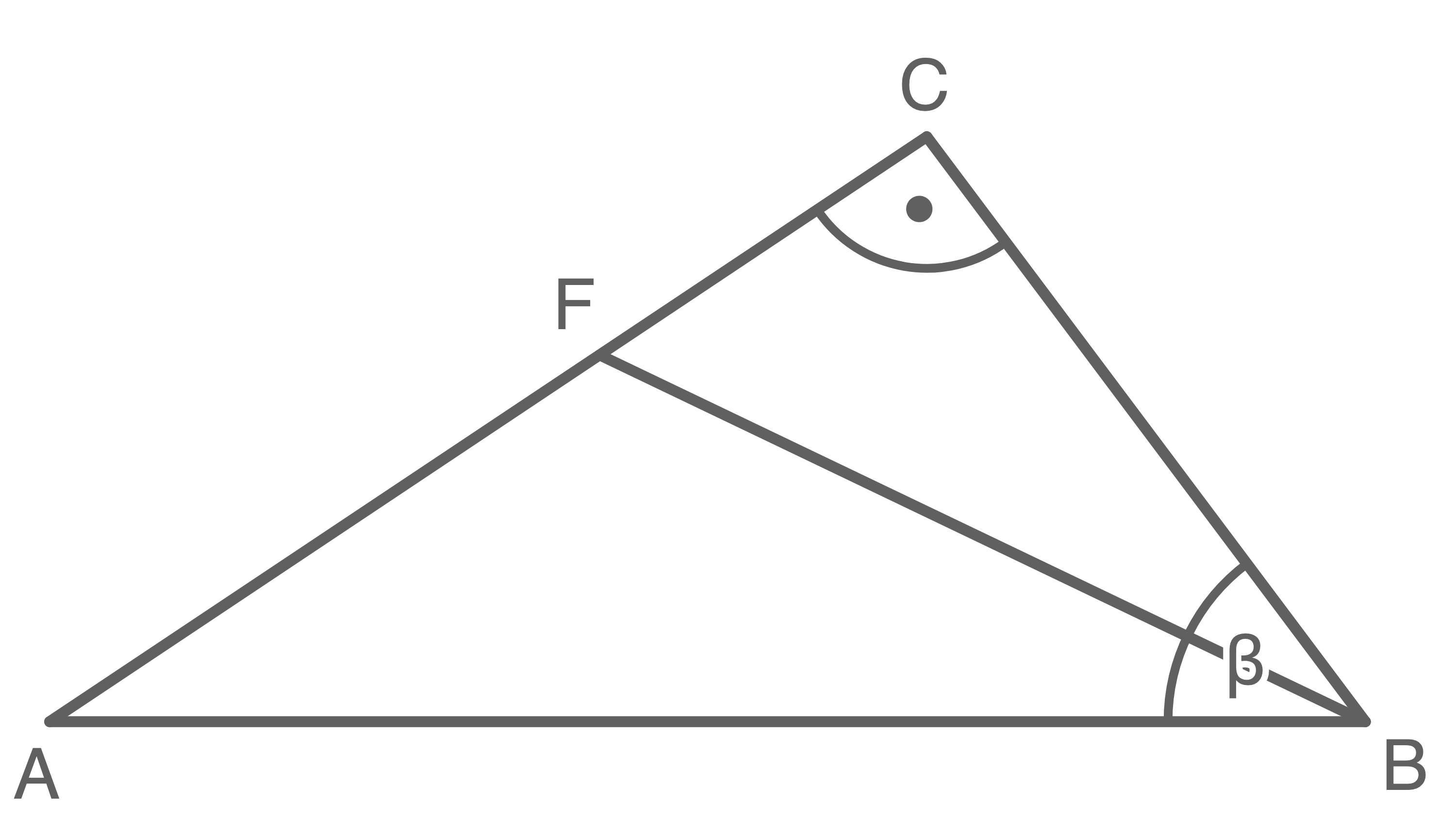 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BC}&=&5,8 \text{ cm} \\[5pt]
\overline{BF}&=&6,6 \text{ cm}
\end{array}\)](https://www.schullv.de/resources/formulas/181e185025f6306743357400f5c9ad44494d31bfd247bc58baadfd6e57a2051e_light.svg)
 halbiert den Winkel
halbiert den Winkel  .
Berechne den Umfang des Dreiecks
.
Berechne den Umfang des Dreiecks  .
.

4 P
Aufgabe P2
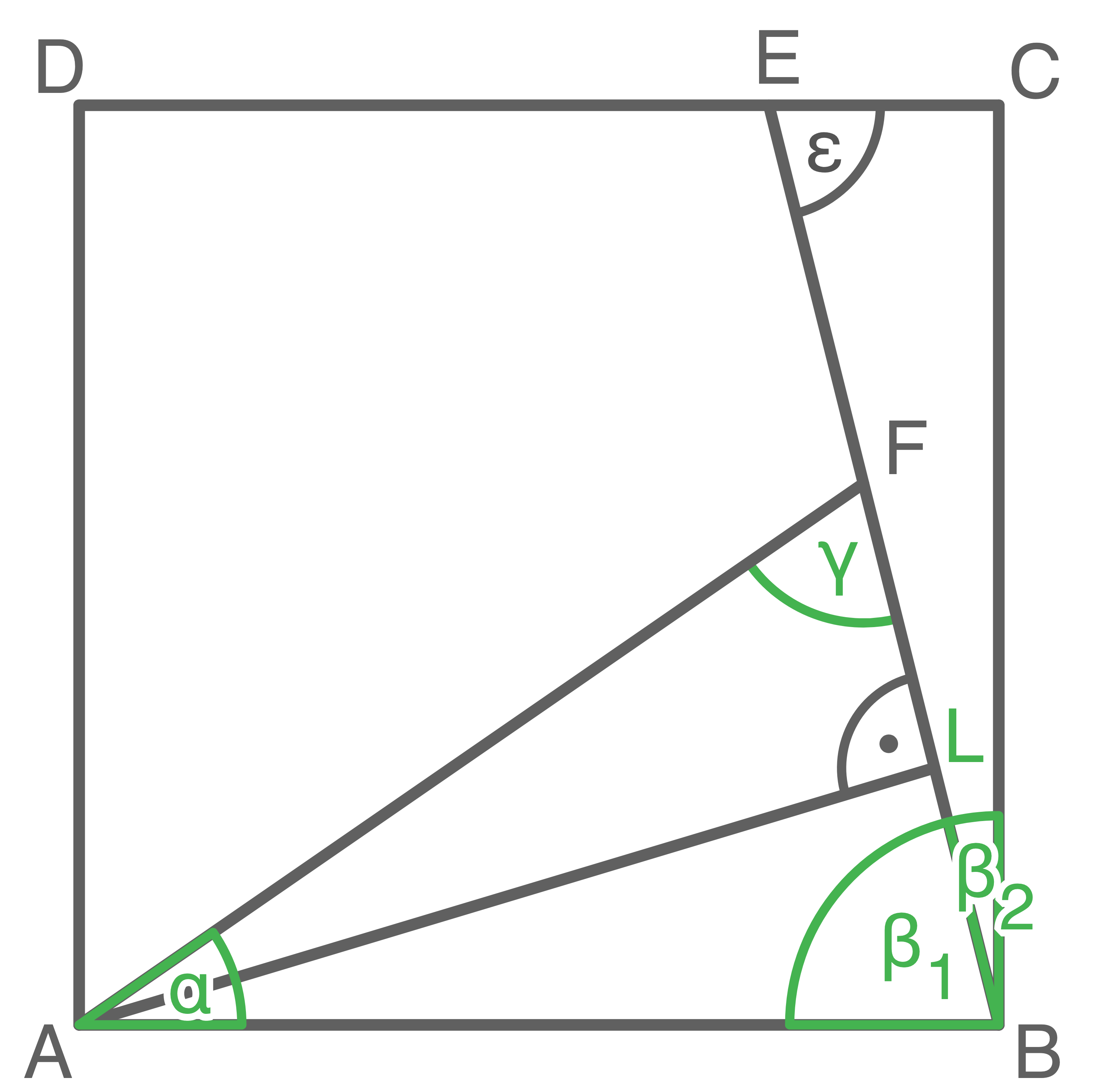
Im Quadrat  liegen das rechtwinklige Dreieck
liegen das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck  .
.
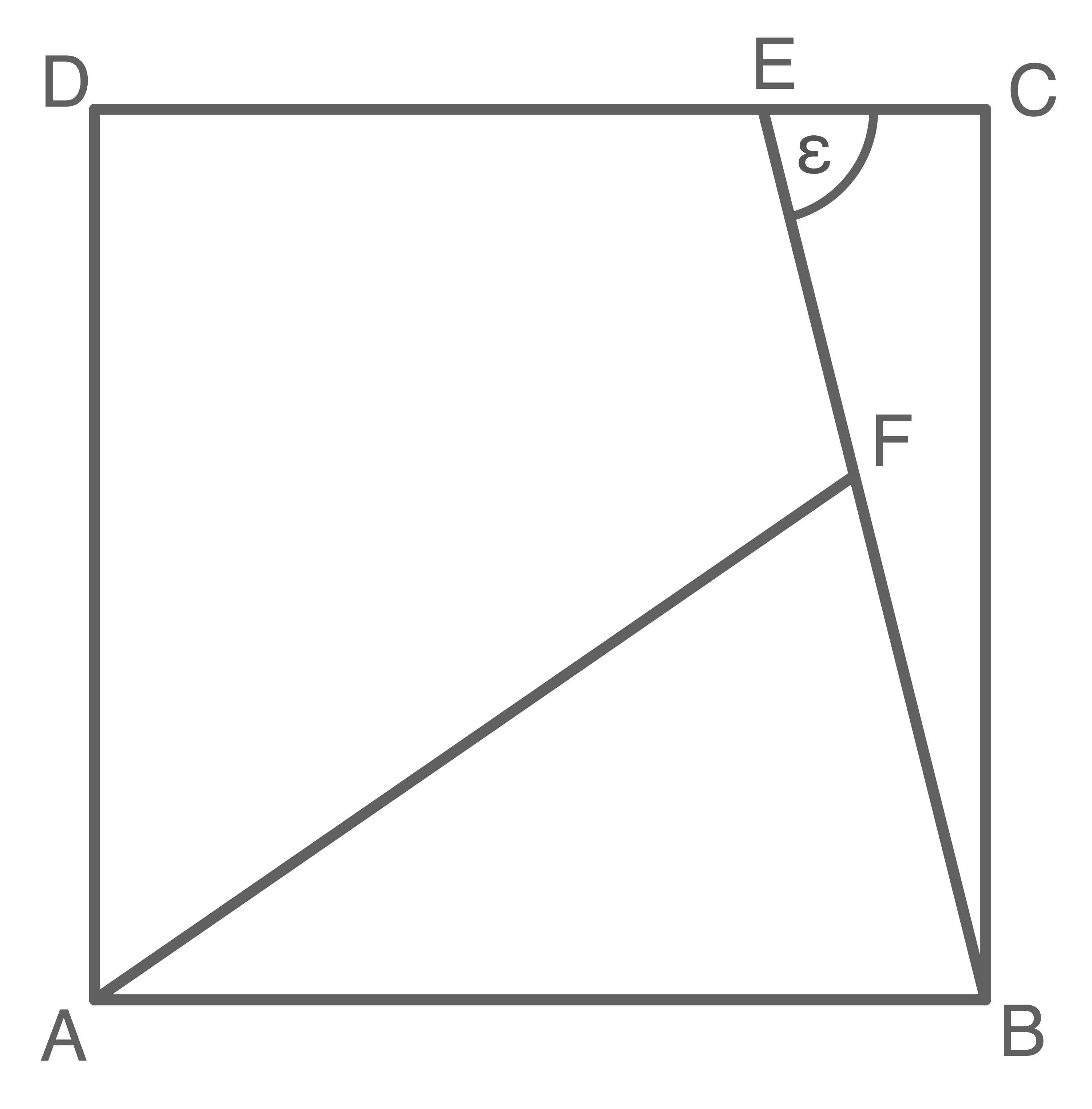 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BC}&=&11,8 \text{ cm} \\[5pt]
\epsilon&=&72,0^{\circ} \\[5pt]
\overline{AB}&=&\overline{AF}
\end{array}\)](https://www.schullv.de/resources/formulas/4fee4a09ce7bf03f388ad365b61442726761f45896f07460de56b68168b9c091_light.svg) Berechne die Länge von
Berechne die Länge von  .
.

4 P
Aufgabe P3
Ein Körper setzt sich aus einem halben Zylinder und einer quadratischen Pyramide zusammen.
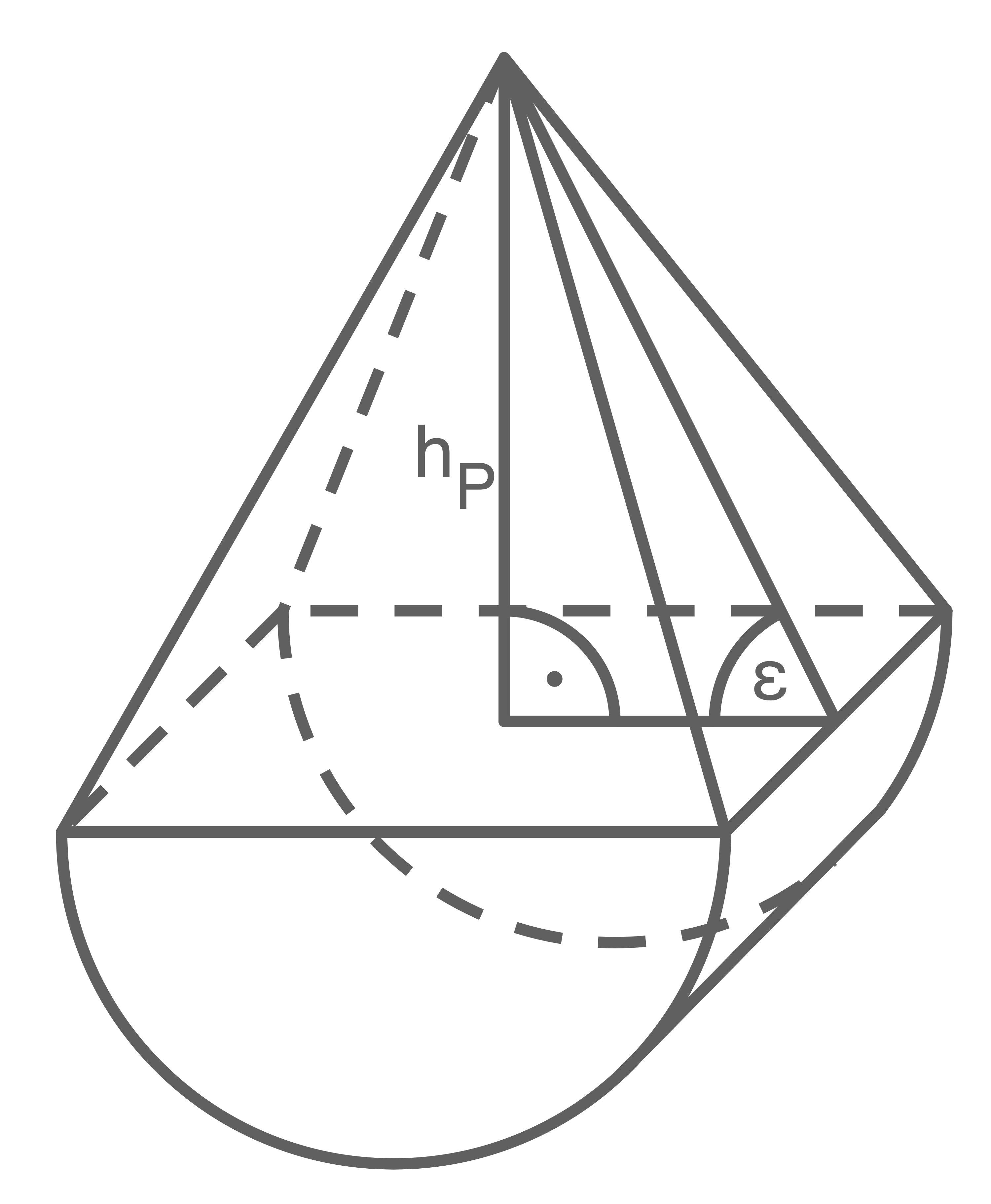 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
h_P&=&16,0 \text{ cm} \\[5pt]
\epsilon&=&58,0 ^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/c5139acfebaf7f889cb8f753abf7409b75d6cbff8cd8a8d6fc16856a7dda67d4_light.svg) Berechne die Oberfläche des zusammengesetzten Körpers.
Berechne die Oberfläche des zusammengesetzten Körpers.

4,5 P
Aufgabe P4
Max und Nele spielen ein Würfelspiel.
Zwei Würfel werden gleichzeitig geworfen.
Die beiden Augenzahlen werden addiert (Augensumme).
Gewonnen hat der Spieler mit der größeren Augensumme. Überprüfe die Aussage:
„Die Wahrscheinlichkeit für Augensumme 6 ist größer als die Wahrscheinlichkeit für Augensumme 9.“
Begründe deine Antwort durch eine Rechnung oder Argumentation. Max hat eine 5 und eine 3 geworfen.
Wie groß ist die Wahrscheinlichkeit, dass Nele mit dem nächsten Wurf das Spiel gewinnt?
Zwei Würfel werden gleichzeitig geworfen.
Die beiden Augenzahlen werden addiert (Augensumme).
Gewonnen hat der Spieler mit der größeren Augensumme. Überprüfe die Aussage:
„Die Wahrscheinlichkeit für Augensumme 6 ist größer als die Wahrscheinlichkeit für Augensumme 9.“
Begründe deine Antwort durch eine Rechnung oder Argumentation. Max hat eine 5 und eine 3 geworfen.
Wie groß ist die Wahrscheinlichkeit, dass Nele mit dem nächsten Wurf das Spiel gewinnt?
3,5 P
Aufgabe P5
Das Schaubild zeigt den Ausschnitt einer verschobenen Normalparapel  .
.
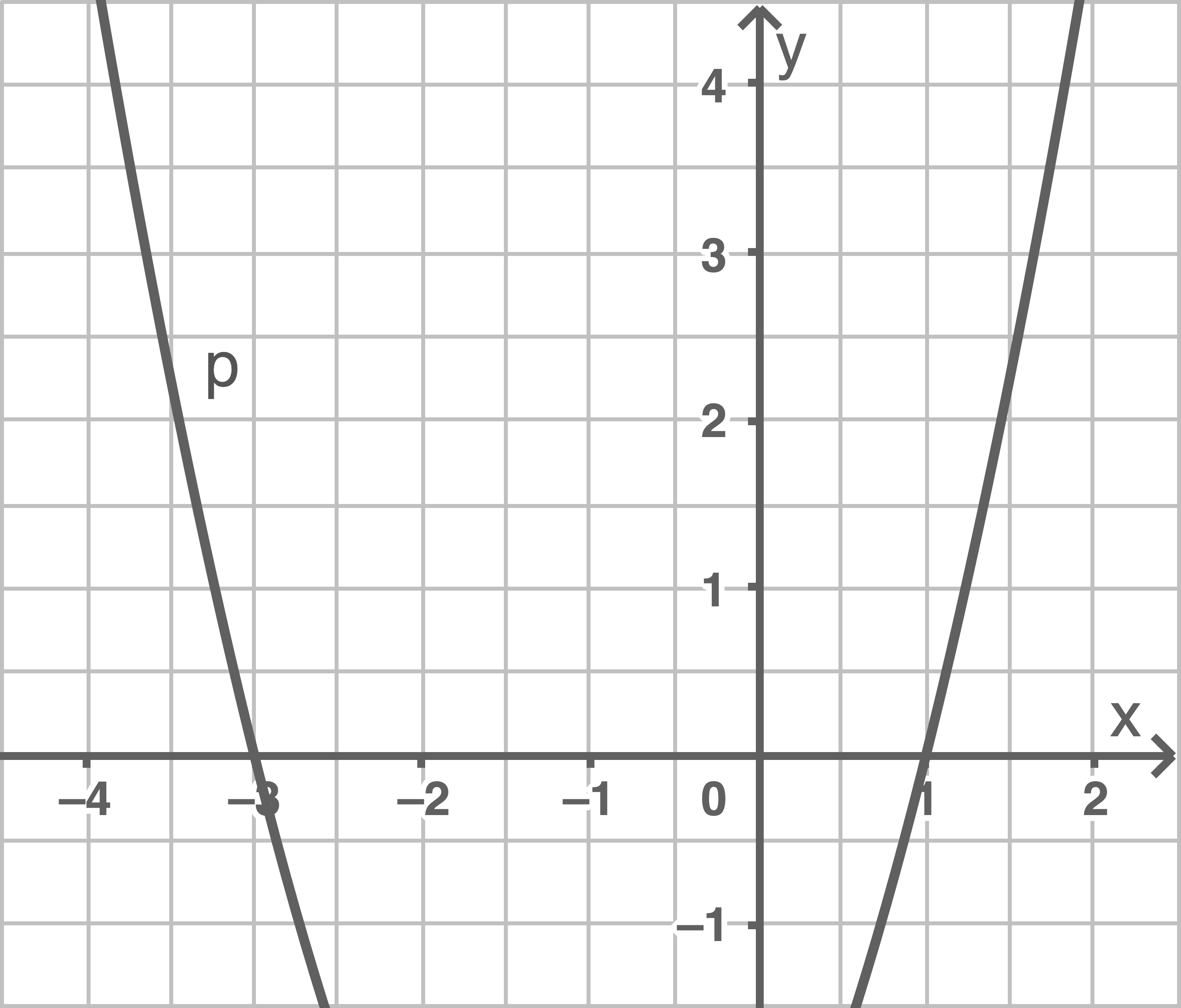 Die Gerade
Die Gerade  mit der Gleichung
mit der Gleichung  geht durch den Scheitelpunkt
geht durch den Scheitelpunkt  der Parabel
der Parabel  .
Berechne die Koordinaten des zweiten Schnittpunktes
.
Berechne die Koordinaten des zweiten Schnittpunktes  von
von  und
und  .
.

3,5 P
Aufgabe P6
Löse die Gleichung:

3,5 P
Aufgabe P7
Bei dem Reiseveranstalter Holiday wurden im Jahr 2015 insgesamt 54 000 Reisen gebucht.
Das Balkendiagramm zeigt die Verteilung der Reisen.
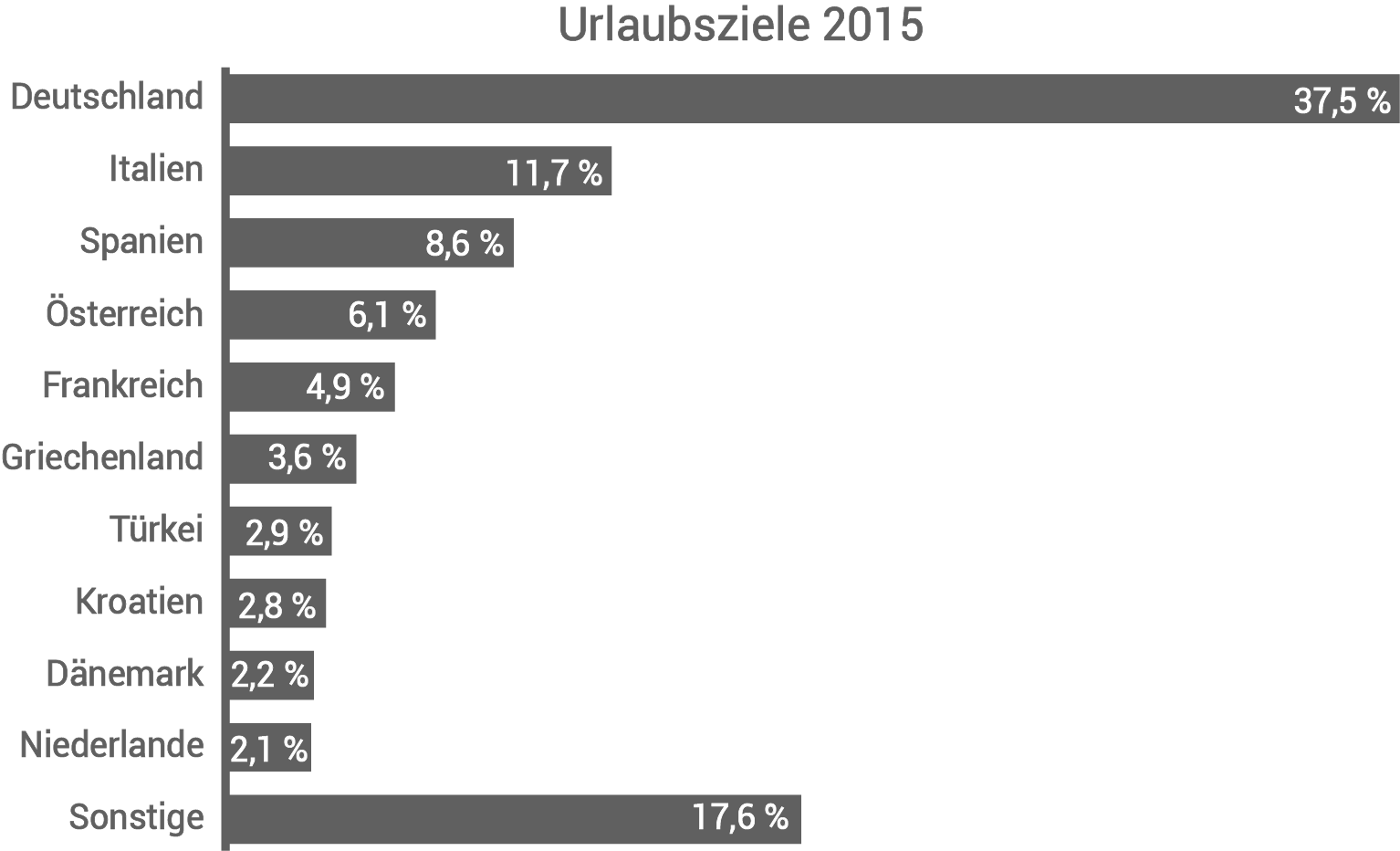 Im Kreisdiagramm sind die Reisen innerhalb Deutschlands dargestellt.
Im Kreisdiagramm sind die Reisen innerhalb Deutschlands dargestellt.
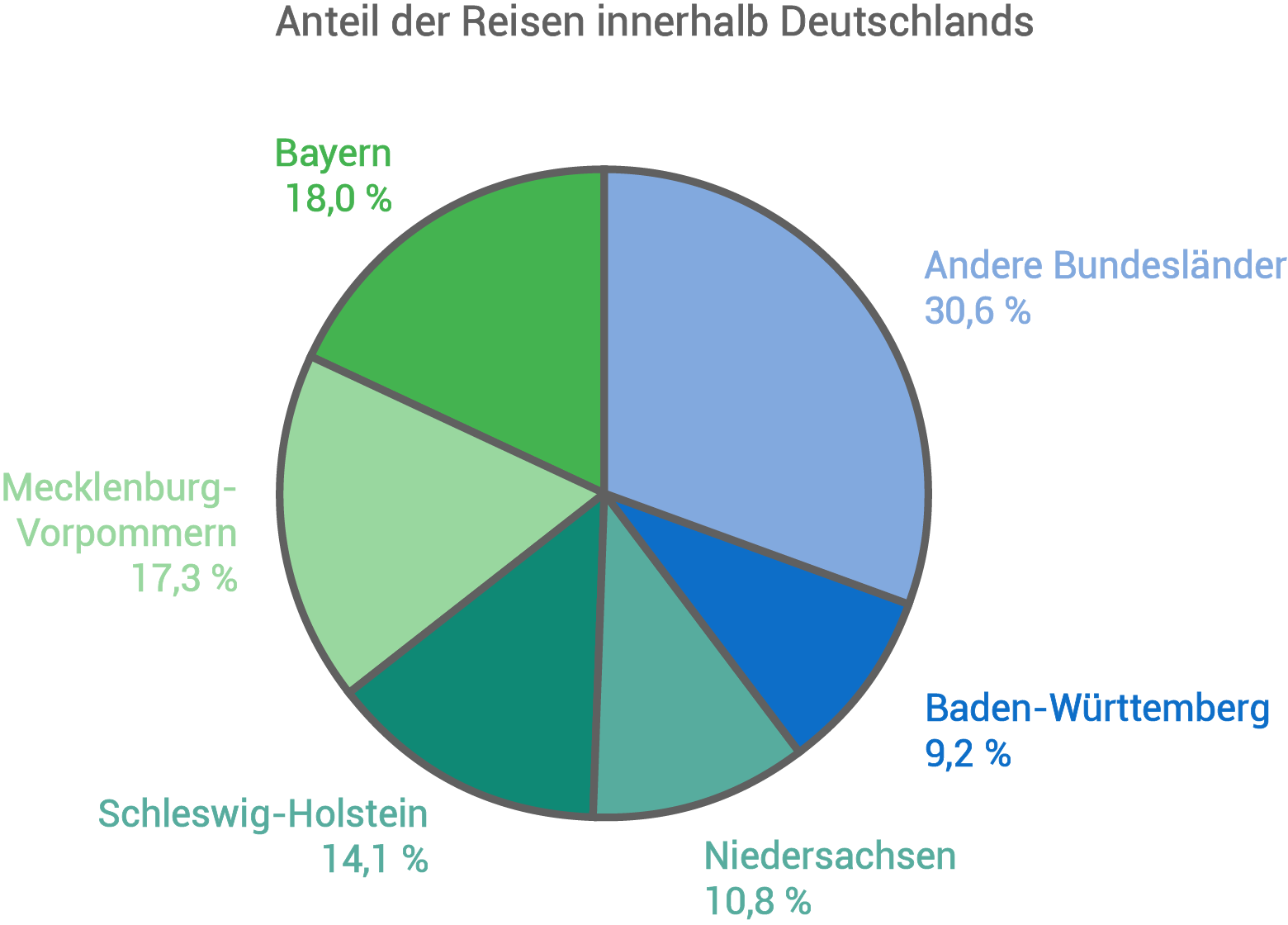 Wie viele Reisen nach Österreich wurden gebucht?
Innerhalb Deutschlands ist Bayern das beliebteste Urlaubsziel.
Wie viele Reisen nach Österreich wurden gebucht?
Innerhalb Deutschlands ist Bayern das beliebteste Urlaubsziel.
Wie viele Reisen gingen nach Bayern? Es wurden 704 Reisen in die USA gebucht.
Wie hoch ist der prozentuale Anteil der Reisen in die USA an den „sonstigen“ Urlaubszielen?
Das Balkendiagramm zeigt die Verteilung der Reisen.


Wie viele Reisen gingen nach Bayern? Es wurden 704 Reisen in die USA gebucht.
Wie hoch ist der prozentuale Anteil der Reisen in die USA an den „sonstigen“ Urlaubszielen?
3,5 P
Aufgabe P8
Die Klasse 10a der Mörike-Realschule hat eine Klassenarbeit geschrieben.
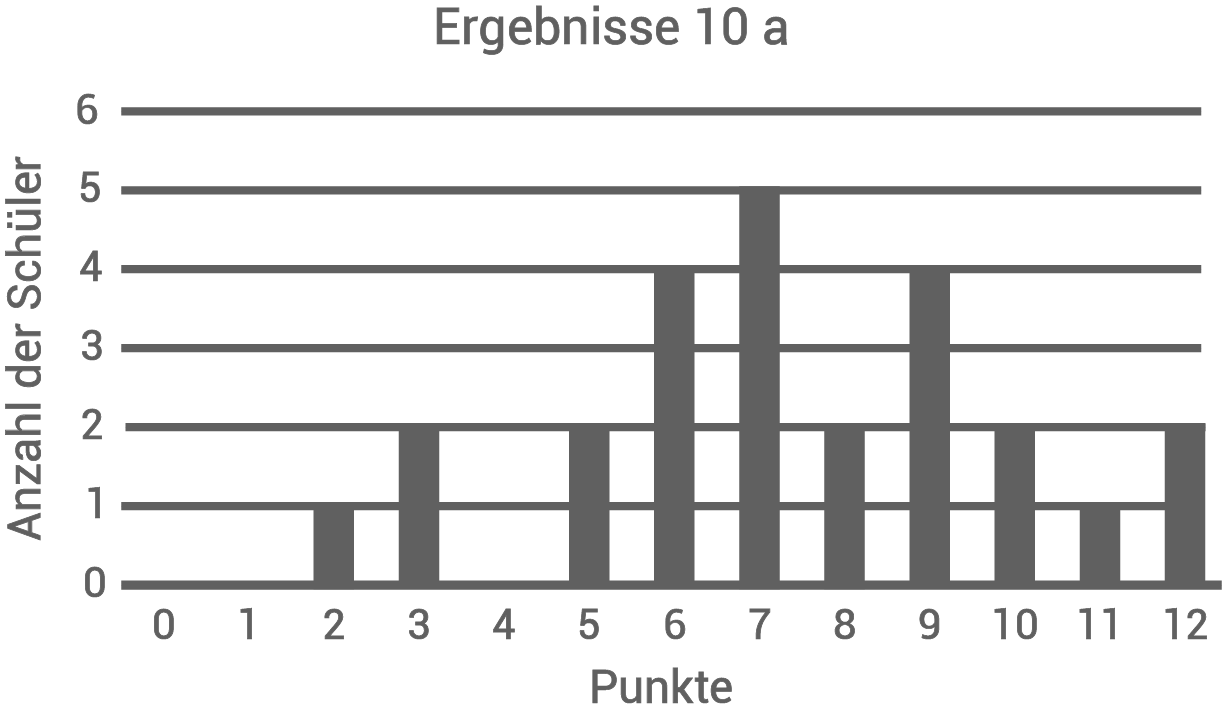
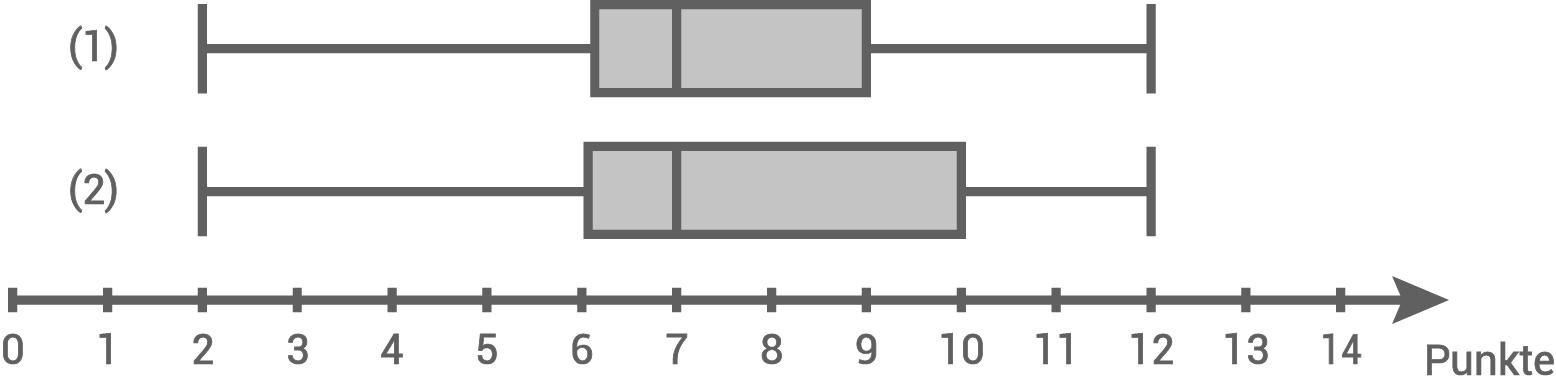 Welcher der beiden folgenden Boxplots zeigt die Verteilung der Ergebnisse der Klasse 10a?
Begründe deine Entscheidung mit Hilfe geeigneter Kennwerte.
Die Klasse 10b mit 29 Schülerinnen und Schülern hat die gleiche Klassenarbeit geschrieben.
Welcher der beiden folgenden Boxplots zeigt die Verteilung der Ergebnisse der Klasse 10a?
Begründe deine Entscheidung mit Hilfe geeigneter Kennwerte.
Die Klasse 10b mit 29 Schülerinnen und Schülern hat die gleiche Klassenarbeit geschrieben.
Das andere Boxplot zeigt die Verteilung der Ergebnisse dieser Klasse.
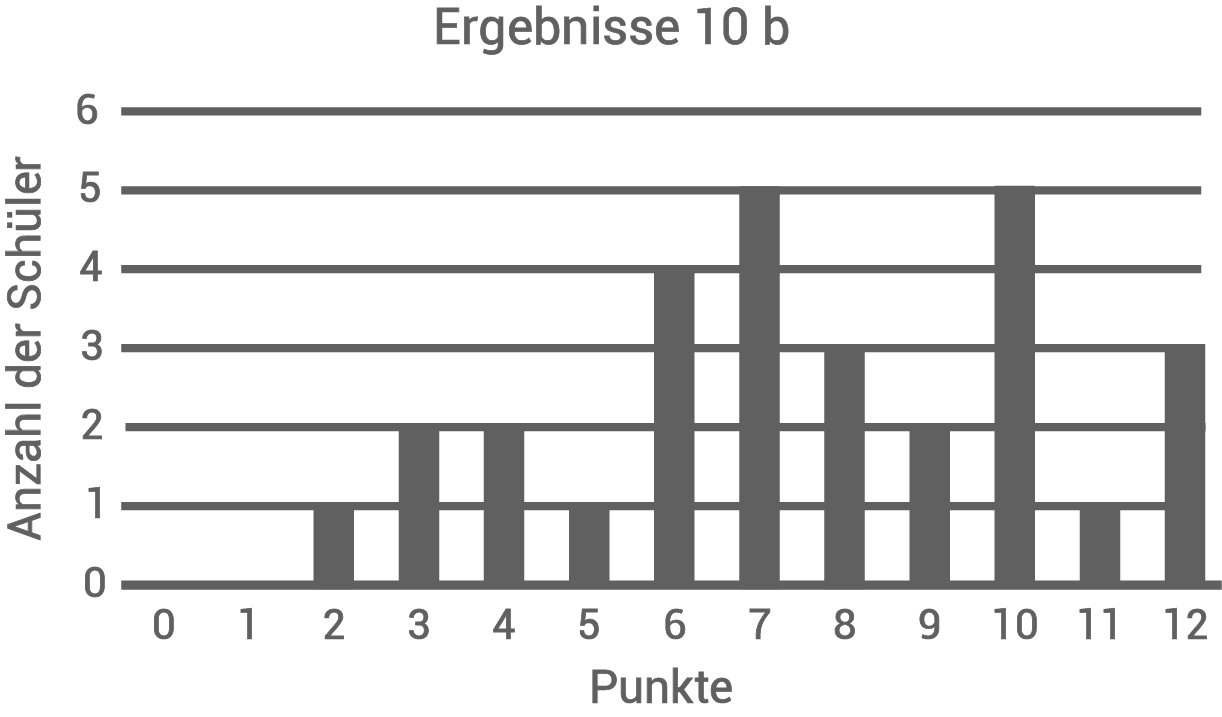
Für die Punktzahlen 9 und 10 fehlen im Diagramm die Säulen.
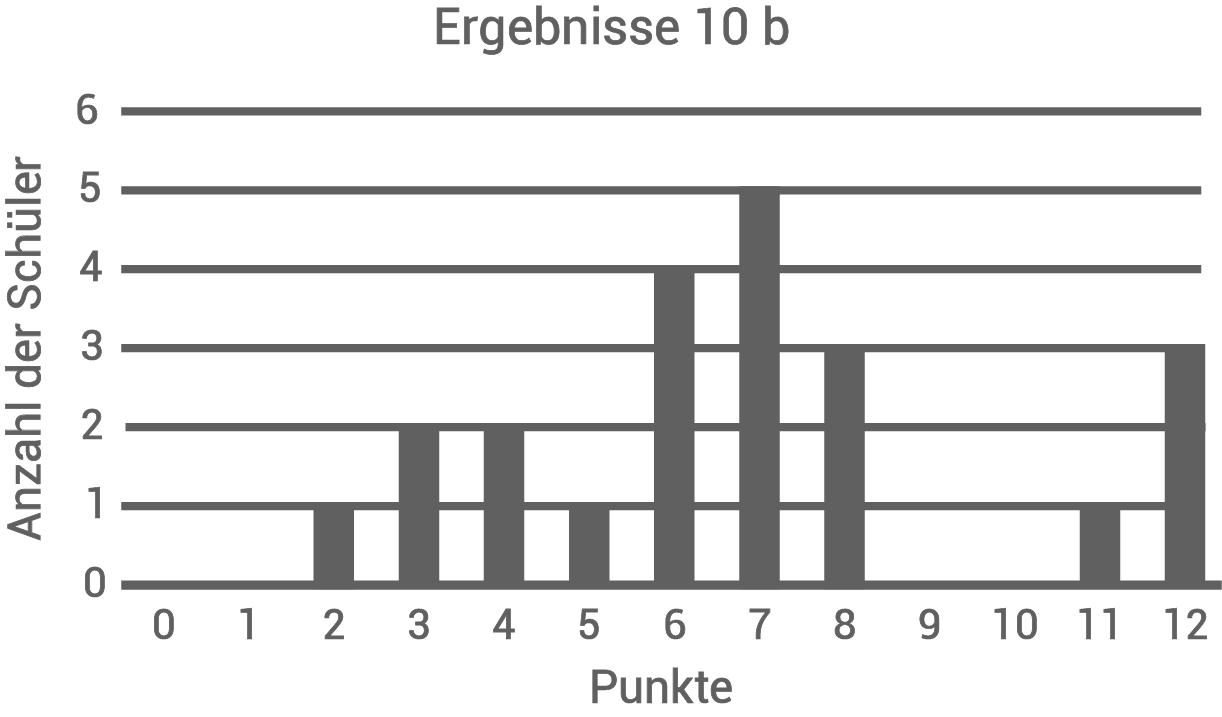 Zeichne eine mögliche Lösung in das nebenstehende Diagramm ein.
Zeichne eine mögliche Lösung in das nebenstehende Diagramm ein.


Das andere Boxplot zeigt die Verteilung der Ergebnisse dieser Klasse.
Für die Punktzahlen 9 und 10 fehlen im Diagramm die Säulen.

3,5 P
Lösung P1
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\beta}{2}\right)&=& \dfrac{\overline{BC}}{\overline{BF}}\\[5pt]
\cos\left(\dfrac{\beta}{2}\right)&=& \dfrac{5,8\,\text{cm}}{6,6 \,\text{cm}} \quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\dfrac{\beta}{2}&=& 28,50 ^{\circ} \\[5pt]
\beta&=& \underline{57 ^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/40e4b220df9404a2d196709f9a113f0feb82b30d9bd0a697ec5ecabb76922e14_light.svg)
Lösung P2
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\varepsilon)&=&\dfrac{\overline{BC}}{\overline{BE}} \quad \scriptsize \mid\; \cdot \overline{BE} \,\,\, \mid\;:\sin(\varepsilon) \\[5pt]
\overline{BE}&=&\dfrac{\overline{BC}}{\sin(\varepsilon)} \\[5pt]
\overline{BE}&=& \dfrac{11,8 \text{ cm}}{\sin(72^{\circ})} \\[5pt]
\overline{BE}&=& \underline{12,41\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/e4b10ac7abb040d41ac491b077573696ac8741d5b96b5719ccf41103d741d591_light.svg)
Lösung P3
1. Schritt: Mantelfläche der Pyramide berechnen
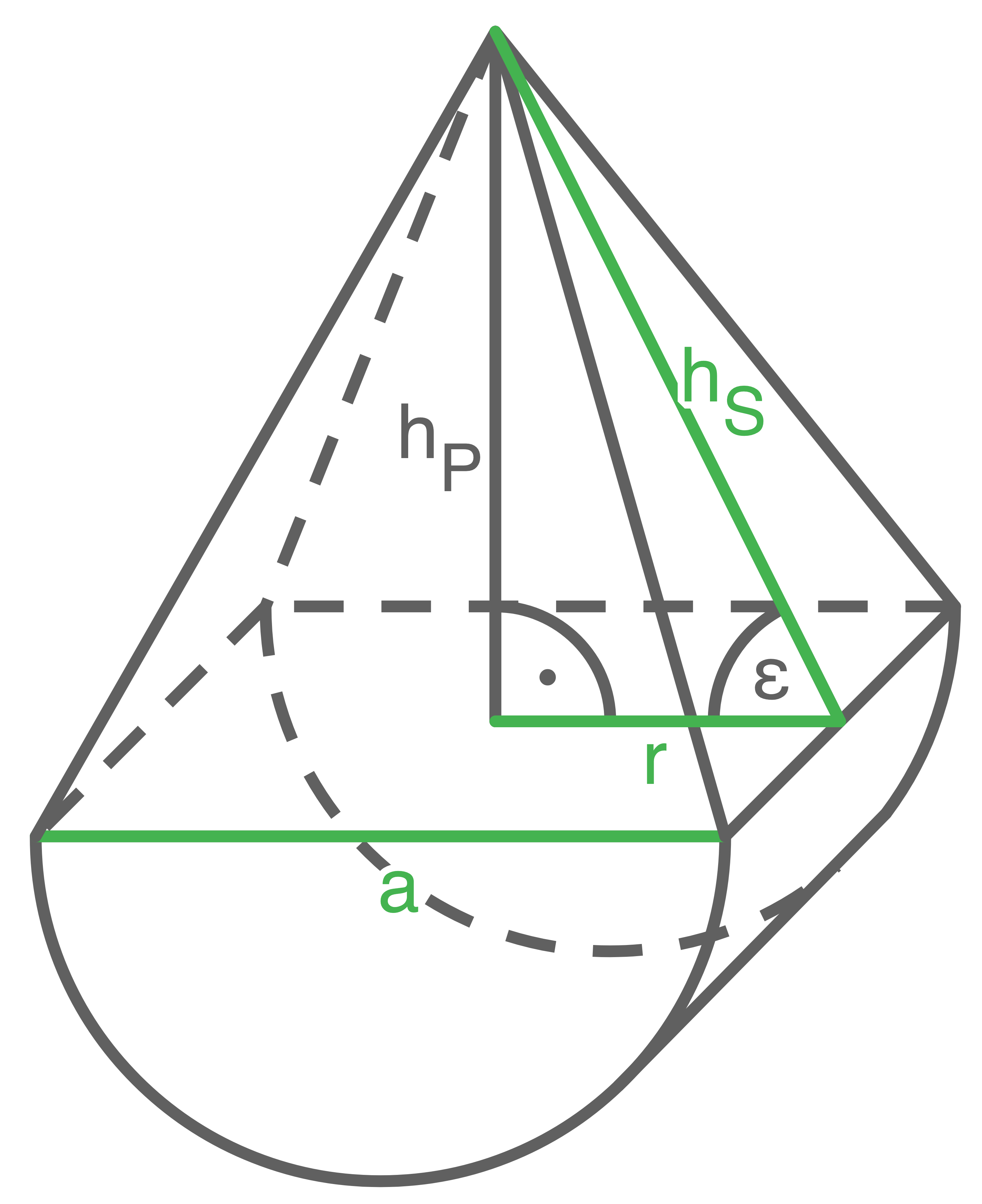 Länge der Strecken
Länge der Strecken  und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_S^2&=& r^2 + h_P^2 \\[5pt]
(18,87\,\text{cm})^2-(16\,\text{cm})^2 &=& r^2 \quad \scriptsize \mid\; \sqrt{\,\,} \\[5pt]
r&=& \underline{10 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/dad1f4d5f0282b96f4aaa3fabe879696c77db9fe123e58c524a64b62982b610b_light.svg) Damit ergibt sich
Damit ergibt sich  Inhalt der Mantelfläche der Pyramide berechnen
Inhalt der Mantelfläche der Pyramide berechnen
![\(\begin{array}[t]{rll}
M_{\,\text{P}}&=& 2 \cdot a \cdot h_S \\[5pt]
&=& 2 \cdot 20 \,\text{cm} \cdot 18,87 \,\text{cm} \\[5pt]
&=& \underline{754,80 \,\text{cm}^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bed0a09ca91c71f3f7821bb67336f5604ee3e3280d35298bacf17136792d86da_light.svg) 2. Schritt: Inhalt der Mantelfläche des Zylinders berechnen
2. Schritt: Inhalt der Mantelfläche des Zylinders berechnen
![\(\begin{array}[t]{rll}
O_Z&=& \dfrac{1}{2} (2 \pi r\cdot (r+a)) \\[5pt]
&=& \frac{1}{2} (2 \pi \cdot 10\,\text{cm}\cdot (10\,\text{cm}+20\,\text{cm} )) \\[5pt]
&=& \underline{942,48 \,\text{cm}^2 }
\end{array}\)](https://www.schullv.de/resources/formulas/889808f555547ad0eb5da5465911b9b13365453fa3c0dbd25c396e507a469f71_light.svg) 3. Schritt: Oberflächeninhalt des zusammengesetzten Körpers berechnen
3. Schritt: Oberflächeninhalt des zusammengesetzten Körpers berechnen
![\(\begin{array}[t]{rll}
O_{\text{gesamt}}&=& M_{\,\text{P}} + O_{\text{Z}} \\[5pt]
&=& 754,80 \,\text{cm}^2 + 942,48 \,\text{cm}^2 \\[5pt]
&=& 1697,28 \,\text{cm}^2\\[5pt]
O_{\text{gesamt}}&=& \underline{\underline{1697,3 \,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/7a334045d3a9f34514e18dfb122ff8edd88a4e885c78d86aaa6ea2bb7240667f_light.svg)
Höhe  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\sin(\varepsilon)&=& \dfrac{h_P}{h_S} \quad \scriptsize \mid\; \cdot h_S \,\, \mid\; :\sin(\varepsilon)\\[5pt]
h_S&=& \dfrac{h_P}{\sin(\varepsilon)} \\[5pt]
&=& \dfrac{16 \,\text{cm}}{\sin(58^{\circ})} \\[5pt]
h_S&=& \underline{18,87\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/1eaeddeaca0135f74b8e1d25fa60fb35ce3c546aa43f6ae4b5483640f7271d69_light.svg)

Lösung P4
Begründung durch Rechnung Wahrscheinlichkeit für die Augensumme 6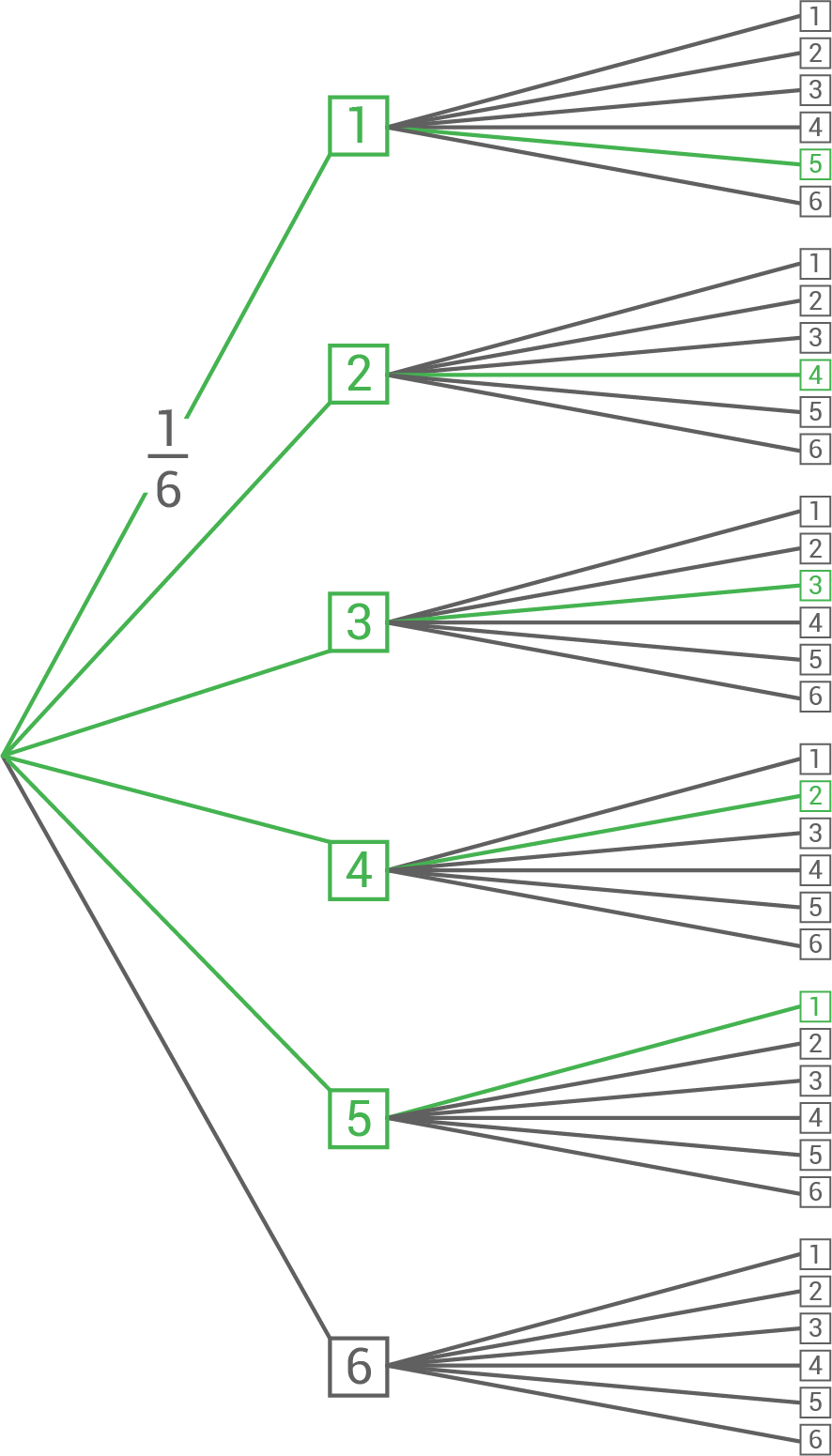
Die Wahrscheinlichkeit jedes Pfades beträgt  Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
&P(\text{Augensumme 6})&=& \left(\dfrac{1}{6}\cdot \dfrac{1}{6}\right) \cdot 5 \\[5pt]
&&=& \dfrac{5}{36} \\[5pt]
&&\approx& 0,1389
\end{array}\)](https://www.schullv.de/resources/formulas/444a1e92865cd8d0c29130f60941612747fd6c3b2ad3429a47244e7226fb132f_light.svg) Die Wahrscheinlichkeit, die Augensumme 6 zu würfeln, beträgt also
Die Wahrscheinlichkeit, die Augensumme 6 zu würfeln, beträgt also 
Wahrscheinlichkeit für die Augensumme 9
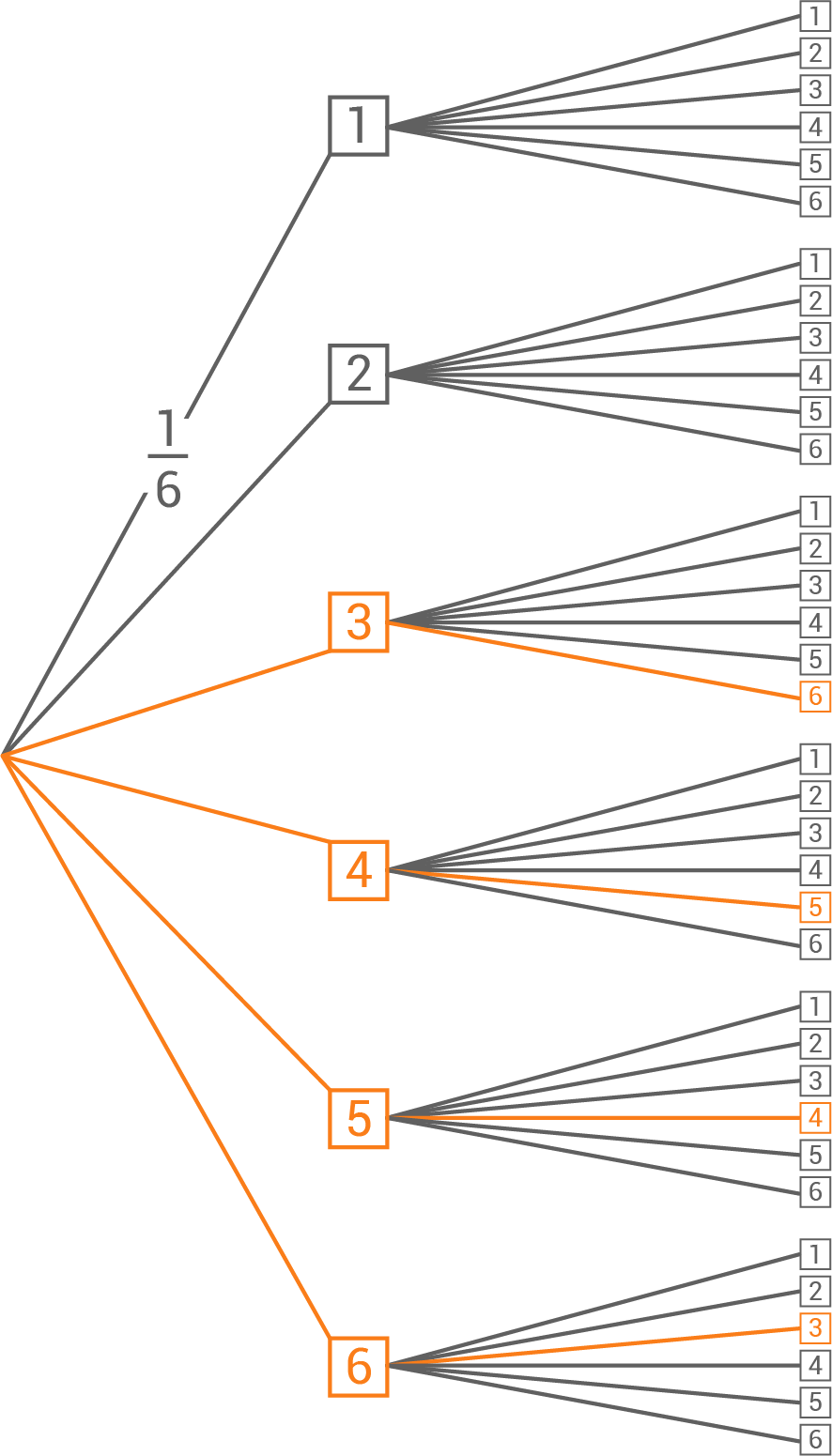
Die Wahrscheinlichkeit jedes Pfades beträgt  Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
&P(\text{Augensumme 9})&=& \left(\dfrac{1}{6}\cdot \dfrac{1}{6}\right) \cdot 4 \\[5pt]
&&=& \dfrac{4}{36} \\[5pt]
&&\approx& 0,1111
\end{array}\)](https://www.schullv.de/resources/formulas/691e2a834a5f03cc99aebf65beb56ade24e63e1bdf82bef156795b502ef12ae0_light.svg) Die Wahrscheinlichkeit, die Augensumme 9 zu würfeln, beträgt also
Die Wahrscheinlichkeit, die Augensumme 9 zu würfeln, beträgt also  Somit stimmt die Aussage.
Somit stimmt die Aussage.
Begründung durch Argumentation
Wahrscheinlichkeit für die Augensumme 6
Es gibt insgesamt fünf Möglichkeiten, die Augensumme 6 zu würfeln:
- 1 und 5
- 2 und 4
- 3 und 3
- 4 und 2
- 5 und 1
Wahrscheinlichkeit für die Augensumme 9
Um die Augensumme 9 zu würfeln, gibt es allerdings nur vier Möglichkeiten:
Für jede dieser Möglichkeiten ist die Wahrscheinlichkeit gleich. Somit reicht es, die Anzahl der Möglichkeiten zu vergleichen, um die Aussage zu bewerten. Für die Augensumme 6 gibt es mehr Möglichkeiten, also stimmt die Aussage.
Wie groß ist die Wahrscheinlichkeit, dass Nele mit dem nächsten Wurf das Spiel gewinnt?
Nele gewinnt dann das Spiel, wenn sie eine größere Augenzahl als 8 würfelt.
- 3 und 6
- 4 und 5
- 5 und 4
- 6 und 3
Dafür gibt es insgesamt zehn Möglichkeiten:
- 3 und 6
- 4 und 5
- 4 und 6
- 5 und 4
- 5 und 5
- 5 und 6
- 6 und 3
- 6 und 4
- 6 und 5
- 6 und 6
Lösung P5
1. Schritt: Scheitelpunktform der verschobenen NormalparabelSomit ist
- Scheitelpunktform:
- Koordinaten des Scheitelpunkts:
2. Schritt: Geradengleichung  aufstellen
Scheitelpunkt in die Geradengleichung
aufstellen
Scheitelpunkt in die Geradengleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-4&=& 3\cdot (-1)+b \\[5pt]
-4&=& -3+b &\quad \scriptsize \mid\; +3 \\[5pt]
b&=&-1
\end{array}\)](https://www.schullv.de/resources/formulas/c7b4d4c485211969761d96866459fdc1d53ed5a31fe705e6afc006a5792a8fa0_light.svg)

![[ALT-TAG]](https://www.schullv.de/resources/images/mathe/desktop/bw_rs2017_p5_lsg.png)
Lösung P6
Lösung P7
Wie viele Reisen nach Österreich wurden gebucht?Lösung P8
Welcher der beiden Boxplots zeigt die Verteilung der Ergebnisse der Klasse 10a? Die beiden Boxplots unterscheiden sich nur im oberen Quartil.Für
1. Schritt: Rangliste für die Klasse 10b erstellen
| Rangplatz | Punkte |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 3 |
| 4 | 4 |
| 5 | 4 |
| 6 | 5 |
| 7 | 6 |
| 8 | 6 |
| 9 | 6 |
| 10 | 6 |
| 11 | 7 |
| 12 | 7 |
| 13 | 7 |
| 14 | 7 |
| 15 | 7 |
| Rangplatz | Punkte |
|---|---|
| 16 | 8 |
| 17 | 8 |
| 18 | 8 |
| 19 | 9 oder 10 |
| 20 | 9 oder 10 |
| 21 | 9 oder 10 |
| 22 | 10 |
| 23 | 10 |
| 24 | 10 |
| 25 | 10 |
| 26 | 11 |
| 27 | 12 |
| 28 | 12 |
| 29 | 12 |
2. Schritt: Fehlende Kennwerte ermitteln und in die Rangliste eintragen



Daraus folgt

Daraus folgt

Daraus folgt in (2) Boxplot ablesen und an Rangplatz 22 eintragen
Für die Rangplätze 19, 20 und 21 kann die Punktzahl 9 oder 10 eingetragen werden.
Für die Rangplätze 23, 24 und 25 muss die Punktzahl 10 eingetragen werden.
in (2) Boxplot ablesen und an Rangplatz 22 eintragen
Für die Rangplätze 19, 20 und 21 kann die Punktzahl 9 oder 10 eingetragen werden.
Für die Rangplätze 23, 24 und 25 muss die Punktzahl 10 eingetragen werden.
3. Schritt: Mögliche Lösung in das Diagramm einzeichnen
Daraus folgt
Daraus folgt
Daraus folgt