Pflichtbereich

Aufgabe P1

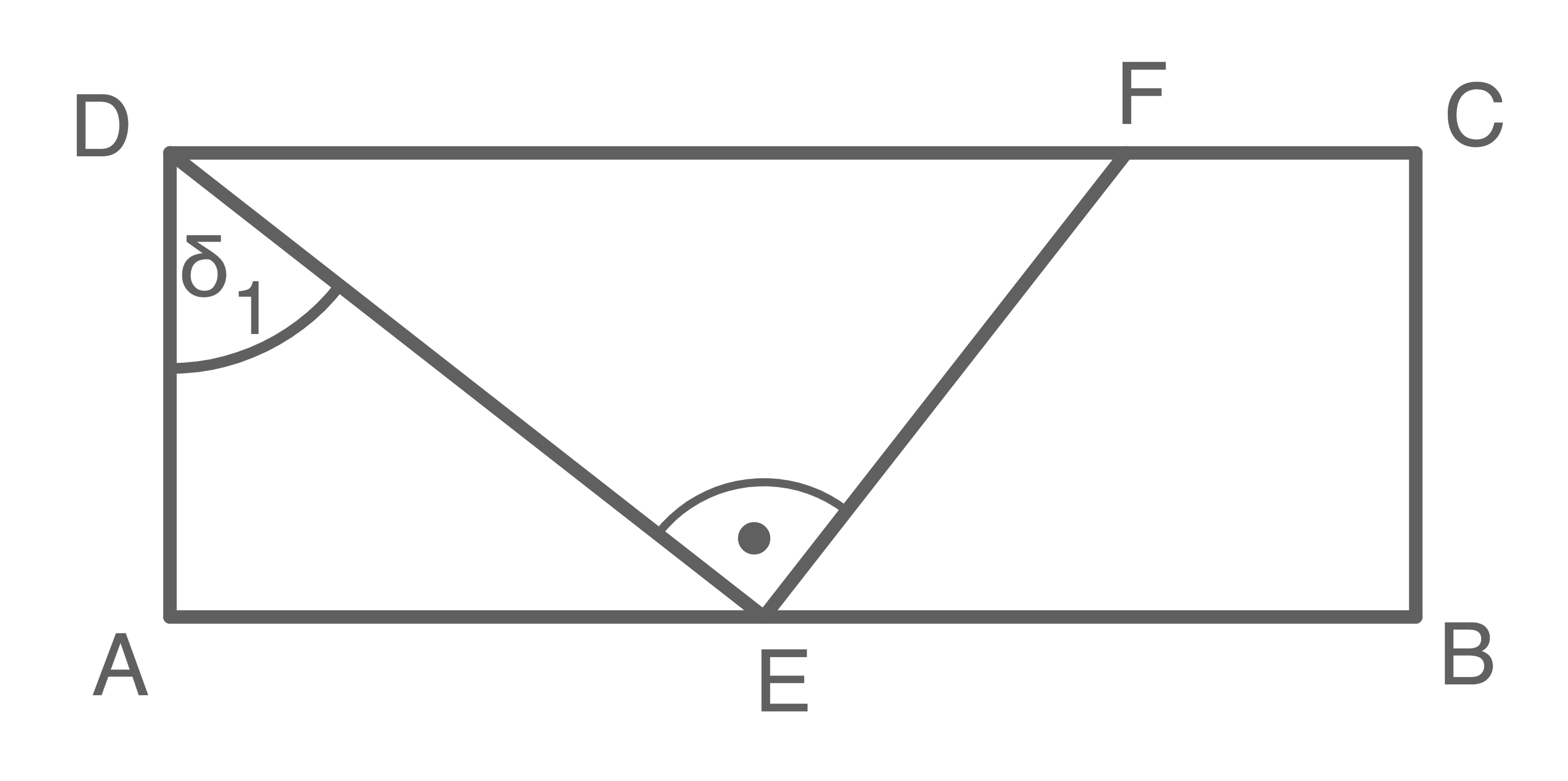
Geometrische Darstellung eines Rechtecks mit beschrifteten Punkten und einem Winkel.

Im Rechteck $ABCD$ gilt:

$\overline{AB} = 14,5\,\text{cm}$
$\overline{AD} = 5,4\,\text{cm}$
$\delta_1= 52,0^{\circ}$

Berechne den Flächeninhalt des Trapezes $EBCF.$

4 P

Aufgabe P2

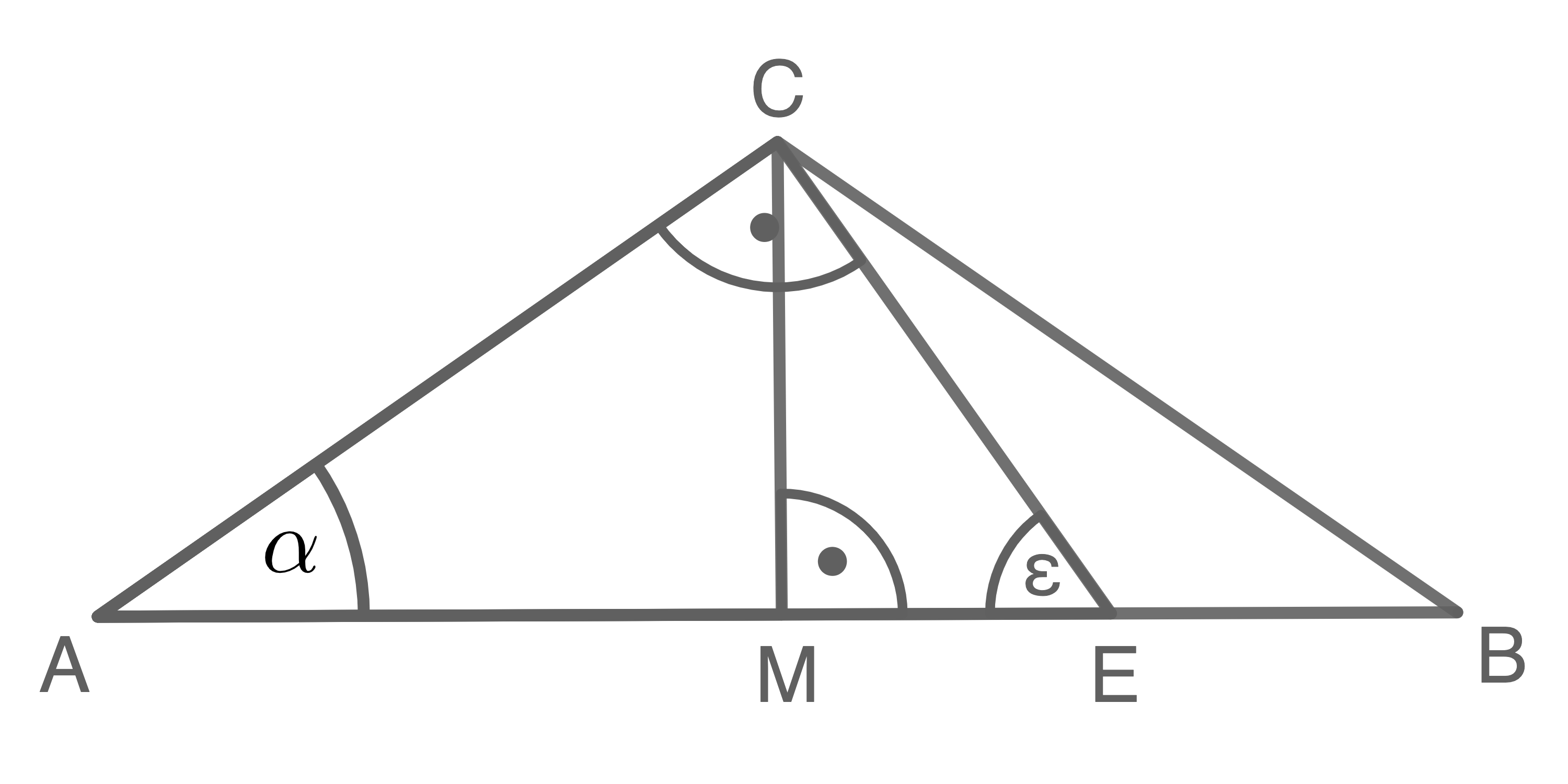
Gegeben sind das gleichschenklige Dreieck $ABC$ und das rechtwinklige Dreieck $AEC.$

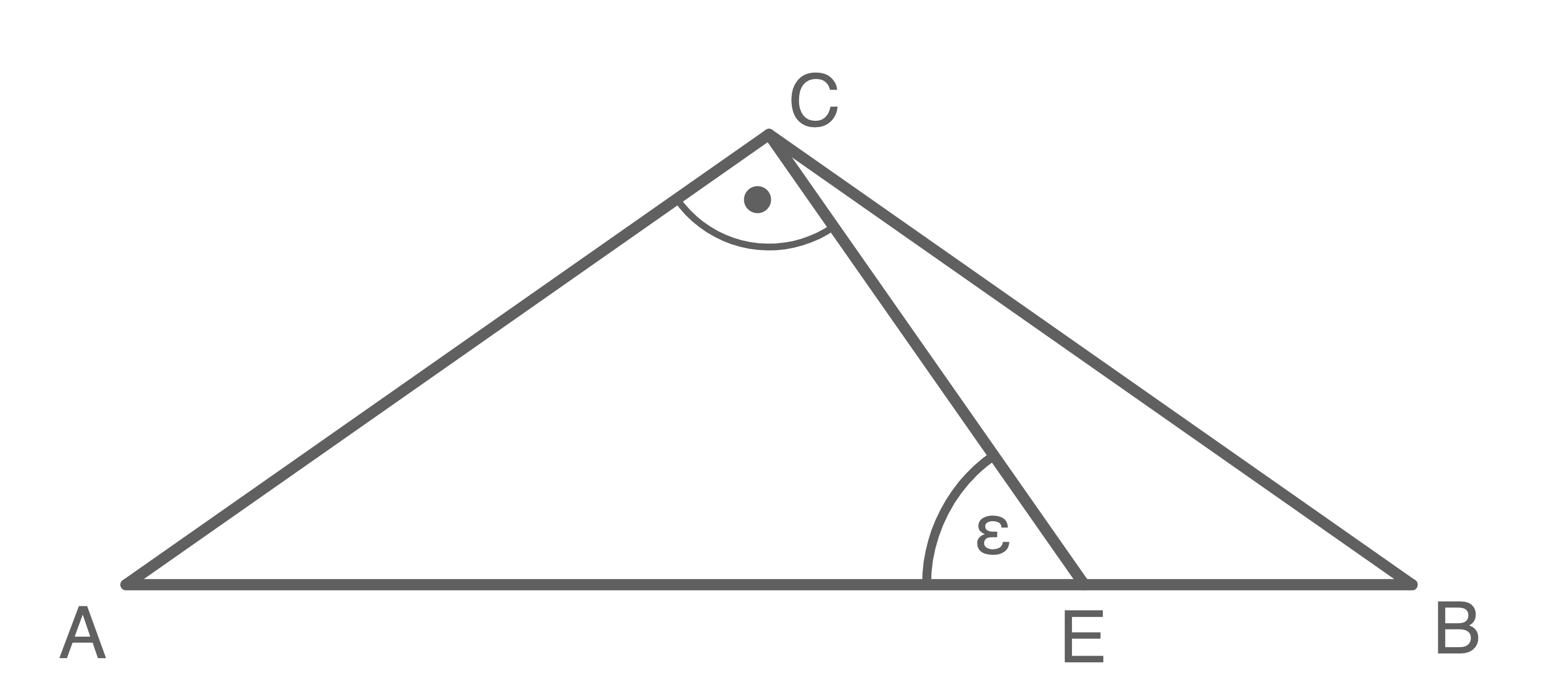
Schematische Darstellung eines Dreiecks mit beschrifteten Punkten und Winkeln.

Es gilt:

$\overline{AE}=9,4\,\text{cm}$
$\epsilon = 55,0^{\circ}$
$\overline{AC} = \overline{BC}$

Berechne die Länge von $\overline{BE}.$

4 P

Aufgabe P3

Die Abbildung zeigt ein quadratisches Prisma und einen zusammengesetzten Körper.

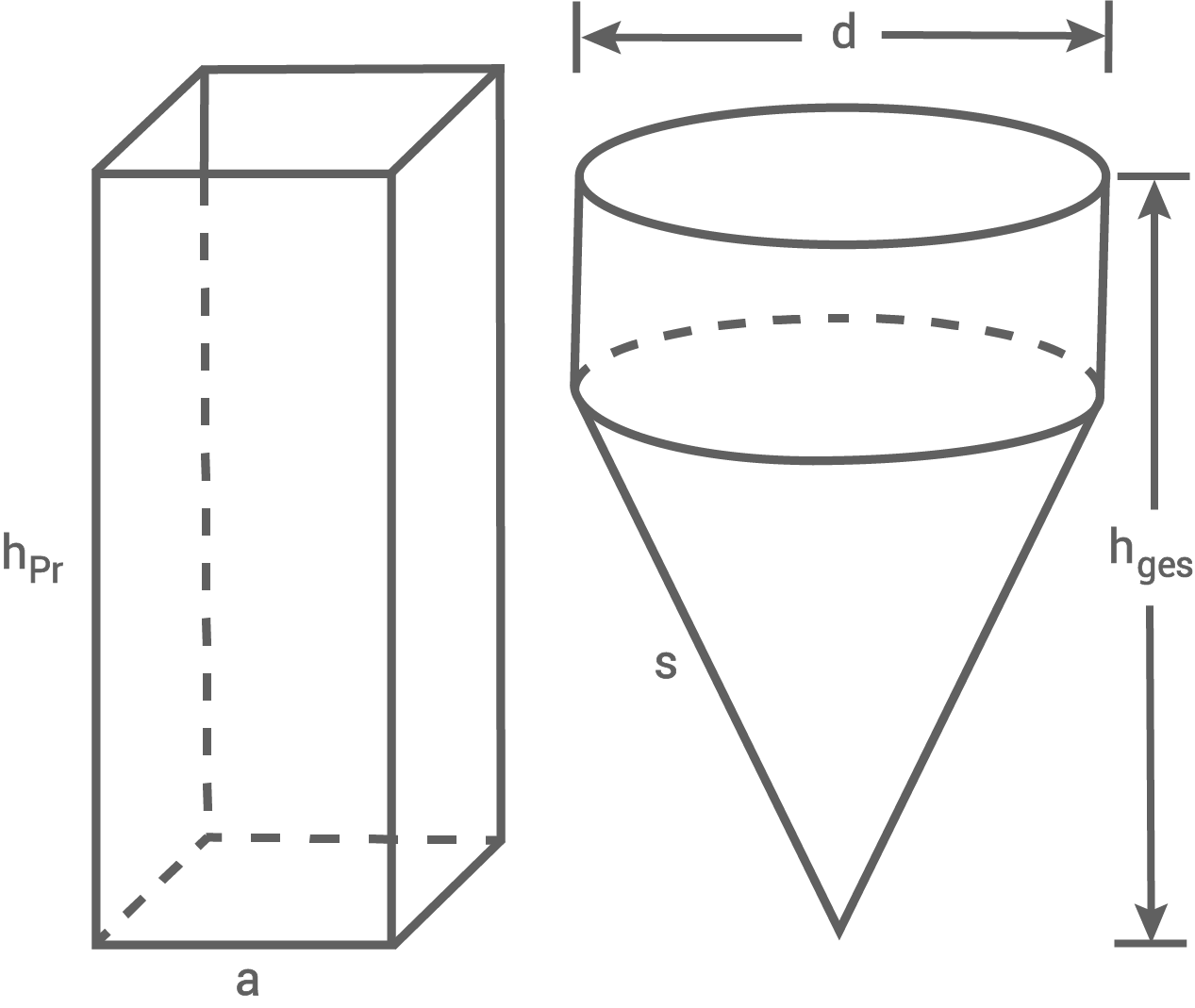Schematische Darstellung eines Quaders und eines Kegels mit Beschriftungen für Maße.

Der zusammengesetzte Körper besteht aus einem Kegel mit aufgesetztem Zylinder.

Das quadratische Prisma ist vollständig mit Wasser gefüllt. Dieses Wasser wird in den zusammengesetzten Körper umgefüllt.
Es gilt:

$a= 10,0\,\text{cm}$
$h_{\,\text{Pr}} = h_{\,\text{ges}} = 25,0\,\text{cm}$
$s= 20,0\,\text{cm}$
$d= 17,8\,\text{cm}$

Wie hoch steht das Wasser im zusammengesetzten Körper?

4 P

Aufgabe P4

Die Grafik zeigt den täglichen Wasserverbrauch pro Kopf in Deutschland.

Entwicklung des Pro-Kopf-Wasserverbrauchs
Angaben in Litern pro Einwohner und Tag in Deutschland

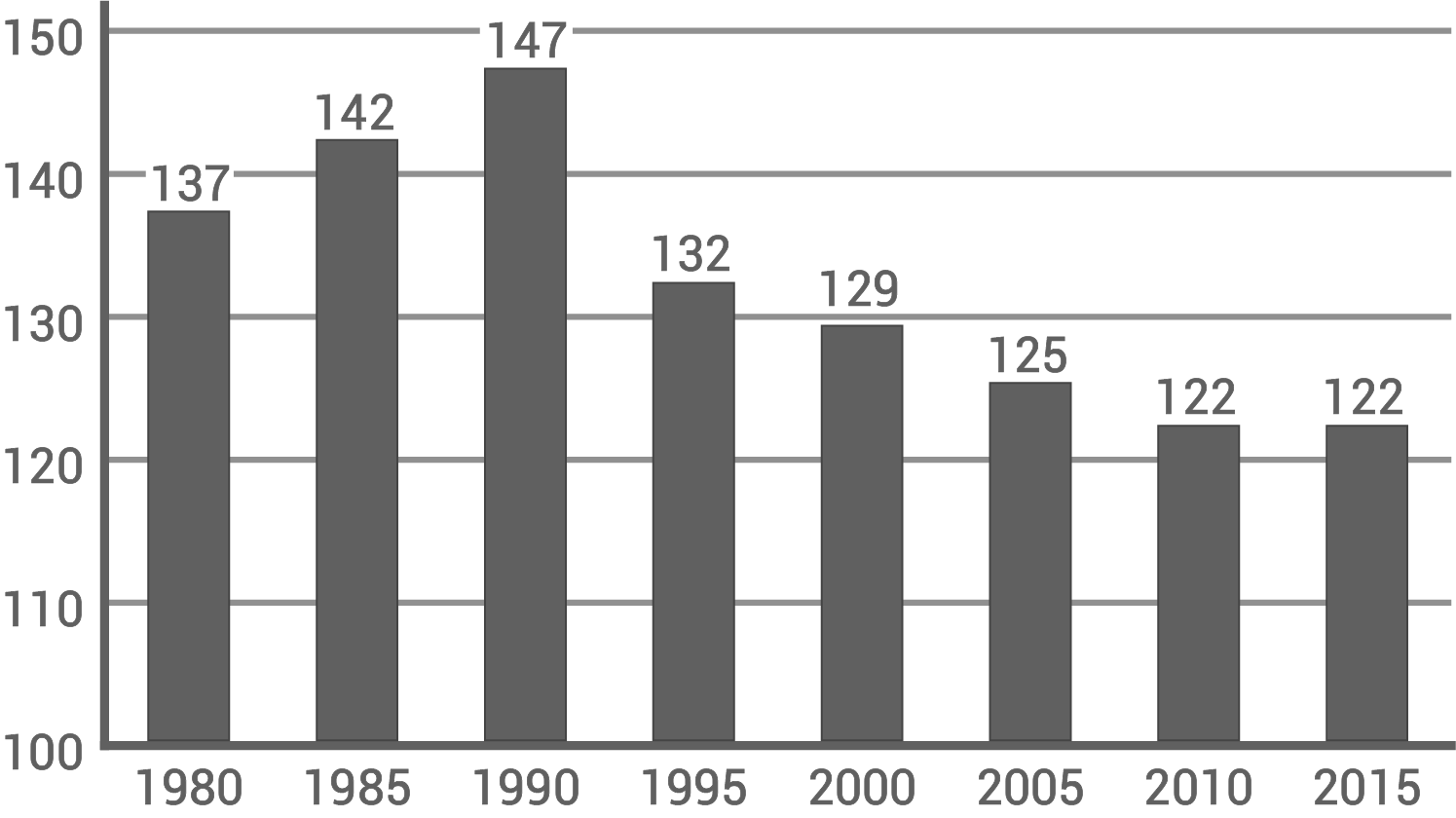
Balkendiagramm zeigt Daten von 1980 bis 2015 mit variierenden Werten.

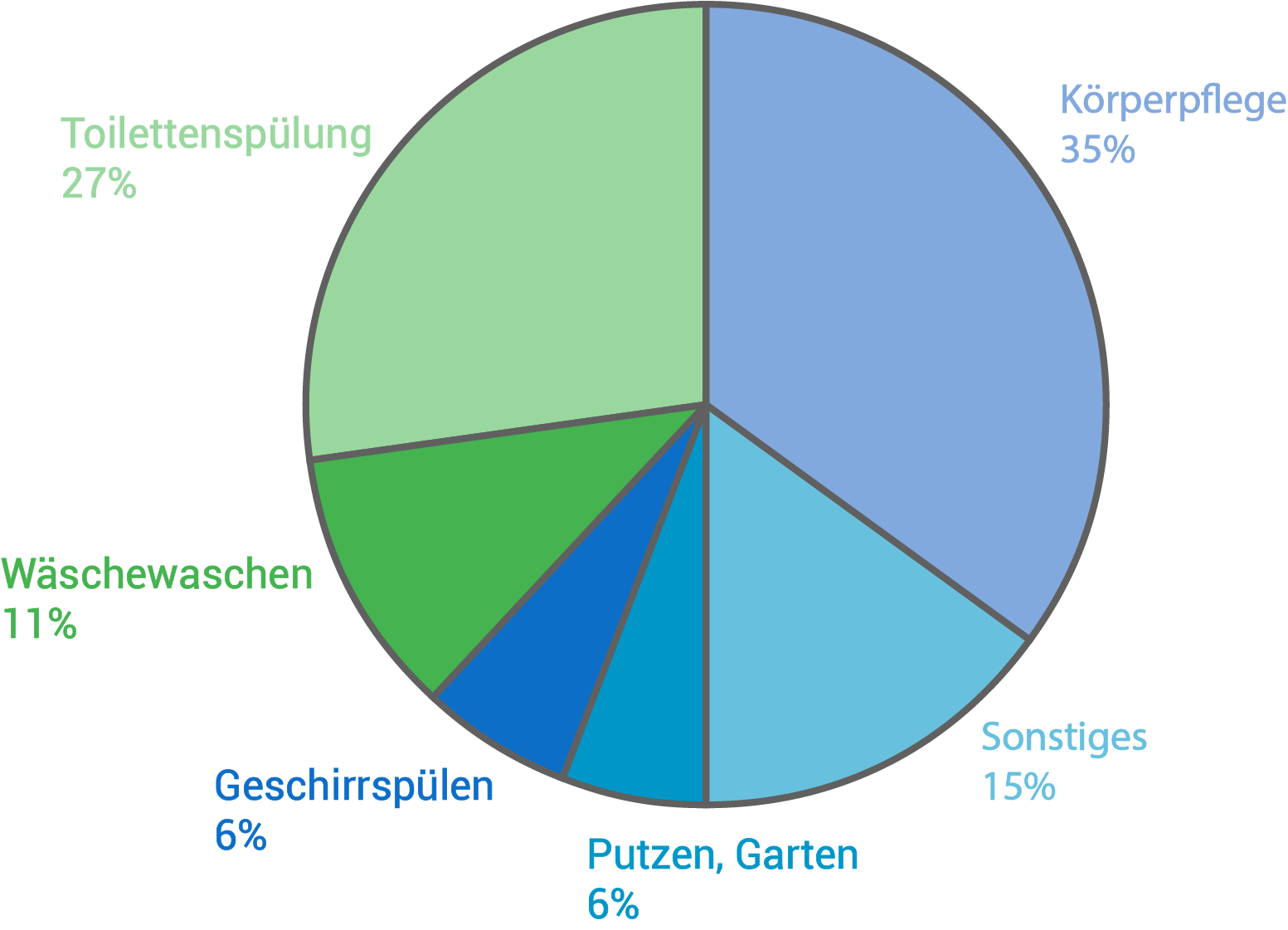
Täglicher Wasserverbrauch pro Einwohner
in Deutschland in Prozent im Jahr 2015

Kreisdiagramm mit verschiedenen Kategorien und Prozentanteilen für Haushaltsaufgaben.

Um wie viel Prozent hat der Wasserverbrauch pro Kopf im Zeitraum von 1990 bis 2010 abgenommen?

Berechne, wie viele Liter Wasser im Jahr 2015 täglich für die Körperpflege pro Einwohner verbraucht wurden.

Einer Studie zufolge nimmt der Wasserverbrauch pro Kopf in den fünf Jahren von 2015 bis 2020 ab. Man geht davon aus, dass sich der Wasserverbrauch um $1\,\%$ pro Jahr, bezogen auf das Vorjahr, verringert.

Mit welchem täglichen Wasserverbrauch pro Kopf ist 2020 zu rechnen?

3,5 P

Aufgabe P5

Gib die Definitions- und Lösungsmenge der Gleichung an:

$\dfrac{4}{x} + \dfrac{2x-2}{x+2} = \dfrac{3x^2}{x^2+2x}$

3,5 P

Aufgabe P6

Zu einer verschobenen, nach oben geöffneten Normalparabel $p$ gehört die teilweise ausgefüllte Wertetabelle.

$x$	$y$
$0$	$5$
$1$
$2$
$3$
$4$
$5$
$6$	$5$

Gib die Funktionsgleichung der Parabel $p$ an.
Ergänze die fehlenden Werte in der Tabelle.
Durch den Schnittpunkt $R$ der Parabel $p$ mit der $y$ -Achse und den Scheitelpunkt $S$ verläuft die Gerade $g.$
Berechne die Steigung $m$ der Geraden $g.$

4 P

Aufgabe P7

In einer Schale liegen rote, grüne und weiße Gummibärchen. Insgesamt sind es 12 Stück. Sofia nimmt, ohne hinzusehen, gleichzeitig zwei Gummibärchen aus der Schale.

Die Grafik zeigt ein unvollständiges Baumdiagramm dieses Zufallsversuchs.

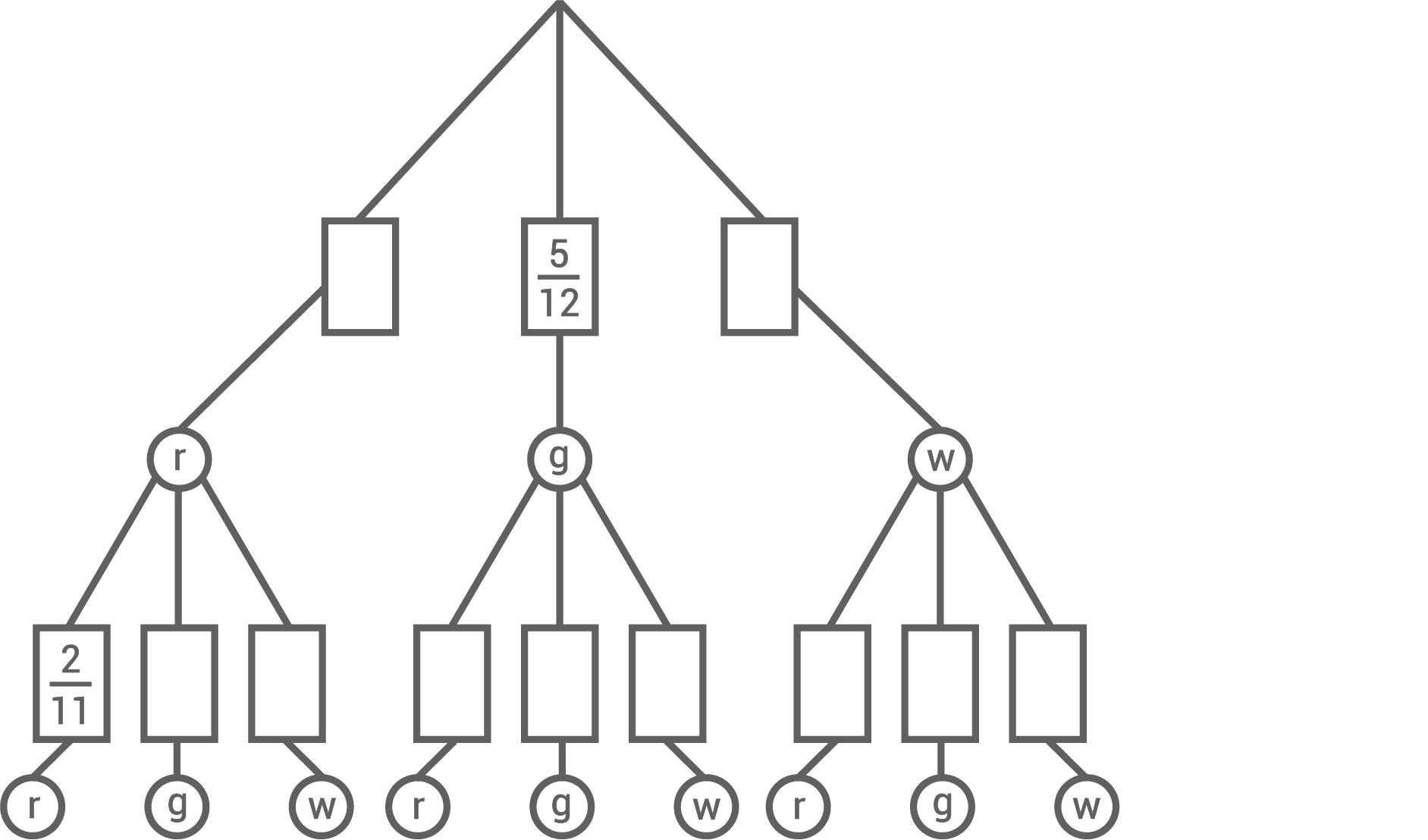Diagramm eines Entscheidungsbaums mit verschiedenen Ästen und Wahrscheinlichkeiten.

Vervollständige dieses Baumdiagramm.

Mit welcher Wahrscheinlichkeit zieht Antonetta bei diesem Zufallsversuch

genau ein rotes Gummibärchen?
höchstens ein weißes Gummibärchen?

3,5 P

Aufgabe P8

Die Jungen der Klassen 7a und 7b werfen im Sportunterricht mit einem 200 - g - Ball.
Die Wurfweiten werden in ganzen Metern erfasst.
Die Verteilungen der Wurfweiten der $17$ Jungen der Klasse 7a und der $13$ Jungen der Klasse 7b sind in den beiden Boxplots dargestellt.

Rangplatz	Klasse 7a
$1$
$2$
$3$
$4$
$5$
$6$	$23$
$7$	$25$
$8$	$28$
$9$	$28$
$10$	$35$
$11$	$36$
$12$	$38$
$13$	$40$
$14$
$15$
$16$
$17$

Rangplatz	Klasse 7b
$1$
$2$
$3$
$4$
$5$	$24$
$6$	$25$
$7$	$28$
$8$	$28$
$9$	$29$
$10$	$36$
$11$	$38$
$12$	$40$
$13$

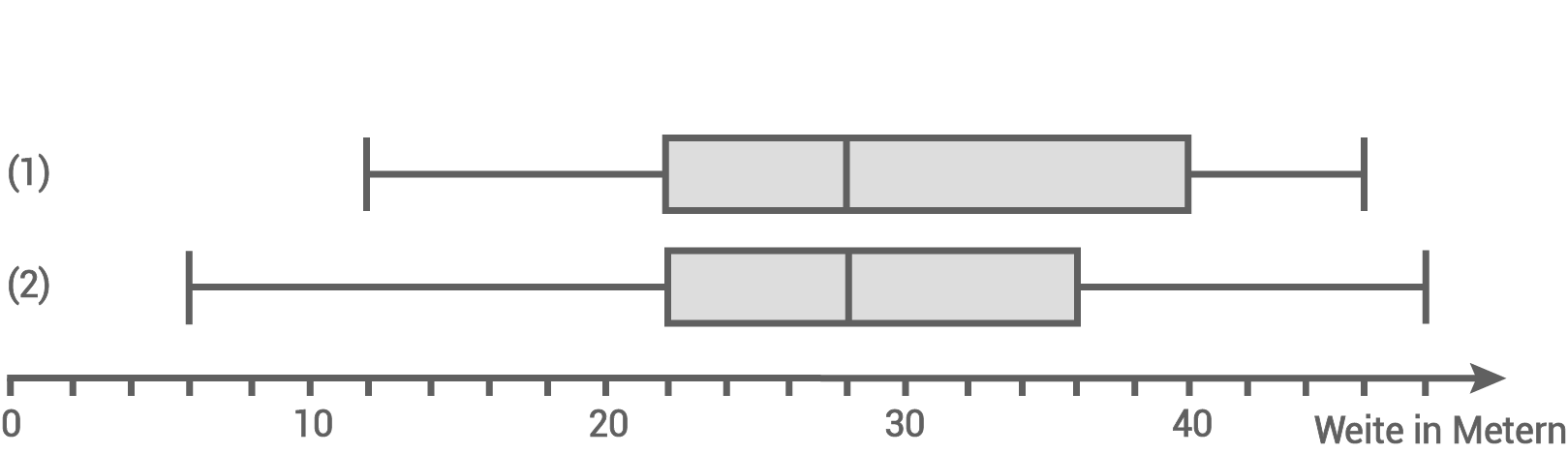
Ordne die Boxplots den unvollständigen Ranglisten der Klassen 7a und 7b zu.
Begründe deine Entscheidung mithilfe geeigneter Kennwerte.
Ergänze die Ranglisten mit möglichen Werten.

Tom und Marc aus der Klasse 7a wurden im Nachhinein aus der Wertung genommen, da sie übertreten hatten. Tom hatte den Ball $23\,\text{m}$ und Marc $36\,\text{m}$ weit geworfen.
Alex behauptet: „Der Zentralwert ändert sich nicht, wenn Tom und Marc aus der Wertung genommen werden.“
Hat Alex recht? Begründe deine Antwort.

3,5 P

Lösung P1

$A_{\,\text{Trapez}}=\dfrac{(a+c)}{2} \cdot h$

$A_{\,\text{EBCF}}=\dfrac{(\overline{EB}+\overline{FC)}}{2} \cdot \overline{BC}$

1. Schritt: Länge der Strecke $\boldsymbol{\overline{EB}}$ berechnen
Länge der Strecke $\overline{AE}$ berechnen

$\begin{array}[t]{rll} \tan (\delta_1) &=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \\[5pt] \tan (52,0^{\circ}) &=& \dfrac{\overline{AE}}{\overline{AD}} \\[5pt] \tan (52,0^{\circ}) &=& \dfrac{\overline{AE}}{5,4\,\text{cm}} \quad \scriptsize \mid\; \cdot 5,4\,\text{cm} \\[5pt] \overline{AE}&=& \underline{ 6,91\,\text{cm}} \end{array}$

Länge der Strecke $\overline{EB}$ berechnen

$\begin{array}[t]{rll} \overline{EB} &=& \overline{AB} - \overline{AE} \\[5pt] &=& 14,5\,\text{cm} - 6,91\,\text{cm} \\[5pt] &=& \underline{ 7,59\,\text{cm}} \\[5pt] \end{array}$

2. Schritt: Länge der Strecke $\boldsymbol{\overline{FC}}$ berechnen

Länge der Strecke $\overline{DE}$ berechnen

Satz des Pythagoras im Dreieck $AED$ :

Rechenweg anzeigen

$\overline{DE} = 8,8\,\text{cm}$

Länge der Strecke $\overline{DF}$ berechnen

$\begin{array}[t]{rll} \delta_2&=& 90^{\circ} - \delta_1 \\[5pt] &=& 90^{\circ} - 52,0^{\circ} \\[5pt] &=& 38,0^{\circ} \end{array}$

$\begin{array}[t]{rll} \cos (\delta_2) &=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \\[5pt] \cos (38^{\circ}) &=& \dfrac{8,77\,\text{cm}}{\overline{DF}} \quad \scriptsize \mid\; \cdot \overline{DF}\\[5pt] \cos (38^{\circ}) \cdot \overline{DF} &=& 8,77\,\text{cm} \quad \scriptsize \mid\; :\cos (38^{\circ}) \\[5pt] \overline{DF} &= & \underline{ 11,13\,\text{cm}} \end{array}$

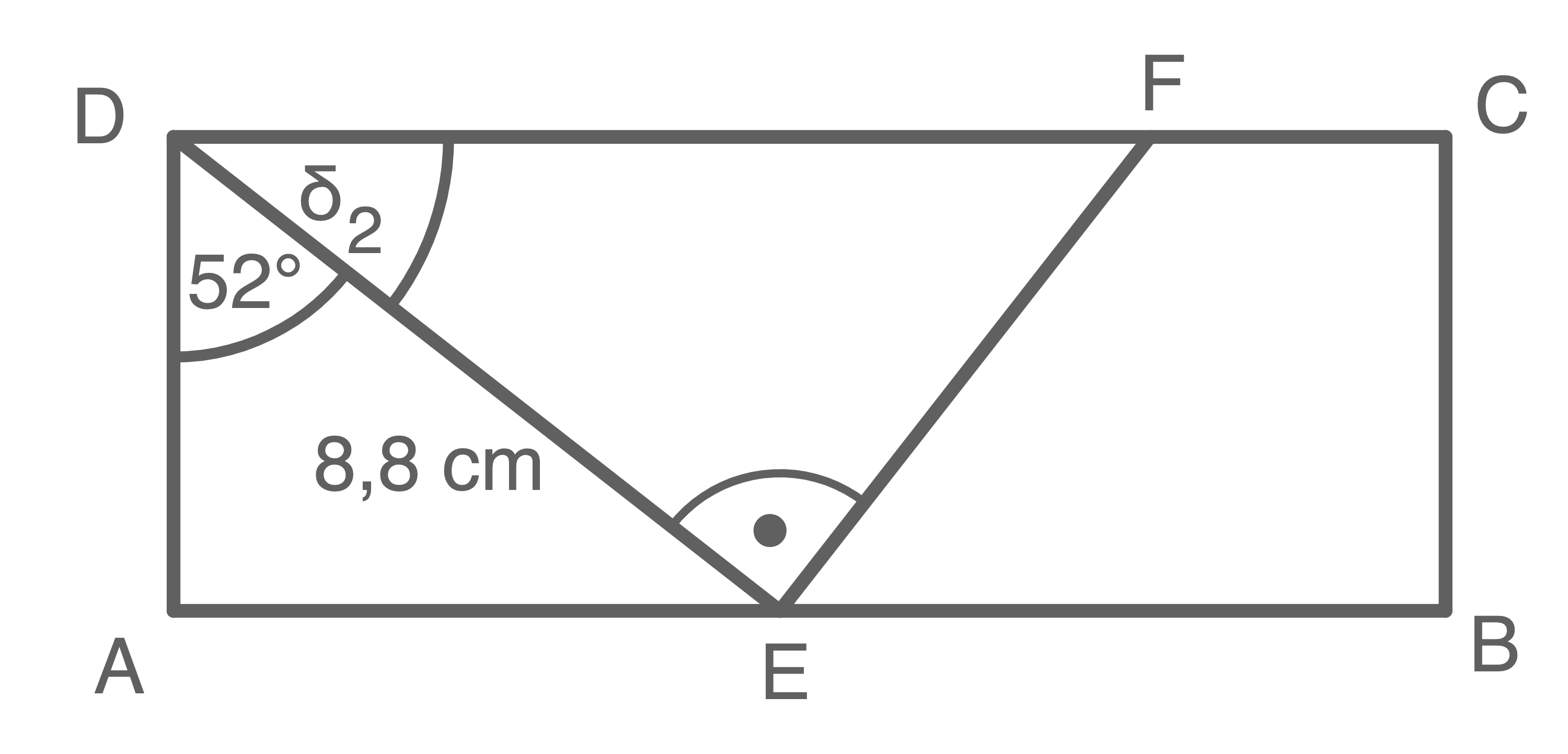
Geometrische Darstellung eines Rechtecks mit Winkeln und Längenangaben.

Länge der Strecke $\overline{FC}$ berechnen

$\begin{array}[t]{rll} \overline{DC}&=& \overline{AB} \\[5pt] \end{array}$

$\begin{array}[t]{rll} \overline{FC}&=& \overline{DC} - \overline{DF} &\quad \scriptsize \\[5pt] &=& 14,5\,\text{cm} - 11,13\,\text{cm}\\[5pt] &=& \underline{ 3,37\,\text{cm}} \end{array}$

3. Schritt: Flächeninhalt berechnen

$\overline{BC} = \overline{AD} = 5,4 \,\text{cm}$

Rechenweg anzeigen

$A_{EBCF}\approx 29,6\,\text{cm}^2$

Der Flächeninhalt des Trapezes $EBCF$ beträgt ca. $29,6\,\text{cm}^2.$

Lösung P2

1. Schritt: Länge der Strecke $\boldsymbol{\overline{AC}}$ berechnen

$\begin{array}[t]{rll} \sin (\epsilon) &=& \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} \\[5pt] \sin (55^{\circ}) &=& \dfrac{\overline{AC}}{9,4\,\text{cm}} \quad \scriptsize \mid\;\cdot 9,4\,\text{cm} \\[5pt] \overline{AC} &=& \underline{ 7,70\,\text{cm}}\\[5pt] \end{array}$

2. Schritt: Größe des Winkels $\boldsymbol{\alpha}$ berechnen

Die Winkelsumme im Dreieck $\,\text{AEC}$ beträgt $180^{\circ}.$

$\begin{array}[t]{rll} \alpha + \epsilon + 90^{\circ} &=& 180^{\circ} \\[5pt] \alpha + 55^{\circ}+ 90^{\circ} &=& 180^{\circ} \\[5pt] \alpha + 145^{\circ} &=& 180^{\circ} &\quad \scriptsize \mid\; -145^{\circ}\\[5pt] \alpha &=& \underline{ 35^{\circ}} \end{array}$

3. Schritt: Länge der Strecke $\boldsymbol{\overline{AM}}$ berechnen

$\begin{array}[t]{rll} \cos(\alpha)&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \\[5pt] \cos(35^{\circ} ) &=& \dfrac{\overline{AM}}{7,7\,\text{cm}} \quad \scriptsize \mid\; \cdot 7,7\,\text{cm} \\[5pt] \overline{AM} &=& \underline{ 6,31 \,\text{cm}}= \overline{BM} \\[5pt] \end{array}$

4. Schritt: Länge der Strecke $\boldsymbol{\overline{AB}}$ berechnen

$\begin{array}[t]{rll} \overline{AB}&=& \overline{AM} + \overline{BM}\\[5pt] &=& 6,31 \,\text{cm} + 6,31 \,\text{cm} \\[5pt] \overline{AB}&=& \underline{ 12,62\,\text{cm}} \end{array}$

5. Schritt: Länge der Seitenlänge $\boldsymbol{\overline{BE}}$ berechnen

$\begin{array}[t]{rll} \overline{BE}&=& \overline{AB} - \overline{AE} \\[5pt] &=& 12,62\,\text{cm} - 9,4\,\text{cm}\\[5pt] &=& 3,22\,\text{cm}\\[5pt] \overline{BE}&=& \underline{\underline{ 3,2\,\text{cm}}} \end{array}$

Die Seite $\overline{BE}$ ist ca. $3,22\,\text{cm}$ lang.

Lösung P3

1. Schritt: Volumen des Wassers berechnen

Volumen des Prismas = Volumen des Wassers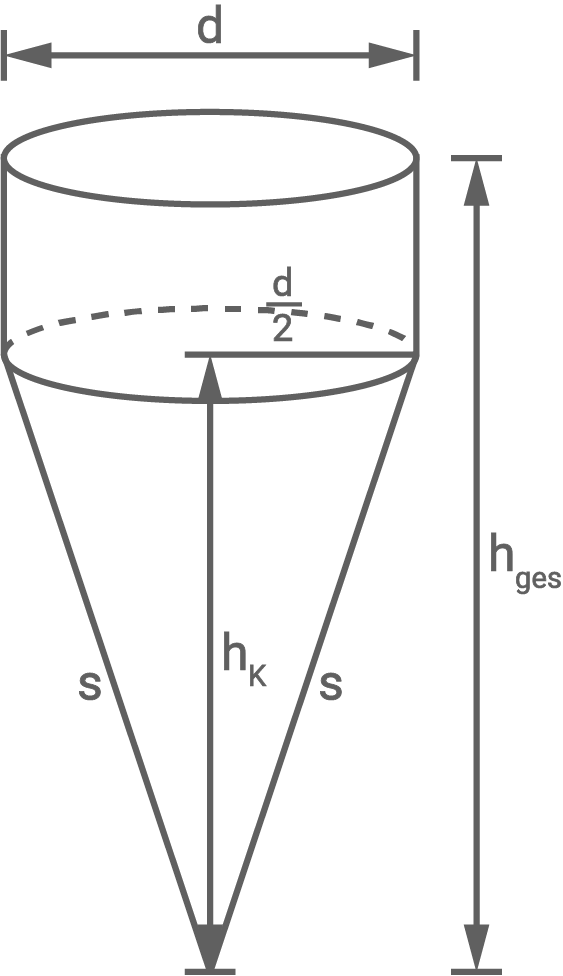

$\begin{array}[t]{rll} V_{\text{Prisma}}&=& a \cdot a\cdot h_{\text{Pr}} \\[5pt] &=& 10\,\text{cm} \cdot 10\,\text{cm} \cdot 25\,\text{cm}\\[5pt] V_{\text{Prisma}}&=& \underline{ 2\,500\,\text{cm}^3} \end{array}$

2. Schritt: Höhe des Kegels berechnen

Rechenweg anzeigen

$h_K= 17,91\,\text{cm}$

3. Schritt: Volumen des Kegels berechnen

$\begin{array}[t]{rll} V_{\text{Kegel}}&=& \frac{1}{3}\cdot \pi \cdot \left(\frac{d}{2}\right)^2\cdot h_{\,\text{K}} \\[5pt] &=& \frac{1}{3}\cdot \pi \cdot \left(\frac{17,8\,\text{cm}}{2}\right)^2\cdot 17,91\,\text{cm} \\[5pt] V_{\text{Kegel}}&=& \underline{ 1\,485,61\,\text{cm}^3}\\[5pt] \end{array}$

4. Schritt: Volumen des Wassers im Zylinder berechnen

Da $1\,485,61\,\text{cm}^3$ Wasser den Kegel füllen, gilt für den Zylinder:

$2\,500\,\text{cm}^3 - 1\,485,61\,\text{cm}^3 = \underline{ 1\,014,39\,\text{cm}^3}$

5. Schritt: Höhe des Wassers im Zylinder berechnen

Das Wasser, das in den Zylinder läuft, bildet einen neuen, kleineren Zylinder. Dieser hat den gleichen Durchmesser $d$ aber eine neue Höhe $h_W.$

$V= \pi \cdot \left(\frac{\,\text{d}}{2}\right)^2 \cdot\,\text{h}_{\text{W}}$

Rechenweg anzeigen

$\,\text{h}_{\text{W}}=\underline{ 4,08\,\text{cm}}$

6. Schritt: Gesamtfüllhöhe des Wassers berechnen

$17,91\,\text{cm} +4,08\,\text{cm} = 21,99\,\text{cm}$

Im zusammengesetzten Körper steht das Wasser also ca. $\underline{\underline{ 22,0\,\text{cm}}}$ hoch.

Lösung P4

Prozentuale Abnahme des Wasserverbrauchs berechnen

Informationen im ersten Diagramm:

Im Jahr 1990 verbrauchte jeder Einwohner pro Tag ca. $147\,\text{Liter}.$
Im Jahr 2010 verbrauchte jeder Einwohner pro Tag ca. $122\,\text{Liter}.$

Differenz im betrachteten Zeitraum: $147\,\text{Liter}-122\,\text{Liter} = 25\,\text{Liter}$
In Prozent entspricht das:

$\dfrac{25\,\text{Liter}}{147\,\text{Liter}} \cdot 100\,\% = \underline{\underline{ 17\,\% }}$

Von 1990 bis 2010 hat der Wasserverbrauch pro Kopf und Tag also um ca. $17\,\%$ abgenommen.

Wasserverbrauch für die Körperpflege berechnen

Information im ersten Diagramm:

Im Jahr 2015 verbrauchte jeder Einwohner pro Tag ca. $122\,\text{Liter}.$

Information im zweiten Diagramm:

Im Jahr 2015 wurde im Schnitt $35\,\%$ des Wassers für Körperpflege benutzt.

$122\,\text{Liter} \cdot \dfrac{35\,\%}{100\,\%} = \underline{\underline{ 42,7\,\text{Liter}}}.$

Im Jahr 2015 wurden täglich $42,7\,\text{Liter}$ Wasser pro Einwohner für die Körperpflege verwendet.

Wasserverbrauch im Jahr 2020 berechnen

Es handelt sich um eine exponentielle Abnahme, daher gilt:

$122\,\text{Liter}\cdot (1-0,01)^5$

$\,\text{n}= 5,$ da $2020-2015=5$

$122\,\text{Liter}\cdot (1-0,01)^5 = \underline{\underline{ 116\,\text{Liter}}}$

Im Jahr 2020 beträgt der durchschnittliche Wasserverbrauch pro Einwohner und pro Kopf voraussichtlich ca. $116\,\text{Liter}$ täglich.

Lösung P5

Definitionsmenge bestimmen

Einschränkung: Der Nenner eines Bruchs darf nicht Null sein.

Der erste Nenner $x$ ist für $x=0$ gleich Null
Der zweite Nenner $x+2$ ist für $x=-2$ gleich Null
Für den dritten Nenner gilt:
$\begin{array}[t]{rll} x^2+2x&=& 0\\[5pt] x\cdot (x+2)&=& 0 \end{array}$
Daraus folgt: $x=0$ und $(x+2)=0$
$\begin{array}[t]{rll} x+2&=& 0 &\quad \scriptsize \mid\;-2 \\[5pt] x&=& -2 \end{array}$

Für $x=0$ und $x=-2$ wird mindestens einer der Nenner gleich Null.

Daraus folgt also $\underline{\underline{ \mathbb{D} = \mathbb{R}\setminus \{-2;0\}}}.$

Lösungsmenge bestimmen

Gemeinsamen Hauptnenner für alle Brüche bestimmen:
Es gilt $x^2+2x = x\cdot (x+2).$ Ein möglicher Hauptnenner ist also $x\cdot(x+2).$

Multiplikation mit dem Hauptnenner:

Rechenweg anzeigen

$x_1=-2 \quad x_2=4$

Da $x=-2$ aus der Definitionsmenge ausgeschlossen ist, ist dieser Wert kein Teil der Lösungsmenge.

$\underline{\underline{ \mathbb{L} = \{4\}}}$

Lösung P6

Funktionsgleichung $\boldsymbol{p}$ ermitteln

$x$ -Koordinate des Scheitelpunkts bestimmen

Funktionsform für eine nach oben geöffnete Normalparabel: $y= (x-x_S)^2 + y_S$

Dabei sind $(x_S\mid y_S)$ die Koordinaten des Scheitelpunkts.

Da eine Normalparabel achsensymmetrisch ist, kann man mit den Werten $x=0$ und $x=6,$ die den gleichen Funktionswert besitzen, die $x$ -Koordinate des Scheitelpunktes berechnen. Dieser muss genau in der Mitte der beiden Werte liegen.

Es ist also $x_S=3.$

$y= (x-3)^2 +y_S$

$y$ -Koordinate des Scheitelpunkts berechnen

$R(0\mid 5)$ einsetzen:

$\begin{array}[t]{rll} y &=& (x-3)^2 + y_S \\[5pt] 5&=& (0-3)^2 + y_S \\[5pt] 5&=& 9+y_S \quad \scriptsize \mid\;-9 \\[5pt] -4&=& y_S \end{array}$

Die Funktionsgleichung der Parabel $p$ lautet also:

$\underline{\underline{ p:y= (x-3)^2 -4}}$

Tabelle ergänzen

Durch Einsetzen der gegebenen $x$ -Werte in die Funktionsgleichung und durch Nutzung der Achsensymmetrie ergibt sich:

$x$	$y$
$0$	$5$
$1$	$0$
$2$	$-3$
$3$	$-4$
$4$	$-3$
$5$	$0$
$6$	$5$

Steigung der Geraden berechnen

Die Parabel $p$ hat an der Stelle $x=0$ den Funktionswert $y=5.$ Sie schneidet die $y$ -Achse also im Punkt $R(0\mid 5).$ Die Koordinaten des Scheitelpunkts sind $S(3\mid -4).$

$\begin{array}[t]{rll} m &=& \dfrac{y_S -y_P}{x_S-x_P} \\[5pt] &=& \dfrac{-4-5}{3-0} \\[5pt] &=& \dfrac{-9}{3} \\[5pt] m&=& -3 \\[5pt] \end{array}$

Die Steigung der Geraden $g$ beträgt $\underline{\underline{ m=-3}}.$

Lösung P7

Baumdiagramm vervollständigen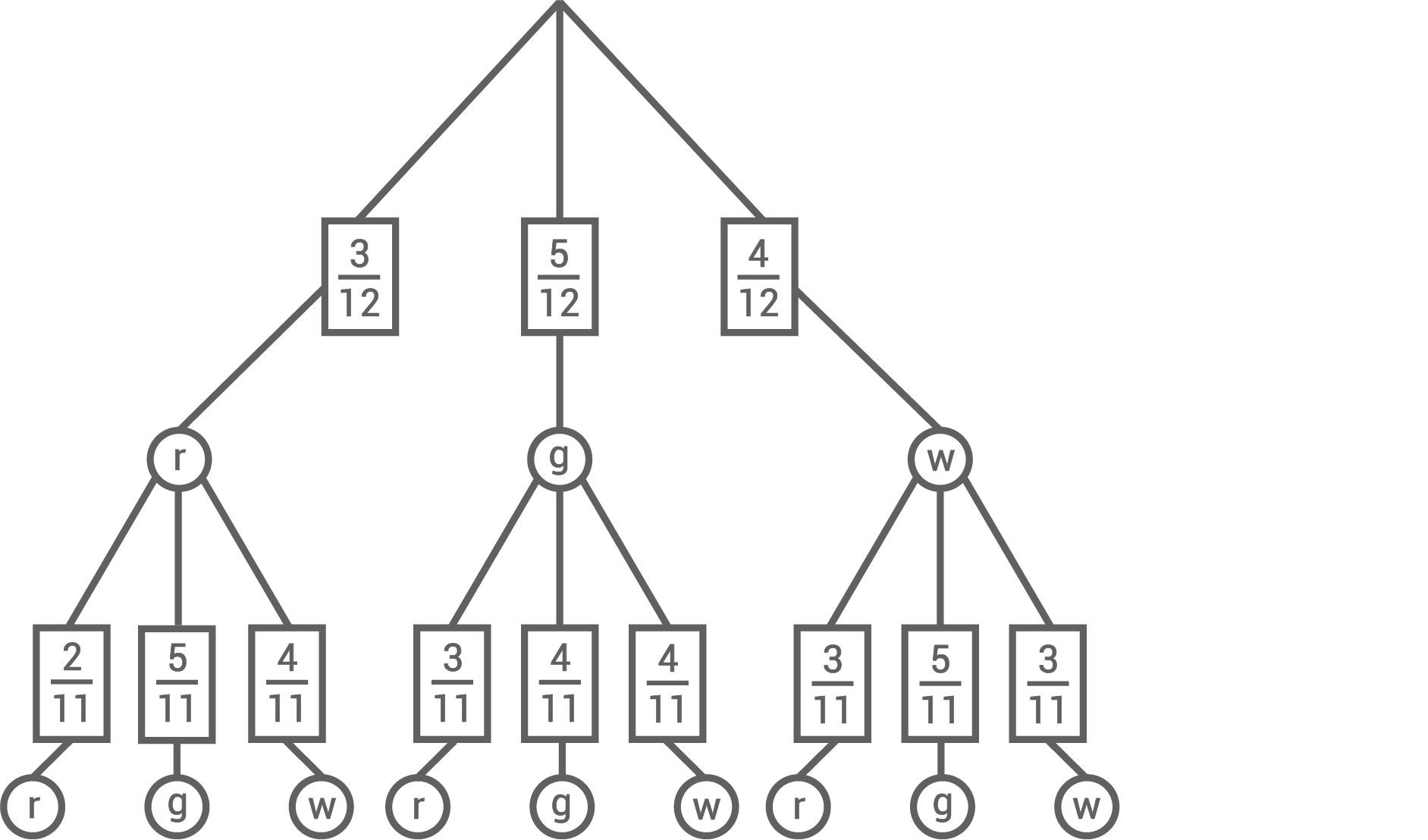

Wahrscheinlichkeiten berechnen

Mit der Produkt- und Summenregel ergibt sich:

Rechenweg anzeigen

$\,\text{P (genau ein rotes Gb)} = \dfrac{9}{22}= 41\%$

Mit einer Wahrscheinlichkeit von $41\%$ zieht Sofia genau ein rotes Gummibärchen.

Dass Sofia höchstens ein weißes Gummibärchen zieht, ist das Gegenereignis dazu, dass sie genau zwei weiße Gummibärchen zieht.

$\begin{array}[t]{rll} \,\text{P (zwei weiße Gb)} &=& P(\,\text{w};\,\text{w}) \\[5pt] &=& \dfrac{4}{12}\cdot \dfrac{3}{11} \\[5pt] &=& \dfrac{1}{11}\\[5pt] \end{array}$

$\,\text{P (höchstens ein weißes Gb)}$ $= 1- \dfrac{1}{11} = \dfrac{10}{11}=\underline{\underline{ 91\,\%}}$

Mit einer Wahrscheinlichkeit von $91\%$ zieht Sofia höchstens ein weißes Gummibärchen.

Lösung P8

Boxplots zuordnen

Wichtige Kennwerte bestimmen:

Da der Zentralwert und das untere Quartil gleich sind, helfen sie bei der Zuordnung nicht.
Minimum und Maximum kann nicht auf den Ranglisten abgelesen werden. Das obere Quartil muss also verwendet werden.

Das obere Quartil der ersten Rangliste ist auf Rangplatz 13 und beträgt daher $40.$
Das obere Quartil der zweiten Rangliste ist auf Rangplatz 10 und beträgt daher $36.$

Vergleichen zeigt, dass das obere Quartil von Boxplot (1) dem der ersten Rangliste entspricht und das obere Quartil von Boxplot (2) dem der zweiten Rangliste entspricht.

Ranglisten ergänzen

Kennwerte von Boxplot (1):

Minimum: $12;$ In der ersten Rangliste von Klasse 7a muss Rangplatz 1 also den Wert $12$ haben.
Maximum: $46;$ In der ersten Rangliste von Klasse 7a muss Rangplatz $17$ also den Wert $46$ haben.
Unteres Quartil: $22;$ In der ersten Rangliste von Klasse 7a muss Rangplatz 5 also den Wert $22$ haben.

Kennwerte von Boxplot (2):

Minimum: $6;$ In der zweiten Rangliste von Klasse 7b muss Rangplatz 1 also den Wert $6$ haben.
Maximum: $48;$ In der zweiten Rangliste von Klasse 7b muss Rangplatz $13$ also den Wert $48$ haben.
Unteres Quartil: $22;$ In der zweiten Rangliste von Klasse 7b muss Rangplatz 4 also den Wert $22$ haben.

Die übrigen Werte können mit Zahlen aufgefüllt werden, die in die Reihenfolge passen.
Eine mögliche Lösung:

Rangplatz	Klasse 7a
$1$	$\color{#db2416}{12 }$
$2$	$\color{#87c800}{14}$
$3$	$\color{#87c800}{16}$
$4$	$\color{#87c800}{18}$
$5$	$\color{#db2416}{22}$
$6$	$23$
$7$	$25$
$8$	$28$
$9$	$28$
$10$	$35$
$11$	$36$
$12$	$38$
$13$	$40$
$14$	$\color{#87c800}{41}$
$15$	$\color{#87c800}{42}$
$16$	$\color{#87c800}{43}$
$17$	$\color{#db2416}{46}$

Rangplatz	Klasse 7b
$1$	$\color{#db2416}{6}$
$2$	$\color{#87c800}{10}$
$3$	$\color{#87c800}{16}$
$4$	$\color{#db2416}{22}$
$5$	$24$
$6$	$25$
$7$	$28$
$8$	$28$
$9$	$29$
$10$	$36$
$11$	$38$
$12$	$40$
$13$	$\color{#db2416}{48}$

Rote Werte müssen exakt übereinstimmen. Grüne Werte können verschieden sein.

Aussage überprüfen

Der Zentralwert der Rangliste von Klasse 7a liegt auf Rangplatz 9. Der Wert $23\,\text{m}$ liegt auf Rangplatz 6, der Wert $36\,\text{m}$ liegt auf Rangplatz 11.
Es wird also jeweis unterhalb und oberhalb des Zentralwerts ein Wert entfernt. Es befinden sich nun noch $7$ Werte unterhalb und $7$ Werte oberhalb des ursprünglichen Zentralwerts. Damit bleibt der Zentralwert erhalten und Alex hat recht.