Wahlbereich
Aufgabe W1
a)
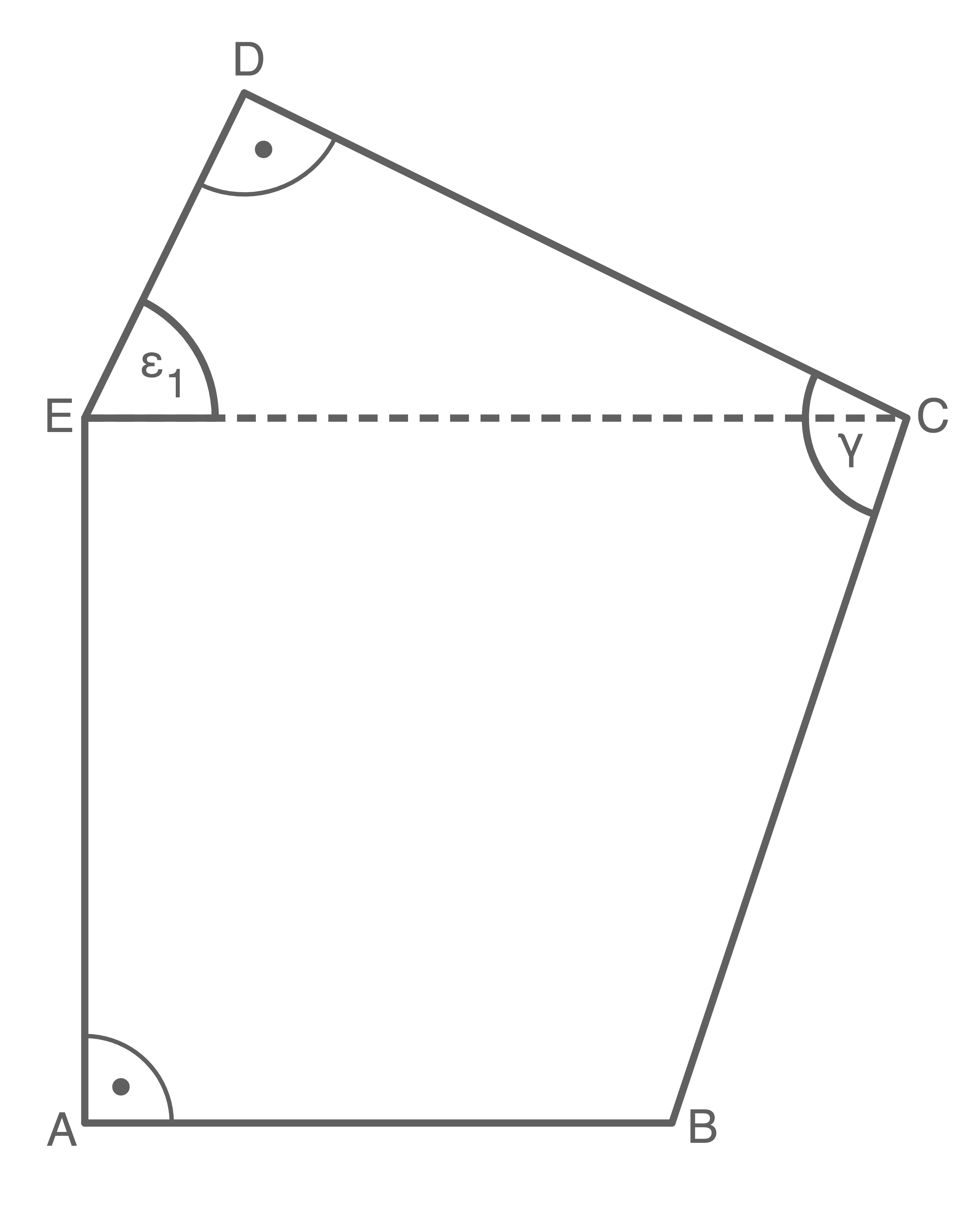
(5,5 P)
b)
lm Rechteck  liegen die gleichseitigen Dreiecke
liegen die gleichseitigen Dreiecke  und
und 
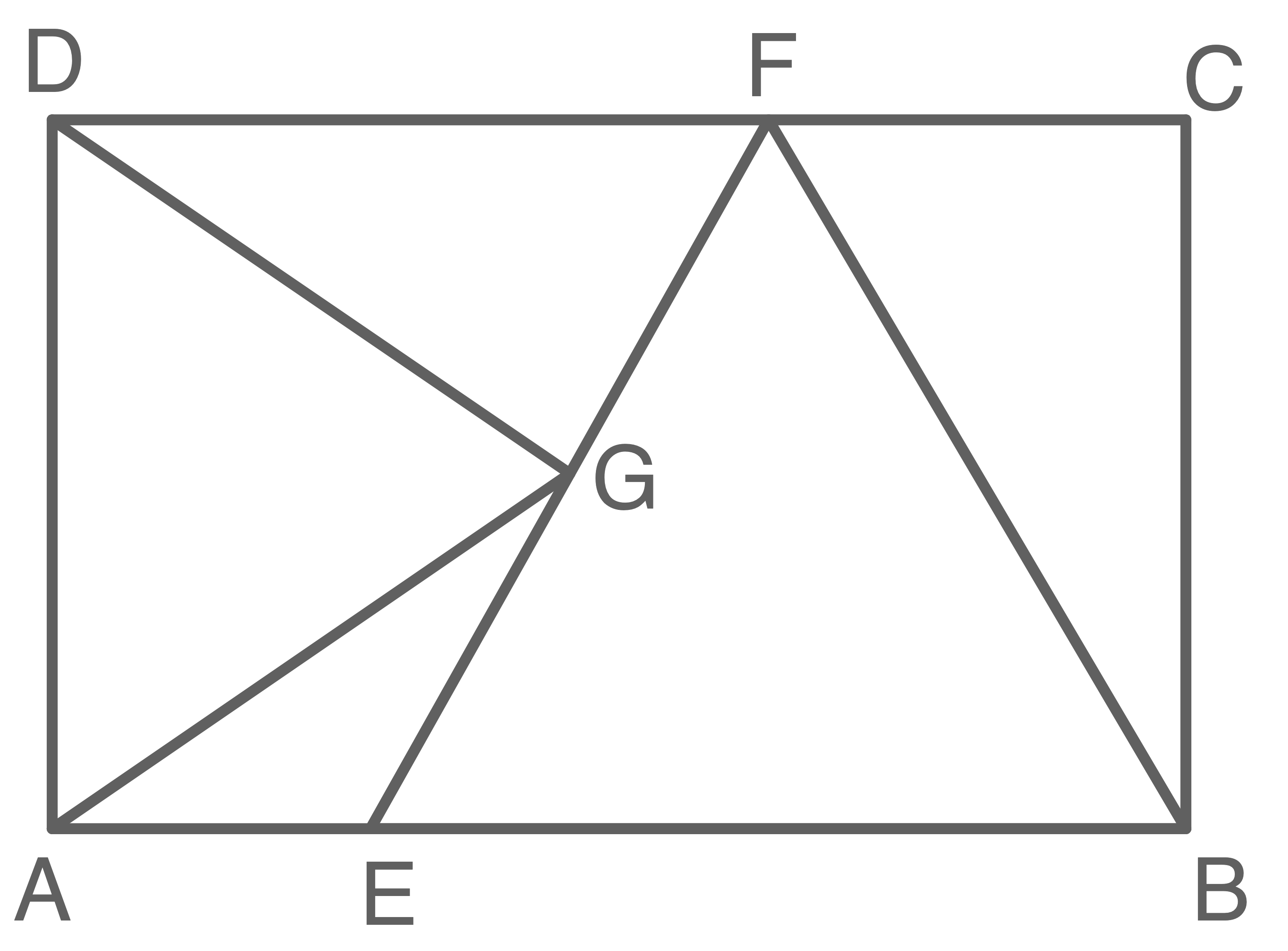 Es gilt:
Es gilt:

Weise ohne Verwendung gerundeter Werte nach, dass für den Flächeninhalt des Rechtecks gilt:
gilt:


Weise ohne Verwendung gerundeter Werte nach, dass für den Flächeninhalt des Rechtecks
(4,5 P)
Aufgabe W2
a)
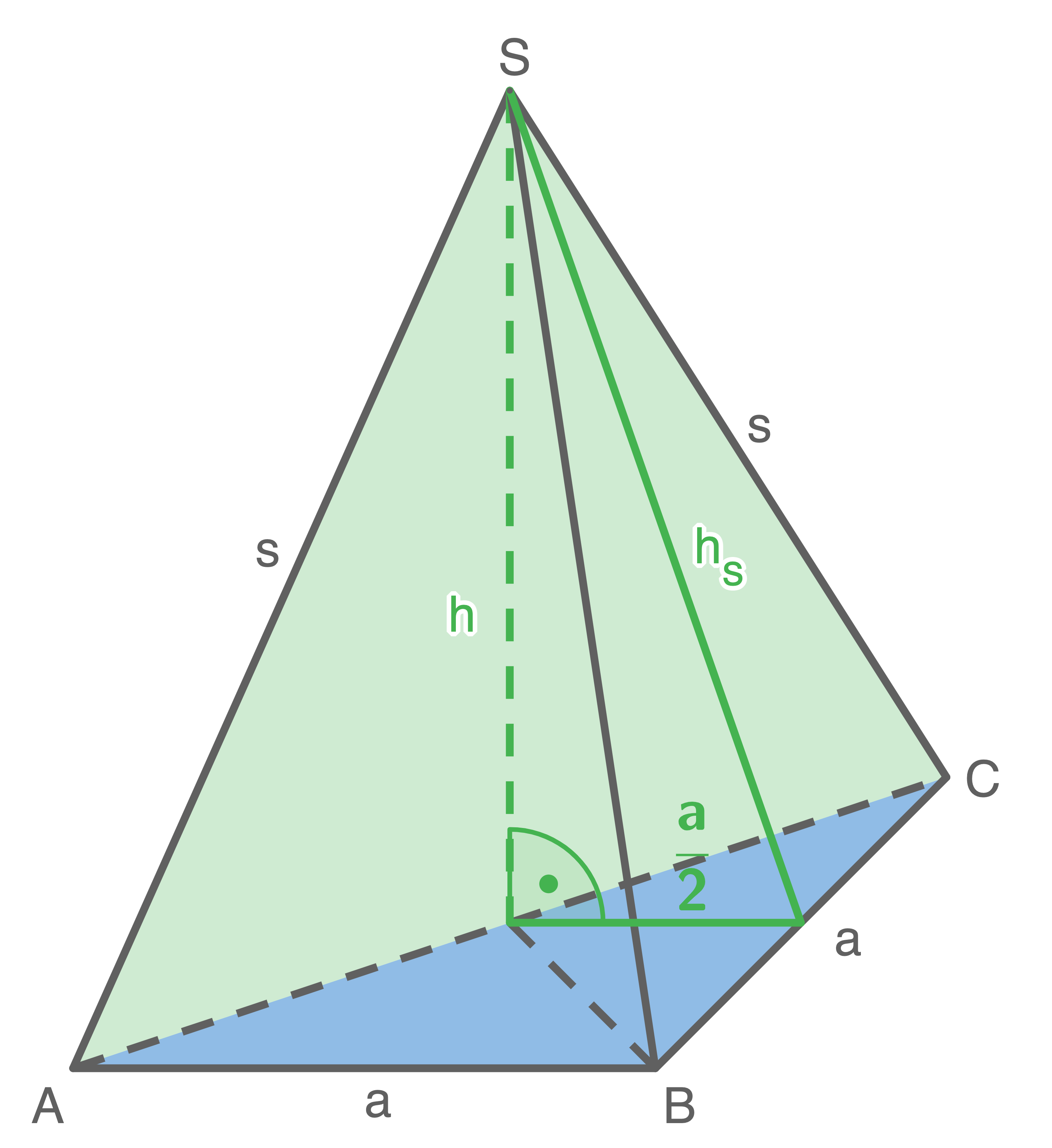
Von einer regelmäßigen achtseitigen Pyramide sind bekannt:


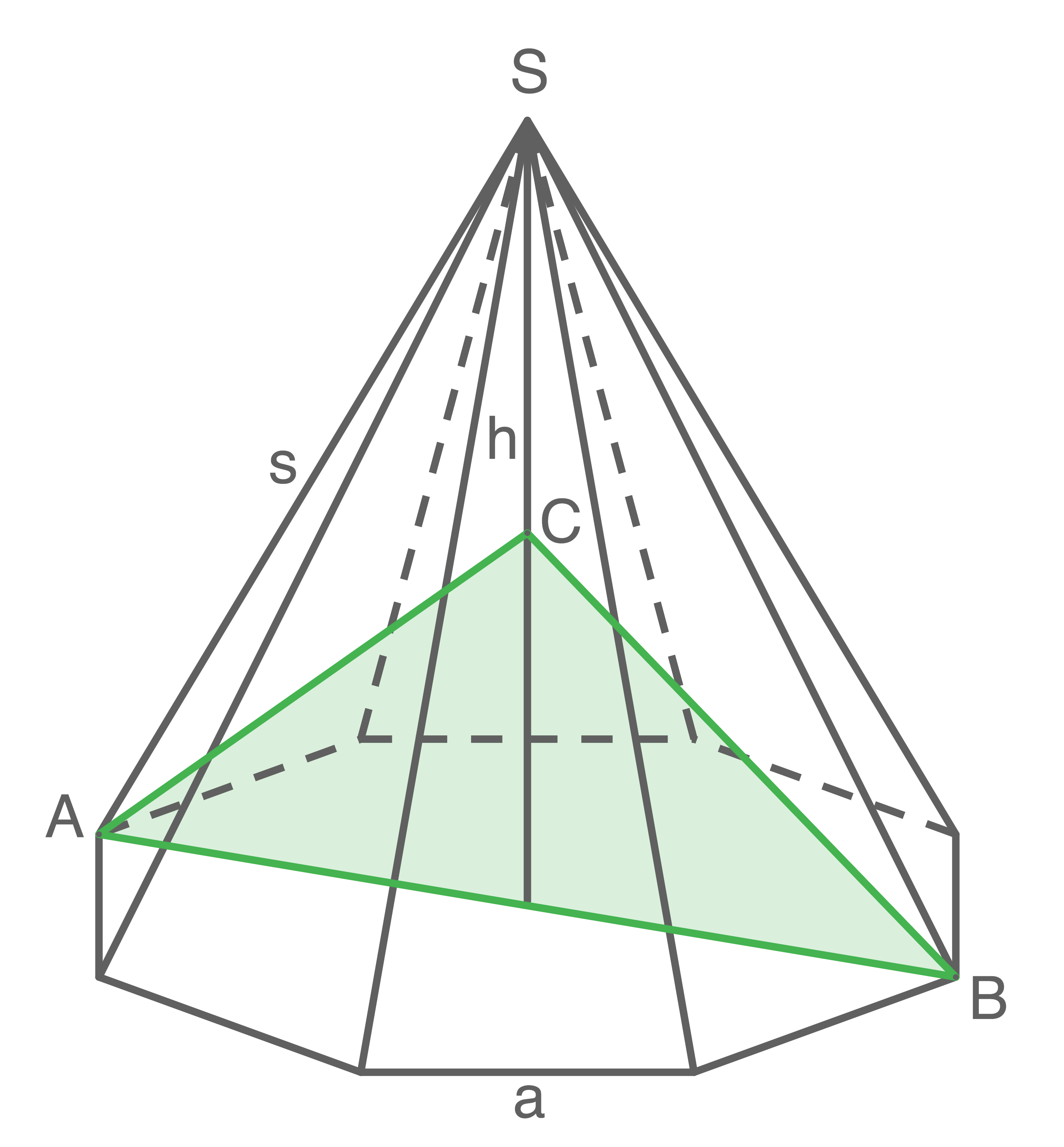 Der Punkt
Der Punkt  liegt auf der Höhe
liegt auf der Höhe  der Pyramide. Das Dreieck
der Pyramide. Das Dreieck  soll den gleichen Flächeninhalt haben wie eines der Manteldreiecke.
Berechne die Länge von
soll den gleichen Flächeninhalt haben wie eines der Manteldreiecke.
Berechne die Länge von 

(5,5 P)
b)
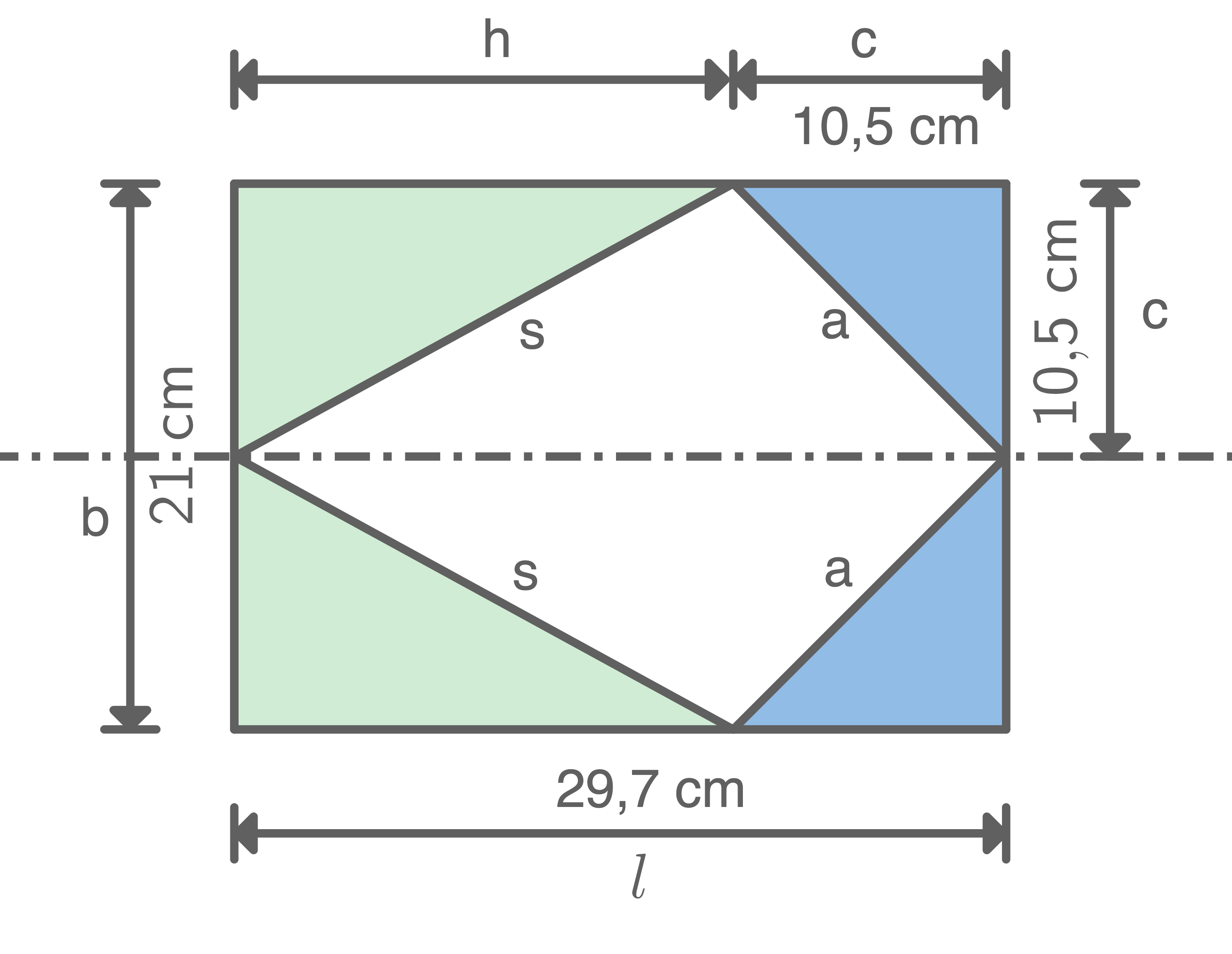
Von einem DIN-A4-Blatt  werden die vier eingefärbten Dreiecke abgeschnitten.
werden die vier eingefärbten Dreiecke abgeschnitten.
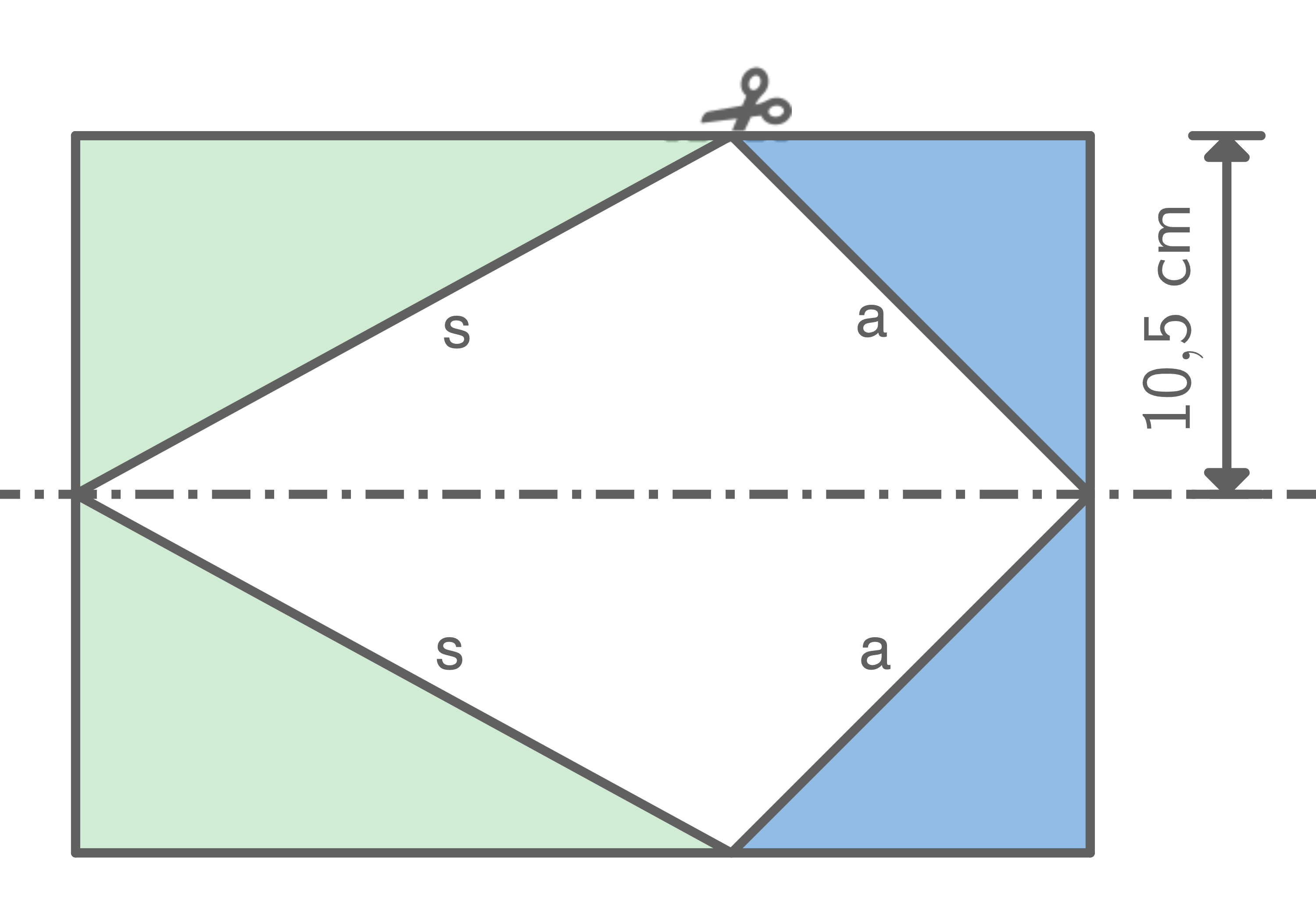
Mit diesen vier Dreiecken werden die Diagonalschnittfläche und die Grundfläche einer halben massiven quadratischen Pyramide vollständig beklebt.
und die Grundfläche einer halben massiven quadratischen Pyramide vollständig beklebt.
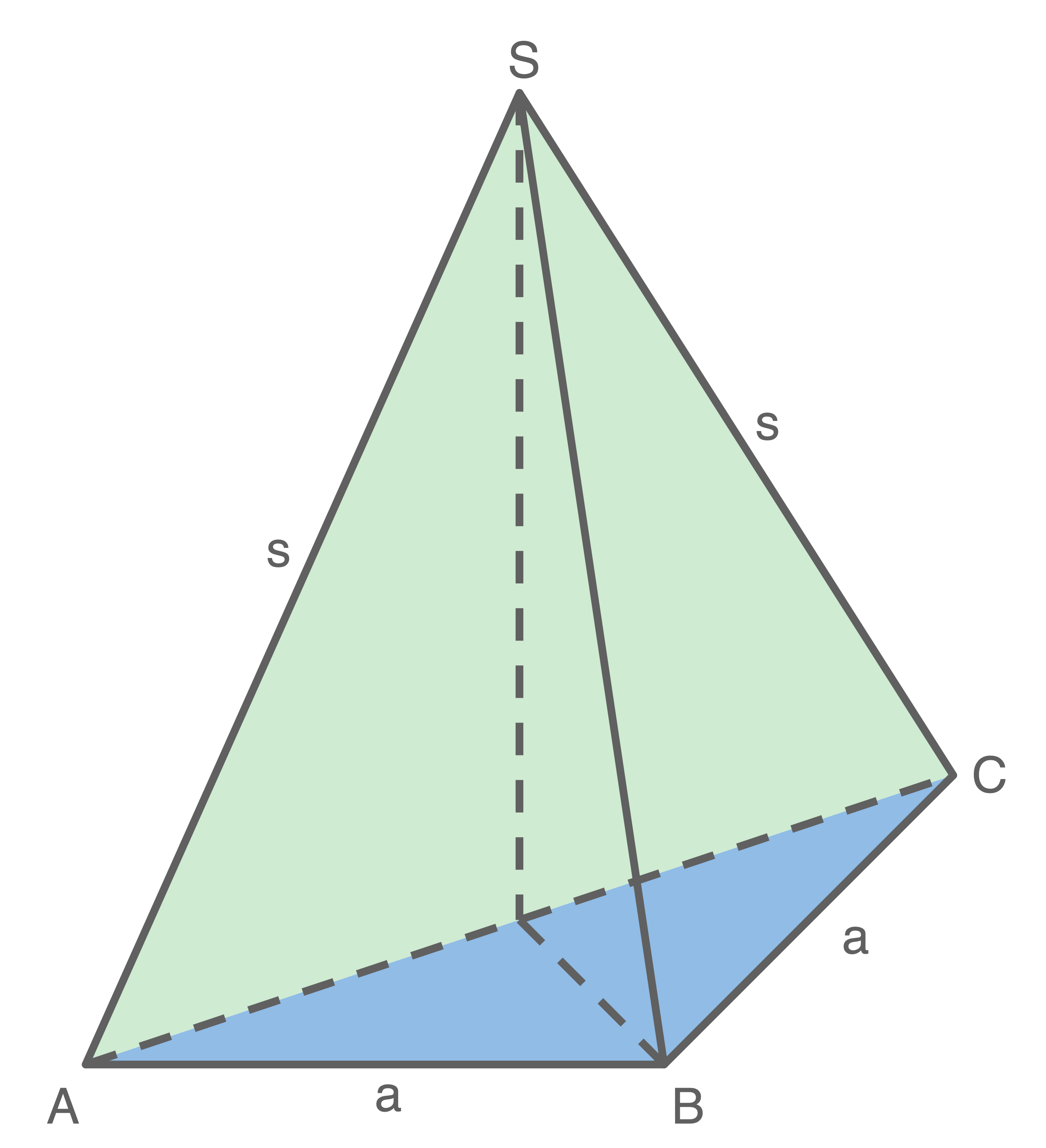 Lena behauptet: „Die beiden Manteldreiecke
Lena behauptet: „Die beiden Manteldreiecke  und
und  haben zusammen den gleichen Flächeninhalt wie die Restfläche des DlN-A4-Blatts.“
Hat Lena Recht? Begründe durch Rechnung.
haben zusammen den gleichen Flächeninhalt wie die Restfläche des DlN-A4-Blatts.“
Hat Lena Recht? Begründe durch Rechnung.

Mit diesen vier Dreiecken werden die Diagonalschnittfläche

(4,5 P)
Aufgabe W3
a)
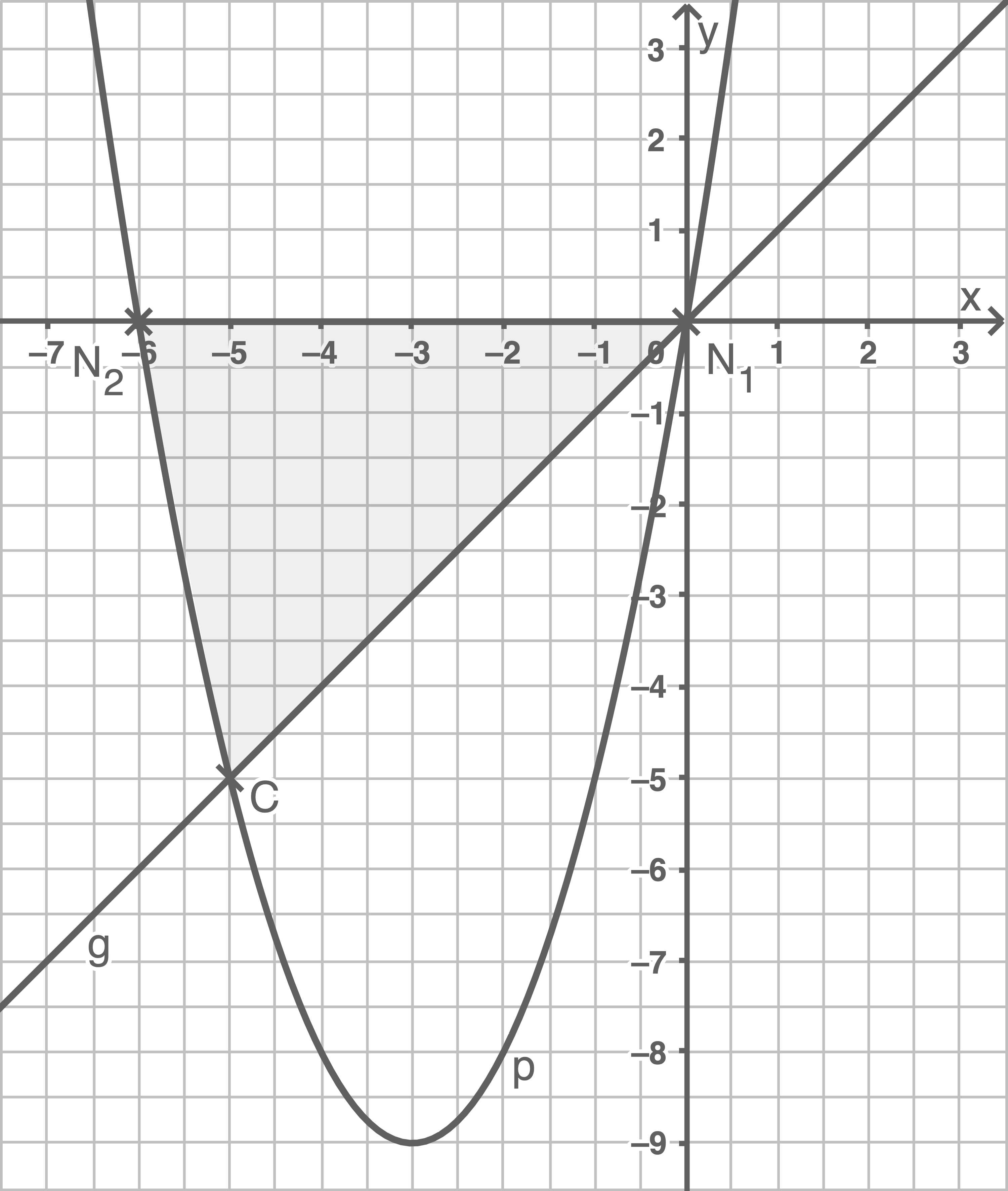
Die nach oben geöffnete Normalparabel  hat mit der
hat mit der  -Achse die Schnittpunkte
-Achse die Schnittpunkte  und
und  Sie schneidet die
Sie schneidet die  -Achse im Punkt
-Achse im Punkt  Die Parabel
Die Parabel  hat die Funktionsgleichung
hat die Funktionsgleichung  und schneidet die
und schneidet die  -Achse im Punkt
-Achse im Punkt  Durch die Scheitelpunkte
Durch die Scheitelpunkte  und
und  der beiden Parabeln verläuft die Gerade
der beiden Parabeln verläuft die Gerade 
Berechne die Funktionsgleichung der Geraden Der Punkt
Der Punkt  ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke 
Die Gerade mit der Steigung
mit der Steigung  geht durch
geht durch 
Unter welchen Winkeln schneiden sich die Geraden und
und  ?
?
Begründe deine Antwort durch Rechnung oder Argumentation.
Berechne die Funktionsgleichung der Geraden
Die Gerade
Unter welchen Winkeln schneiden sich die Geraden
Begründe deine Antwort durch Rechnung oder Argumentation.
(5,5 P)
b)
Die Parabel  mit der Funktionsgleichung
mit der Funktionsgleichung  schneidet die
schneidet die  -Achse in den Punkten
-Achse in den Punkten  und
und 
Die Gerade mit der Funktionsgleichung
mit der Funktionsgleichung  schneidet die Parabel in den Punkten
schneidet die Parabel in den Punkten  und
und 
Berechne den Flächeninhalt des Dreiecks Die Gerade
Die Gerade  mit der Funktionsgleichung
mit der Funktionsgleichung  schneidet die Parabel in den Punkten
schneidet die Parabel in den Punkten  und
und  Peter behauptet: „Die Steigung der Geraden
Peter behauptet: „Die Steigung der Geraden  ist nur halb so groß wie die der Geraden
ist nur halb so groß wie die der Geraden  Daher ist der Flächeninhalt des Dreiecks
Daher ist der Flächeninhalt des Dreiecks  auch nur halb so groß wie der des Dreiecks
auch nur halb so groß wie der des Dreiecks 
Hat Peter Recht? Begründe rechnerisch.
Die Gerade
Berechne den Flächeninhalt des Dreiecks
Hat Peter Recht? Begründe rechnerisch.
(4,5 P )
Aufgabe W4
a)
Die beiden Glücksräder werden gedreht. Nachdem sie stehen bleiben, erkennt man im Sichtfenster eine Kombination zweier Symbole.
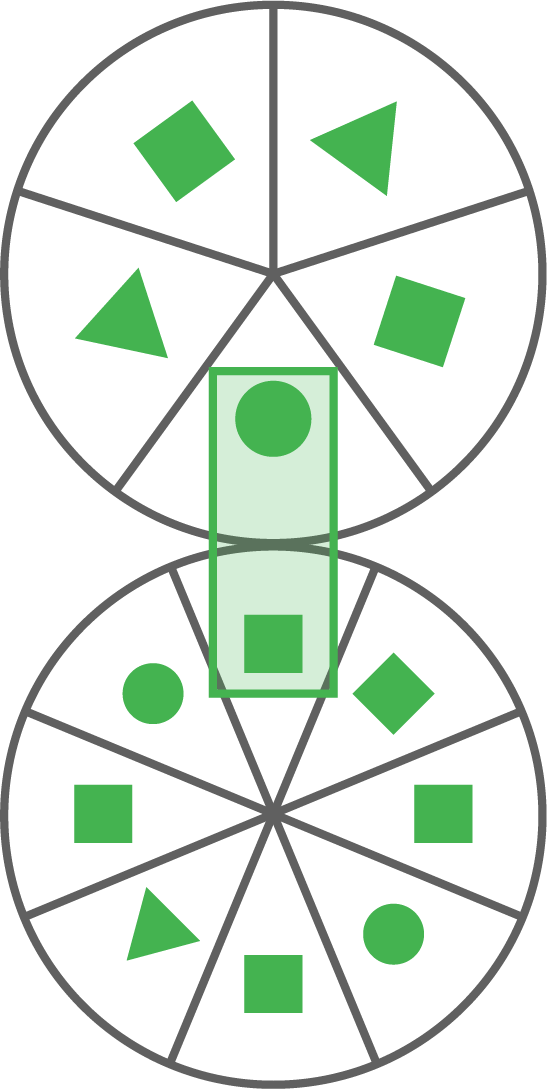 Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole im Sichtfenster zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird der abgebildete Gewinnplan geprüft.
Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole im Sichtfenster zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird der abgebildete Gewinnplan geprüft.
Berechne den Erwartungswert.
Der Gewinnplan soll so verändert werden, dass das Spiel fair wird.
Wie hoch muss dann der Gewinn für das Ereignis „Kreis und Dreieck“ sein, wenn alles andere unverändert bleibt?

| Ereignis | Gewinn |
|---|---|
| gleiche Symbole | |
| Kreis und Dreieck | |
| restliche Möglichkeiten | kein Gewinn |
| Einsatz pro Spiel: |
|
(5,5 P)
b)
Thea trainiert Aufschläge beim Volleyball (siehe Skizze).
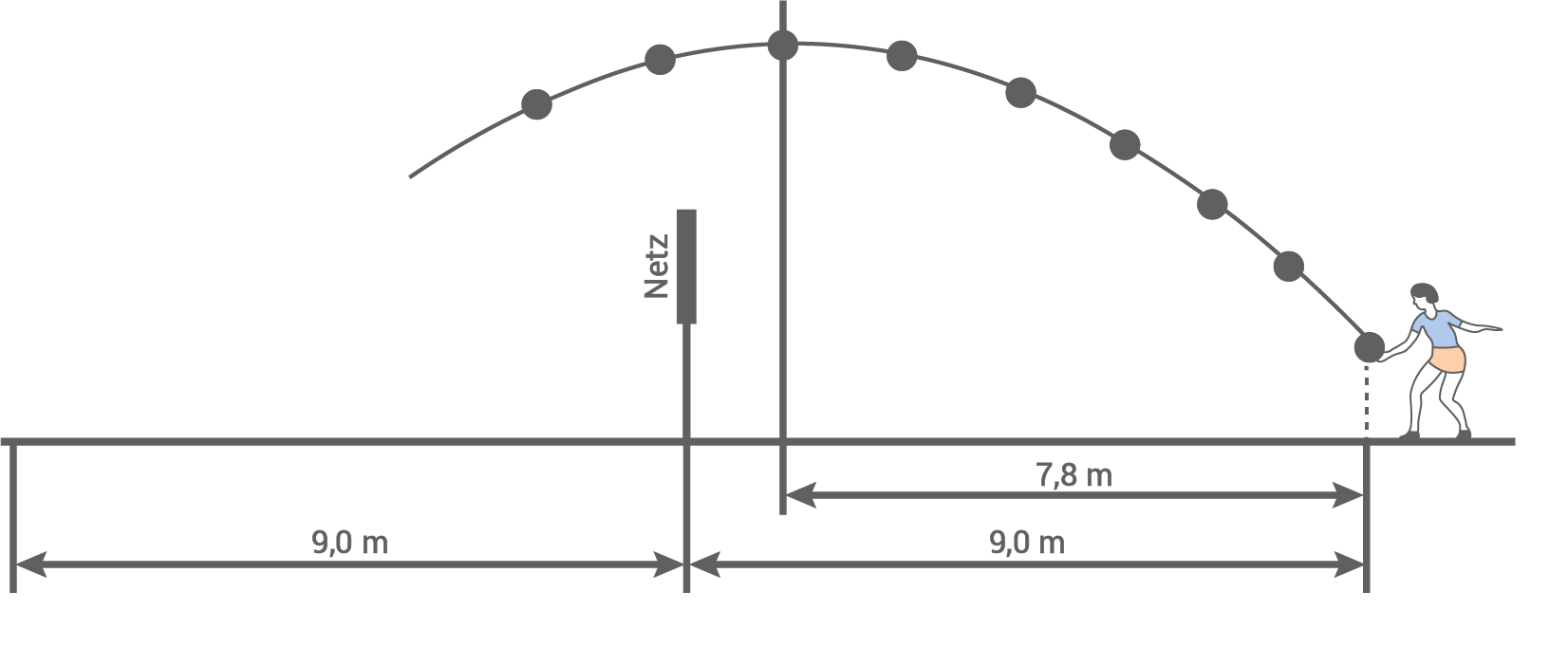 Die Flugkurve des Balles lässt sich mit einer Funktionsgleichung der Form
Die Flugkurve des Balles lässt sich mit einer Funktionsgleichung der Form  annähernd beschreiben. Der Ball verlässt beim Aufschlag von unten die Hand in einer Höhe von
annähernd beschreiben. Der Ball verlässt beim Aufschlag von unten die Hand in einer Höhe von  über der Grundlinie.
über der Grundlinie.
Nach (horizontal gemessen) erreicht die Flugkurve des Balles ihre maximale Höhe von
(horizontal gemessen) erreicht die Flugkurve des Balles ihre maximale Höhe von 
Gib eine mögliche Funktionsgleichung der zugehörigen Parabel an.
ln welchem Abstand überquert der Ball das
an.
ln welchem Abstand überquert der Ball das  hohe Netz?
Die Grundlinien des Volleyballspielfeldes sind jeweils
hohe Netz?
Die Grundlinien des Volleyballspielfeldes sind jeweils  vom Netz entfernt (siehe Skizze).
vom Netz entfernt (siehe Skizze).
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?

Nach
Gib eine mögliche Funktionsgleichung der zugehörigen Parabel
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
(4,5 P)
Lösung W1
a)
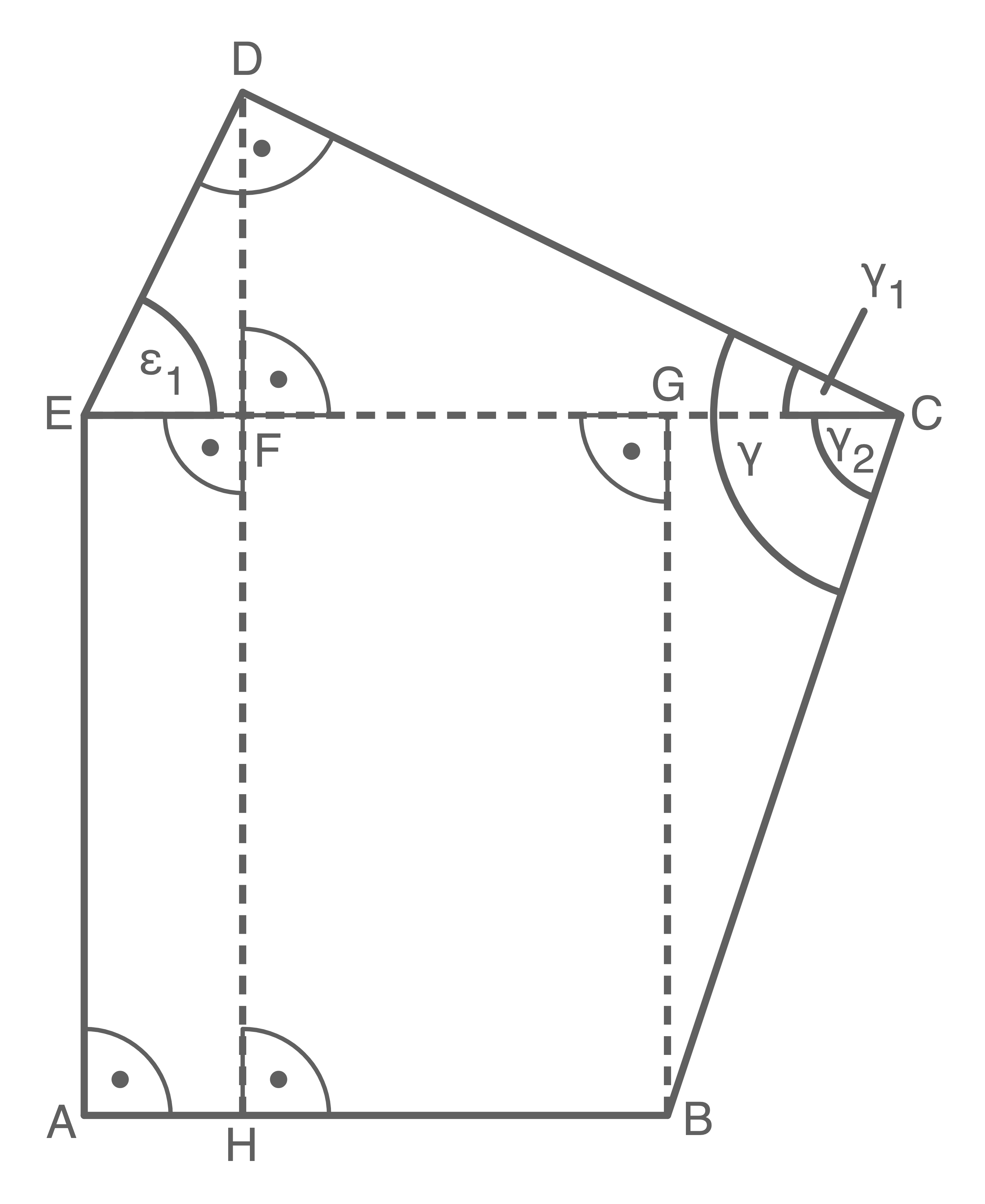
b)
Formel zur Berechnung des Flächeninhalts:  In einem gleichseitigen Dreieck sind alle Winkel
In einem gleichseitigen Dreieck sind alle Winkel  groß:
groß:
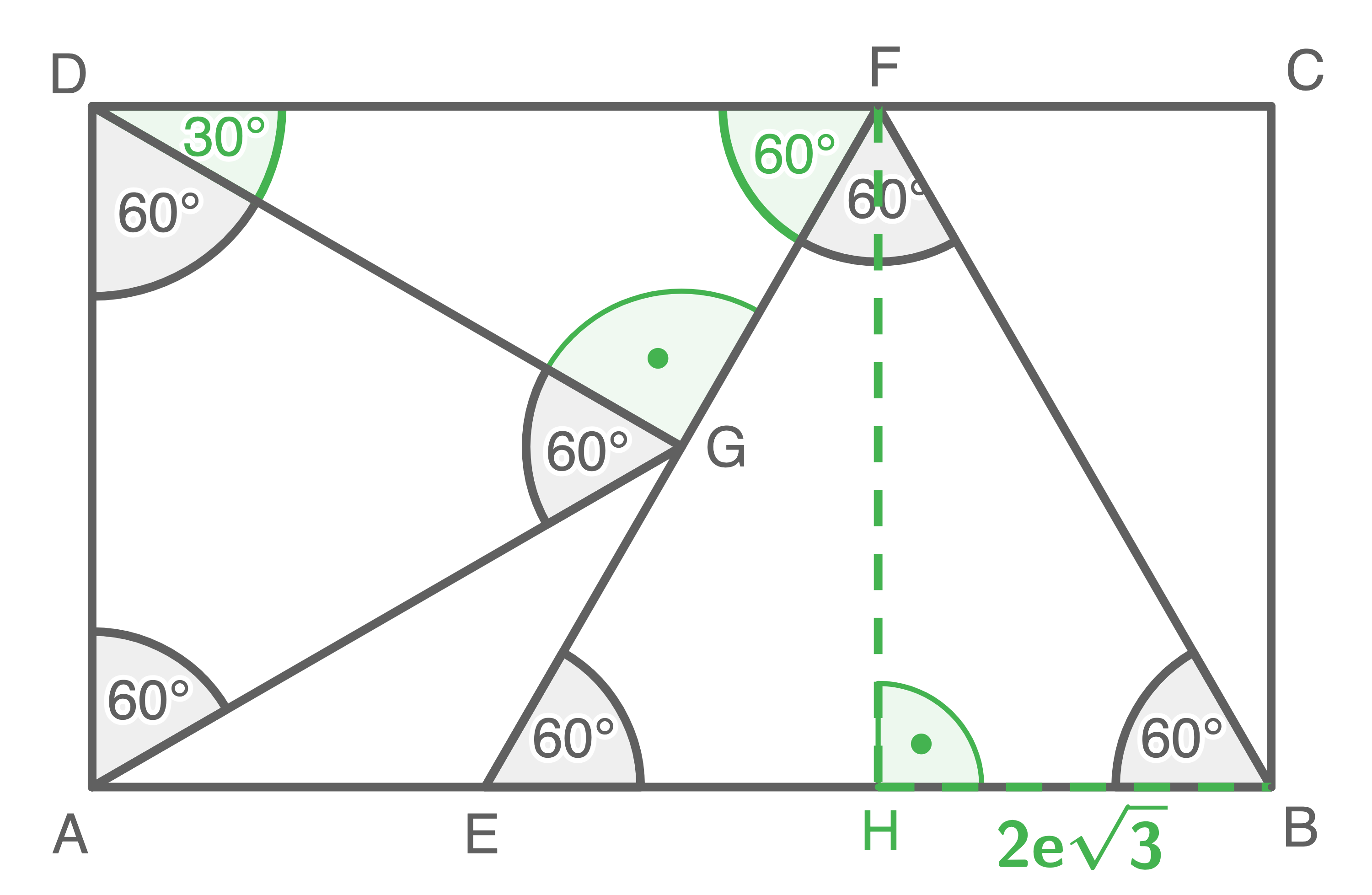 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\tan(60^{\circ})&=&\dfrac{\overline{HF}}{2\mathrm{e}\sqrt{3}} \quad \scriptsize \mid\; \cdot 2 \mathrm{e}\sqrt{3} \\[5pt]
\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3} &=& \overline{HF}\\[5pt]
\overline{HF} &=&\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3}\\[5pt]
\overline{HF}&=&\underline{ 6\mathrm{e}} \quad = \overline{AD} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f997c82a1f730ef4e12dee8337ab28128c28652c047b585890ecd112753a6279?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Da in einem gleichseitigen Dreieck alle Seiten gleich lang sind, gilt
berechnen
Da in einem gleichseitigen Dreieck alle Seiten gleich lang sind, gilt 
![\(\begin{array}[t]{rll}
\cos(30^{\circ}) &=& \dfrac{\overline{DG}}{\overline{DF}} \\[5pt]
\cos(30^{\circ}) &=& \dfrac{6\mathrm{e}}{\overline{DF}}\quad \scriptsize \mid\; \cdot \overline{DF}\\[5pt]
\cos(30^{\circ}) \cdot \overline{DF} &=& 6\mathrm{e} \quad \scriptsize \mid\; :\cos(30^{\circ}) \\[5pt]
\overline{DF} &=& \dfrac{6\mathrm{e}}{\cos(30^{\circ})} \\[5pt]
\overline{DF} &=& \underline{ 4 \mathrm{e}\sqrt{3}}
\end{array}\)](https://mathjax.schullv.de/c64f3b29f550f2f74e9d1070e1478d57d94cb82bbafb8c3c587fdf9963cc7a35?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\overline{DC}&=& \overline{DF} + \overline{FC}\\[5pt]
&=& 4 \mathrm{e}\sqrt{3} + 2 \mathrm{e}\sqrt{3}\\[5pt]
&=& \underline{ 6\mathrm{e}\sqrt{3}}
\end{array}\)](https://mathjax.schullv.de/85682e3d34adf3dc1aac7a56ea4696dcabf3cc01033157731b0d2c346ec6588a?color=5a5a5a) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& \overline{AD} \cdot \overline{DC} \\[5pt]
&=& 6\mathrm{e} \cdot 6\mathrm{e}\sqrt{3} \\[5pt]
&=& \underline{\underline{ 36\mathrm{e}^2\sqrt{3}}}
\end{array}\)](https://mathjax.schullv.de/f157043d0028e83389606a3be4906c36a67460f457fb334132e65f48ac7c30d4?color=5a5a5a) Damit ist die Aussage bewiesen.
Damit ist die Aussage bewiesen.

Lösung W2
a)
1. Schritt: Flächeninhalt des Manteldreiecks berechnen
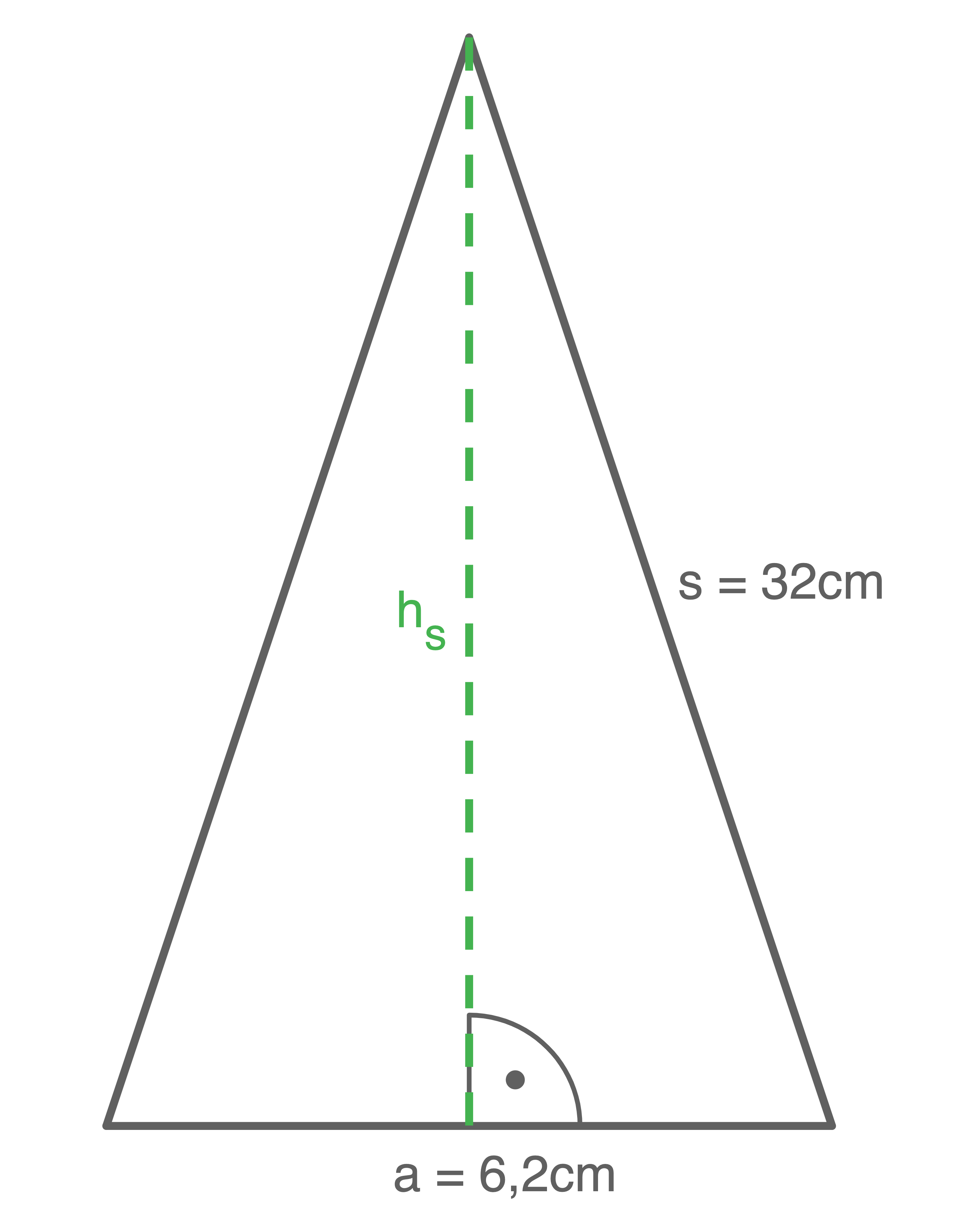 Da die Pyramide regelmäßig ist, sind die Manteldreiecke gleichschenklig und es gilt:
Da die Pyramide regelmäßig ist, sind die Manteldreiecke gleichschenklig und es gilt:
![\(\begin{array}[t]{rll}
A_{\,\text{Manteldreieck}}&=&\dfrac{1}{2} \cdot a \cdot h_s \\[5pt]
&=&\dfrac{1}{2} \cdot 6,2\,\text{cm} \cdot 31,85\,\text{cm} \\[5pt]
&= &\underline{ 98,74\,\text{cm}^2}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8128474d47eb08f86f8e8314aa41bd71ecdaf0cbc951ccfac7a05ef4323a901c?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Die Grundfläche der Pyramide lässt sich in acht gleichschenklige Dreiecke einteilen:
berechnen
Die Grundfläche der Pyramide lässt sich in acht gleichschenklige Dreiecke einteilen:
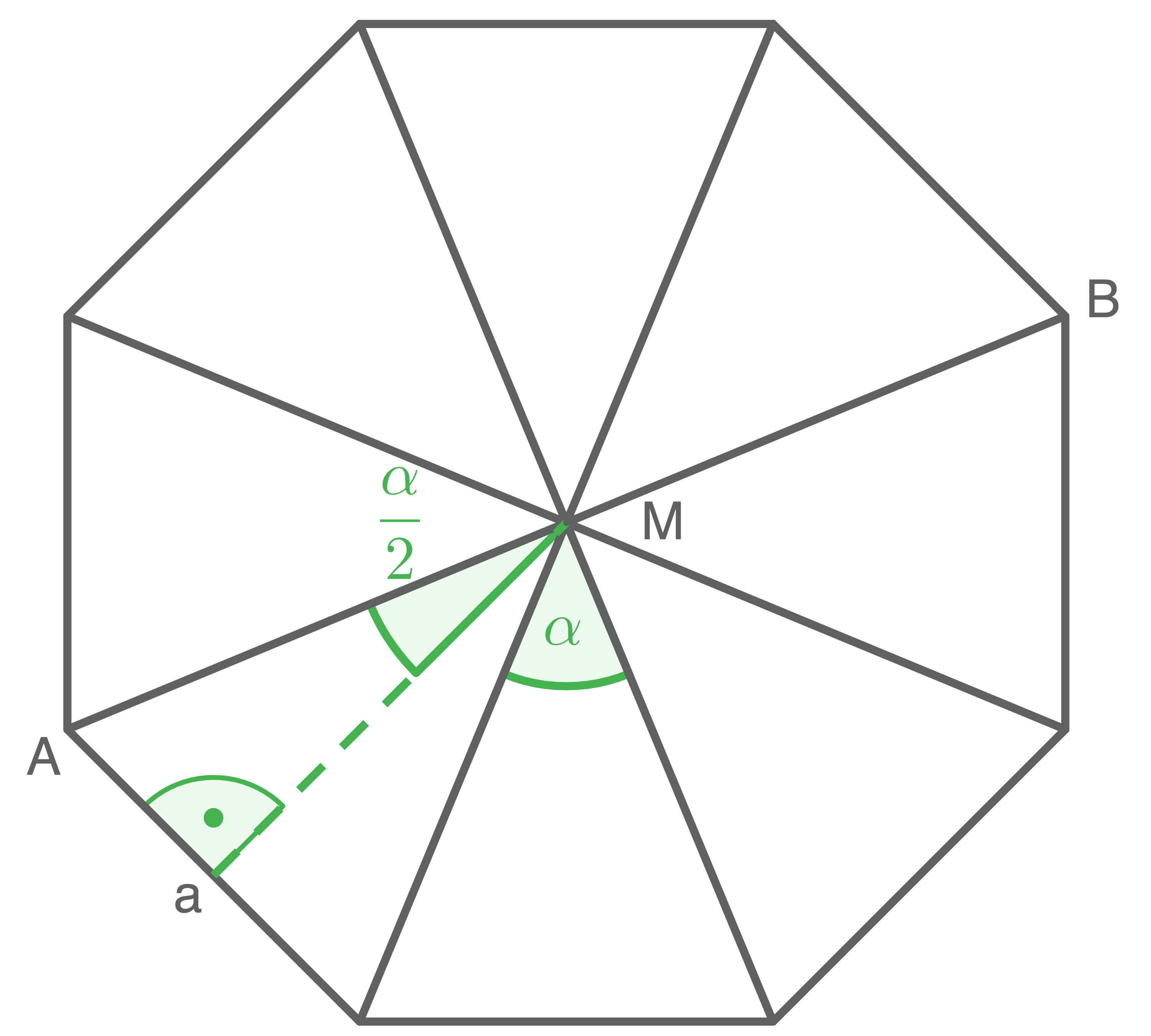
![\(\begin{array}[t]{rll}
\alpha&=& 360^{\circ}:8 \\[5pt]
&=& 45^{\circ}
\end{array}\)](https://mathjax.schullv.de/be2ddfc757b74964274e70b9de13be6519698b1301ea5459119f8dc9070011fe?color=5a5a5a)
![\(\begin{array}[t]{rll}
\sin\left(\dfrac{\alpha}{2}\right)&=&\dfrac{\dfrac{a}{2}}{\overline{AM}} \\[5pt]
\sin(22,5°)&=&\dfrac{3,1\,\text{cm}}{\overline{AM}} \quad \scriptsize \mid\; \cdot \overline{AM}\\[5pt]
\sin(22,5°)\cdot \overline{AM} &=& 3,1\,\text{cm} \quad \scriptsize \mid\; : \sin(22,5^{\circ} ) \\[5pt]
\overline{AM} &=& \dfrac{3,1\,\text{cm}}{ \sin(22,5^{\circ}) } \\[5pt]
\overline{AM} &= &8,1\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a1c210361b5570e016187e8d54c623b3b2f30e7601226ba18b080e7fca9d011a?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overline{AB}&=& \overline{AM}\cdot 2 \\[5pt]
&=& 8,1\,\text{cm} \cdot 2 \\[5pt]
&=& \underline{ 16,2\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/be84e74c04eb056dcc3c7cb17a35099b6f1c336f3f9d66aadf1f0c933860e0ec?color=5a5a5a) 3. Schritt: Höhe des Dreiecks
3. Schritt: Höhe des Dreiecks  berechnen
berechnen
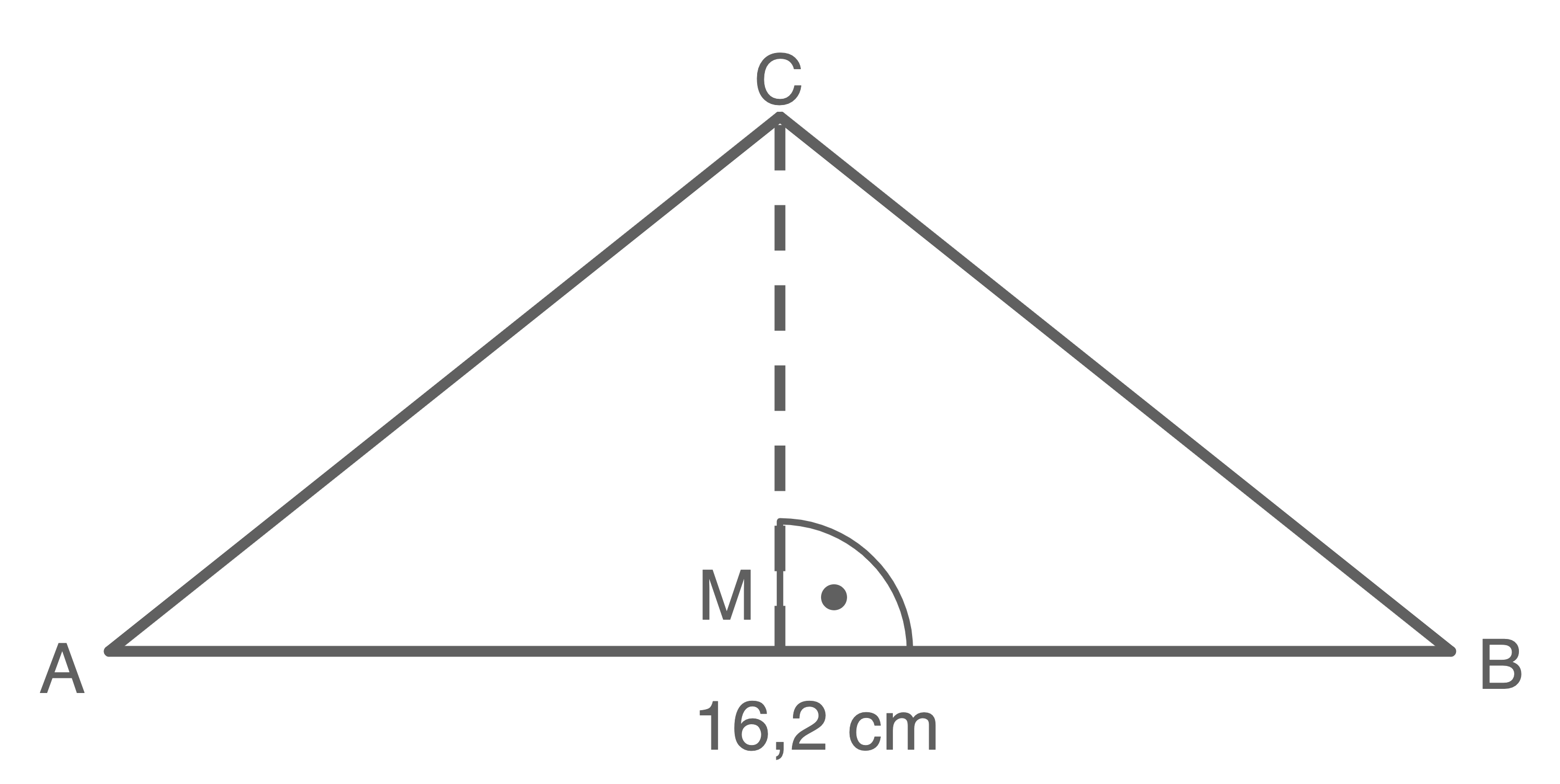

![\(\begin{array}[t]{rll}
A_{ABC}&=&\dfrac{1}{2} \cdot \overline{AB} \cdot \overline{MC} \\[5pt]
98,74\,\text{cm}^2&=&\dfrac{1}{2} \cdot 16,2\,\text{cm} \cdot \overline{MC} \\[5pt]
98,74\,\text{cm}^2&=& 8,1\,\text{cm} \cdot \overline{MC} \quad \scriptsize \mid\; :8,1 \,\text{cm} \\[5pt]
\dfrac{ 98,74\,\text{cm}^2}{ 8,1\,\text{cm}} &=& \overline{MC} \\[5pt]
\overline{MC} &=& \dfrac{ 98,74\,\text{cm}^2}{ 8,1\,\text{cm}}\\[5pt]
\overline{MC} &=& \underline{ 12,19\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/eda3ce87d60a1d42169806145e6e82cda5b03b1be0284f351d90b2331bed99e8?color=5a5a5a) 4. Schritt: Höhe der Pyramide berechnen
4. Schritt: Höhe der Pyramide berechnen
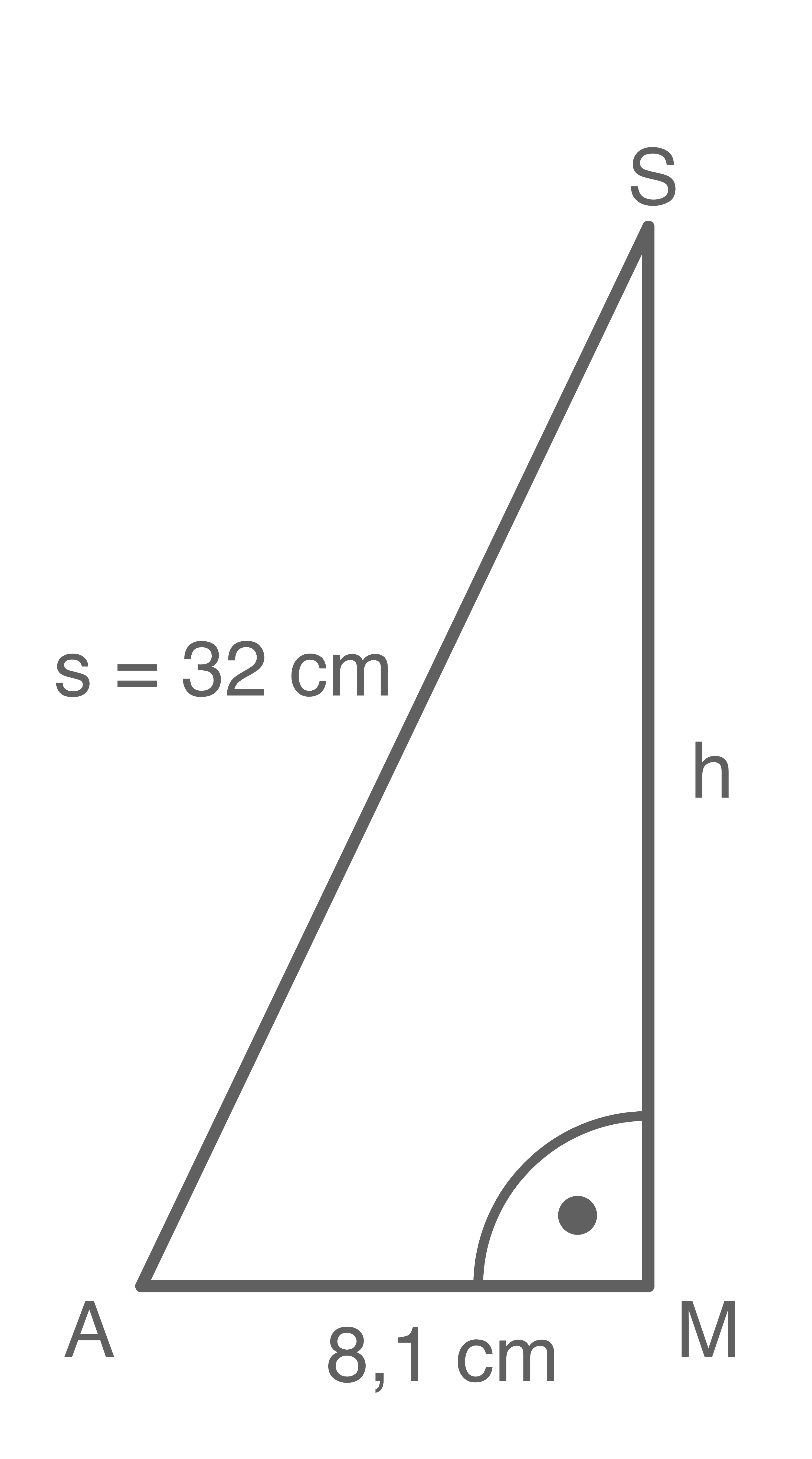 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{SC}&=& h-\overline{MC} \\[5pt]
&=& 30,96\,\text{cm}-12,19\,\text{cm} \\[5pt]
&=&18,77\,\text{cm}\\[5pt]
\overline{SC}&=& \underline{\underline{ 18,8\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/a15342055a4c8ecdebd9068d0732f689e3f741a51d9fefb083ffa1524a7a99f9?color=5a5a5a)




b)
Lösung W3
a)
Funktionsgleichung der Geraden  berechnen
1. Schritt: Scheitelpunkt von
berechnen
1. Schritt: Scheitelpunkt von  bestimmen
bestimmen
 Durch Einsetzen der Koordinaten von
Durch Einsetzen der Koordinaten von  und
und  ergibt sich ein lineares Gleichungssystem:
ergibt sich ein lineares Gleichungssystem:
 Einsetzen von
Einsetzen von  in
in 
![\(\begin{array}[t]{rll}
0 &=& 1-b +c &\quad \scriptsize \mid\;b=6 \\[5pt]
0 &=& 1-6 +c \\[5pt]
0&=& -5 +c &\quad \scriptsize \mid\; +5 \\[5pt]
5 &=& c \\[5pt]
c &=& 5
\end{array}\)](https://mathjax.schullv.de/1713e51ee5bfaf353324a62f5d4aea5580a96c9bc913585702df903fb38aabd0?color=5a5a5a)
 Durch quadratische Ergänzung kann die Funktionsgleichung von
Durch quadratische Ergänzung kann die Funktionsgleichung von  in die Scheitelpunktform gebracht werden:
in die Scheitelpunktform gebracht werden:
![\(\begin{array}[t]{rll}
p_1:\; y&=& x^2+6x+5 \\[5pt]
&=& x^2+2\cdot 3x+5\\[5pt]
&=& x^2+2\cdot 3x +3^2 -3^2+5\\[5pt]
&=& (x+3)^2-3^2 + 5\\[5pt]
y&=& (x+3)^2-4
\end{array}\)](https://mathjax.schullv.de/2cd5f039e215960530b23741b6487d88c24d4c7c4d050ad1b63b8dae6fedfb9b?color=5a5a5a)
 2. Schritt: Scheitelpunkt von
2. Schritt: Scheitelpunkt von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
p_2:\; y&=&x^2-6x+11 \\[5pt]
&=&x^2-2\cdot 3x+11\\[5pt]
&=&x^2-2\cdot 3x +3^2 -3^2+11\\[5pt]
&=&(x-3)^2-3^2+11\\[5pt]
y&=&(x-3)^2+2
\end{array}\)](https://mathjax.schullv.de/78d7e463709fcd891ee86fc3da82fbf9a729e63543861b14dd5bff2ca11808c6?color=5a5a5a)
 3. Schritt: Funktionsgleichung der Geraden
3. Schritt: Funktionsgleichung der Geraden  berechnen
berechnen

![\(\begin{array}[t]{rll}
g: \; y &=& m \cdot x + c \\[5pt]
y &=& 1 \cdot x +c &\quad \scriptsize \mid\; S_2(3\mid2) \\[5pt]
2 &=& 1 \cdot 3 + c &\quad \scriptsize \mid\;-3\\[5pt]
-1 &=& c \\[5pt]
c &=& -1
\end{array}\)](https://mathjax.schullv.de/46c54dccb8fd9445a0c7bdf76fe735969c028a53cd7aeb8bb9ca42fbafb06b3c?color=5a5a5a)
 Schnittwinkel von
Schnittwinkel von  und
und  bestimmen
Zwei Geraden schneiden sich senkrecht, wenn das Produkt ihrer Steigungen
bestimmen
Zwei Geraden schneiden sich senkrecht, wenn das Produkt ihrer Steigungen  ergibt.
Steigung
ergibt.
Steigung  Steigung
Steigung 
 Die beiden Geraden stehen senkrecht zueinander. Daher ist jeder der vier Schnittwinkel
Die beiden Geraden stehen senkrecht zueinander. Daher ist jeder der vier Schnittwinkel  groß.
groß.
b)
Die Länge der Grundseite ergibt sich deshalb aus den
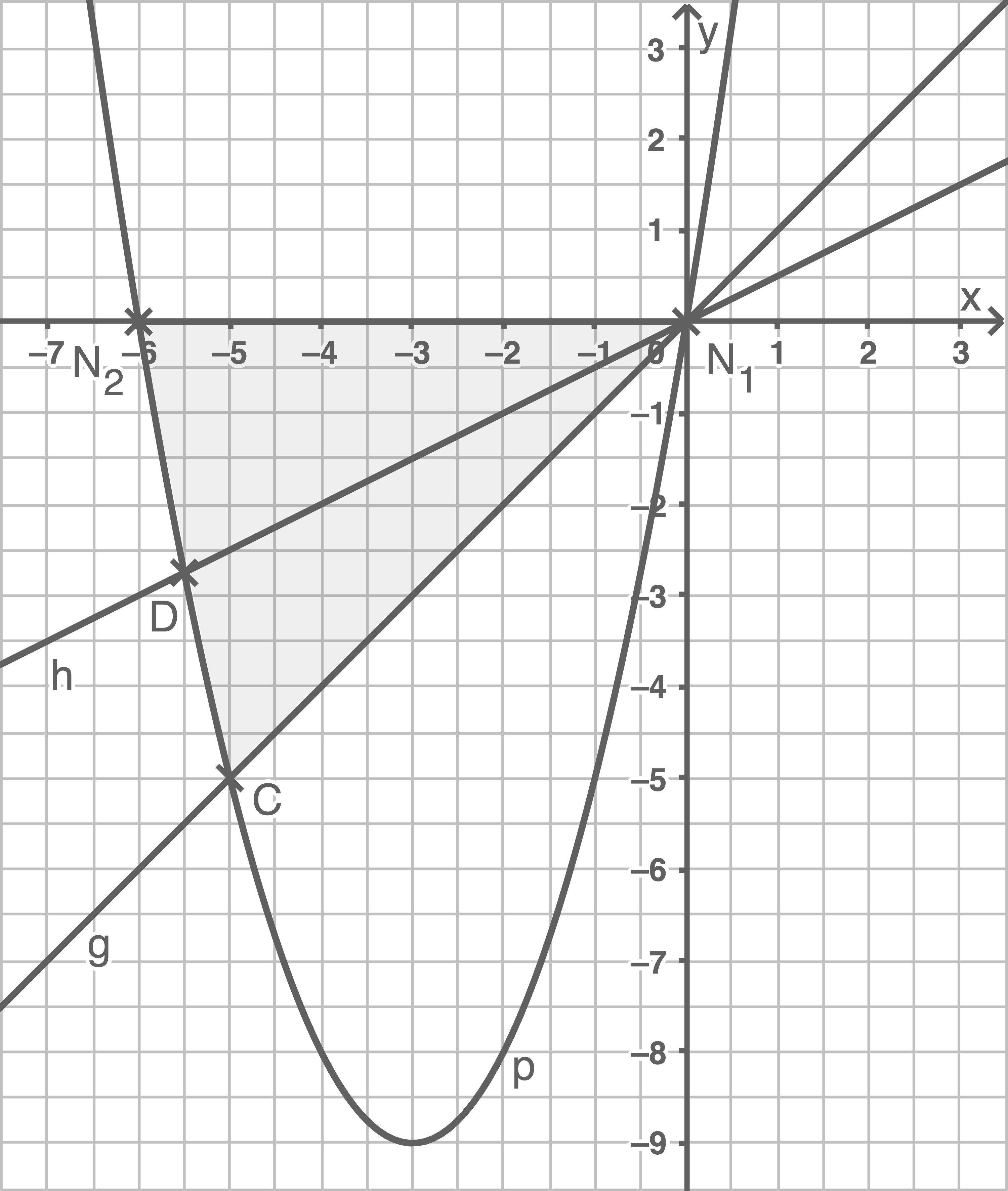
Peter hat also nicht recht.
Lösung W4
a)
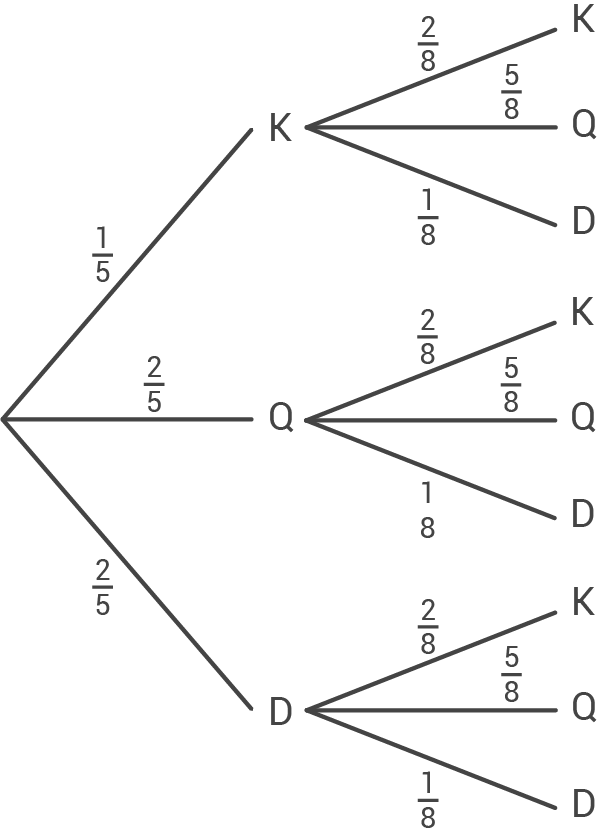
b)
Mögliche Funktionsgleichung berechnen
Der höchste Punkt der Flugbahn entspricht dem Scheitelpunkt der Parabel:
Scheitelpunkt:  Da dieser auf der
Da dieser auf der  -Achse liegt, gilt
-Achse liegt, gilt  Aufschlagspunkt:
Aufschlagspunkt: 
![\(\begin{array}[t]{rll}
p \; y&=& ax^2+c &\quad \scriptsize \mid\;c=4 \\[5pt]
y&=& ax^2+4 &\quad \scriptsize \mid\;P(7,8\mid0,9) \\[5pt]
0,9&=& a \cdot 7,8^2 +4&\quad \scriptsize \mid\;-4 \\[5pt]
-3,1&=& a \cdot 7,8^2 &\quad \scriptsize \mid\;:7,8^2 \\[5pt]
-\dfrac{3,1}{7,8^2}&=& a \\[5pt]
a &=& -\dfrac{3,1}{7,8^2} \\[5pt]
a &=& -\dfrac{155}{3042}
\end{array}\)](https://mathjax.schullv.de/100233be7a22fb675784e35ef4aade5ff3cda7e87f8e9020c2526d6c2dee8b92?color=5a5a5a) Eine mögliche Funktionsgleichung der Parabel
Eine mögliche Funktionsgleichung der Parabel  lautet also:
lautet also:
 ln welchem Abstand überquert der Ball das Netz?
Berechnung der
ln welchem Abstand überquert der Ball das Netz?
Berechnung der  -Koordinate des Überflugpunkts:
-Koordinate des Überflugpunkts:

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& -\dfrac{155}{3042}\cdot (-1,2)^2+4 \\[5pt]
y&= & 3,93
\end{array}\)](https://mathjax.schullv.de/0b19b557ed06862aa15015fbc9c2039df4d3693a2a2046ecea6edc3a9fcb7aa4?color=5a5a5a) Abstand
Abstand  zum Netz berechnen:
zum Netz berechnen:
![\(\begin{array}[t]{rll}
d &=& 3,93\,\text{m}- 2,24\,\text{m} \\[5pt]
&=& 1,69\,\text{m}
\\[5pt]
d&=& \underline{\underline{ 1,7\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/7f2326fd72e27a9cf0716f22d5d45797f5826b9cfe2e2c4cb0d92142e5a69c9e?color=5a5a5a) Der Ball überquert das Netz mit einem Abstand von
Der Ball überquert das Netz mit einem Abstand von  ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
Der Boden wird durch die
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
Der Boden wird durch die  -Achse dargestellt.
-Achse dargestellt.
![\(\begin{array}[t]{rll}
-\dfrac{155}{3042}x^2+4 &=& 0 &\quad \scriptsize \mid\;-4 \\[5pt]
-\dfrac{155}{3042}x^2&=& -4 &\quad \scriptsize \mid\;\cdot \left(-\dfrac{3042}{155}\right)\\[5pt]
x^2&=& \dfrac{12168}{155} &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x_1&=& 8,86 \\[5pt]
x_2&=& -8,86
\end{array}\)](https://mathjax.schullv.de/2e69966e5681d55cd0e75f55eeb102a77c7efbff6efba69aefe332529119fbb9?color=5a5a5a) Abstand der Grundlinie zum Netz
Abstand der Grundlinie zum Netz  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
n&=& 9\,\text{m}+1,2\,\text{m} \\[5pt]
&=& 10,2\,\text{m}
\end{array}\)](https://mathjax.schullv.de/7b0f1cecdfe794ba8720cc8f91f69ebc498a940c875dad310e6f6758ad71998b?color=5a5a5a) Die Grundlinie des Gegners ist
Die Grundlinie des Gegners ist  vom Nullpunkt entfernt.
Abstand der gegenerischen Grundlinie und des Aufprallpunkts
vom Nullpunkt entfernt.
Abstand der gegenerischen Grundlinie und des Aufprallpunkts  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
g&=& 10,2\,\text{m}-8,86\,\text{m} \\[5pt]
&=& 1,34\,\text{m}
\end{array}\)](https://mathjax.schullv.de/457f342e00d44a1a34ec19816e9855e8fb14c1661c04aa69b43f052558915fb5?color=5a5a5a) ln einer Entfernung von
ln einer Entfernung von  zur gegnerischen Grundlinie trifft der Ball auf dem Boden auf.
Abstand der eigenen Grundlinie und des Aufprallpunkts
zur gegnerischen Grundlinie trifft der Ball auf dem Boden auf.
Abstand der eigenen Grundlinie und des Aufprallpunkts  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
e&=& 7,8\,\text{m} + 8,86\,\text{m} \\[5pt]
&=& 16,66\,\text{m}
\\[5pt]
&=& \underline{\underline{ 16,7\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/05be47dad39a20a4ca54d28a2f526d83c77c61fda2f993e1e3c6dda37c1bc5c9?color=5a5a5a) ln einer Entfernung von
ln einer Entfernung von  zur eigenen Grundlinie trifft der Ball auf dem Boden auf.
zur eigenen Grundlinie trifft der Ball auf dem Boden auf.