Pflichtteil 2
Pflichtaufgabe 1
a)
Ermittle die Lösung des linearen Gleichungssystems.

b)
Der Berliner Fernsehturm ist  hoch. Das höchste Gebäude der Welt ist ein Hochhaus in Dubai mit einer Höhe von
hoch. Das höchste Gebäude der Welt ist ein Hochhaus in Dubai mit einer Höhe von 
Berechne, um wie viel Prozent das Hochhaus in Dubai höher ist als der Berliner Fernsehturm.
Berechne, um wie viel Prozent das Hochhaus in Dubai höher ist als der Berliner Fernsehturm.
c)
Gegeben ist ein Dreieck  mit folgenden Stücken:
mit folgenden Stücken:


 Ermittle die Länge der Seite
Ermittle die Länge der Seite  dieses Dreiecks durch Konstruktion und überprüfe diese rechnerisch.
dieses Dreiecks durch Konstruktion und überprüfe diese rechnerisch.
d)
Schreibe als Gleichung.
Das Produkt aus dem Vorgänger und dem Nachfolger einer natürlichen Zahl  ist gleich dem Vorgänger des Quadrates der Zahl
ist gleich dem Vorgänger des Quadrates der Zahl 
e)
In einer Lostrommel befinden sich Lose. Ein Los ist entweder ein Gewinnlos oder eine Niete. Die Wahrscheinlichkeit, ein Gewinnlos zu ziehen, beträgt  Untersuche, ob für den Inhalt der Lostrommel folgende Beschreibung zutreffen kann.
„In der Lostrommel sind genau
Untersuche, ob für den Inhalt der Lostrommel folgende Beschreibung zutreffen kann.
„In der Lostrommel sind genau  Nieten und genau
Nieten und genau  Gewinnlose.“
Gewinnlose.“
12 BE erreichbar
Pflichtaufgabe 2
Gegeben ist eine quadratische Funktion  durch die Gleichung
durch die Gleichung 
a)
Gib die Scheitelpunktkoordinaten des Graphen der Funktion  an und zeichne den Graphen der Funktion
an und zeichne den Graphen der Funktion  in ein Koordinatensystem mindestens im Intervall
in ein Koordinatensystem mindestens im Intervall 
b)
Gib den Wertebereich der Funktion  an.
an.
c)
Zeige, dass die Funktion  auch durch die Gleichung
auch durch die Gleichung  beschrieben wird.
beschrieben wird.
d)
Der Graph der Funktion  mit der Gleichung
mit der Gleichung  schneidet den Graphen der Funktion
schneidet den Graphen der Funktion  in genau einem Punkt.
in genau einem Punkt.
Ermittle die Koordinaten dieses Schnittpunktes.
Ermittle die Koordinaten dieses Schnittpunktes.
7 BE erreichbar
Pflichtaufgabe 3
Ein  tiefer Swimmingpool hat die Form eines Quaders und fasst bei vollständiger Befüllung bis zum Rand
tiefer Swimmingpool hat die Form eines Quaders und fasst bei vollständiger Befüllung bis zum Rand  Liter Wasser.
Liter Wasser.
a)
Ermittle eine mögliche Länge und die dazugehörige Breite, die ein solcher Swimmingpool haben kann.
b)
Das vollständige Befüllen des Swimmingpools erfolgt gleichzeitig mit zwei Pumpen in  Stunden. Eine der Pumpen fördert
Stunden. Eine der Pumpen fördert  Liter Wasser pro Minute.
Liter Wasser pro Minute.
Ermittle, wie viel Liter Wasser die andere Pumpe pro Minute fördern muss, um den Swimmingpool in der vorgegebenen Zeit vollständig zu befüllen.
Ermittle, wie viel Liter Wasser die andere Pumpe pro Minute fördern muss, um den Swimmingpool in der vorgegebenen Zeit vollständig zu befüllen.
5 BE erreichbar
Lösung 1
a)
Es bietet sich das Einsetzungsverfahren an. Durch Einsetzen der Gleichung  in die Gleichung
in die Gleichung  folgt:
folgt:
![\(\begin{array}[t]{rll}
0,5x-2+4x&=& 7&\quad \scriptsize \mid\; +2\\[5pt]
4,5x&=& 9&\quad \scriptsize \mid\; :4,5\\[5pt]
x&=& 2
\end{array}\)](https://mathjax.schullv.de/83a9747b96f1835e9481aea14e497f1fdd620f5e6d2ba8dedfe6cb9ee95ce392?color=5a5a5a) Mit
Mit  folgt mit der Gleichung
folgt mit der Gleichung  :
:
![\(\begin{array}[t]{rll}
y&=& 0,5 \cdot 2 -2\\[5pt]
&=& -1
\end{array}\)](https://mathjax.schullv.de/2653928bf2cfd4e77ca5f81cd0c0d835ac587dcb80a4b93b04d193497a310960?color=5a5a5a) Somit lautet die Lösung des linearen Gleichungssystems
Somit lautet die Lösung des linearen Gleichungssystems  und
und 
b)
Lösung mit Dreisatz




![\(\begin{array}{rcl}
365\,\text{m} & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1\,\text{m} & \mathrel{\widehat{=}}& \dfrac{100}{365}\,\%\\[5pt]
828\,\text{m} & \mathrel{\widehat{\approx}}& 226,85\,\%
\end{array}\)](https://mathjax.schullv.de/a7d141f43d76110b013e33761026126342a736a54419d001b5b567e22f90725a?color=5a5a5a)




 Lösung mit Prozentformel
Lösung mit Prozentformel


![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{828\,\text{m}}{365\,\text{m}}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 226,85\,\%
\end{array}\)](https://mathjax.schullv.de/8ebadfa87c6d9221cb02b304d3d704c4b3a12b02ac2b4a008ad8ca75ebb99876?color=5a5a5a)
 Damit ist das Hochhaus in Dubai etwa um
Damit ist das Hochhaus in Dubai etwa um  größer als der Berliner Fernsehturm.
größer als der Berliner Fernsehturm.
c)
Länge der Seite zeichnerisch ermitteln
Durch Konstruktion des Dreiecks  folgt die Darstellung:
folgt die Darstellung:
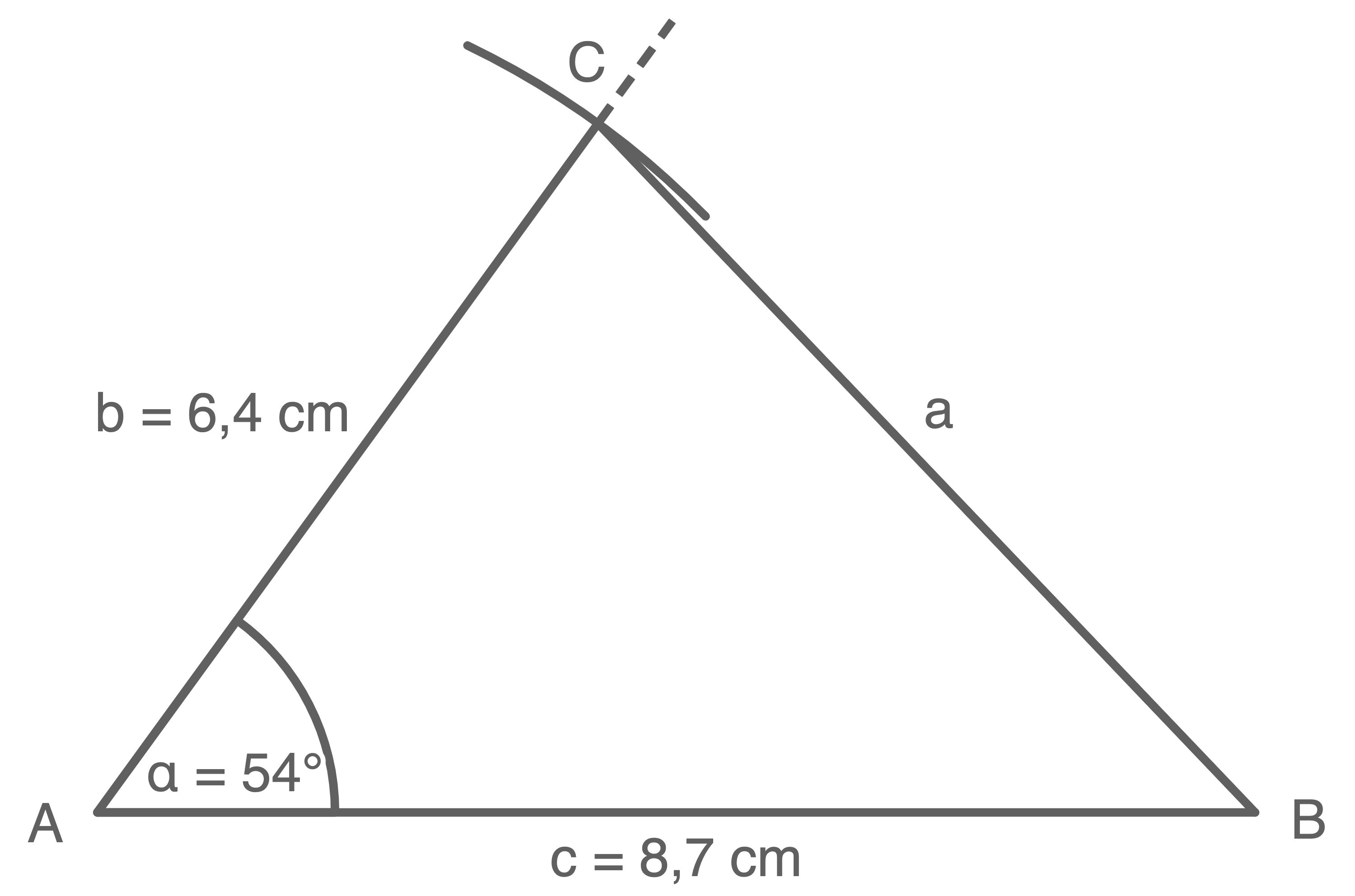 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Somit folgt mit der Konstruktion durch Abmessen
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Somit folgt mit der Konstruktion durch Abmessen  Länge der Seite rechnerisch bestimmen
Mit dem Kosinussatz für das Dreieck
Länge der Seite rechnerisch bestimmen
Mit dem Kosinussatz für das Dreieck  folgt:
Damit gilt durch Rechnung
folgt:
Damit gilt durch Rechnung  Die bestimmte Länge
Die bestimmte Länge  durch Konstruktion ist also korrekt.
durch Konstruktion ist also korrekt.

d)
e)
Gesamtanzahl der Lose:  Anzahl der Gewinnlose:
Anzahl der Gewinnlose:  Wahrscheinlichkeit
Wahrscheinlichkeit  für ein Gewinnlos berechnen:
für ein Gewinnlos berechnen:
![\(\begin{array}[t]{rll}
p&=&\dfrac{\text{Anzahl der Gewinnlose}}{\text{Gesamtanzahl der Lose}} \\[5pt]
&=&\dfrac{20}{120} \\[5pt]
&=& \dfrac{1}{6} \\[5pt]
&\approx& 0,167
\end{array}\)](https://mathjax.schullv.de/580572943c395e723178829cf0e6f0e344a313201fb6d7f8d1f849c7412091fe?color=5a5a5a) Somit kann für den Inhalt der Lostrommel die gegebene Beschreibung nicht zutreffen, da die Wahrscheinlichkeit für ein Gewinnlos nicht
Somit kann für den Inhalt der Lostrommel die gegebene Beschreibung nicht zutreffen, da die Wahrscheinlichkeit für ein Gewinnlos nicht  beträgt.
beträgt.
Lösung 2
a)
Scheitelpunktkoordinaten angeben
Die Funktion  ist bereits in der Scheitelpunktform gegeben. Somit lauten die Scheitelpunktkoordinaten
ist bereits in der Scheitelpunktform gegeben. Somit lauten die Scheitelpunktkoordinaten  Graphen zeichnen
Graphen zeichnen
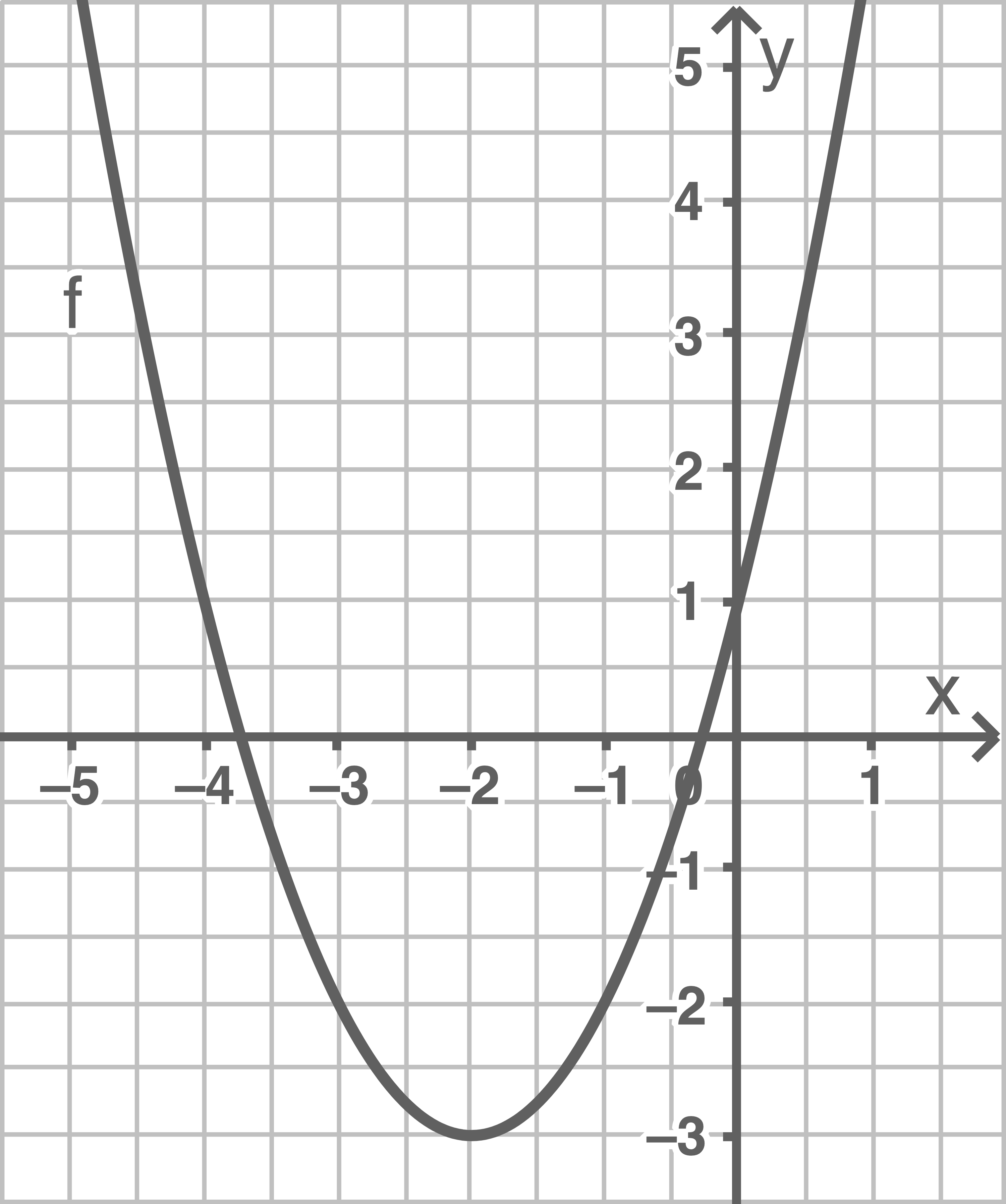

b)
Der Graph der Funktion  ist eine nach oben geöffnete Parabel mit dem Scheitelpunkt
ist eine nach oben geöffnete Parabel mit dem Scheitelpunkt  . Somit folgt:
Wertebereich:
. Somit folgt:
Wertebereich: 
c)
Mit der gegebenen Funktionsgleichung  folgt:
folgt:
![\( \begin{array}[t]{rll}
y&=& (x+2)^2-3\\[5pt]
&=& x^2+4x+4-3\\[5pt]
&=& x^2+4x+1\\[5pt]
\end{array}\)](https://mathjax.schullv.de/c86747eea0362a451a1ee91a1f2d1b78136379611ac8a8a465eaf87e50ce1b8a?color=5a5a5a) Somit kann die Funktion
Somit kann die Funktion  auch durch die Gleichung
auch durch die Gleichung  beschrieben werden.
beschrieben werden.
d)
Durch Gleichsetzen der Funktionsgleichungen der Funktion  und der Funktion
und der Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
f(x)&=& g(x)\\[5pt]
x^2+4x+1&=& x^2-2x+1 \quad \scriptsize \mid \, -x^2\\[5pt]
4x+1&=& -2x+1 \quad \scriptsize \mid \, -1\\[5pt]
4x&=& -2x \quad \scriptsize \mid \, +2x\\[5pt]
6x&=& 0 \quad \scriptsize \mid \, :6\\[5pt]
x&=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/bc7ba8f72b5cbb37f1153100c27ab70c43c88e8ec60881c8feedd3c558486d2f?color=5a5a5a) Für die
Für die  -Koordinate folgt durch Einsetzen in die Funktionsgleichung der Funktion
-Koordinate folgt durch Einsetzen in die Funktionsgleichung der Funktion  :
:
 Somit lauten die Koordinaten des Schnittpunktes
Somit lauten die Koordinaten des Schnittpunktes 
Lösung 3
a)
Volumen des Swimmingpools:
 Ein Quader mit einer Höhe von
Ein Quader mit einer Höhe von  und einem Volumen von
und einem Volumen von  erfüllt für die Breite
erfüllt für die Breite  und die Länge
und die Länge  die folgende Gleichung:
die folgende Gleichung:
 Es gibt viele Möglichkeiten, diese Gleichung zu erfüllen. Eine ist beispielsweise die Folgende:
Es gibt viele Möglichkeiten, diese Gleichung zu erfüllen. Eine ist beispielsweise die Folgende:

b)