Wahlpflichtaufgaben
Wahlpflichtaufgabe 1
Eine Bakterienkultur verdoppelt sich stündlich. Zu Beobachtungsbeginn gibt es vier Bakterien.
a)
Erstelle für diesen Wachstumsprozess eine Wertetabelle für die ersten vier Stunden seit Beobachtungsbeginn.
| Zeit in Stunden | 0 | ||||
|---|---|---|---|---|---|
| Anzahl der Bakterien | 4 |
b)
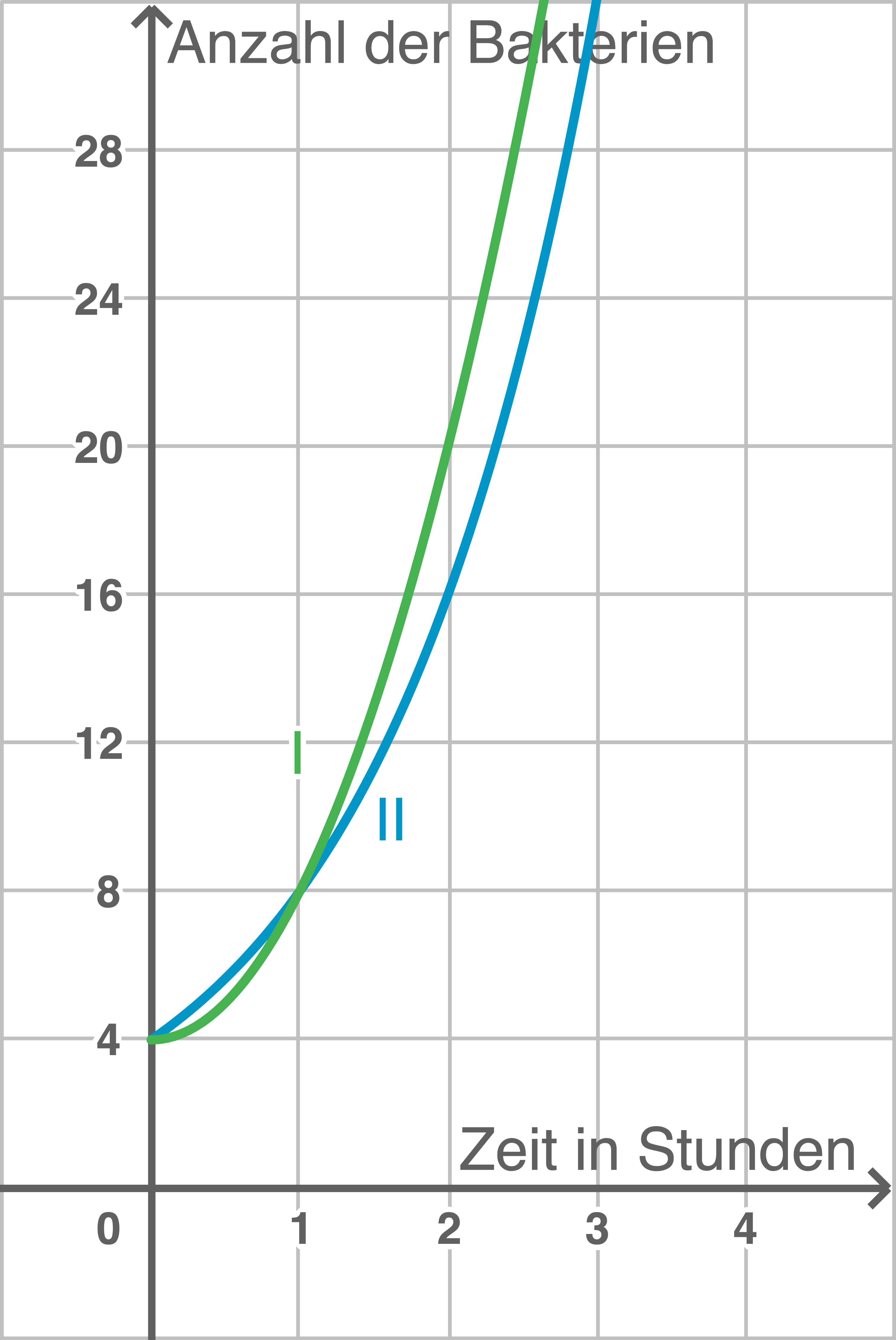
Einer der abgebildeten Graphen beschreibt den Wachstumsprozess.
Gib diesen Graphen an und begründe.
Gib diesen Graphen an und begründe.

c)
Ermittle, nach wie vielen Stunden mindestens 1000 Bakterien vorhanden sind.
d)
Der Wachstumsprozess kann durch eine Funktion  mit
mit  beschrieben werden.
beschrieben werden.
Gib die Bedeutung der Variablen und
und  im beschriebenen Sachzusammenhang an und ermittle den Wert des Parameters
im beschriebenen Sachzusammenhang an und ermittle den Wert des Parameters 
Gib die Bedeutung der Variablen
8 BE erreichbar
Wahlpflichtaufgabe 2
Abflussrinnen bestehen aus baugleichen Betonelementen. Ein Betonelement hat eine Länge von einem Meter. Für den Transport werden die Betonelemente auf Paletten zu je 30 Stück verpackt.
In der Abbildung ist der Querschnitt eines solchen Betonelements vereinfacht dargestellt (Angaben in Millimeter).
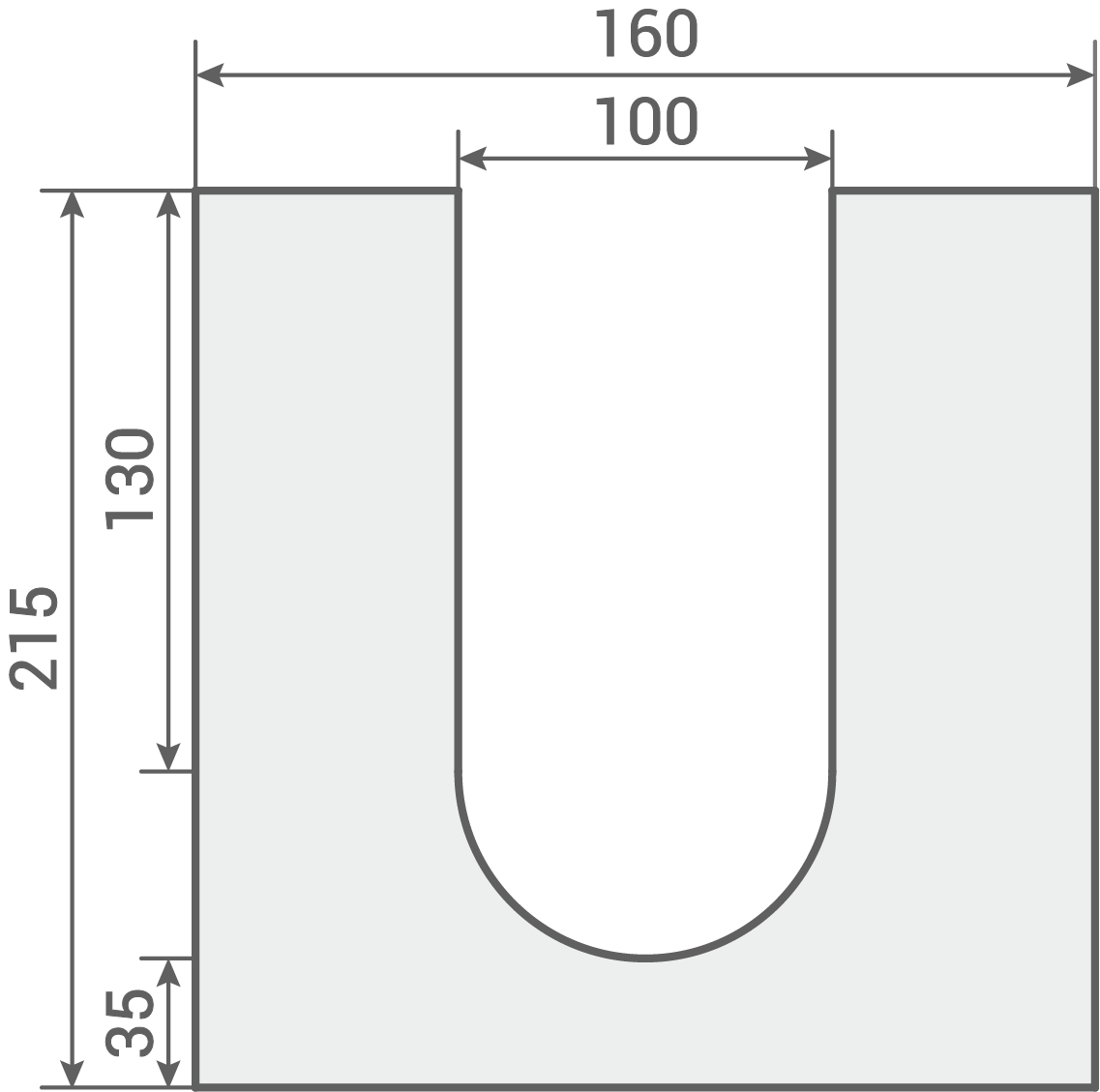

Abbildung (nicht maßstäblich)
a)
Zeige, dass das Volumen eines Betonelements ca.  beträgt.
beträgt.
b)
Für die Auslieferung der Betonelemente steht ein LKW mit einer Ladefähigkeit von  zur Verfügung.
zur Verfügung.
Ermittle die größtmögliche Anzahl an Paletten, die mit diesem LKW pro Fahrt transportiert werden kann. Hinweis: Ein Kubikdezimeter Beton hat eine Masse von zwei Kilogramm.
Ermittle die größtmögliche Anzahl an Paletten, die mit diesem LKW pro Fahrt transportiert werden kann. Hinweis: Ein Kubikdezimeter Beton hat eine Masse von zwei Kilogramm.
8 BE erreichbar
Wahlpflichtaufgabe 3
Beim Spiel „Hüpf mein Hütchen“ legt der aktive Spieler zweimal nacheinander ein Hütchen auf ein Katapult und schleudert es auf ein Spielfeld mit Öffnungen (siehe Abbildung).
Ziel ist es, dass das Hütchen jeweils mit der Spitze nach unten in einer Öffnung landet.
Der Spieler erhält die in der jeweiligen Öffnung angezeigte Punktzahl. Landet ein Hütchen in einer bereits besetzten Öffnung, erhält der Spieler erneut die angezeigte Punktzahl.
Gewonnen hat bei diesem Spiel derjenige Spieler, der die größte Gesamtpunktzahl erreicht. Vereinfacht wird angenommen, dass ein Hütchen jedes Mal in einer der Öffnungen landet.
Ziel ist es, dass das Hütchen jeweils mit der Spitze nach unten in einer Öffnung landet.
Der Spieler erhält die in der jeweiligen Öffnung angezeigte Punktzahl. Landet ein Hütchen in einer bereits besetzten Öffnung, erhält der Spieler erneut die angezeigte Punktzahl.
Gewonnen hat bei diesem Spiel derjenige Spieler, der die größte Gesamtpunktzahl erreicht. Vereinfacht wird angenommen, dass ein Hütchen jedes Mal in einer der Öffnungen landet.
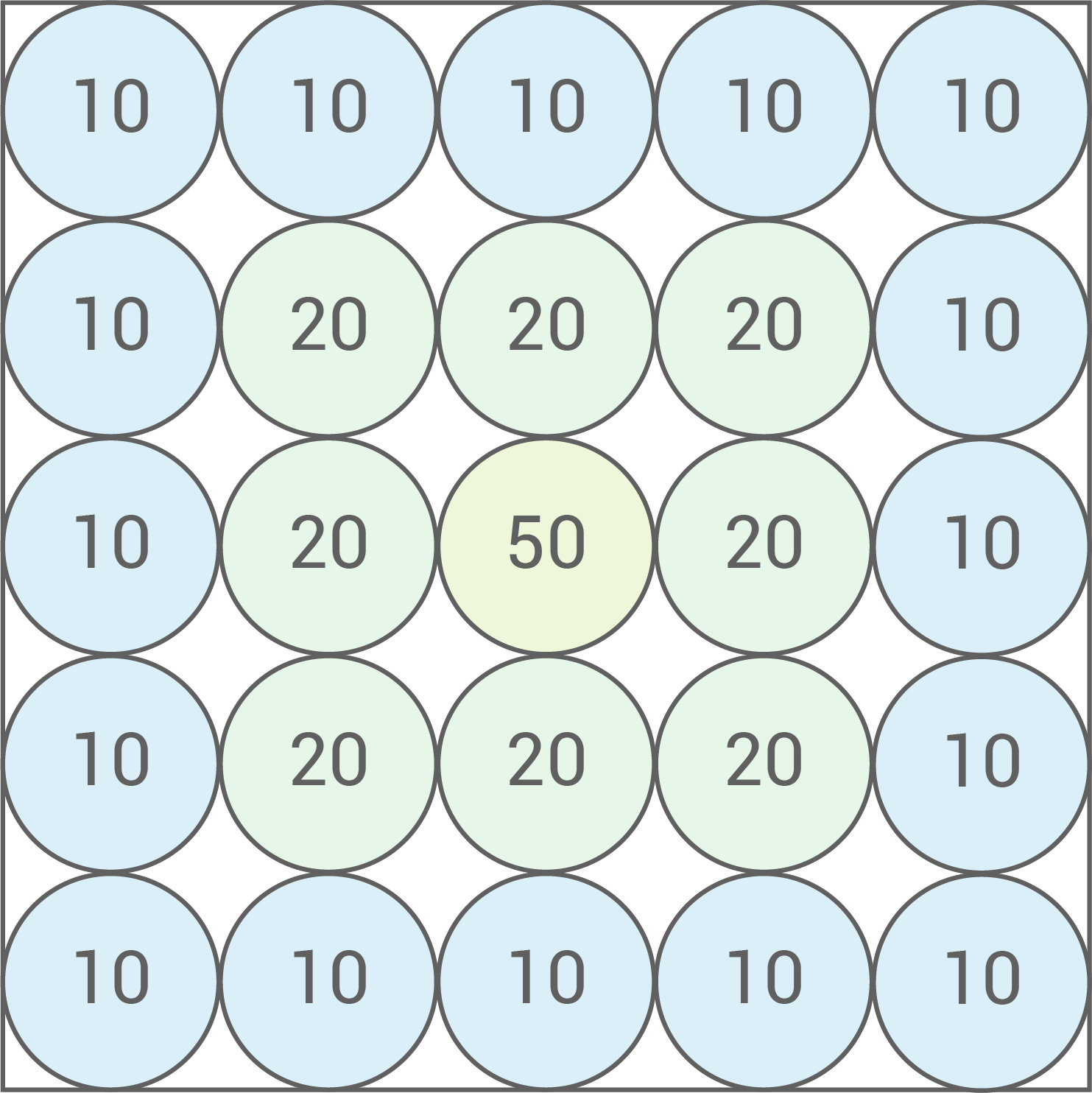
a)
Gib die Gesamtpunktzahlen an, die ein Spieler in diesem Spiel erreichen kann.
b)
Berechne die Wahrscheinlichkeit für das Erreichen der Gesamtpunktzahl 20.
c)
Zeige, dass es neben der Gesamtpunktzahl 20 eine weitere Gesamtpunktzahl mit gleicher Wahrscheinlichkeit gibt, und gib diese Gesamtpunktzahl an.
d)
Beschreibe eine reale Situation, bei der ein Spieler bei diesem Spiel im Vorteil ist.
8 BE erreichbar
Lösung 1
a)
| Zeit in Stunden | |||||
|---|---|---|---|---|---|
| Anzahl der Bakterien |
b)
Die Punkte  und
und  liegen auf beiden Graphen. Ab der zweiten Stunde erfüllt jedoch nur noch Graph
liegen auf beiden Graphen. Ab der zweiten Stunde erfüllt jedoch nur noch Graph  die berechneten Werte der Wertetabelle.
die berechneten Werte der Wertetabelle.
c)
Fortführen der Wertetabelle:
Nach  Stunden sind mindestens
Stunden sind mindestens  Bakterien vorhanden.
Bakterien vorhanden.
| Zeit in Stunden | |||||
|---|---|---|---|---|---|
| Anzahl der Bakterien |
d)
Bedeutung der Variablen im Sachzusammenhang angeben
 beschreibt die Zeit in Stunden und
beschreibt die Zeit in Stunden und  die Anzahl der Bakterien.
Wert des Parameters
die Anzahl der Bakterien.
Wert des Parameters  ermitteln
Um den Parameter zu ermitteln, wird ein bekannter Wert in die Funktionsgleichung eingesetzt und nach
ermitteln
Um den Parameter zu ermitteln, wird ein bekannter Wert in die Funktionsgleichung eingesetzt und nach  umgestellt.
umgestellt.
![\(\begin{array}[t]{rll}
y&=&a\cdot 2^x \quad \scriptsize \mid\; (0\mid 4) \\[5pt]
4&=&a\cdot 2^0 \\[5pt]
4&=&a
\end{array}\)](https://mathjax.schullv.de/5d717f1a271534617ce86bd17815db3069a6a51257b160bc046f0c73f79c070d?color=5a5a5a) Die Funktionsgleichung lautet:
Die Funktionsgleichung lautet:

Lösung 2
a)
Die Betonelemente haben die Form eines Prismas mit einer Höhe von einem Meter. Die Grundfläche ist gegeben durch die in der Abbildung grau gefärbte Fläche in der Form eines Rechtecks, aus der ein kleineres Rechteck mit anschließendem Halbkreis ausgeschnitten ist.
Fläche des ausgeschnittenen Rechtecks:
![\(\begin{array}[t]{rll}
A_R&=& 100\,\text{mm}\cdot 130\,\text{mm} \\[5pt]
&=& 13\,000\,\text{mm}^2
\end{array}\)](https://mathjax.schullv.de/ba01ce13b47406a5c9a4998691151b0c9587b5420163de58a21ec531f1fdb773?color=5a5a5a) Fläche des ausgeschnittenen Halbkreises:
Fläche des ausgeschnittenen Halbkreises:
![\(\begin{array}[t]{rll}
A_H&=&\dfrac{1}{2}\cdot \pi\cdot \left(\dfrac{100\,\text{mm}}{2}\right)^2 \\[5pt]
&\approx & 3\,927\,\text{mm}^2
\end{array}\)](https://mathjax.schullv.de/184fe666b3323d6a5424fa0ba565ff03ac8a8abea64f77beb585c48130e02dff?color=5a5a5a) Für die Grundfläche des Prismas ergibt sich damit:
Für das Volumen gilt dann mit
Für die Grundfläche des Prismas ergibt sich damit:
Für das Volumen gilt dann mit 
![\(\begin{array}[t]{rll}
V&=& G\cdot h\\[5pt]
&=& 1,7473~\text{dm}^2\cdot 10~\text{dm}\\[5pt]
&\approx& 17,5~\text{dm}^3
\end{array}\)](https://mathjax.schullv.de/d79159ed11f0e102a5b5a51cf11f94bc97a010b282211ed21a5392c4ee0a0478?color=5a5a5a)
b)
Masse eines Betonelements:
 Auf eine Palette passen
Auf eine Palette passen  dieser Elemente. Gewicht einer Palette:
dieser Elemente. Gewicht einer Palette:
 Damit kann berechnet werden, wie viele dieser Paletten auf den LKW passen:
Damit kann berechnet werden, wie viele dieser Paletten auf den LKW passen:
 Da keine Teilpaletten transportiert werden können, muss die Anzahl der Paletten abgerundet werden. Es können also
Da keine Teilpaletten transportiert werden können, muss die Anzahl der Paletten abgerundet werden. Es können also  Paletten pro Fahrt transportiert werden.
Paletten pro Fahrt transportiert werden.
Lösung 3
a)
Pro Spiel hat ein Spieler zwei Hütchen. Da eine Öffnung auch doppelt belegt werden kann, können folgende Gesamtpunktzahlen erreicht werden:
b)
Die Gesamtpunktzahl  kann nur durch zwei 10er erreicht werden.
Anzahl Öffnungen mit 10 Punkten:
kann nur durch zwei 10er erreicht werden.
Anzahl Öffnungen mit 10 Punkten: 
Gesamtanzahl Öffnungen: Die Wahrscheinlichkeit, einmal
Die Wahrscheinlichkeit, einmal  Punkte zu treffen, ist also:
Punkte zu treffen, ist also:
 Mit der Pfadmultiplikationsregel lässt sich die Wahrscheinlichkeit für zweimal hintereinander
Mit der Pfadmultiplikationsregel lässt sich die Wahrscheinlichkeit für zweimal hintereinander  Punkte berechnen:
Punkte berechnen:
![\(\begin{array}[t]{rll}
P(10;10)&=& \dfrac{16}{25}\cdot \dfrac{16}{25} \\[5pt]
&=& 0,4096 \\[5pt]
&=& 40,96\,\%
\end{array}\)](https://mathjax.schullv.de/5e33436f8a039b3ce33e0910bc7069dd954159fa5f0e8914a3d5d85600c2928a?color=5a5a5a) Die Wahrscheinlichkeit beträgt
Die Wahrscheinlichkeit beträgt  .
.
Gesamtanzahl Öffnungen:
c)
Um die Gesamtpunktzahl 30 zu erreichne, muss eine 10er und eine 20er Öffnung getroffen werden. Es gibt nur halb so viele 20er wie 10er Öffnungen. Dafür gibt es jedoch zwei Möglichkeiten, die Summe 30 zu erreichen. Es gilt:
![\(\begin{array}[t]{rll}
P(30)&=& P(20;10)+P(10;20) \\[5pt]
&=& \dfrac{8}{25}\cdot \dfrac{16}{25}+\dfrac{16}{25}\cdot \dfrac{8}{25} \\[5pt]
&=& \dfrac{128}{625}+\dfrac{128}{625} \\[5pt]
&=& 0,4096 \\[5pt]
&=& 40,96\,\%
\end{array}\)](https://mathjax.schullv.de/2c5d440cf34f395b56b99b4af9fa81a28d856adf9acaf762cb2f3e29e9c9633f?color=5a5a5a) Die Gesamtpunktzahl 30 hat die gleiche Wahrscheinlichkeit wie die Gesamtpunktzahl 20.
Die Gesamtpunktzahl 30 hat die gleiche Wahrscheinlichkeit wie die Gesamtpunktzahl 20.
d)
Wenn der Gegenspieler eine Gesamtpunktzahl von  erreicht hat, kann nur eine höhere oder die gleiche Punktzahl erreicht werden. Der Spieler ist also im Vorteil.
erreicht hat, kann nur eine höhere oder die gleiche Punktzahl erreicht werden. Der Spieler ist also im Vorteil.