Pflichtteil 2
Pflichtaufgabe 1
a)
Gegeben ist eine lineare Funktion  durch
durch 
Zeichne den Graphen von mindestens im Intervall
mindestens im Intervall  in ein Koordinatensystem.
in ein Koordinatensystem.
Zeichne den Graphen von
b)
In der Abbildung ist ein Viertel einer Kreisfläche als schraffierte Fläche dargestellt. Der Radius des zugehörigen Kreises beträgt 
Berechne den Umfang der schraffierten Fläche.
Berechne den Umfang der schraffierten Fläche.
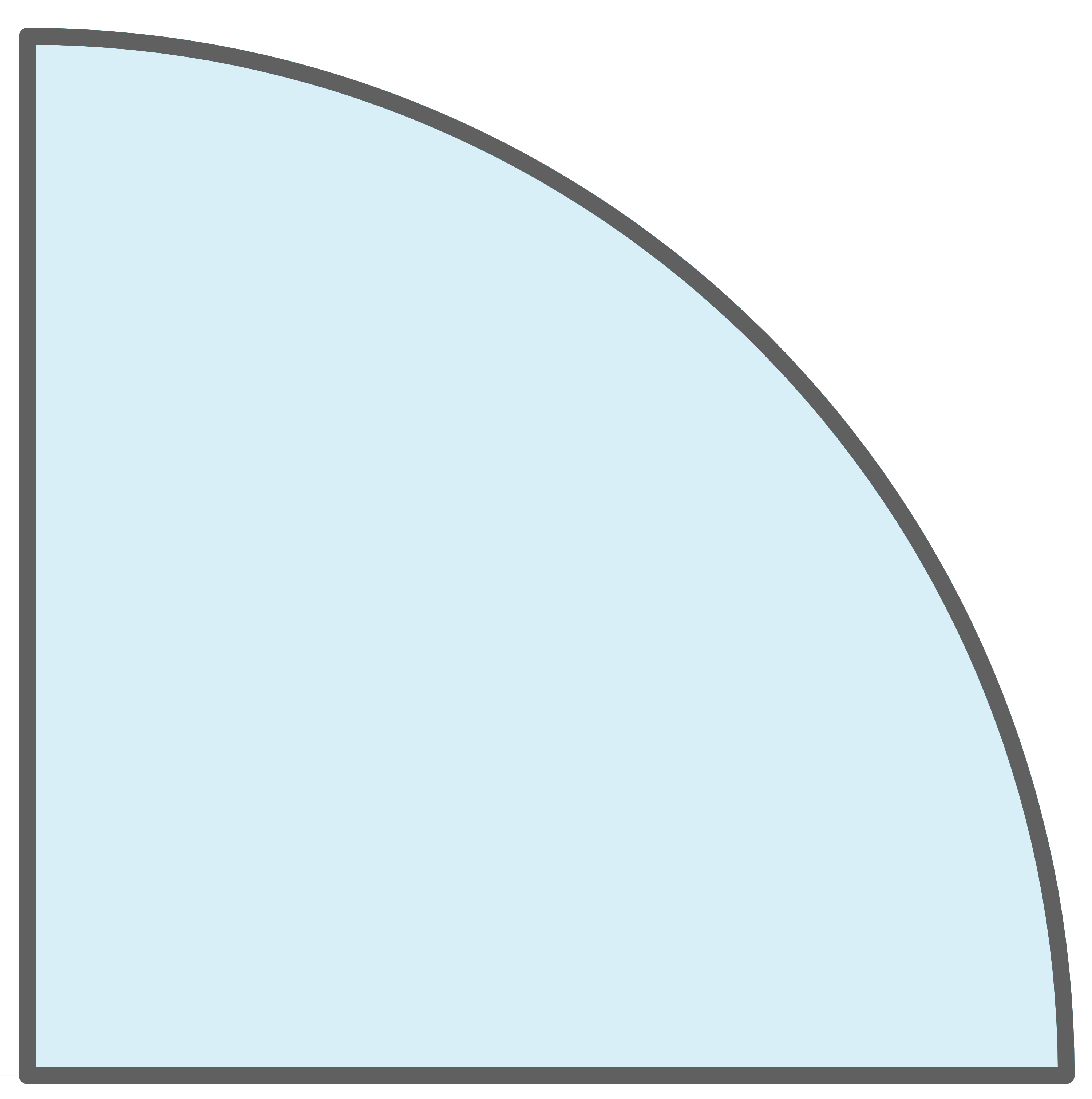
Abbildung (nicht maßstäblich)
c)
In der Tabelle sind Ergebnisse einer Verkehrszählung dargestellt. Erfasst wurde jeweils die Anzahl der Fahrzeuge, die einen Straßenabschnitt in den angegebenen Zeiträumen passieren.
| Mo | Mi | Fr | So | |
|---|---|---|---|---|
| 6 bis 9 Uhr | ||||
| 9 bis 12 Uhr | ||||
| 12 bis 15 Uhr | ||||
| 15 bis 18 Uhr |
(I)
Ermittle die Spannweite dieser Daten.
(II)
Berechne die durchschnittliche Anzahl der Fahrzeuge pro Stunde für den Beobachtungszeitraum von 6 bis 18 Uhr am Montag.
d)
Vereinfache den Term so weit wie möglich.

e)
Gegeben ist eine Pyramide mit rechteckiger Grundfläche. Die Seitenlängen des Rechtecks sind  und
und  Die Körperhöhe beträgt
Die Körperhöhe beträgt 
Zeichne ein Schrägbild dieser Pyramide.
Zeichne ein Schrägbild dieser Pyramide.
10 BE erreichbar
Pflichtaufgabe 2
Gegeben ist ein Dreieck  mit
mit  und
und 
a)
Konstruieren Sie das Dreieck 
b)
Berechne die Länge der Seite  sowie den Flächeninhalt des Dreiecks
sowie den Flächeninhalt des Dreiecks 
c)
Die Mittelpunkte der Seiten des Dreiecks  werden wie folgt bezeichnet.
werden wie folgt bezeichnet.
Ermittle das Verhältnis der Flächeninhalte der beiden Dreiecke  und
und  zueinander.
zueinander.
| Seite | Mittelpunkt der Seite |
|---|---|
8 BE erreichbar
Pflichtaufgabe 3
a)
Laut einer Studie tippen 4,5 Prozent der Autofahrer während der Fahrt auf ihrem Handy. Wissenschaftler hatten an 30 zufällig ausgewählten Standorten knapp 12000 Autofahrer beobachtet.
Gib die Anzahl der Autofahrer in dieser Studie an, die beim Tippen auf dem Handy beobachtet wurden.
Gib die Anzahl der Autofahrer in dieser Studie an, die beim Tippen auf dem Handy beobachtet wurden.
b)
Ein Autofahrer fährt auf einer Landstraße mit einer Geschwindigkeit von  und schaut dabei ca. 4 Sekunden auf das Display seines Handys.
und schaut dabei ca. 4 Sekunden auf das Display seines Handys.
Berechne den Weg, den er in dieser Zeit ohne Blick auf die Straße zurücklegt.
Berechne den Weg, den er in dieser Zeit ohne Blick auf die Straße zurücklegt.
c)
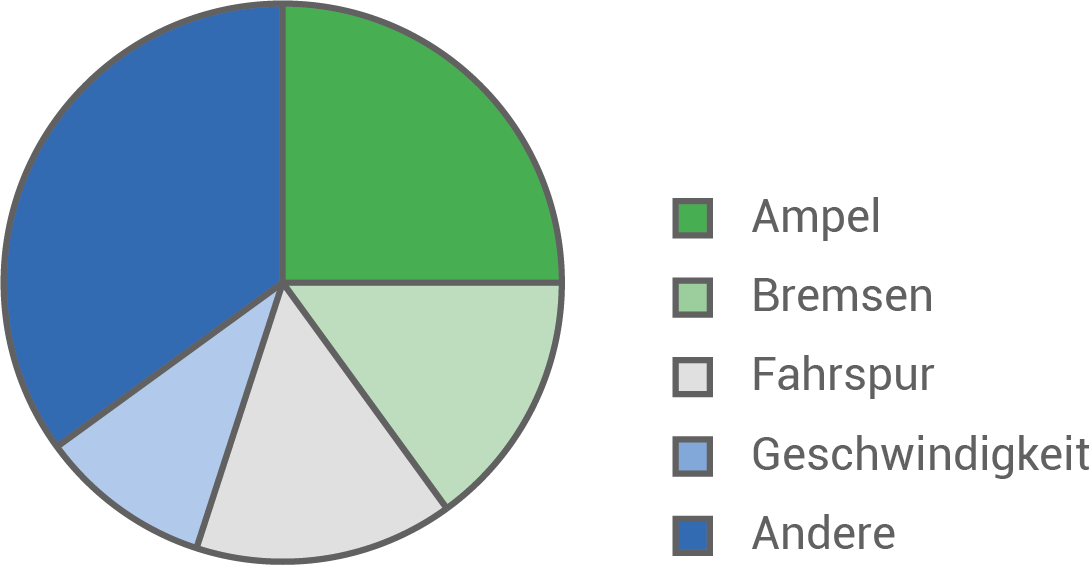
Die Tabelle zeigt durch Handy-Nutzung am Steuer entstehende kritische Situationen und deren prozentuales Auftreten.
Stelle diesen Sachverhalt in einem Kreisdiagramm dar.
| Situation | Angabe in % |
|---|---|
| Umschalten der Ampel zu spät erkannt | |
| Verkehrsbedingtes Bremsen zu spät erkannt | |
| Von der Fahrspur abgekommen | |
| Geschwindigkeitsbegrenzung übersehen | |
| Andere |
6 BE erreichbar
Lösung 1
1.
a)
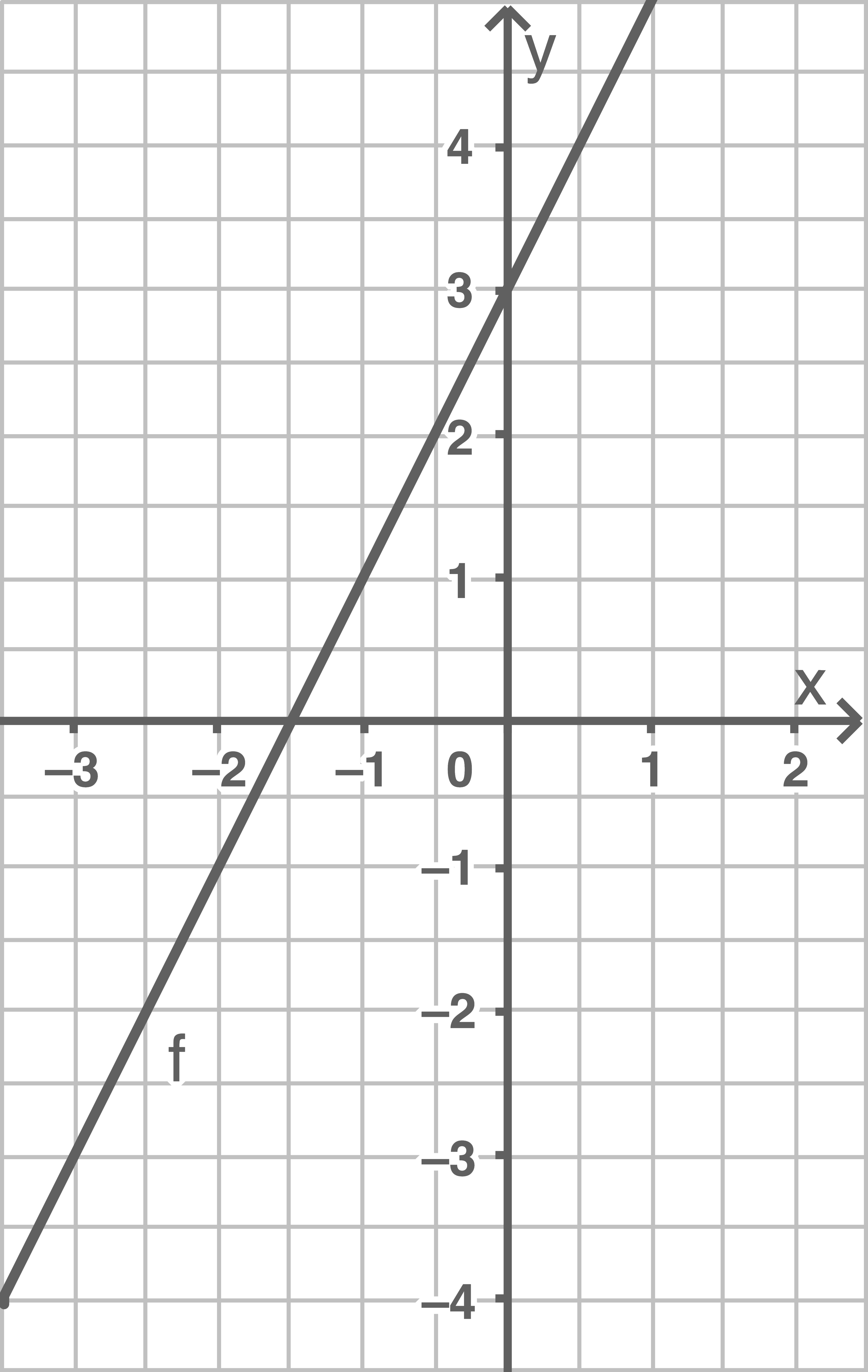
b)
Der Umfang der schraffierten Fläche setzt sich aus zwei Radien und einem Viertel des Umfangs des Kreises zusammen.
![\(\begin{array}[t]{rll}
u&=& 2\cdot r+\dfrac{1}{4}\cdot 2\cdot \pi\cdot r \\[5pt]
&=& 2\cdot 6\,\text{cm}+\dfrac{1}{4}\cdot 2\cdot \pi\cdot 6\,\text{cm} \\[5pt]
&\approx& 21,4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/1a485cf3f9605ce2af4eaab9493c6cf9157f32c5222fe23d115b05e44e753d8b?color=5a5a5a) Die Kreisfläche hat einen Umfang von
Die Kreisfläche hat einen Umfang von 
c)
(I)
(II)
Anzahl Stunden:  Gesamtanzahl Fahrzeuge im Zeitraum:
Gesamtanzahl Fahrzeuge im Zeitraum: 
![\(\begin{array}[t]{rll}
\overline{x}&=& \dfrac{\text{Gesamtanzahl Fahrzeuge}}{\text{Anzahl Stunden}} \\[5pt]
&=& \dfrac{14\,072}{12} \\[5pt]
&\approx& 1\,172,7
\end{array}\)](https://mathjax.schullv.de/b7dec34c2c9fe432b65b2493f7f81f6b90151e1c0ac85cf3341c51ed902ead9b?color=5a5a5a) Die Durchschnittliche Anzahl der Fahrzeuge pro Stunde beträgt
Die Durchschnittliche Anzahl der Fahrzeuge pro Stunde beträgt 
d)
e)
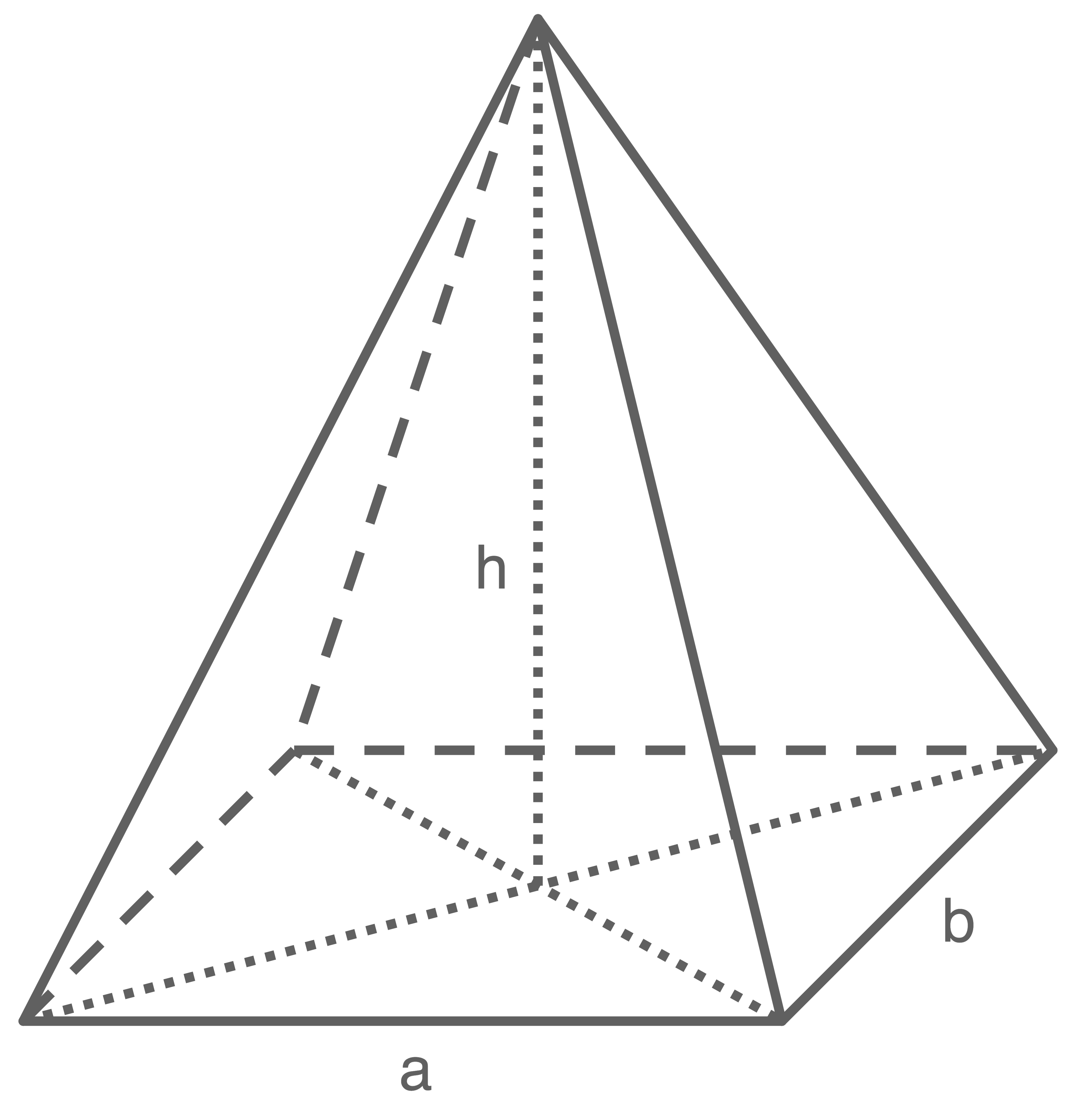
Lösung 2
a)
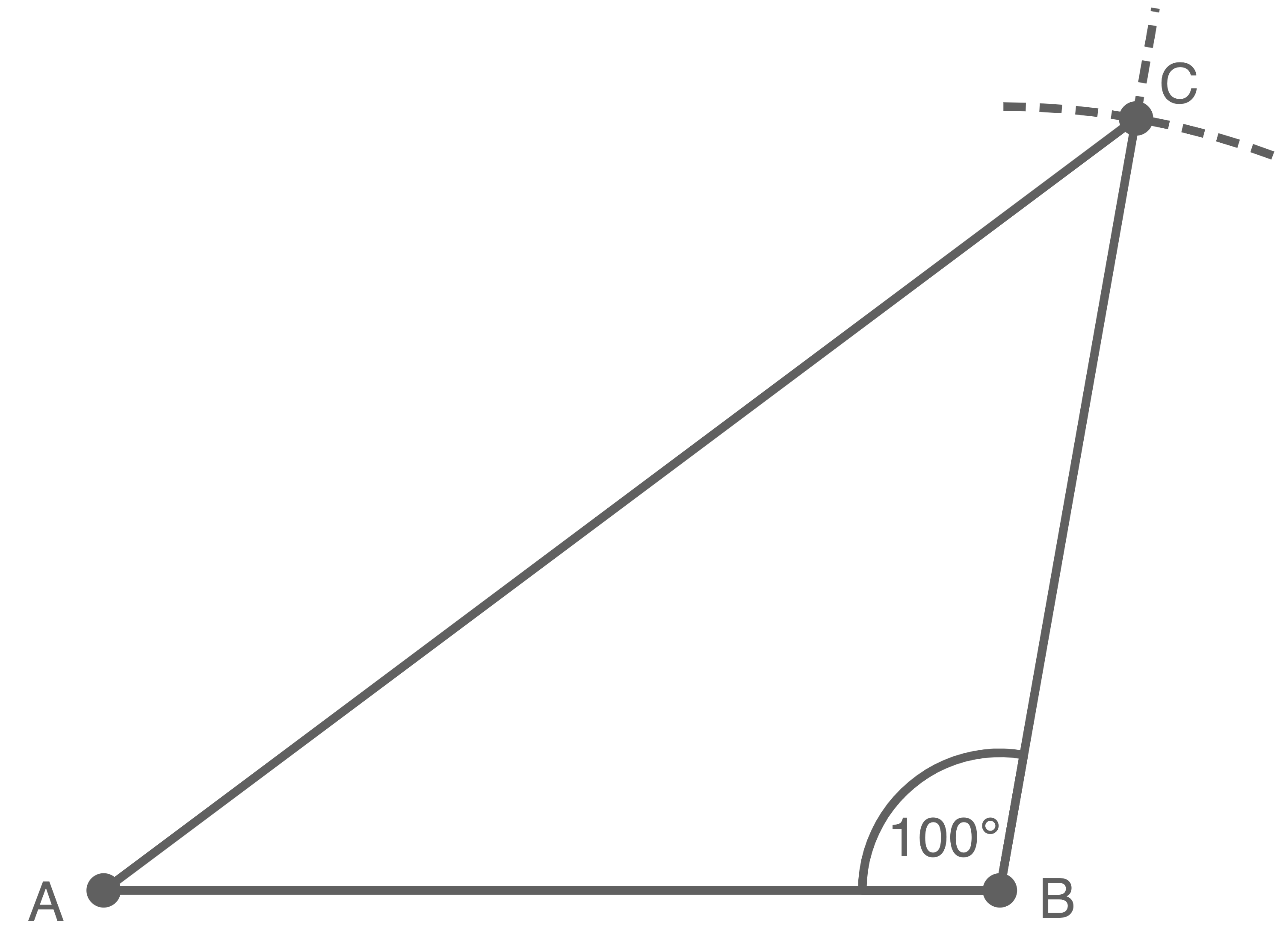
b)
Länge der Seite  berechnen
Mit dem Kosinussatzes gilt:
Die Seite
berechnen
Mit dem Kosinussatzes gilt:
Die Seite  ist ungefähr
ist ungefähr  lang.
Flächeninhalt des Dreiecks
lang.
Flächeninhalt des Dreiecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot \overline{AB}\cdot \overline{BC} \cdot \sin(\beta) \\[5pt]
&=&\dfrac{1}{2} \cdot 8~\text{cm} \cdot 7~\text{cm} \cdot \sin(100^{\circ}) \\[5pt]
&\approx& 27,6\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/8f6677d4daa66fc55ecc4f1c9ae7049c06ad3a1c7041c316e1c544405944589b?color=5a5a5a) Das Dreieck hat einen Flächeninhalt von ungefähr
Das Dreieck hat einen Flächeninhalt von ungefähr 
c)
Das Dreieck lässt sich in 4 gleich große Dreiecke unterteilen, die alle kongruent sind zum Dreieck 
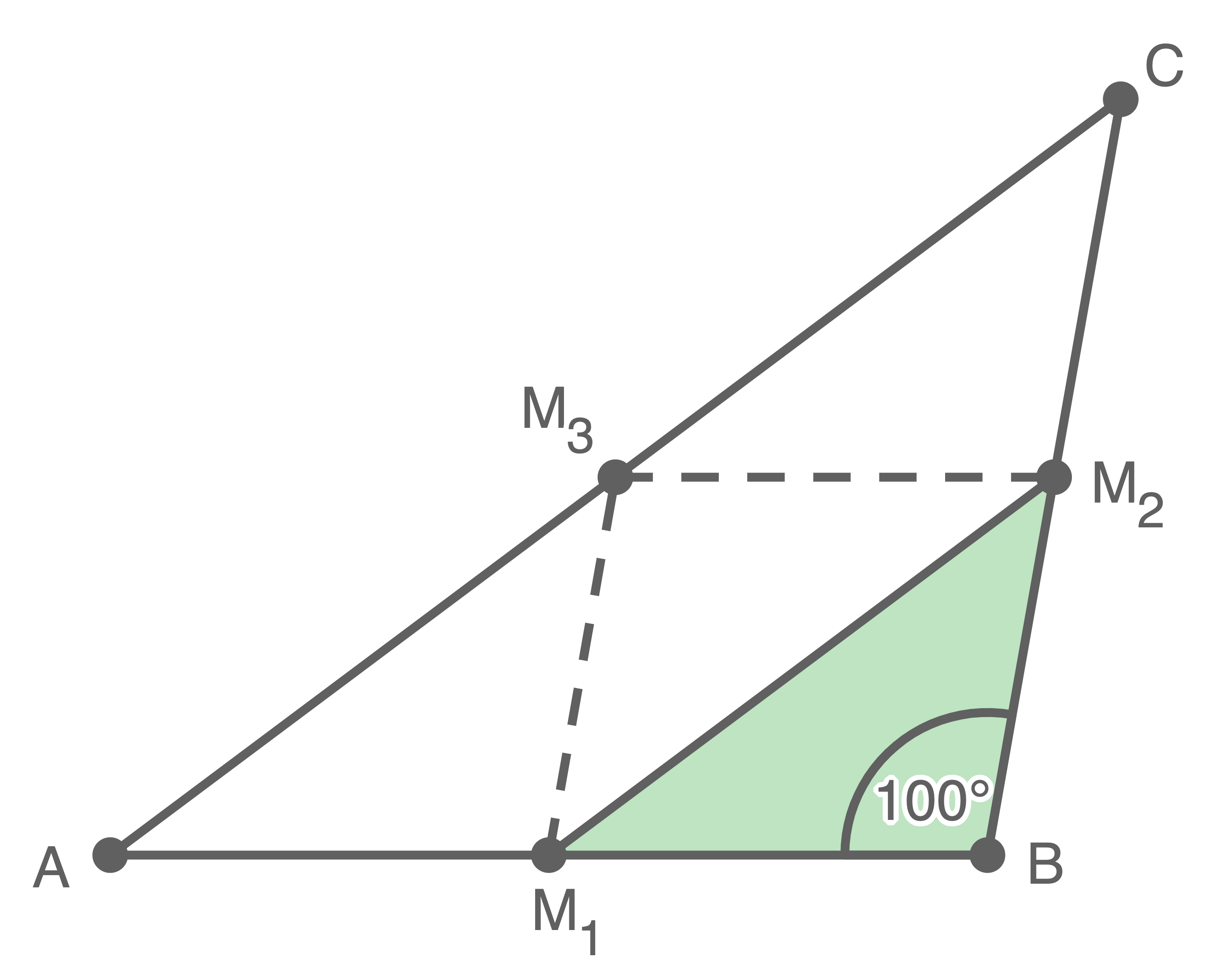 Die Flächeninhalte der beiden Dreiecke haben daher ein Verhältnis von
Die Flächeninhalte der beiden Dreiecke haben daher ein Verhältnis von 

Lösung 3
a)
Lösung mit Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 12\,000\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 120 \\[5pt]
4,5\,\% & \mathrel{\widehat{=}}& 540
\end{array}\)](https://mathjax.schullv.de/f080458d7d3d6047e610bf2e3f1dcb2ce9e0ba022b46bdd0190c0df4fdc6b764?color=5a5a5a)



 Lösung mit Prozentformel
Lösung mit Prozentformel


![\(\begin{array}[t]{rll}
W&=& \dfrac{p\,\%}{100\,\%}\cdot G \\[5pt]
W&=& \dfrac{4,5\,\%}{100\,\%}\cdot 12\,000 \\[5pt]
W&=& 540
\end{array}\)](https://mathjax.schullv.de/0aa5b26b22d2d34392832c317a9192ad6fb95071f0a3209ff3a92743d47b0bd6?color=5a5a5a) Es wurden
Es wurden  Autofahrer beim Tippen auf dem Handy beobachtet.
Autofahrer beim Tippen auf dem Handy beobachtet.
b)
Für den Zusammenhang zwischen Geschwindigkeit  , Strecke
, Strecke  und Zeit
und Zeit  gilt:
gilt:
![\(\begin{array}[t]{rll}
s&=& v\cdot t \\[5pt]
&=& 90\dfrac{\text{km}}{\text{h}}\cdot 4\,\text{s} \\[5pt]
&=& 90\,\dfrac{1\,000\text{m}}{3\,600\text{s}}\cdot 4\,\text{s} \\[5pt]
&=& 100\,\text{m}
\end{array}\)](https://mathjax.schullv.de/5ca560474b52210a6183e532c2868673da0e83c12776cf24b0fbf99de126ca1b?color=5a5a5a) Der Autofahrer legt in der Zeit
Der Autofahrer legt in der Zeit  zurück.
zurück.
c)
Prozentzahlen in Grad umrechnen:
![\(\begin{array}[t]{rll}
25\,\%&:& 0,25\cdot 360^{\circ}=90^{\circ} \\[5pt]
15\,\%&:& 0,15\cdot 360^{\circ}=54^{\circ} \\[5pt]
10\,\%&:& 0,10\cdot 360^{\circ}=36^{\circ}
\end{array}\)](https://mathjax.schullv.de/aa783048e28622aab1965f38285b06fd607d5b10d081f680087268c1aa37be99?color=5a5a5a)