Pflichtteil 2
Pflichtaufgabe 1
a)
Die Abbildung zeigt ein Dreieck 
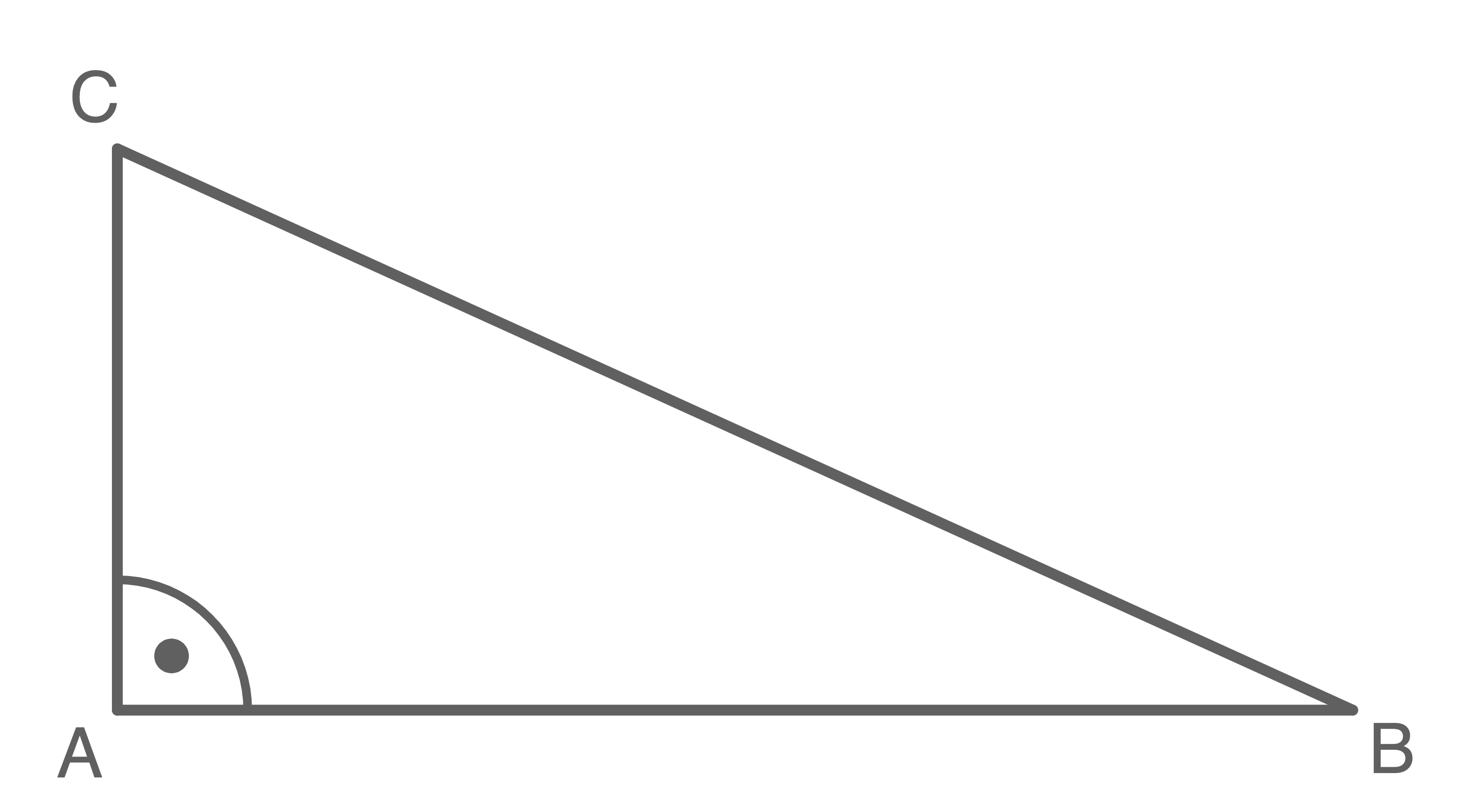
Es gilt:


Abbildung (nicht maßstäblich)
b)
Die Einwohnerzahl einer Gemeinde ist um  gestiegen. Die Gemeinde zählt nun
gestiegen. Die Gemeinde zählt nun  Einwohner.
Einwohner.
Ermittle die Anzahl der Einwohner, die hinzugekommen sind.
Ermittle die Anzahl der Einwohner, die hinzugekommen sind.
c)
Flüssigdünger wird in konzentrierter Form angeboten. Ein Hersteller empfiehlt folgende Dosierung:
„Für 1000 Liter Gießwasser werden vier Liter Flüssigdünger benötigt.“
Untersuche, ob  Flüssigdünger pro
Flüssigdünger pro  Liter Gießwasser der empfohlenen Dosierung entsprechen.
Liter Gießwasser der empfohlenen Dosierung entsprechen.
d)
Bestimme  sodass
sodass  eine Lösung der Gleichung
eine Lösung der Gleichung  ist.
ist.
e)
Betrachtet werden reelle Zahlen  und
und  mit
mit 

Untersuche, ob die Differenz der Quadrate von und
und  und das Quadrat der Differenz von
und das Quadrat der Differenz von  und
und  zueinander äquivalent sind.
zueinander äquivalent sind.
Untersuche, ob die Differenz der Quadrate von
11 BE erreichbar
Pflichtaufgabe 2
Gegeben sind die linearen Funktionen  und
und  durch
durch
 und
und  schneiden einander im Punkt
schneiden einander im Punkt  .
.
Eine Längeneinheit im Koordinatensystem entspricht
.
- Der Graph der Funktion
verläuft durch die Punkte
und
Eine Längeneinheit im Koordinatensystem entspricht
a)
Zeichne die Graphen von  und
und  mindestens im Intervall von
mindestens im Intervall von  in ein und dasselbe Koordinatensystem.
in ein und dasselbe Koordinatensystem.
b)
Der Graph von  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  .
.
Der Punkt ist der Bildpunkt von
ist der Bildpunkt von  bei Spiegelung an der
bei Spiegelung an der  -Achse.
Zeichne das Viereck
-Achse.
Zeichne das Viereck  in das unter a) angelegte Koordinatensystem.
in das unter a) angelegte Koordinatensystem.
Bestimme den Flächeninhalt des Vierecks
Der Punkt
Bestimme den Flächeninhalt des Vierecks
c)
Gib eine Gleichung einer linearen Funktion an, deren Graph parallel zum Graphen von  verläuft.
verläuft.
7 BE erreichbar
Pflichtaufgabe 3
Die Abbildung zeigt eine gerade Pyramide mit quadratischer Grundfläche.
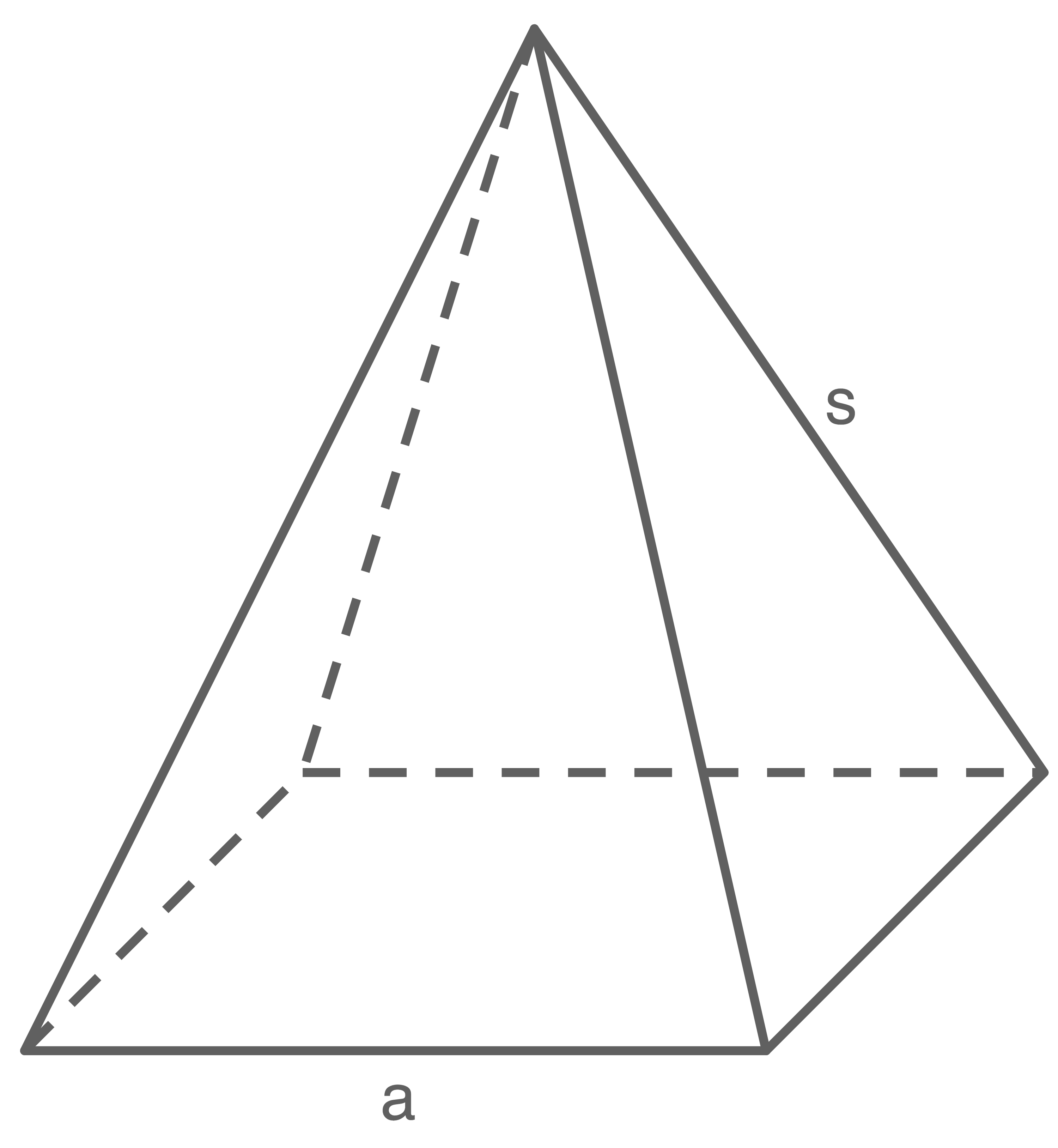
Eine Grundkante hat die Länge  eine Seitenkante hat die Länge
eine Seitenkante hat die Länge 

Abbildung (nicht maßstäblich)
a)
Zeichne ein Netz der Pyramide.
b)
Berechne die Größe der Innenwinkel einer Seitenfläche.
6 BE erreichbar
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rll}
\overline{\,\text{BC}}^2&=&\overline{\,\text{AC}}^2+\overline{\,\text{AB}}^2 \\[5pt]
\overline{\,\text{BC}}^2 &=& (4 \,\text{cm})^2+ (8\,\text{cm})^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{\,\text{BC}} &=& \sqrt{(4 \,\text{cm})^2+ (8\,\text{cm})^2} \\[5pt]
\overline{\,\text{BC}} &\approx& 8,9 \,\text{cm}
\end{array}\)](https://mathjax.schullv.de/899e6546825857c41839183fa655b0a54424a786833aabab9f1ba8415391dd04?color=5a5a5a) Die Seite
Die Seite  ist etwa
ist etwa  lang.
lang.
b)
Lösung mit Dreisatz
Ursprüngliche Einwohnerzahl ermitteln:




![\(\begin{array}{rcl}
104\,\% & \mathrel{\widehat{=}}& 23\,400\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 225\\[5pt]
100\,\% & \mathrel{\widehat{=}}& 22\,500
\end{array}\)](https://mathjax.schullv.de/33b3f99555c0ece3fd17f140e813733fb741ba0dc6eaf6c1b490b203134ff3b6?color=5a5a5a)




 Lösung mit Lösungsformel
Ursprüngliche Einwohnerzahl ermitteln:
Lösung mit Lösungsformel
Ursprüngliche Einwohnerzahl ermitteln:


![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&=& \dfrac{23\,400\cdot 100\,\%}{104\,\%} \\[5pt]
G&\approx& 22\,500
\end{array}\)](https://mathjax.schullv.de/124acd85ebb132bb792d3711c60be7fea79c4635d6b6fff414b57d279690b2fe?color=5a5a5a)
 Es sind 900 Menschen in die Gemeinde eingetreten.
Es sind 900 Menschen in die Gemeinde eingetreten.
c)
d)
e)
Beispielwerte: 
 Differenz der Quadrate von
Differenz der Quadrate von  und
und 
 Quadrat der Differenz von
Quadrat der Differenz von  und
und 
 Die Terme sind zueinander nicht äquivalent, da
Die Terme sind zueinander nicht äquivalent, da  gilt.
gilt.
Lösung 2
a)
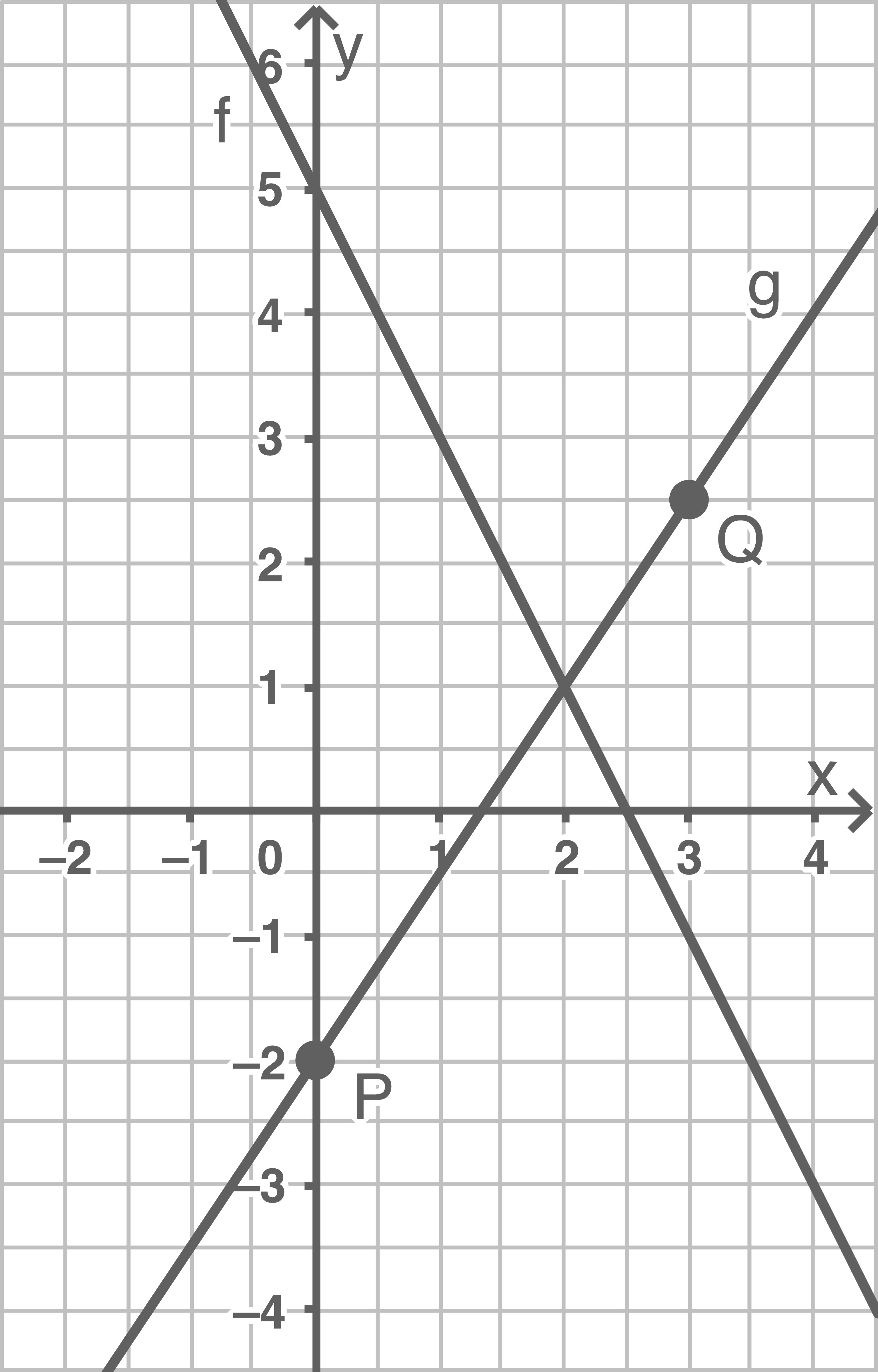
b)
Viereck einzeichnen
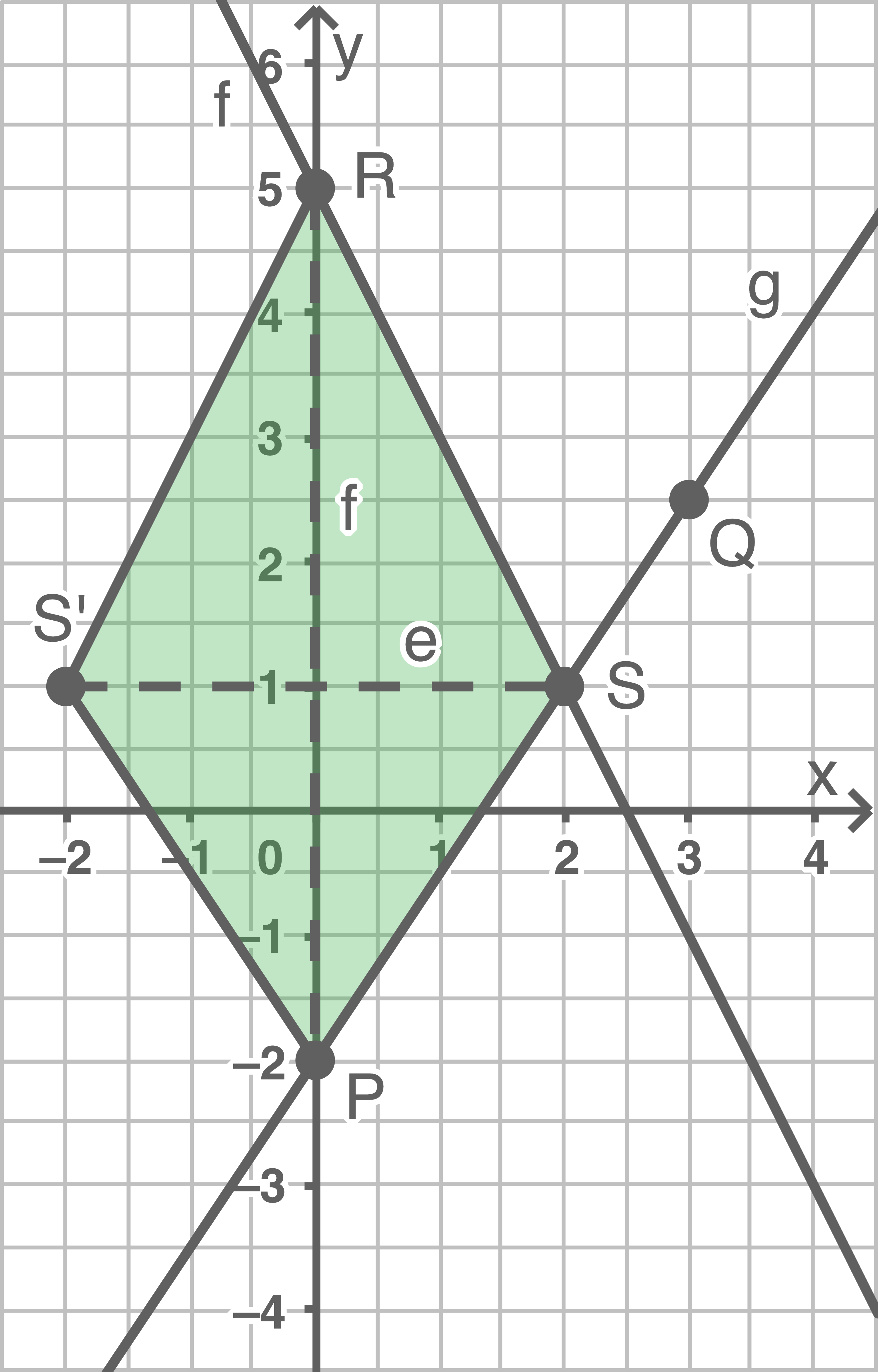 Flächeninhalt berechnen
Mit der Formel für den Flächeninhalt eines Drachenvierecks folgt:
Flächeninhalt berechnen
Mit der Formel für den Flächeninhalt eines Drachenvierecks folgt:
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot e\cdot f \\[5pt]
&=& \dfrac{1}{2}\cdot 4\,\text{cm}\cdot 7\,\text{cm} \\[5pt]
&=& 14\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/c63594acc74303512231796b1b24ac4933f78794ea8732c09cc46d9d8f5a6049?color=5a5a5a) Der Flächeninhalt des Vierecks beträgt
Der Flächeninhalt des Vierecks beträgt 

c)
Der Abbildung aus Teilaufgabe b) kann die Steigung  und der
und der  -Achsenabschnitt
-Achsenabschnitt  entnommen werden.
Jede lineare Funktion, die die gleiche Steigung, aber einen anderen
entnommen werden.
Jede lineare Funktion, die die gleiche Steigung, aber einen anderen  -Achsenabschnitt hat, ist eine Parallele zu
-Achsenabschnitt hat, ist eine Parallele zu  Eine mögliche Lösung ist beispielsweise:
Eine mögliche Lösung ist beispielsweise:

Lösung 3
a)
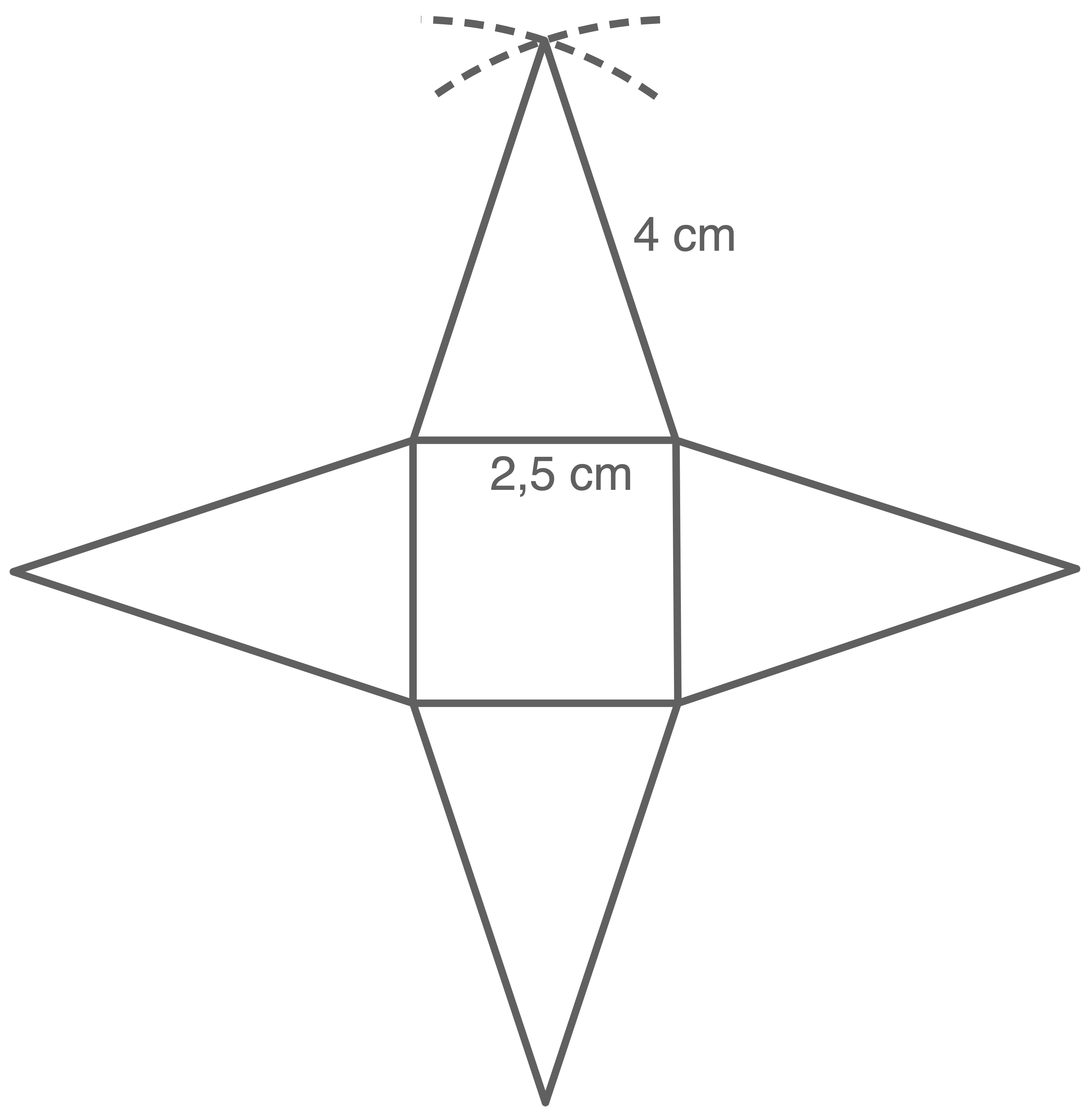
b)
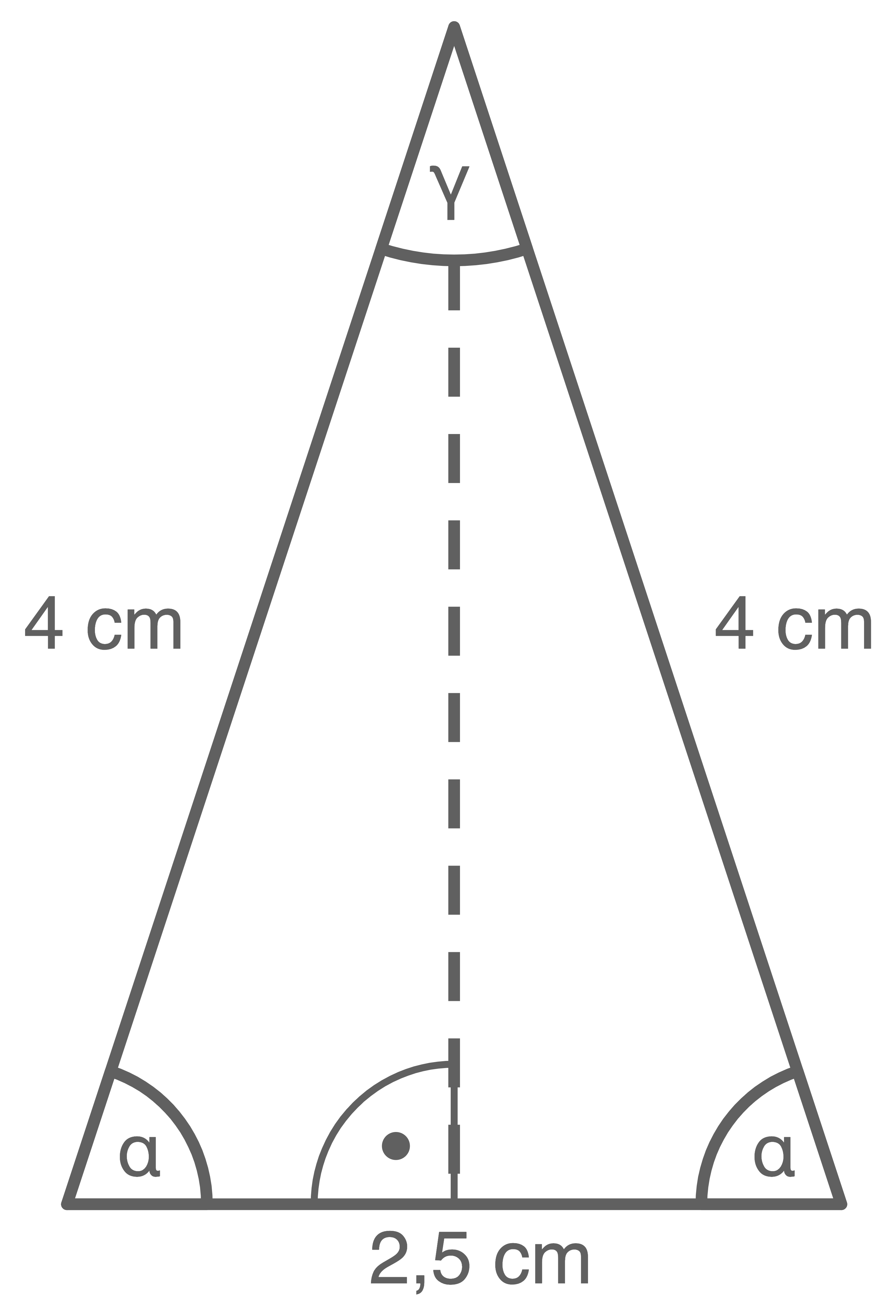
Skizze einer Seitenfläche