Wahlpflichtaufgaben
Wahlpflichtaufgabe 1
Der Mond ist durchschnittlich 
von der Erde entfernt und hat einen Durchmesser von ca. 
a)
Die Umlaufbahn des Mondes um die Erde wird vereinfacht als kreisförmig betrachtet.
Berechne die Länge dieser Umlaufbahn.
Berechne die Länge dieser Umlaufbahn.
b)
Ermittle annähernd den Oberflächeninhalt des Mondes und gib den Oberflächeninhalt in der Schreibweise 
an.
c)
Zeige rechnerisch, dass ein vom Auge eines Beobachters 
entfernter kreisförmiger Gegenstand mit einem Durchmesser von 
den Mond verdeckt.
8 BE erreichbar
Wahlpflichtaufgabe 2
Gegeben sind die Funktionen 
und 
durch:
- Der Graph der Funktion
und
a)
Zeichne die Graphen beider Funktionen mindestens im Intervall 
in ein und dasselbe Koordinatensystem.
b)
Begründe, dass die Funktion an der Stelle 
nicht definiert ist.
c)
Weise nach, dass 
eine Gleichung der Funktion ist.
d)
Die Gleichung 
stellt im Zusammenhang mit den Funktionen und einen Lösungsansatz einer Aufgabe dar.
Ermittle die Lösungen der Gleichung und formuliere eine zum Lösungsansatz passende Aufgabenstellung.
Ermittle die Lösungen der Gleichung und formuliere eine zum Lösungsansatz passende Aufgabenstellung.
8 BE erreichbar
Wahlpflichtaufgabe 3
Die Abbildung zeigt das Netz eines Würfels. Dieser Würfel wird zweimal nacheinander geworfen.
Nach jedem Wurf wird notiert, ob die Augenzahl 6 fällt oder nicht.
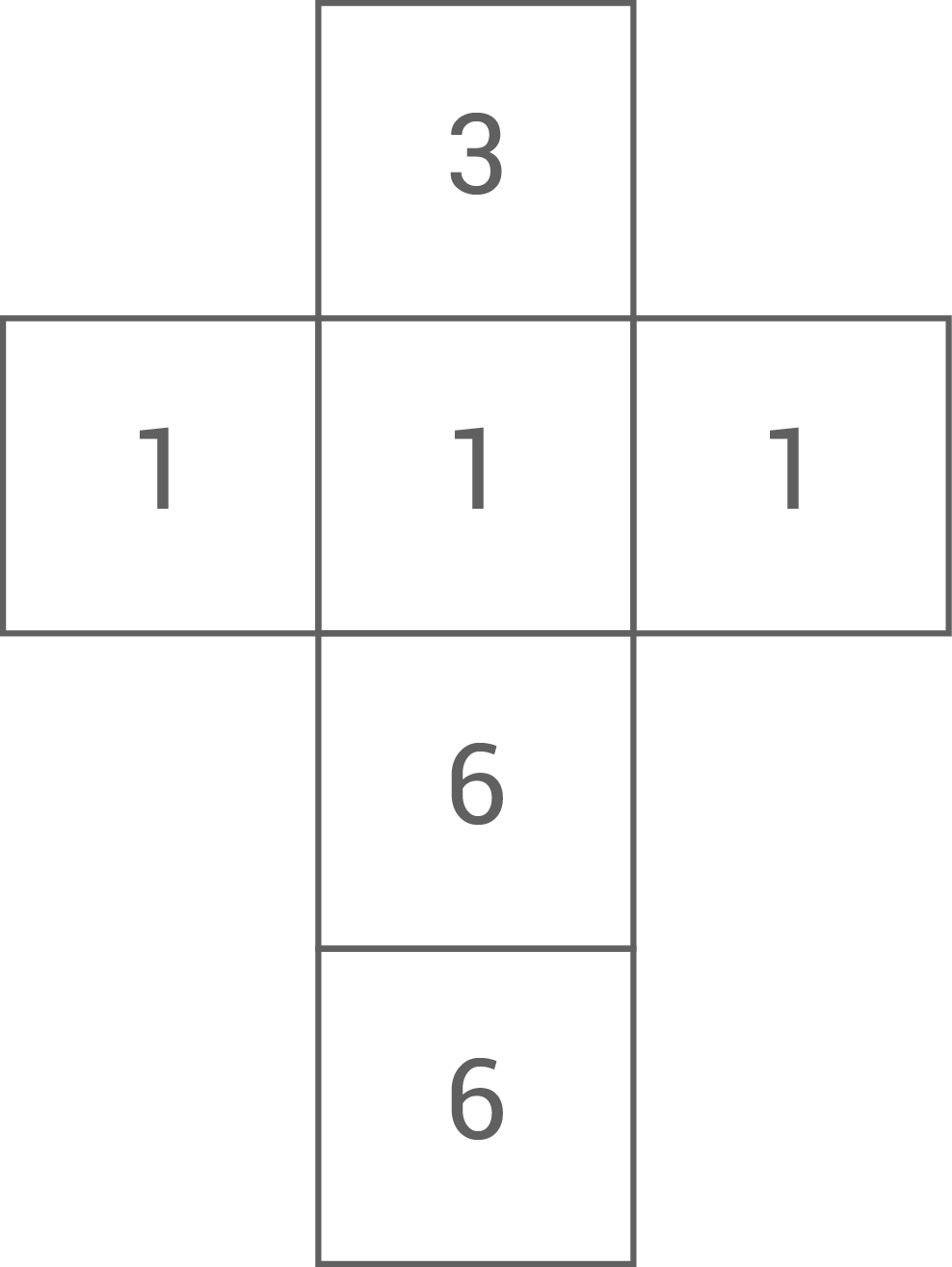
Abbildung
a)
Zeichne für diesen zweistufigen Zufallsversuch ein Baumdiagramm, und trage die Wahrscheinlichkeiten an allen Pfaden an.
b)
Berechne die Wahrscheinlichkeit, dass die Augenzahl 6 bei diesem Zufallsversuch genau einmal auftritt.
Nach jedem Wurf wird nun die gefallene Augenzahl notiert.
c)
Ermittle die Wahrscheinlichkeit des Ereignisses „Die Summe der beiden Augenzahlen ist eine Primzahl."
8 BE erreichbar
Lösung 1
a)
Der Radius 
der Umlaufbahn entspricht der Entfernung der Erde zum Mond. Mit der Formel für dem Umfang eines Kreises folgt:
Die Länge der Umlaufbahn beträgt ungefähr 
b)
Mit der Formel für den Oberflächeninhalt einer Kugel gilt:
![\(\begin{array}[t]{rll}
O&=& 4\cdot \pi\cdot \left(\dfrac{3\,500\,\text{km}}{2}\right)^2 \\[5pt]
&\approx& 38\,484\,510\,\text{km}^2 \\[5pt]
&\approx& 3,8\,\cdot10^7\,\text{km}^2
\end{array}\)](https://mathjax.schullv.de/6281c7ada0786001972f1e89047f61776f3cd4c966752bd94e4bc0564d872739?color=5a5a5a)
Der Mond hat ungefähr einen Oberflächeninhalt von 
c)
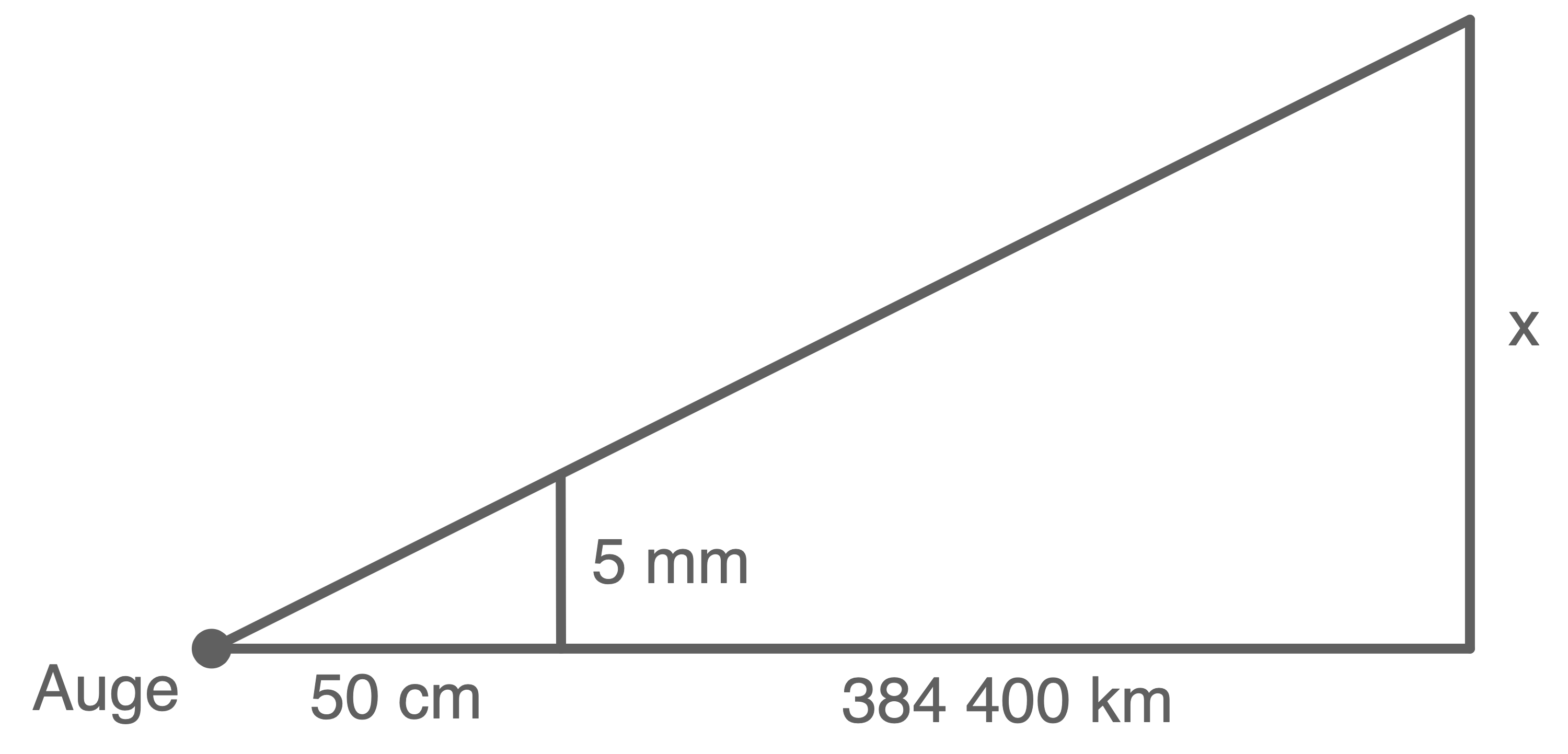
Lösung 2
a)
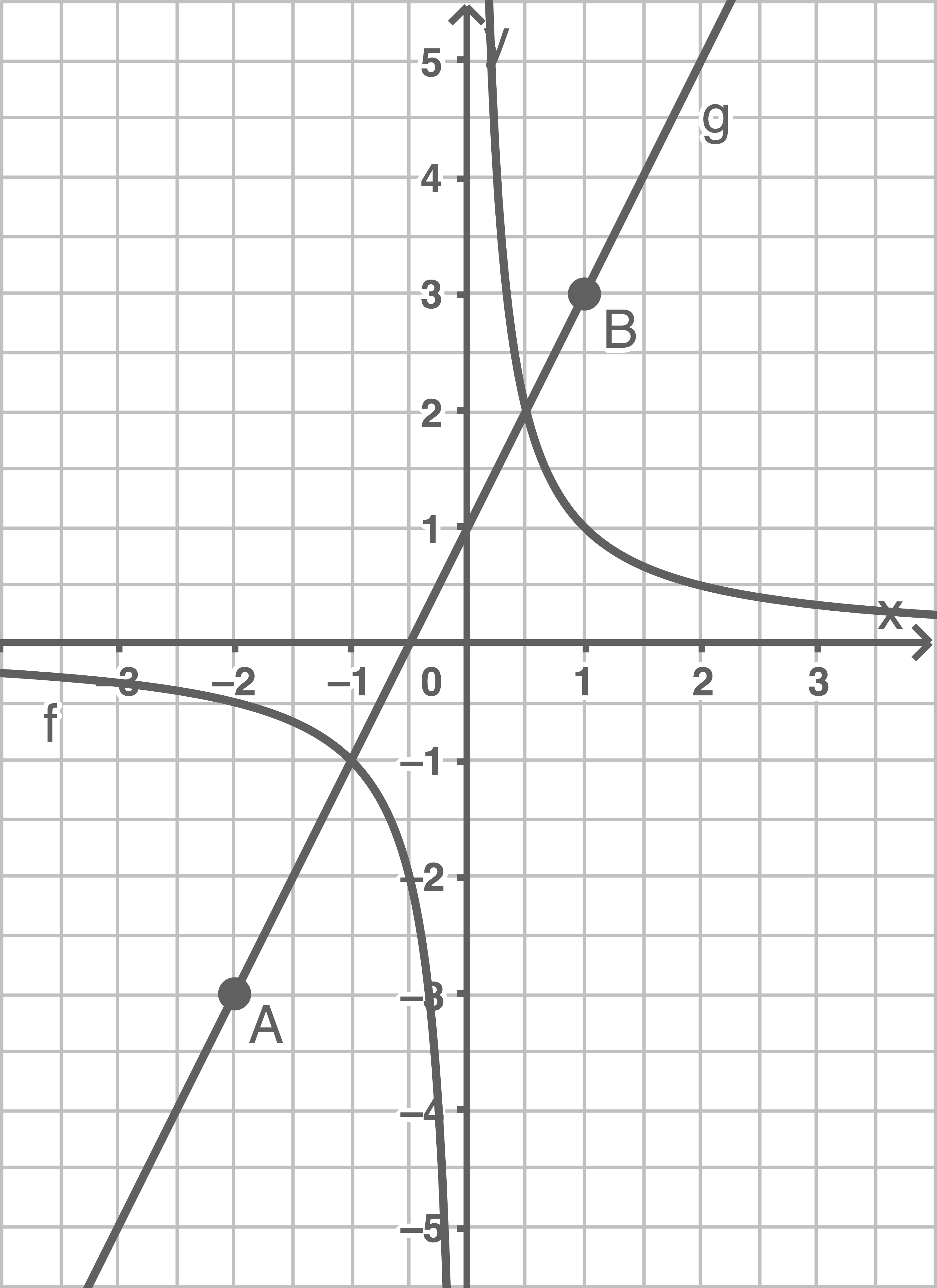
b)
Der Nenner eines Bruches darf nach Definition nicht sein. Daher ist die Funktion mit der Funktionsgleichung 
an der Stelle 
nicht definiert.
c)
Der 
-Achsenabschnitt 
von lässt sich direkt aus dem Koordinatensystem aus Teilaufgabe a) ablesen:
Mit dem Steigungsdreieck lässt sich außerdem die Steigung 
bestimmen:
Einsetzen in die allgemeine Geradengleichung 
liefert die Funktionsgleichung 
d)
Lösungen der Gleichung ermitteln
![\(\begin{array}[t]{rll}
\dfrac{1}{x}&=& 2x+1 \quad \scriptsize \mid\;\cdot x \\[5pt]
1&=& 2x^2+x \quad \scriptsize \mid\;-1 \\[5pt]
0&=& 2x^2+x-1 \quad \scriptsize \mid\;:2 \\[5pt]
0&=& x^2+\dfrac{1}{2}x-\dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/2702b9d500a39a3fc3665240f6210d627162b1956cea07366194720ba3c8b900?color=5a5a5a)
Mit der 
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{1}{4}\pm\sqrt{\left(\dfrac{1}{4}\right)^2-\left(-\dfrac{1}{2}\right)} \\[5pt]
&=& -\dfrac{1}{4}\pm\sqrt{\dfrac{9}{16}} \\[5pt]
x_1&=& -\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{1}{2} \\[5pt]
x_2&=& -\dfrac{1}{4}-\dfrac{3}{4}=-1
\end{array}\)](https://mathjax.schullv.de/0fcba42b58e4173e130fa59592331d054d5322a0c52d9a37f377202346a30e1e?color=5a5a5a)
Die Gleichung hat die Lösungen 
und 
Mögliche Aufgabenstellung angeben
„Bestimme die Schnittstellen der beiden Funktionen und 
“
Lösung 3
a)
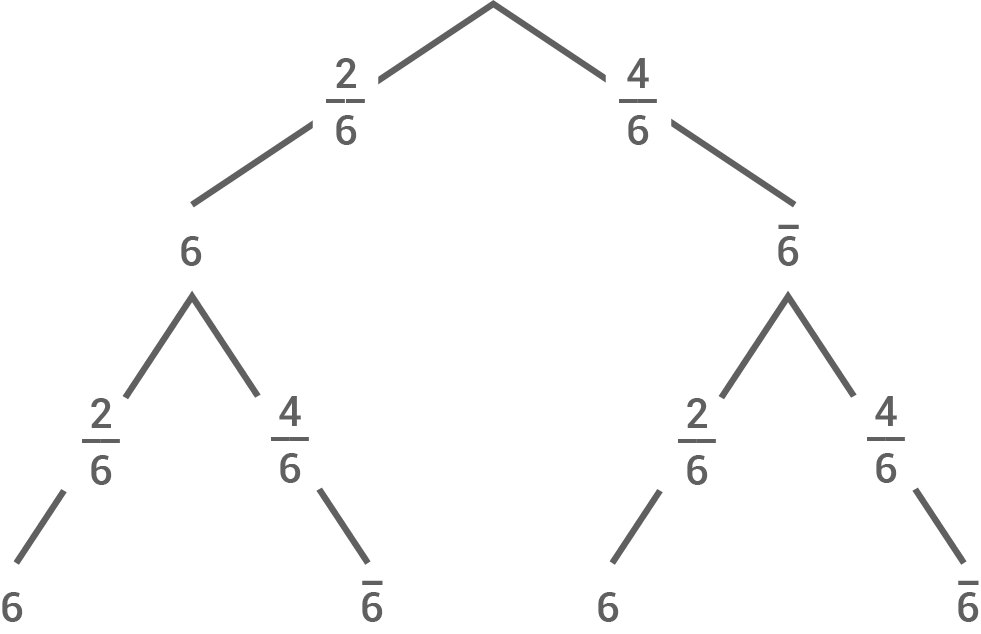
b)
c)