Wahlpflichtaufgaben
Wahlpflichtaufgabe 1
Fibonacci-Zahlen sind die Zahlen der Folge 1, 1, 2, 3, 5, 8, ...
Mit einer Tabellenkalkulation werden die Fibonacci-Zahlen erzeugt.
Mit einer Tabellenkalkulation werden die Fibonacci-Zahlen erzeugt.
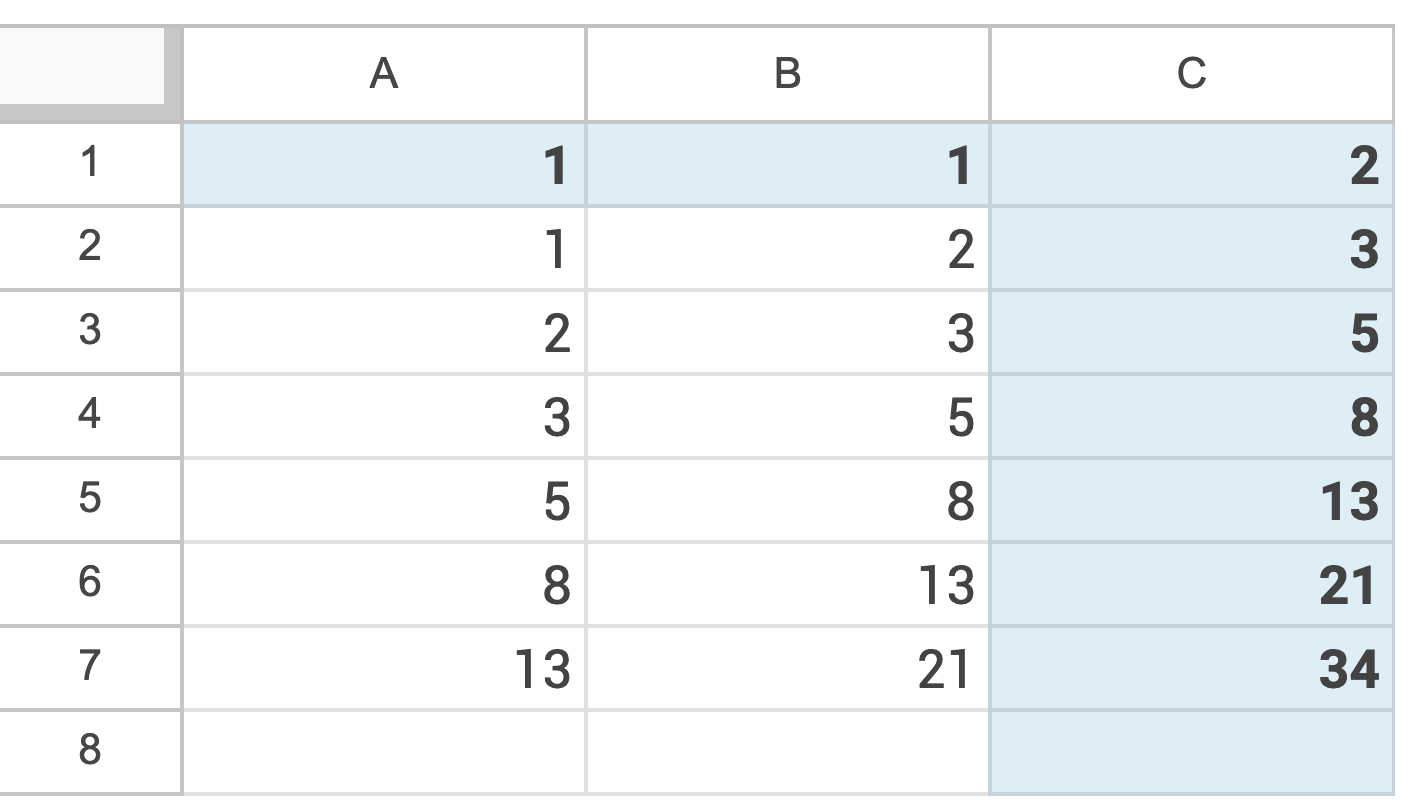
a)
Die nächste Fibonacci-Zahl wird in Zelle C8 erzeugt.
Gib diese Fibonacci-Zahl sowie eine zugehörige Formel zur Berechnung der Zelle C8 an. Hinweis: In der Formel sind Zellbezüge zu verwenden.
Gib diese Fibonacci-Zahl sowie eine zugehörige Formel zur Berechnung der Zelle C8 an. Hinweis: In der Formel sind Zellbezüge zu verwenden.
b)
Der Quotient aus einer Fibonacci-Zahl und der vorhergehenden Fibonacci-Zahl ergibt annähernd die Verhältniszahl des Goldenen Schnitts.
Berechne unter Verwendung der Fibonacci-Zahlen 89, 144, 233 die Verhältniszahl auf Hundertstel genau.
Berechne unter Verwendung der Fibonacci-Zahlen 89, 144, 233 die Verhältniszahl auf Hundertstel genau.
c)
Bei dem im 16. Jahrhundert erbauten Leipziger Rathaus teilt der Turm die Fassade im Verhältnis des Goldenen Schnitts (siehe Abbildung). Die Fassade hat eine Gesamtlänge von  Meter.
Meter.
 Die zugehörigen Streckenverhältnisse (siehe Abbildung) können mit der Gleichung
Die zugehörigen Streckenverhältnisse (siehe Abbildung) können mit der Gleichung  berechnet werden.
Durch Umformen ergibt sich die Gleichung
berechnet werden.
Durch Umformen ergibt sich die Gleichung  Berechne die Längen der beiden Teilstrecken und zeige, dass diese die unter b) ermittelte Verhältniszahl liefern.
Berechne die Längen der beiden Teilstrecken und zeige, dass diese die unter b) ermittelte Verhältniszahl liefern.

Abbildung (nicht maßstäblich)
8 BE erreichbar
Wahlpflichtaufgabe 2
Die Abbildung zeigt den Kreis durch die Punkte  und
und 
 ist der Mittelpunkt des Kreises.
ist der Mittelpunkt des Kreises.
Der grau gefärbte Anteil des Kreises hat einen Flächeninhalt von
Der grau gefärbte Anteil des Kreises hat einen Flächeninhalt von
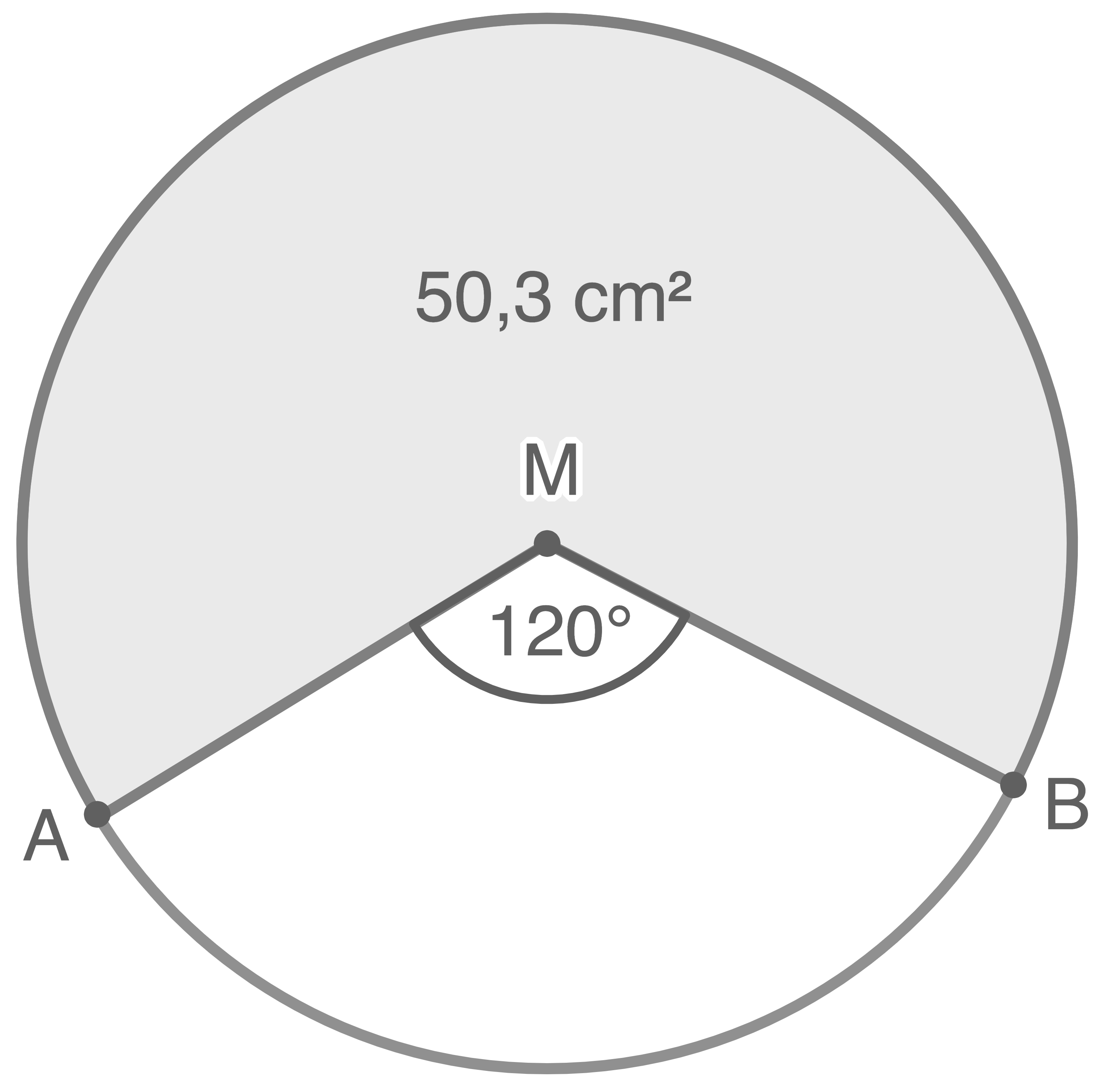
Abbildung (nicht maßstäblich)
a)
Begründe, dass der Kreis einen Flächeninhalt von  hat.
hat.
b)
Die Punkte 
 und
und  bilden das Dreieck
bilden das Dreieck 
Berechne den Flächeninhalt des Dreiecks
Berechne den Flächeninhalt des Dreiecks
c)
Der Punkt  wird auf dem Kreis verschoben.
wird auf dem Kreis verschoben.
Gib eine Bedingung dafür an, dass ein gleichseitiges Dreieck entsteht.
Begründe deine Angabe.
Gib eine Bedingung dafür an, dass ein gleichseitiges Dreieck entsteht.
Begründe deine Angabe.
8 BE erreichbar
Wahlpflichtaufgabe 3
Im Jahr 2020 lagerten in Deutschland rund  Millionen ungenutzte Handys. Ein Handy enthält durchschnittlich
Millionen ungenutzte Handys. Ein Handy enthält durchschnittlich  Gold.
Gold.
Im Folgenden wird angenommen, dass dieses Gold wiederverwendet wird.
Werkstück l besteht aus Gold und Eisen. Es hat eine Masse von Der Anteil der Masse des Goldes im Werkstück l beträgt
Der Anteil der Masse des Goldes im Werkstück l beträgt 
Werkstück ll besteht aus Gold und Silber.
Im Folgenden wird angenommen, dass dieses Gold wiederverwendet wird.
a)
Das Gold wird zu Goldbarren mit einer Masse von je  verarbeitet.
verarbeitet.
Berechne die Anzahl der Goldbarren, die aus Millionen Handys hergestellt werden.
Millionen Handys hergestellt werden.
Berechne die Anzahl der Goldbarren, die aus
b)
Aus dem Gold von  ungenutzten Handys wird ein Ring mit einer Masse von
ungenutzten Handys wird ein Ring mit einer Masse von  hergestellt. Auf diesem Ring soll der Feingehalt eingraviert werden.
Der Feingehalt gibt den Goldanteil an der Gesamtmasse des Ringes an (siehe Tabelle).
hergestellt. Auf diesem Ring soll der Feingehalt eingraviert werden.
Der Feingehalt gibt den Goldanteil an der Gesamtmasse des Ringes an (siehe Tabelle).
Ermittle den Feingehalt, der auf diesem Ring eingraviert werden muss.
Zwei Werkstücke mit gleicher Masse und gleichem Volumen werden im Folgenden betrachtet.
| Feingehalt | |||
|---|---|---|---|
| Goldanteil in % |
Werkstück l besteht aus Gold und Eisen. Es hat eine Masse von
Werkstück ll besteht aus Gold und Silber.
Die Tabelle enthält die Dichten der jeweiligen Bestandteile.
Hinweis:
Zum Beispiel hat ein Kubikzentimeter Gold eine Masse von Gramm.
Gramm.
Zum Beispiel hat ein Kubikzentimeter Gold eine Masse von
| Metall | Dichte in |
|---|---|
| Gold | |
| Silber | |
| Eisen |
c)
Berechne das Volumen  des Werkstücks l.
des Werkstücks l.
d)
Gib die Bedeutung der Variable  in der Formel
in der Formel

im Sachzusammenhang an. Begründe deine Angabe.
im Sachzusammenhang an. Begründe deine Angabe.
8 BE erreichbar
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Nächste Fibonacci-Zahl angeben
Die nächste Fibonacci-Zahl ergibt sich immer aus der Addition der beiden vorangegangenen Zahlen. Damit ergibt sich die nächste Zahl wie folgt:
 Formel zur Berechnung von C8 angeben
Formel:
Formel zur Berechnung von C8 angeben
Formel: 
b)
c)
Längen der beiden Teilstrecken berechnen
Die Länge der Teilstrecke  kann mit der
kann mit der  -Formel berechnet werden.
-Formel berechnet werden.
![\(\begin{array}[t]{rll}
x^2 &=& 93 \cdot (93-x) \\[5pt]
x^2 &=& 8\,649 - 93x \quad \scriptsize \mid\;+93x \\[5pt]
x^2+93x &=& 8\,649 \quad \scriptsize \mid\;-8\,649 \\[5pt]
x^2+ 93x -8649&=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c00e889f71650a25013aeac27514bff5297d0f1dffaf644f2f7a2810c0ae591d?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{93}{2}\pm \sqrt{\left(\dfrac{93}{2}\right)^2-(-8649)} \\[5pt]
x_{1}&=& -\dfrac{93}{2}+ \sqrt{10811,25} \, \approx 57,5 \\[5pt]
x_{2}&=& -\dfrac{93}{2}- \sqrt{10811,25} \, \approx -150,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b2868f5396677ca21d30fa86c6897ecb145614ea3870afbce52a4b07728759fa?color=5a5a5a) Die Lösung
Die Lösung  entfällt im Sachzusammenhang. Die Länge der Strecke
entfällt im Sachzusammenhang. Die Länge der Strecke  beträgt
beträgt  Somit gilt für die zweite Teilstrecke:
Somit gilt für die zweite Teilstrecke:
![\(\begin{array}[t]{rll}
y&=& 93\,\text{m}-x_1 & \\[5pt]
&\approx& 93\,\text{m}-57,5\,\text{m} & \\[5pt]
&=& 35,5\,\text{m}
\end{array}\)](https://mathjax.schullv.de/2cabe2346f1762c8988f0e35e51f9335b43fcedfd398b045281f0085d5859570?color=5a5a5a) Verhältniszahl ermitteln
Verhältniszahl ermitteln
 Damit ist gezeigt, dass die Verhältniszahl mit der Verhältniszahl des goldenen Schnitts übereinstimmt.
Damit ist gezeigt, dass die Verhältniszahl mit der Verhältniszahl des goldenen Schnitts übereinstimmt.
Lösung 2
a)
Der Innenwinel eines Kreises beträgt  Der Anteil der grau gefärbten Fläche beträgt damit
Der Anteil der grau gefärbten Fläche beträgt damit 
 des Flächeninhalts des Kreises beträgt
des Flächeninhalts des Kreises beträgt  Da die beiden Flächeninhalte übereinstimmen, muss der Kreis einen Flächeninhalt von
Da die beiden Flächeninhalte übereinstimmen, muss der Kreis einen Flächeninhalt von  haben.
haben.
b)
Die Länge der Schenkel des Dreiecks entspricht dem Raduis des Kreises. Dieser lässt sich mit der Formel für den Flächeninhalt berechnen:
![\(\begin{array}[t]{rll}
A&=& \pi \cdot r^2 \quad \scriptsize \mid\;:\pi \\[5pt]
\dfrac{A}{\pi}&=& r^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
\sqrt{\dfrac{A}{\pi}}&=& r \\[5pt]
\sqrt{\dfrac{75,45\,\text{cm}^2}{\pi}}&=& r\\[5pt]
4,9\,\text{cm}&\approx& r
\end{array}\)](https://mathjax.schullv.de/1f57f47f9f481fd25589c7ded7dcec3d048e387a49d5cb2f1fe008d304f2ef4b?color=5a5a5a) Damit lässt sich der Flächeninhalt des Dreiecks berechnen:
Damit lässt sich der Flächeninhalt des Dreiecks berechnen:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2} \cdot \overline{AM} \cdot \overline{BM} \cdot \sin(120°) \\[5pt]
&\approx& \dfrac{1}{2} \cdot 4,9\,\text{cm} \cdot 4,9\,\text{cm} \cdot \sin(120^{\circ}) \\[5pt]
&\approx& 10,4\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/e83a7dffa7e67d9b584f046e218351e305ed64028de74f328ca78db759dd345c?color=5a5a5a) Der Flächeninhalt des Dreiecks beträgt etwa
Der Flächeninhalt des Dreiecks beträgt etwa 
c)
Bei einem gleichseitigen Dreieck ist jeder Innenwinkel  groß. Da
groß. Da  gilt, ist dies bereits durch
gilt, ist dies bereits durch  erfüllt.
Bedingung:
erfüllt.
Bedingung: 
Lösung 3
a)
Gesamtmasse des Goldes:
 Anzahl der Goldbarren berechnen:
Anzahl der Goldbarren berechnen:
 Es werden
Es werden  Goldbarren hergestellt.
Goldbarren hergestellt.
b)
Gold aus 117 Handys:
 Anteil an Gold am
Anteil an Gold am  schweren Ring:
schweren Ring:
 Aus der Tabelle lässt sich ablesen, dass auf dem Ring der Feingehalt 585 eingraviert werden muss.
Aus der Tabelle lässt sich ablesen, dass auf dem Ring der Feingehalt 585 eingraviert werden muss.
c)
Der Anteil der Masse des Goldes im Werkstück I beträgt  Das entspricht einer Masse von
Das entspricht einer Masse von  Der Anteil an Eisen hat also eine Masse von
Der Anteil an Eisen hat also eine Masse von  Mit den Dichten der jeweiligen Bestandteile folgt:
Mit den Dichten der jeweiligen Bestandteile folgt:
![\(\begin{array}[t]{rll}
V&=& \dfrac{60\,\text{g}}{19,3\frac{\,\text{g}}{\,\text{cm}^3}}+\dfrac{20\,\text{g}}{7,68\frac{\,\text{g}}{\,\text{cm}^3}} \\[5pt]
&\approx& 5,71\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/416c3f38409aea8b2eb763a43fc6b809d39559165410a47a3e3cfcc4b6f1b0a7?color=5a5a5a) Das Volumen des Werkstücks l beträgt
Das Volumen des Werkstücks l beträgt 
d)
Die Formel gibt das Volumen des Werkstücks II an.
![\(\begin{array}[t]{rll}
V&=& V_{\,\text{Gold}}+ V_{\,\text{Silber}} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3d643d7c9217da0d92d02069f585dcea3dcadf0fdeea997ab5703a7f8d962315?color=5a5a5a) Dabei gibt
Dabei gibt  die Masse des Goldes im Werkstück II an.
die Masse des Goldes im Werkstück II an.