Pflichtteil 2
Pflichtaufgabe 1
a)
Bei einem Geldinstitut werden  Euro für zwei Jahre zu folgenden Zinssätzen angelegt.
1. Jahr Zinssatz:
Euro für zwei Jahre zu folgenden Zinssätzen angelegt.
1. Jahr Zinssatz:  2. Jahr Zinssatz:
2. Jahr Zinssatz:  Berechne das Guthaben nach dem 1. Jahr und das Guthaben nach dem 2. Jahr, wenn die Zinsen gutgeschrieben und mit verzinst werden.
Berechne das Guthaben nach dem 1. Jahr und das Guthaben nach dem 2. Jahr, wenn die Zinsen gutgeschrieben und mit verzinst werden.
b)
In der Abbildung ist ein Kreiszylinder dargestellt.
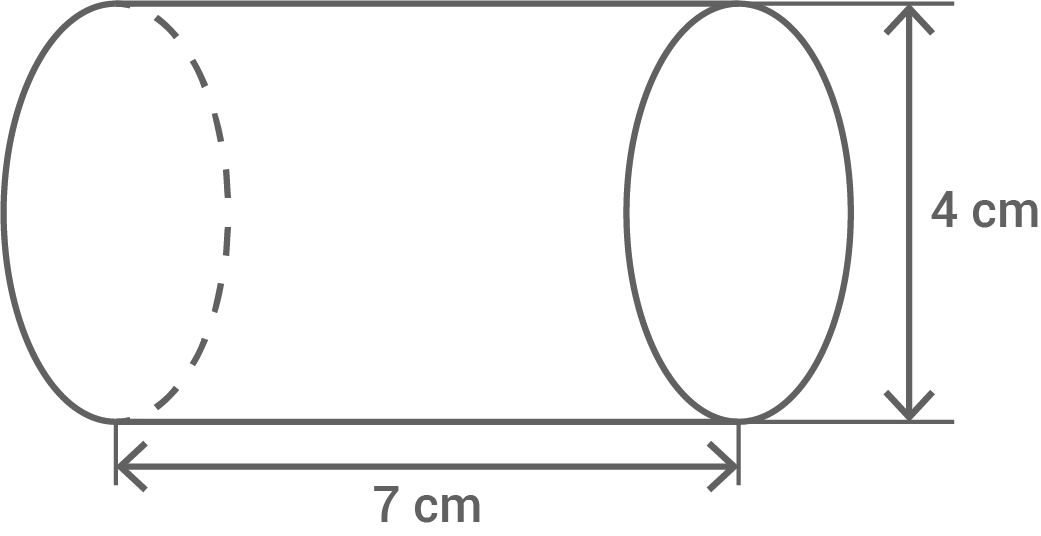 Zeichne ein Netz dieses Kreiszylinders.
Zeichne ein Netz dieses Kreiszylinders.

Abbildung nicht maßstäblich
c)
Bei einer Ziehung der Lottozahlen  aus
aus  wurden bereits die Zahlen
wurden bereits die Zahlen 



 gezogen.
gezogen.
Ermittle die Wahrscheinlichkeit, dass als sechste Zahl die gezogen wird.
gezogen wird.
Ermittle die Wahrscheinlichkeit, dass als sechste Zahl die
d)
Ein Chip für eine Digitalkamera hat eine Speicherkapazität von  Gigabyte (GB).
Gigabyte (GB).
Gib diese Speicherkapazität in Megabyte (MB) an.
Gib diese Speicherkapazität in Megabyte (MB) an.
e)
Das soziale Netzwerk „Facebook“ verkündete im Januar  die Absicht, an die Börse gehen
die Absicht, an die Börse gehen zu wollen. Unmittelbar danach protestierten
zu wollen. Unmittelbar danach protestierten  Millionen der
Millionen der  Millionen Mitglieder gegen diese Absicht. Dennoch ist „Facebook“ an die Börse gegangen.
Millionen Mitglieder gegen diese Absicht. Dennoch ist „Facebook“ an die Börse gegangen.
Eine Zeitung stellt fest: „Es haben nicht genug Mitglieder protestiert, um den Gang an die Börse aufzuhalten.“
Beurteile diese Feststellung mithilfe einer mathematischen Betrachtung.
Eine Zeitung stellt fest: „Es haben nicht genug Mitglieder protestiert, um den Gang an die Börse aufzuhalten.“
Beurteile diese Feststellung mithilfe einer mathematischen Betrachtung.
9 BE erreichbar
1 „An die Börse gehen“ heißt, ein Unternehmen verkauft erstmalig Aktien.
Pflichtaufgabe 2
Gegeben sind die linearen FunktionenVon der Funktion
a)
Zeichne die Graphen der beiden Funktionen  und
und  in ein und dasselbe Koordinatensystem mindestens im Intervall
in ein und dasselbe Koordinatensystem mindestens im Intervall 
b)
Begründe, dass  eine Gleichung der Funktion
eine Gleichung der Funktion  ist.
ist.
c)
Die Graphen der Funktionen  und
und  schneiden einander im Punkt
schneiden einander im Punkt  Berechne die Koordinaten des Punktes
Berechne die Koordinaten des Punktes  mithilfe eines linearen Gleichungssystems.
mithilfe eines linearen Gleichungssystems.
d)
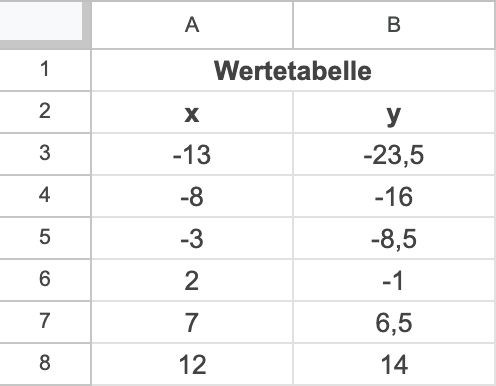
In einem Tabellenkalkulationsprogramm werden Funktionswerte in der folgenden Wertetabelle mit der Formel  aus Zelle B3 durch Kopieren erzeugt.
aus Zelle B3 durch Kopieren erzeugt.
Begründe, dass beim Prüfen der Formel in Zelle B7 nicht mehr die Formel aus Zelle B3 steht.
Begründe, dass beim Prüfen der Formel in Zelle B7 nicht mehr die Formel aus Zelle B3 steht.

8 BE erreichbar
Pflichtaufgabe 3
Im Vermessungswesen werden Streckenlängen und Winkelgrößen im Gelände ermittelt. Durch trigonometrische Berechnungen können daraus weitere interessierende Größen bestimmt werden.
a)
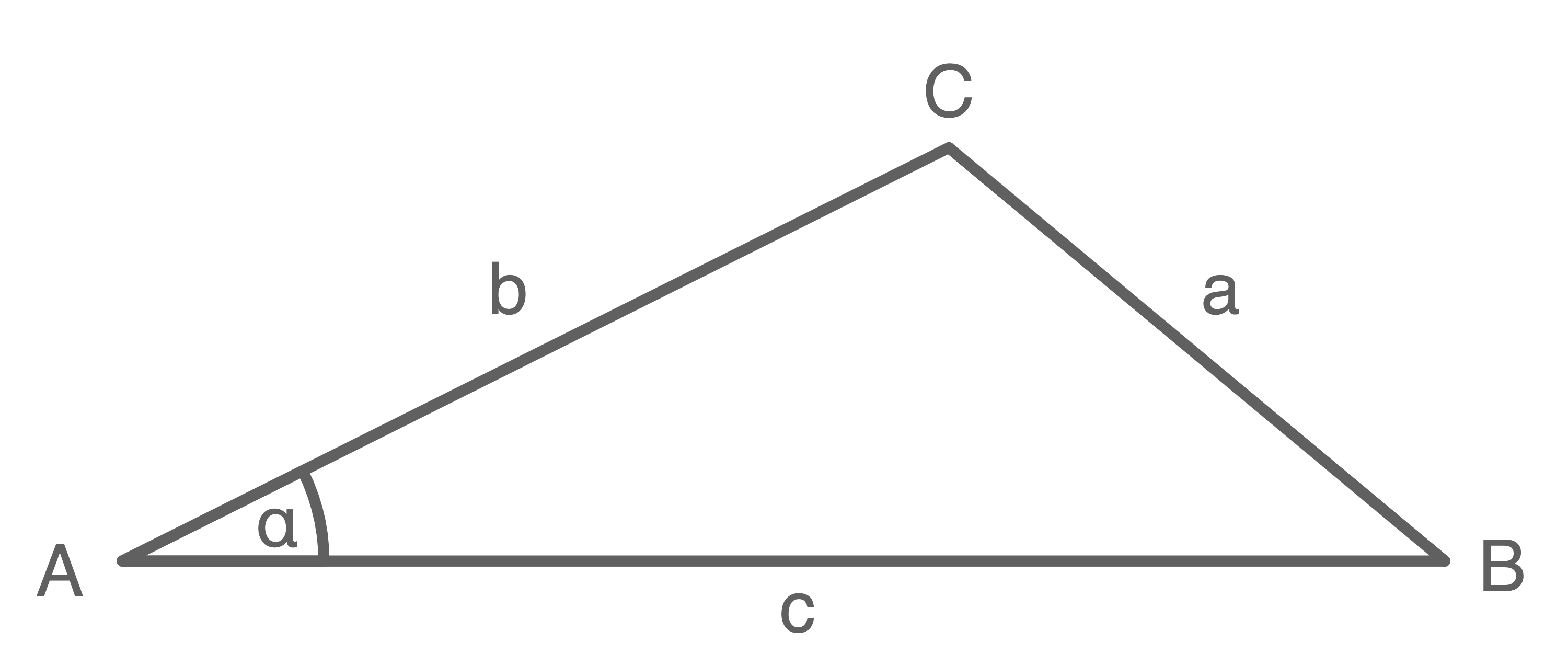
Es wurde ein Gelände in Form eines Dreiecks mit den Eckpunkten 
 und
und  vermessen, wobei sich folgende Messwerte ergaben.
vermessen, wobei sich folgende Messwerte ergaben.


 Ermittle von diesem Gelände die Länge der Strecke
Ermittle von diesem Gelände die Länge der Strecke  sowohl rechnerisch als auch konstruktiv.
sowohl rechnerisch als auch konstruktiv.
b)
In der folgenden Abbildung ist ein Prinzip der Bestimmung von Entfernungen dargestellt.
Es wird der Winkel für einen Abschnitt auf der Messlatte gemessen.
für einen Abschnitt auf der Messlatte gemessen.
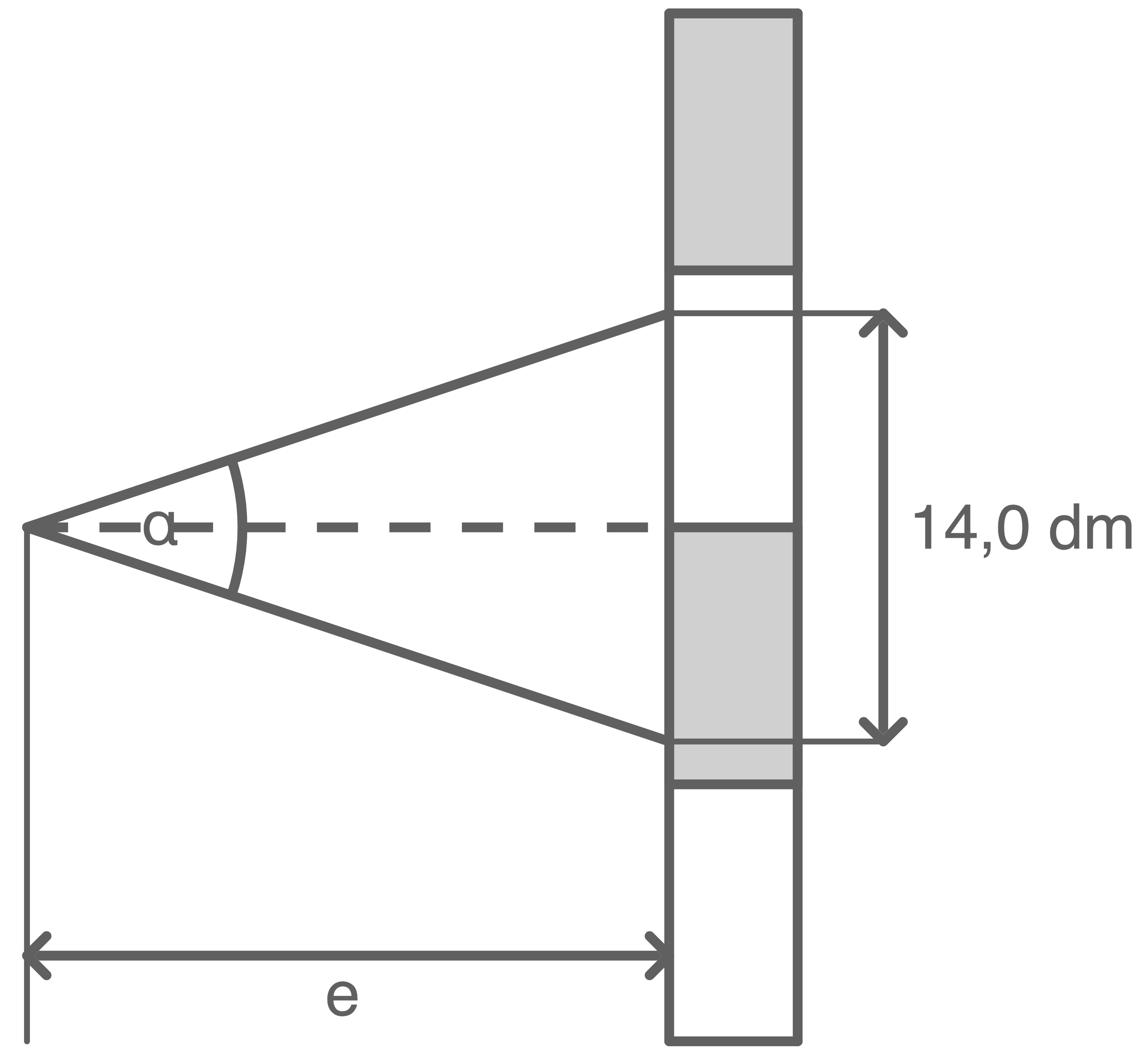 Berechne die Entfernung
Berechne die Entfernung  für den Fall, dass zu einem Abschnitt von
für den Fall, dass zu einem Abschnitt von  auf der Messlatte der Winkel
auf der Messlatte der Winkel  von
von  gemessen wird.
gemessen wird.
Es wird der Winkel

Abbildung nicht maßstäblich
7 BE erreichbar
Lösung 1
a)
Guthaben nach dem 1. Jahr


 Mit der Zinseszinsformel
Mit der Zinseszinsformel  folgt:
folgt:
![\(\begin{array}[t]{rll}
K_1 &=& 1\,800\,€ \cdot \left(1+\dfrac{1,3\,\%}{100\,\%}\right)^1 \\[5pt]
&=& 1\,800\,€ \cdot 1,013\\[5pt]
&=& 1823,40\,€
\end{array}\)](https://mathjax.schullv.de/8fddb96468dd2a63ee1dfdd95e6e2c775fc98a318ace147458969dbceef240a0?color=5a5a5a) Das Guthaben nach dem ersten Jahr beträgt
Das Guthaben nach dem ersten Jahr beträgt  Guthaben nach dem 2. Jahr berechnen
Guthaben nach dem 2. Jahr berechnen


 Mit der Zinseszinsformel
Mit der Zinseszinsformel  folgt:
folgt:
![\(\begin{array}[t]{rll}
K_1 &=& 1\,823,40\,€ \cdot \left(1+\dfrac{1,6\,\%}{100\,\%}\right)^1 \\[5pt]
&=& 1\,823,40\,€ \cdot 1,016\\[5pt]
&\approx& 1\,852,57\,€
\end{array}\)](https://mathjax.schullv.de/1dcaf247ebb783df30fae999f122d161dd8b16e9c419df90ae807ba984bbbe4f?color=5a5a5a) Das Guthaben nach dem zweiten Jahr beträgt
Das Guthaben nach dem zweiten Jahr beträgt 
b)
Die Länge der Rechteckseiten, die an die Kreise angrenzen, entsprechen dem Umfang der Kreise.

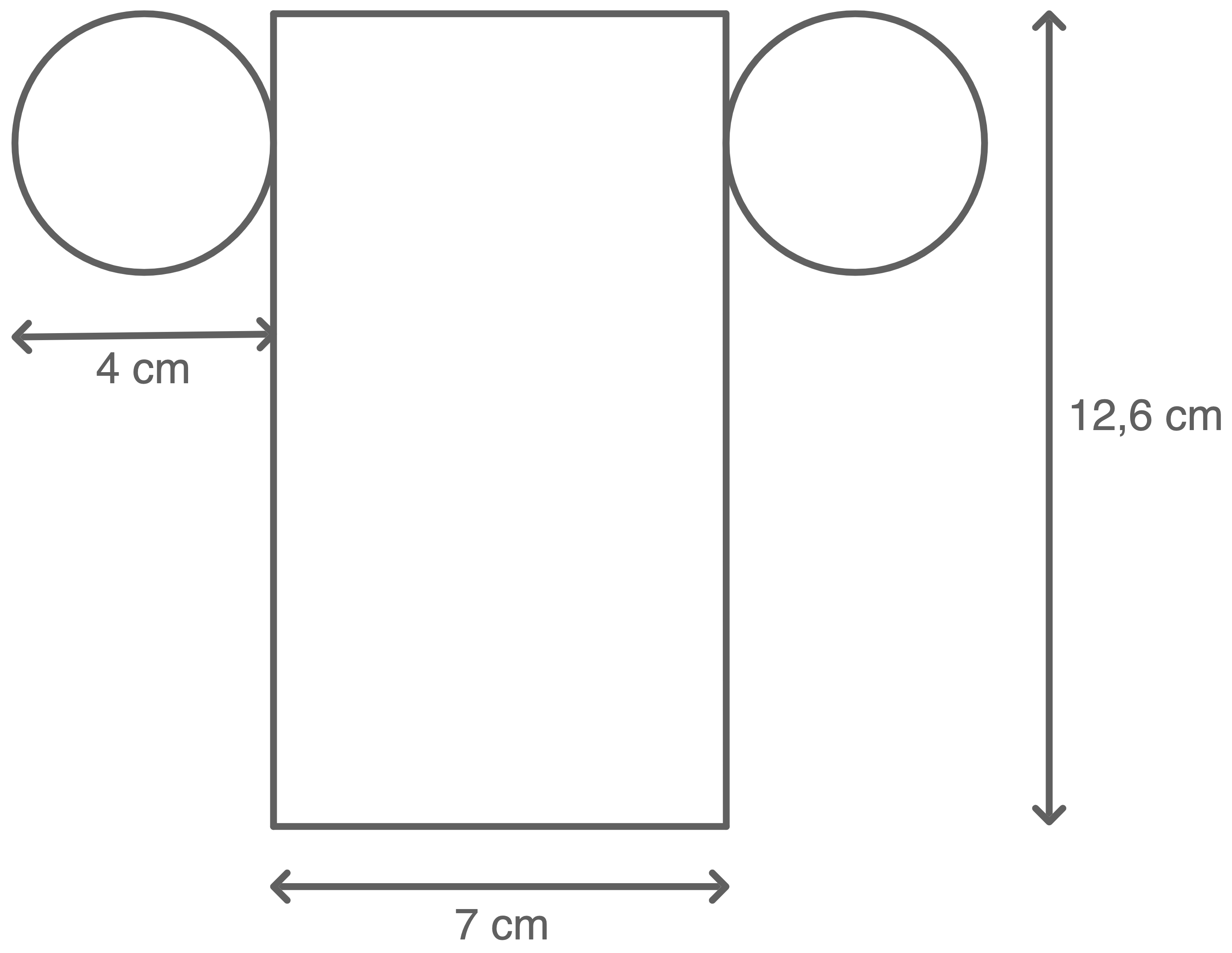 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

c)
Noch verfügbare Kugeln:  Damit folgt für die Wahrscheinlichkeit, die Kugel mit der 20 zu ziehen:
Damit folgt für die Wahrscheinlichkeit, die Kugel mit der 20 zu ziehen:

d)
e)
Lösung 2
a)
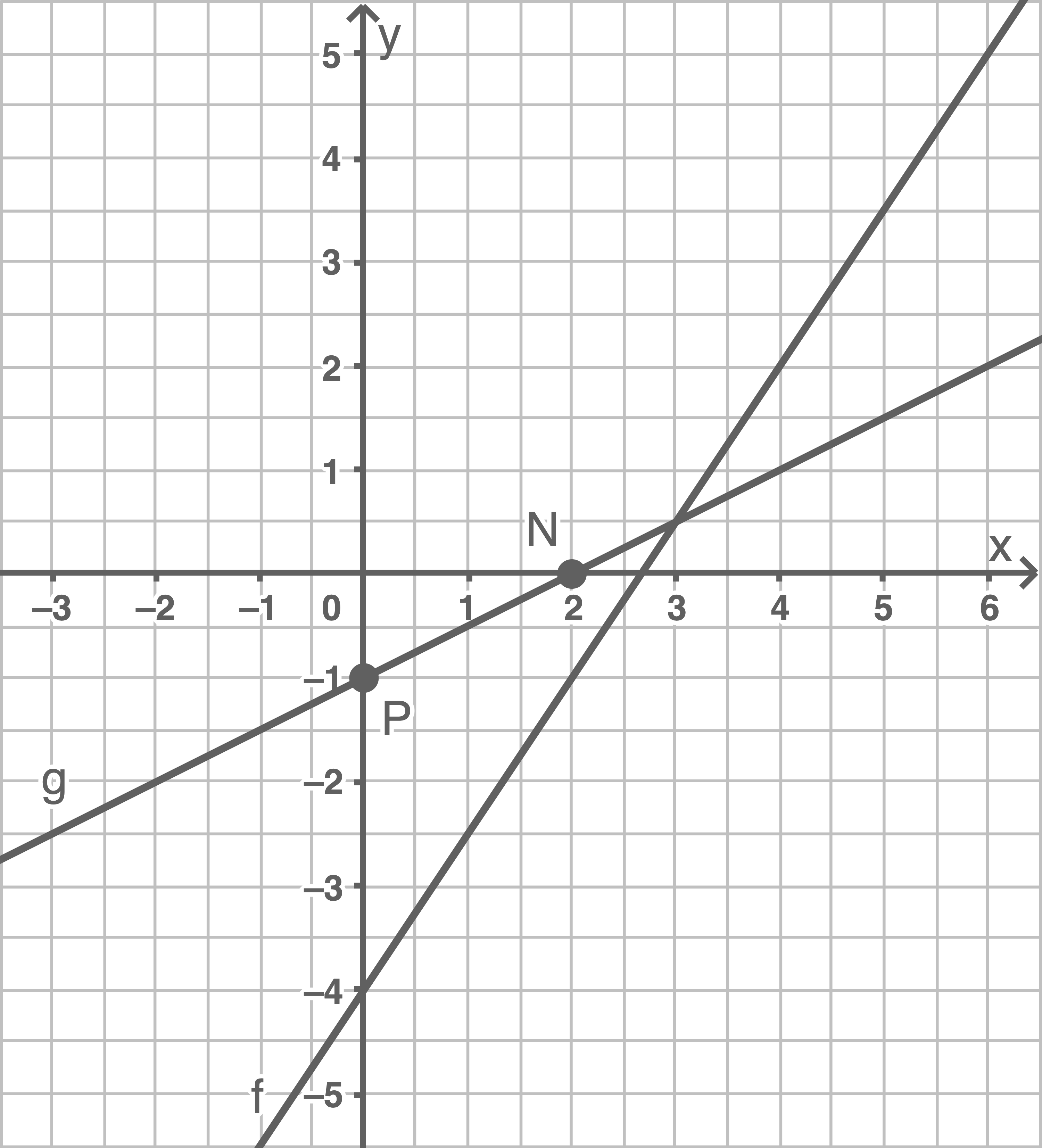
b)
Falls die Gleichung zu der Geraden gehört, müssen beide bekannten Punkte auf der Geraden zu der Gleichung liegen.
Punktprobe mit  und der Nullstelle
und der Nullstelle 

 Beide Punkte des Graphen von
Beide Punkte des Graphen von  liegen auf dem Graphen der Funktion der Gleichung
liegen auf dem Graphen der Funktion der Gleichung  Damit ist
Damit ist  eine Gleichung der Funktion
eine Gleichung der Funktion 
c)
Gleichsetzen der Funktionsterme und auflösen nach  liefert:
liefert:
![\(\begin{array}[t]{rll}
f(x)&=& g(x) \\[2pt]
1,5x-4&=&\dfrac{1}{2}x-1 \quad \scriptsize \mid\; +4 \\[2pt]
1,5x&=&\dfrac{1}{2}x+3 \quad \scriptsize \mid\; -\dfrac{1}{2}x \\[2pt]
x&=& 3
\end{array}\)](https://mathjax.schullv.de/d74db6db0f10d217d44a4161f0c743a4cca5c68c944c0b778b95df266f45ccbd?color=5a5a5a) Einsetzen von
Einsetzen von  in
in  oder in
oder in 
![\(\begin{array}[t]{rll}
y=f(3)&=& 1,5 \cdot 3 -4 \\[2pt]
&=& 4,5-4\\[2pt]
&=& 0,5
\end{array}\)](https://mathjax.schullv.de/40ba3794b6893acda5ffddaccab42b53046d2913a7b2ac05ba53209f10f128a6?color=5a5a5a) Der Schnittpunkt beider Graphen ist
Der Schnittpunkt beider Graphen ist 
d)
Würde in Zelle  die gleiche Formel wie in
die gleiche Formel wie in  stehen, so wäre auch der Wert in Zelle
stehen, so wäre auch der Wert in Zelle  der gleiche wie in Zelle
der gleiche wie in Zelle  Es gilt jedoch
Es gilt jedoch  Beim Kopieren einer Formel in einem Tabellenkalkulations-Programm wird automatisch der Bezug hergestellt: Bezieht sich
Beim Kopieren einer Formel in einem Tabellenkalkulations-Programm wird automatisch der Bezug hergestellt: Bezieht sich  auf
auf  , muss sich
, muss sich  auf
auf  beziehen.
Die Formel in Zelle
beziehen.
Die Formel in Zelle  lautet daher:
lautet daher: 
Lösung 3
a)
Länge der Strecke  rechnerisch ermitteln
rechnerisch ermitteln
 Die fehlende Seite kann über den Kosinussatz berechnet werden:
Die Länge der Strecke
Die fehlende Seite kann über den Kosinussatz berechnet werden:
Die Länge der Strecke  beträgt
beträgt  Länge der Strecke
Länge der Strecke  konstruktiv ermitteln
Es bietet sich an, das Dreieck im Maßstab
konstruktiv ermitteln
Es bietet sich an, das Dreieck im Maßstab  zu zeichnen. Dann gilt für die Seitenlängen:
zu zeichnen. Dann gilt für die Seitenlängen:


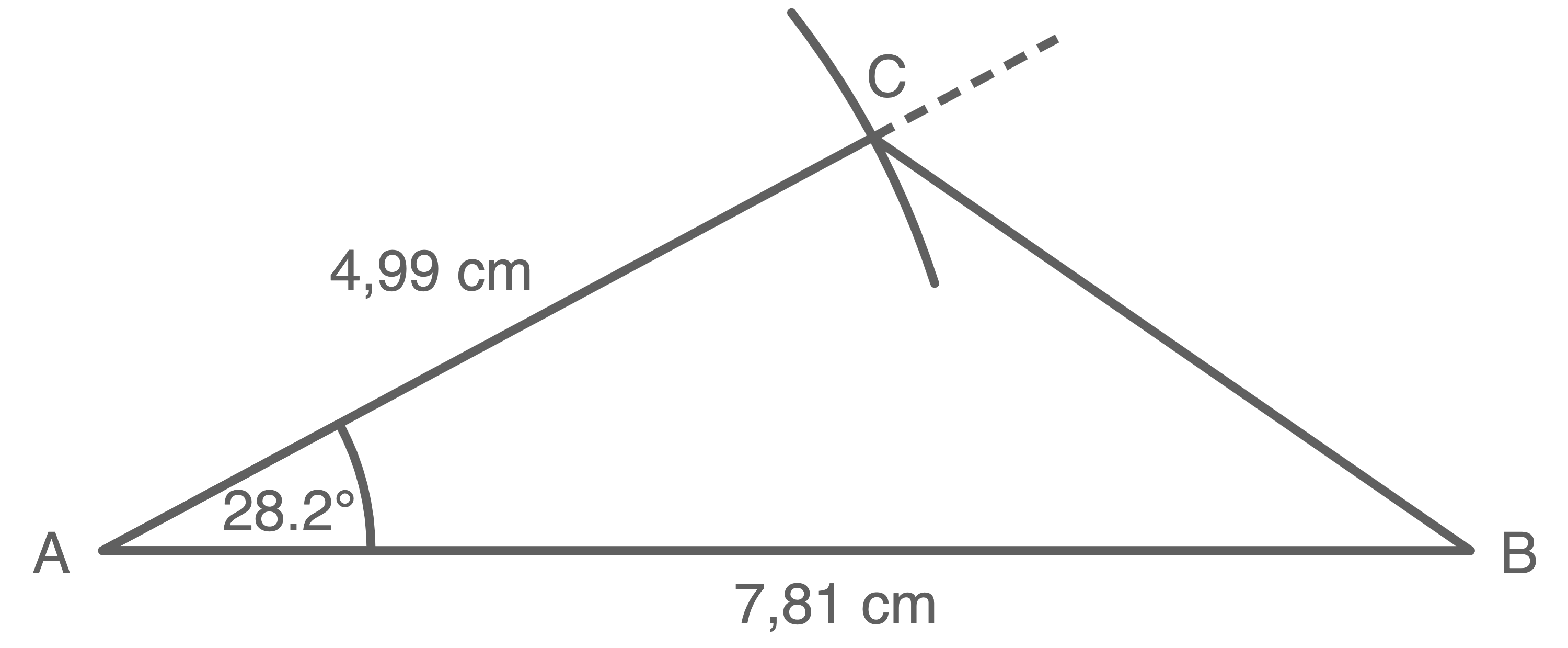 Die Strecke
Die Strecke  ist ungefähr
ist ungefähr  lang. Beim Maßstab
lang. Beim Maßstab  entspricht dies
entspricht dies  .
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Skizze

b)
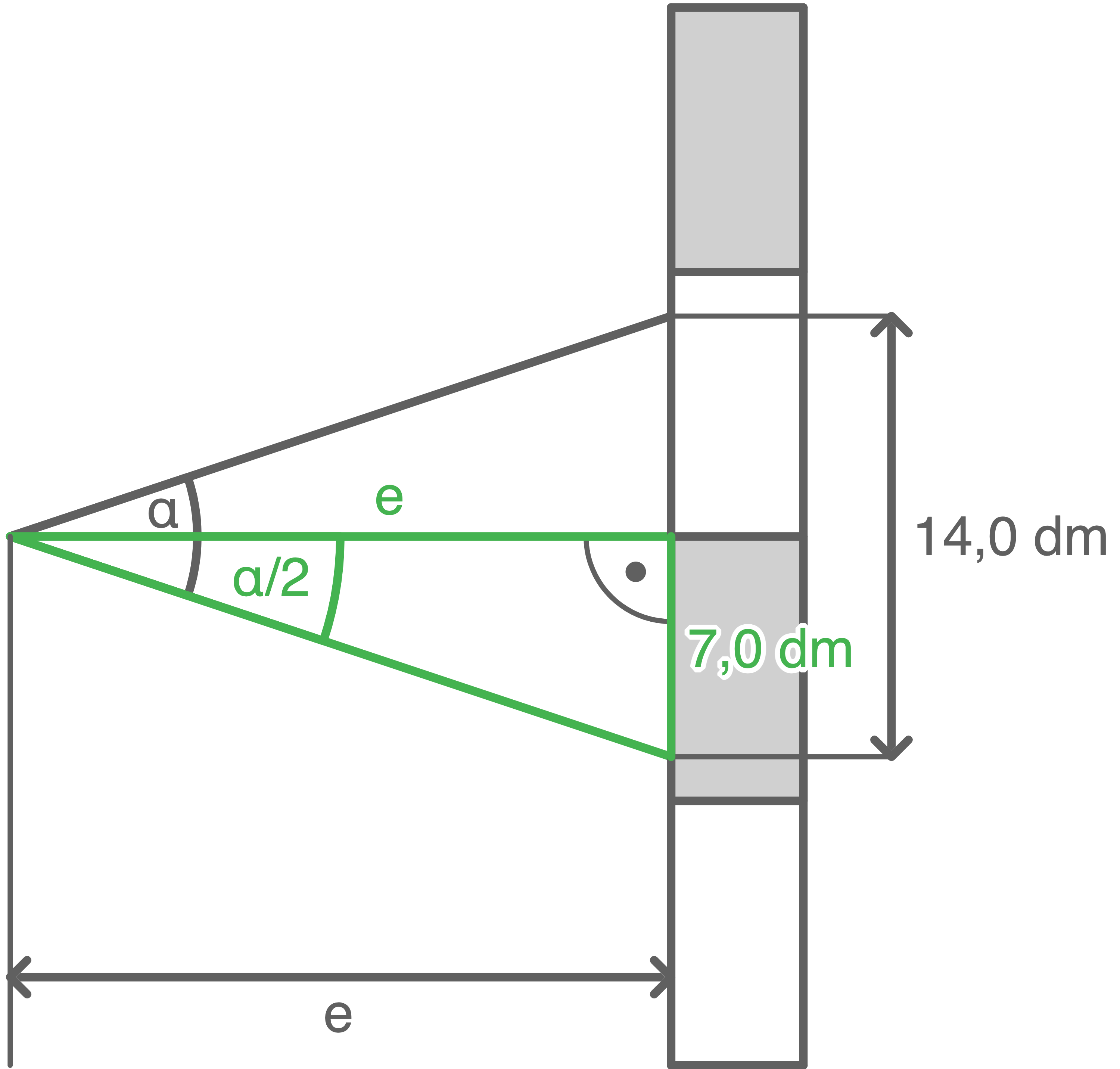
Skizze