Wahlpflichtteil
Wahlpflichtaufgabe 1
Messing ist eine Legierung, die aus Kupfer und Zink besteht.Für eine Messingschmelze werden zunächst
a)
Berechne den prozentualen Anteil von Kupfer in dieser Messingschmelze.
b)
Der Kupferanteil dieser Messingschmelze soll auf  erhöht werden.
erhöht werden.
Ermittle, wie viel Kilogramm Kupfer hinzugefügt werden müssen.
Ermittle, wie viel Kilogramm Kupfer hinzugefügt werden müssen.
c)
Die Dichte von Zink beträgt  und die Dichte von Kupfer
und die Dichte von Kupfer  Tom berechnet die Dichte der ursprünglichen Messingschmelze bestehend aus
Tom berechnet die Dichte der ursprünglichen Messingschmelze bestehend aus  Zink und
Zink und  Kupfer, indem er wie folgt einen Mittelwert bildet.
Kupfer, indem er wie folgt einen Mittelwert bildet.
![\(\begin{array}[t]{rll}
P_{\text{Messing}}&=& 7,13\frac{\text{kg}}{\text{dm}^3}\cdot\dfrac{15}{50}+8,96\frac{\text{kg}}{\text{dm}^3}\cdot\dfrac{35}{50} \\[5pt]
&\approx& 8,41\frac{\text{kg}}{\text{dm}^3}
\end{array}\)](https://mathjax.schullv.de/bc89b794feef4e9fd65afa51ba02cf3f6ff66854c498589030727909dc369afa?color=5a5a5a) Weise rechnerisch unter Verwendung der Volumina nach, dass dieser Ansatz zur Berechnung der Dichte ein falsches Ergebnis liefert.
Weise rechnerisch unter Verwendung der Volumina nach, dass dieser Ansatz zur Berechnung der Dichte ein falsches Ergebnis liefert.
8 BE erreichbar
Wahlpflichtaufgabe 2
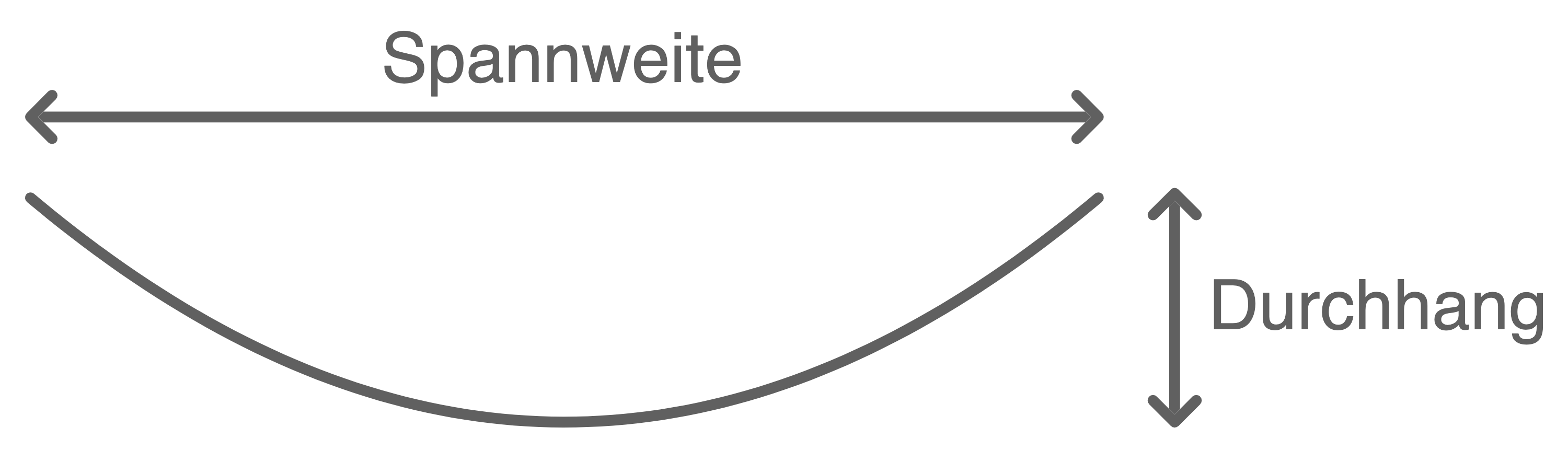
Der Querschnitt einer Hängebrücke auf einem Spielplatz kann annähernd als Parabel betrachtet werden. Diese Parabel wird durch die Funktion
a)
Zeichne den Graphen der Funktion  in ein Koordinatensystem mindestens im Intervall
in ein Koordinatensystem mindestens im Intervall  .
.
Berechne den Funktionswert .
.
Berechne den Funktionswert
b)
Die Spannweite der dargestellten Hängebrücke beträgt  .
Gib die Koordinaten zweier Punkte des Graphen der Funktion
.
Gib die Koordinaten zweier Punkte des Graphen der Funktion  an, die für die Ermittlung des Durchhangs der Hängebrücke geeignet sind.
Ermittle den Durchhang der Hängebrücke.
an, die für die Ermittlung des Durchhangs der Hängebrücke geeignet sind.
Ermittle den Durchhang der Hängebrücke.
c)
Ein Konstrukteur plant für einen anderen Spielplatz eine Hängebrücke mit einer Spannweite von  und einem Durchhang von
und einem Durchhang von  Der parabelförmige Querschnitt soll durch eine Funktion mit der Gleichung
Der parabelförmige Querschnitt soll durch eine Funktion mit der Gleichung  beschrieben werden.
beschrieben werden.
Ermittle
Ermittle
8 BE erreichbar
Wahlpflichtaufgabe 3
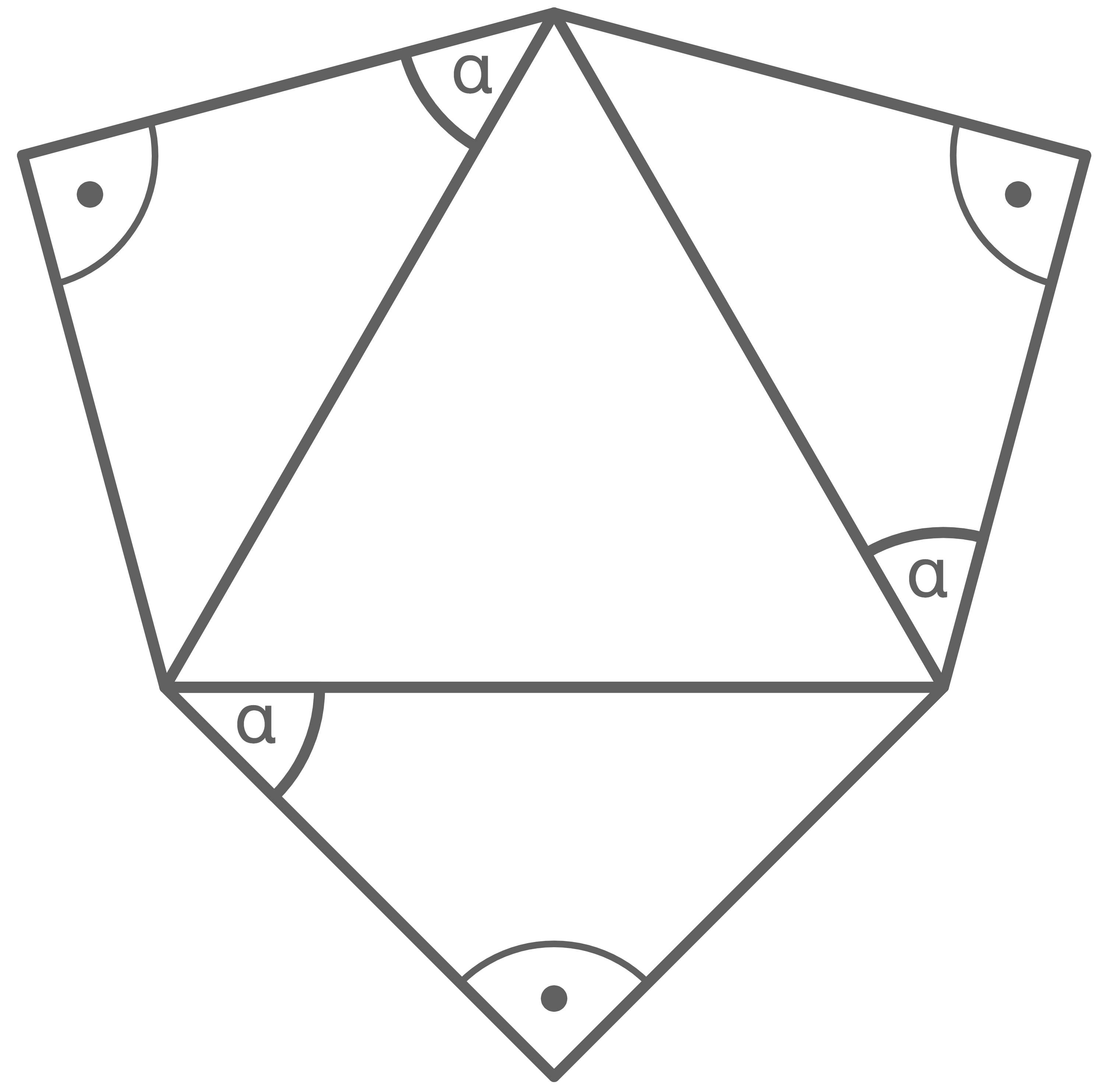
Eine dreiseitige Pyramide werde von einem gleichseitigem Dreieck und drei zueinander kongruenten rechtwinklig-gleichschenkligen Dreiecken begrenzt.Die folgende Abbildung zeigt ein Netz einer solchen Pyramide.
a)
Begründe, dass der Winkel  stets eine Größe von
stets eine Größe von  hat.
hat.
b)
Die Seitenlänge des gleichseitigen Dreiecks sei 
Berechne den Flächeninhalt eines der rechtwinkligen Dreiecke.
Berechne den Flächeninhalt eines der rechtwinkligen Dreiecke.
c)
Stellt man eine solche Pyramide auf eine der rechtwinklig-gleichschenkligen Dreiecksflächen, so erkennt man, dass das Volumen der Pyramide mit dem folgenden Ansatz berechnet werden kann:
 , wobei
, wobei  die Länge einer Kathete im rechtwinklig-gleichschenkligen Dreieck ist.
Erkläre, wie man auf diesen Ansatz kommt.
die Länge einer Kathete im rechtwinklig-gleichschenkligen Dreieck ist.
Erkläre, wie man auf diesen Ansatz kommt.
8 BE erreichbar
Lösung 1
a)
Gesamtgewicht:  Gewicht an Kupfer:
Gewicht an Kupfer:  Prozentualen Anteil berechnen:
Prozentualen Anteil berechnen:
 Der prozentuale Anteil an Kupfer in der Messingschmelze beträgt
Der prozentuale Anteil an Kupfer in der Messingschmelze beträgt 
b)
c)
Berechne das Volumen von  Zink mit der Formel
Zink mit der Formel 
 Volumen von
Volumen von  Kupfer berechnen:
Kupfer berechnen:
 Dichte der Messingschmelze berechnen:
Dichte der Messingschmelze berechnen:



 Die Dichte der ursprünglichen Messingschmelze beträgt
Die Dichte der ursprünglichen Messingschmelze beträgt  . Damit liefert Toms Ansatz zur Berechnung der Dichte mit
. Damit liefert Toms Ansatz zur Berechnung der Dichte mit  ein falsches Ergebnis.
ein falsches Ergebnis.
Lösung 2
a)
Graphen der Funktion  zeichnen
zeichnen
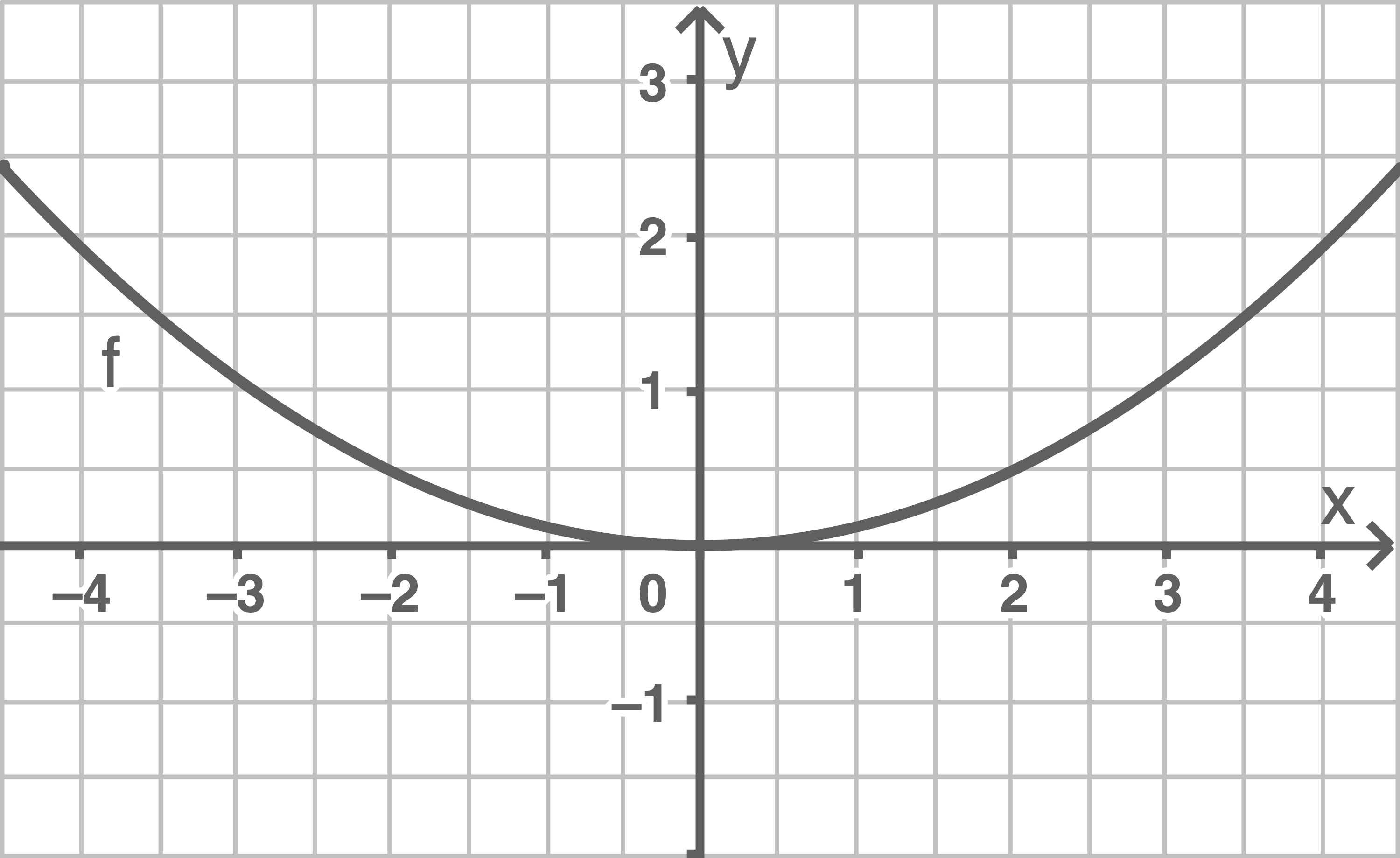 Funktionswert berechnen
Funktionswert berechnen

| -3 | 1,08 |
| -2 | 0,48 |
| -1 | 0,12 |
| 0 | 0 |
| 1 | 0,12 |
| 2 | 0,48 |
| 3 | 1,08 |

b)
Geeignete Koordinaten angeben
Um den Durchhang der Hängebrücke zu ermitteln, wird die Differenz zwischen dem höchsten und dem niedrigsten Punkt benötigt.
Tiefster Punkt: Scheitelpunkt  Die Spannweite beträgt
Die Spannweite beträgt  . Also liegt der höchste Punkt bei
. Also liegt der höchste Punkt bei  und bei
und bei  Aus a) ist
Aus a) ist  bekannt.
Folglich lauten die Koordinaten des höchsten Punktes
bekannt.
Folglich lauten die Koordinaten des höchsten Punktes  Durchhang ermitteln
Die
Durchhang ermitteln
Die  -Achse steht für die Höhe des Durchhangs. Der
-Achse steht für die Höhe des Durchhangs. Der  -Wert beträgt beim höchsten Punkt
-Wert beträgt beim höchsten Punkt  und beim tiefsten Punkt
und beim tiefsten Punkt  . Also beträgt der Durchhang
. Also beträgt der Durchhang 
c)
In ein Koordinatensystem übertragen, erstreckt sich die Parabel bei einer Spannweite von  von
von  bis
bis  .
.
Die Gleichung der Funktion hat die Form , also liegt der Scheitelpunkt ihres Graphen bei
, also liegt der Scheitelpunkt ihres Graphen bei 
Der Durchhang soll betragen, also gibt es den Punkt
betragen, also gibt es den Punkt  .
Einsetzen der Koordinaten von
.
Einsetzen der Koordinaten von  in
in  und umstellen nach
und umstellen nach  liefert:
liefert:
![\(\begin{array}[t]{rll}
y&=& a \cdot x^2 \quad \scriptsize \mid\; : x^2\\[5pt]
\dfrac{y}{x^2}&=& a\\[5pt]
\dfrac{0,5}{2,5^2}&=& a \\[5pt]
0,08&=& a
\end{array}\)](https://mathjax.schullv.de/62dc26b5dfd395ddb20d95ca8a563e2cd11ca4f37043436d898f623046973e55?color=5a5a5a) Die Funktion lautet
Die Funktion lautet  .
.
Die Gleichung der Funktion hat die Form
Der Durchhang soll
Lösung 3
a)
Die Winkelsumme in einem Dreieck beträgt  Da das Dreieck rechtwinklig ist, gilt
Da das Dreieck rechtwinklig ist, gilt 
Die verbleibenden verteilen sich auf zwei Winkel. Diese sind bei einem gleichschenkligen Dreieck immer gleich groß:
verteilen sich auf zwei Winkel. Diese sind bei einem gleichschenkligen Dreieck immer gleich groß:  .
.
Die verbleibenden
b)
Gegeben ist ein rechtwinklig-gleichschenkliges Dreieck mit:
 berechnet werden:
Damit folgt:
berechnet werden:
Damit folgt:


- Seitenlänge Hypotenuse
- Winkel
- Kathete
Kathete
c)
Die Formel zur Berechnung des Volumens einer Pyramide lautet  Die Grundfläche eines der rechtwinklig-gleichschenkligen Dreiecke kann über
Die Grundfläche eines der rechtwinklig-gleichschenkligen Dreiecke kann über  berechnet werden.
Für die Basis
berechnet werden.
Für die Basis  gilt im rechtwinklig-gleichschenkligen Dreieck mit dem Satz des Pythagoras:
gilt im rechtwinklig-gleichschenkligen Dreieck mit dem Satz des Pythagoras:
![\(\begin{array}[t]{rll}
c^2&=& a^2+a^2\\[2pt]
c^2&=& 2a^2
\end{array}\)](https://mathjax.schullv.de/c18b39fe7d99db86c1ac7cd3596f292870cf809a3ec4608bf7763a9fe1555989?color=5a5a5a) Einsetzen in die Formel für die Grundfläche:
Einsetzen in die Formel für die Grundfläche:
 .
Es gilt also:
.
Es gilt also:
![\(\begin{array}[t]{rll}
V&=&\dfrac{1}{3} \cdot A \cdot h \\[4pt]
&=&\dfrac{1}{3} \cdot \dfrac{a^2}{2} \cdot h\\[4pt]
&=& \dfrac{a^2}{6} \cdot h
\end{array}\)](https://mathjax.schullv.de/a29dc2f4dfd4517c7d2e85cc21e41a95863c63014a0379c1ad7835e59b56e226?color=5a5a5a) Die Pyramide wird so zusammengeklappt, dass die Seiten mit rechtem Winkel aneinander liegen. Die Seite
Die Pyramide wird so zusammengeklappt, dass die Seiten mit rechtem Winkel aneinander liegen. Die Seite  steht somit senkrecht auf der Grundfläche
steht somit senkrecht auf der Grundfläche  .
.
Also ist die Höhe und es gilt:
die Höhe und es gilt:  .
.
![\(\begin{array}[t]{rll}
V&=& \dfrac{a^2}{6} \cdot h &\quad \scriptsize \mid\; h=a \\[2pt]
&=& \dfrac{a^2}{6} \cdot a \\[2pt]
&=& \dfrac{a^3}{6}
\end{array}\)](https://mathjax.schullv.de/3da9d6f0419b8a402d90cd52acea8a01c0669af1ead08db3abe5b431fbb62f00?color=5a5a5a)
Also ist