Teil B2
Ein Wohngebäude kann modellhaft durch den Körper  dargestellt werden (vgl. Abbildung). Der untere Teil des Gebäudes entspricht dem Quader
dargestellt werden (vgl. Abbildung). Der untere Teil des Gebäudes entspricht dem Quader  das Dach dem ebenflächig begrenzten Körper
das Dach dem ebenflächig begrenzten Körper  Gegeben sind die Punkte
Gegeben sind die Punkte 




 und
und  Im verwendeten Koordinatensystem stellt die
Im verwendeten Koordinatensystem stellt die  -Ebene den ebenen Untergrund dar.
Die Ebene mit der Gleichung
-Ebene den ebenen Untergrund dar.
Die Ebene mit der Gleichung  stellt im Modell die Symmetrieebene des Gebäudes dar.
Eine Längeneinheit im Koordinatensystem entspricht 1 Meter in der Wirklichkeit.
stellt im Modell die Symmetrieebene des Gebäudes dar.
Eine Längeneinheit im Koordinatensystem entspricht 1 Meter in der Wirklichkeit.
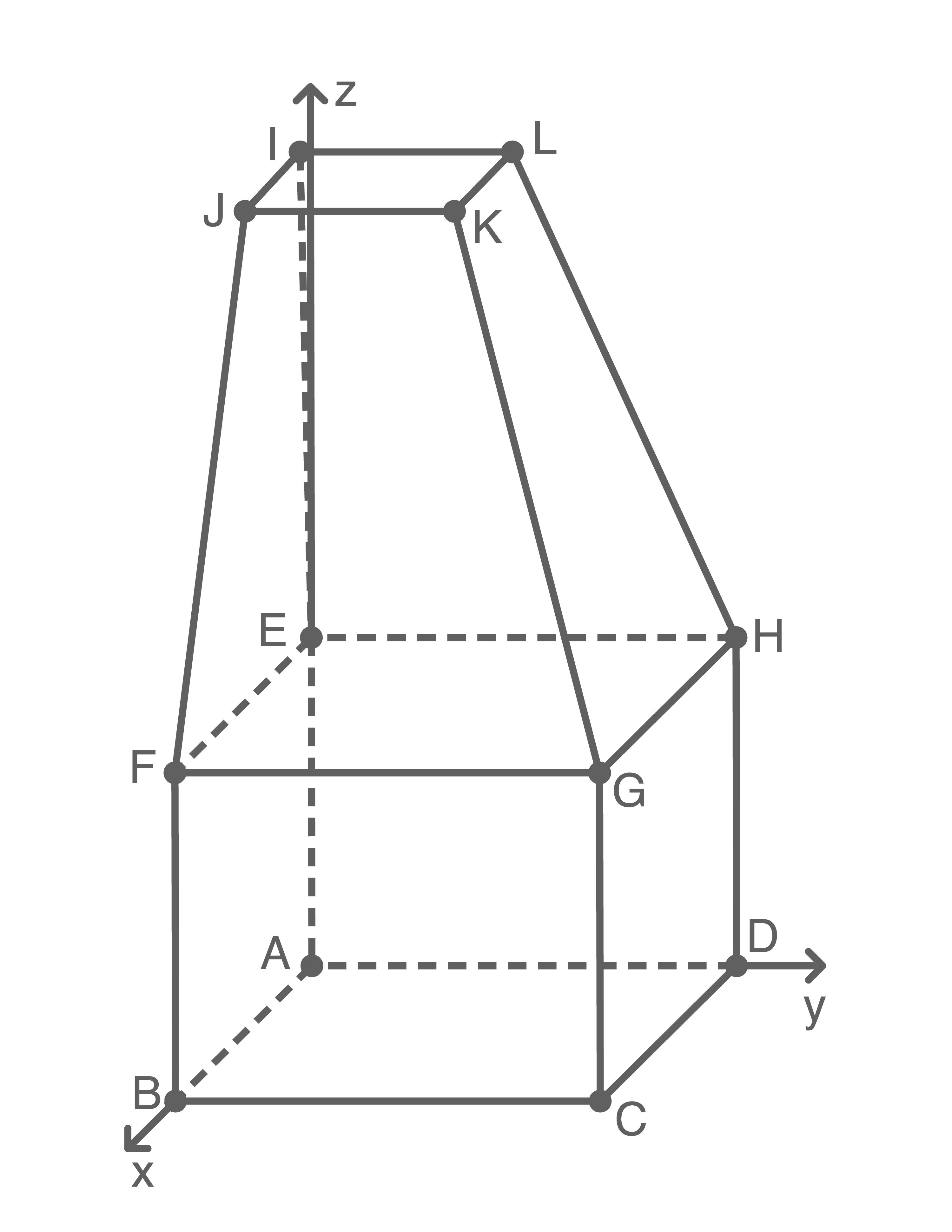
Abbildung (nicht maßstäblich)
2.1
Zeige, dass  die Koordinaten
die Koordinaten  hat.
Gib eine Gleichung an, welche die Strecke
hat.
Gib eine Gleichung an, welche die Strecke  beschreibt.
beschreibt.
(4 BE)
2.2
Berechne den Inhalt der Dachfläche, die im Modell durch das Viereck  beschrieben wird.
beschrieben wird.
(4 BE)
2.3
Die Gleichungen  und
und  liefern gemeinsam den Ansatz zur Lösung einer Aufgabe im Sachzusammenhang.
liefern gemeinsam den Ansatz zur Lösung einer Aufgabe im Sachzusammenhang.

 Formuliere eine passende Aufgabenstellung im Sachzusammenhang.
Beschreibe die Bedeutung der beiden Gleichungen im Zusammenhang mit dieser Aufgabenstellung.
Formuliere eine passende Aufgabenstellung im Sachzusammenhang.
Beschreibe die Bedeutung der beiden Gleichungen im Zusammenhang mit dieser Aufgabenstellung.
(4 BE)
2.4
Jede der vier Seitenkanten des Körpers  liegt jeweils auf einer Geraden.
Begründe, dass folgende Aussage wahr ist:
Für den Nachweis, dass sich diese vier Geraden in einem Punkt schneiden, ist es ausreichend zu zeigen, dass der Schnittpunkt der beiden Geraden durch die Punkte G und
liegt jeweils auf einer Geraden.
Begründe, dass folgende Aussage wahr ist:
Für den Nachweis, dass sich diese vier Geraden in einem Punkt schneiden, ist es ausreichend zu zeigen, dass der Schnittpunkt der beiden Geraden durch die Punkte G und  bzw. durch die Punkte
bzw. durch die Punkte  und
und  die
die  -Koordinate 4 hat.
-Koordinate 4 hat.
(3 BE)
2.5
Berechne den Rauminhalt des Wohngebäudes.
(7 BE)
2.6
Ermittle die Länge der kürzesten Verbindungslinie, die vom Punkt  über einen Punkt der Kante
über einen Punkt der Kante  zum Punkt
zum Punkt  verläuft.
verläuft.
Die Fassade des Gebäudes wird mit Ziegeln in verschiedenen Farben verkleidet.
(5 BE)
2.7
Für eine Reihe aus sechs Ziegeln stehen drei weiße  zwei gelbe
zwei gelbe  und ein brauner
und ein brauner  Ziegel zur Verfügung. Die Ziegel werden nacheinander zufällig ausgewählt und in dieser Reihe von links nach rechts am Gebäude angebracht.
Berechne die Wahrscheinlichkeit
Ziegel zur Verfügung. Die Ziegel werden nacheinander zufällig ausgewählt und in dieser Reihe von links nach rechts am Gebäude angebracht.
Berechne die Wahrscheinlichkeit  mit der dabei die Farbanordnung "wgwbwg" entsteht.
Beurteile folgende Aussage:
Jede Farbanordnung mit diesen sechs Ziegeln, bei denen die zwei gelben Ziegel zuerst ausgewählt werden, entsteht mit der Wahrscheinlichkeit
mit der dabei die Farbanordnung "wgwbwg" entsteht.
Beurteile folgende Aussage:
Jede Farbanordnung mit diesen sechs Ziegeln, bei denen die zwei gelben Ziegel zuerst ausgewählt werden, entsteht mit der Wahrscheinlichkeit 
(6 BE)
2.8
Die verwendeten Ziegel weisen zum Teil Farbfehler oder Maßfehler auf.
Für einen zufällig ausgewählten Ziegel gilt:
Die Wahrscheinlichkeit dafür, dass ein Maßfehler vorliegt, beträgt 
Die Wahrscheinlichkeit dafür, dass beide Fehler auftreten, beträgt
Die Wahrscheinlichkeit dafür, dass mindestens einer der beiden Fehler auftritt, beträgt Gib die Wahrscheinlichkeit dafür an, dass ein zufällig ausgewählter Ziegel keinen Fehler hat.
Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Ziegel mit Farbfehler einen Maßfehler hat.
Untersuche, ob die beiden Fehler stochastisch abhängig sind.
Gib die Wahrscheinlichkeit dafür an, dass ein zufällig ausgewählter Ziegel keinen Fehler hat.
Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Ziegel mit Farbfehler einen Maßfehler hat.
Untersuche, ob die beiden Fehler stochastisch abhängig sind.
Die Wahrscheinlichkeit dafür, dass beide Fehler auftreten, beträgt
Die Wahrscheinlichkeit dafür, dass mindestens einer der beiden Fehler auftritt, beträgt
(7 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
Koordinaten zeigen
Da  ein bezüglich der Symmetrieebene symmetrischer und benachbarter Punkt von
ein bezüglich der Symmetrieebene symmetrischer und benachbarter Punkt von  ist und das Dach ein ebenflächig begrenzter Körper ist, besitzt
ist und das Dach ein ebenflächig begrenzter Körper ist, besitzt  die gleiche
die gleiche  - und
- und  -Koordinate wie
-Koordinate wie  Die Symmetrieebene
Die Symmetrieebene  beeinflusst nur die
beeinflusst nur die  -Koordinate.
Da die Symmetrieebene des Gebäudes durch die Gleichung
-Koordinate.
Da die Symmetrieebene des Gebäudes durch die Gleichung  gegeben ist, muss der Punkt
gegeben ist, muss der Punkt  außerdem den gleichen Abstand entlang der
außerdem den gleichen Abstand entlang der  -Achse wie
-Achse wie  zur Symmetrieebene haben. Für die
zur Symmetrieebene haben. Für die  -Koordinate von
-Koordinate von  gilt
gilt  Aufgrund der Symmetrie muss der Punkt
Aufgrund der Symmetrie muss der Punkt  auf der anderen Seite der Ebene ebenfalls 2 Einheiten entfernt liegen und die
auf der anderen Seite der Ebene ebenfalls 2 Einheiten entfernt liegen und die  -Koordinate von
-Koordinate von  folgt also mit
folgt also mit 
 besitzt somit die Koordinaten
besitzt somit die Koordinaten  Gleichung angeben
Gleichung angeben
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OG}+t\cdot \overrightarrow{GK}& \\[5pt]
&=& \pmatrix{8\\9\\7}+t\cdot \pmatrix{-2\\-4\\11}
\end{array}\)](https://mathjax.schullv.de/0147c5ddc4977781751b1756feddfb43647147978d0a9985e7b13bdbeee79cd7?color=5a5a5a) Für
Für  beschreibt die Geradengleichung
beschreibt die Geradengleichung  die Strecke
die Strecke 
2.2
Die Dachfläche  ist trapezförmig und ihr Flächeninhalt kann somit mit folgender Formel berechnet werden:
ist trapezförmig und ihr Flächeninhalt kann somit mit folgender Formel berechnet werden:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot (a+b)\cdot h& \\[5pt]
&=& \dfrac{1}{2}\cdot (|\overline{GH}|+|\overline{KL}|)\cdot h
\end{array}\)](https://mathjax.schullv.de/209f5239db9716b5f3a82915ab5e02a366d0b99cac06ca1d878829b0c84c7144?color=5a5a5a) Aus der Abbildung ergeben sich die Koordinaten von
Aus der Abbildung ergeben sich die Koordinaten von  mit
mit  Da sich die Koordinaten von
Da sich die Koordinaten von  und
und  nur in ihrer
nur in ihrer  -Koordinate unterscheiden, gilt
-Koordinate unterscheiden, gilt 
 Der Flächeninhalt der Dachfläche, die im Modell durch das Viereck
Der Flächeninhalt der Dachfläche, die im Modell durch das Viereck  beschrieben wird, beträgt somit etwa 70,2 Quadratmeter.
beschrieben wird, beträgt somit etwa 70,2 Quadratmeter.
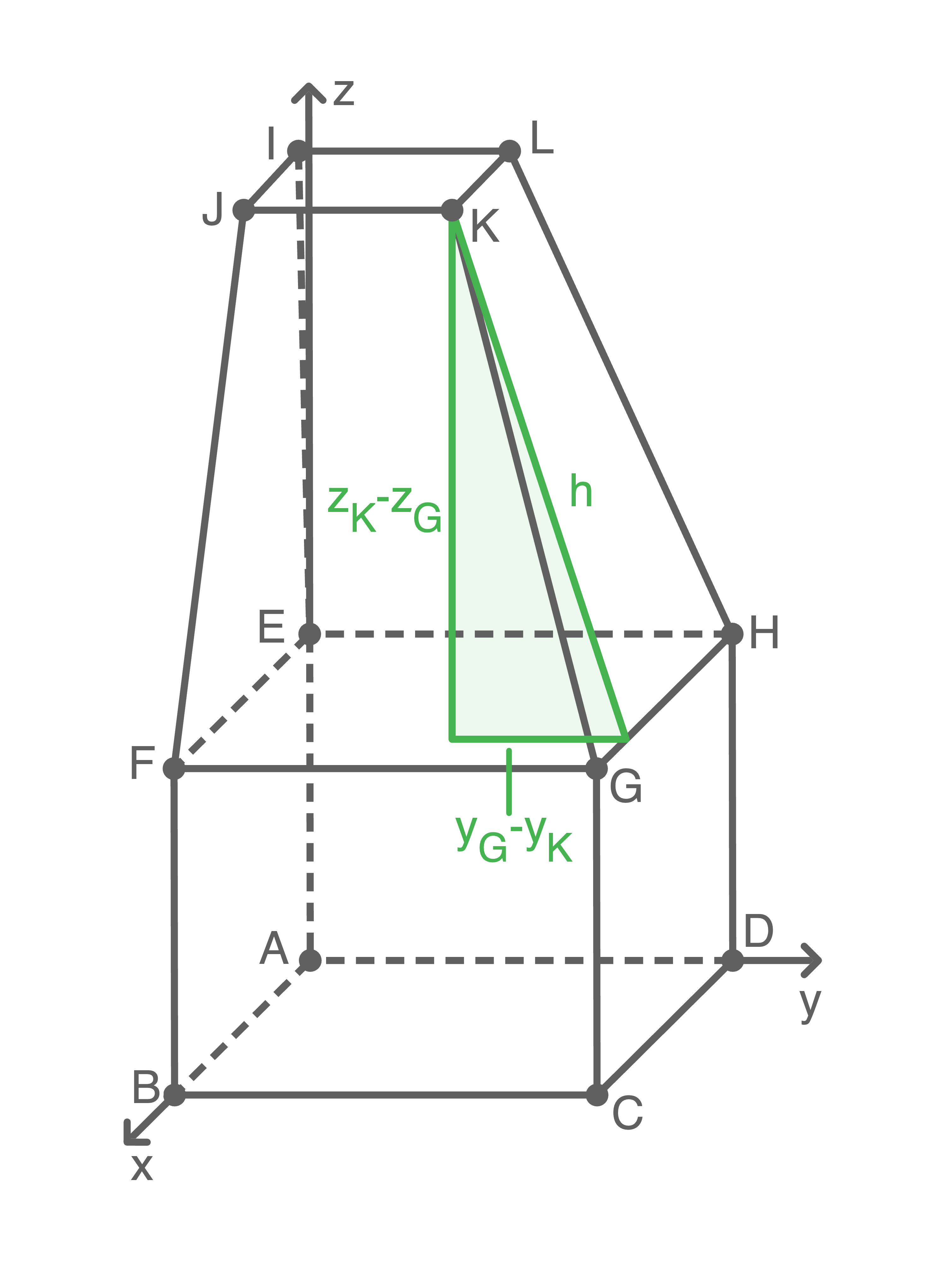
Analog gilt  Für die Höhe des Trapez kann ein Hilfsdreieck eingezeichnet werden.
Mit dem Satz des Pythagoras folgt so:
Für die Höhe des Trapez kann ein Hilfsdreieck eingezeichnet werden.
Mit dem Satz des Pythagoras folgt so:
![\(\begin{array}[t]{rll}
a^2+b^2&=& c^2 &\\[5pt]
(y_G-y_K)^2+(z_K-z_G)^2&=& h^2 &\\[5pt]
(9-5)^2+(18-7)^2&=& h^2 &\\[5pt]
137&=& h^2 &\quad \scriptsize \mid \; \sqrt{\,}\\[5pt]
11,7&\approx& h
\end{array}\)](https://mathjax.schullv.de/bf4fa9b121f074fd3633a466382be8a210b5bf7b06e7ef1924a8b4f1073ea186?color=5a5a5a) Der Flächeninhalt der Dachfläche ergibt sich somit zu:
Der Flächeninhalt der Dachfläche ergibt sich somit zu:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot (|\overline{GH}|+|\overline{KL}|)\cdot h & \\[5pt]
&=& \dfrac{1}{2}\cdot (8+ 4)\cdot 11,7 & \\[5pt]
&=& 70,2 \; [\,\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/c7bb37c4f87887d8ef40a6b7b8618a1a04a049a5049d4f191518e1e2f999682b?color=5a5a5a)

Hilfsskizze
2.3
Aufgabenstellung formulieren
Berechne den Winkel, in dem die Dachfläche, die durch das Viereck  beschrieben wird, zur Grundfläche des quaderförmigen unteren Teils des Gebäudes geneigt ist.
Bedeutung beschreiben
Die Gleichung
beschrieben wird, zur Grundfläche des quaderförmigen unteren Teils des Gebäudes geneigt ist.
Bedeutung beschreiben
Die Gleichung  beschreibt den Normalenvektor
beschreibt den Normalenvektor  der Ebene, in welcher das Viereck
der Ebene, in welcher das Viereck  liegt.
In Gleichung
liegt.
In Gleichung  wird anschließend der Schnittwinkel dieser Ebene mit der
wird anschließend der Schnittwinkel dieser Ebene mit der  -Ebene berechnet. Die
-Ebene berechnet. Die  -Ebene besitzt den Normalenvektor
-Ebene besitzt den Normalenvektor  und entspricht dem Untergrund.
Der Schnittwinkel
und entspricht dem Untergrund.
Der Schnittwinkel  entspricht somit dem Neigungswinkel der Dachfläche zum Untergrund bzw. zur parallelen Oberfläche des unteren Teils des Gebäudes.
entspricht somit dem Neigungswinkel der Dachfläche zum Untergrund bzw. zur parallelen Oberfläche des unteren Teils des Gebäudes.
2.4
Schneiden sich die Geraden durch die Punkte  und
und  bzw.
bzw.  und
und  in einem Punkt, der in der Symmetrieebene
in einem Punkt, der in der Symmetrieebene  liegt, so gilt dies auch für die andere Seite der Symmetrieebene.
Die Geraden durch die Punkte
liegt, so gilt dies auch für die andere Seite der Symmetrieebene.
Die Geraden durch die Punkte  und
und  bzw.
bzw.  und
und  haben in diesem Fall aus Symmetriegründen den gleichen Schnittpunkt in der Symmetrieebene.
haben in diesem Fall aus Symmetriegründen den gleichen Schnittpunkt in der Symmetrieebene.
2.5
1. Schritt: Rauminhalt des unteren Teils berechnen
Der untere Teil des Gebäudes entspricht einem Quader mit der Länge  der Breite
der Breite  und der Höhe
und der Höhe  Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
V_{\text{Quader}}&=& 9\cdot 8\cdot 7& \\[5pt]
&=& 504 \; [\,\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/1afe6a911295d0e80e43db3de10b04f5eef72d86fdf13cfda583ed95ba5776fa?color=5a5a5a) 2. Schritt: Höhe der Pyramide berechnen
2. Schritt: Höhe der Pyramide berechnen
 Die Höhe der Pyramide beträgt somit
Die Höhe der Pyramide beträgt somit  Meter.
3. Schritt: Volumen der gesamten Pyramide ermitteln
Die Grundfläche der Pyramide
Meter.
3. Schritt: Volumen der gesamten Pyramide ermitteln
Die Grundfläche der Pyramide  ist das Quadrat
ist das Quadrat  mit mit der Länge
mit mit der Länge  und der Breite
und der Breite  Der Flächeninhalt
Der Flächeninhalt  der Grundfläche folgt also mit
der Grundfläche folgt also mit ![\(g=9\cdot 8=72 \;\,[\text{m}^2].\)](https://mathjax.schullv.de/808b474608ec221367d93a5b584f3dc70a766c1fb0df738a82b766e63760ca9e?color=5a5a5a) Somit ergibt sich das Volumen der Pyramide zu:
Somit ergibt sich das Volumen der Pyramide zu:
![\(\begin{array}[t]{rll}
V_{EFGHS}&=& \dfrac{1}{3}\cdot g\cdot h&\\[5pt]
&=& \dfrac{1}{3}\cdot 72 \cdot 22&\\[5pt]
&=& 528 \; [\,\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/3d6cce78425c77da6c758b8b35e0f002c7f3905b178108d096c05325ad5d00c9?color=5a5a5a) 4. Schritt: Volumen des oberen Teils der Pyramide bestimmen
Die Spitze der Pyramide
4. Schritt: Volumen des oberen Teils der Pyramide bestimmen
Die Spitze der Pyramide  entspricht der kleineren Pyramide
entspricht der kleineren Pyramide  Dieser Teil der Pyramide gehört nicht mehr zum Wohngebäude.
Aus den Koordinaten der Punkte
Dieser Teil der Pyramide gehört nicht mehr zum Wohngebäude.
Aus den Koordinaten der Punkte  und
und  ergibt sich die Länge der rechteckigen Grundfläche mit
ergibt sich die Länge der rechteckigen Grundfläche mit ![\(y_K-y_J=5-0,5=4,5 \,[\,\text{m}]\)](https://mathjax.schullv.de/38c8f85d7f6feb7143e4847e81026a6142142761ab2204be666ad7cdea074beb?color=5a5a5a) und die Breite mit
und die Breite mit ![\(x_K-x_L=6-2=4 \,[\,\text{m}].\)](https://mathjax.schullv.de/59c1bad19510cf0824ed6fff9f1b79dbb27b463c42cb5250aea0c74d988fa512?color=5a5a5a) Die Höhe der Pyramide ergibt sich mit
Die Höhe der Pyramide ergibt sich mit ![\(z_S-z_J=29-18=11 \,[\,\text{m}].\)](https://mathjax.schullv.de/1977def6dc98d9eda61060d077e4b22aacbfc903141cf92522f8adf5178492ea?color=5a5a5a) Somit folgt das Volumen mit:
Somit folgt das Volumen mit:
![\(\begin{array}[t]{rll}
V_{IJKLS}&=& \dfrac{1}{3}\cdot g\cdot h& \\[5pt]
&=& \dfrac{1}{3}\cdot (4,5\cdot 4)\cdot 11& \\[5pt]
&=& 66 \; [\,\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/e89b611f8f5f899b9fb9b5b0d5ee2106416e33c4cca11487432ebbc49f558bef?color=5a5a5a) 5. Schritt: Gesamtes Volumen berechnen
Der Rauminhalt
5. Schritt: Gesamtes Volumen berechnen
Der Rauminhalt  des Wohngebäudes ergibt sich zu:
des Wohngebäudes ergibt sich zu:
![\(\begin{array}[t]{rll}
V&=& V_{Quader}+(V_{EFGHS}-V_{IJKLS})& \\[5pt]
&=& 504 \,\text{m}^2+( 528 \,\text{m}^2-66 \,\text{m}^2)& \\[5pt]
&=& 966 \,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/eb0a954b9cf1f7813ece34b3c7a03d6a390424dfbc834efde49cb62e4b45234c?color=5a5a5a)
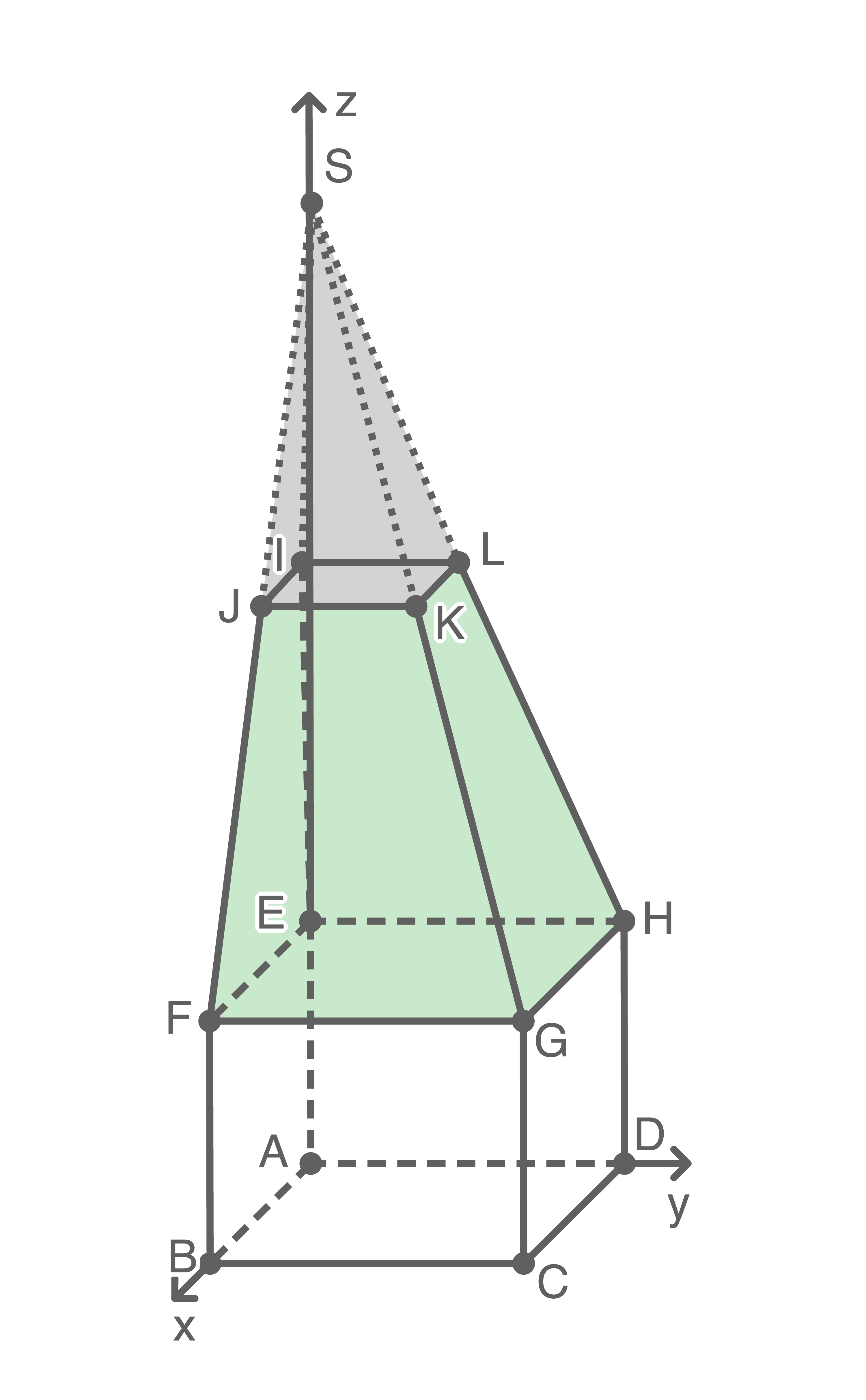
Der obere Teil des Gebäudes entspricht einem Pyramidenstumpf. Um das Volumen des Stumpfs zu berechnen, muss das Volumen der gesamten Pyramide sowie das Volumen der grauen Spitze der Pyramide berechnet werden.
Die Spitze der Pyramide entspricht hierbei dem Schnittpunkt der vier Geraden, auf denen die Kanten des Körpers liegen. Aufgrund der Symmetrie reicht es aus, den Schnittpunkt der Geraden, die die Kante  beinhaltet, mit der Symmetrieebene
beinhaltet, mit der Symmetrieebene  zu berechnen. Mit der Geradengleichung aus Aufgabe 2.1 folgt:
zu berechnen. Mit der Geradengleichung aus Aufgabe 2.1 folgt:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:
![\(\begin{array}[t]{rll}
4&=& 8-2t&\quad \scriptsize \mid\; -8\\[5pt]
-4&=& -2t&\quad \scriptsize \mid\; :(-2)\\[5pt]
2&=& t
\end{array}\)](https://mathjax.schullv.de/8a64bd705f501402cae37506090e0b4dea860918a7ffd4e660f75177bed26fea?color=5a5a5a) Somit ergeben sich die Koordinaten der Pyramidenspitze
Somit ergeben sich die Koordinaten der Pyramidenspitze  zu:
zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \pmatrix{8\\9\\7}+2\cdot \pmatrix{-2\\-4\\11} &\\[5pt]
&=& \pmatrix{4\\1\\29}
\end{array}\)](https://mathjax.schullv.de/964d7c9b2d5f0c7fa41839b73e873bf9131512ce19de77a06aff66b200cd6e7f?color=5a5a5a)

Hilfsskizze
2.6
1. Schritt: Geradengleichung aufstellen
Die Strecke  liegt auf der Geraden, die durch folgende Gleichung beschrieben werden kann:
liegt auf der Geraden, die durch folgende Gleichung beschrieben werden kann:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OG}+t\cdot \overrightarrow{GH} & \\[5pt]
&=& \pmatrix{8\\9\\7}+t\cdot \pmatrix{-8\\0\\0} & \\[5pt]
&=& \pmatrix{8-8t\\9\\7}
\end{array}\)](https://mathjax.schullv.de/9f330dbca4326e1fb8c669cff4e966d2dfa5ce6489e4d1f1c15a89c58acc8764?color=5a5a5a) Für
Für  liegt der entsprechende Punkt auf der Kante
liegt der entsprechende Punkt auf der Kante  2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  beschreiben
Der Punkt
beschreiben
Der Punkt  entspricht einem Punkt auf der Kante
entspricht einem Punkt auf der Kante  Für den Abstand von
Für den Abstand von  zu einem beliebigen
zu einem beliebigen  gilt:
3. Schritt: Länge der Strecke
gilt:
3. Schritt: Länge der Strecke  beschreiben
Für den Abstand von
beschreiben
Für den Abstand von  zu einem beliebigen
zu einem beliebigen  gilt:
4. Schritt: Abstandsfunktion minimieren
Der gesamte Abstand von Punkt
gilt:
4. Schritt: Abstandsfunktion minimieren
Der gesamte Abstand von Punkt  über einen Punkt
über einen Punkt  auf der Kante
auf der Kante  zu Punkt
zu Punkt  beträgt für
beträgt für  somit:
somit:
![\(\begin{array}[t]{rll}
d(t)&=& \sqrt{64t^2+49}+\sqrt{(6-8t)^2+137} &\\[5pt]
&=& (64t^2+49)^{\frac{1}{2}} + ((6-8t)^2+137)^{\frac{1}{2}}
\end{array}\)](https://mathjax.schullv.de/718eb8716bb708adea3bef98828f50bf5f4d813f0c599f1670fef938f0912978?color=5a5a5a) Mit dem GTR kann das Minimum der Abstandsfunktion graphisch bestimmt werden. Die Koordinaten des Tiefpunkts folgen mit
Mit dem GTR kann das Minimum der Abstandsfunktion graphisch bestimmt werden. Die Koordinaten des Tiefpunkts folgen mit  Da
Da  gilt, beträgt die kürzeste Verbindungslinie, die vom Punkt
gilt, beträgt die kürzeste Verbindungslinie, die vom Punkt  über einen Punkt der Kante
über einen Punkt der Kante  zum Punkt
zum Punkt  verläuft, etwa
verläuft, etwa  Meter.
Meter.
2.7
Wahrscheinlichkeit berechnen
Bei der Farbanordnung handelt es sich um Ziehen ohne Zurücklegen und mit Beachtung der Reihenfolge. Nach jedem gezogenen Ziegel verringert sich die Gesamtanzahl somit um eins.
Mit den Anfangswahrscheinlichkeiten 
 und
und  ergibt sich also:
ergibt sich also:
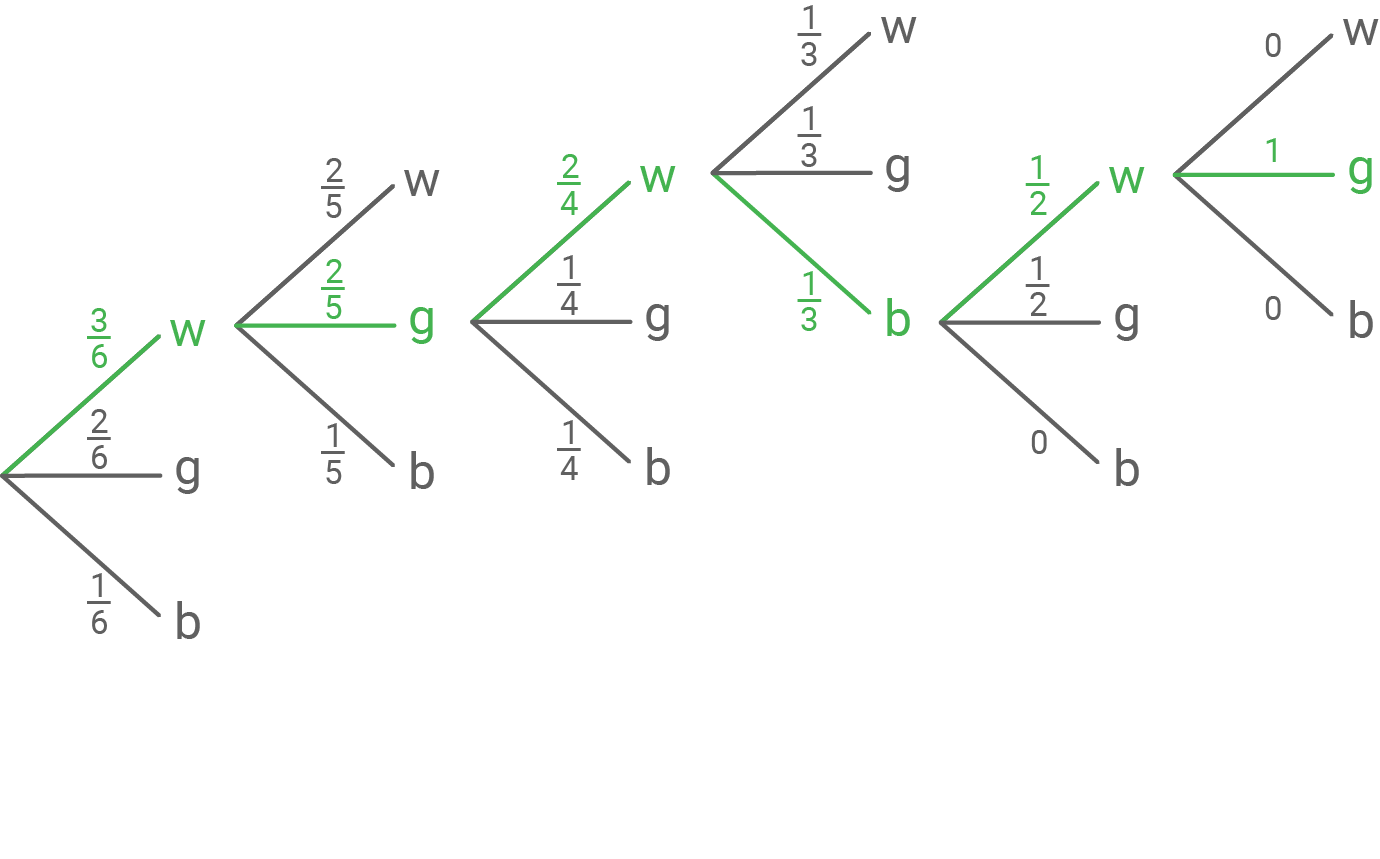
![\(\begin{array}[t]{rll}
P(\text{wgwbwg})&=& \dfrac{3}{6}\cdot \dfrac{2}{5}\cdot \dfrac{2}{4}\cdot \dfrac{1}{3}\cdot \dfrac{1}{2}\cdot 1 & \\[5pt]
&=& \dfrac{1}{60} & \\[5pt]
&\approx& 0,017
\end{array}\)](https://mathjax.schullv.de/3ab598bd26f09f4e1792d5e1f827766d123060570ea9e06ae96a22b33b5c65d4?color=5a5a5a) Die Wahrscheinlichkeit
Die Wahrscheinlichkeit  , mit der die Farbanordnung "wgwbwg" entsteht, entspricht somit etwa
, mit der die Farbanordnung "wgwbwg" entsteht, entspricht somit etwa  Aussage beurteilen
Wenn die beiden zuerst ausgewählten Ziegel gelb sind, gibt es für die übrigen vier Stellen noch 3 weiße und einen braunen Ziegel. Der braune Ziegel kann hierbei an dritter, vierter, fünfter oder sechster Stelle ausgewählt werden, während die restlichen Ziegel alle weiß sind.
Es gibt somit genau vier Möglichkeiten, bei denen die beiden gelben Ziegel zuerst gewählt werden.
Da die Wahrscheinlichkeit für eine beliebige Reihenfolge wie zuvor berechnet
Aussage beurteilen
Wenn die beiden zuerst ausgewählten Ziegel gelb sind, gibt es für die übrigen vier Stellen noch 3 weiße und einen braunen Ziegel. Der braune Ziegel kann hierbei an dritter, vierter, fünfter oder sechster Stelle ausgewählt werden, während die restlichen Ziegel alle weiß sind.
Es gibt somit genau vier Möglichkeiten, bei denen die beiden gelben Ziegel zuerst gewählt werden.
Da die Wahrscheinlichkeit für eine beliebige Reihenfolge wie zuvor berechnet  beträgt, gilt für die vier möglichen Farbanordnungen:
beträgt, gilt für die vier möglichen Farbanordnungen:
 Die Aussage ist somit korrekt.
Die Aussage ist somit korrekt.

2.8