Teil A – Pflichtbereich

In den Teilaufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Für alle $x$ aus dem größtmöglichen Definitionsbereich der Funktion $f$ mit $f(x)=\sqrt{x+1}$ gilt: $x \in \mathbb{R}$ und

	$x \leq -1$
	$x \geq -1$
	$x\gt -1$
	$x\geq 0$
	$x \gt0$

1.2

Ein möglicher Funktionsterm der ersten Ableitungsfunktion von $f$ mit $f(x)=\dfrac{2}{3 \cdot x} \quad\left(x \in D_f\right)$ ist:

	$\dfrac{2}{3}\cdot \ln\|x\|$
	$\dfrac{3}{2}\cdot \ln(x)$
	$\dfrac{2}{3\cdot x^2}$
	$-\dfrac{2}{3\cdot x^2}$
	$-\dfrac{3}{2\cdot x^2}$

1.3

Für welche Funktion $f$ mit größtmöglichem Definitionsbereich gilt: $\lim\limits_{x\to+\infty} f(x)=1 \; ?$

	$f(x)=\dfrac{x+1}{x-1}$
	$f(x)=\dfrac{1+x}{1-x}$
	$f(x)=-\dfrac{1}{x}$
	$f(x)=\dfrac{1+x^2}{1-x}$
	$f(x)=\dfrac{1+x}{1-x^2}$

1.4

In der Abbildung ist der Graph der ersten Ableitungsfunktion $\(f$ einer in $\mathbb{R}$ definierten ganzrationalen Funktion $f$ dritten Grades dargestellt.

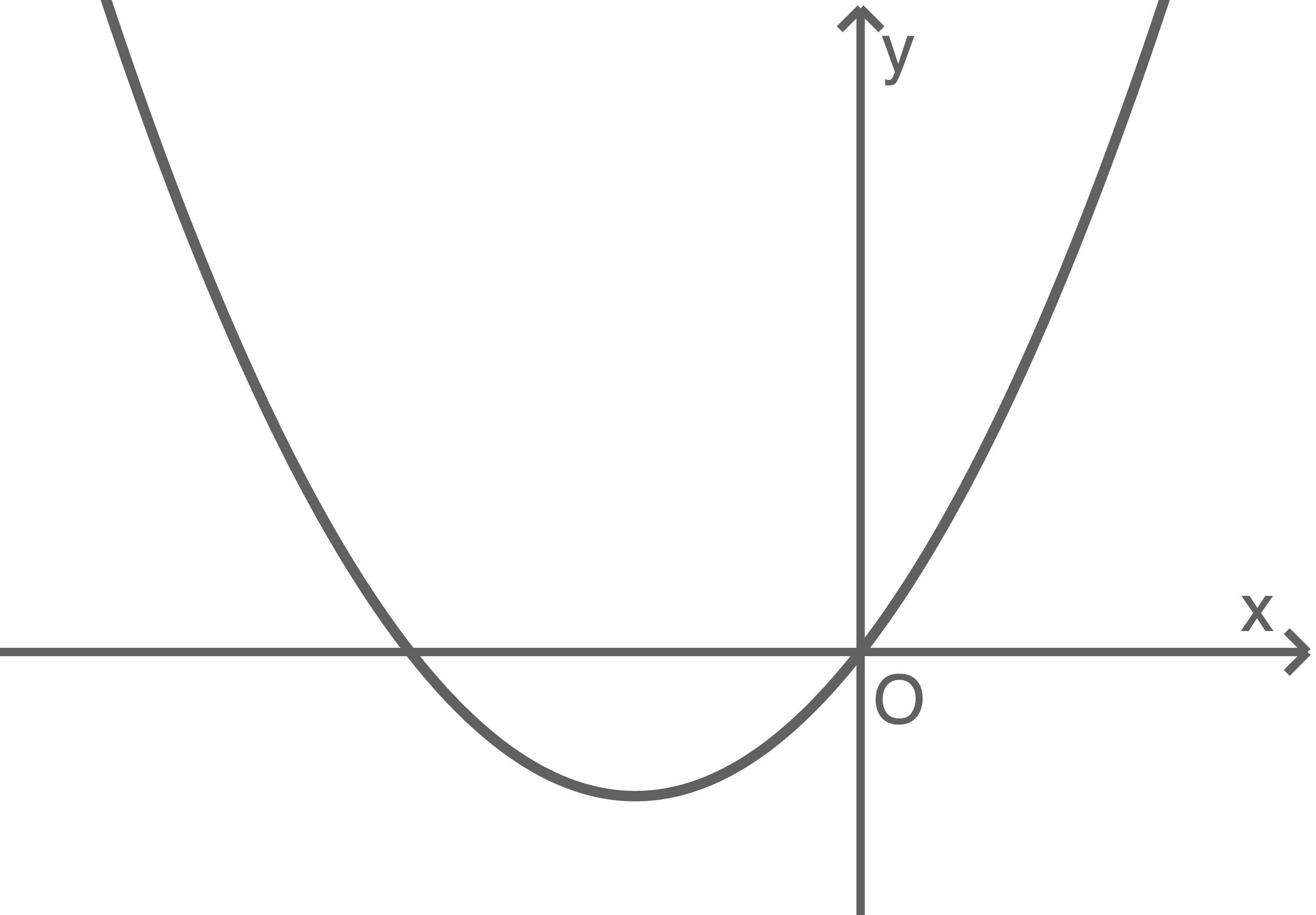
Pflichtteil Mathe Abi Sachsen 2024 Graph Ableitungsfunktion

Welche der folgenden Aussagen ist falsch?

	$f$ ist in $\mathbb{R}$ stetig.
	$f$ ist in $\mathbb{R}$ differenzierbar.
	$f$ hat genau eine Wendestelle.
	$f$ hat genau eine lokale Extremstelle.
	$f$ hat mindestens eine Nullstelle.

1.5

Die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\mathrm{e}^x \cdot\left(2 \cdot x+x^2\right)$ hat die Nullstellen:

	0 und 1
	0 und 2
	0 und -2
	1 und -2
	2 und -2

(5 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^3-4 \cdot x.$

2.1

Zeige anhand des Funktionsterms, dass der Graph von $f$ symmetrisch bezüglich des Koordinatenursprungs ist.

(2 BE)

2.2

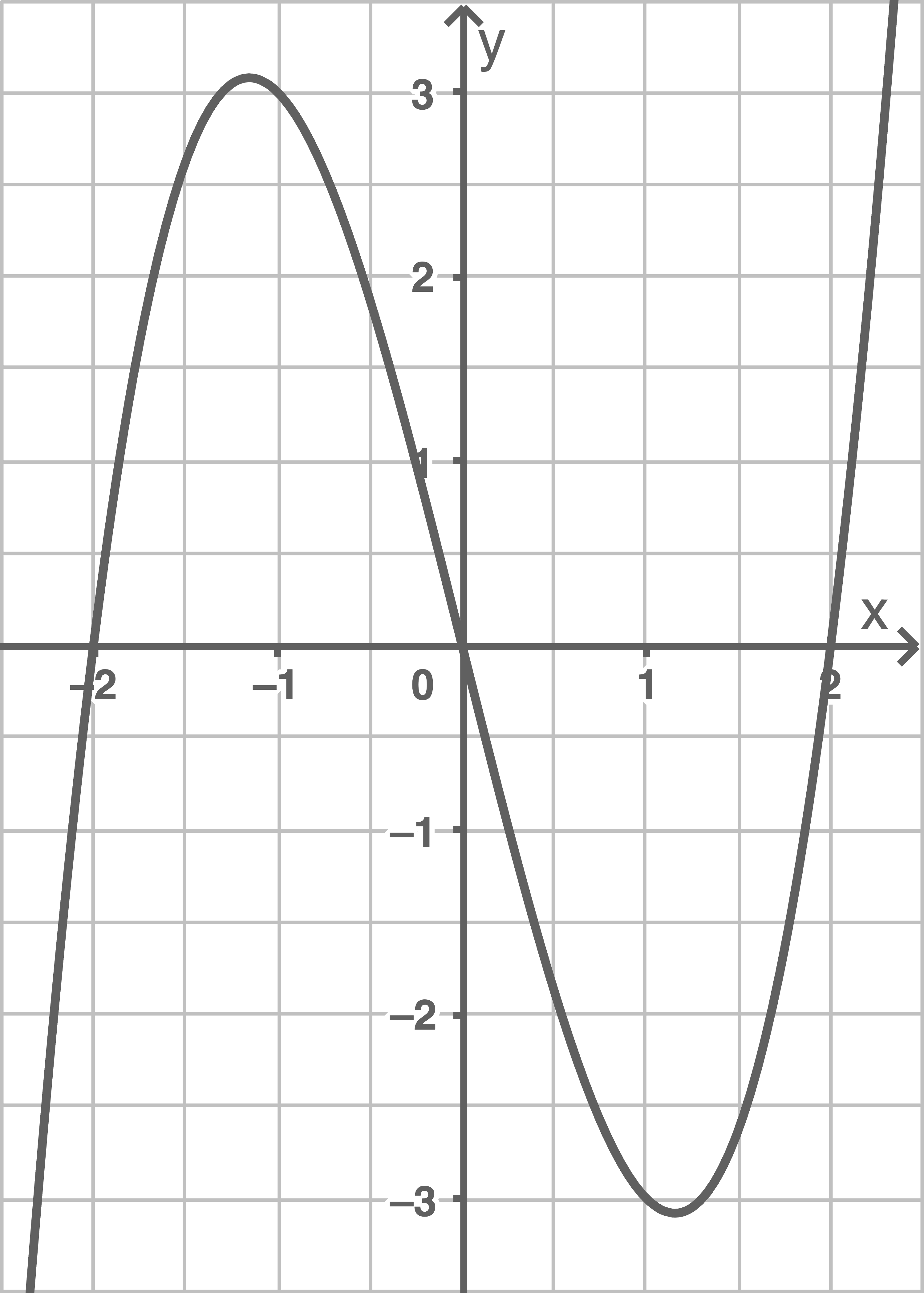
In der Abbildung ist der Graph von $f$ dargestellt.

Ermittle grafisch mit Hilfe der Abbildung den Wert des Integrals $\displaystyle\int_{-0,5}^{1}f(x)\;\mathrm dx.$

Veranschauliche das Vorgehen in der Abbildung.

(3 BE)

Gegeben sind die Ebenen $E: 3 \cdot x+y-2 \cdot z=5\;$ und $\;F:-5 \cdot x+y+2 \cdot z=-7.$

3.1

Begründe, dass $E$ und $F$ nicht parallel zueinander verlaufen.

(1 BE)

3.2

Es gibt eine Gerade, die in beiden Ebenen liegt.

Bestimme eine Gleichung dieser Gerade.

(4 BE)

Es werden die Behälter A, B und C betrachtet. In diesen Behältern befinden sich schwarze und weiße Kugeln mit folgender Aufteilung:

Behälter A: $\;$ 3 schwarze, 2 weiße Kugeln

Behälter B: $\;$ 1 schwarze, 1 weiße Kugel

Behälter C: $\;$ 1 schwarze, 4 weiße Kugeln

Es wird ein Behälter zufällig ausgewählt und anschließend daraus eine Kugel zufällig gezogen.

4.1

Zeige, dass die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen, $\dfrac{13}{30}$ beträgt.

(2 BE)

4.2

Es wird eine schwarze Kugel gezogen.

Ermittle die Wahrscheinlichkeit dafür, dass diese Kugel aus Behälter A stammt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

	$x \leq -1$
	$x \geq -1$
	$x\gt -1$
	$x\geq 0$
	$x \gt0$

Lösungsweg:

Da die Wurzel einer negativen Zahl im reellen Zahlenbereich nicht definiert ist, muss der Ausdruck $x+1$ unter der Wurzel größer oder gleich Null sein. Es muss also gelten:

$\begin{array}[t]{rll} x+1&\geq& 0 &\quad \scriptsize \mid\; -1 \\[5pt] x&\geq& -1 \end{array}$

1.2

	$\dfrac{2}{3}\cdot \ln\|x\|$
	$\dfrac{3}{2}\cdot \ln(x)$
	$\dfrac{2}{3\cdot x^2}$
	$-\dfrac{2}{3\cdot x^2}$
	$-\dfrac{3}{2\cdot x^2}$

Lösungsweg:

$f(x)= \dfrac{2}{3\cdot x}= \dfrac{2}{3}\cdot \dfrac{1}{x}= \dfrac{2}{3}\cdot x^{-1}$

Die Ableitung folgt also also mit:

$\(\begin{array}[t]{rll} f$

1.3

	$f(x)=\dfrac{x+1}{x-1}$
	$f(x)=\dfrac{1+x}{1-x}$
	$f(x)=-\dfrac{1}{x}$
	$f(x)=\dfrac{1+x^2}{1-x}$
	$f(x)=\dfrac{1+x}{1-x^2}$

Lösungsweg:

Für $x\rightarrow\infty$ nähert sich sowohl der Nenner als auch der Zähler unendlich an.

Da der Einfluss von $+1$ und $-1$ mit $x\rightarrow\infty$ immer geringer wird und das Verhältnis von Nenner und Zähler somit immer ähnlicher wird, gilt:

$\lim\limits_{x\to+\infty} \dfrac{x+1}{x-1}=1$

1.4

	$f$ ist in $\mathbb{R}$ stetig
	$f$ ist in $\mathbb{R}$ differenzierbar
	$f$ hat genau eine Wendestelle
	$f$ hat genau eine lokale Extremstelle
	$f$ hat mindestens eine Nullstelle

Lösungsweg:

Die Extremstellen von $f$ entsprechen den Nullstellen der Ableitungsfunktion $\(f$

Da der Graph von $\(f$ genau zweimal die $x$ -Achse schneidet und $\(f$ somit zwei lokale Nullstellen hat, besitzt $f$ folglich zwei lokale Extremstellen.

1.5

	0 und 1
	0 und 2
	0 und -2
	1 und -2
	2 und -2

Lösungsweg:

An den Nullstellen gilt:

$0=\mathrm e^x\cdot (2\cdot x+x^2)$

Wegen $\mathrm e^x\gt 0$ muss gelten:

$\begin{array}[t]{rll} 0&=& 2\cdot x+x^2 & \\[5pt] 0&=& x\cdot (2+x) \end{array}$

Mit dem Satz vom Nullprodukt folgen die Nullstellen mit $x_1=0$ und $x_2=-2.$

2.1

Für Punktsymmetrie bezüglich des Koordinatenursprungs muss gelten:

$f(-x)=-f(x)$

Für die gegebene Funktion gilt aufgrund des ungeraden Exponents:

$\begin{array}[t]{rll} f(-x)&=& (-x)^3-4\cdot (-x)& \\[5pt] &=& -x^3+4\cdot x& \\[5pt] &=& -(x^3-4\cdot x)& \\[5pt] &=& -f(x)& \\[5pt] \end{array}$

Somit ist der Graph von $f$ punktsymmetrisch bezüglich des Koordinatenursprungs.

2.2

Der Wert des Integrals entspricht der Fläche zwischen dem Graphen von $f$ und der $x$ -Achse. Für diejenigen Abschnitte, in denen der Graph unterhalb der $x$ -Achse verläuft, ist der zugehörige Wert des Integrals negativ.

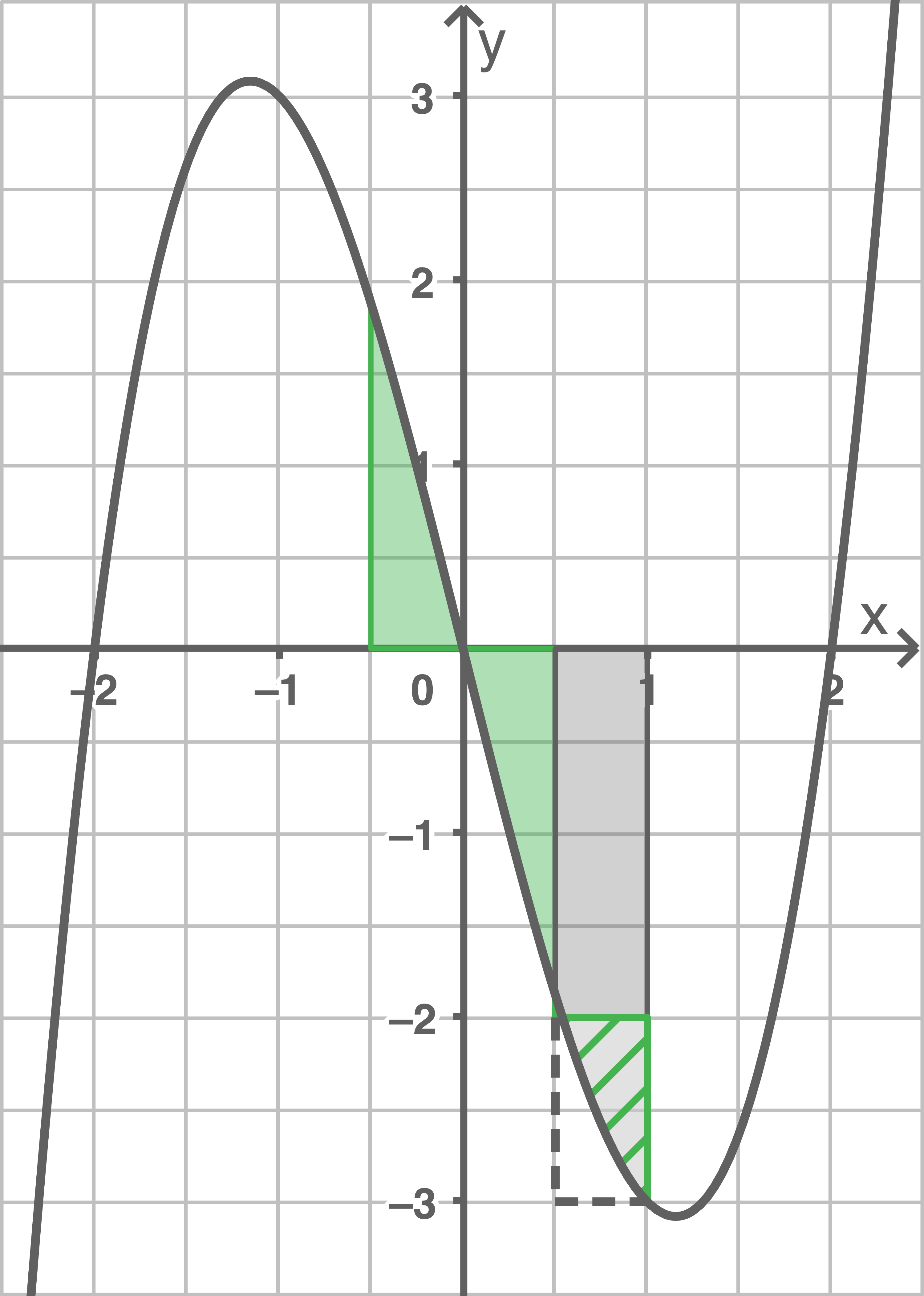
Da der Graph von $f$ punktsymmetrisch bezüglich des Koordinatenursprungs ist, ist der Betrag des Flächeninhalts im Intervall $[-0,5;0]$ gleich groß wie der Betrag des Flächeninhalts im Intervall $[0;0,5].$ Für die in der Abbildung grün markierte Fläche gilt also $\displaystyle\int_{-0,5}^{0,5}f(x)\;\mathrm dx=0.$

Ein Kästchen in der Abbildung entspricht $0,5\cdot 0,5=0,25 \;\text{FE}.$

Die Fläche im Intervall $[0,5;1]$ kann durch ein Rechteck und ein Dreieck angenähert werden. Das grau markierte Rechteck besitzt den Flächeninhalt $1 \;\text{FE}.$ Das grün schraffierte Dreieck kann durch Verdopplung zu einem Rechteck mit 2 Kästchen ergänzt werden, der Flächeninhalt des Dreiecks entspricht somit einem Kästchen, also etwa $0,25\;\text{FE}.$

Da diese Flächen unterhalb der $x$ -Achse liegen, folgt $\displaystyle\int_{-0,5}^{1}f(x)\;\mathrm dx=-1,25.$

Sachsen Mathe Abi 2024 Integral Vorgehen

3.1

Zwei Ebenen verlaufen genau dann parallel zueinander, wenn ihre Normalenvektoren Vielfache voneinander sind. Aus den Koordinatengleichungen kann abgelesen werden:

$\overrightarrow{n_E}=\pmatrix{3\\1\\-2}$ und $\; \overrightarrow{n_F}=\pmatrix{-5\\1\\2}$

Für Parallelität müsste gelten:

$\pmatrix{3\\1\\-2}=a\cdot \pmatrix{-5\\1\\2}$

Da diese Gleichung für keinen Wert von $a$ gilt, verlaufen die Ebenen $E$ und $F$ nicht parallel zueinander.

3.2

Die Gerade, die in beiden Ebenen liegt, ist genau die Schnittgerade von $E$ und $F.$ Diese entspricht der Lösung des Gleichungssystems der beiden Koordinatengleichungen:

$\begin{array}{lrll} \text{I:}\quad& 3x+y-2z&=& 5 &\quad \\ \text{II:}\quad&-5x+y+2z&=& -7&\quad \\ \end{array}$

Mit dem Additionsverfahren folgt für $\text{I}+\text{II}:$

$\text{I}+\text{II}:\quad -2x+2y = -2$

Rechenweg anzeigen

Das Gleichungssystem enthält drei Variablen, aber nur zwei Gleichungen und ist somit unterbestimmt. Ein solches Gleichungssystem besitzt unendlich viele Lösungen, wobei jede dieser Lösungen ein Punkt auf der Schnittgeraden der beiden Ebenen ist.

Setze also beispielsweise $x=t.$ Dann gilt:

$\begin{array}[t]{rll} -2t+2y&=& -2&\quad \scriptsize \mid\; +2t \\[5pt] 2y&=& -2+2t&\quad \scriptsize \mid\; :2\\[5pt] y&=& -1+t \end{array}$

Einsetzen von $x=t$ und $y=-1+t$ in die Gleichung $\text{I}$ liefert:

$\begin{array}[t]{rll} 3t+(-1+t)-2z&=& 5 & \\[5pt] 4t-1-2z&=& 5 &\quad \scriptsize \mid\; -4t \quad \scriptsize \mid\;+1 \\[5pt] -2z&=& 6-4t &\quad \scriptsize \mid\; :(-2)\\[5pt] z&=& -3+2t \end{array}$

Die Lösungen für $x,y$ und $z$ können nun als Vektor geschrieben werden und in eine Parameterform einer Geraden umgewandelt werden:

$\begin{array}[t]{rll} g: \quad \pmatrix{x\\y\\z}&=& \pmatrix{t\\-1+t\\-3+2t} &\\[5pt] &=& \pmatrix{0+t\cdot 1\\-1+t\cdot 1\\-3+t\cdot 2} &\\[5pt] &=& \pmatrix{0\\-1\\-3}+t\cdot \pmatrix{1\\1\\2}& \\[5pt] \end{array}$

Eine mögliche Gleichung der Geraden, die in beiden Ebenen liegt, ist somit gegeben durch $g: \overrightarrow{x}= \pmatrix{0\\-1\\-3}+t\cdot \pmatrix{1\\1\\2}.$

4.1

S: schwarze Kugel

W: weiße Kugel

Baumdiagramm Kugeln Sachsen Mathe Abi 2024

Die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen, ergibt sich mit:

$\begin{array}[t]{rll} P(S)&=& P(A,S)+P(B,S)+P(C,S)& \\[5pt] &=& \dfrac{1}{3}\cdot \dfrac{3}{5}+\dfrac{1}{3}\cdot \dfrac{1}{2}+\dfrac{1}{3}\cdot \dfrac{1}{5}& \\[5pt] &=& \dfrac{3}{15}+\dfrac{1}{6}+\dfrac{1}{15}& \\[5pt] &=& \dfrac{6}{30}+\dfrac{5}{30}+\dfrac{2}{30}& \\[5pt] &=& \dfrac{13}{30} \end{array}$

4.2

$\begin{array}[t]{rll} P(A \mid S)&=& \dfrac{P(A \cap S)}{P(S)}&\\[5pt] &=& \dfrac{\dfrac{1}{3}\cdot \dfrac{3}{5}}{ \dfrac{13}{30}}&\\[5pt] &=& \dfrac{3}{15}\cdot \dfrac{30}{13}&\\[5pt] &=& \dfrac{6}{30}\cdot \dfrac{30}{13} &\\[5pt] &=& \dfrac{6}{13} \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?