Teil B1

Auf einer Waldfläche wurden Fichten gepflanzt. Alle Fichten hatten zum Zeitpunkt der Pflanzung eine Höhe von $50$ $\text{cm}$ .

Betrachtet wird die Wachstumsrate der Höhe der Fichten in Abhängigkeit von der Zeit. Diese Wachstumsrate wird für $t\geq 0$ modellhaft durch die in $\mathbb{R}$ definierte Funktion $w$ mit $w(t)=60\cdot \mathrm e^{-\frac{(t-40)^{2}}{3000}}$ beschrieben.

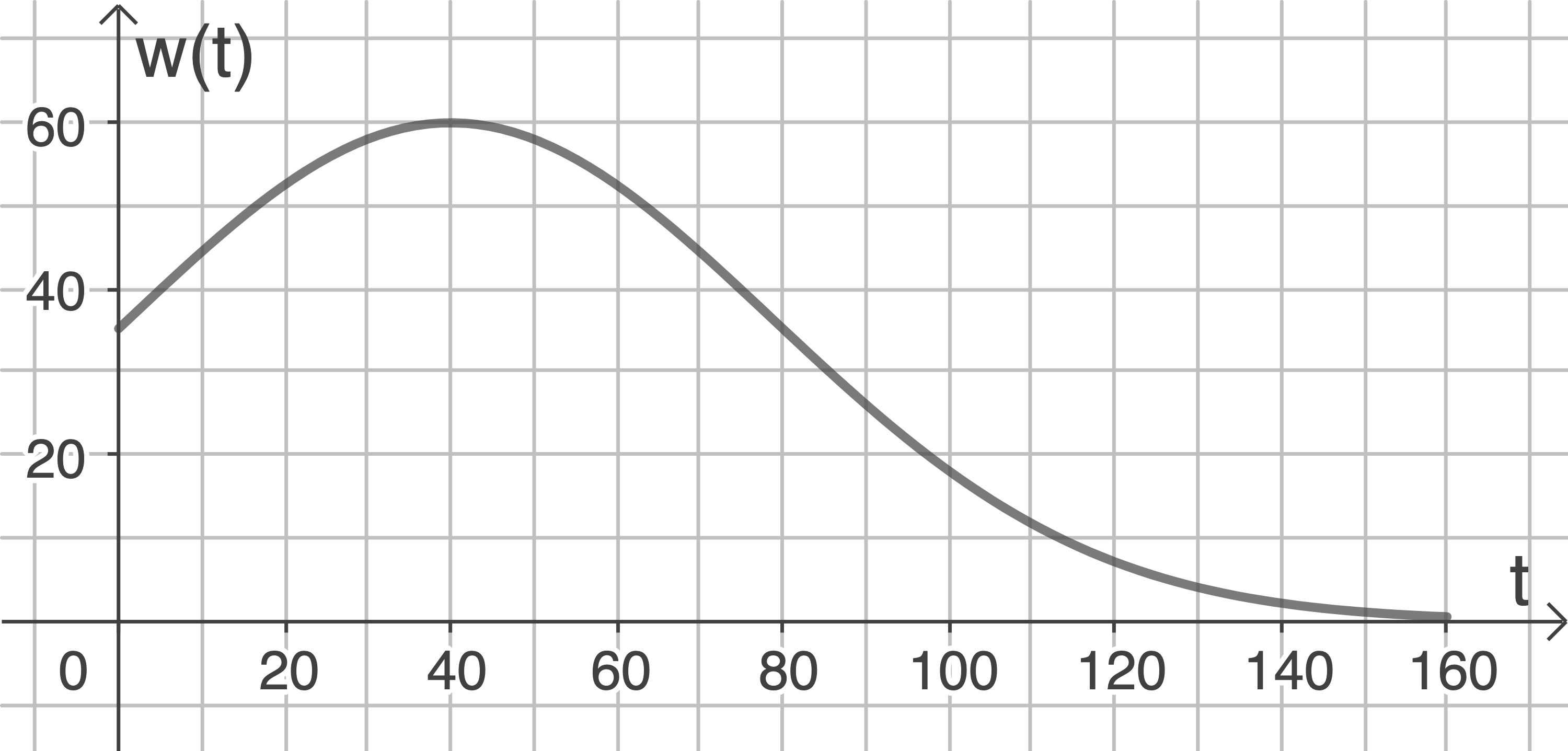
Dabei gilt:

$t$ ... seit der Pflanzung vergangene Zeit in Jahren

$w(t)$ ... Wachstumsrate zur Zeit $t$ in Zentimeter pro Jahr

Diagramm zeigt eine Kurve von w(t) über t in einem Koordinatensystem.

1.1

Ermittle die Wachstumsrate, die $2$ Jahre nach der Pflanzung vorliegt. Weise nach, dass die Wachstumsrate $40$ Jahre nach der Pflanzung am größten ist. Gib diese größte Wachstumsrate an.

Erreichbare BE-Anzahl: 07

1.2

Bestimme den Zeitraum, in dem die Wachstumsrate größer als $47$ $\text{cm}$ pro Jahr ist.

Begründe die folgende Aussage:
Innerhalb der ersten $80$ Jahre nach der Pflanzung sind für zwei beliebige Zeitpunkte, die den gleichen zeitlichen Abstand zum Zeitpunkt der größten Wachstumsrate haben, die modellhaften Wachstumsraten gleich groß.

Erreichbare BE-Anzahl: 06

1.3

Gib die Bedeutung des Terms $\displaystyle \frac{1}{100}\cdot \left(50+\int_{0}^{60}w(t)\,\mathrm dt\right)$
im Sachzusammenhang an.
Begründe deine Angabe.

Eine Funktion beschreibt die Höhe der Fichten in Abhängigkeit von der Zeit in den ersten $160$ Jahren nach der Pflanzung.
Skizziere den Graphen dieser Funktion.

Erreichbare BE-Anzahl: 08

1.4

Die Höhe der Fichten $40$ Jahre nach der Pflanzung soll mit dem Term

$50+\displaystyle \frac{w(40)+w(0)}{2}\cdot 40$ berechnet werden.

Beurteile, ob der Term zur Berechnung dieser Höhe der Fichten geeignet ist.

Erreichbare BE-Anzahl: 05

In einem anderen Modell wird die Höhe der Fichten in Abhängigkeit von der Zeit mithilfe der Funktion $h$ mit $h(t)=\displaystyle \frac{50\cdot e^{0,1\cdot t}}{e^{0,1\cdot t}+99}$ $(t\in \mathbb{R},t\geq 0)$ beschrieben.
Dabei ist $t$ die seit der Pflanzung vergangene Zeit in Jahren und $h(t)$ die Höhe der Fichten zur Zeit $t$ in Metern.

1.5

Bestimme die Koordinaten des Wendepunktes des Graphen von $h$ .
Gib die Bedeutung des Wendepunktes für den Graphen von $h$ an.

Erreichbare BE-Anzahl: 07

1.6

Für $40\leq t\leq 50$ kann der Graph von $h$ näherungsweise durch den Verlauf der Tangente $k$ an den Graphen von $h$ im Punkt $P(46\mid h(46))$ beschrieben werden.

Für jeden Wert von $t$ mit $40\leq t\leq 50$ gibt es eine prozentuale Abweichung der Funktionswerte von $k$ und $h$ bezüglich der Funktionswerte von $h.$
Bestimme einen Näherungswert für die maximale prozentuale Abweichung.

Erreichbare BE-Anzahl: 07

1.7

Der Brusthöhendurchmesser von $30$ -jährigen Fichten ist normalverteilt mit den Parametern $\mu$ und $\sigma.$ Der Erwartungswert ist $\mu=30 \;\text{cm}$ . Die Abbildung stellt den Graphen der zugehörigen Dichtefunktion $\varphi$ dar.

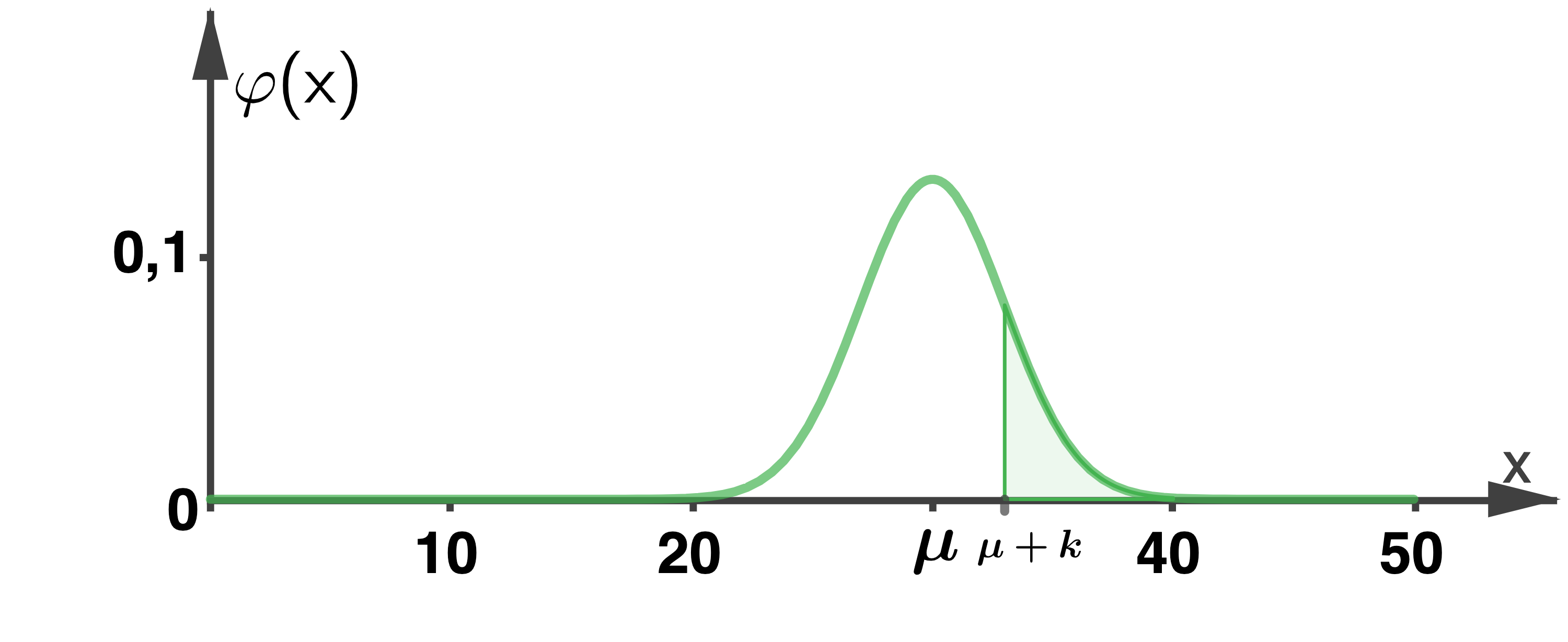
Graf einer Funktion mit einer Kurve, die auf der x-Achse verläuft und Werte zwischen 0 und 0,1 zeigt.

Gib einen Term an, mit dem der lnhalt der in der Abbildung grün unterlegten nach rechts unbegrenzten Fläche berechnet werden kann.

Der lnhalt der in der Abbildung grau unterlegten nach rechts unbegrenzten Fläche beträgt $0,15.$
Bestimme den Wert von $k$ für $\sigma=3 \;\text{cm}.$

Erreichbare BE-Anzahl: 05

1.8

ln einem Mischwald sind $40\,\%$ aller Bäume Fichten. Eine Untersuchung aufgrund starken Borkenkäferbefalls ergab, dass $18\,\%$ dieser Fichten von Borkenkäfern befallen sind. lnsgesamt sind $14\,\%$ der Bäume in diesem Mischwald von Borkenkäfern befallen.

Ein zufällig und unabhängig von der Baumart ausgewählter Baum ist nicht von Borkenkäfern befallen. Berechne die Wahrscheinlichkeit, dass dieser Baum keine Fichte ist.

Erreichbare BE-Anzahl: 05

1.9

Aufgrund des Borkenkäferbefalls sollen Laubbäume gepflanzt werden. Jeder gepflanzte Laubbaum wächst mit einer Wahrscheinlichkeit von $40\,\%$ an. Ermittle, wie viele Laubbäume mindestens gepflanzt werden müssen, damit mit einer Wahrscheinlichkeit von mindestens $98\,\%$ mindestens $200$ Laubbäume anwachsen.

Erreichbare BE-Anzahl: 03

1.1

Wachstumsrate nach 2 Jahren

$w(2)= 60 \cdot \mathrm e^{\frac{-(2-40)^2}{3000}} \approx 37,1\,\frac{\text{cm}}{\text{Jahr}}$

2 Jahre nach der Pflanzung beträgt die Wachstumsrate ca. $37,1\,\frac{\text{cm}}{\text{Jahr}}.$

Zeitpunkt mit der größten Wachstumsrate

Gesucht wird das Maximum der Funktion im Bereich $0 \leq t \leq 160.$ Die Ableitung von $w$ lautet:

$\(\begin{array}[t]{rll} w$

Mit der notwendigen Bedingung für Extremstellen folgt:

$\(\begin{array}[t]{rll} w$

Da die $\mathrm e$ -Funktion auf $\mathbb{R}$ nie den Wert $0$ annimmt, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rll} \dfrac{t - 40}{25}&=& 0&\quad \scriptsize \mid\; \cdot 25 \\[5pt] t - 40&=& 0& \quad \scriptsize \mid\; +40 \\[5pt] t& =& 40 \end{array}$

$t=40$ ist also die einzige mögliche Extremstelle und gemäß der gegebenen Abbildung auch ein Maximum. Nun müssen noch die Intervallränder überprüft werden:

$w(0) = 60\cdot \mathrm e^{-\frac{(0-40)^2}{3000}} \approx 35,2$

$w(40) = 60\cdot \mathrm e^{-\frac{(40-40)^2}{3000}} = 60$

$w(160) = 60\cdot \mathrm e^{-\frac{(160-40)^2}{3000}} \approx 0,5$

40 Jahre nach der Pflanzung ist die Wachstumsrate also am größten und beträgt zu diesem Zeitpunkt $60$ Zentimeter pro Jahr.

1.2

Zeitraum mit angegebener Wachstumsrate

Gesucht sind die Werte von $t,$ für die $w(t) \gt 47$ gilt. Dies lässt sich mit dem GTR lösen:

$12,93 \lt t \lt 67,07$

Im Zeitraum ab 13 Jahre nach Pflanzung bis 67 Jahre nach Pflanzung ist die Wachstumsrate größer als $47$ Zentimeter pro Jahr.

Begründung der Aussage

Der Exponent der Exponentialfunktion $w$ ist $-\frac{(t-40)^2}{3000}.$ Dieser Term beschreibt eine nach unten geöffnete Parabel mit dem Scheitelpunkt $(40\mid 0).$ Diese Parabel verläuft achsensymmetrisch zur Geraden zu $t=40.$
Für alle beliebigen zwei Zeitpunkte $t_1$ und $t_2$ mit $0 \leq t_1, t_2 \leq 80,$ die den gleichen zeitlichen Abstand zum Zeitpunkt der größten Wachstumsrate $(t=40)$ haben, ist also der Exponent der Exponentialfunktion identisch und damit auch der Funktionswert von $w.$ Die Wachstumsrate ist also für solche Zeitpunkte gleich.

1.3

Der Term gibt die Höhe der Fichten in Metern, 60 Jahre nach der Pflanzung an.

50 ist die Höhe der Fichten zum Zeitpunkt der Pflanzung in Zentimetern. Der Wert des Integrals gibt den Zuwachs der Höhe innerhalb der ersten 60 Jahre nach der Pflanzung in Zentimetern an. Der Faktor $\dfrac{1}{100}$ führt zu einem Wert in Metern.

Die Funktion für die Höhe der Fichte ist gerade ein Integral von $w.$ Da die Fichte bei $c=50 \; [\text{cm}]$ startet folgt der Graph der Funktion:

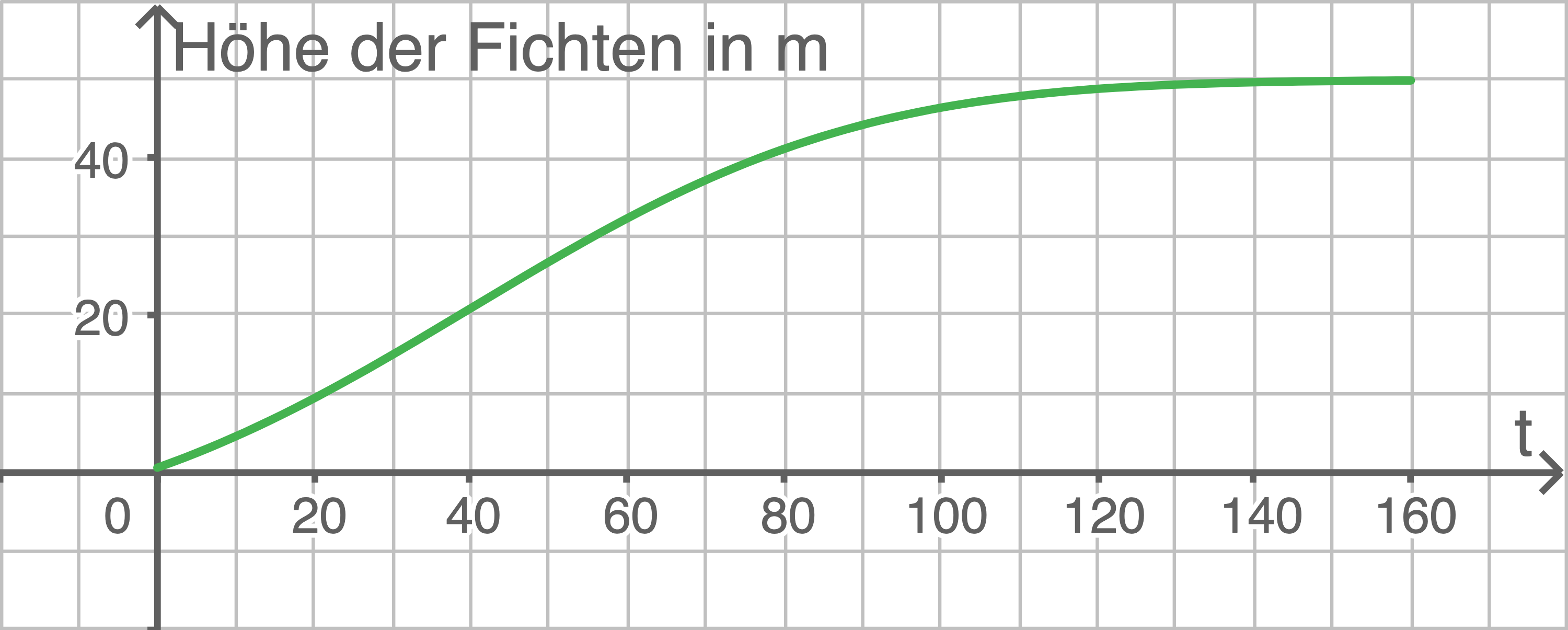Dabei kann das Integral durch folgendem Befehl mit dem GTR berechnet werden:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

1.4

Der Term $\dfrac{w(0)+w(40)}{2}$ beschreibt gerade den Mittelwert zwischen den Funktionswerten $w(0)$ und $w(40).$ Im Kontext ist das die mittlere Wachstumsrate der Fichten in den ersten $40$ Jahren.
Da in diesem Zeitraum der Wachstum der Pflanzen nahezu linear verläuft, ergibt die Mulitplikation mit der Anzahl der Jahre $(40)$ also eine gute Näherung für den Höhenzuwachs der Fichten in den ersten 40 Jahren. Mit der Addition der ursprünglichen Höhe $(50)$ folgt eine Näherung für die Höhe der Fichten nach $40$ Jahren.
Insgesamt ist der Term nicht zur genauen Berechnung der Fichtenhöhe nach 40 Jahren geeignet, liefert aber eine angemessene Näherung, die im Anwendungsfall genügen könnte.

1.5

Mit Hilfe des GTR lässt sich die zweite Ableitungen von $h$ berechnen:

$\( h$
Anschließend lässt sich mit folgendem Befehl die notwendige Bedingung für Wendestellen bestimmen:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 2: zero

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F1: ROOT

$\(\begin{array}[t]{rll} h$

Da dies die einzige Lösung ist, muss es sich dabei um die Wendestelle von $h$ handeln.
Die zugehörige $y$ -Koordinate ergibt sich ebenfalls mit dem GTR:

$h(46) \approx 25$

Die Koordinaten des Wendepunkts des Graphen von $h$ lauten also $W(46\mid 25).$

Der Wendepunkt ist der Punkt des Graphen von $h$ mit der größten Steigung. Zu diesem Zeitpunkt wachsen die Fichten also am schnellsten.

1.6

1. Schritt: Tangentengleichung aufstellen

Mit Aufgabe 1.5 folgt: $P(46 \mid h(46)) = P(46 \mid 25)$

Die Tangente $k$ hat die allgemeine Gleichung $k(t)= m \cdot t +b$ .
Die Steigung lässt sich mit dem GTR bestimmen: $\(m=h$

Durch Eisetzen von $P$ in $k(t)$ folgt:

$\begin{array}[t]{rll} 25&=&1,25 \cdot 46 +b \\[5pt] 25&=& 57,5 +b&\quad \scriptsize \mid -57,5 \\[5pt] -32,5&=&b \\[5pt] \end{array}$

Das ergibt die Tangentengleichung:
$k(t)= 1,25 \cdot t -32,5$

2. Schritt: Maximale Abweichung bestimmen

Die prozentuale Abweichung der Funktionswerte von $h$ und $k$ im Verhältnis zu $h$ kann durch die folgende Funktion $d$ beschrieben werden:

$d(t)= \dfrac{h(t) - k(t)}{h(t)}$

Mit dem GTR lassen sich mögliche Maxima und Minima von $d(t)$ bestimmen.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 3: minimum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F3: MIN

Dies ergibt keine Extrempunkte. Durch Überprüfen der Intervallränder folgt:

$\begin{array}[t]{rll} d(40)&\approx& 0,01\\[5pt] d(50)&\approx& -0,002\\[5pt] \end{array}$

An der Stelle $t=50$ weicht der Funktionswert von $k$ von dem von $h$ um etwa $0,2\,\%$ nach unten ab. An der Stelle $t=40$ weicht der Funktionswert von $k$ von dem von $h$ um etwa $1\,\%$ nach oben ab.
Die größte prozentuale Abweichung beträgt also ca. $1\,\%.$

1.7

Term angeben

Der Flächeninhalt einer Fläche, die vom Graphen der Dichtefunktion einer Normalverteilung mit dem Erwartungswert $\mu$ und der Standardabweichung $\sigma$ mit der x-Achse im Bereich $(-\infty;a]$ eingeschlossen wird, lässt sich mit Hilfe der Verteilungsfunktion $\Phi$ der Standardnormalverteilung berechnen: $\Phi(\frac{a-\mu}{\sigma}).$ Aus der Abbildung ist $a=\mu +k$ zu entnehmen, gesucht ist allerdings der Flächeninhalt im Bereich $[\mu +k; \infty).$

Da es sich bei $\varphi$ um die Dichtefunktion einer Wahrscheinlichkeitsverteilung handelt, beträgt der Gesamtflächeninhalt, den der Graph von $\varphi$ mit der $x$ -Achse einschließt, $1.$
Der Flächeninhalt der grauen Fläche lässt sich also wie folgt berechnen:

$1-\Phi\left(\frac{\mu+k-\mu}{\sigma}\right) = 1- \Phi\left(\frac{k}{\sigma}\right)$

Wert von $k$ bestimmen

Gleichsetzen des Terms von oben mit dem angegebenen Wert ergibt:

$\begin{array}[t]{rll} 1- \Phi\left(\frac{k}{\sigma}\right) &=& 0,15 & \scriptsize \mid\;-1 \quad \mid\;\cdot (-1) \\[5pt] \Phi\left(\frac{k}{\sigma}\right) &=& 0,85 \end{array}$

Die Gleichung lässt sich entweder mit Hilfe der inversen Normalverteilung des Taschenrechners oder mit Hilfe einer Tabelle zu Standardnormalverteilung lösen. Mit Hilfe der Standardnormalverteilung folgt:

$\Phi(1,04)\approx 0,85 .$

Also gilt:

$\begin{array}[t]{rll} \frac{k}{\sigma} &\approx& 1,04 &\quad \scriptsize \mid\; \sigma = 3\,\text{cm}\\[5pt] \frac{k}{3\,\text{cm}} &\approx & 1,04 &\quad \scriptsize \mid\;\cdot 3\,\text{cm} \\[5pt] k &\approx& 3,12\,\text{cm} \end{array}$

1.8

Folgendes Baumdiagramm dient zur Übersicht. Hierbei steht $F$ für Fichte und $B$ für befallen.

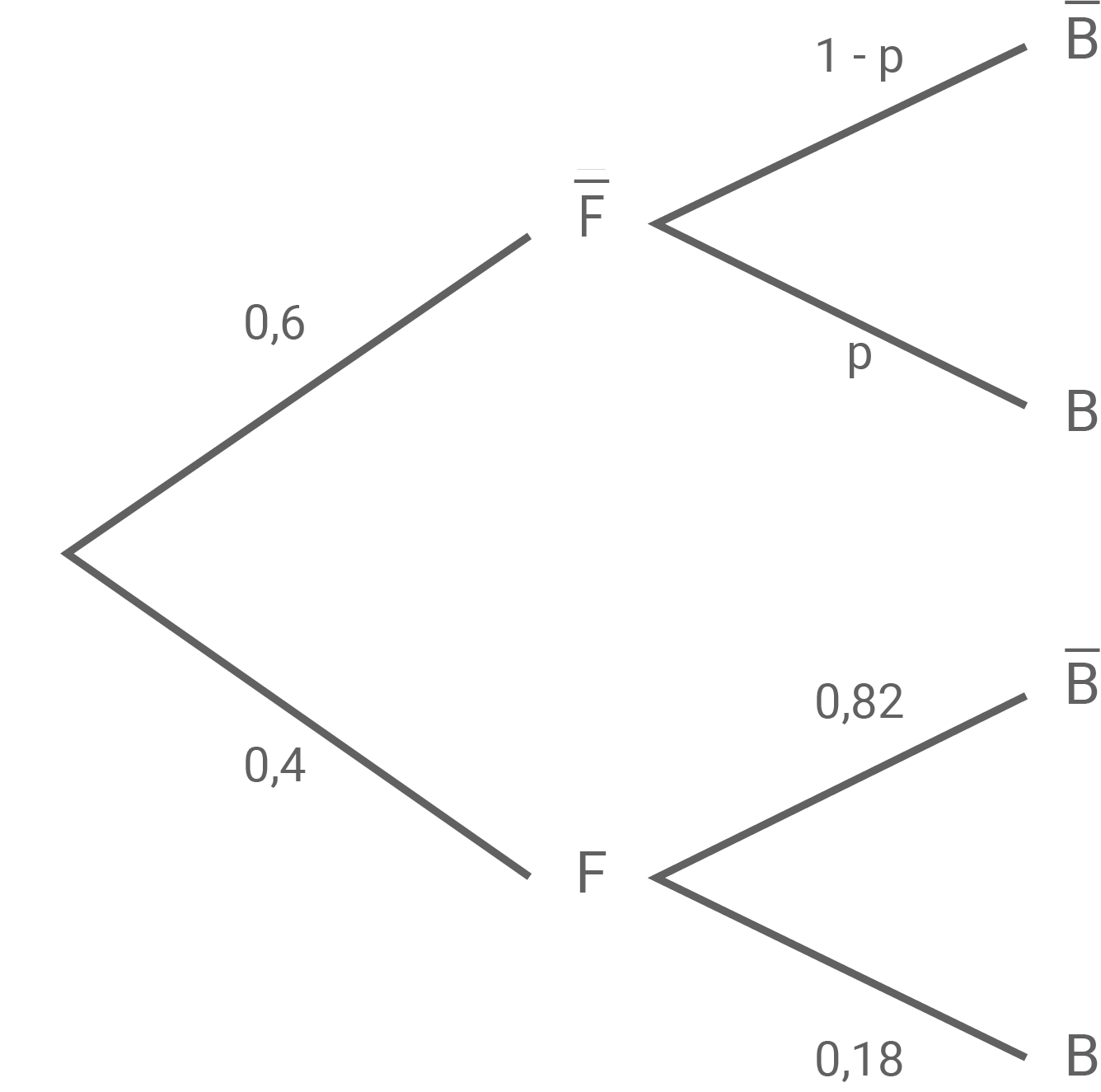Es gilt:

$P(\overline{B}) = 1- P(B) = 1-0,14 = 0,86$

$P(\overline{F}) = 0,6$

Dann folgt:

$\begin{array}[t]{rll} P(B)&=& 0,14&\quad \scriptsize \\[5pt] 0,4 \cdot 0,18 + 0,6 \cdot p&=& 0,14 \quad \scriptsize \mid \; -0,072 \\[5pt] 0,6 \cdot p & = & 0,068 \quad \scriptsize \mid \; :0,6 \\[5pt] p& \approx & 0,1133 \end{array}$

Mit dem Satz von Bayes gilt:

$P_{\overline{B}}(\overline{F}) = \dfrac{P(\overline{B} \cap \overline{F})}{P(\overline{B})}$ $= \dfrac{0,6 \cdot (1-0,1133)}{0,86}$ $= 0.6181$

Mit einer Wahrscheinlichkeit von ca. 61,86 % handelt es sich bei einem zufällig ausgewählten Baum, der nicht befallen ist, nicht um eine Fichte.

1.9

Die Zufallsgröße $X,$ die die zufällige Anzahl der Laubbäume, die anwachsen, unter $n$ eingepflanzten Laubbäumen beschreibt kann als binomialverteilt mit $p=0,4$ und unbekanntem $n$ angenommen werden. Gesucht ist die kleinste Anzahl $n,$ sodass $P(X\geq 200)\geq 0,98$ gilt.

Durch strategisches Ausprobieren on $n$ folgt:

$n = 558: \; P(X \leq 199) \approx 0,0198$

$n = 557: \; P(X \leq 199) \approx 0,0214$

Also muss $n \geq 558$ gelten. Es müssen mindestens $558$ Laubbäume geplanzt werden, damit darunter mit einer Wahrscheinlichkeit von mindestens 98 % mindestens 200 Laubbäume anwachsen.