Teil B2

Die Abbildung zeigt einen von ebenen Flächen begrenzten Glaskörper, der für optische Experimente verwendet wird. In diesen Glaskörper mit $ABCDEF$ mit $A(0\mid 0\mid0),$ $B(4,5\mid0\mid0),$ $D(0\mid0\mid12),$ $E(4,5\mid0\mid9)$ und $F(0\mid6\mid10,5)$ wird ein kartesisches Koordinatensystem (1 Längeneinheit enspricht 1 Zentimeter) gelegt.
Die Grundfläche $ABC$ liegt in der $x$ - $y$ -Ebene, die Seitenflächen $ABED,$ $BCFE$ und $ACFD$ stehen dazu senkrecht. Die Punkte $G$ und $H$ liegen auf den Kanten $\overline{AD}$ bzw. $\overline{CF}$ und haben die gleiche $z$ -Koordinate wie $E.$

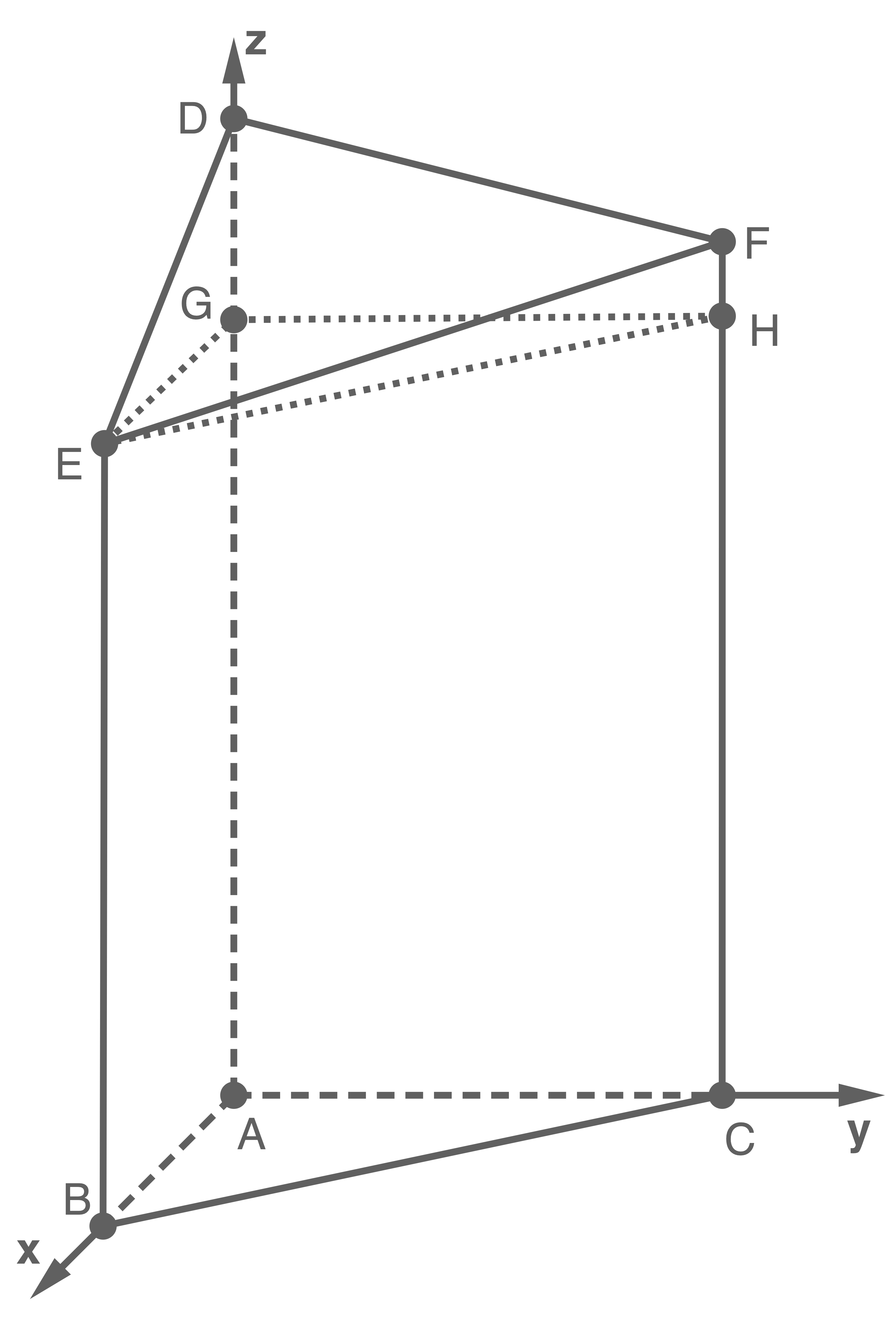
3D-Darstellung eines geometrischen Körpers mit Punkten und Linien in einem Koordinatensystem.

Abbildung (nicht maßstäblich)

2.1

Begründe, dass das Viereck $DGHF$ ein Trapez ist.
Berechne das Volumen des Teilkörpers $DGHFE.$

Erreichbare BE-Anzahl: 05

2.2

Die Punkte $G,$ $E$ und $H$ liegen in der Ebene $\epsilon.$ Durch die Punkte $E$ und $D$ verläuft eine Gerade, die $\epsilon$ im Winkel $\alpha$ schneidet. Durch die Punkte $F$ und $D$ verläuft eine weitere Gerade, die $\epsilon$ im Winkel $\beta$ schneidet. Zeige, dass gilt: $\dfrac{\tan \alpha}{\tan \beta}=\dfrac{8}{3}.$

Erreichbare BE-Anzahl: 04

2.3

Der Punkt $M(m_1\mid m_2\mid 0)$ hat von allen Seiten des Dreiecks $ABC$ den gleichen Abstand.
Begründe, dass $m_1=m_2$ gilt.
Die Schritte I bis IV liefern gemeinsam die Koordinaten von $M$ :

$g:\overrightarrow{x_g}=s\cdot\pmatrix{1\\1\\0}$ $(s\in\mathbb{R})$

II:

Gleichung anzeigen

$h: \overrightarrow{x_h}=$

III:

$\overrightarrow{x_g}=\overrightarrow{x_h} \Rightarrow s=\dfrac{3}{2}; t=\dfrac{15}{8}$

IV:

$\overrightarrow{OM}=\dfrac{3}{2}\cdot\pmatrix{1\\1\\0}\Rightarrow M(1,5\mid1,5\mid0)$

Beschreibe die Bedeutung der Schritte I bis IV zur Bestimmung der Koordinaten von $M.$

Ereichbare BE-Anzahl: 06

Bei den optischen Experimenten können mithilfe von Laserstrahlen ebene Flächen und Linien in den Glaskörper graviert werden. Eine Laserquelle ist so installiert, dass die Laserstrahlen dieser Laserquelle für bestimmte reelle Werte $a$ im Inneren des Glaskörpers in der Ebene

$W_a:\overrightarrow{x}=\pmatrix{4,5\\0\\0}+r\cdot\pmatrix{-1,5\\2\\a}+s\cdot\pmatrix{0\\-1\\2}$ $(r,s\in\mathbb{R})$ verlaufen.

2.4

Für $a=0$ schneiden die Laserstrahlen der Ebene $W_0$ die Strecke $\overline{GH}$ des Glaskörpers.
Berechne in welchem Verhältnis der Schnittpunkt diese Strecke teilt.

Erreichbare BE-Anzahl: 04

2.5

Bestimme den Wert von $a$ so, dass die Ebene $W_a$ parallel zur Kante $\overline{EF}$ verläuft.

Errreichbare BE-Anzahl: 05

2.6

Betrachtet wird eine Schar von Laserstrahlen, die auf den Geraden

$g_b: \overrightarrow{x}= \pmatrix{1,5\\1,5\\0}+ t \cdot \pmatrix{-1,5\\2-2\cdot b\\4\cdot b}$ mit $t\in\mathbb{R}$ und $b\in\mathbb{R}$ liegen. Diese Laserstrahlen treffen im Punkt $M$ auf die Grundfläche $ABC$ .
Ermittle die Werte von $b$ so, dass die Laserstrahlen die Grundfläche $ABC$ in einem Winkel von $30^{\circ}$ treffen.

Erreichbare BE-Anzahl: 04

2.7

Die optischen Experimente werden in einem „Science Center“ durchgeführt. Für den Besuch im „Science Center“ gibt es Dauerkarten für Erwachsene und Dauerkarten für andere Besucher. $40\,\%$ aller Besucher des „Science Centers“ besitzen eine Dauerkarte. $23\,\%$ der Besucher, die eine Dauerkarte besitzen, sind Erwachsene. $38\,\%$ aller Besucher des „Science Centers“ sind Erwachsene.
Ein Besucher des „Science Centers“ wird zufällig ausgewählt und besitzt keine Dauerkarte.
Ermittle die Wahrscheinlichkeit dafür, dass dieser Besucher ein Erwachsener ist.
Ein Besucher des „Science Centers“ wird zufällig ausgewählt und ist kein Erwachsener.
Ermittle die Wahrscheinlichkeit dafür, dass dieser Besucher keine Dauerkarte besitzt.

Erreichbare BE-Anzahl: 06

2.8

Der Zeitpunkt, zu dem ein zufällig ausgewählter Besucher das „Science Center“ an einem beliebigen Tag betritt, kann mithilfe einer normalverteilten Zufallsgröße $t$ beschrieben werden. Dabei ist $t$ die seit 00:00 Uhr vergangene Zeit in Stunden. Die Zufallsgröße $t$ besitzt den Erwartungswert $14,5$ und die Standardabweichung $2,0$ (jeweils in Stunden).
Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Besucher zwischen 12:00 Uhr und 16:00 Uhr das „Science Center“ betritt.
An einem bestimmten Tag wird das „Science Center“ von $2500$ Besuchern betreten.
Ermittle näherungsweise die Uhrzeit, zu der mit dem Eintritt des eintausendfünfhundertsten Besuchers an diesem Tag zu rechnen ist.

Erreichbare BE-Anzahl: 06

Verteilungsfunktion der Standardnormalverteilung

$\phi(z)=\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{z}\mathbb{e}^{-\dfrac{1}{2}t^2}dt$

$\phi(-z)=1-\phi(z)$

Grafik eines Kurvenverlaufs mit gekennzeichneten Achsen und einem schattierten Bereich.

	B	C	D	E	F	G	H	I	J	K	L
2
3	z	0	1	2	3	4	5	6	7	8	9
4	0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
5	0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
6	0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
7	0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
8	0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
9	0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
10	0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
11	0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
12	0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
13	0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
14	1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
15	1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
16	1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
17	1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
18	1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
19	1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
20	1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
21	1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
22	1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
23	1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
24	2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
25	2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
26	2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
27	2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
28	2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
29	2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
30	2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
31	2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
32	2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
33	2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
34	3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
35	3,1	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
36	3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995
37	3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997
38	3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998
39	3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
40	3,6	0,9998	0,9998	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
41	3,7	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
42	3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
43	3,9	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

2.1

Trapezform begründen

$H$ hat die gleiche $z$ -Koordinate wie $E$ und liegt auf der Kante $\overline{CF},$ also gilt $H(0\mid 6\mid 9).$ Damit folgt:

$\overrightarrow{HF}=\pmatrix{0-0\\6-6\\10,5-9}=\pmatrix{0\\0\\1,5}$

$G$ hat auch die gleiche $z$ -Koordinate wie $E$ und liegt auf der Kante $\overline{AD},$ also gilt $G(0\mid 0\mid 9).$ Damit gilt:

$\overrightarrow{GD}=\pmatrix{0-0\\0-0\\12-9}=\pmatrix{0\\0\\3}$

Es gilt also $2\cdot \overrightarrow{HF}=\overrightarrow{GD},$ also sind die Kanten $\overline{HF}$ und $\overline{GD}$ parallel.

Damit hat das Viereck $DGHF$ ein Paar gegenüberliegender Seiten, die parallel zueinander sind, und ist somit ein Trapez.

Volumen des Teilkörpers berechnen

Bei dem Teilkörper $DGHFE$ handelt es sich um eine Pyramide mit der Grundfläche $DGHF$ und der Spitze $E.$

1. Schritt: Größe der Grundfläche berechnen

Da die beiden Punkte $G$ und $D$ auf der $z$ -Achse liegen und $G$ und $H$ die gleichen $x$ - und $z-$ Koordinaten haben, besitzt das Trapez bei $G$ einen rechten Winkel. Die Länge der Strecke $\overline{GH}$ ist also die Höhe des Trapezes. Außerdem gilt:

$\begin{array}[t]{rll} \overline{GD}&=& \left|\overrightarrow{GD} \right| \\[5pt] &=& \left|\pmatrix{0\\0\\3} \right| \\[5pt] &=& \sqrt{0^2+0^2 +3^2} \\[5pt] &=& 3 \\[10pt] \overline{HF}&=& \left|\overrightarrow{HF} \right| \\[5pt] &=& \left|\pmatrix{0\\0\\1,5} \right| \\[5pt] &=& \sqrt{0^2+0^2 +1,5^2} \\[5pt] &=& 1,5 \\[10pt] \overline{GH}&=& \left|\overrightarrow{GH} \right| \\[5pt] &=& \left|\pmatrix{0\\6\\0} \right| \\[5pt] &=& \sqrt{0^2+6^2 +0^2} \\[5pt] &=& 6 \\[10pt] \end{array}$

Mit der Formel für den Flächeninhalt eines Trapezes folgt:

$\begin{array}[t]{rll} G &=& \dfrac{1}{2}\cdot \left( \overline{HF}+ \overline{GD}\right)\cdot \overline{GH} \\[5pt] &=& \dfrac{1}{2}\cdot \left( 1,5 + 3\right)\cdot 6 \\[5pt] &=& 13,5\,[\text{cm}^2]\\[5pt] \end{array}$

2. Schritt: Höhe bestimmen

$D,$ $G,$ $H$ und $F$ besitzen alle die gleiche $x$ -Koordinate Null. Die Grundfläche liegt daher vollständig in der $yz$ -Ebene. Die Höhe der Pyramide ist der Abstand der Spitze $E$ zur Grundfläche und ergibt sich daher aus der $x$ -Koordinate von $E.$
Die Höhe der Pyramide ist also $h = 4,5\,\text{cm}.$

3. Schritt: Volumen berechnen

Mithilfe der Formel für das Volumen einer Pyramide ergibt sich nun:

$\begin{array}[t]{rll} V &=& \dfrac{1}{3} \cdot G \cdot h \\[5pt] &=& \dfrac{1}{3} \cdot 13,5\,\text{cm}^2\cdot 4,5\,\text{cm} \\[5pt] &=& 20,25\,\text{cm}^3 \\[5pt] \end{array}$

Das Volumen des Teilkörpers $DGHFE$ beträgt $20,25\,\text{cm}^3 .$

2.2

Die Punkte $E,$ $G$ und $H$ haben alle die gleiche $z$ -Koordinate $9$ und liegen daher in der Ebene $\epsilon$ mit der Gleichung $z=9.$ Ein Normalenvektor von $\epsilon$ ist daher $\overrightarrow{n}_{\epsilon} = \pmatrix{0\\0\\1}.$

1. Schritt: Schnittwinkel $\alpha$ bestimmen

Ein Richtungsvektor der Geraden durch $E$ und $D$ ist $\overrightarrow{ED} = \pmatrix{-4,5\\0\\3}.$ Für $\alpha$ gilt aufgrund der Formel für den Schnittwinkel einer Gerade und einer Ebene:

$\begin{array}[t]{rll} \sin \alpha &=& \dfrac{\left|\overrightarrow{n}_{\epsilon} \circ \overrightarrow{ED} \right|}{\left|\overrightarrow{n}_{\epsilon}\right|\cdot \left|\overrightarrow{ED} \right| } \\[5pt] \sin \alpha &=& \dfrac{\left|\pmatrix{0\\0\\1}\circ \pmatrix{-4,5\\0\\3} \right|}{\left|\pmatrix{0\\0\\1}\right|\cdot \left|\pmatrix{-4,5\\0\\3} \right| } \\[5pt] \sin \alpha &=& \dfrac{3}{\sqrt{29,25} } \quad \scriptsize \mid \; \sin^{-1} \\[5pt] \alpha &=& \sin^{-1}\dfrac{3}{\sqrt{29,25} } \quad \scriptsize \mid \; \tan \\[5pt] \tan \alpha &=& \tan \sin^{-1}\dfrac{3}{\sqrt{29,25} } \\[5pt] \end{array}$

2. Schritt: Schnittwinkel $\beta$ bestimmen

Ein Richtungsvektor der Geraden durch $F$ und $D$ ist $\overrightarrow{FD} = \pmatrix{0\\-6\\1,5}.$ Für $\beta$ gilt aufgrund der Formel für den Schnittwinkel einer Gerade und einer Ebene:

$\begin{array}[t]{rll} \sin \beta &=& \dfrac{\left|\overrightarrow{n}_{\epsilon} \circ \overrightarrow{FD} \right|}{\left|\overrightarrow{n}_{\epsilon}\right|\cdot \left|\overrightarrow{FD} \right| } \\[5pt] \sin \beta &=& \dfrac{\left|\pmatrix{0\\0\\1}\circ \pmatrix{0\\-6\\1,5} \right|}{\left|\pmatrix{0\\0\\1}\right|\cdot \left|\pmatrix{0\\-6\\1,5} \right| } \\[5pt] \sin \beta &=& \dfrac{1,5}{\sqrt{38,25} } \quad \scriptsize \mid \; \sin^{-1} \\[5pt] \beta &=& \sin^{-1}\dfrac{1,5}{\sqrt{38,25} } \quad \scriptsize \mid \; \tan \\[5pt] \tan \beta &=& \tan \sin^{-1}\dfrac{1,5}{\sqrt{38,25} } \\[5pt] \end{array}$

3. Schritt: Quotient berechnen

$\begin{array}[t]{rll} \dfrac{\tan \alpha}{\tan \beta} &=& \dfrac{\tan \sin^{-1}\dfrac{3}{\sqrt{29,25} }}{\tan \sin^{-1}\dfrac{1,5}{\sqrt{38,25}}} \\[5pt] &=& \dfrac{8}{3} \\[5pt] \end{array}$

2.3

Gleiche Koordinaten begründen

Der Punkt $C$ hat die gleichen $x$ - und $y$ -Koordinaten wie $F$ und liegt in der $xy$ -Ebene. Er hat also die Koordinaten $C(0\mid 6\mid 0).$

Der Punkt $B$ liegt auf der $x$ -Achse, der Punkt $C$ liegt auf der $y$ -Achse, $A$ ist der Koordinatenursprung. Daher liegt die Strecke $\overline{AB}$ auf der $x$ -Achse, die Strecke $\overline{AC}$ liegt auf der $y$ -Achse.
Der Punkt $M$ muss innerhalb des Dreiecks $ABC$ liegen. Damit er innerhalb des Dreiecks liegt und von $\overline{AB}$ und $\overline{AC}$ den gleichen Abstand hat, muss er auf der Winkelhalbierenden des Winkels bei $A$ liegen. Bei allen Punkten auf dieser Winkelhalbierenden sind die $x$ - und die $y$ -Koordinate identisch, da $\overline{AB}$ auf der $x$ -Achse und $\overline{AC}$ auf der $y$ -Achse liegt.

Bedeutung der Schritte beschreiben

$\text{I}$

$g: \, \overrightarrow{x_g} = s\cdot \pmatrix{1\\1\\0}$ beschreibt die Winkelhalbierende des Winkels, der im Dreieck $ABC$ bei $A$ liegt.

$\text{II}$

Gleichung anzeigen

$h: \, \overrightarrow{x_h} = \, ...$

beschreibt die Winkelhalbierende des Winkels, der im Dreieck $ABC$ bei $B$ liegt.

$\text{III}$

Der Punkt $M$ ist der Mittelpunkt des Dreiecks $ABC.$ Dieser ist der Schnittpunkt der drei Winkelhalbierenden des Dreiecks. Die beiden Geradendarstellungen von $g$ und $h$ werden hier also nun gleichgesetzt und das darausentstehende Gleichungssystem nach den beiden Geradenparametern $s$ und $t$ gelöst.

$\text{IV}$

Der Parameterwert, der im dritten Schritt für $s$ berechnet wurde, wird nun in die Geradengleichung von $g$ eingesetzt, um die Koordinaten des Schnittpunkts von $g$ und $h$ zu bestimmen. Dieser Schnittpunkt ist dann der Schnittpunkt der beiden Winkelhalbierenden und damit der Mittelpunkt $M$ des Dreiecks $ABC.$ Er hat von allen drei Dreiecksseiten den gleichen Abstand.

2.4

Streckenverhältnis berechnen

1. Schritt: Geradengleichung zur Strecke aufstellen

Die Strecke $\overline{GH}$ liegt auf der Geraden mit der Gleichung:

$\begin{array}[t]{rll} GH: \, \overrightarrow{x} &=& \overrightarrow{OG} + u\cdot \overrightarrow{GH} \\[5pt] &=& \pmatrix{0\\0\\9} + u\cdot\pmatrix{0\\6\\0} \end{array}$

2. Schritt: Schnittpunkt bestimmen

Gleichsetzen von Geradengleichung und Ebenengleichung liefert:

Rechenweg anzeigen

$\pmatrix{-4,5\\0\\9}=\, ...$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& -4,5 &=& -1,5r \\ \text{II}\quad& 0 &=& 2r-s-6u \\ \text{III}\quad& 9 &=& 2s \\ \end{array}$

Aus der ersten Gleichung ergibt sich:

$\begin{array}[t]{rll} -4,5 &=& -1,5r &\quad \scriptsize \mid\; :(-1,5) \\[5pt] 3 &=& r \end{array}$

Aus der dritten Gleichung folgt:

$\begin{array}[t]{rll} 9 &=& 2s &\quad \scriptsize \mid\; :2 \\[5pt] 4,5 &=& s \end{array}$

Diese beiden Ergebnisse können nun in die zweite Gleichung eingesetzt werden:

$\begin{array}[t]{rll} 0 &=& 2r-s-6u \quad \scriptsize \mid\; r = 3; s = 4,5\\[5pt] 0 &=& 2\cdot 3 -4,5 -6u\\[5pt] 0 &=& 1,5 - 6u \quad \scriptsize \mid\;+6u \\[5pt] 6u &=& 1,5 \quad \scriptsize \mid\; :6 \\[5pt] u &=& 0,25 \end{array}$

Einsetzen von $u$ in die Geradengleichung liefert:

$\pmatrix{0\\0\\9} + 0,25\cdot\pmatrix{0\\6\\0} = \pmatrix{0\\1,5\\ 9 }$

Der Schnittpunkt der Laserebene mit der Strecke $\overline{GH}$ des Glaskörpers hat die Koordinaten $S(0\mid 1,5 \mid 9).$

3. Schritt: Längen der Teilstrecken berechnen

Die Längen der Teilstrecken können über die entsprechenden Vektorbeträge berechnet werden:

$\begin{array}[t]{rll} \overline{GS}&=& \left|\overrightarrow{GS} \right| \\[5pt] &=& \left| \pmatrix{0\\1,5\\0} \right| \\[5pt] &=& 1,5 \\[10pt] \overline{SH}&=& \left|\overrightarrow{SH} \right| \\[5pt] &=& \left| \pmatrix{0\\4,5\\0} \right| \\[5pt] &=& 4,5 \\[10pt] \end{array}$

4. Schritt: Teilungsverhältnis berechnen

Die Laserebene teilt die Strecke $\overline{GH}$ des Glaskörpers im Verhältnis $1,5:4,5 = 1:3.$

2.5

Die Ebene $W_a$ verläuft parallel zur Kante $\overline{EF},$ wenn die beiden Spannvektoren und der Vektor $\overrightarrow{EF}$ linear abhängig sind, wenn es also Werte $r$ und $s$ gibt, für die gilt:

$r\cdot \pmatrix{-1,5\\ 2\\a} + s\cdot \pmatrix{0\\-1\\2} = \pmatrix{-4,5\\6\\1,5}$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& -4,5 &= -1,5\cdot r \\ \text{II}\quad& 6 &= 2r -s \\ \text{III}\quad& 1,5 &= a\cdot r +2s \\ \end{array}$

Aus der ersten Gleichung folgt:

$\begin{array}[t]{rll} -4,5 &=& -1,5r \quad \scriptsize \mid\;:(-1,5) \\[5pt] 3 &=& r \end{array}$

Dies kann in die zweite Gleichung eingesetzt werden:

$\begin{array}[t]{rll} 6 &=& 2r -s \quad \scriptsize \mid\;r = 3 \\[5pt] 6 &=& 2\cdot 3 -s \\[5pt] 6 &=& 6 -s \quad \scriptsize \mid\;-6 \\[5pt] 0 &=& -s \quad \scriptsize \mid\;\cdot (-1) \\[5pt] 0 &=& s \end{array}$

Beide Parameter können nun in die dritte Gleichung eingesetzt werden:

$\begin{array}[t]{rll} 1,5 &=& a\cdot r +2\cdot s \quad \scriptsize \mid\; r=3; s = 0 \\[5pt] 1,5 &=& 3a \quad \scriptsize \mid\; :3 \\[5pt] 0,5 &=& a \end{array}$

Die Ebene $W_a$ mit $a=0,5$ verläuft parallel zur Kante $\overline{EF}.$

2.6

Die Grundfläche $ABC$ liegt in der $xy$ -Ebene. Ein Normalenvektor dieser Ebene ist $\overrightarrow{n}_z = \pmatrix{0\\0\\1}.$
Mit der Formel für den Schnittwinkel einer Gerade und einer Ebene ergibt sich folgende Gleichung:

Rechenweg anzeigen

$6,25 -8b - 44b^2 = 0$

Die Gleichung kann mit dem GTR nach $b$ gelöst werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 2: zero

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F1: ROOT

Der Taschenrechner liefert:

$\begin{array}[t]{rll} b_1 &\approx& -0,48 \\[5pt] b_2 &\approx& 0,30 \\[5pt] \end{array}$

Für $b_1 \approx -0,48$ und $b_2 \approx 0,30$ treffen die Laserstrahlen in einem Winkel von ca. $30^{\circ}$ auf die Grundfläche $ABC.$

2.7

Wahrscheinlichkeit für einen Erwachsenen ermitteln

Bekannt sind folgende Wahrscheinlichkeiten:

$P(E) = 0,38$
$P(D) = 0,4$ und daher $P(\overline{D}) = 0,6$
$P_D(E) = 0,23$

Mit den Pfadregeln ergibt sich:

Rechenweg anzeigen

$P_{\overline{D}}(E)=0,48$

$D:$ Ein zufällig ausgewählter Besucher besitzt eine Dauerkarte.
$E:$ Ein zufällig ausgewählter Besucher ist ein Erwachsener.

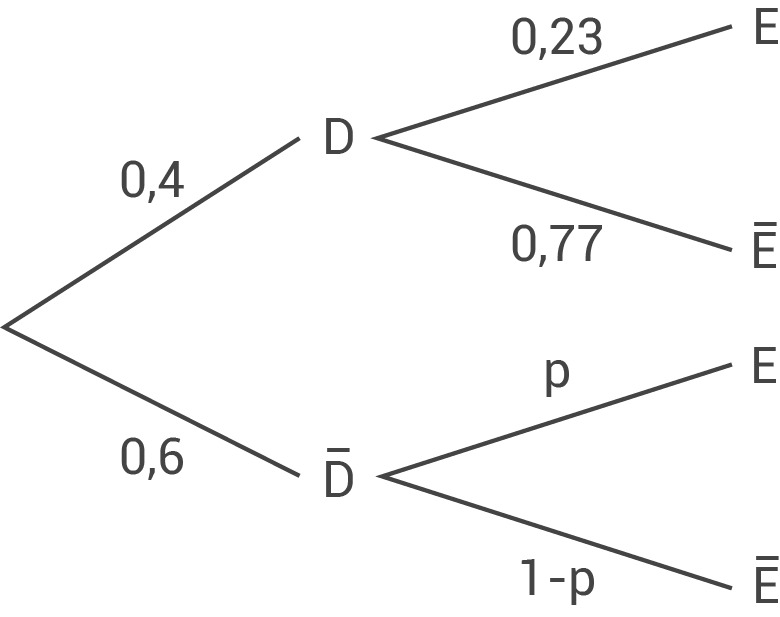baumdiagramm, wahrscheinlichkeiten berechnen, pfadregeln, teil b2

Mit einer Wahrscheinlichkeit von $0,48 = 48\,\%$ ist ein zufällig ausgewählter Besucher ohne Dauerkarte ein Erwachsener.

Wahrscheinlichkeit für keine Dauerkarte ermitteln

Das Baumdiagramm kann mit obiger Rechnung vervollständigt werden.

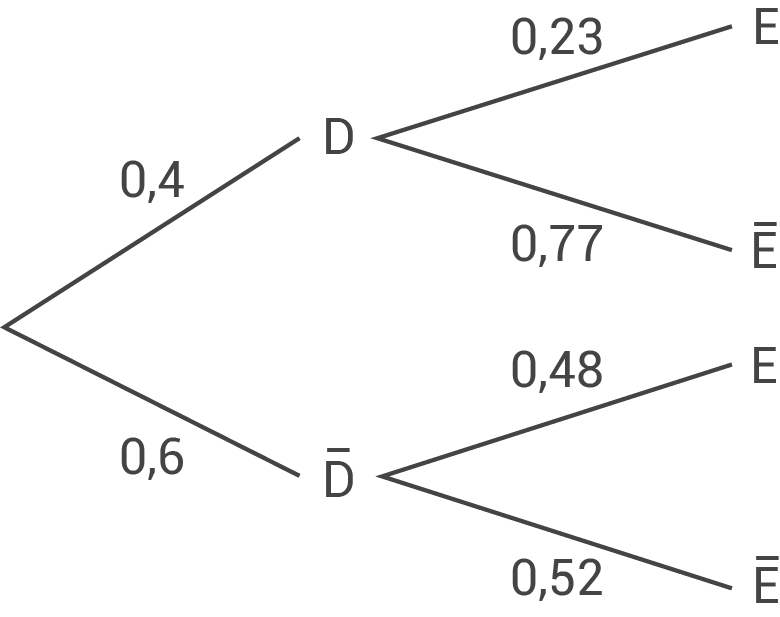baumdiagramm, wahrscheinlichkeiten berechnen, pfadregeln, teil a

Gesucht ist $P_{\overline{E}}(\overline{D}).$ Es kann der Satz von Bayes angewendet werden:

$\begin{array}[t]{rll} P_{\overline{E}}(\overline{D}) &=& \dfrac{P_{\overline{D}}(\overline{E})\cdot P(\overline{D})}{P(\overline{E})} \\[5pt] &=& \dfrac{0,52\cdot 0,6}{1-0,38} \\[5pt] &\approx& 0,5032 \\[5pt] \end{array}$

Mit einer Wahrscheinlichkeit von ca. $0,5032=50,32\,\%$ hat ein zufällig ausgewählter Besucher, der kein Erwachsener ist, keine Dauerkarte.

2.8

Wahrscheinlichkeit berechnen

Die Wahrscheinlichkeiten von $t$ können durch die Standardnormalverteilung angenähert werden. Für $t$ gilt:

$\mu = 14,5$
$\sigma = 2$

Mit der Tabelle aus dem Material folgt:

Rechenweg anzeigen

$P(12\leq t \leq 16) \approx 0,6678$

Mit einer Wahrscheinlichkeit von ca. $0,6678=66,78\,\%$ betritt ein zufällig ausgewählter Besucher das Science Center zwischen 12:00 Uhr und 16:00 Uhr.

Uhrzeit näherungsweise ermitteln

Am gesamten Tag kommen $2500$ Besucher. Für den Zeitpunkt, zu dem der $2500.$ Besucher das Center betritt, besitzt die Zufallsgröße $t$ näherungsweise die Wahrscheinlichkeit $100\,\%.$
Für den Zeitpunkt $x,$ an dem mit dem $1500.$ Besucher zu rechnen ist, nimmt $t$ also die Wahrscheinlichkeit $P(t\leq x) \approx \dfrac{1500}{2500} = 0,6$ an. Gesucht ist also $x$ mit $\Phi\left(\dfrac{x-14,5}{2}\right) \approx 0,6.$

Aus der Tabelle im Material folgt:

$\Phi(0,25)\approx 0,5987$
$\Phi(0,26)\approx 0,6026$

Der Wert für $0,25$ liegt näher an $0,6.$ Es muss also $0,25 = \dfrac{x-14,5}{2}$ gelten:

$\begin{array}[t]{rll} 0,25 &=& \dfrac{x-14,5}{2} &\quad \scriptsize \mid\; \cdot 2\\[5pt] 0,5 &=& x-14,5 &\quad \scriptsize \mid\;+14,5 \\[5pt] 15&=& x \end{array}$

Um ca. 15:00 Uhr kann man also mit dem eintausendfünfhundertsten Besucher rechnen.

Bildnachweise [nach oben]

[1],[2]