Teil A – Wahlbereich

Gegeben ist die Schar der Geraden $g_a$ mit $g_a(x)=-\dfrac{1}{4} \cdot x+a \quad(x \in \mathbb{R} ; \; a \in \mathbb{R}).$

5.1

Begründe, dass alle Geraden der Schar parallel zueinander verlaufen.

(1 BE)

5.2

Untersuche, für welche Werte von $a$ die Geraden der Schar genau einen gemeinsamen Punkt mit dem Graphen der Funktion $h$ mit $h(x)=\dfrac{1}{x} \quad(x \in \mathbb{R}, x \neq 0)\;$ besitzen.

(4 BE)

Betrachtet werden in $\mathbb{R}$ definierte und differenzierbare Funktionen $g,$ die bei $x=1$ ein lokales Minimum haben.

6.1

Gib eine Gleichung einer solchen Funktion $g$ an.

(1 BE)

6.2

Zeige, dass jede in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\mathrm e^{-g(x)}$ bei $x=1$ ein lokales Extremum besitzt und bestimme dessen Art.

(4 BE)

Für jedes $k \in \mathbb{R}$ ist der Punkt $P_k\left(0\mid k+1\mid -k^2+4\right)$ gegeben.

7.1

Bestimme die Koordinaten des Punkts $P_k,$ der auf der $z$ -Achse liegt.

(2 BE)

7.2

Stelle die Menge der Punkte $P_k$ in einem kartesischen Koordinatensystem dar.

(3 BE)

Für jeden reellen Wert von $u$ sind $A_u(u\mid -1\mid 3)$ und $C_u(u\mid 5\mid 3)$ zwei gegenüberliegende Eckpunkte eines Quadrats, welches in der Ebene $E: z=3$ liegt.

8.1

Die Punkte $A_u$ und $C_u$ liegen bezüglich der Ebene $F$ zueinander symmetrisch.

Bestimme eine Gleichung von $F.$

(2 BE)

8.2

Gib die Koordinaten eines weiteren Eckpunkts des Quadrats in Abhängigkeit von $u$ an und begründe deine Angabe.

(3 BE)

Ein Glücksrad hat zwei Sektoren, von denen einer schwarz und einer gelb ist. Bei jeder Drehung des Glücksrads wird der gelbe Sektor mit der Wahrscheinlichkeit $p$ erzielt. Das Glücksrad wird mehrmals gedreht und die Farbe des erzielten Sektors notiert.

9.1

Gib ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $3 \cdot p \cdot(1-p)^2$ berechnet werden kann.

(2 BE)

9.2

Betrachtet wird das Ereignis A: Beim zweimaligen Drehen des Glücksrads wird genau einmal der gelbe Sektor erzielt.

Ermittle denjenigen Wert von $p,$ für den die Wahrscheinlichkeit des Eintretens von A am größten ist.

(3 BE)

Betrachtet werden die binomialverteilten Zufallsgrößen $X$ und $Y.$

10.1

Die Zufallsgröße $X$ hat die Parameter $n$ und $p=\dfrac{1}{5}$ sowie die Standardabweichung 4.

Berechne $n.$

(2 BE)

10.2

Die Zufallsgröße $Y$ hat die Parameter $n=10$ und $p>0.$

Berechne denjenigen Wert $p,$ für den $P(Y=9)=30 \cdot P(Y=10)$ gilt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5.1

Die Geraden der Schar haben alle die gleiche Steigung von $-\dfrac{1}{4}.$ Der Parameter $a$ beeinflusst nur den $y$ -Achsenabschnitt der Geraden, ändert jedoch nichts an der Steigung.

Somit verlaufen alle Geraden der Schar parallel zueinander.

5.2

Für die gemeinsamen Punkte der Schar mit dem Graphen der Funktion $h$ gilt:

$\begin{array}[t]{rll} g_a(x)&=& h(x) &\\[5pt] -\dfrac{1}{4}x+a&=& \dfrac{1}{x} &\quad \scriptsize \mid\; \cdot x \\[5pt] -\dfrac{1}{4}x^2+ax&=& 1 &\quad \scriptsize \mid\; -1 \\[5pt] -\dfrac{1}{4}x^2+ax-1&=& 0 & \quad \scriptsize \mid\;\cdot (-4)\\[5pt] x^2-4ax+4&=& 0 & \\[5pt] \end{array}$

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rll} x_{1;2}&=& -\dfrac{(-4a)}{2} \pm \sqrt{\left(\dfrac{-4a}{2}\right)^2-4} \\[5pt] &=& 2a\pm \sqrt{\dfrac{16a^2}{4}-4} &\\[5pt] &=& 2a\pm \sqrt{4a^2-4} \end{array}$

Die Gleichung hat genau dann nur eine Lösung, wenn gilt:

$\begin{array}[t]{rll} \sqrt{4a^2-4}&=& 0&\quad \scriptsize \mid\; (\,)^2\\[5pt] 4a^2-4&=& 0&\quad \scriptsize \mid\; +4\\[5pt] 4a^2&=& 4&\quad \scriptsize \mid\; :4\\[5pt] a^2&=& 1&\quad \scriptsize \mid\; \sqrt{\,}\\[5pt] a&=& \pm1 \end{array}$

Für die Werte $a=1$ und $a=-1$ haben die Geraden der Schar folglich genau einen gemeinsamen Punkt mit dem Graphen der Funktion.

6.1

Eine Gleichung einer solchen Funktion ist beispielsweise die verschobene Normalparabel $g(x)=(x-1)^2.$

Möglich sind alle Funktionen, für die gilt:

$g^{\prime}(1)=0$ (notwendige Bedingung für ein lokales Extremum)
$g^{\prime \prime}(1)>0$ (hinreichende Bedingung für ein lokales Minimum)

6.2

1. Schritt: Ableitungen bilden

Mit der Ketten- und Produktregel ergibt sich:

$\(f$

$\( f$

Rechenweg anzeigen

2. Schritt: Notwendige Bedingung für Extremstellen prüfen

An der Stelle $x=1$ gilt:

$\(f$

Da $g$ an der Stelle $x=1$ ein lokales Minimum besitzt, gilt $\(g$

Somit folgt:

$\(f$

Damit ist die notwendige Bedingung für ein Extremum erfüllt.

3. Schritt: Hinreichende Bedingung für Extremstellen prüfen

An der Stelle $x=1$ gilt:

$\( f$

Rechenweg anzeigen

Wegen $\mathrm{e}^{-g(1)}\gt 0$ und $\(-g$ folgt: $\(f$

Jede in $\mathbb{R}$ definierte Funktion $f$ besitzt somit bei $x=1$ ein lokales Maximum.

7.1

Punkte, die auf der $z$ -Achse liegen, haben folgende Form: $P(0\mid 0\mid z)$

Da für alle Punkte $P_k$ bereits $x=0$ gegeben ist, muss weiterhin gelten:

$\begin{array}[t]{rll} y&=& 0 & \\[5pt] k+1&=& 0 &\quad \scriptsize \mid\; -1 \\[5pt] k&=& -1 \end{array}$

Die $y$ -Koordinate folgt nun mit $-(-1)^2+4=3.$

Die Koordinaten des Punkts $P_k,$ der auf der $z$ -Achse liegt, ergeben sich somit zu $P_{-1}(0\mid 0\mid 3).$

7.2

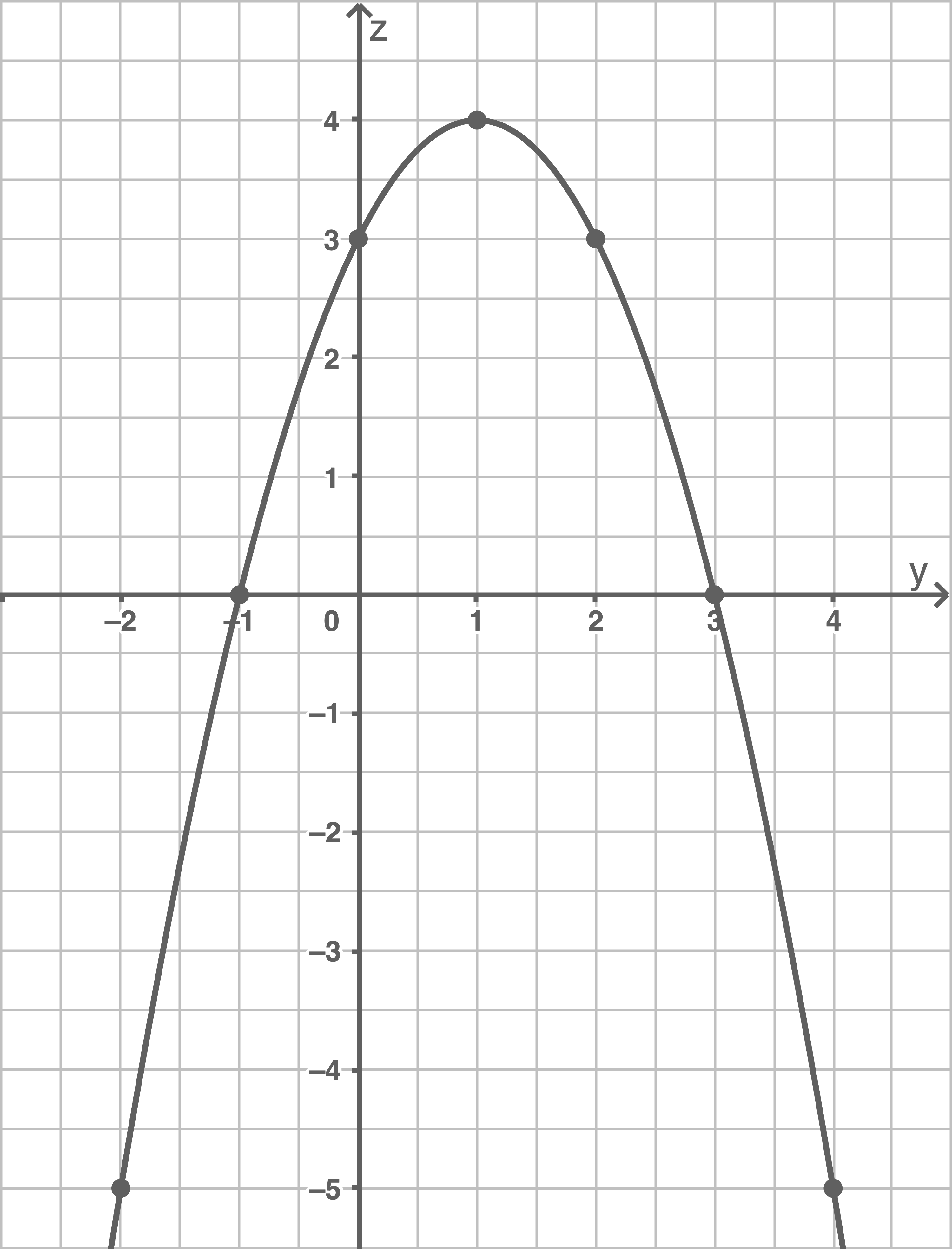
Da die $x$ -Koordinate für alle $k$ Null ist, kann die Menge der Punkte in einem zweidimensionalen kartesischen Koordinatensystem dargestellt werden.

Einsetzen verschiedener Werte für $k$ und Einzeichnen der entsprechenden Punkte liefert:

Sachsen Mathe Abi 2024 Punkte Koordinaten

8.1

1. Schritt: Mittelpunkt $\boldsymbol{M}$ berechnen

$\overrightarrow{OM}=\pmatrix{\dfrac{u+u}{2}\\\dfrac{-1+5}{2}\\\dfrac{3+3}{2}}=\pmatrix{u\\2\\3}$

2. Schritt: Normalenvektor $\boldsymbol{\overrightarrow{n}}$ bestimmen

Da die Ebene $F$ senkrecht zur Strecke $\overline{A_uC_u}$ liegen muss, ergibt sich ein Normalenvektor der Ebene mit:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \overrightarrow{A_uC_u}& \\[5pt] &=& \pmatrix{u-u\\5-(-1)\\3-3}& \\[5pt] &=& \pmatrix{0\\6\\0}&\\[5pt] &=& 6\cdot \pmatrix{0\\1\\0} \end{array}$

3. Schritt: Koordinatengleichung ermitteln

Einsetzen des gekürzten Normalenvektors in die allgemeine Koordinatenform ergibt:

$\begin{array}[t]{rll} F: \quad 0\cdot x+1\cdot y+0\cdot z&=& c &\\[5pt] y&=& c \end{array}$

Da die Ebene durch den Punkt $M$ verläuft und dieser die $y$ -Koordinate $y=2$ besitzt, folgt auch $c=2.$

Eine Gleichung von $F$ ist somit gegeben durch $F: y=2.$

8.2

$A_u(u\mid -1\mid 3)$ und $C_u(u\mid 5\mid 3)$ sind gegenüberliegende Eckpunkte des Quadrats, dessen Diagonalen parallel zur $x$ - bzw. $y$ -Achse verlaufen. Da das Quadrat in der Ebene $z=3$ liegt, müssen außerdem alle Punkte des Quadrats die $z$ -Koordinate 3 besitzen.

Der Mittelpunkt $M$ des Quadrats ist bereits bekannt: $M(u\mid 2\mid 3)$

Die beiden gegebenen Punkte $A_u$ und $C_u$ unterscheiden sich nur in ihrer $y$ -Koordinate und sind jeweils um 3 Längeneinheiten entlang der $y$ -Achse vom Mittelpunkt $M$ aus verschoben.

Die anderen beiden Eckpunkte müssen somit um genau 3 Einheiten vom Punkt $M$ aus entlang der $x$ -Achse verschoben werden und die $y$ -Koordinate $y=2$ sowie die $z$ -Koordinate $z=3$ besitzen.

Die Koordinaten eines weiteren Eckpunkts des Quadrats ergeben sich somit zu $B_u(u-3\mid2\mid3).$

Analog hierzu ergibt sich der vierte Eckpunkt mit $D_u(u+3\mid2\mid3).$

9.1

Beim dreimaligen Drehen des Glücksrads wird genau einmal der gelbe Sektor und zweimal der schwarze Sektor erzielt.

9.2

1. Schritt: Formel aufstellen

Da der gelbe Sektor entweder beim ersten oder beim zweiten Drehen erzielt werden kann, ergibt sich:

$\begin{array}[t]{rll} P(A)&=& 2\cdot p\cdot (1-p)&\\[5pt] &=& 2p-2p^2 \end{array}$

2. Schritt: Ableitungen bestimmen

$\(\begin{array}[t]{rll} f(p)&=& 2p-2p^2 & \\[5pt] f$

3. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Da aus der zweiten Ableitung bereits hervorgeht, dass diese für alle Werte von $p$ negativ ist, gilt, dass die Funktion $f$ und somit die Wahrscheinlichkeit $P(A)$ für $p=\dfrac{1}{2}$ maximal ist.

10.1

Für die Standardabweichung gilt:

$\begin{array}[t]{rll} \sigma(x)&=& \sqrt{n\cdot p\cdot (1-p)}&\\[5pt] 4&=& \sqrt{n\cdot \dfrac{1}{5}\cdot \dfrac{4}{5}} &\quad \scriptsize \mid\; (\,)^2 \\[5pt] 16&=& n\cdot \dfrac{4}{25}&\quad \scriptsize \mid\;\cdot \dfrac{25}{4} \\[5pt] \dfrac{16\cdot 25}{4}&=& n& \\[5pt] 4\cdot 25&=& n& \\[5pt] 100&=& n \end{array}$

10.2

Es gilt:

$\begin{array}[t]{rll} P(Y=9)&=& \pmatrix{10\\9}\cdot p^9\cdot (1-p)^{1}& \\[5pt] &=& 10\cdot p^9\cdot (1-p) \end{array}$

$\begin{array}[t]{rll} P(Y=10)&=& \pmatrix{10\\10}\cdot p^{10}\cdot (1-p)^{0}& \\[5pt] &=& p^{10} \end{array}$

Einsetzen in die Gleichung aus der Aufgabenstellung ergibt nun:

$\begin{array}[t]{rll} P(Y=9)&=& 30\cdot P(Y=10) & \\[5pt] 10\cdot p^9\cdot (1-p)&=& 30\cdot p^{10} \quad \scriptsize \mid\; :10p^9 \\[5pt] 1-p&=& 3p \quad \scriptsize \mid\;+p \\[5pt] 1&=& 4p \quad \scriptsize \mid\; :4\\[5pt] \dfrac{1}{4}&=& p \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?