Teil B2
In einem kartesischen Koordinatensystem mit dem Ursprung  sind die Punkte
sind die Punkte 
 und
und  sowie die Ebene
sowie die Ebene  mit
mit  gegeben.
gegeben.
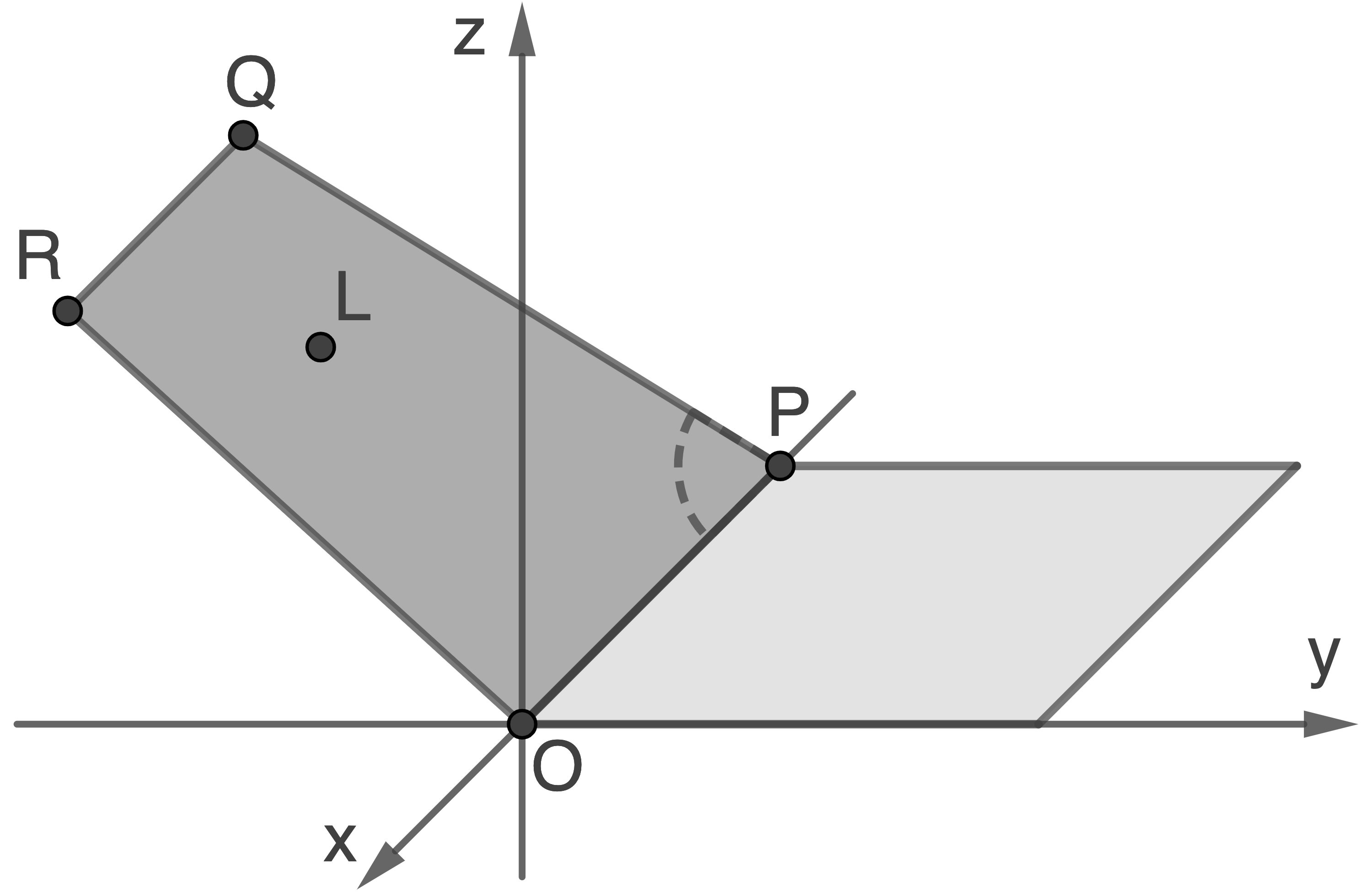
 und ein Rechteck stellen modellhaft die beiden Teile einer Minigolfbahn dar. Eine Seite des Rechtecks ist
und ein Rechteck stellen modellhaft die beiden Teile einer Minigolfbahn dar. Eine Seite des Rechtecks ist  Der Punkt
Der Punkt  liegt in dem Rechteck.
Der Punkt
liegt in dem Rechteck.
Der Punkt  stellt das Loch dieser Minigolfbahn dar. lm verwendeten Koordinatensystem entspricht eine Längeneinheit
stellt das Loch dieser Minigolfbahn dar. lm verwendeten Koordinatensystem entspricht eine Längeneinheit  in der Realität.
in der Realität.
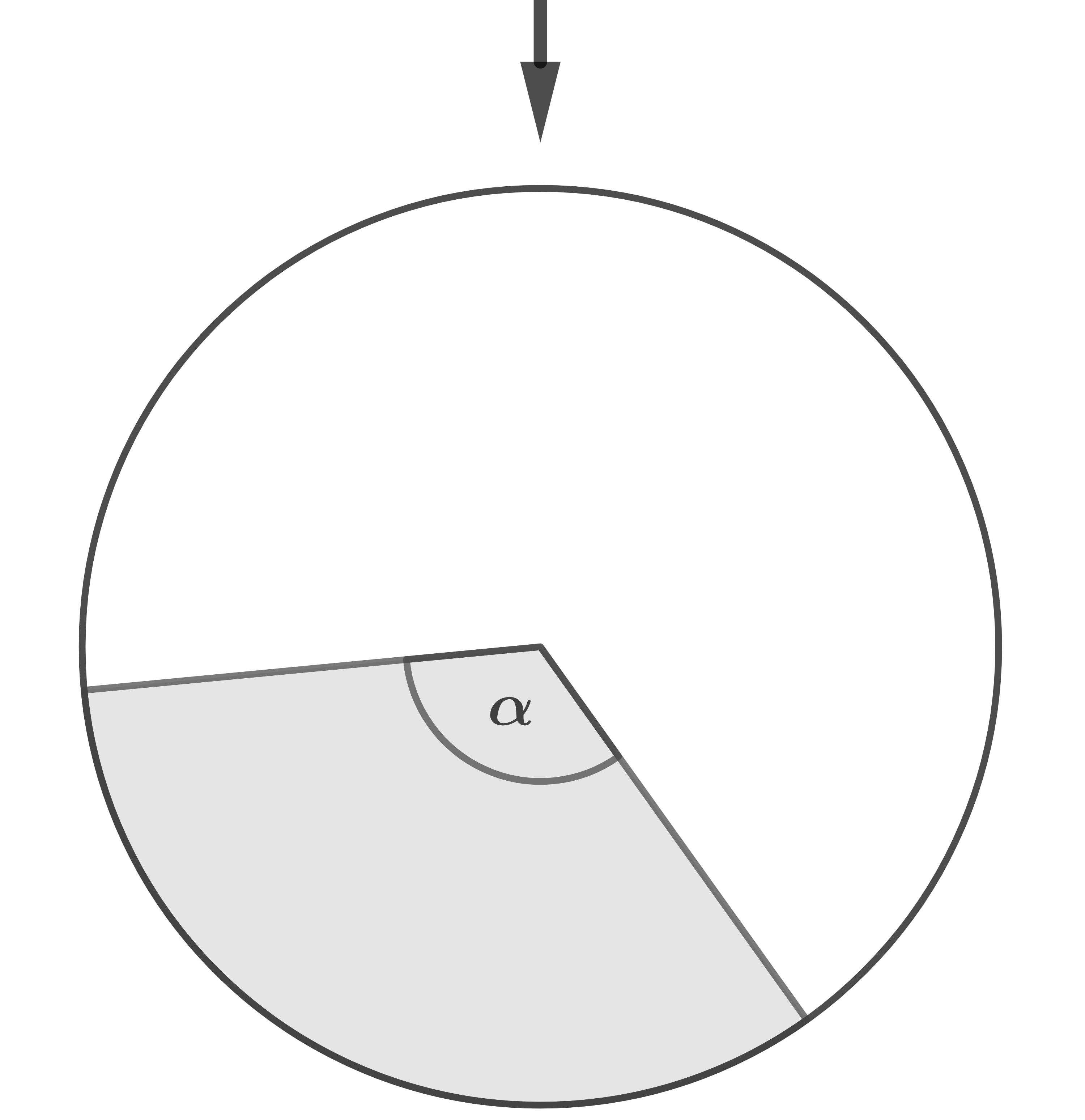

 gewonnen werden. Für einen Einsatz von
gewonnen werden. Für einen Einsatz von 
 wird das Glücksrad dreimal gedreht. Ein Minigolfkurs wird nur dann gewonnen, wenn dabei genau zweimal der grau unterlegte Sektor angezeigt wird.
wird das Glücksrad dreimal gedreht. Ein Minigolfkurs wird nur dann gewonnen, wenn dabei genau zweimal der grau unterlegte Sektor angezeigt wird.




2.1
Beschreibe die besondere Lage der Geraden  mit
mit

 im Koordinatensystem.
Weise nach, dass die Ebene
im Koordinatensystem.
Weise nach, dass die Ebene  durch den Punkt
durch den Punkt  und die Gerade
und die Gerade  eindeutig festgelegt ist.
eindeutig festgelegt ist.
Erreichbare BE-Anzahl: 04
In der Abbildung sind der Punkt  und das Viereck
und das Viereck  dargestellt. Das Viereck
dargestellt. Das Viereck  liegt in der Ebene
liegt in der Ebene 

Abbildung nicht maßstäblich
2.2
Das Viereck  ist ein achsensymmetrisches Trapez.
ist ein achsensymmetrisches Trapez.  und
und  liegen auf
liegen auf 
Berechne die Koordinaten des Punktes
Berechne die Koordinaten des Punktes
Erreichbare BE-Anzahl: 04
2.3
Es gibt Punkte  mit folgenden zwei Eigenschaften:
mit folgenden zwei Eigenschaften:
 liegen.
liegen.
Das Viereck - Die Punkte
liegen im Viereck
- Das Dreieck
hat den Flächeninhalt
Erreichbare BE-Anzahl: 04
2.4
Berechne die Größe des stumpfen Winkels, den die beiden Teile der Minigolfbahn einschließen.
Im Folgenden werden verschiedene Wege von Minigolfbällen betrachtet. Jeder Ball wird dabei als punktförmig angenommen.
Erreichbare BE-Anzahl: 03
2.5
Nach einem Abschlag in  wird ein Ball an der seitlichen Begrenzung des rechteckigen Teils der Bahn, die auf der
wird ein Ball an der seitlichen Begrenzung des rechteckigen Teils der Bahn, die auf der  -Achse liegt, in einem Punkt
-Achse liegt, in einem Punkt  entsprechend des Reflexionsgesetzes reflektiert und erreicht
entsprechend des Reflexionsgesetzes reflektiert und erreicht  im Punkt
im Punkt  Ermittle die Koordinaten des Punktes B.
Ermittle die Koordinaten des Punktes B.
Erreichbare BE-Anzahl: 04
2.6
ln der obigen Abbildung ist ein Teil des Wegs eines anderen Balls gestrichelt dargestellt. Seine Positionen auf dem dargestellten Weg können mithilfe der Punkte


 mit
mit  und
und  beschrieben werden.
Weise nach, dass der Ball auf dem betrachteten Teil seines Wegs durchgehend Kontakt zur Minigolfbahn hat.
beschrieben werden.
Weise nach, dass der Ball auf dem betrachteten Teil seines Wegs durchgehend Kontakt zur Minigolfbahn hat.
Ermittle rechnerisch, um wie viele Zentimeter der Ball das Loch verfehlt.
Ermittle rechnerisch, um wie viele Zentimeter der Ball das Loch verfehlt.
Erreichbare BE-Anzahl: 06
Bei der Jubiläumsfeier der Minigolfanlage werden Glücksräder (siehe folgende Abbildung) verwendet. Die als binomialverteilt angenommene Zufallsgröße  gibt jeweils an, wie oft beim mehrmaligen Drehen eines Glücksrades der grau unterlegte Sektor angezeigt wird.
gibt jeweils an, wie oft beim mehrmaligen Drehen eines Glücksrades der grau unterlegte Sektor angezeigt wird.

2.7
Ein Glücksrad mit  wird
wird  -mal gedreht.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Ereignis
-mal gedreht.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Ereignis  Der grau unterlegte Sektor wird genau dreimal angezeigt.
Der grau unterlegte Sektor wird genau dreimal angezeigt.
Ereignis Der grau unterlegte Sektor wird häufiger angezeigt als zu erwarten ist.
Der grau unterlegte Sektor wird häufiger angezeigt als zu erwarten ist.
Bei einem vom Betreiber durchgeführten Spiel mit einem der Glücksräder können Minigolfkurse im Wert von Ereignis
Erreichbare BE-Anzahl: 04
2.8
Zeige, dass die Wahrscheinlichkeit dafür, bei diesem Spiel einen Minigolfkurs zu gewinnen, mithilfe des Terms  berechnet werden kann.
berechnet werden kann.
Erreichbare BE-Anzahl: 03
2.9
Zeige, dass bei Verwendung des Glücksrades mit  auf lange Sicht bei diesem Spiel ein Verlust für den Betreiber entsteht.
auf lange Sicht bei diesem Spiel ein Verlust für den Betreiber entsteht.
Ermittle alle möglichen Werte von für die der Betreiber auf lange Sicht bei diesem Spiel einen Verlust haben wird.
für die der Betreiber auf lange Sicht bei diesem Spiel einen Verlust haben wird.
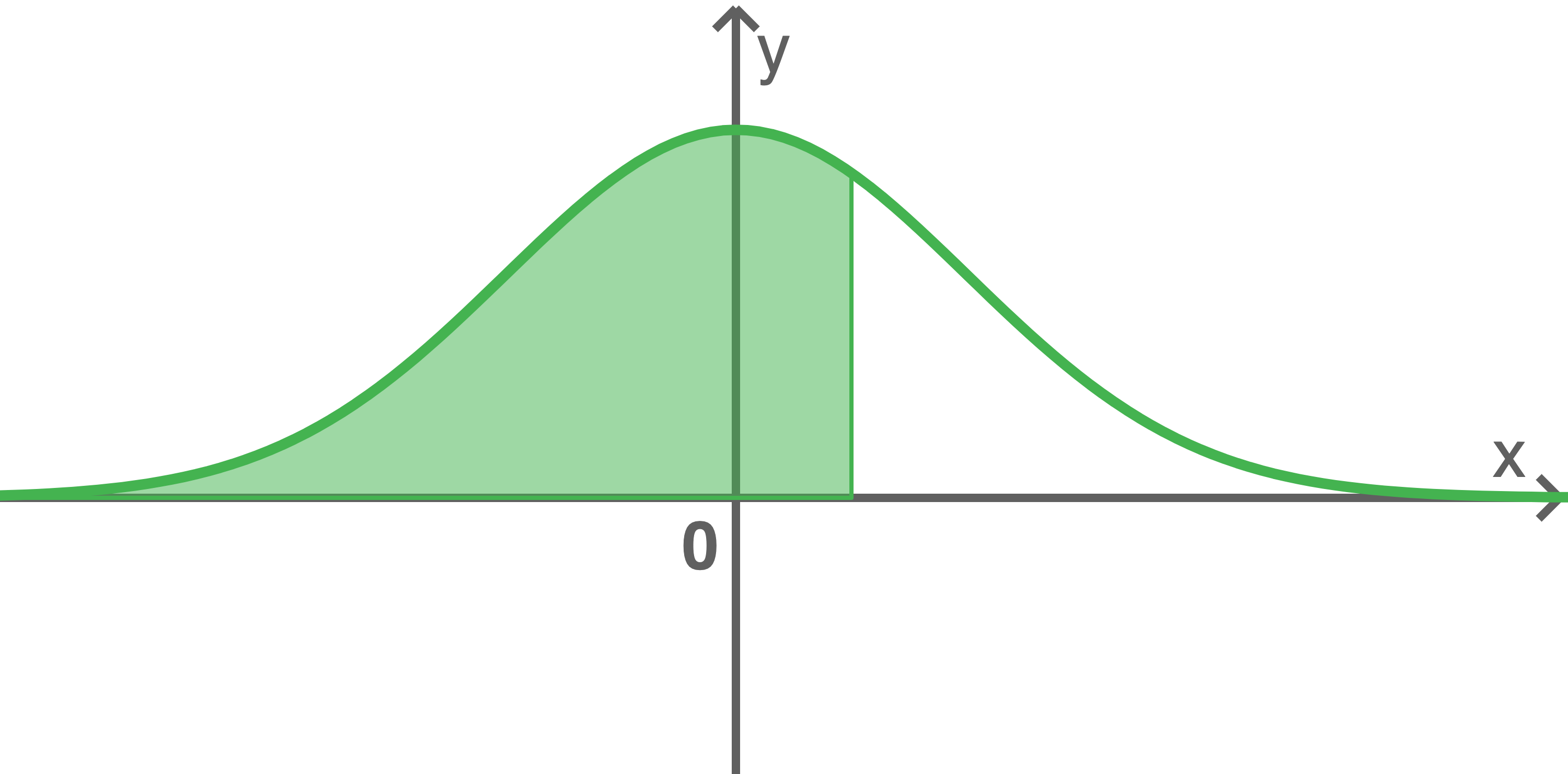
Verteilungsfunktion der Standardnormalverteilung
Ermittle alle möglichen Werte von
Erreichbare BE-Anzahl: 05
