Teil A
1
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1.1
Welchen Anstieg besitzt die Funktion  mit
mit  an der Stelle
an der Stelle 
1.2
Betrachtet werden in  definierte quadratische Funktionen
definierte quadratische Funktionen  welche genau eine reelle Nullstelle
welche genau eine reelle Nullstelle  besitzen.
Für jede derartige Funktion
besitzen.
Für jede derartige Funktion  mit der ersten Ableitungsfunktion
mit der ersten Ableitungsfunktion  gilt:
gilt:
1.3
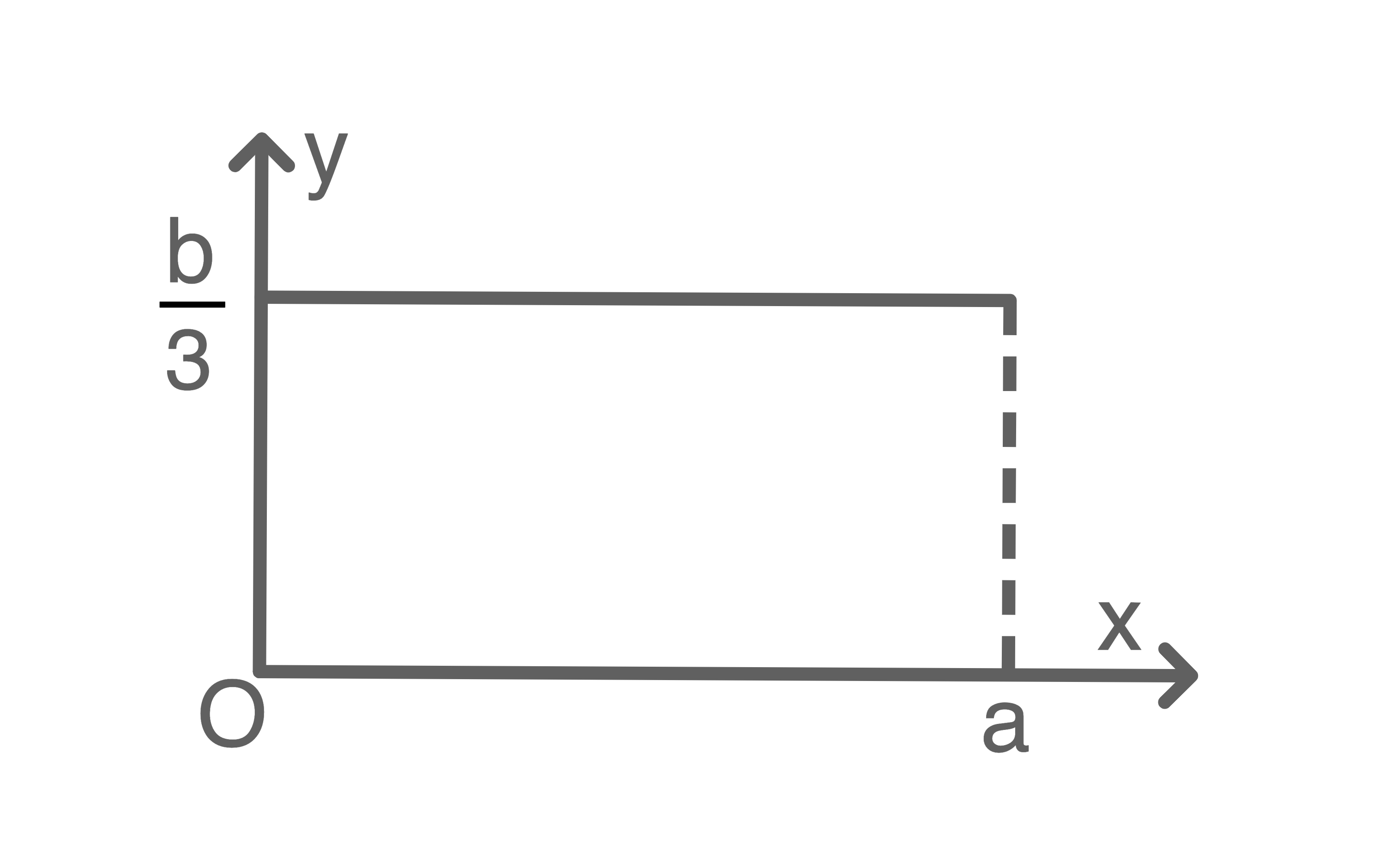
Die Fläche zwischen einer Strecke und der  -Achse rotiert um die
-Achse rotiert um die  -Achse. Der dabei entstehende Körper hat das Volumen
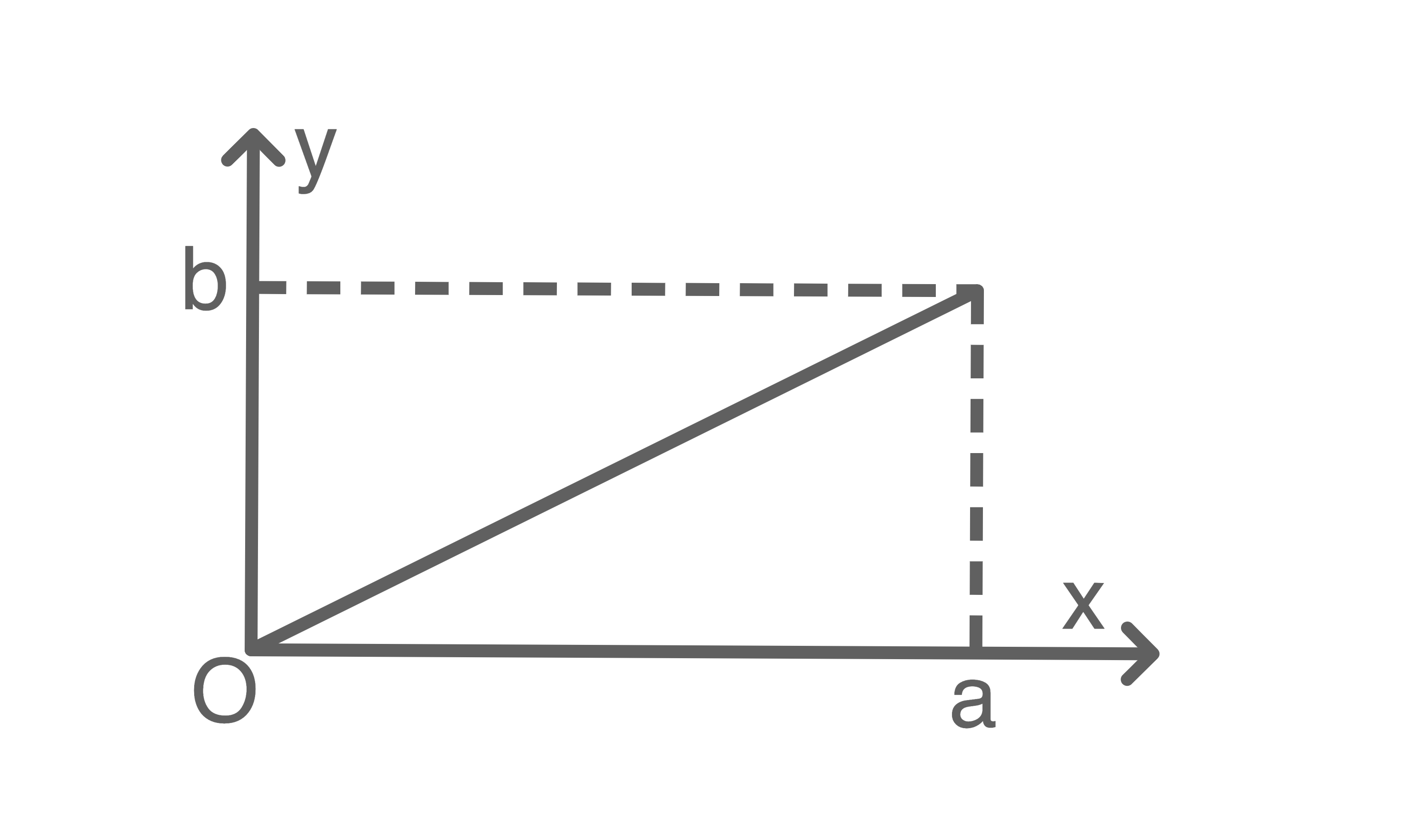
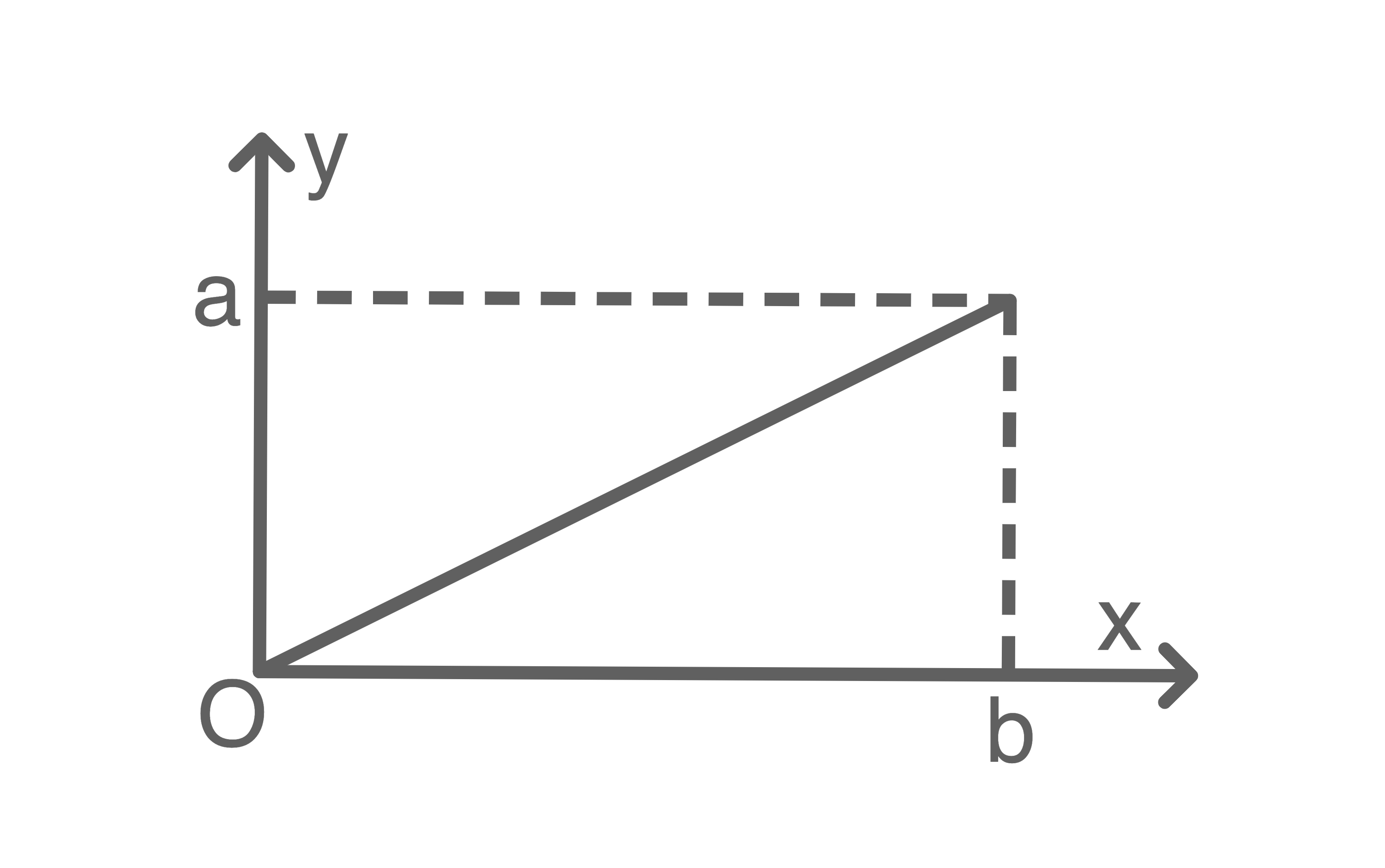
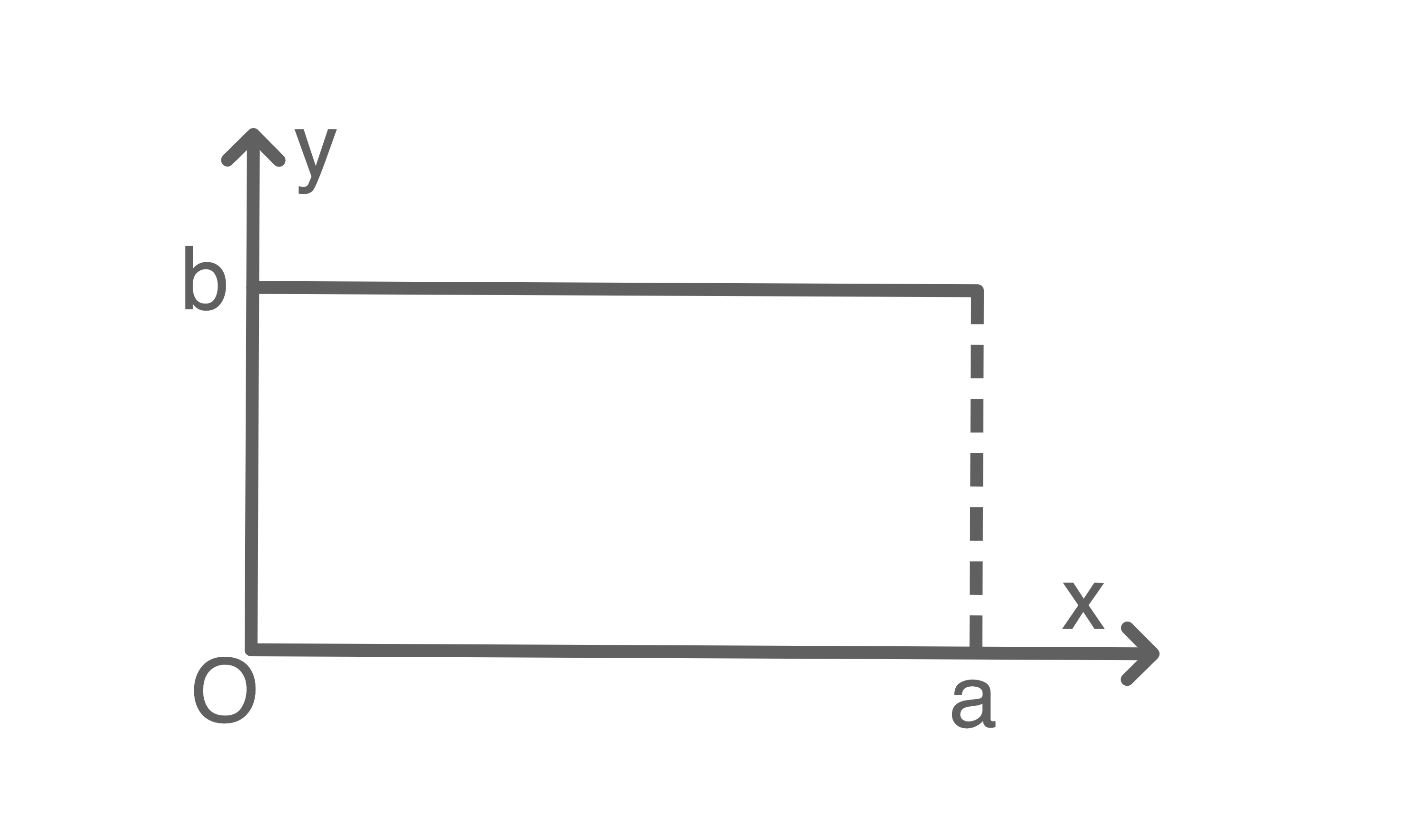
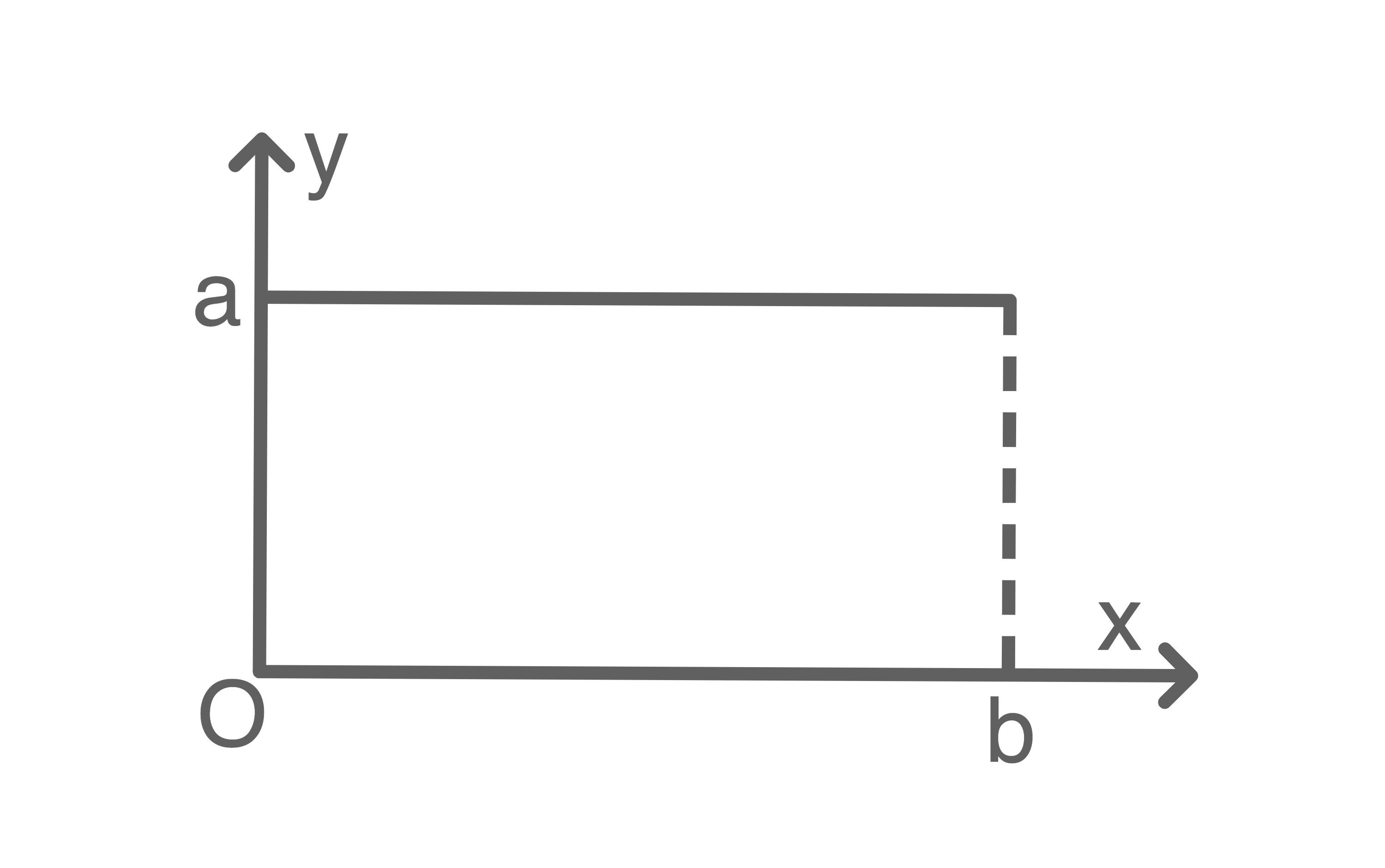
-Achse. Der dabei entstehende Körper hat das Volumen  Welche Abbildung passt zu diesem Sachverhalt?
Welche Abbildung passt zu diesem Sachverhalt?
|
|
|
|
|
|
|
|
|
1.4
Die Gerade  schneidet die Ebene
schneidet die Ebene  im Punkt
im Punkt
1.5
Betrachtet wird ein Punkt  der nicht in der
der nicht in der  -Ebene liegt. Bei Spiegelung von
-Ebene liegt. Bei Spiegelung von  an dieser Ebene entsteht der Punkt
an dieser Ebene entsteht der Punkt  Die Gerade durch
Die Gerade durch  und
und  verläuft
verläuft
| parallel zur |
|
| parallel zur |
|
| parallel zur |
|
| senkrecht zur |
|
| senkrecht zur |
(5 BE)
2
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  und
und  . Die Nullstellen von
. Die Nullstellen von  sind
sind  und
und  .
.
2.1
Zeige, dass das Flächenstück, das der Graph von  mit der
mit der  -Achse einschließt, den Inhalt
-Achse einschließt, den Inhalt  hat.
hat.
(2 BE)
2.2
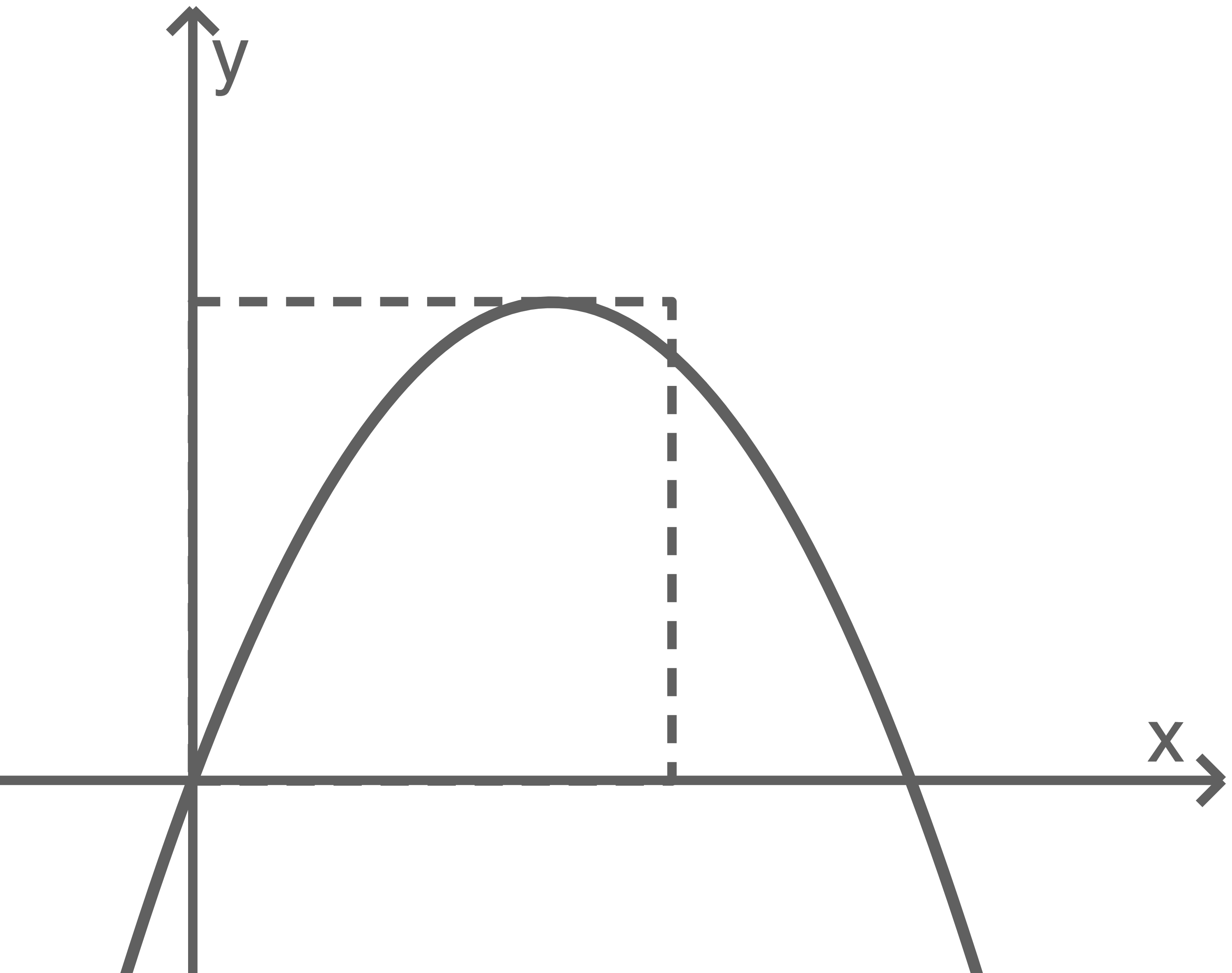
Der Hochpunkt des Graphen von  liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung).
Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von
liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung).
Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von  mit der
mit der  -Achse einschließt, überein.
Bestimme den Wert von
-Achse einschließt, überein.
Bestimme den Wert von 
(3 BE)
3
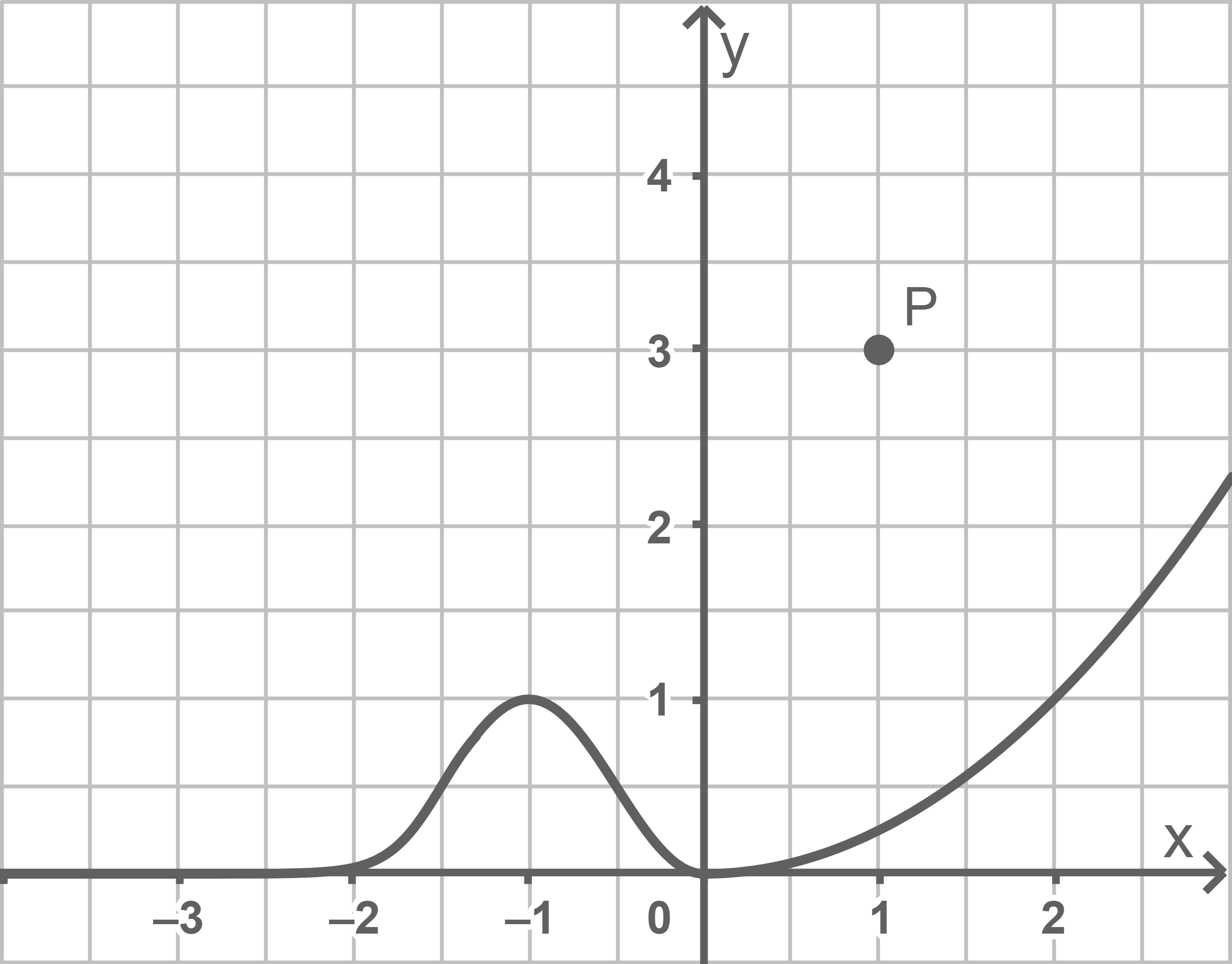
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion  dessen einzige Extrempunkte
dessen einzige Extrempunkte  und
und  sind, sowie den Punkt
sind, sowie den Punkt 
3.1
Gib die Koordinaten des Tiefpunkts des Graphen der in  definierten Funktion
definierten Funktion  mit
mit  an.
an.
(2 BE)
3.2
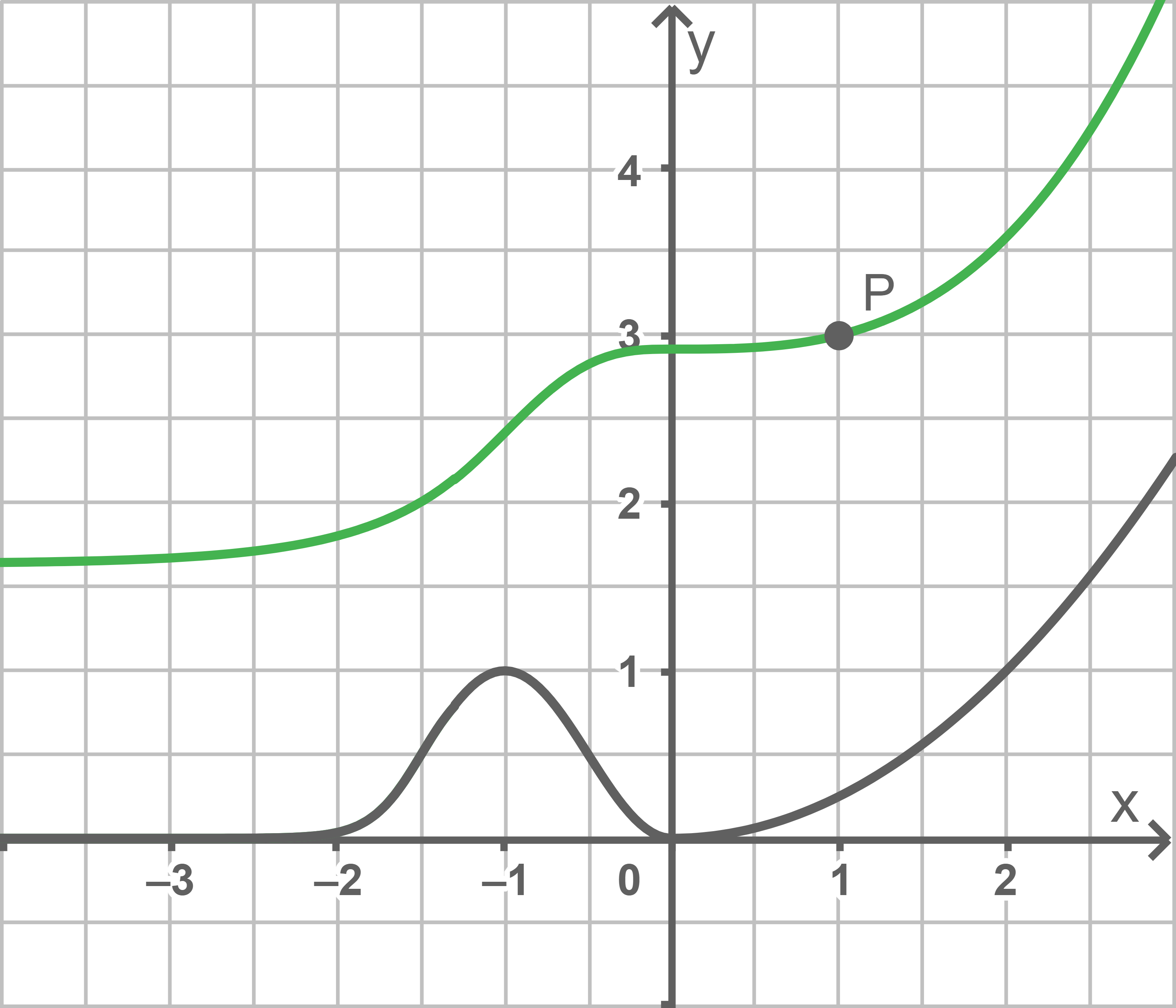
Der Graph einer Stammfunktion von  verläuft durch
verläuft durch  Skizziere diesen Graphen in der Abbildung.
Skizziere diesen Graphen in der Abbildung.
(3 BE)
4
Gegeben ist die Gerade  mit
mit 
4.1
Zeige, dass  in der Ebene mit der Gleichung
in der Ebene mit der Gleichung  liegt.
liegt.
(2 BE)
4.2
Gegeben ist außerdem die Schar der Geraden  mit
mit  und
und  Weise nach, dass
Weise nach, dass  und
und  für jeden Wert von
für jeden Wert von  windschief sind.
windschief sind.
(3 BE)
5
Gegeben sind die Punkte  und
und  sowie die Geraden
sowie die Geraden  und
und  , die sich in
, die sich in  schneiden. Die Gerade
schneiden. Die Gerade  hat den Richtungsvektor
hat den Richtungsvektor  die Gerade
die Gerade  den Richtungsvektor
den Richtungsvektor 
5.1
Weise nach, dass  auf
auf  liegt.
liegt.
(1 BE)
5.2
Bestimme die Koordinaten zweier Punkte  und
und  so, dass
so, dass  auf
auf  liegt und das Viereck
liegt und das Viereck  eine Raute ist.
eine Raute ist.
(4 BE)
6
Gegeben sind die Geraden  und
und  mit
mit 
6.1
Begründe, dass  und
und  nicht identisch sind.
nicht identisch sind.
(1 BE)
6.2
Die Gerade  soll durch Spiegelung an einer Ebene auf die Gerade
soll durch Spiegelung an einer Ebene auf die Gerade  abgebildet werden.
Bestimme eine Gleichung einer geeigneten Ebene und erläutere dein Vorgehen.
abgebildet werden.
Bestimme eine Gleichung einer geeigneten Ebene und erläutere dein Vorgehen.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Rechnungen

 Die Funktion
Die Funktion  besitzt an der Stelle
besitzt an der Stelle  somit den Ansteig
somit den Ansteig 
1.2
Lösungsweg
Besitzt der Graph einer quadratischen Funktion genau eine Nullstelle, so entspricht diese ihrem Maximum bzw. Minimum. Für Maxima bzw. Minima gilt mit der notwendigen Bedingung:
Besitzt der Graph einer quadratischen Funktion genau eine Nullstelle, so entspricht diese ihrem Maximum bzw. Minimum. Für Maxima bzw. Minima gilt mit der notwendigen Bedingung:
1.3

|
|

|
|

|
|

|
|

|
Lösungsweg
Für einen Kegel gilt: Da
Da  hier dem Radius
hier dem Radius  und
und  der Höhe des entstehenden Kegels entsprechen soll, passt die zweite Abbildung zum Sachverhalt.
der Höhe des entstehenden Kegels entsprechen soll, passt die zweite Abbildung zum Sachverhalt.
Für einen Kegel gilt:
1.4
1.5
| parallel zur |
|
| parallel zur |
|
| parallel zur |
|
| senkrecht zur |
|
| senkrecht zur |
2.1
Der Inhalt des Flächenstücks lässt sich wie folgt berechnen:
2.2
1. Schritt: Koordinaten des Hochpunkts ermitteln
Aus den Nullstellen bei  und
und  ergibt sich aufgrund der Symmetrie ein Hochpunkt mit den Koordinaten
ergibt sich aufgrund der Symmetrie ein Hochpunkt mit den Koordinaten  Die
Die  -Koordinate ergibt sich zu:
-Koordinate ergibt sich zu:
![\(\begin{array}[t]{rll}
f(a)&=& -a^2+2a\cdot a& \\[5pt]
&=& a^2
\end{array}\)](https://mathjax.schullv.de/1fdff1ec86f7930b53cc12bf125b98ffe63ac768387207047bb19083d322d418?color=5a5a5a) 2. Schritt: Wert von
2. Schritt: Wert von  bestimmen
Für den Flächeninhalt des Quadrates gilt:
bestimmen
Für den Flächeninhalt des Quadrates gilt:
![\(A_Q=A=\dfrac{4}{3}a^3 \; [\text{FE}]\)](https://mathjax.schullv.de/a31d9e95c211883f892551b2f73c15b20628e04f8cd9a72cd30dccdef36b1307?color=5a5a5a) Mit den Koordinaten des Hochpunkts
Mit den Koordinaten des Hochpunkts  ergeben sich die Höhe und somit auch die Breite des Quadrats mit
ergeben sich die Höhe und somit auch die Breite des Quadrats mit  Es folgt
Es folgt  und somit:
und somit:
![\(\begin{array}[t]{rll}
A_Q&=& \dfrac{4}{3}a^3&\\[5pt]
a^2\cdot a^2&=& \dfrac{4}{3}a^3 & \\[5pt]
a^4&=& \dfrac{4}{3}a^3&\quad \scriptsize \mid\; :a^3\\[5pt]
a&=&\dfrac{4}{3}
\end{array}\)](https://mathjax.schullv.de/85c8031930e5bd4dca46d4fcbb59cfb743f8438db06e6ac4eada96325c3f119d?color=5a5a5a)
3.1
Der Graph von  ergibt sich aus dem Graphen von
ergibt sich aus dem Graphen von  durch Verschiebung um 3 Längeneinheiten in positive
durch Verschiebung um 3 Längeneinheiten in positive  -Richtung und Spiegelung an der
-Richtung und Spiegelung an der  -Achse.
Aufgrund der Spiegelung entspricht der Hochpunkt des Graphen von
-Achse.
Aufgrund der Spiegelung entspricht der Hochpunkt des Graphen von  nach entsprechender Verschiebung also dem Tiefpunkt des Graphen von
nach entsprechender Verschiebung also dem Tiefpunkt des Graphen von  Durch Spiegelung an der
Durch Spiegelung an der  -Achse ergeben sich die Koordinaten des Tiefpunkts des Graphen von
-Achse ergeben sich die Koordinaten des Tiefpunkts des Graphen von  mit
mit 
3.2
4.1
Aus der Geradengleichung  lassen sich
lassen sich 
 und
und  herauslesen.
Einsetzen in die Ebenengleichung ergibt:
herauslesen.
Einsetzen in die Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
E: \lambda+1+(1-\lambda)&=& 2& \\[5pt]
2&=& 2
\end{array}\)](https://mathjax.schullv.de/b2a6549a57bd092be0f1a5c6cb318d1e2234913bfc690c28900709ee2605901b?color=5a5a5a) Somit liegt die Gerade
Somit liegt die Gerade  in der Ebene
in der Ebene 
4.2
Zwei Geraden sind genau dann windschief, wenn sie nicht parallel bzw. identisch parallel zueinander sind und keinen gemeinsamen Schnittpunkt haben.
Parallelität überprüfen:
Es muss gelten:
 Da aus der ersten Zeile
Da aus der ersten Zeile  , aus der zweiten Zeile
, aus der zweiten Zeile  und aus der dritten Zeile
und aus der dritten Zeile  folgt, hat diese Gleichung keine Lösung.
Die Gerade
folgt, hat diese Gleichung keine Lösung.
Die Gerade  und die Geraden der Schar
und die Geraden der Schar  sind folglich unabhängig von
sind folglich unabhängig von  weder parallel noch identisch parallel zueinander.
Schnittpunkt prüfen:
Aus der dritten Zeile folgt
weder parallel noch identisch parallel zueinander.
Schnittpunkt prüfen:
Aus der dritten Zeile folgt  und eingesetzt in die erste Zeile
und eingesetzt in die erste Zeile  Einsetzen in die zweite Zeile ergibt jedoch
Einsetzen in die zweite Zeile ergibt jedoch  was zu einem Widerspruch führt.
Die Gerade
was zu einem Widerspruch führt.
Die Gerade  und die Geraden der Schar
und die Geraden der Schar  haben somit keinen Schnittpunkt miteinander und sind folglich für jeden Wert von
haben somit keinen Schnittpunkt miteinander und sind folglich für jeden Wert von  windschief.
windschief.
5.1
Da die Gerade  laut Aufgabenstellung durch den Punkt
laut Aufgabenstellung durch den Punkt  verläuft, ergibt sich die Geradengeichung von
verläuft, ergibt sich die Geradengeichung von  mit:
mit:
 Punktprobe mit
Punktprobe mit  liefert:
liefert:
![\(\begin{array}[t]{rll}
\pmatrix{3\\5\\5}&=& \pmatrix{1\\1\\1}+s\cdot \pmatrix{1\\2\\2}&\\[5pt]
\pmatrix{3\\5\\5}&=& \pmatrix{1+s\\1+2s\\1+2s}
\end{array}\)](https://mathjax.schullv.de/e13902413fe377f15cda23470bb94e0e3bcbb4f3ebc123554e9fddec8965db64?color=5a5a5a) Aus der ersten Zeile folgt
Aus der ersten Zeile folgt  und somit
und somit  Kontrolle durch Einsetzen von
Kontrolle durch Einsetzen von  in Zeile 2 und 3:
in Zeile 2 und 3:
![\(\begin{array}[t]{rll}
5&=& 1+2\cdot 2& \\[5pt]
5&=& 5
\end{array}\)](https://mathjax.schullv.de/b8316107ee07e1ae0495884d80a594a3dca25694082210c5a0a87d050a503b8a?color=5a5a5a) Da
Da  also eine Lösung des Gleichungssystems ist, liegt
also eine Lösung des Gleichungssystems ist, liegt  folglich auf
folglich auf 
5.2
Da die Seiten einer Raute alle gleich lang sind, muss gelten:
 Da die Koordinaten von
Da die Koordinaten von  und
und  bereits gegeben sind, folgt:
Da der Punkt
bereits gegeben sind, folgt:
Da der Punkt  auf der Geraden
auf der Geraden  liegt und den Abstand 6 zu Punkt
liegt und den Abstand 6 zu Punkt  haben soll, folgt:
haben soll, folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OC}&=& \overrightarrow{OB}+6\cdot \pmatrix{1\\0\\0} & \\[5pt]
&=& \pmatrix{1\\1\\1}+ \pmatrix{6\\0\\0} & \\[5pt]
&=& \pmatrix{7\\1\\1}
\end{array}\)](https://mathjax.schullv.de/221980c6e718444d2d639e850fb1a215f4fa025f674f8b6afaccee74b7dde71b?color=5a5a5a) Da die gegenüberliegenden Seiten einer Raute parallel zueinander sind, muss gelten:
Da die gegenüberliegenden Seiten einer Raute parallel zueinander sind, muss gelten:
 Es folgt also:
Es folgt also:
![\(\begin{array}[t]{rll}
\overrightarrow{OD}&=& \overrightarrow{OA}+6\cdot \pmatrix{1\\0\\0} & \\[5pt]
&=& \pmatrix{3\\5\\5}+ \pmatrix{6\\0\\0} & \\[5pt]
&=& \pmatrix{9\\5\\5}
\end{array}\)](https://mathjax.schullv.de/1faae5edb49bf1f6c9b43c3d9742427a772dd4901f71df149e804aa1dec30a6e?color=5a5a5a) Die Koordinaten der Punkte
Die Koordinaten der Punkte  und
und  sind somit gegeben durch
sind somit gegeben durch  und
und 
6.1
6.2
Da die Richtungsvektoren der beiden Geraden gleich lang sind, ergibt sich ein Normalenvektor aus der Differenz der beiden Vektoren:
 Einsetzen des gemeinsamen Stützpunkts
Einsetzen des gemeinsamen Stützpunkts  in die allgemeine Ebenengleichung liefert:
in die allgemeine Ebenengleichung liefert:
![\(\begin{array}[t]{rll}
E: n_1\cdot x+n_2\cdot y+n_3\cdot z&=& c& \\[5pt]
1\cdot 1-1\cdot 1+0\cdot 1&=& c& \\[5pt]
0&=& c
\end{array}\)](https://mathjax.schullv.de/8887cedd6c3270cd251d96b1456e8e04ee4ecba4647d719c2a0f40fb27e9fe21?color=5a5a5a) Die Koordinatengleichung folgt also mit:
Die Koordinatengleichung folgt also mit:
