Teil B2
In einem kartesischen Koordinatensystem werden die Pyramiden  mit
mit



 und
und 
mit
 betrachtet. Die gemeinsame Grundfläche
betrachtet. Die gemeinsame Grundfläche  dieser Pyramiden ist quadratisch. Die Abbildung zeigt beispielhaft eine dieser Pyramiden.
dieser Pyramiden ist quadratisch. Die Abbildung zeigt beispielhaft eine dieser Pyramiden.
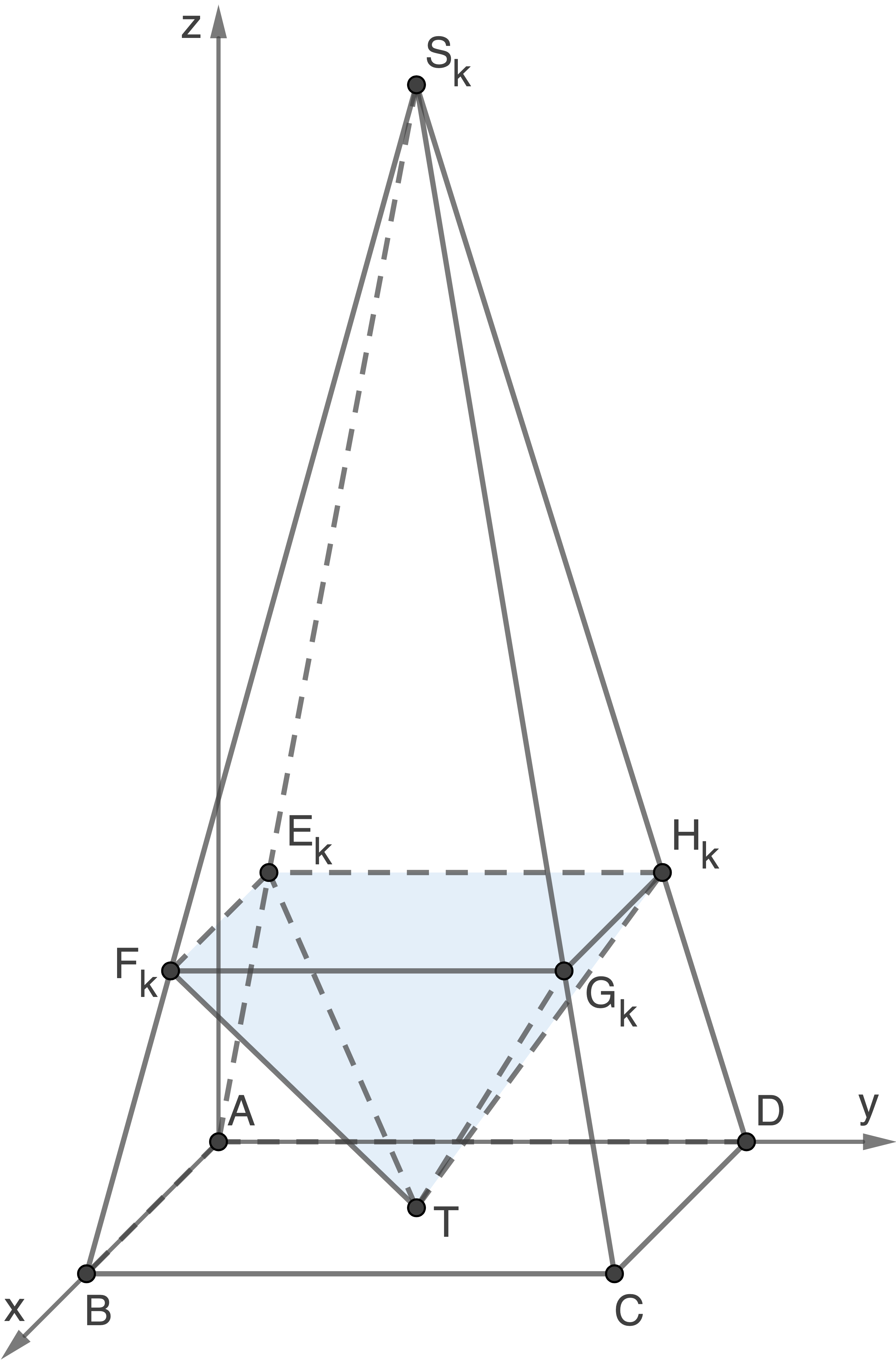
 ist der Schnittpunkt der Diagonalen der Grundfläche
ist der Schnittpunkt der Diagonalen der Grundfläche 
mit
2.1
Berechne für  den Inhalt der Mantelfläche der geraden Pyramide
den Inhalt der Mantelfläche der geraden Pyramide 
Gib für eine Symmetrieebene der Pyramide eine Gleichung in parameterfreier Form an.
eine Gleichung in parameterfreier Form an.
Begründe, dass die Gleichung mit
mit  keine Symmetriebene der Pyramide
keine Symmetriebene der Pyramide  beschreibt.
beschreibt.
Gib für eine Symmetrieebene der Pyramide
Begründe, dass die Gleichung

Abbildung (nicht maßstäblich)
(6 BE)
2.2
Begründe, dass jede der Pyramiden  gerade ist.
gerade ist.
(2 BE)
2.3
Die Seitenfläche  liegt in einer Ebene.
liegt in einer Ebene.
Zeige, dass diese Ebene durch die Gleichung beschrieben werden kann.
beschrieben werden kann.
Bestimme denjenigen Wert von für den die Seitenfläche
für den die Seitenfläche  gegenüber der Grundfläche
gegenüber der Grundfläche  um einen Winkel der Größe 60 °C geneigt ist.
um einen Winkel der Größe 60 °C geneigt ist.
Der abgebildete Punkt Zeige, dass diese Ebene durch die Gleichung
Bestimme denjenigen Wert von
(6 BE)
2.4
Der Mittelpunkt der Strecke  wird mit
wird mit  bezeichnet. Für einen Wert von
bezeichnet. Für einen Wert von  ist
ist  von der Grundfläche
von der Grundfläche  dreimal so weit entfernt wie von jeder der vier Seitenflächen der Pyramide
dreimal so weit entfernt wie von jeder der vier Seitenflächen der Pyramide 
Ermittle diesen Wert von
Ermittle diesen Wert von
(4 BE)
2.5
Die Ebene mit der Gleichung  schneidet die vier vom Punkt
schneidet die vier vom Punkt  ausgehenden Kanten der Pyramide
ausgehenden Kanten der Pyramide  in den Punkten
in den Punkten 

 und
und  (siehe Abbildung).
(siehe Abbildung).
Berechne die - und
- und  -Koordinate von
-Koordinate von 
Bestimme diejenigen Werte von für die das Verhältnis des Volumens der Pyramide
für die das Verhältnis des Volumens der Pyramide  zum Volumen der Pyramide
zum Volumen der Pyramide 
 beträgt.
beträgt.
Eine Werbefirma produziert Schlüsselanhänger in Form von Pyramiden, wobei 75 % dieser Pyramiden ein Firmenlogo besitzen. Die Anzahl der Pyramiden mit Firmenlogo unter den der Produktion zufällig entnommenen Pyramiden wird als binomialverteilt angenommen.
Berechne die
Bestimme diejenigen Werte von
(7 BE)
2.6
Der Produktion werden 200 Pyramiden zufällig entnommen.
Bestimme die Wahrscheinlichkeit dafür, dass mehr als 50 % und weniger als 70 % dieser Pyramiden ein Firmenlogo besitzen.
Bestimme die Wahrscheinlichkeit dafür, dass mehr als 50 % und weniger als 70 % dieser Pyramiden ein Firmenlogo besitzen.
(3 BE)
2.7
Ermittle, wie viele Pyramiden der Produktion mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mehr als 95 % mindestens 10 dieser Pyramiden ein Firmenlogo besitzen.
(3 BE)
2.8
70 % aller produzierten Pyramiden bestehen aus durchsichtigem Material. Der Anteil derjenigen Pyramiden, die aus durchsichtigem Material bestehen und grün sind, beträgt 14 %.
Von allen produzierten Pyramiden sind 26 % grün.
Der Produktion der Werbefirma wird eine Pyramide zufällig entnommen.
Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
Untersuche die Ereignisse „Die Pyramide besteht aus durchsichtigem Material.“ und „Die Pyramide ist grün.“ auf stochastische Abhängigkeit.
Bestimme die Wahrscheinlichkeit dafür, dass eine entnommene Pyramide aus durchsichtigem Material besteht, unter der Bedingung, dass sie nicht grün ist.
Von allen produzierten Pyramiden sind 26 % grün.
Der Produktion der Werbefirma wird eine Pyramide zufällig entnommen.
Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
Untersuche die Ereignisse „Die Pyramide besteht aus durchsichtigem Material.“ und „Die Pyramide ist grün.“ auf stochastische Abhängigkeit.
Bestimme die Wahrscheinlichkeit dafür, dass eine entnommene Pyramide aus durchsichtigem Material besteht, unter der Bedingung, dass sie nicht grün ist.
(7 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
2.2
Die quadratische Grundfläche liegt in der  -Ebene. Die Körperhöhe steht senkrecht auf der Mitte der Grundfläche, da der Schnittpunkt der Diagonalen der Grundflächen die gleichen
-Ebene. Die Körperhöhe steht senkrecht auf der Mitte der Grundfläche, da der Schnittpunkt der Diagonalen der Grundflächen die gleichen  - und
- und  -Koordianten, wie
-Koordianten, wie  hat.
hat.
2.3
Punktprobe für die Punkte  ,
,  und
und  :
Punkt
:
Punkt  :
:  Punkt
Punkt  :
:  Punkt
Punkt  :
:  Die Koordinaten der Punkte
Die Koordinaten der Punkte  ,
,  und
und  erfüllen die Gleichung
erfüllen die Gleichung  , sodass die Ebene
, sodass die Ebene  durch die gegebene Gleichung beschrieben werden kann.
Mit
durch die gegebene Gleichung beschrieben werden kann.
Mit  und
und  und
und  ergibt sich für
ergibt sich für  :
Mit der Vorraussetzung
:
Mit der Vorraussetzung  ergibt sich: Für
ergibt sich: Für  ist die Seitenfläche
ist die Seitenfläche  gegenüber der Grundfläche
gegenüber der Grundfläche  um
um  geneigt.
geneigt.
2.4
2.5
Gerade durch  :
:
 mit
mit  Gerade
Gerade  mit der Gleichung
mit der Gleichung  gleichsetzen:
gleichsetzen:
 Dies liefert
Dies liefert  .
.

 Die Koordinaten von
Die Koordinaten von  lauten
lauten  .
Das Volumen der Pyramide
.
Das Volumen der Pyramide  berechnet sich wie folgt:
berechnet sich wie folgt:
 Das Volumen der Pyramide
Das Volumen der Pyramide  berechnet sich wie folgt:
berechnet sich wie folgt:

 Verhältnis des Volumens der Pyramiden mit
Verhältnis des Volumens der Pyramiden mit  :
:
![\(\begin{array}[t]{rll}
\dfrac{V_{E_kF_kG_kH_kT}}{V_{ABCDS_k}}&=&\dfrac{1}{8}&\quad \scriptsize \\[5pt]
\dfrac{\dfrac{1}{3}\cdot \left(2-\dfrac{2}{k}\right)^2}{\dfrac{1}{3}\cdot 2^2\cdot k}&=&\dfrac{1}{8}&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a1e3e2746d3b0f0efbc8a2d4bcd7e0d6039d72b95f22eec4e44d9ca784d7420d?color=5a5a5a) Mit dem Taschenrechner folgt:
Mit dem Taschenrechner folgt:
Für und
und  beträgt das Verhältnis des Volumens der Pyramiden
beträgt das Verhältnis des Volumens der Pyramiden  .
.
Für
2.6
Die Zufallsgröße  beschreibt die Anzahl an Pyramiden mit Firmenlogo.
beschreibt die Anzahl an Pyramiden mit Firmenlogo.  ist binomialverteilt mit
ist binomialverteilt mit  .
.
 und
und 
 Die Wahrscheinlichkeit, dass mehr als
Die Wahrscheinlichkeit, dass mehr als  , aber weniger als
, aber weniger als  der Pyramiden ein Firmenlogo haben, beträgt
der Pyramiden ein Firmenlogo haben, beträgt  .
.
2.7
Die Zufallsgröße  beschreibt die Anzahl an Pyramiden mit Firmenlogo.
beschreibt die Anzahl an Pyramiden mit Firmenlogo.  ist binomialverteilt mit
ist binomialverteilt mit  .
.
 Für
Für  ist
ist  das erste Mal größer als
das erste Mal größer als  . Es müssen also mindesten
. Es müssen also mindesten  Pyramiden entnommen werden.
Pyramiden entnommen werden.
2.8
| grün | nicht grün | ||
|---|---|---|---|
| durchsichtig | |||
| nicht durchsichtig | |||