Teil B1

Betrachtet werden alle in $\mathbb{R}$ definierten Funktionen $f_{p}$ der Schar mit

$f_p(x)=...$

Funktionenschar anzeigen

und $p \in \mathbb{R}$ .

Die Graphen von $f_{p}$ werden mit $G_{p}$ bezeichnet.

1.1

Zeige, dass die $y$ -Koordinate des Schnittpunkts von $G_{p}$ mit der Ordinatenachse unabhängig von $p$ ist.

Bestimme den Wert von $p$ , für den $G_{p}$ symmetrisch zur Ordinatenachse ist.

Gib das Verhalten von $f_{p}$ für $x \rightarrow+\infty$ in Abhängigkeit von $p$ an.

(7 BE)

1.2

Betrachtet werden die folgenden drei Aussagen für $p>0$ :

Aussagen anzeigen

Aus diesen drei Aussagen ergibt sich eine Eigenschaft von $G_{p}$ .

Gib diese Eigenschaft an.

Begründe deine Angabe unter Verwendung der drei Aussagen.

(5 BE)

1.3

Die Tangente an $G_{p}$ an der Stelle $x=1$ wird durch die Gleichung $y=-90 \cdot x+\frac{p}{4}+270$ beschrieben.

Diese Tangente schließt für $p \neq-1080$ mit den Koordinatenachsen eine Fläche ein.

Bestimme einen Wert von $p$ , für den der Inhalt dieser Fläche 500 beträgt.

(5 BE)

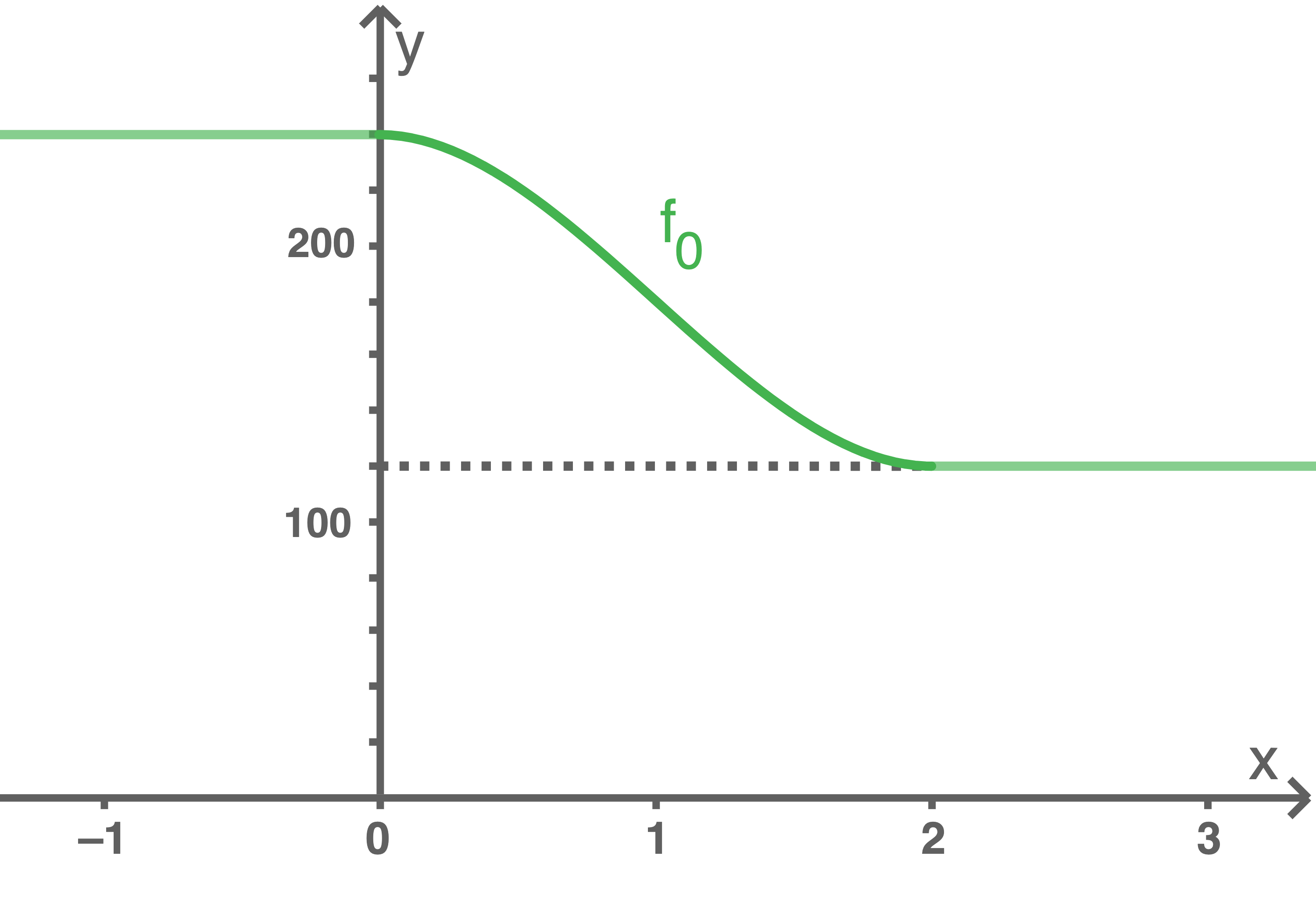
Ein ICE fährt bis 15:00 Uhr mit konstanter Geschwindigkeit. Von 15:00 Uhr bis 15:02 Uhr nimmt seine Geschwindigkeit ab. Ab 15:02 Uhr fährt der ICE wieder mit konstanter Geschwindigkeit. Zur modellhaften Beschreibung der Entwicklung der Geschwindigkeit des ICE im Zeitraum von 15:00 Uhr bis 15:02 Uhr wird die Funktion $f_{0}$ mit $f_{0}(x)=30 \cdot x^{3}-90 \cdot x^{2}+240$ verwendet. Dabei ist $x$ die seit 15:00 Uhr vergangene Zeit in Minuten und $f_{0}(x)$ die Geschwindigkeit in Kilometer pro Stunde. Die Abbildung 1 zeigt für $0 \leq x \leq 2$ den Graphen von $f_{0}$ ; außerdem stellt sie die Geschwindigkeiten des ICE vor 15:00 Uhr und nach 15:02 Uhr dar.

Abbildung 1

1.4

Bestimme die Geschwindigkeit, die der ICE eine halbe Minute nach 15:00 Uhr hat. Zeigen Sie, dass die Geschwindigkeit in der ersten halben Minute nach 15:00 Uhr um einen kleineren Betrag abnimmt als in der darauffolgenden halben Minute.

(4 BE)

1.5

Ermittle den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt.

(3 BE)

1.6

Interpretiere die Gleichung $f_{0}(x+0,5)=f_{0}(x)-20$ im Sachzusammenhang.

Gib eine Lösung der Gleichung an.

(3 BE)

1.7

Berechne die Länge der Strecke, die der ICE in den ersten drei Minuten nach 15:00 Uhr zurücklegt.

(5 BE)

1.8

Untersuche, ob die folgende Aussage wahr ist:

Wenn sich die Abnahme der Geschwindigkeit von 15:01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.

(4 BE)

Betrachtet wird die in $\mathbb{R}$ definierte Funktion $s$ mit $s(x)=2 \cdot \sin \left(\frac{\pi}{4} \cdot x\right)+1$

1.9

Gib die Koordinaten und die Art zweier direkt aufeinanderfolgender Extrempunkte des Graphen von $s$ an.

(5 BE)

1.10

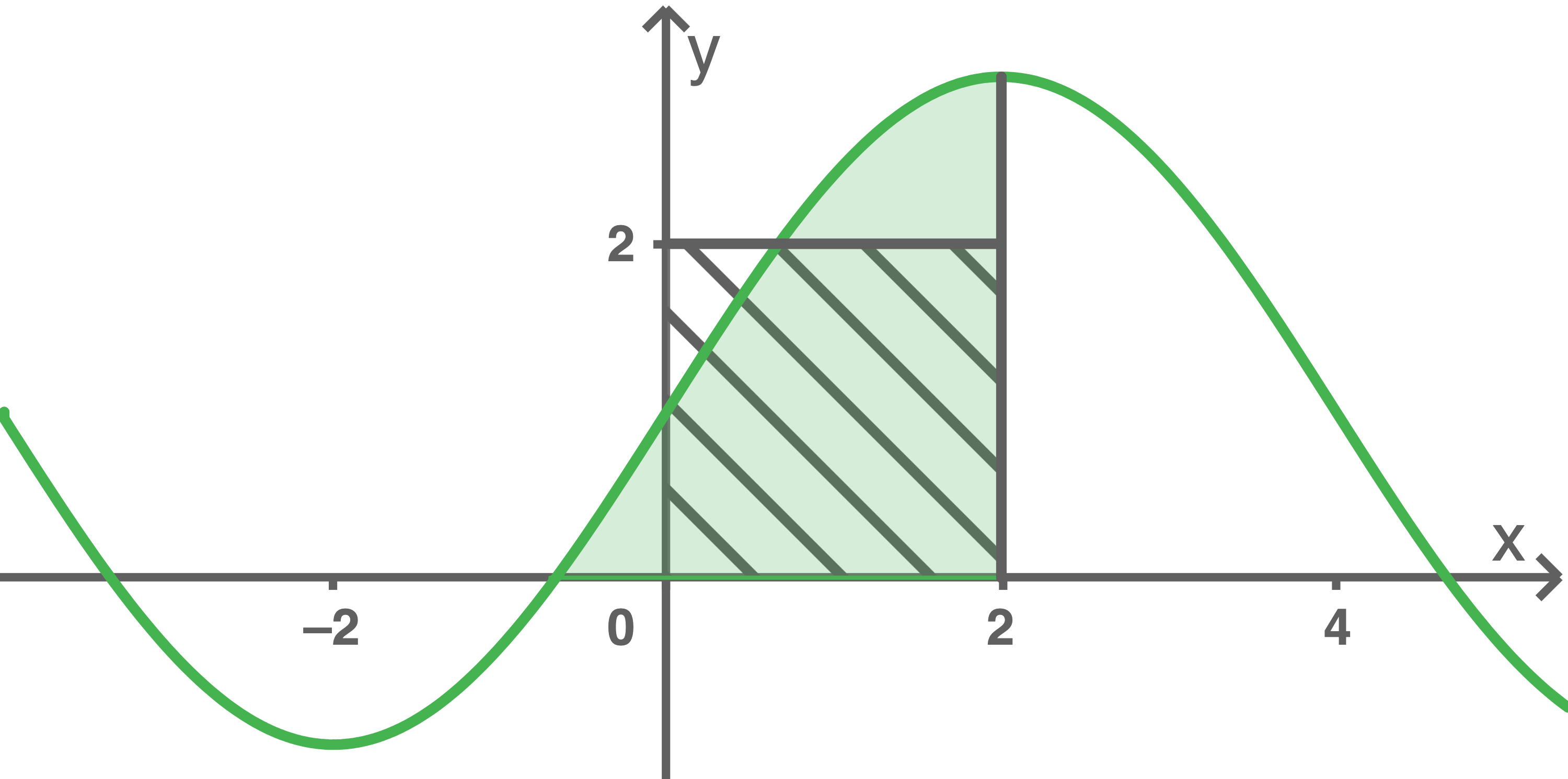
Berechne den Wert des Terms $\int_{-2}^{2} s(x) d x$ .

Beschreibe mithilfe der Abbildung 2, wie man zum Wert dieses Terms mit geometrischen Überlegungen gelangen kann.

Sachsen Abi 2022 LK Term geometrische Überlegung

Abbildung 2

(6 BE)

1.11

Der Graph von $s$ hat in jedem seiner Wendepunkte $(4 \cdot k \mid 1)$ mit $k \in \mathbb{Z}$ entweder die Steigung $-\frac{\pi}{2}$ oder die Steigung $\frac{\pi}{2}$ .

Für jeden Wendepunkt des Graphen von $s$ wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt $P(2022 \mid 2022)$ verläuft.

Untersuche, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von $s$ ist.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Schnittpunkt mit der Ordinatenachse

Rechenweg anzeigen

$f_p(0)=240$

Der Schnittpunkt mit der Ordinatenachse ist unabhängig von $p$ immer $240.$

Wert von $p$ bestimmen

Bedingung für Symmetrie zur Ordinatenachse:

$f(-x)=f(x)$

Rechenweg anzeigen

$(30-p) \cdot (-x)^{3}= (30-p) \cdot x^{3}$

Diese Gleichung lässt sich nur für $(30-p)=0$ und somit $p=30$ lösen.

Verhalten für $x\rightarrow\infty$ bestimmen

$p\lt 0$ : für $x\rightarrow+\infty$ gilt $f_p(x)\rightarrow -\infty$

$p\geq 0$ : für $x\rightarrow+\infty$ gilt $f_p(x)\rightarrow +\infty$

1.2

Aus den drei Aussagen folgt, dass $G_p$ einen Tiefpunkt bei $(2|120)$ besitzt.

Bei Aussage $II$ wurde die notwendige Bedingung für Extremstellen angewendet, bei Aussage $III$ die hinreichende Bedingung für Extremstellen.

Aus $p\gt0$ und somit $\(III:f_p$ ergibt sich, dass es sich hierbei um einen Tiefpunkt handelt.

1.3

Schnittstelle mit der $x-$ Achse berechnen

$\begin{array}[t]{rll} y&=& 0& \\[5pt] -90\cdot x+\dfrac{p}{4}+270&=& 0& \\[5pt] \end{array}$

Mit dem solve Befehl des CAS folgt $x= 3 +\dfrac{p}{360}.$

Schnittstelle mit der $y-$ Achse berechnen

$\begin{array}[t]{rll} y&=&-90\cdot 0+\dfrac{p}{4}+270 &\\[5pt] &=&\dfrac{p}{4}+270 \end{array}$

Flächeninhalt des eingeschlossenen Dreiecks bestimmen

$\begin{array}[t]{rll} A&=& 500& \\[5pt] \dfrac{1}{2}\cdot \left(\dfrac{p}{4}+270\right) \cdot \left(3 +\dfrac{p}{360}\right) &=& 500& \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS folgt $p=120.$

Für $p=120$ beträgt der Inhalt der eingeschlossenen Fläche $500.$

1.4

Geschwindigkeit bestimmen

$\begin{array}[t]{rll} f(0,5) &=& 30 \cdot 0,5^3 - 90 \cdot 0,5^2 + 240 \\[5pt] &=& 221,25 \end{array}$

Die Geschwindigkeit des ICE beträgt eine halbe Minute nach 15:00 ca. $221 \; \frac{\text{km}}{\text{h}}.$

Geschwindigkeitsabnahme im ersten Intervall

Rechenweg anzeigen

$f(0)-f(0,5)=18,75$

Geschwindigkeitsabnahme im zweiten Intervall

Rechenweg anzeigen

$f(0,5)-f(1)= 41,25$

Folglich ist die Geschwindigkeitabnahme im zweiten Intervall größer als im ersten Intervall.

1.5

Zu bestimmen ist das Minimum.

Dies erfolgt mit dem Einsatz des CAS.

$\(f$ nimmt ihr Minimum an der Stelle $x=1$ an.

1.6

Die Gleichung beschreibt das Intervall einer halben Minute, in welcher die Geschwindigkeit um $20 \; \frac{\text{km}}{\text{h}}$ abnimmt.

Lösung der Gleichung angeben

Rechenweg anzeigen

Mit dem solve Befehl des CAS folgt $x_1=\dfrac{-\sqrt{77}+9}{12}.$

1.7

Es gilt: $2 \,\text{min}= \dfrac{1}{30}\,\text{h}$

Die zurückgelegte Strecke in den ersten beiden Minuten entspricht dem Flächeninhalt der Fläche, die der Graph von $f_0(x)$ im Intervall $\left[0,\dfrac{1}{30}\right]$ mit der $x$ -Achse einschließt.

Rechenweg anzeigen

Mit dem solve-Befehl des CAS folgt:

$\displaystyle\int_{0}^{\dfrac{1}{30}}f_0(x)\;\mathrm dx\approx 8 \;[\,\text{km}]$

Zurückgelegte Strecke in der dritten Minute:

$1 \,\text{min}\mathrel{\widehat{=}} \dfrac{1}{60}\,\text{h}$

$\begin{array}[t]{rll} s&=&\dfrac{1}{60}\cdot 120 & \\[5pt] &=&2 \; [\text{km}] \end{array}$

Der ICE legt in den ersten drei Minuten folglich $8 \; \text{km} +2 \; \text{km} =10 \; \text{km}$ zurück.

1.8

Tangente bei $x_0=1$ aufstellen

Anwenden der Tangentengleichung ergibt:

$\(\begin{array}[t]{rll} y&=& f$

Nullstelle der Tangente bestimmen

$\begin{array}[t]{rll} y&=& 0 \\[5pt] -90 \cdot x+ 270 &=& 0 &\quad \scriptsize \mid\; -270 \\[5pt] -90 \cdot x &=& -270 &\quad \scriptsize \mid\; :90 \\[5pt] x &=& 3 \end{array}$

Zurückgelegte Strecke berechnen

Die zurückgelegte Strecke $s$ entspricht dem Flächeninhalt, den der Graph von $y$ mit der $x$ -Achse im Intervall $[1;3]$ einschließt.

$\begin{array}[t]{rll} s&=& \dfrac{1}{60} \cdot \dfrac{1}{2} \cdot 2 \cdot f(1)& \\[5pt] s&=& \dfrac{1}{60} \cdot 180 \\[5pt] s&=& 3 \; [\text{km} ] \end{array}$

Die Aussage ist richtig.

1.9

Mit dem CAS können die Koordinaten eines Hochpunkts bestimmt werden:

Es ergibt sich der Hochpunkt $H(2|3).$

Aufeinanderfolgende Extremstellen untersuchen

Periodenlänge bestimmen:

$p=\dfrac{2\pi}{b}=\dfrac{2\pi}{\dfrac{\pi}{4}}=8$

Aus der Periodenlänge $8$ folgt, dass sich die Extrempunkte im Abstand von $4 \; [\text{LE}]$ zueinander befinden.

Auf die Extremstelle $x_1=2$ folgt demnach die Extremstelle $x_2=6.$

Durch die Sinus Funktion ist bestimmt, dass der folgende Extrempunkt an der Stelle $x_2$ also ein Tiefpunkt sein muss.

Koordinaten bestimmen

$\begin{array}[t]{rll} s(6)&=&2\cdot \sin \left(\dfrac{\pi}{4}\cdot 6\right)+1 & \\[5pt] &=&2\cdot (-1)+1 & \\[5pt] &=& -1 \end{array}$

Somit ergeben sich folgende aufeinanderfolgende Extrempunkte:

$H(2|3)$ und $T(6|-1)$

1.10

Wert des Terms berechnen

Rechenweg anzeigen

$\displaystyle\int_{-2}^{2}s(x)\;\mathrm dx =2$

Geometrische Überlegungen beschreiben

Der Graph von $s$ ist symmetrisch bezüglich des Punktes $(0\mid 1).$

Damit haben die Flächenstücke $A_{1}$ und $A_{4}$ ebenso den gleichen Inhalt wie die Flächenstücke $A_{2}$ und $A_{3}.$

Aufgrund der Lage dieser Flächenstücke bezüglich der $x$ -Achse und bezüglich des abgebildeten Quadrats, stimmt der Wert des Terms mit dem Flächeninhalt des Quadrats überein, ist also $2^{2}=4$ .

Also gilt:

$\displaystyle\int_{-2}^{2}s(x)\;\mathrm dx = 4$

1.11

Koordinaten der Wendepunkte

Dem Text kann entnommen werden, dass die Wendepunkte die Koordinaten $(4k \mid 1)$ mit $k \in \mathbb{Z}$ besitzen.

Steigung der Geraden

Die betrachteten Geraden haben folgende Steigung:

$\begin{array}[t]{rll} m &=& \dfrac{\Delta y}{\Delta x}\\[5pt] m &=& \dfrac{2022 - 1}{2022-4k} \\[5pt] m &=& \dfrac{2021}{2022-4k} \\[5pt] \end{array}$

Folglich ist die Steigung für jedes $k \in \mathbb{Z}$ rational. Die Steigung in den Wendestellen ist nach Aufgabenstellung $\pm \frac{\pi}{2}$ und somit irrational. Folglich ist keine der Geraden eine Tangente einer Wendestelle.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?