Teil B1

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f_a$ und $g_a$ mit

$f_a(x)= -\frac{a}{250}\cdot x^4 + \frac{1}{25}\cdot x^3$ $(a\in \mathbb{R}; a\gt 0)$

sowie

$g_a(x) = f_a(x) - \frac{3}{5}\cdot x.$

Die Abbildung 1 zeigt die Graphen von $f_1$ und $g_1.$

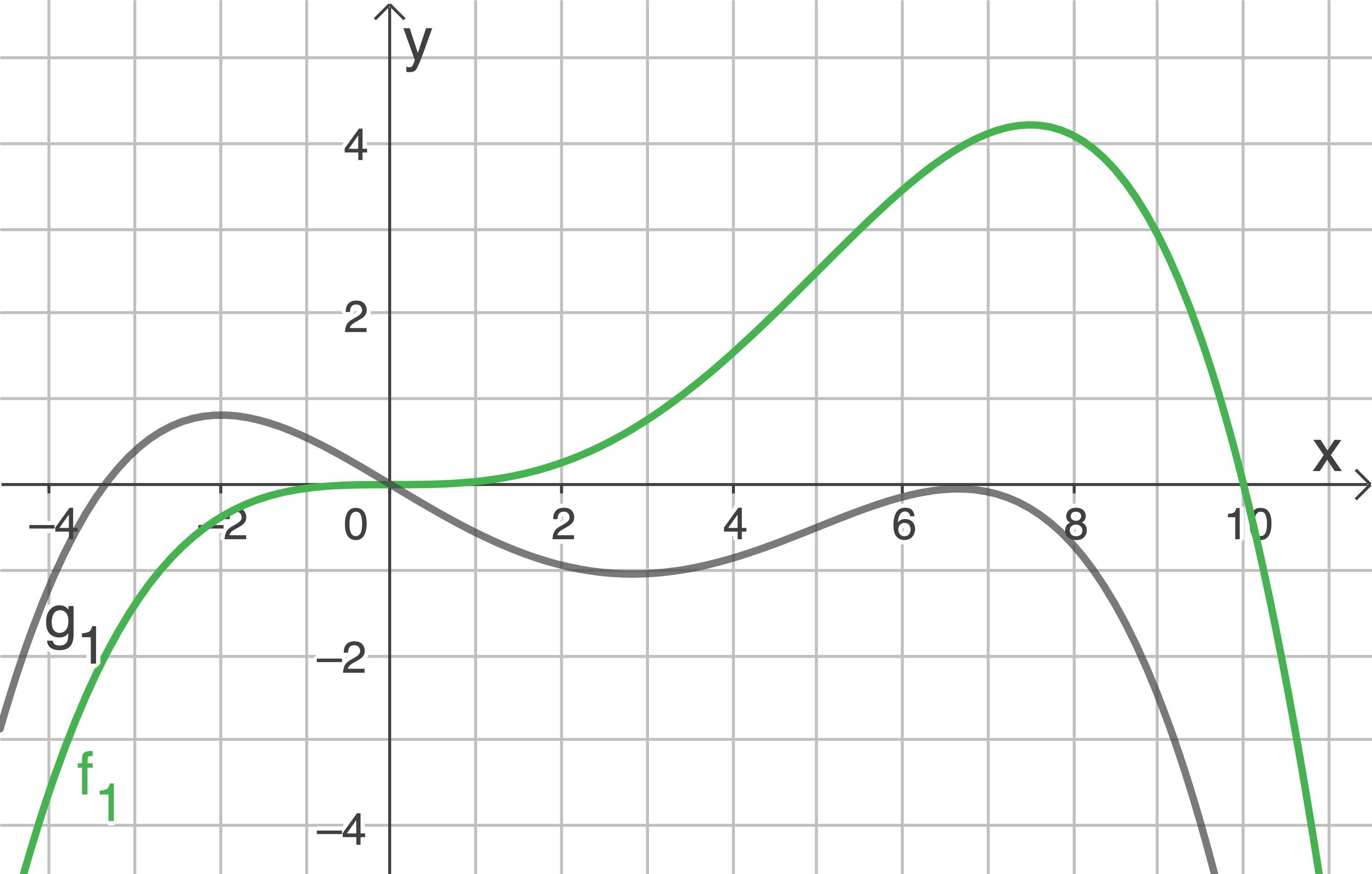
Zweidimensionales Diagramm mit zwei Kurven, einer grünen und einer grauen, in einem Koordinatensystem.

Abbildung 1 (nicht maßstäblich)

1.1

Gib für den Graphen von $f_1$ die Koordinaten der Schnittpunkte mit den Koordinatenachsen sowie die Koordinaten des Extrempunkts an.
Gib an, für welche Werte von $x$ der Graph von $f_1$ oberhalb des Graphen von $g_1$ verläuft und für welche unterhalb.
Begründe deine Angabe anhand der Funktionsgleichung $g_1(x)=f_1(x) - \frac{3}{5}\cdot x.$

(8 BE)

1.2

Für jeden Wert von $a$ gilt:

Die Funktionsterme von $f_a$ und $g_a$ unterscheiden sich nur um den Summanden $-\frac{3}{5}\cdot x.$

Der Graph von $f_a$ hat genau zwei Wendepunkte, deren $x$ -Koordinaten 0 und $\frac{5}{a}$ sind.

Gib an, was sich aus I und II hinsichtlich der Anzahl und der Koordinaten der Wendepunkte des Graphen von $g_a$ im Vergleich zu den Wendepunkten des Graphen von $f_a$ folgern lässt.
Begründe deine Angabe.

(5 BE)

Die Tangente $t_f$ an den Graphen von $f_a$ an der Stelle $x= \frac{5}{a}$ wird durch die Gleichung

$y= \dfrac{1}{ a^2}\cdot x - \dfrac{5}{2\cdot a^3}$ $(x\in \mathbb{R})$ beschrieben.

Die Tangente $t_g$ an den Graphen von $g_a$ an der Stelle $x= \frac{5}{a}$ wird durch die Gleichung

$y= \dfrac{5-3\cdot a^2}{5\cdot a^2}\cdot x - \dfrac{5}{2\cdot a^3}$ $(x\in \mathbb{R})$ beschrieben.

Der Schnittpunkt $S$ dieser beiden Tangenten liegt für jeden Wert von $a$ auf der $y$ -Achse.

1.3

Gib die Koordinaten von $S$ an.
Berechne für $a=1$ den Schnittwinkel der Tangenten $t_f$ und $t_g$ in $S.$

(6 BE)

1.4

Die Gerade mit der Gleichung $x=\frac{5}{a}$ schneidet $t_f$ im Punkt $F$ und $t_g$ im Punkt $G.$
Bestimme einen reellen Wert $a\gt 0,$ für den das Dreieck $SGF$ rechtwinklig ist.

(6 BE)

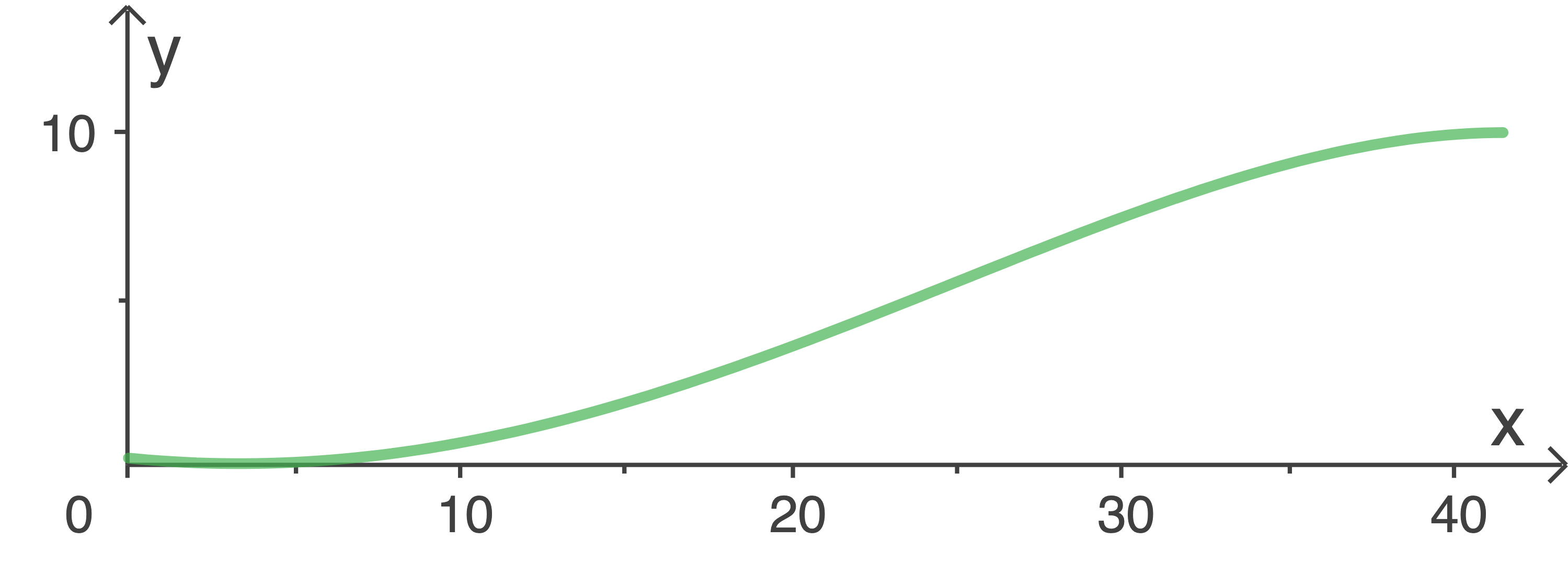
Die Abbildung 2 zeigt schematisch die Profillinie des Längsschnitts einer Skipiste in einer Skihalle. Die Skipiste ist in Querrichtung nicht geneigt und durchgehend 30 m breit.

Ein Diagramm mit einer grünen Kurve, die eine ansteigende Funktion darstellt. Achsen sind beschriftet mit x und y.

Abbildung 2 (nicht maßstäblich)

Die Profillinie wird für $0\leq x \leq 41,5$ modellhaft durch den Graphen der in $\mathbb{R}$ definierten Funktion $p$ mit

Formel anzeigen

$p(x)=...$

dargestellt.

Im verwendeten Koordinatensystem beschreibt die $x$ -Achse die Horizontale; eine Längeneinheit im Koordinatensystem entspricht 10 m in der Realität.

1.5

Ermittle die Größe des größten Neigungswinkels der Skipiste gegenüber der Horizontalen.

(4 BE)

1.6

Der Verlauf eines Seils über der Profillinie der Skipiste kann modellhaft mithilfe der Funktion $h$ mit

$h(x)= 1,818 \cdot 1,049^x$ $(x\in \mathbb{R}; 5\leq x\leq 37)$

beschrieben werden. Das Seil ist an den beiden Punkten $A(5\mid h(5))$ und $B(37\mid h(37))$ befestigt.

Zeige, dass der vertikale Abstand des Seils zur Skipiste im Befestigungspunkt $A$ größer als 20 m ist.

Untersuche, in welchem Bereich der vertikale Abstand des Seils zur Skipiste höchstens 3 m beträgt.

Ermittle die Höhendifferenz, um die die beiden Befestigungspunkte gemeinsam mindestens angehoben werden müssten, damit das Seil an jeder Stelle von der Skipiste einen vertikalen Abstand von mindestens 3 m hat.

(10 BE)

1.7

Die Abbildung 3 zeigt grau markiert die Schneeauflage im unteren Bereich der Skipiste; dazu wurde die Abbildung 2 in Richtung der $y$ -Achse stärker vergrößert als in Richtung der $x$ -Achse.

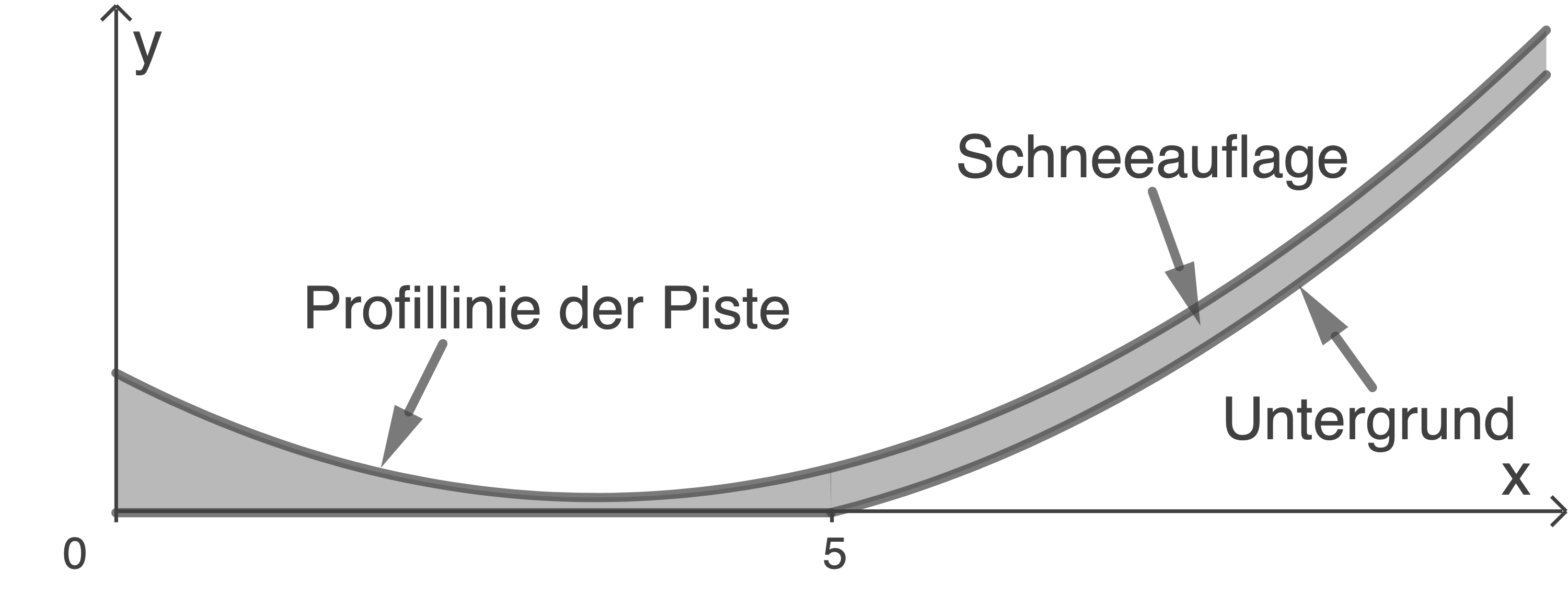
Diagramm zur Profilinie einer Piste mit Beschriftungen für Schneeauflage und Untergrund.

Abbildung 3 (nicht maßstäblich)

Der Untergrund, auf dem der Schnee aufgebracht ist, wird für $0\leq x\leq 5$ durch die $x$ -Achse dargestellt. Für den übrigen Teil der Skipiste soll davon ausgegangen werden, dass die in vertikaler Richtung gemessene Schneehöhe 60 cm beträgt.
Bestimme das Volumen der Schneeauflage der gesamten Skipiste.

(5 BE)

Die Höhe der Schneeauflage wird regelmäßig an verschiedenen Stellen der Skipiste durch Messung überprüft.

1.8

Die Höhe der Schneeauflage an einer bestimmten Stelle kann mithilfe einer normalverteilten Zufallsgröße $X$ beschrieben werden. Die Zufallsgröße $X$ besitzt den Erwartungswert 60 cm und die Standardabweichung 10 cm.
Berechne die Wahrscheinlichkeit dafür, dass bei einer Messung die Höhe der Schneeauflage mehr als 80 cm beträgt.
Beurteile ohne Rechnung die Richtigkeit der folgenden Aussage:

„Die Wahrscheinlichkeit, dass bei einer Messung die Höhe der Schneeauflage weniger als 45 cm beträgt, ist ebenso groß wie die Wahrscheinlichkeit, dass die Höhe der Schneeauflage mehr als 75 cm beträgt.“

(5 BE)

1.9

Die Höhe der Schneeauflage an einer anderen Stelle kann mithilfe einer normalverteilten Zufallsgröße $Y$ mit dem Erwartungswert 60 cm beschrieben werden. Die Wahrscheinlichkeit dafür, dass bei einer Messung die Höhe der Schneeauflage höchstens 50 cm beträgt, ist 22 %.
Ermittle die zugehörige Standardabweichung.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Die Schnittpunkte mit den Koordinatenachsen sind $S_1(0\mid 0)$ und $S_2(10\mid 0)$ .

Berechnung des Extrempunktes:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 6: Graph analysieren $\to$ 3: Maximum

$\blacktriangleright$ Casio Classpad II

Analyse $\to$ Grafische Lösung $\to$ Maximum

Der Taschenrechner liefert den Hochpunkt $H \left(\dfrac{15}{2}\,\bigg \vert \, \dfrac{135}{32}\right)$ .

Für $x\lt 0$ verläuft der Graph von $f_1$ unterhalb des Graphen von $g_1$ , denn es gilt:

$-\dfrac{3}{5}\cdot x \gt 0 \quad$ und somit $\quad f_1(x) \lt f_1(x) - \dfrac{3}{5} \cdot x$ .

Für $x\gt 0$ verläuft der Graph von $f_1$ oberhalb des Graphen von $g_1$ , denn es gilt:

$-\dfrac{3}{5}\cdot x \lt 0 \quad$ und somit $\quad f_1(x) \gt f_1(x) - \dfrac{3}{5} \cdot x$ .

1.2

Der Graph von $g_a$ hat dieselbe Anzahl an Wendepunkten wie der Graph von $f_a$ . Außerdem entsprechen die $x$ -Koordinaten der Wendepunkte der Graphen $g_a$ denen der Wendepunkte der Graphen $f_a$ .
Dies wird durch die Aussage $I$ begründet, da $\(f_a$ gilt. Durch die Aussage $II$ folgt, dass der Graph $g_a$ auch bei $0$ und $\dfrac {5}{a}$ Wendestellen vorliegen hat und aus $-\dfrac{3}{5} \cdot 0=0$ folgt, dass $g_a$ und $f_a$ an der Stelle $x=0$ denselben Funktionswert haben.

Insgesamt gilt also: $g_a$ hat zwei Wendepunkte: $W_{g_a 1} (0 \mid f_a(0))$ und $W_{g_a 2} \left( \dfrac{5}{a} \,\bigg \vert \, f_a \left( \dfrac{5}{a} \right) - \dfrac{3}{a} \right)$ .

1.3

Schnittpunkt der Tangenten $t_f$ und $t_g$ :

Da der Schnittpunkt $S$ auf der y-Achse liegt, gilt für die $x$ -Koordinate von $S$ : $x = 0$ .
Durch Einsetzen in $t_f$ folgt die y-Koordinate:

$y=\dfrac{1}{a^2}\cdot 0-\dfrac{5}{2a^3}=-\dfrac{5}{2a^3}$

Die Tangenten $t_f$ und $t_g$ schneiden sich im Punkt $S\left(0\,\bigg \vert \, -\dfrac{5}{2a^3}\right)$ .

Berechnung des Schnittwinkels:

$y_f=x-\dfrac{5}{2}$ und $y_g=\dfrac{2}{5}x-\dfrac{5}{2}$

$\begin{array}[t]{rll} \tan(\alpha)&=& \,\bigg \vert \, \dfrac{m_1-m_2}{1+m_1\cdot m_2}\,\bigg \vert \, &\quad \scriptsize \\[5pt] &=& \,\bigg \vert \, \dfrac{1-\frac{2}{5}}{1+1\cdot \frac{2}{5}}\,\bigg \vert \, &\quad \scriptsize \\[5pt] &=& \dfrac{3}{7} &\quad \scriptsize \mid \tan^{-1} \\[5pt] \alpha&\approx& 23,2 ^{\circ} \end{array}$

Die Tangenten $t_f$ und $t_g$ schneiden sich für $a=1$ in $S$ mit einem Winkel von etwa $23,2^{\circ}$ .

1.4

Für ein rechtwinkliges Dreieck bietet sich ein rechter Winkel in den Punkten $G$ oder $F$ an, da dort die anliegende Dreiecksseite $\overline{QF}$ senkrecht zur $x$ -Achse steht.

Damit dort ein rechter Winkel vorliegt, muss dann die Seite $\overline{SF}$ bzw. $\overline{SG}$ parallel zur $x$ -Achse verlaufen.
Mit anderen Worten: Die $y$ -Koordinate von $S$ muss der $y$ -Koordinate von $G$ bzw. $F$ entsprechen.

Rechter Winkel in Punkt $G$ :

$\begin{array}[t]{rll} g_a \left(\dfrac{5}{a} \right)& =& - \dfrac{5}{2a^3}& \quad \scriptsize \mid\; \text{Einsetzen} \\[5pt] \dfrac{5-3a^2}{a^3}&=& 0& \quad \scriptsize \mid\; \cdot a^3 \\[5pt] 5 - 3a^2 & =& 0 & \quad \scriptsize \mid \; + 3a^2 \\[5pt] 5 & =& 3a^2& \quad \scriptsize \mid\; :3 \\[5pt] \dfrac{5}{3}& =& a^2 & \quad \scriptsize \mid \; \sqrt{\;} \\[5pt] \pm \sqrt{\dfrac{5}{3}}& =& a& \end{array}$

Folglich liegt für $a= \sqrt{\dfrac{5}{3}}$ in $G$ ein rechter Winkel vor.

Rechter Winkel in Punkt F:

$\begin{array}[t]{rll} f_a(\dfrac{5}{a})& =& - \dfrac{5}{2a^3}&\quad \scriptsize \mid\; \text{Einsetzen} \\[5pt] \dfrac{5}{2a^3}& = & - \dfrac{5}{2a^3}& \end{array}$

Dies ist für keine reelle Zahl $a$ möglich.

Insgesamt gilt also: Das Dreieck ist für $a = \sqrt{\dfrac{5}{3}}$ rechtwinklig.

1.5

$\(p$

Zu Berechnen ist das Maximum der ersten Ableitung:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Taschenrechner liefert ein Maximum an der Stelle $x=25$ .

Die Steigung wird durch das Einsetzen von $x=25$ in $\(p$ berechnet:

$\(p$ $=0,4$

Berechnung des Neigungswinkels:

$\begin{array}[t]{rll} \tan(\alpha)&=& 0,4 &\quad \scriptsize \mid \tan^{-1}\\[5pt] \alpha&\approx& 22^{\circ} \end{array}$

Der größte Neigungswinkel der Skipiste beträgt etwa $22^{\circ}$ .

1.6

$h(5)=1,818\cdot 1,049^5\approx2,309$

Vollständigen Rechenweg anzeigen

$p(5)= 0,06$

$h(5)-p(5)=2,309-0,06=2,249$

$2,249\cdot 10\,\text{m}=22,49\,\text{m}$ .

Folglich beträgt der Abstand zwischen dem Seil und der Piste im Punkt $A$ mehr als $20\,\text{m}$ .

Der vertikale Abstand des Seils zur Skipiste kann durch die Funktion $d$ mit $d(x)=h(x)-p(x)$ beschrieben werden.
Für $5\leq x\leq 37$ liefert $d\leq0,3$ den gesuchten Bereich im Modell $x_1\leq x \leq x_2$ mit $x_1\approx 27,24$ und $x_2 \approx 32,64$ .

Für den Bereich $x_1\leq x \leq x_2$ ist der Tiefpunkt des Seils zu bestimmen:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 3: minimum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F3: MIN

Der Tiefpunkt liegt an der Stelle $x=30,09$ vor.

Mit $0,3-d(30,09)\approx 0,11$ folgt, dass die Befestigungspunkte um etwa $1,1\,\text{m}$ angehoben werden müssen.

1.7

In dem Bereich von $0$ bis $5$ wird das Integral der Funktion $p(x)$ berechnet.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

Vollständigen Rechenweg anzeigen

$V = 7500$

Das Volumen der Schneeauflage beträgt $7500\,\text{m}^3$ .

1.8

Mit Hilfe des Taschenrechners folgt:

$P(X\gt 80\,\text{cm}) \approx 0,0228$

Die Wahrscheinlichkeit, dass bei einer Messunge die Schneeauflage mehr als $80\,\text{cm}$ ist, beträgt $2,28\,\%$ .

Die Aussage ist war, da die Werte für die Höhe der Schneeauflage den gleichen Abstand zum Erwartungswert besitzen. Dadurch entstehen zwei zum Erwartungswert symmetrische Intervalle und die Wahrscheinlichkeiten sind gleich groß.

1.9

$P(X\leq50\,\text{cm})=\Phi\left(\dfrac{50\,\text{cm}-60\,\text{cm}}{\sigma}\right)$ $=0,22$

Dies liefert $\sigma =13\,\text{cm}$ für die zugehörige Standardabweichung.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?