Teil A
1
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig.
Kreuze das jeweilige Feld an.
1.1
Für welchen reellen Wert  hat die Funktion
hat die Funktion  mit
mit  an der Stelle
an der Stelle  den Anstieg 1?
den Anstieg 1?
1.2
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Die erste Ableitungsfunktion von
Die erste Ableitungsfunktion von  ist
ist  .
Der Wert von
.
Der Wert von  ist:
ist:
1.3
Für welche Funktion  mit größtmöglichem Definitionsbereich gilt
mit größtmöglichem Definitionsbereich gilt  ?
?
1.4
Für die Gerade  gilt:
gilt:
1.5
Für welchen positiven Wert  besitzt der zum Punkt
besitzt der zum Punkt  gehörende Ortsvektor die Länge 6?
gehörende Ortsvektor die Länge 6?
(5 BE)
2
Wird der Punkt  an der Ebene
an der Ebene  gespiegelt, so ergibt sich der Punkt
gespiegelt, so ergibt sich der Punkt  .
.
2.1
Bestimme eine Gleichung von  in parameterfreier Form.
in parameterfreier Form.
(3 BE)
2.2
Auf der Gerade durch  und
und  liegen die Punkte
liegen die Punkte  und
und  symmetrisch bezüglich
symmetrisch bezüglich  ; dabei liegt
; dabei liegt  bezüglich
bezüglich  auf der gleichen Seite wie
auf der gleichen Seite wie  .
Der Abstand von
.
Der Abstand von  und
und  ist doppelt so groß wie der Abstand von
ist doppelt so groß wie der Abstand von  und
und  .
Bestimme die Koordinaten von
.
Bestimme die Koordinaten von  .
.
(2 BE)
3
Gegeben sind die Punkte  und
und  . Gib die Koordinaten des Mittelpunkts der Strecke
. Gib die Koordinaten des Mittelpunkts der Strecke  an.
Bestimme eine Gleichung derjenigen Mittelsenkrechte von
an.
Bestimme eine Gleichung derjenigen Mittelsenkrechte von  , die parallel zur
, die parallel zur  -Ebene verläuft.
-Ebene verläuft.
(5 BE)
4
Betrachtet werden die in  definierten Funktionen
definierten Funktionen  und
und  , wobei
, wobei  eine Stammfunktion von
eine Stammfunktion von  ist.
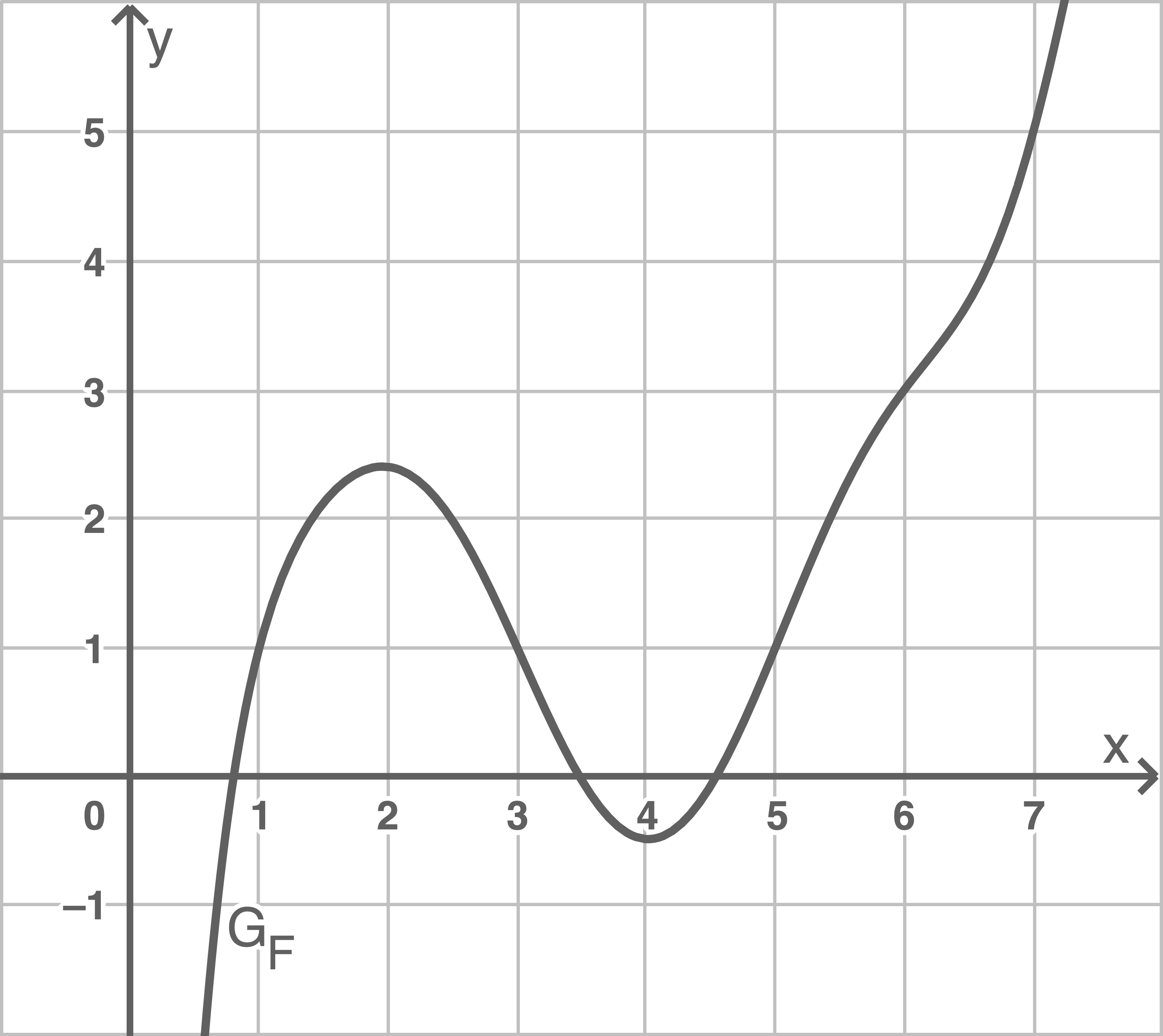
Die Abbildung zeigt den Graphen
ist.
Die Abbildung zeigt den Graphen  von
von  .
.
4.1
Bestimme den Wert des Integrals  .
.
(2 BE)
4.2
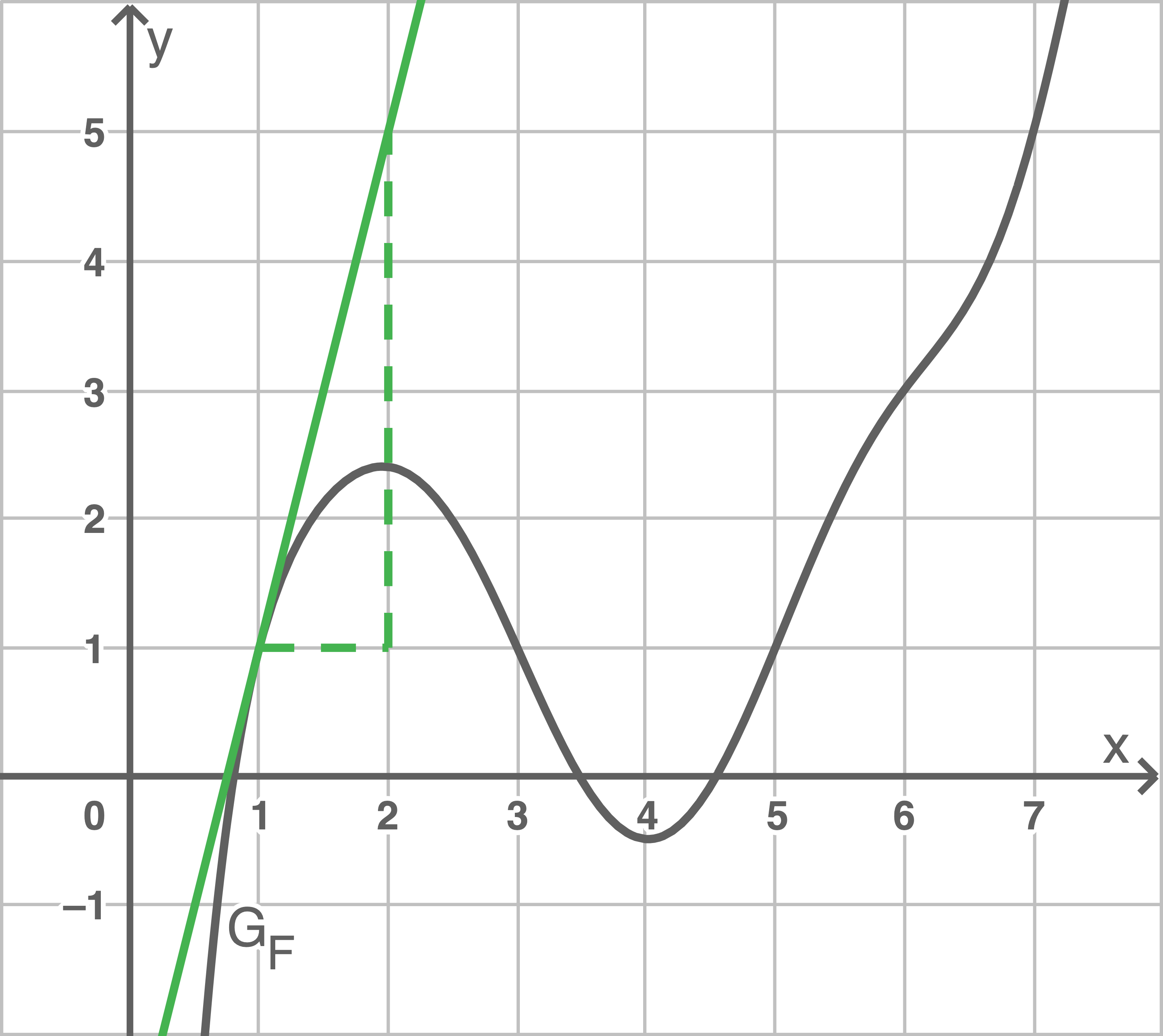
Bestimme den Funktionswert von  an der Stelle
an der Stelle  Veranschauliche dein Vorgehen in der Abbildung.
Veranschauliche dein Vorgehen in der Abbildung.
(3 BE)
5
Betrachtet werden die in  definierten Funktionen
definierten Funktionen  mit
mit 
5.1
Zeige, dass  gilt.
gilt.
(1 BE)
5.2
Bestimme diejenigen Werte von  , für die die Tangente im Punkt
, für die die Tangente im Punkt  an den Graphen von
an den Graphen von  eine positive Steigung hat und ihre Schnittstelle mit der
eine positive Steigung hat und ihre Schnittstelle mit der  -Achse größer als
-Achse größer als  ist.
ist.
(4 BE)
6
Ermittle eine Gleichung der quadratischen Funktion  , die die beiden folgenden Eigenschaften hat:
I
, die die beiden folgenden Eigenschaften hat:
I  Der Graph von
Der Graph von  schneidet die Gerade mit der Gleichung
schneidet die Gerade mit der Gleichung  im Punkt
im Punkt  unter einem rechten Winkel.
II
unter einem rechten Winkel.
II  Die
Die  - und die
- und die  -Koordinate des Extrempunkts des Graphen von
-Koordinate des Extrempunkts des Graphen von  stimmen überein.
stimmen überein.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Ableitung bilden:

![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/db26c40db404768b7ef5ba8c7901253287483a26259fcd5a25aaadd4c86d8d8b?color=5a5a5a) Die Funktion
Die Funktion  hat für
hat für  an der Stelle
an der Stelle  die Steigung
die Steigung 
1.2
1.3
Die dritte Antwortmöglichkeit ist richtig.

1.4
Die vierte Antwortmöglichkeit ist richtig.
Die  -Koordinate jedes Punktes, der auf der Geraden liegt, entspricht der Zahl 7. Somit verläuft die Gerade parallel zur
-Koordinate jedes Punktes, der auf der Geraden liegt, entspricht der Zahl 7. Somit verläuft die Gerade parallel zur  -Ebene und ist somit senkrecht zur
-Ebene und ist somit senkrecht zur  -Achse.
-Achse.
1.5
2.1
1. Schritt: Einen Normalenvektor von  bestimmen
Ein Normalenvektor von
bestimmen
Ein Normalenvektor von  ist gegeben durch
ist gegeben durch 
 2. Schritt: Punkt aus
2. Schritt: Punkt aus  ermitteln
Der Mittelpunkt
ermitteln
Der Mittelpunkt  der Strecke
der Strecke  liegt in der Ebene
liegt in der Ebene  Die Koordinaten von
Die Koordinaten von  ergeben sich zu:
ergeben sich zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OP}+\dfrac{1}{2}\cdot \overrightarrow{PQ} & \\[5pt]
&=&\pmatrix{1\\2\\3}+\dfrac{1}{2}\cdot \pmatrix{6\\0\\8} & \\[5pt]
&=&\pmatrix{4\\2\\7}
\end{array}\)](https://mathjax.schullv.de/8f17aabcd499d84dad3f64233ed504449a40b2e71bf437ae2ba1bea2d0093db3?color=5a5a5a)
 3. Schritt:
3. Schritt:  in
in  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
E: 6\cdot x_1+8\cdot x_3&=&c & \\[5pt]
6\cdot 4+8\cdot 7&=&c & \\[5pt]
80&=&c
\end{array}\)](https://mathjax.schullv.de/f876ac7e7dd3a68ee0a6bddcd0c07c0efb3b3b834613f2915208c00c13440936?color=5a5a5a) Eine parameterfreie Gleichung für
Eine parameterfreie Gleichung für  ist somit gegeben durch:
ist somit gegeben durch:

2.2
3
1. Schritt: Koordinaten des Mittelpunktes bestimmen
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\frac{1}{2}\cdot \left(\overrightarrow{OA}+ \overrightarrow{OB}\right) \\[5pt]
&=&\frac{1}{2}\cdot \left(\pmatrix{-5\\5\\-3}+\pmatrix{-1\\1\\-1}\right) \\[5pt]
&=&\pmatrix{-3\\3\\-2}
\end{array}\)](https://mathjax.schullv.de/1af40a174eae729730aec4af8655e20dcecf7cd449abc8e09f7b2ce743a0d37c?color=5a5a5a)
 2. Schritt: Richtungsvektor bestimmen
Damit der Richtungsvektor
2. Schritt: Richtungsvektor bestimmen
Damit der Richtungsvektor  parallel zur
parallel zur  -Ebene ist, muss
-Ebene ist, muss  gelten. Außerdem muss er senkrecht zu
gelten. Außerdem muss er senkrecht zu  sein:
sein:
![\(\begin{array}[t]{rlll}
\overrightarrow{r}\circ \overrightarrow{AB}&=& 0 \\[5pt]
4x -4\cdot 0 + 2z &=& 0 \\[5pt]
4x + 2z &=& 0
\end{array}\)](https://mathjax.schullv.de/516afc7a8b3b4ee1093f95a5f92225500ce9a99cd8106c71976d4fc0fdcf50b9?color=5a5a5a) Werte, die diese Gleichung erfüllen, sind beispielsweise
Werte, die diese Gleichung erfüllen, sind beispielsweise  und
und  3. Schritt: Geradengleichung für die Mittelsenkrechte aufstellen
3. Schritt: Geradengleichung für die Mittelsenkrechte aufstellen
![\(\begin{array}[t]{rll}
s: \overrightarrow{x}&=&\overrightarrow{OM}+ t\cdot \overrightarrow{r} & \\[5pt]
\overrightarrow{x}&=&\pmatrix{-3\\3\\-2} + t\cdot \pmatrix{1\\0\\-2}
\end{array}\)](https://mathjax.schullv.de/10b8bab9fc71b08cd493a790dbdb4945856a73f4664322d9e2e471e038de5578?color=5a5a5a)
4.1
4.2
5.1
Ableitung bilden:

![\(\begin{array}[t]{rll}
f_k](https://mathjax.schullv.de/a5500765f732b91287bca413401b6faea16dac4e7f51e25b870774733bfe550f?color=5a5a5a)
5.2
6
Gleichung einer quadratischen Funktion:
 Aus dem Schnittpunkt mit der Gerade
Aus dem Schnittpunkt mit der Gerade  folgt, dass die Gerade ebenfalls durch den Punkt
folgt, dass die Gerade ebenfalls durch den Punkt  verläuft.
verläuft.
![\(\begin{array}[t]{rll}
g(0)&=& 1& \\[5pt]
a\cdot 0^2+b\cdot 0+c&=& 1& \\[5pt]
c&=&1
\end{array}\)](https://mathjax.schullv.de/7c84273a2b22990fc82adf63eaf652535ba9b97f7bc247a6aa88b6a103f909a1?color=5a5a5a) Der Schnittwinkel von
Der Schnittwinkel von  weist auf Orthogonalität hin. Für
weist auf Orthogonalität hin. Für  gilt also:
gilt also:
 Eingesetzt in
Eingesetzt in  ergibt sich so:
ergibt sich so:
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/ca3d93070dc422593543a9c93e5108d3ea68eb7516ea0b8e60010561660ab62f?color=5a5a5a) Extrempunkt bestimmen:
Notwendige Bedingung für einen Extrempunkt anwenden:
Extrempunkt bestimmen:
Notwendige Bedingung für einen Extrempunkt anwenden:
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/629348ef3ebb291e4edd77eb48e681460c59cfe6e8b33910a509300db7b70de1?color=5a5a5a) Da bereits vorausgesetzt ist, dass ein Extrempunkt existiert, ist das Prüfen der hinreichenden Bedingung hier nicht mehr nötig.
Da bereits vorausgesetzt ist, dass ein Extrempunkt existiert, ist das Prüfen der hinreichenden Bedingung hier nicht mehr nötig.
![\(\begin{array}[t]{rll}
g\left(\dfrac{2}{a}\right)&=&\dfrac{2}{a} & \\[5pt]
a\cdot\left(\dfrac{2}{a}\right)^2-4\cdot \left(\dfrac{2}{a}\right)+1&=&\dfrac{2}{a} & \\[5pt]
a\cdot\dfrac{4}{a^2}-\dfrac{8}{a}+1&=&\dfrac{2}{a} & \\[5pt]
-\dfrac{4}{a}+1&=&\dfrac{2}{a} &\quad \scriptsize \mid\; \cdot a \\[5pt]
-4+a&=& 2 &\quad \scriptsize \mid\; +4 \\[5pt]
a&=& 6 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9093b82b4baa3e36ac61cd6600fc9ec1cff8754e6eff04f89f03968305b908b8?color=5a5a5a) Somit folgt:
Somit folgt: 