Teil B2
In einem Wald ist ein Baumwipfelpfad geplant.
Er soll vier Aussichtsplattformen besitzen. Die Aussichtsplattformen sind in der Planung untereinander durch Brücken verbunden, welche jeweils in einer Aussichtsplattform beginnen bzw. enden. Die Aussichtsplattformen werden als Punkte, die Brücken als Strecken angenommen.
Der geplante Baumwipfelpfad kann in einem kartesischen Koordinatensystem dargestellt werden (1 Längeneinheit entspricht 1 Meter). Drei der Aussichtsplattformen sollen sich in den Punkten ,
,  und
und  befinden. Die vierte Aussichtsplattform ist in Abhängigkeit von
befinden. Die vierte Aussichtsplattform ist in Abhängigkeit von  im Punkt
im Punkt  geplant.
geplant.
Die Punkte ,
,  und
und  liegen in der Ebene
liegen in der Ebene  . Der ebene Waldboden liegt in der
. Der ebene Waldboden liegt in der  -
- -Koordinatenebene.
-Koordinatenebene.
Er soll vier Aussichtsplattformen besitzen. Die Aussichtsplattformen sind in der Planung untereinander durch Brücken verbunden, welche jeweils in einer Aussichtsplattform beginnen bzw. enden. Die Aussichtsplattformen werden als Punkte, die Brücken als Strecken angenommen.
Der geplante Baumwipfelpfad kann in einem kartesischen Koordinatensystem dargestellt werden (1 Längeneinheit entspricht 1 Meter). Drei der Aussichtsplattformen sollen sich in den Punkten
Die Punkte
2.1 Begründe, dass die Aussichtsplattformen in den Punkten  ,
,  und
und  in der Ebene
in der Ebene  mit
mit  liegen.
liegen.
Ermittle die Gesamtlänge der drei Brücken, welche die Aussichtsplattformen in den Punkten ,
,  und
und  untereinander verbinden sollen.
untereinander verbinden sollen.
Bestimme den Neigungswinkel der Brücke zwischen den Aussichtsplattformen in den Punkten und
und  gegenüber dem ebenen Waldboden.
gegenüber dem ebenen Waldboden.
Ermittle die Gesamtlänge der drei Brücken, welche die Aussichtsplattformen in den Punkten
Bestimme den Neigungswinkel der Brücke zwischen den Aussichtsplattformen in den Punkten
(9P)
2.2 Die Brücken, die von der Aussichtsplattform im Punkt  zu den Aussichtsplattformen in den Punkten
zu den Aussichtsplattformen in den Punkten  ,
,  und
und  führen, sollen in einer Planungsvariante I ebenfalls in der Ebene
führen, sollen in einer Planungsvariante I ebenfalls in der Ebene  liegen.
liegen.
Ermittle dafür den Wert von .
.
Ermittle dafür den Wert von
(3P)
2.3 Bestimme die Koordinaten desjenigen Punktes auf der Brücke zwischen den Aussichtsplattformen in den Punkten  und
und  , der den geringsten Abstand zum Punkt
, der den geringsten Abstand zum Punkt  besitzt.
besitzt.
Die Brücke zwischen den Aussichtsplattformen in den Punkten und
und  liegt auf der Geraden
liegt auf der Geraden  . Die Brücke zwischen den Aussichtsplattformen in den Punkten
. Die Brücke zwischen den Aussichtsplattformen in den Punkten  und
und  liegt auf der Geraden
liegt auf der Geraden  .
Der Abstand
.
Der Abstand  der Geraden
der Geraden  und
und  beträgt
beträgt  .
Es gibt einen Wert von
.
Es gibt einen Wert von  , für den der Abstand der Geraden
, für den der Abstand der Geraden  und
und  maximal ist.
maximal ist.
Bestimme diesen Wert von und gib den maximalen Abstand an.
und gib den maximalen Abstand an.
Die Brücke zwischen den Aussichtsplattformen in den Punkten
Bestimme diesen Wert von
(6P)
2.4 In der Planungsvariante II soll der Wert von  so gewählt werden, dass für den zugehörigen Punkt
so gewählt werden, dass für den zugehörigen Punkt  folgende Bedingungen gelten:
folgende Bedingungen gelten:
 .
.
- Der Abstand der Aussichtsplattform im Punkt
zur Ebene
soll höchstens
betragen.
- Die Brücken von der Aussichtsplattform im Punkt
zu den Aussichtsplattformen in den Punkten
und
sollen einen Winkel von mindestens
einschließen
(8P)
2.5 Ausgehend von den Aussichtsplattformen sollen geradlinige Sicherungsseile gespannt werden.
Ein Sicherungsseil soll vom Punkt  so zum Waldboden gespannt werden, dass es unter einem Winkel von
so zum Waldboden gespannt werden, dass es unter einem Winkel von  auf dem Waldboden auftrifft.
Ermittle die Koordinaten eines möglichen Auftreffpunktes dieses Sicherungsseiles auf dem Waldboden.
Alle Punkte in der
auf dem Waldboden auftrifft.
Ermittle die Koordinaten eines möglichen Auftreffpunktes dieses Sicherungsseiles auf dem Waldboden.
Alle Punkte in der  -
- -Koordinatenebene, die als Auftreffpunkte dieses Sicherungsseiles auf dem Waldboden in Frage kommen, schließen eine Fläche vollständig ein.
Bestimme den Inhalt dieser Fläche.
-Koordinatenebene, die als Auftreffpunkte dieses Sicherungsseiles auf dem Waldboden in Frage kommen, schließen eine Fläche vollständig ein.
Bestimme den Inhalt dieser Fläche.
(8P)
2.6 Die Reißfestigkeit der vorgesehenen Sicherungsseile ist annähernd normalverteilt.
Der Hersteller der Seile gibt an, dass der Erwartungswert für die Reißfestigkeit dieser Seile bei  liegt. Außerdem gibt der Hersteller an, dass die Wahrscheinlichkeit dafür, dass ein Sicherungsseil bei einer Belastung von mehr als
liegt. Außerdem gibt der Hersteller an, dass die Wahrscheinlichkeit dafür, dass ein Sicherungsseil bei einer Belastung von mehr als  reißt, bei ca.
reißt, bei ca.  liegt.
Bestimme auf der Grundlage dieser Angaben, mit welcher Wahrscheinlichkeit davon ausgegangen werden muss, dass ein Sicherungsseil bei einer Belastung zwischen
liegt.
Bestimme auf der Grundlage dieser Angaben, mit welcher Wahrscheinlichkeit davon ausgegangen werden muss, dass ein Sicherungsseil bei einer Belastung zwischen  und
und  reißt.
reißt.
(6P)
2.7 Es wird erwartet, dass ca.  der zukünftigen Besucher des Baumwipfelpfades aus der näheren Umgebung kommen. Außerdem wird erwartet, dass der Anteil von Kindern unter den zukünftigen Besuchern, die nicht aus der näheren Umgebung kommen, bei ca.
der zukünftigen Besucher des Baumwipfelpfades aus der näheren Umgebung kommen. Außerdem wird erwartet, dass der Anteil von Kindern unter den zukünftigen Besuchern, die nicht aus der näheren Umgebung kommen, bei ca.  liegen wird. Der Gesamtanteil der Kinder unter allen zukünftigen Besuchern wird mit ca.
liegen wird. Der Gesamtanteil der Kinder unter allen zukünftigen Besuchern wird mit ca.  prognostiziert.
An Ferientagen werden pro Tag ca.
prognostiziert.
An Ferientagen werden pro Tag ca.  Kinder aus der näheren Umgebung als zukünftige Besucher erwartet.
Ermittle, mit welcher Gesamtbesucherzahl an einem Ferientag geplant wird.
Kinder aus der näheren Umgebung als zukünftige Besucher erwartet.
Ermittle, mit welcher Gesamtbesucherzahl an einem Ferientag geplant wird.
(5P)
Materialien für Aufgaben zur Stochastik
Verteilungsfunktion der Standardnormalverteilung
|
|
|
|
|

| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2
|
||||||||||||
|
3
|
z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|
4
|
0,0 | 0,5000 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 | |
|
5
|
0,1 | 0,5398 | 0,5438 | 0,5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0,5714 | 0,5753 | |
|
6
|
0,2 | 0,5793 | 0,5832 | 0,5871 | 0,5910 | 0,5948 | 0,5987 | 0,6026 | 0,6064 | 0,6103 | 0,6141 | |
|
7
|
0,3 | 0,6179 | 0,6217 | 0,6255 | 0,6293 | 0,6331 | 0,6368 | 0,6406 | 0,6443 | 0,6480 | 0,6517 | |
|
8
|
0,4 | 0,6554 | 0,6591 | 0,6628 | 0,6664 | 0,6700 | 0,6736 | 0,6772 | 0,6808 | 0,6844 | 0,6879 | |
|
9
|
0,5 | 0,6915 | 0,6950 | 0,6985 | 0,7019 | 0,7054 | 0,7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 | |
|
10
|
0,6 | 0,7257 | 0,7291 | 0,7324 | 0,7357 | 0,7389 | 0,7422 | 0,7454 | 0,7486 | 0,7517 | 0,7549 | |
|
11
|
0,7 | 0,7580 | 0,7611 | 0,7642 | 0,7673 | 0,7704 | 0,7734 | 0,7764 | 0,7794 | 0,7823 | 0,7852 | |
|
12
|
0,8 | 0,7881 | 0,7910 | 0,7939 | 0,7967 | 0,7995 | 0,8023 | 0,8051 | 0,8078 | 0,8106 | 0,8133 | |
|
13
|
0,9 | 0,8159 | 0,8186 | 0,8212 | 0,8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0,8365 | 0,8389 | |
|
14
|
1,0 | 0,8413 | 0,8438 | 0,8461 | 0,8485 | 0,8508 | 0,8531 | 0,8554 | 0,8577 | 0,8599 | 0,8621 | |
|
15
|
1,1 | 0,8643 | 0,8665 | 0,8686 | 0,8708 | 0,8729 | 0,8749 | 0,8770 | 0,8790 | 0,8810 | 0,8830 | |
|
16
|
1,2 | 0,8849 | 0,8869 | 0,8888 | 0,8907 | 0,8925 | 0,8944 | 0,8962 | 0,8980 | 0,8997 | 0,9015 | |
|
17
|
1,3 | 0,9032 | 0,9049 | 0,9066 | 0,9082 | 0,9099 | 0,9115 | 0,9131 | 0,9147 | 0,9162 | 0,9177 | |
|
18
|
1,4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 | |
|
19
|
1,5 | 0,9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0,9406 | 0,9418 | 0,9429 | 0,9441 | |
|
20
|
1,6 | 0,9452 | 0,9463 | 0,9474 | 0,9484 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 | |
|
21
|
1,7 | 0,9554 | 0,9564 | 0,9573 | 0,9582 | 0,9591 | 0,9599 | 0,9608 | 0,9616 | 0,9625 | 0,9633 | |
|
22
|
1,8 | 0,9641 | 0,9649 | 0,9656 | 0,9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0,9699 | 0,9706 | |
|
23
|
1,9 | 0,9713 | 0,9719 | 0,9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9761 | 0,9767 | |
|
24
|
2,0 | 0,9772 | 0,9778 | 0,9783 | 0,9788 | 0,9793 | 0,9798 | 0,9803 | 0,9808 | 0,9812 | 0,9817 | |
|
25
|
2,1 | 0,9821 | 0,9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0,9846 | 0,9850 | 0,9854 | 0,9857 | |
|
26
|
2,2 | 0,9861 | 0,9864 | 0,9868 | 0,9871 | 0,9875 | 0,9878 | 0,9881 | 0,9884 | 0,9887 | 0,9890 | |
|
27
|
2,3 | 0,9893 | 0,9896 | 0,9898 | 0,9901 | 0,9904 | 0,9906 | 0,9909 | 0,9911 | 0,9913 | 0,9916 | |
|
28
|
2,4 | 0,9918 | 0,9920 | 0,9922 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 | |
|
29
|
2,5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 | |
|
30
|
2,6 | 0,9953 | 0,9955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 | |
|
31
|
2,7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 | |
|
32
|
2,8 | 0,9974 | 0,9975 | 0,9976 | 0,9977 | 0,9977 | 0,9978 | 0,9979 | 0,9979 | 0,9980 | 0,9981 | |
|
33
|
2,9 | 0,9981 | 0,9982 | 0,9982 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 | |
|
34
|
3,0 | 0,9987 | 0,9987 | 0,9987 | 0,9988 | 0,9988 | 0,9989 | 0,9989 | 0,9989 | 0,9990 | 0,9990 | |
|
35
|
3,1 | 0,9990 | 0,9991 | 0,9991 | 0,9991 | 0,9992 | 0,9992 | 0,9992 | 0,9992 | 0,9993 | 0,9993 | |
|
36
|
3,2 | 0,9993 | 0,9993 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9995 | 0,9995 | 0,9995 | |
|
37
|
3,3 | 0,9995 | 0,9995 | 0,9995 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9997 | |
|
38
|
3,4 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9998 | |
|
39
|
3,5 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | |
|
40
|
3,6 | 0,9998 | 0,9998 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
41
|
3,7 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
42
|
3,8 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
43
|
3,9 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Aufgabe B 2
2.1  Begründe, dass Punkte in der Ebene liegen
Du sollst zeigen, dass die Punkte
Begründe, dass Punkte in der Ebene liegen
Du sollst zeigen, dass die Punkte  ,
,  und
und  in der Ebene
in der Ebene  liegen. Die Ebene
liegen. Die Ebene  lautet
lautet
 Eine Punktprobe liefert:
Eine Punktprobe liefert:
![\(\begin{array}[t]{rll}
7 \cdot 30 - 2 \cdot 5 + 20 \cdot 15&=& 210-10+300 \\[5pt]
&=&500\ \checkmark\\[10pt]
7 \cdot 0 - 2 \cdot 0 + 20 \cdot 25&=&0-0+500 \\[5pt]
&=&500\ \checkmark\\[10pt]
7 \cdot 0 - 2 \cdot 50 + 20 \cdot 30&=& 0-100+600 \\[5pt]
&=&500\ \checkmark
\end{array}\)](https://mathjax.schullv.de/70a4ffd822a0e710932b198678f9e919a9d07737efd29c94727d104d3c257318?color=5a5a5a) Die Punkte liegen somit in der Ebene E.
Die Punkte liegen somit in der Ebene E.
 Gesamtlänge der Brücken berechnen
Du sollst die Gesamtlänge der drei Brücken, die die drei Punkte
Gesamtlänge der Brücken berechnen
Du sollst die Gesamtlänge der drei Brücken, die die drei Punkte  ,
,  und
und  verbinden, berechnen. Stelle dafür zunächst die Vektoren, die die Brücken darstellen auf und berechne dann deren Länge.
1. Schritt: Vektoren aufstellen
verbinden, berechnen. Stelle dafür zunächst die Vektoren, die die Brücken darstellen auf und berechne dann deren Länge.
1. Schritt: Vektoren aufstellen
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=&\overrightarrow{OB}-\overrightarrow{OA} \\[5pt]
&=&\begin{pmatrix}0-30\\0-5\\25-15\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}-30\\-5\\10\end{pmatrix}\\[10pt]
\overrightarrow{BD}&=&\overrightarrow{OD}-\overrightarrow{OB} \\[5pt]
&=&\begin{pmatrix}0-0\\50-0\\30-25\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}0\\50\\5\end{pmatrix}\\[10pt]
\overrightarrow{DA}&=&\overrightarrow{OA}-\overrightarrow{OD} \\[5pt]
&=&\begin{pmatrix}30-0\\5-50\\15-30\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}30\\-45\\-15\end{pmatrix}\\[10pt]
\end{array}\)](https://mathjax.schullv.de/4507746a8843995ac0fc4c826d5f39a057b91e29e4dadea0b47395298a2f726a?color=5a5a5a) 2. Schritt: Längen berechnen
Um die Länge der Brücken zu berechnen, bestimmst du die Beträge der gerade aufgestellten Vektoren.
2. Schritt: Längen berechnen
Um die Länge der Brücken zu berechnen, bestimmst du die Beträge der gerade aufgestellten Vektoren.
![\(\begin{array}[t]{rll}
\left|\overrightarrow{AB}\right|&=&\sqrt{(-30)^2 + (-5)^2 + 10^2} \\[5pt]
&=&\sqrt{1025}\\[10pt]
\left|\overrightarrow{BD}\right|&=&\sqrt{0^2 + 50^2 + 5^2} \\[5pt]
&=&\sqrt{2525}\\[10pt]
\left|\overrightarrow{DA}\right|&=&\sqrt{30^2 + (-45)^2 + (-15)^2} \\[5pt]
&=&\sqrt{3150}
\end{array}\)](https://mathjax.schullv.de/e2f5c7538d2fbd84492db72199889622c07ae20595476c16d3b1edbb5fb7a8ac?color=5a5a5a) Die Gesamtlänge der Brücken ergibt sich durch addieren der drei berechneten Längen.
Die Gesamtlänge der Brücken ergibt sich durch addieren der drei berechneten Längen.

 .
Die Gesamtlänge der Brücken beträgt ungefähr
.
Die Gesamtlänge der Brücken beträgt ungefähr  m.
m.
 Neigungswinkel bestimmen
Du sollst den Neigungswinkel zwischen der Brücke von
Neigungswinkel bestimmen
Du sollst den Neigungswinkel zwischen der Brücke von  nach
nach  und der
und der  -Ebene bestimmen. Den Winkel
-Ebene bestimmen. Den Winkel  zwischen einem Vektor
zwischen einem Vektor  und einer Ebene mit Normalenvektor
und einer Ebene mit Normalenvektor  berechnest du mit folgender Formel:
berechnest du mit folgender Formel:
 Ein Normalenvektor der
Ein Normalenvektor der  -Ebene ist
-Ebene ist  . Der Vektor, der die Brücke von
. Der Vektor, der die Brücke von  nach
nach  beschreibt lautet
beschreibt lautet  .
Berechne also den gesuchten Winkel mit der oben angegebenen Formel.
.
Berechne also den gesuchten Winkel mit der oben angegebenen Formel.
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\left|\begin{pmatrix}-30\\-5\\10\end{pmatrix} \cdot \begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\left|\begin{pmatrix}-30\\-5\\10\end{pmatrix}\right| \cdot \left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}\\[5pt]
&=&\dfrac{\left|(-30) \cdot 0 +(-5) \cdot 0 + 10\cdot 1\right|}{\sqrt{(-30)^2 + (-5)^2 + 10^2} \cdot 1}\\[5pt]
&=&\dfrac{10}{\sqrt{1025}}
\end{array}\)](https://mathjax.schullv.de/fbce760285de44dfc5f5e3a9b6e2b6e705a7c02c6a5bd4e4c290780bebe446f2?color=5a5a5a) Für den Winkel gilt:
Für den Winkel gilt:  .
.
2.2  Wert von
Wert von  bestimmen
Du sollst den Wert für
bestimmen
Du sollst den Wert für  bestimmen, sodass die Brücken von der Plattform in
bestimmen, sodass die Brücken von der Plattform in  zu den Plattformen in
zu den Plattformen in  ,
,  und
und  in der Ebene
in der Ebene  liegen. Die Punkte
liegen. Die Punkte  ,
,  und
und  liegen in der Ebene
liegen in der Ebene  , damit die Brücken in
, damit die Brücken in  liegen, muss also der Punkt
liegen, muss also der Punkt  in
in  liegen.
Um den Wert für
liegen.
Um den Wert für  zu bestimmen, führe eine Punktprobe durch und bestimme
zu bestimmen, führe eine Punktprobe durch und bestimme  so, dass diese eine wahre Aussage liefert.
Setze
so, dass diese eine wahre Aussage liefert.
Setze  in
in  ein und löse nach
ein und löse nach  auf.
auf.
![\(\begin{array}[t]{rll}
7 \cdot (-15) - 2\cdot 45 + 20 \cdot h&=& 500\\[5pt]
-105-90+20\cdot h&=&500\\[5pt]
-195 + 20\cdot h&=&500\quad \scriptsize \mid\; +195\\[5pt]
20\cdot h &=&695\quad \scriptsize \mid\;:20\\[5pt]
h&=&34,75
\end{array}\)](https://mathjax.schullv.de/132c0c58ae82477649419c70b325ab4f11926e8393373b6ecb773c94e0116288?color=5a5a5a) Für
Für  liegen die Brücken in der Ebene
liegen die Brücken in der Ebene  .
.
2.3  Koordinaten des Punkts mit minimalem Abstand bestimmen
Deine Aufgabe ist es den Punkt zwischen
Koordinaten des Punkts mit minimalem Abstand bestimmen
Deine Aufgabe ist es den Punkt zwischen  und
und  zu finden, der den geringsten Abstand zum Punkt
zu finden, der den geringsten Abstand zum Punkt  hat. Du kannst in folgenden Schritten vorgehen:
hat. Du kannst in folgenden Schritten vorgehen:
 und
und  auf.
auf.
![\(\begin{array}[t]{rll}
j:\quad \vec{x}&=&\overrightarrow{OB}+ r \cdot \overrightarrow{BD}\\[5pt]
&=&\begin{pmatrix}0\\0\\25\end{pmatrix} + r \begin{pmatrix}0-0\\50-0\\30-25\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}0\\0\\25\end{pmatrix} + r \begin{pmatrix}0\\50\\5\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/248dcd2bc54f0e762a238165feafc3af2bdd5cd969dfc8ceeb8df15c46d5eb0e?color=5a5a5a) 2. Schritt: Hilfsebene aufstellen
Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt
2. Schritt: Hilfsebene aufstellen
Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt  als Stützpunkt.
als Stützpunkt.
![\(F: \quad \begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \left[\vec{x}- \begin{pmatrix}30\\5\\15\end{pmatrix}\right]=0\)](https://mathjax.schullv.de/a6c2c6210517f83cee7a642c02232cd8453456ab4ab5226b71080c16d87e5d4c?color=5a5a5a) 3. Schritt: Ebenengelichung in Koordinatenform umwandeln
Wandle die Normalenform in Koordinatenform um, indem du das Skalarprodukt berechnest.
3. Schritt: Ebenengelichung in Koordinatenform umwandeln
Wandle die Normalenform in Koordinatenform um, indem du das Skalarprodukt berechnest.
![\(\begin{array}[t]{rll}
\begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \left[\vec{x}- \begin{pmatrix}30\\5\\15\end{pmatrix}\right]&=&0\\[5pt]
\begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \begin{pmatrix}x-30\\y-5\\z-15\end{pmatrix}&=&0\\[5pt]
0\cdot(x-30) + 50 \cdot (y-5)+ 5\cdot (z-15) &=&0\\[5pt]
50y-250+5z-75 &=& 0 \\[5pt]
50y+5z-325&=&0 \quad \scriptsize \mid\; +325\\[5pt]
50y+5z&=&325
\end{array}\)](https://mathjax.schullv.de/59eff27fa14d630cdfa538032b34093da381ea44ce7532b6bd18ffac97623014?color=5a5a5a) 4. Schritt: Berechne
4. Schritt: Berechne  Setze die Gerade in die Koordinatenform ein und berechne
Setze die Gerade in die Koordinatenform ein und berechne  .
.
![\(\begin{array}[t]{rll}
50\cdot50 r+5\cdot (25+5r)&=&325\\[5pt]
2500r+125+25r&=&325\\[5pt]
2525r+125&=&325 \quad \scriptsize \mid\; -125\\[5pt]
2525r&=&200 \quad \scriptsize \mid\; :2525\\[5pt]
r&=&\dfrac{8}{101} \approx 0,08
\end{array}\)](https://mathjax.schullv.de/d20ed7e5921df11e325a23130af2f517ee935878d4efa1604aa7694f0d3aae73?color=5a5a5a) Setze
Setze  in die Geradengleichung ein, um die Koordinaten des Punkts
in die Geradengleichung ein, um die Koordinaten des Punkts  mit dem minimalen Abstand zu
mit dem minimalen Abstand zu  zu bestimmen.
zu bestimmen.

 Setzt du
Setzt du  in die Geradengleichung ein, erhältst du die Koordinaten des Punkts
in die Geradengleichung ein, erhältst du die Koordinaten des Punkts  . Setzt du
. Setzt du  in die Geradengleichung ein, erhältst du die Koordinaten des Punkts
in die Geradengleichung ein, erhältst du die Koordinaten des Punkts  . Da
. Da  liegt der Punkt
liegt der Punkt  tatsächlich zwischen den Punkten
tatsächlich zwischen den Punkten  und
und  .
Der Punkt
.
Der Punkt  mit dem minimalen Abstand zu
mit dem minimalen Abstand zu  lautet
lautet  .
.
 Wert für
Wert für  bestimmen, sodass Abstand maximal
Der Abstand zwischen den Geraden
bestimmen, sodass Abstand maximal
Der Abstand zwischen den Geraden  und
und  soll maximal sein. Du hast die Funktionsgleichung für den Abstand dieser beiden Geraden gegeben:
soll maximal sein. Du hast die Funktionsgleichung für den Abstand dieser beiden Geraden gegeben:
 für
für  gilt
gilt  .
Zeichne dir die Funktion
.
Zeichne dir die Funktion  in deinem GTR und bestimme das Maximum.
in deinem GTR und bestimme das Maximum.
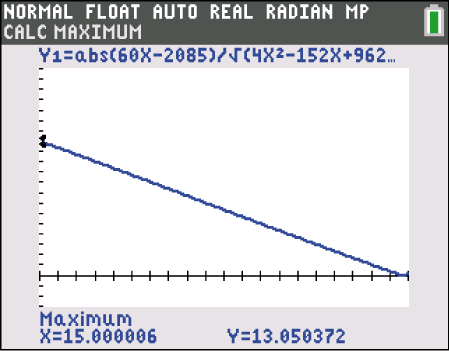 Der Wert für
Der Wert für  , sodass die beiden Geraden den maximalen Abstand haben lautet
, sodass die beiden Geraden den maximalen Abstand haben lautet  . Der maximale Abstand beträgt
. Der maximale Abstand beträgt  m.
m.
- Stelle die Gleichung der Geraden durch
und
auf.
- Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt
als Stützpunkt.
- Wandle die Normalenform in Koordinatenform um.
- Setze die Gerade in die Koordinatenform ein und berechne
.

2.4  Werte für
Werte für  bestimmen
Für eine weitere Planungsvariante sollen folgende Bedingungen erfüllt sein:
bestimmen
Für eine weitere Planungsvariante sollen folgende Bedingungen erfüllt sein:
 bestimmen.
1. Bedingung
Der Abstand von
bestimmen.
1. Bedingung
Der Abstand von  zur Ebene
zur Ebene  soll höchstens 7m betragen.
Um die Werte für
soll höchstens 7m betragen.
Um die Werte für  bestimmen zu können, die diese Bedingung erfüllen, berechnest du zunächst die Hessesche Normalform der Ebene
bestimmen zu können, die diese Bedingung erfüllen, berechnest du zunächst die Hessesche Normalform der Ebene  , indem du durch den Betrag des Normalenvektors teils.
Ein Normalenvektor der Ebene
, indem du durch den Betrag des Normalenvektors teils.
Ein Normalenvektor der Ebene  lautet:
lautet:  Die Länge des Normalenvektors ist:
Die Länge des Normalenvektors ist:
 Die Hessesche Normalform der Ebene
Die Hessesche Normalform der Ebene  lautet somit:
lautet somit:
![\(E: \quad \dfrac{1}{\sqrt{453}} \left[7 \cdot x - 2\cdot y + 20 \cdot z -500\right] = 0\)](https://mathjax.schullv.de/634d95bce34af32f25d18bd8d4c9f794fc516c6c3c1b8b2bbcda9e0df0f3129b?color=5a5a5a) Setze nun den Punkt
Setze nun den Punkt  in die Hessesche Normalform ein, der Betrag dieses Ausdrucks soll dann kleiner gleich 7 sein.
in die Hessesche Normalform ein, der Betrag dieses Ausdrucks soll dann kleiner gleich 7 sein.
![\(\begin{array}[t]{rrrll}
&&\left|d\right| &\leq&7\\[5pt]
&&\dfrac{1}{\sqrt{453}} \left|7 \cdot (-15) - 2\cdot 45 + 20 \cdot h -500\right|&\leq&7\\[5pt]
&&\dfrac{1}{\sqrt{453}} \left|-695 + 20h \right|&\leq&7\quad \scriptsize \mid\; \cdot \sqrt{453}\\[5pt]
&&\left|-695+20h\right|&\leq&7\cdot \sqrt{453} \\[5pt]
-7\cdot \sqrt{453}&\leq & -695+20h&\leq&7\cdot \sqrt{453}\quad \scriptsize \mid\;+695\\[5pt]
546,0134 &\leq&20h&\leq&843,9866\quad \scriptsize \mid\;:20\\[5pt]
27,30&\leq& h &\leq&42,12
\end{array}\)](https://mathjax.schullv.de/eed1b851b48a6980b2ee1b5970069e36144b844ceca3576a82c70ed944bdea21?color=5a5a5a) Die 1. Bedingung ist für
Die 1. Bedingung ist für  erfüllt.
2. Bedingung
Damit die Brücken von der Aussichtsplattform im Punkt
erfüllt.
2. Bedingung
Damit die Brücken von der Aussichtsplattform im Punkt  zu den Aussichtsplattformen in den Punkten
zu den Aussichtsplattformen in den Punkten  und
und  einen Winkel von mindestens 90° einschließen, müssen die Vektoren
einen Winkel von mindestens 90° einschließen, müssen die Vektoren  und
und  einen Winkel von mindestens 90° einschließen.
Der Winkel
einen Winkel von mindestens 90° einschließen.
Der Winkel  zwischen zwei Vektoren
zwischen zwei Vektoren  und
und  wird folgendermaßen berechnet:
wird folgendermaßen berechnet:
 Stelle die Vektoren
Stelle die Vektoren  und
und  auf.
auf.



 Es soll
Es soll  gelten, mit der oben angegebenen Formel und
gelten, mit der oben angegebenen Formel und  erhältst du
erhältst du
![\(\begin{array}[t]{rll}
90^{\circ}&\leq& \alpha \\[5pt]
90^{\circ}&\leq& \cos^{-1}\left(\dfrac{\overrightarrow{C_hB} \cdot\overrightarrow{C_hD}}{\left|\overrightarrow{C_hB}\right|\cdot \left|\overrightarrow{C_hD}\right|} \right) \\[5pt]
0&\geq&\dfrac{\overrightarrow{C_hB} \cdot\overrightarrow{C_hD}}{\left|\overrightarrow{C_hB}\right|\cdot \left|\overrightarrow{C_hD}\right|} \\[5pt]
0&\geq&\dfrac{\begin{pmatrix}15\\-45 \\25-h\end{pmatrix} \cdot\begin{pmatrix}15\\5 \\30-h\end{pmatrix}}{\left|\begin{pmatrix}15\\-45 \\25-h\end{pmatrix}\right|\cdot \left|\begin{pmatrix}15\\5 \\30-h\end{pmatrix}\right|}\\[5pt]
0&\geq&\dfrac{15^2+ (-45)\cdot 5 + (25-h)(30-h)}{\sqrt{15^2+(-45)^2+(25-h)^2}\cdot \sqrt{15^2+5^2+(30-h)^2}}\\[5pt]
0&\geq&\dfrac{(25-h)(30-h)}{\sqrt{2250+(25-h)^2}\cdot \sqrt{250+(30-h)^2}}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/92c5a6f7fb3cd8a293de05531842be6e8d636412008bf23a3d600528bf3e7689?color=5a5a5a) Zeichne die Funktion mit deinem GTR und berechne die Nullstellen.
Zeichne die Funktion mit deinem GTR und berechne die Nullstellen.
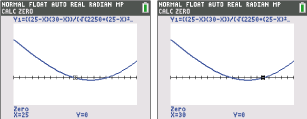 Die 2. Bedingung ist erfüllt für
Die 2. Bedingung ist erfüllt für  Nimmst du nun die beiden Ergebnisse zusammen, sind beide Bedingungen erfüllt, wenn
Nimmst du nun die beiden Ergebnisse zusammen, sind beide Bedingungen erfüllt, wenn 
- Der Abstand der Aussichtsplattform im Punkt
zur Ebene
soll höchstens 7m betragen.
- Die Brücken von der Aussichtsplattform im Punkt
zu den Aussichtsplattformen in den Punkten
und
sollen einen Winkel von mindestens 90° einschließen.

2.5  Punkt des Sicherungsseils bestimmen
Du sollst die Koordinaten eines Punktes bestimmen, in welchem das Sicherungsseil von der Aussichtsplattform in Punkt
Punkt des Sicherungsseils bestimmen
Du sollst die Koordinaten eines Punktes bestimmen, in welchem das Sicherungsseil von der Aussichtsplattform in Punkt  den Boden in einem Winkel von 60° trifft.
Der Auftreffpunkt auf der
den Boden in einem Winkel von 60° trifft.
Der Auftreffpunkt auf der  -Ebene hat die Koordinaten
-Ebene hat die Koordinaten  . Die Gerade durch den Punkt
. Die Gerade durch den Punkt  und den Punkt
und den Punkt  , die also das Sicherungsseil beschreibt, hat dann folgende Form:
, die also das Sicherungsseil beschreibt, hat dann folgende Form:
 Für den Winkel
Für den Winkel  zwischen einer Ebene mit Normalenvektor
zwischen einer Ebene mit Normalenvektor  und einer Gerade mit Richtungsvektor
und einer Gerade mit Richtungsvektor  gilt folgende Formel:
gilt folgende Formel:
 Ein Normalenvektor zur
Ein Normalenvektor zur  - Ebene ist beispielsweise
- Ebene ist beispielsweise  .
Setze den Winkel und die beiden Vektoren in die Formel ein und löse nach
.
Setze den Winkel und die beiden Vektoren in die Formel ein und löse nach  auf.
auf.
![\(\begin{array}[t]{rll}
\sin(60^{\circ})&=&\dfrac{\left|\begin{pmatrix}0\\0\\1\end{pmatrix} \cdot \begin{pmatrix}l_1\\l_2-50\\-30\end{pmatrix}\right|}{\left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right| \cdot \left|\begin{pmatrix}l_1\\l_2-50\\-30\end{pmatrix}\right|}\\[5pt]
\dfrac{\sqrt{3}}{2}&=&\dfrac{30}{1\cdot \sqrt{l_1^2 + (l_2-50)^2 + (-30)^2}} \quad \scriptsize \mid\; \cdot \sqrt{l_1^2 + (l_2-50)^2 + (-30)^2}\\[5pt]
\dfrac{\sqrt{3}}{2}\cdot \sqrt{l_1^2 + (l_2-50)^2 + 900}&=&30 \quad \scriptsize \mid\; \cdot \dfrac{2}{\sqrt{3}} \\[5pt]
\sqrt{l_1^2 + (l_2-50)^2 + 900}&=&\dfrac{60}{\sqrt{3}} \quad \scriptsize \mid\; ()^2 \\[5pt]
l_1^2 + (l_2-50)^2 +900&=&\dfrac{3600}{3} \quad \scriptsize \mid\; -((l_2-50)^2 + 900) \\[5pt]
l_1^2 &=&1200 -900 - (l_2-50)^2\quad \scriptsize \mid\; \sqrt{ } \\[5pt]
l_1 &=&\pm \sqrt{300 - (l_2-50)^2}
\end{array}\)](https://mathjax.schullv.de/9cab77d9d6ca8af1faf12e6537668340e4578474d7f1c91f5797bcf18da60b11?color=5a5a5a) Wähle nun einen Wert für
Wähle nun einen Wert für  , sodass die Diskriminante positiv ist und berechne das zugehörige
, sodass die Diskriminante positiv ist und berechne das zugehörige  .
Ein Auftreffpunkt hat die Koordinaten
.
Ein Auftreffpunkt hat die Koordinaten  und
und

 .
Der Punkt lautet dann
.
Der Punkt lautet dann  .
.
 Flächeninhalt bestimmen
Alle möglichen Auftreffpunkte schließen eine Fläche ein, du sollst deren Inhalt bestimmen.
Die allgemeine Funktionsgleichung für einen Kreis mit Radius
Flächeninhalt bestimmen
Alle möglichen Auftreffpunkte schließen eine Fläche ein, du sollst deren Inhalt bestimmen.
Die allgemeine Funktionsgleichung für einen Kreis mit Radius  und Mittelpunkt
und Mittelpunkt  lautet
lautet
 Betrachtest du die Funktionsgleichung für
Betrachtest du die Funktionsgleichung für  , so erkennst du, dass es sich dabei gerade um die eines Kreises mit Radius
, so erkennst du, dass es sich dabei gerade um die eines Kreises mit Radius  und Mittelpunkt
und Mittelpunkt  handelt.
Berechne den Flächeninhalt dieses Kreises:
handelt.
Berechne den Flächeninhalt dieses Kreises:
![\(\begin{array}[t]{rll}
A&=&\pi r^2 \\[5pt]
&=&\pi \cdot 300 \\[5pt]
&\approx&942,478
\end{array}\)](https://mathjax.schullv.de/54512b3392730d927900976bf7ebc96fd10073eb0032be95793d24dacdf499f5?color=5a5a5a) Die Fläche hat einen Inhalt von 942,478 m2.
Die Fläche hat einen Inhalt von 942,478 m2.
2.6  Wahrscheinlichkeit bestimmen
Die Reißfestigkeit der Sicherungsseile ist annähernd normalverteilt. Sei also
Wahrscheinlichkeit bestimmen
Die Reißfestigkeit der Sicherungsseile ist annähernd normalverteilt. Sei also  die Zufallsvariable, die die Reißfestigkeit der Sicherungsseile beschreibt. Der Erwartungswert
die Zufallsvariable, die die Reißfestigkeit der Sicherungsseile beschreibt. Der Erwartungswert  liegt bei 145 kN, außerdem weist du, dass
liegt bei 145 kN, außerdem weist du, dass  ist.
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein Sicherungsseil bei einer Belastung zwischen 142 kN und 150 kN reißt.
Führe dafür eine
ist.
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein Sicherungsseil bei einer Belastung zwischen 142 kN und 150 kN reißt.
Führe dafür eine  -Transformation durch, dabei ist
-Transformation durch, dabei ist  dann eine standard-normalverteilte Zufallsvariable.
dann eine standard-normalverteilte Zufallsvariable.
 Für die Transformation fehlt dir also noch die Varianz
Für die Transformation fehlt dir also noch die Varianz  . Diese kannst du mit Hilfe der gegebenen Wahrscheinlichkeit und der Tabelle zur Standard-Normalverteilung berechnen:
. Diese kannst du mit Hilfe der gegebenen Wahrscheinlichkeit und der Tabelle zur Standard-Normalverteilung berechnen:
![\(\begin{array}[t]{rll}
P(X>140)&=&0,973 \\[5pt]
P\left(\dfrac{X-145}{\sigma}>\dfrac{140-145}{\sigma}\right)&=&0,973\\[5pt]
P\left(Z>-\dfrac{5}{\sigma}\right)&=&0,973\\[5pt]
1-P\left(Z\leq-\frac{5}{\sigma}\right)&=&0,973\\[5pt]
1-\phi\left(-\frac{5}{\sigma}\right)&=&0,973\\[5pt]
1-\left(1-\phi\left(\frac{5}{\sigma}\right)\right)&=&0,973\quad \\[5pt]
\phi\left(\frac{5}{\sigma}\right)&=&0,973
\end{array}\)](https://mathjax.schullv.de/891180ec59772e87f55b844117789c424b00df6cd38cf819614958cbe79b289c?color=5a5a5a) Suche nun in der Tabelle für die Standard-Normalverteilung nach der Wahrscheinlichkeit 0,973 um anschließend
Suche nun in der Tabelle für die Standard-Normalverteilung nach der Wahrscheinlichkeit 0,973 um anschließend  zu bestimmen. Du findest
zu bestimmen. Du findest
 Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
1,93&=&\frac{5}{\sigma} \quad \scriptsize \mid\; \cdot \sigma\\[5pt]
1,93 \sigma&=&5 \quad \scriptsize \mid\; :1,93\\[5pt]
\sigma &\approx& 2,5907
\end{array}\)](https://mathjax.schullv.de/07061f54f71f35d0d85f037c429ce3e34e85e06af0a858aaf6395781bfe50bdd?color=5a5a5a) Du sollst nun die Wahrscheinlichkeit
Du sollst nun die Wahrscheinlichkeit  bestimmen. Führe die
bestimmen. Führe die  -transformation durch und nutze dann die Tabelle für die Standard-Normalverteilung um die gesuchte Wahrscheinlichkeit zu berechnen.
-transformation durch und nutze dann die Tabelle für die Standard-Normalverteilung um die gesuchte Wahrscheinlichkeit zu berechnen.
![\(\begin{array}[t]{rll}
P(142 \leq X \leq 150)&=&P(X\leq 150) - P(X \leq 142) \\[5pt]
&=&P\left(\dfrac{X-145}{2,5907}\leq \dfrac{150-145}{2,5907}\right)-P\left(\dfrac{X-145}{2,5907}\leq \dfrac{142-145}{2,5907}\right)\\[5pt]
&=&P\left(Z\leq \dfrac{150-145}{2,5907}\right)-P\left(Z\leq \dfrac{142-145}{2,5907}\right)\\[5pt]
&=&P\left(Z\leq 1,93\right)-P\left(Z\leq -1,16\right)\\[5pt]
&=&\phi(1,93)-\phi(-1,16)\\[5pt]
&=&\phi(1,93)- (1-\phi(1,16))\\[5pt]
&=&0,9732 - (1-0,8770)\\[5pt]
&=&0,8502
\end{array}\)](https://mathjax.schullv.de/69b5c602731066e9ea8c4b9d2ff237462ec046c5774069e13fd737470c87dfef?color=5a5a5a) Die Wahrscheinlichkeit, dass das Seil bei einer Belastung zwischen 142 kN und 150 kN reißt beträgt 85,02%.
Die Wahrscheinlichkeit, dass das Seil bei einer Belastung zwischen 142 kN und 150 kN reißt beträgt 85,02%.
2.7  Gesamtbesucherzahl bestimmen
Du sollst die erwartete Gesamtbesucherzahl an einem Ferientag berechnen, wenn 100 Kinder aus der näheren Umgebung in den Hochseilgarten kommen. Außerdem kennst du die folgenden Anteile
Gesamtbesucherzahl bestimmen
Du sollst die erwartete Gesamtbesucherzahl an einem Ferientag berechnen, wenn 100 Kinder aus der näheren Umgebung in den Hochseilgarten kommen. Außerdem kennst du die folgenden Anteile
![\(\begin{array}[t]{rll}
P(K)&=&P(U)\cdot P(UK) + P(\overline{U})\cdot P(\overline{U}K) \\[5pt]
0,485&=&0,65 \cdot P(UK) + 0,35\cdot 0,55 \\[5pt]
0,485&=&0,65 \cdot P(UK) + 0,1925 \quad \scriptsize \mid\;-0,1925\\[5pt]
0,2925&=&0,65 \cdot P(UK)\quad \scriptsize \mid\;:0,65\\[5pt]
P(UK) &=& 0,45
\end{array}\)](https://mathjax.schullv.de/6baa5bb69c0029bf77720fce4b59d9264a27207371fcc9bef5e30a249c111ee6?color=5a5a5a) 45% der Besucher aus der näheren Umgebung sind Kinder. Dieser Anteil entspricht hier 100 Kindern. Berechne die Anzahl der Besucher aus der näheren Umgebung.
45% der Besucher aus der näheren Umgebung sind Kinder. Dieser Anteil entspricht hier 100 Kindern. Berechne die Anzahl der Besucher aus der näheren Umgebung.
![\(\begin{array}[t]{rll}
\text{Anzahl }U \cdot P(UK)&=&100 \\[5pt]
\text{Anzahl }U \cdot 0,45&=&100\quad \scriptsize \mid\; :0,45\\[5pt]
\text{Anzahl }U &=& \dfrac{100}{0,45} = 222,\overline{2}
\end{array}\)](https://mathjax.schullv.de/0ad786241b4b1398f99b88f58aa7a1998f08e435baf8f609dea706c2f4b011f4?color=5a5a5a) Das entspricht 65% der Gesamtbesucherzahl, diese berechnet sich somit folgendermaßen
Das entspricht 65% der Gesamtbesucherzahl, diese berechnet sich somit folgendermaßen
![\(\begin{array}[t]{rll}
\text{Anzahl Besucher} \cdot P(U)&=&222,\overline{2} \\[5pt]
\text{Anzahl Besucher} \cdot 0,65&=&222,\overline{2}\quad \scriptsize \mid\;: 0,65\\[5pt]
\text{Anzahl Besucher} &=& \dfrac{222,\overline{2}}{0,65} \approx 341,88
\end{array}\)](https://mathjax.schullv.de/59545f7bd6dade7a20c8961758659a55ad16dba3298c87947aee55b8793cd2f8?color=5a5a5a) Die erwartete Besucherzahl an einem Ferientag liegt bei 342 Besuchern.
Die erwartete Besucherzahl an einem Ferientag liegt bei 342 Besuchern.
- 65% der Besucher kommen aus der näheren Umgebung (
).
- 55% der Besucher, die nicht aus der näheren Umgebung kommen, sind Kinder (
).
- 48,5% der Besucher sind Kinder (
).
Aufgabe B 2
2.1  Begründe, dass Punkte in der Ebene liegen
Du sollst zeigen, dass die Punkte
Begründe, dass Punkte in der Ebene liegen
Du sollst zeigen, dass die Punkte  ,
,  und
und  in der Ebene
in der Ebene  liegen. Die Ebene
liegen. Die Ebene  lautet
lautet
 Eine Punktprobe liefert:
Eine Punktprobe liefert:
![\(\begin{array}[t]{rll}
7 \cdot 30 - 2 \cdot 5 + 20 \cdot 15&=& 210-10+300 \\[5pt]
&=&500\ \checkmark\\[10pt]
7 \cdot 0 - 2 \cdot 0 + 20 \cdot 25&=&0-0+500 \\[5pt]
&=&500\ \checkmark\\[10pt]
7 \cdot 0 - 2 \cdot 50 + 20 \cdot 30&=& 0-100+600 \\[5pt]
&=&500\ \checkmark
\end{array}\)](https://mathjax.schullv.de/70a4ffd822a0e710932b198678f9e919a9d07737efd29c94727d104d3c257318?color=5a5a5a) Die Punkte liegen somit in der Ebene E.
Die Punkte liegen somit in der Ebene E.
 Gesamtlänge der Brücken berechnen
Du sollst die Gesamtlänge der drei Brücken, die die drei Punkte
Gesamtlänge der Brücken berechnen
Du sollst die Gesamtlänge der drei Brücken, die die drei Punkte  ,
,  und
und  verbinden, berechnen. Stelle dafür zunächst die Vektoren, die die Brücken darstellen auf und berechne dann deren Länge.
1. Schritt: Vektoren aufstellen
verbinden, berechnen. Stelle dafür zunächst die Vektoren, die die Brücken darstellen auf und berechne dann deren Länge.
1. Schritt: Vektoren aufstellen
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=&\overrightarrow{OB}-\overrightarrow{OA} \\[5pt]
&=&\begin{pmatrix}0-30\\0-5\\25-15\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}-30\\-5\\10\end{pmatrix}\\[10pt]
\overrightarrow{BD}&=&\overrightarrow{OD}-\overrightarrow{OB} \\[5pt]
&=&\begin{pmatrix}0-0\\50-0\\30-25\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}0\\50\\5\end{pmatrix}\\[10pt]
\overrightarrow{DA}&=&\overrightarrow{OA}-\overrightarrow{OD} \\[5pt]
&=&\begin{pmatrix}30-0\\5-50\\15-30\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}30\\-45\\-15\end{pmatrix}\\[10pt]
\end{array}\)](https://mathjax.schullv.de/4507746a8843995ac0fc4c826d5f39a057b91e29e4dadea0b47395298a2f726a?color=5a5a5a) 2. Schritt: Längen berechnen
Um die Länge der Brücken zu berechnen, bestimmst du die Beträge der gerade aufgestellten Vektoren.
2. Schritt: Längen berechnen
Um die Länge der Brücken zu berechnen, bestimmst du die Beträge der gerade aufgestellten Vektoren.
![\(\begin{array}[t]{rll}
\left|\overrightarrow{AB}\right|&=&\sqrt{(-30)^2 + (-5)^2 + 10^2} \\[5pt]
&=&\sqrt{1025}\\[10pt]
\left|\overrightarrow{BD}\right|&=&\sqrt{0^2 + 50^2 + 5^2} \\[5pt]
&=&\sqrt{2525}\\[10pt]
\left|\overrightarrow{DA}\right|&=&\sqrt{30^2 + (-45)^2 + (-15)^2} \\[5pt]
&=&\sqrt{3150}
\end{array}\)](https://mathjax.schullv.de/e2f5c7538d2fbd84492db72199889622c07ae20595476c16d3b1edbb5fb7a8ac?color=5a5a5a) Die Gesamtlänge der Brücken ergibt sich durch addieren der drei berechneten Längen.
Die Gesamtlänge der Brücken ergibt sich durch addieren der drei berechneten Längen.

 .
Die Gesamtlänge der Brücken beträgt ungefähr
.
Die Gesamtlänge der Brücken beträgt ungefähr  m.
m.
 Neigungswinkel bestimmen
Du sollst den Neigungswinkel zwischen der Brücke von
Neigungswinkel bestimmen
Du sollst den Neigungswinkel zwischen der Brücke von  nach
nach  und der
und der  -Ebene bestimmen. Den Winkel
-Ebene bestimmen. Den Winkel  zwischen einem Vektor
zwischen einem Vektor  und einer Ebene mit Normalenvektor
und einer Ebene mit Normalenvektor  berechnest du mit folgender Formel:
berechnest du mit folgender Formel:
 Ein Normalenvektor der
Ein Normalenvektor der  -Ebene ist
-Ebene ist  . Der Vektor, der die Brücke von
. Der Vektor, der die Brücke von  nach
nach  beschreibt lautet
beschreibt lautet  .
Berechne also den gesuchten Winkel mit der oben angegebenen Formel.
.
Berechne also den gesuchten Winkel mit der oben angegebenen Formel.
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\left|\begin{pmatrix}-30\\-5\\10\end{pmatrix} \cdot \begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\left|\begin{pmatrix}-30\\-5\\10\end{pmatrix}\right| \cdot \left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}\\[5pt]
&=&\dfrac{\left|(-30) \cdot 0 +(-5) \cdot 0 + 10\cdot 1\right|}{\sqrt{(-30)^2 + (-5)^2 + 10^2} \cdot 1}\\[5pt]
&=&\dfrac{10}{\sqrt{1025}}
\end{array}\)](https://mathjax.schullv.de/fbce760285de44dfc5f5e3a9b6e2b6e705a7c02c6a5bd4e4c290780bebe446f2?color=5a5a5a) Für den Winkel gilt:
Für den Winkel gilt:  .
.
2.2  Wert von
Wert von  bestimmen
Du sollst den Wert für
bestimmen
Du sollst den Wert für  bestimmen, sodass die Brücken von der Plattform in
bestimmen, sodass die Brücken von der Plattform in  zu den Plattformen in
zu den Plattformen in  ,
,  und
und  in der Ebene
in der Ebene  liegen. Die Punkte
liegen. Die Punkte  ,
,  und
und  liegen in der Ebene
liegen in der Ebene  , damit die Brücken in
, damit die Brücken in  liegen, muss also der Punkt
liegen, muss also der Punkt  in
in  liegen.
Um den Wert für
liegen.
Um den Wert für  zu bestimmen, führe eine Punktprobe durch und bestimme
zu bestimmen, führe eine Punktprobe durch und bestimme  so, dass diese eine wahre Aussage liefert.
Setze
so, dass diese eine wahre Aussage liefert.
Setze  in
in  ein und löse nach
ein und löse nach  auf.
auf.
![\(\begin{array}[t]{rll}
7 \cdot (-15) - 2\cdot 45 + 20 \cdot h&=& 500\\[5pt]
-105-90+20\cdot h&=&500\\[5pt]
-195 + 20\cdot h&=&500\quad \scriptsize \mid\; +195\\[5pt]
20\cdot h &=&695\quad \scriptsize \mid\;:20\\[5pt]
h&=&34,75
\end{array}\)](https://mathjax.schullv.de/132c0c58ae82477649419c70b325ab4f11926e8393373b6ecb773c94e0116288?color=5a5a5a) Für
Für  liegen die Brücken in der Ebene
liegen die Brücken in der Ebene  .
.
2.3  Koordinaten des Punkts mit minimalem Abstand bestimmen
Deine Aufgabe ist es den Punkt zwischen
Koordinaten des Punkts mit minimalem Abstand bestimmen
Deine Aufgabe ist es den Punkt zwischen  und
und  zu finden, der den geringsten Abstand zum Punkt
zu finden, der den geringsten Abstand zum Punkt  hat. Du kannst in folgenden Schritten vorgehen:
hat. Du kannst in folgenden Schritten vorgehen:
 und
und  auf.
auf.
![\(\begin{array}[t]{rll}
j:\quad \vec{x}&=&\overrightarrow{OB}+ r \cdot \overrightarrow{BD}\\[5pt]
&=&\begin{pmatrix}0\\0\\25\end{pmatrix} + r \begin{pmatrix}0-0\\50-0\\30-25\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}0\\0\\25\end{pmatrix} + r \begin{pmatrix}0\\50\\5\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/248dcd2bc54f0e762a238165feafc3af2bdd5cd969dfc8ceeb8df15c46d5eb0e?color=5a5a5a) 2. Schritt: Hilfsebene aufstellen
Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt
2. Schritt: Hilfsebene aufstellen
Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt  als Stützpunkt.
als Stützpunkt.
![\(F: \quad \begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \left[\vec{x}- \begin{pmatrix}30\\5\\15\end{pmatrix}\right]=0\)](https://mathjax.schullv.de/a6c2c6210517f83cee7a642c02232cd8453456ab4ab5226b71080c16d87e5d4c?color=5a5a5a) 3. Schritt: Ebenengelichung in Koordinatenform umwandeln
Wandle die Normalenform in Koordinatenform um, indem du das Skalarprodukt berechnest.
3. Schritt: Ebenengelichung in Koordinatenform umwandeln
Wandle die Normalenform in Koordinatenform um, indem du das Skalarprodukt berechnest.
![\(\begin{array}[t]{rll}
\begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \left[\vec{x}- \begin{pmatrix}30\\5\\15\end{pmatrix}\right]&=&0\\[5pt]
\begin{pmatrix}0\\50\\5\end{pmatrix}\cdot \begin{pmatrix}x-30\\y-5\\z-15\end{pmatrix}&=&0\\[5pt]
0\cdot(x-30) + 50 \cdot (y-5)+ 5\cdot (z-15) &=&0\\[5pt]
50y-250+5z-75 &=& 0 \\[5pt]
50y+5z-325&=&0 \quad \scriptsize \mid\; +325\\[5pt]
50y+5z&=&325
\end{array}\)](https://mathjax.schullv.de/59eff27fa14d630cdfa538032b34093da381ea44ce7532b6bd18ffac97623014?color=5a5a5a) 4. Schritt: Berechne
4. Schritt: Berechne  Setze die Gerade in die Koordinatenform ein und berechne
Setze die Gerade in die Koordinatenform ein und berechne  .
.
![\(\begin{array}[t]{rll}
50\cdot50 r+5\cdot (25+5r)&=&325\\[5pt]
2500r+125+25r&=&325\\[5pt]
2525r+125&=&325 \quad \scriptsize \mid\; -125\\[5pt]
2525r&=&200 \quad \scriptsize \mid\; :2525\\[5pt]
r&=&\dfrac{8}{101} \approx 0,08
\end{array}\)](https://mathjax.schullv.de/d20ed7e5921df11e325a23130af2f517ee935878d4efa1604aa7694f0d3aae73?color=5a5a5a) Setze
Setze  in die Geradengleichung ein, um die Koordinaten des Punkts
in die Geradengleichung ein, um die Koordinaten des Punkts  mit dem minimalen Abstand zu
mit dem minimalen Abstand zu  zu bestimmen.
zu bestimmen.

 Setzt du
Setzt du  in die Geradengleichung ein, erhältst du die Koordinaten des Punkts
in die Geradengleichung ein, erhältst du die Koordinaten des Punkts  . Setzt du
. Setzt du  in die Geradengleichung ein, erhältst du die Koordinaten des Punkts
in die Geradengleichung ein, erhältst du die Koordinaten des Punkts  . Da
. Da  liegt der Punkt
liegt der Punkt  tatsächlich zwischen den Punkten
tatsächlich zwischen den Punkten  und
und  .
Der Punkt
.
Der Punkt  mit dem minimalen Abstand zu
mit dem minimalen Abstand zu  lautet
lautet  .
.
 Wert für
Wert für  bestimmen, sodass Abstand maximal
Der Abstand zwischen den Geraden
bestimmen, sodass Abstand maximal
Der Abstand zwischen den Geraden  und
und  soll maximal sein. Du hast die Funktionsgleichung für den Abstand dieser beiden Geraden gegeben:
soll maximal sein. Du hast die Funktionsgleichung für den Abstand dieser beiden Geraden gegeben:
 für
für  gilt
gilt  .
Zeichne dir die Funktion
.
Zeichne dir die Funktion  in deinem GTR und bestimme das Maximum.
in deinem GTR und bestimme das Maximum.
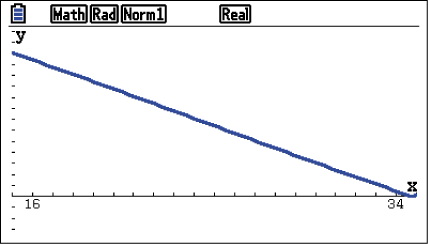 Der GTR findet kein globales Maximum im Definitionsbereich von
Der GTR findet kein globales Maximum im Definitionsbereich von  , somit wird der maximale Wert an einem der Randpunkte angenommen. Der Graphik kannst du entnehmen, dass dieser bei
, somit wird der maximale Wert an einem der Randpunkte angenommen. Der Graphik kannst du entnehmen, dass dieser bei  liegt. Berechne noch den zugehörigen Funktionswert.
liegt. Berechne noch den zugehörigen Funktionswert.
 Der Wert für
Der Wert für  , sodass die beiden Geraden den maximalen Abstand haben lautet
, sodass die beiden Geraden den maximalen Abstand haben lautet  . Der maximale Abstand beträgt
. Der maximale Abstand beträgt  m.
m.
- Stelle die Gleichung der Geraden durch
und
auf.
- Stelle die Hilfsebene auf, indem du den Richtungsvektor der Geraden als Normalenvektor verwendest und den Punkt
als Stützpunkt.
- Wandle die Normalenform in Koordinatenform um.
- Setze die Gerade in die Koordinatenform ein und berechne
.

2.4  Werte für
Werte für  bestimmen
Für eine weitere Planungsvariante sollen folgende Bedingungen erfüllt sein:
bestimmen
Für eine weitere Planungsvariante sollen folgende Bedingungen erfüllt sein:
 bestimmen.
1. Bedingung
Der Abstand von
bestimmen.
1. Bedingung
Der Abstand von  zur Ebene
zur Ebene  soll höchstens 7m betragen.
Um die Werte für
soll höchstens 7m betragen.
Um die Werte für  bestimmen zu können, die diese Bedingung erfüllen, berechnest du zunächst die Hessesche Normalform der Ebene
bestimmen zu können, die diese Bedingung erfüllen, berechnest du zunächst die Hessesche Normalform der Ebene  , indem du durch den Betrag des Normalenvektors teils.
Ein Normalenvektor der Ebene
, indem du durch den Betrag des Normalenvektors teils.
Ein Normalenvektor der Ebene  lautet:
lautet:  Die Länge des Normalenvektors ist:
Die Länge des Normalenvektors ist:
 Die Hessesche Normalform der Ebene
Die Hessesche Normalform der Ebene  lautet somit:
lautet somit:
![\(E: \quad \dfrac{1}{\sqrt{453}} \left[7 \cdot x - 2\cdot y + 20 \cdot z -500\right] = 0\)](https://mathjax.schullv.de/634d95bce34af32f25d18bd8d4c9f794fc516c6c3c1b8b2bbcda9e0df0f3129b?color=5a5a5a) Setze nun den Punkt
Setze nun den Punkt  in die Hessesche Normalform ein, der Betrag dieses Ausdrucks soll dann kleiner gleich 7 sein.
in die Hessesche Normalform ein, der Betrag dieses Ausdrucks soll dann kleiner gleich 7 sein.
![\(\begin{array}[t]{rrrll}
&&\left|d\right| &\leq&7\\[5pt]
&&\dfrac{1}{\sqrt{453}} \left|7 \cdot (-15) - 2\cdot 45 + 20 \cdot h -500\right|&\leq&7\\[5pt]
&&\dfrac{1}{\sqrt{453}} \left|-695 + 20h \right|&\leq&7\quad \scriptsize \mid\; \cdot \sqrt{453}\\[5pt]
&&\left|-695+20h\right|&\leq&7\cdot \sqrt{453} \\[5pt]
-7\cdot \sqrt{453}&\leq & -695+20h&\leq&7\cdot \sqrt{453}\quad \scriptsize \mid\;+695\\[5pt]
546,0134 &\leq&20h&\leq&843,9866\quad \scriptsize \mid\;:20\\[5pt]
27,30&\leq& h &\leq&42,12
\end{array}\)](https://mathjax.schullv.de/eed1b851b48a6980b2ee1b5970069e36144b844ceca3576a82c70ed944bdea21?color=5a5a5a) Die 1. Bedingung ist für
Die 1. Bedingung ist für  erfüllt.
2. Bedingung
Damit die Brücken von der Aussichtsplattform im Punkt
erfüllt.
2. Bedingung
Damit die Brücken von der Aussichtsplattform im Punkt  zu den Aussichtsplattformen in den Punkten
zu den Aussichtsplattformen in den Punkten  und
und  einen Winkel von mindestens 90° einschließen, müssen die Vektoren
einen Winkel von mindestens 90° einschließen, müssen die Vektoren  und
und  einen Winkel von mindestens 90° einschließen.
Der Winkel
einen Winkel von mindestens 90° einschließen.
Der Winkel  zwischen zwei Vektoren
zwischen zwei Vektoren  und
und  wird folgendermaßen berechnet:
wird folgendermaßen berechnet:
 Stelle die Vektoren
Stelle die Vektoren  und
und  auf.
auf.



 Es soll
Es soll  gelten, mit der oben angegebenen Formel und
gelten, mit der oben angegebenen Formel und  erhältst du
erhältst du
![\(\begin{array}[t]{rll}
90^{\circ}&\leq& \alpha \\[5pt]
90^{\circ}&\leq& \cos^{-1}\left(\dfrac{\overrightarrow{C_hB} \cdot\overrightarrow{C_hD}}{\left|\overrightarrow{C_hB}\right|\cdot \left|\overrightarrow{C_hD}\right|} \right) \\[5pt]
0&\geq&\dfrac{\overrightarrow{C_hB} \cdot\overrightarrow{C_hD}}{\left|\overrightarrow{C_hB}\right|\cdot \left|\overrightarrow{C_hD}\right|} \\[5pt]
0&\geq&\dfrac{\begin{pmatrix}15\\-45 \\25-h\end{pmatrix} \cdot\begin{pmatrix}15\\5 \\30-h\end{pmatrix}}{\left|\begin{pmatrix}15\\-45 \\25-h\end{pmatrix}\right|\cdot \left|\begin{pmatrix}15\\5 \\30-h\end{pmatrix}\right|}\\[5pt]
0&\geq&\dfrac{15^2+ (-45)\cdot 5 + (25-h)(30-h)}{\sqrt{15^2+(-45)^2+(25-h)^2}\cdot \sqrt{15^2+5^2+(30-h)^2}}\\[5pt]
0&\geq&\dfrac{(25-h)(30-h)}{\sqrt{2250+(25-h)^2}\cdot \sqrt{250+(30-h)^2}}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/92c5a6f7fb3cd8a293de05531842be6e8d636412008bf23a3d600528bf3e7689?color=5a5a5a) Zeichne die Funktion mit deinem GTR und berechne die Nullstellen.
Zeichne die Funktion mit deinem GTR und berechne die Nullstellen.
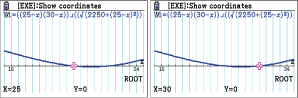 Die 2. Bedingung ist erfüllt für
Die 2. Bedingung ist erfüllt für  Nimmst du nun die beiden Ergebnisse zusammen, sind beide Bedingungen erfüllt, wenn
Nimmst du nun die beiden Ergebnisse zusammen, sind beide Bedingungen erfüllt, wenn 
- Der Abstand der Aussichtsplattform im Punkt
zur Ebene
soll höchstens 7m betragen.
- Die Brücken von der Aussichtsplattform im Punkt
zu den Aussichtsplattformen in den Punkten
und
sollen einen Winkel von mindestens 90° einschließen.

2.5  Punkt des Sicherungsseils bestimmen
Du sollst die Koordinaten eines Punktes bestimmen, in welchem das Sicherungsseil von der Aussichtsplattform in Punkt
Punkt des Sicherungsseils bestimmen
Du sollst die Koordinaten eines Punktes bestimmen, in welchem das Sicherungsseil von der Aussichtsplattform in Punkt  den Boden in einem Winkel von 60° trifft.
Der Auftreffpunkt auf der
den Boden in einem Winkel von 60° trifft.
Der Auftreffpunkt auf der  -Ebene hat die Koordinaten
-Ebene hat die Koordinaten  . Die Gerade durch den Punkt
. Die Gerade durch den Punkt  und den Punkt
und den Punkt  , die also das Sicherungsseil beschreibt, hat dann folgende Form:
, die also das Sicherungsseil beschreibt, hat dann folgende Form:
 Für den Winkel
Für den Winkel  zwischen einer Ebene mit Normalenvektor
zwischen einer Ebene mit Normalenvektor  und einer Gerade mit Richtungsvektor
und einer Gerade mit Richtungsvektor  gilt folgende Formel:
gilt folgende Formel:
 Ein Normalenvektor zur
Ein Normalenvektor zur  - Ebene ist beispielsweise
- Ebene ist beispielsweise  .
Setze den Winkel und die beiden Vektoren in die Formel ein und löse nach
.
Setze den Winkel und die beiden Vektoren in die Formel ein und löse nach  auf.
auf.
![\(\begin{array}[t]{rll}
\sin(60^{\circ})&=&\dfrac{\left|\begin{pmatrix}0\\0\\1\end{pmatrix} \cdot \begin{pmatrix}l_1\\l_2-50\\-30\end{pmatrix}\right|}{\left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right| \cdot \left|\begin{pmatrix}l_1\\l_2-50\\-30\end{pmatrix}\right|}\\[5pt]
\dfrac{\sqrt{3}}{2}&=&\dfrac{30}{1\cdot \sqrt{l_1^2 + (l_2-50)^2 + (-30)^2}} \quad \scriptsize \mid\; \cdot \sqrt{l_1^2 + (l_2-50)^2 + (-30)^2}\\[5pt]
\dfrac{\sqrt{3}}{2}\cdot \sqrt{l_1^2 + (l_2-50)^2 + 900}&=&30 \quad \scriptsize \mid\; \cdot \dfrac{2}{\sqrt{3}} \\[5pt]
\sqrt{l_1^2 + (l_2-50)^2 + 900}&=&\dfrac{60}{\sqrt{3}} \quad \scriptsize \mid\; ()^2 \\[5pt]
l_1^2 + (l_2-50)^2 +900&=&\dfrac{3600}{3} \quad \scriptsize \mid\; -((l_2-50)^2 + 900) \\[5pt]
l_1^2 &=&1200 -900 - (l_2-50)^2\quad \scriptsize \mid\; \sqrt{ } \\[5pt]
l_1 &=&\pm \sqrt{300 - (l_2-50)^2}
\end{array}\)](https://mathjax.schullv.de/9cab77d9d6ca8af1faf12e6537668340e4578474d7f1c91f5797bcf18da60b11?color=5a5a5a) Wähle nun einen Wert für
Wähle nun einen Wert für  , sodass die Diskriminante positiv ist und berechne das zugehörige
, sodass die Diskriminante positiv ist und berechne das zugehörige  .
Ein Auftreffpunkt hat die Koordinaten
.
Ein Auftreffpunkt hat die Koordinaten  und
und

 .
Der Punkt lautet dann
.
Der Punkt lautet dann  .
.
 Flächeninhalt bestimmen
Alle möglichen Auftreffpunkte schließen eine Fläche ein, du sollst deren Inhalt bestimmen.
Die allgemeine Funktionsgleichung für einen Kreis mit Radius
Flächeninhalt bestimmen
Alle möglichen Auftreffpunkte schließen eine Fläche ein, du sollst deren Inhalt bestimmen.
Die allgemeine Funktionsgleichung für einen Kreis mit Radius  und Mittelpunkt
und Mittelpunkt  lautet
lautet
 Betrachtest du die Funktionsgleichung für
Betrachtest du die Funktionsgleichung für  , so erkennst du, dass es sich dabei gerade um die eines Kreises mit Radius
, so erkennst du, dass es sich dabei gerade um die eines Kreises mit Radius  und Mittelpunkt
und Mittelpunkt  handelt.
Berechne den Flächeninhalt dieses Kreises:
handelt.
Berechne den Flächeninhalt dieses Kreises:
![\(\begin{array}[t]{rll}
A&=&\pi r^2 \\[5pt]
&=&\pi \cdot 300 \\[5pt]
&\approx&942,478
\end{array}\)](https://mathjax.schullv.de/54512b3392730d927900976bf7ebc96fd10073eb0032be95793d24dacdf499f5?color=5a5a5a) Die Fläche hat einen Inhalt von 942,478 m2.
Die Fläche hat einen Inhalt von 942,478 m2.
2.6  Wahrscheinlichkeit bestimmen
Die Reißfestigkeit der Sicherungsseile ist annähernd normalverteilt. Sei also
Wahrscheinlichkeit bestimmen
Die Reißfestigkeit der Sicherungsseile ist annähernd normalverteilt. Sei also  die Zufallsvariable, die die Reißfestigkeit der Sicherungsseile beschreibt. Der Erwartungswert
die Zufallsvariable, die die Reißfestigkeit der Sicherungsseile beschreibt. Der Erwartungswert  liegt bei 145 kN, außerdem weist du, dass
liegt bei 145 kN, außerdem weist du, dass  ist.
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein Sicherungsseil bei einer Belastung zwischen 142 kN und 150 kN reißt.
Führe dafür eine
ist.
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein Sicherungsseil bei einer Belastung zwischen 142 kN und 150 kN reißt.
Führe dafür eine  -Transformation durch, dabei ist
-Transformation durch, dabei ist  dann eine standard-normalverteilte Zufallsvariable.
dann eine standard-normalverteilte Zufallsvariable.
 Für die Transformation fehlt dir also noch die Varianz
Für die Transformation fehlt dir also noch die Varianz  . Diese kannst du mit Hilfe der gegebenen Wahrscheinlichkeit und der Tabelle zur Standard-Normalverteilung berechnen:
. Diese kannst du mit Hilfe der gegebenen Wahrscheinlichkeit und der Tabelle zur Standard-Normalverteilung berechnen:
![\(\begin{array}[t]{rll}
P(X>140)&=&0,973 \\[5pt]
P\left(\dfrac{X-145}{\sigma}>\dfrac{140-145}{\sigma}\right)&=&0,973\\[5pt]
P\left(Z>-\dfrac{5}{\sigma}\right)&=&0,973\\[5pt]
1-P\left(Z\leq-\frac{5}{\sigma}\right)&=&0,973\\[5pt]
1-\phi\left(-\frac{5}{\sigma}\right)&=&0,973\\[5pt]
1-\left(1-\phi\left(\frac{5}{\sigma}\right)\right)&=&0,973\quad \\[5pt]
\phi\left(\frac{5}{\sigma}\right)&=&0,973
\end{array}\)](https://mathjax.schullv.de/891180ec59772e87f55b844117789c424b00df6cd38cf819614958cbe79b289c?color=5a5a5a) Suche nun in der Tabelle für die Standard-Normalverteilung nach der Wahrscheinlichkeit 0,973 um anschließend
Suche nun in der Tabelle für die Standard-Normalverteilung nach der Wahrscheinlichkeit 0,973 um anschließend  zu bestimmen. Du findest
zu bestimmen. Du findest
 Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
1,93&=&\frac{5}{\sigma} \quad \scriptsize \mid\; \cdot \sigma\\[5pt]
1,93 \sigma&=&5 \quad \scriptsize \mid\; :1,93\\[5pt]
\sigma &\approx& 2,5907
\end{array}\)](https://mathjax.schullv.de/07061f54f71f35d0d85f037c429ce3e34e85e06af0a858aaf6395781bfe50bdd?color=5a5a5a) Du sollst nun die Wahrscheinlichkeit
Du sollst nun die Wahrscheinlichkeit  bestimmen. Führe die
bestimmen. Führe die  -transformation durch und nutze dann die Tabelle für die Standard-Normalverteilung um die gesuchte Wahrscheinlichkeit zu berechnen.
-transformation durch und nutze dann die Tabelle für die Standard-Normalverteilung um die gesuchte Wahrscheinlichkeit zu berechnen.
![\(\begin{array}[t]{rll}
P(142 \leq X \leq 150)&=&P(X\leq 150) - P(X \leq 142) \\[5pt]
&=&P\left(\dfrac{X-145}{2,5907}\leq \dfrac{150-145}{2,5907}\right)-P\left(\dfrac{X-145}{2,5907}\leq \dfrac{142-145}{2,5907}\right)\\[5pt]
&=&P\left(Z\leq \dfrac{150-145}{2,5907}\right)-P\left(Z\leq \dfrac{142-145}{2,5907}\right)\\[5pt]
&=&P\left(Z\leq 1,93\right)-P\left(Z\leq -1,16\right)\\[5pt]
&=&\phi(1,93)-\phi(-1,16)\\[5pt]
&=&\phi(1,93)- (1-\phi(1,16))\\[5pt]
&=&0,9732 - (1-0,8770)\\[5pt]
&=&0,8502
\end{array}\)](https://mathjax.schullv.de/69b5c602731066e9ea8c4b9d2ff237462ec046c5774069e13fd737470c87dfef?color=5a5a5a) Die Wahrscheinlichkeit, dass das Seil bei einer Belastung zwischen 142 kN und 150 kN reißt beträgt 85,02%.
Die Wahrscheinlichkeit, dass das Seil bei einer Belastung zwischen 142 kN und 150 kN reißt beträgt 85,02%.
2.7  Gesamtbesucherzahl bestimmen
Du sollst die erwartete Gesamtbesucherzahl an einem Ferientag berechnen, wenn 100 Kinder aus der näheren Umgebung in den Hochseilgarten kommen. Außerdem kennst du die folgenden Anteile
Gesamtbesucherzahl bestimmen
Du sollst die erwartete Gesamtbesucherzahl an einem Ferientag berechnen, wenn 100 Kinder aus der näheren Umgebung in den Hochseilgarten kommen. Außerdem kennst du die folgenden Anteile
![\(\begin{array}[t]{rll}
P(K)&=&P(U)\cdot P(UK) + P(\overline{U})\cdot P(\overline{U}K) \\[5pt]
0,485&=&0,65 \cdot P(UK) + 0,35\cdot 0,55 \\[5pt]
0,485&=&0,65 \cdot P(UK) + 0,1925 \quad \scriptsize \mid\;-0,1925\\[5pt]
0,2925&=&0,65 \cdot P(UK)\quad \scriptsize \mid\;:0,65\\[5pt]
P(UK) &=& 0,45
\end{array}\)](https://mathjax.schullv.de/6baa5bb69c0029bf77720fce4b59d9264a27207371fcc9bef5e30a249c111ee6?color=5a5a5a) 45% der Besucher aus der näheren Umgebung sind Kinder. Dieser Anteil entspricht hier 100 Kindern. Berechne die Anzahl der Besucher aus der näheren Umgebung.
45% der Besucher aus der näheren Umgebung sind Kinder. Dieser Anteil entspricht hier 100 Kindern. Berechne die Anzahl der Besucher aus der näheren Umgebung.
![\(\begin{array}[t]{rll}
\text{Anzahl }U \cdot P(UK)&=&100 \\[5pt]
\text{Anzahl }U \cdot 0,45&=&100\quad \scriptsize \mid\; :0,45\\[5pt]
\text{Anzahl }U &=& \dfrac{100}{0,45} = 222,\overline{2}
\end{array}\)](https://mathjax.schullv.de/0ad786241b4b1398f99b88f58aa7a1998f08e435baf8f609dea706c2f4b011f4?color=5a5a5a) Das entspricht 65% der Gesamtbesucherzahl, diese berechnet sich somit folgendermaßen
Das entspricht 65% der Gesamtbesucherzahl, diese berechnet sich somit folgendermaßen
![\(\begin{array}[t]{rll}
\text{Anzahl Besucher} \cdot P(U)&=&222,\overline{2} \\[5pt]
\text{Anzahl Besucher} \cdot 0,65&=&222,\overline{2}\quad \scriptsize \mid\;: 0,65\\[5pt]
\text{Anzahl Besucher} &=& \dfrac{222,\overline{2}}{0,65} \approx 341,88
\end{array}\)](https://mathjax.schullv.de/59545f7bd6dade7a20c8961758659a55ad16dba3298c87947aee55b8793cd2f8?color=5a5a5a) Die erwartete Besucherzahl an einem Ferientag liegt bei 342 Besuchern.
Die erwartete Besucherzahl an einem Ferientag liegt bei 342 Besuchern.
- 65% der Besucher kommen aus der näheren Umgebung (
).
- 55% der Besucher, die nicht aus der näheren Umgebung kommen, sind Kinder (
).
- 48,5% der Besucher sind Kinder (
).