Teil B1
Eine Spielzeugfabrik stellt Puppenwagen her. Die beiden zueinander kongruenten Seitenteile eines solchen Puppenwagens bestehen aus Holzplatten.
Die Außenfläche eines dieser Seitenteile kann in einem kartesischen Koordinatensystem mit dem Koordinatenursprung  (1 Längeneinheit entspricht 1 Dezimeter) dargestellt werden (siehe Abbildung 1).
(1 Längeneinheit entspricht 1 Dezimeter) dargestellt werden (siehe Abbildung 1).
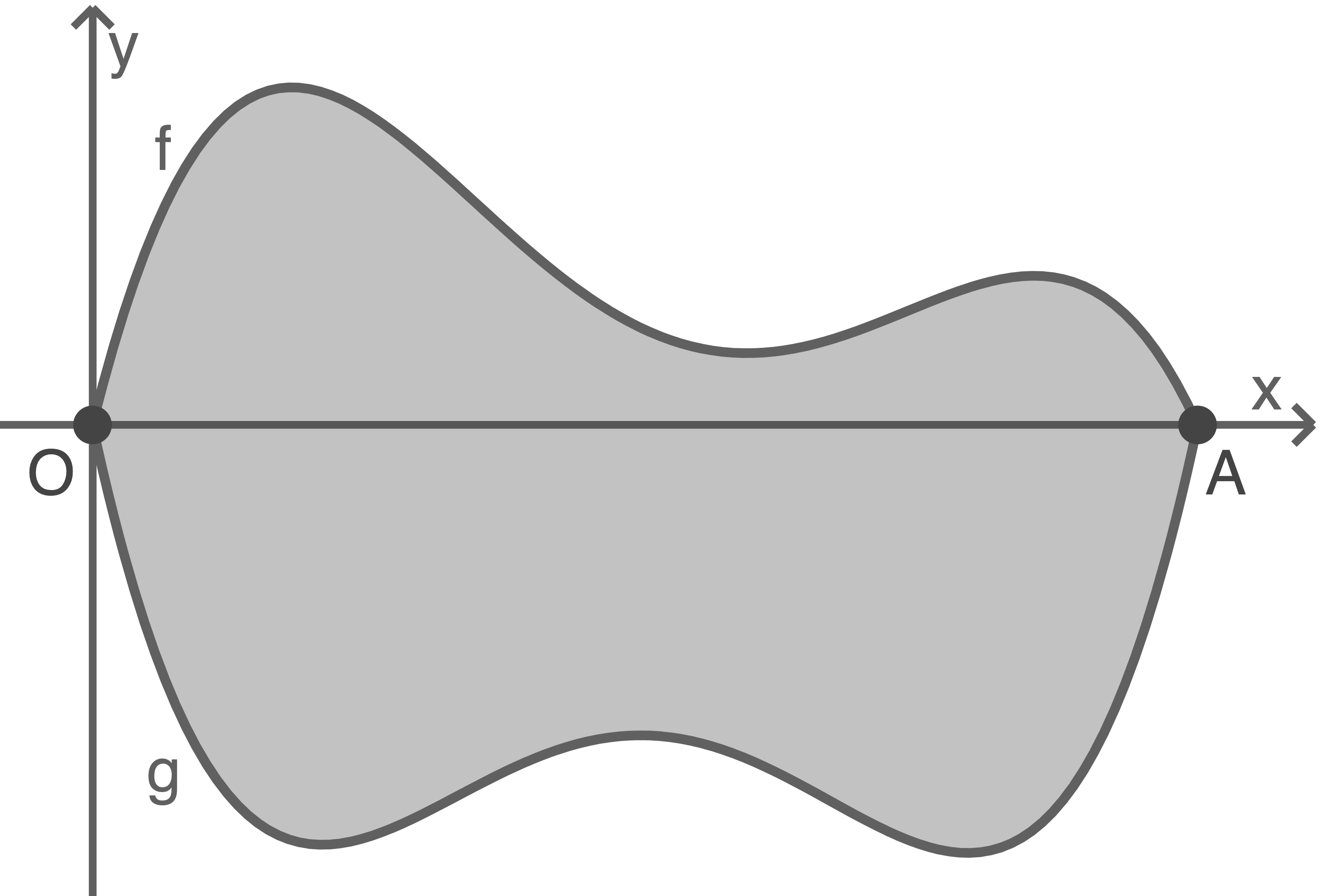
Abbildung 1 (nicht maßstäblich)
1.1
Begründe, dass die Strecke  näherungsweise die Länge
näherungsweise die Länge  besitzt.
besitzt.
Jedes Seitenteil des Puppenwagens wird aus einer rechteckigen Holzplatte ausgesägt.
Die Strecke verläuft dabei parallel zu zwei gegenüberliegenden Seiten dieser Rechteckfläche.
verläuft dabei parallel zu zwei gegenüberliegenden Seiten dieser Rechteckfläche.
Ermittle Mindestlänge und Mindestbreite der rechteckigen Holzplatte.
Jedes Seitenteil des Puppenwagens wird aus einer rechteckigen Holzplatte ausgesägt.
Die Strecke
Ermittle Mindestlänge und Mindestbreite der rechteckigen Holzplatte.
(7 P)
1.2
Jedes  dicke Seitenteil des Puppenwagens soll vollständig (Außenfläche, Innenfläche und Randfläche) mit einem für Kleinkinder gefahrlosen Speziallack überzogen werden.
dicke Seitenteil des Puppenwagens soll vollständig (Außenfläche, Innenfläche und Randfläche) mit einem für Kleinkinder gefahrlosen Speziallack überzogen werden.
Ermittle den Inhalt der zu lackierenden Fläche eines Seitenteils des Puppenwagens.
Ermittle den Inhalt der zu lackierenden Fläche eines Seitenteils des Puppenwagens.
(12 P)
1.3
Jedes Seitenteil soll auf der Außenfläche mit einem Zierstreifen beklebt werden. Die parallelen Begrenzungen des Zierstreifens sollen dabei vollständig auf der Außenfläche des Seitenteils zu sehen und unter einem Winkel von  gegenüber der Abszissenachse geneigt sein (siehe Abbildung 2).
Bestimme die maximal mögliche Breite des Zierstreifens.
gegenüber der Abszissenachse geneigt sein (siehe Abbildung 2).
Bestimme die maximal mögliche Breite des Zierstreifens.
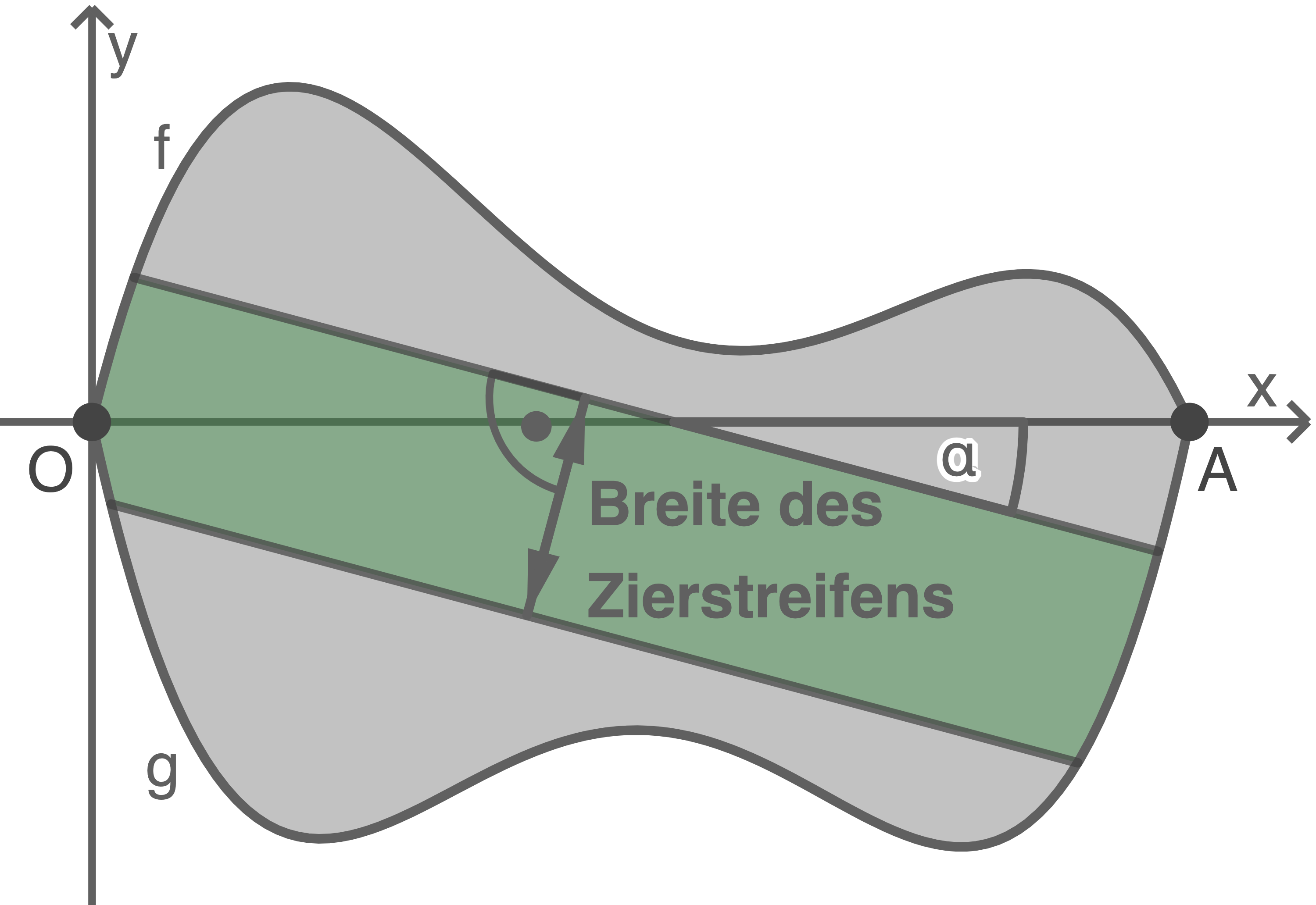
Abbildung 2 (nicht maßstäblich)
(10 P)
1.4
Für die Befestigung des Haltegriffs am Puppenwagen wird eine Metallstrebe verwendet. Zwischen den Punkten  und
und  kann die Metallstrebe durch einen Teil des Graphen einer linearen Funktion
kann die Metallstrebe durch einen Teil des Graphen einer linearen Funktion  beschrieben werden. Im Punkt
beschrieben werden. Im Punkt  geht der Graph der Funktion
geht der Graph der Funktion  tangential in den Graphen der Funktion
tangential in den Graphen der Funktion  über.
über.
Bestimme die Länge der Metallstrebe zwischen den Punkten und
und  .
.
Puppenwagen aus der laufenden Produktion können Oberflächen- oder Farbgestaltungsfehler besitzen.
Bestimme die Länge der Metallstrebe zwischen den Punkten
(7 P)
Erfahrungsgemäß werden bei
1.5
Ermittle, mit welcher Wahrscheinlichkeit ein der Produktion zufällig entnommener Puppenwagen keinen der beiden Fehler aufweist.
(4 P)
1.6
Nach einer Veränderung des Produktionsablaufes wird von Seiten der Spielzeugfabrik behauptet, dass von den produzierten Puppenwagen statt bisher  nun weniger fehlerhaft sind. In einem Test mit
nun weniger fehlerhaft sind. In einem Test mit  der Produktion zufällig entnommenen Puppenwagen soll die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens
der Produktion zufällig entnommenen Puppenwagen soll die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens  “ auf ein Signifikanzniveau von
“ auf ein Signifikanzniveau von  überprüft werden.
überprüft werden.
Bestimme den Ablehnungsbereich der Nullhypothese für den beschriebenen Test.
Bestimme den Ablehnungsbereich der Nullhypothese für den beschriebenen Test.
(5 P)
Aufgabe B 1
1.1  Länge der Strecke bestimmen
In der ersten Aufgabe sind zwei Funktion
Länge der Strecke bestimmen
In der ersten Aufgabe sind zwei Funktion  und
und  gegeben, diese begrenzen die Fläche der Seitenteile eines Puppenwagens. Du sollst zeigen, dass die Strecke
gegeben, diese begrenzen die Fläche der Seitenteile eines Puppenwagens. Du sollst zeigen, dass die Strecke  ungefähr 4,71 dm lang ist. Der Punkt
ungefähr 4,71 dm lang ist. Der Punkt  ist der Koordinatenursprung und
ist der Koordinatenursprung und  ist der Punkt, in dem
ist der Punkt, in dem  und
und  die
die  -Achse schneiden.
Die Länge der Strecke ist somit gerade die
-Achse schneiden.
Die Länge der Strecke ist somit gerade die  -Koordinate des Punkts
-Koordinate des Punkts  . Du musst also eine der folgenden Gleichungen lösen
. Du musst also eine der folgenden Gleichungen lösen
 oder
oder  Definiere dir die Funktion in deinem GTR und berechne die Nullstellen.
Definiere dir die Funktion in deinem GTR und berechne die Nullstellen.
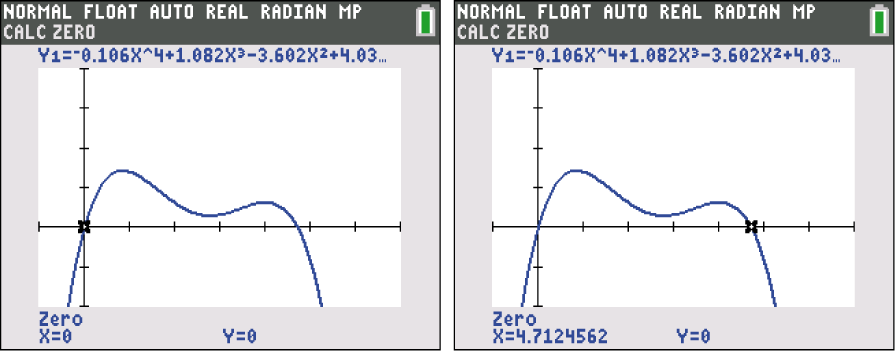 Die Strecke
Die Strecke  hat somit eine Länge von ungefähr 4,71 dm.
hat somit eine Länge von ungefähr 4,71 dm.
 Mindestlänge und -breite berechnen
Das Seitenteil wird aus einer rechteckigen Holzplatte ausgesägt. Du sollst nun die Mindestlänge und -breite für diese Holzplatte berechnen.
Die Mindestlänge hast du bereits berechnet, da diese der Länge der Strecke
Mindestlänge und -breite berechnen
Das Seitenteil wird aus einer rechteckigen Holzplatte ausgesägt. Du sollst nun die Mindestlänge und -breite für diese Holzplatte berechnen.
Die Mindestlänge hast du bereits berechnet, da diese der Länge der Strecke  entspricht.
Die Mindestbreite setzt sich aus dem maximalen Abstand der Funktion
entspricht.
Die Mindestbreite setzt sich aus dem maximalen Abstand der Funktion  zur
zur  -Achse und dem maximalen Abstand der Funktion
-Achse und dem maximalen Abstand der Funktion  zur
zur  -Achse zusammen. Berechne also von der Funktion
-Achse zusammen. Berechne also von der Funktion  den maximalen Funktionswert in
den maximalen Funktionswert in  und für
und für  den minimalen Funktionswert in
den minimalen Funktionswert in  . Dafür kannst du deinen GTR verwenden.
. Dafür kannst du deinen GTR verwenden.
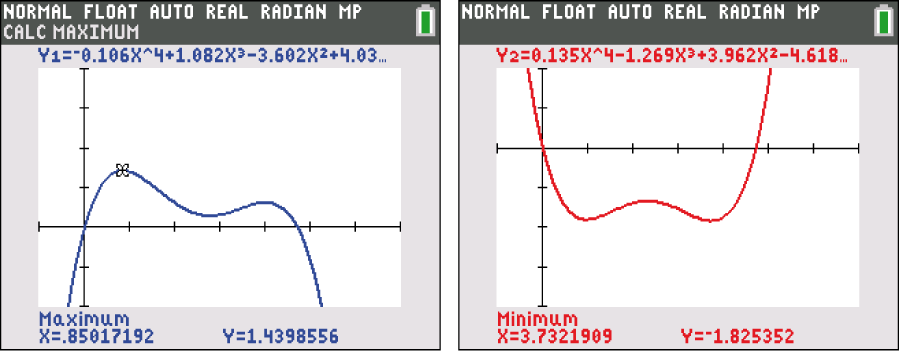 Der maximale Abstand der Funktion
Der maximale Abstand der Funktion  zur
zur  -Achse beträgt
-Achse beträgt
 .
Der maximale Abstand der Funktion
.
Der maximale Abstand der Funktion  zur
zur  - Achse beträgt
- Achse beträgt
 .
Für die Mindestbreite gilt somit:
.
Für die Mindestbreite gilt somit:
 Die Mindestbreite beträgt ungefähr 3,27 dm und die Mindestlänge beträgt ungefähr 4,71 dm.
Die Mindestbreite beträgt ungefähr 3,27 dm und die Mindestlänge beträgt ungefähr 4,71 dm.
2nd  TRACE (CALC)
TRACE (CALC)  2: zero
2: zero

2nd  TRACE (CALC)
TRACE (CALC)  3: minimum/4: maximum
3: minimum/4: maximum

1.2  Inhalt der zu lackierenden Fläche berechnen
Die Seitenfläche soll komplett lackiert werden. Du sollst die zu lackierende Fläche berechnen. Berechne zunächst den Inhalt der Innenseite bzw. Außenseite und dann den Inhalt der Randfläche.
1. Schritt: Flächeninhalt der Innenseite bzw. Außenseite berechnen
Die Fläche der Innenseite bzw. Außenseite wird durch die Funktionen
Inhalt der zu lackierenden Fläche berechnen
Die Seitenfläche soll komplett lackiert werden. Du sollst die zu lackierende Fläche berechnen. Berechne zunächst den Inhalt der Innenseite bzw. Außenseite und dann den Inhalt der Randfläche.
1. Schritt: Flächeninhalt der Innenseite bzw. Außenseite berechnen
Die Fläche der Innenseite bzw. Außenseite wird durch die Funktionen  und
und  begrenzt. Du kannst die Fläche zwischen diesen beiden Funktionen mit Hilfe ihrer Differenzenfunktion im Bereich
begrenzt. Du kannst die Fläche zwischen diesen beiden Funktionen mit Hilfe ihrer Differenzenfunktion im Bereich  berechnen:
berechnen:
 Dafür kannst du deinen GTR verwenden.
Dafür kannst du deinen GTR verwenden.
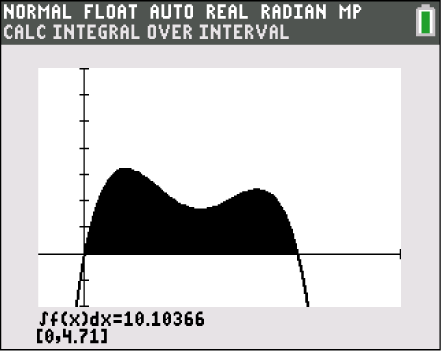 Du erhältst für den Inhalt einer Seitenfläche also
Du erhältst für den Inhalt einer Seitenfläche also  dm2.
2. Schritt: Randfläche berechnen
Um den Inhalt der Randfläche berechnen zu können, benötigst du zunächst den Umfang der Seitenfläche. Dieser Umfang setzt sich aus der Länge der Kurve
dm2.
2. Schritt: Randfläche berechnen
Um den Inhalt der Randfläche berechnen zu können, benötigst du zunächst den Umfang der Seitenfläche. Dieser Umfang setzt sich aus der Länge der Kurve  und der Länge der Kurve
und der Länge der Kurve  zusammen. Die Länge einer Kurve
zusammen. Die Länge einer Kurve  im Intervall
im Intervall ![\([a,b]\)](https://mathjax.schullv.de/c487989b0b629aea171018db737fb06843ac124c02828a0d3639596c70713937?color=5a5a5a) wird mit folgender Formel berechnet:
wird mit folgender Formel berechnet:
 Zeichne den Graphen zu der Wurzelfunktion und berechne das Integral für die Länge der Kurve jeweils für
Zeichne den Graphen zu der Wurzelfunktion und berechne das Integral für die Länge der Kurve jeweils für  und
und  .
.
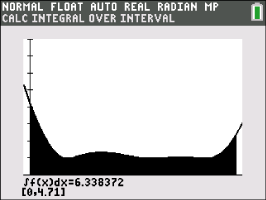
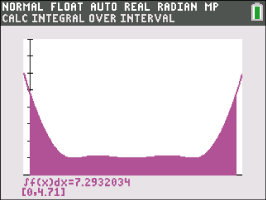 Die Kurvenlängen betragen
Die Kurvenlängen betragen
 dm
dm
 dm
Die Seitenfläche hat also einen Umfang von
dm
Die Seitenfläche hat also einen Umfang von
 Die Randfläche ist dann ein Rechteck mit Länge
Die Randfläche ist dann ein Rechteck mit Länge  dm und Breite
dm und Breite  cm
cm  dm. Nun kannst du den Inhalt
dm. Nun kannst du den Inhalt  dieser Fläche berechnen.
dieser Fläche berechnen.
 Der gesuchte Flächeninhalt berechnet sich dann wie folgt
Der gesuchte Flächeninhalt berechnet sich dann wie folgt
 Die zu lackierende Fläche ist ungefähr
Die zu lackierende Fläche ist ungefähr  dm2 groß.
dm2 groß.
2nd  TRACE (CALC)
TRACE (CALC)  7:
7: 

MATH  8: nDeriv
2nd
8: nDeriv
2nd  TRACE (CALC)
TRACE (CALC)  7:
7: 


1.3  Maximale Breite des Zierstreifens
Du sollst die maximale Breite des Zierstreifens auf der Seitenfläche berechnen. Dieser Zierstreifen wird begrenzt von zwei Geraden mit einem Schnittwinkel mit der
Maximale Breite des Zierstreifens
Du sollst die maximale Breite des Zierstreifens auf der Seitenfläche berechnen. Dieser Zierstreifen wird begrenzt von zwei Geraden mit einem Schnittwinkel mit der  -Achse von
-Achse von  . Die gesuchte Breite ist also der Abstand zwischen diesen beiden Geraden. Stelle also die Funktionsgleichungen der beiden Geraden auf und berechne anschließend den Abstand dieser Geraden.
1. Schritt: Geradengleichungen aufstellen
Für den Steigungswinkel
. Die gesuchte Breite ist also der Abstand zwischen diesen beiden Geraden. Stelle also die Funktionsgleichungen der beiden Geraden auf und berechne anschließend den Abstand dieser Geraden.
1. Schritt: Geradengleichungen aufstellen
Für den Steigungswinkel  und die Steigung
und die Steigung  einer Funktion gilt folgender Zusammenhang
einer Funktion gilt folgender Zusammenhang
 Ist die Steigung positiv, so ist der Schnittwinkel mit der
Ist die Steigung positiv, so ist der Schnittwinkel mit der  -Achse gleich dem Steigungswinkel. Ist die Steigung jedoch negativ gilt
Steigungswinkel =
-Achse gleich dem Steigungswinkel. Ist die Steigung jedoch negativ gilt
Steigungswinkel = - Schnittwinkel
Der Steigungswinkel der beiden Geraden ist also
- Schnittwinkel
Der Steigungswinkel der beiden Geraden ist also  . Berechne die Steigung der beiden Geraden mit der oben angegebenen Formel.
. Berechne die Steigung der beiden Geraden mit der oben angegebenen Formel.
 Die Geraden haben dann folgende Form:
Die Geraden haben dann folgende Form:  und
und  .
Bestimme nun
.
Bestimme nun  so, dass die Gerade
so, dass die Gerade  den Graphen von
den Graphen von  von unten berührt und
von unten berührt und  so, dass die Gerade
so, dass die Gerade  den Graphen von
den Graphen von  von oben berührt.
Zwei Funktionen berühren sich in einem gemeinsamen Punkt, wenn sie dort dieselbe Steigung besitzen. Bestimme also zunächst die Stelle, an der die Funktion
von oben berührt.
Zwei Funktionen berühren sich in einem gemeinsamen Punkt, wenn sie dort dieselbe Steigung besitzen. Bestimme also zunächst die Stelle, an der die Funktion  bzw.
bzw.  eine Steigung von -0,27 hat, beachte dabei, dass die Stelle gesucht ist, sodass die Gerade innerhalb der Fläche verläuft. Für
eine Steigung von -0,27 hat, beachte dabei, dass die Stelle gesucht ist, sodass die Gerade innerhalb der Fläche verläuft. Für  muss gelten, dass die Gerade den Graphen von unten berührt, das bedeutet, dass der Graph der Funktion vorher eine größere negative Steigung hat als nach der Stelle mit Steigung -0,27. Für den Graphen von
muss gelten, dass die Gerade den Graphen von unten berührt, das bedeutet, dass der Graph der Funktion vorher eine größere negative Steigung hat als nach der Stelle mit Steigung -0,27. Für den Graphen von  gilt das Umgekehrte. Der Graph hat vorher eine kleinere negative Steigung als nach der Stelle mit Steigung -0,27.
Zeichne die Ableitung der Funktionen und die Gerade
gilt das Umgekehrte. Der Graph hat vorher eine kleinere negative Steigung als nach der Stelle mit Steigung -0,27.
Zeichne die Ableitung der Funktionen und die Gerade  , berechne dann den Schnittpunkt. Dafür kannst du deinen GTR verwenden.
, berechne dann den Schnittpunkt. Dafür kannst du deinen GTR verwenden.
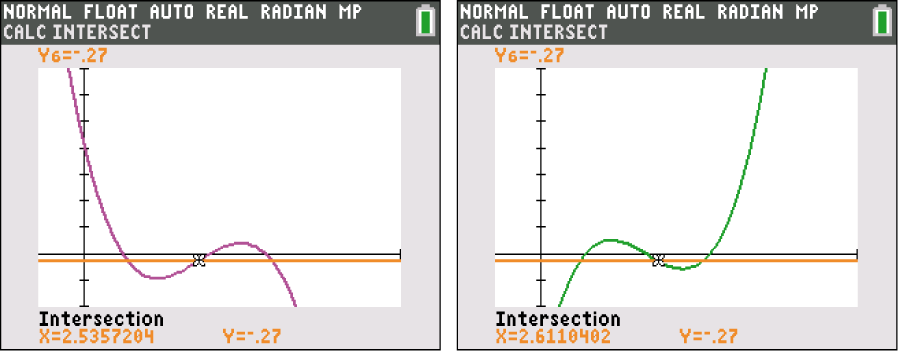 Du erhältst für
Du erhältst für  der zugehörige Funktionswert ist
der zugehörige Funktionswert ist  . Der Berührpunkt von
. Der Berührpunkt von  und dem Graphen von
und dem Graphen von  ist also
ist also  . Setze diese Werte in die Geradengleichung zu
. Setze diese Werte in die Geradengleichung zu  ein und berechne
ein und berechne  :
:
![\(\begin{array}[t]{rll}
0,3403&=&-0,27 \cdot 2,5357 + b_1\\[5pt]
0,3403&=&-0,684639 + b_1\quad \scriptsize \mid\;+0,684639 \\[5pt]
b_1 &\approx&1,02
\end{array}\)](https://mathjax.schullv.de/9a348cbd4ecb9b9338f91be88d38562e2b34af72e301ffe205d3998d915f586c?color=5a5a5a) Die Geradengleichung für
Die Geradengleichung für  lautet also
lautet also  .
Außerdem erhältst du für
.
Außerdem erhältst du für  der zugehörige Funktionswert ist
der zugehörige Funktionswert ist  . Der Berührpunkt von
. Der Berührpunkt von  und dem Graphen von
und dem Graphen von  ist also
ist also  . Setze diese Werte in die Geradengleichung zu
. Setze diese Werte in die Geradengleichung zu  ein und berechne
ein und berechne  :
:
![\(\begin{array}[t]{rll}
-1,3614&=&-0,27 \cdot 2,6110 + b_2\\[5pt]
-1,3614&=&-0,70497 + b_2\quad \scriptsize \mid\;+0,70497 \\[5pt]
b_2 &\approx&-0,66
\end{array}\)](https://mathjax.schullv.de/881e0929fe7c6bb36e584d3d56083de1ba847111a2327be796c3f396c9cb73b1?color=5a5a5a) Die Geradengleichung lautet demnach
Die Geradengleichung lautet demnach  .
2. Schritt: Abstand zwischen den Geraden
Der Abstand zwischen den Geraden entspricht dem Abstand zwischen dem Berührpunkt
.
2. Schritt: Abstand zwischen den Geraden
Der Abstand zwischen den Geraden entspricht dem Abstand zwischen dem Berührpunkt  und der Gerade
und der Gerade  . Um diesen zu berechnen, stelle eine Lotgerade
. Um diesen zu berechnen, stelle eine Lotgerade  durch den Punkt
durch den Punkt  auf, welche orthogonal zu der Geraden
auf, welche orthogonal zu der Geraden  verläuft. Zwei Geraden sind orthogonal zueinander, wenn für die Steigungen folgendes gilt:
verläuft. Zwei Geraden sind orthogonal zueinander, wenn für die Steigungen folgendes gilt:
 Daher ist die Stiegung der Lotgeraden gegeben durch
Daher ist die Stiegung der Lotgeraden gegeben durch  . Berechne nun noch die
. Berechne nun noch die  -Achsenverschiebung
-Achsenverschiebung  wie oben durch Punktprobe mit
wie oben durch Punktprobe mit  :
:
![\(\begin{array}[t]{rll}
n_1: y&=& \frac{1}{0,27}x+ b &\quad \scriptsize \\[5pt]
0,3403&=&\frac{1}{0,27}\cdot2,5357+b &\quad \scriptsize \mid\;- \frac{1}{0,27}\cdot2,5357 \\[5pt]
-9,05118&=& b &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5be63d5224a889955c86bde33f0de183ad442c0415eed84fc646c06321742a2b?color=5a5a5a) Die Geradengleichung der Lotgerade lautet dann
Die Geradengleichung der Lotgerade lautet dann  .
.
Berechne nun den Lotfußpunkt, also den Schnittpunkt von und
und  . Der Abstand zwischen dem Lotfußpunkt
. Der Abstand zwischen dem Lotfußpunkt  und
und  ist dann der gesuchte Abstand.
ist dann der gesuchte Abstand.
![\(\begin{array}[t]{rll}
\frac{1}{0,27}x-9,05118&=& -0,27x - 0,66&\quad \scriptsize \mid\; +0,27x; +9,05118 \\[5pt]
\frac{1}{0,27}x+0,27x &=& 9,05118-0,66 &\quad \scriptsize \mid\; :(\frac{1}{0,27} + 0,27) \\[5pt]
x&=& 2,11168&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/06858f1409cd93bcdc6d591be84ac8f7e4ebd78daeae2213b671c103b959c4e5?color=5a5a5a) Die
Die  -Koordinate ist dann
-Koordinate ist dann  . Damit sind die Koordinaten des Lotfußpunktes
. Damit sind die Koordinaten des Lotfußpunktes  . Gesucht ist nun der Abstand zwischen
. Gesucht ist nun der Abstand zwischen  und
und  . Den Abstand zwischen zwei Punkten kannst du mit folgender Formel berechnen:
. Den Abstand zwischen zwei Punkten kannst du mit folgender Formel berechnen:
 Damit ergibt sich nun:
Damit ergibt sich nun:
![\(\begin{array}[t]{rll}
d&=& \sqrt{(2,11168-2,5357)^2+(-1,23015-0,3403)^2} &\quad \scriptsize \\[5pt]
&\approx& 1,63&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4f48b3b7592009cda738a59a47652feb49796c1aad619fa27385cf2b97ef9322?color=5a5a5a) Der Zierstreifen darf maximal
Der Zierstreifen darf maximal  dm breit sein.
dm breit sein.
2nd  TRACE (CALC)
TRACE (CALC)  5: intersect
5: intersect

Berechne nun den Lotfußpunkt, also den Schnittpunkt von
1.4  Länge der Metallstrebe berechnen
Um die Länge der Metallstrebe zu berechnen, stellst du zuerst die Gleichung der Geraden
Länge der Metallstrebe berechnen
Um die Länge der Metallstrebe zu berechnen, stellst du zuerst die Gleichung der Geraden  auf und berechnest dann den Abstand zwischen den Punkten
auf und berechnest dann den Abstand zwischen den Punkten  und
und  .
1. Schritt: Geradengleichung bestimmen
Die Gerade
.
1. Schritt: Geradengleichung bestimmen
Die Gerade  geht tangential in die Funktion
geht tangential in die Funktion  über, das bedeutet, dass diese im Punkt
über, das bedeutet, dass diese im Punkt  die gleiche Steigung haben.
die gleiche Steigung haben.
 Außerdem verläuft die Gerade durch den Punkt
Außerdem verläuft die Gerade durch den Punkt  . Damit kannst du die Geradengleichung aufstellen.
. Damit kannst du die Geradengleichung aufstellen.
![\(\begin{array}[t]{rll}
h(4,71)&=&0\\[5pt]
0&=&4,672 \cdot 4,71 + b\\[5pt]
0&=&22,00512 + b\quad \scriptsize \mid\; -22,00512\\[5pt]
b&=&-22,00512
\end{array}\)](https://mathjax.schullv.de/67ba0610eaf927b11c453650ca4284d686c8bac2239fc3168fa503dc107f06f7?color=5a5a5a) Die Geradengleichung von
Die Geradengleichung von  lautet:
lautet:  2. Schritt: Länge berechnen
Um die Länge der Metallstrebe berechnen zu können, bestimme zunächst die
2. Schritt: Länge berechnen
Um die Länge der Metallstrebe berechnen zu können, bestimme zunächst die  -Koordinate von Punkt
-Koordinate von Punkt  .
.
 Den Abstand
Den Abstand  zwischen zwei Punkten
zwischen zwei Punkten  und
und  berechnest du mit folgender Formel
berechnest du mit folgender Formel
 Die gesuchte Länge berechnet sich folgendermaßen
Die gesuchte Länge berechnet sich folgendermaßen
![\(\begin{array}[t]{rll}
d&=& \sqrt{(5,25-4,71)^2 + (2,52-0)^2} \\[5pt]
&\approx&2,58
\end{array}\)](https://mathjax.schullv.de/7ad408fbbd22dfb0396aad0c6be2add3aea16182494e35d1cd19004aa4d214a8?color=5a5a5a) Die Länge der Metallstrebe beträgt ungefähr
Die Länge der Metallstrebe beträgt ungefähr  dm.
dm.
1.5  Wahrscheinlichkeit bestimmen
Du sollst die Wahrscheinlichkeit für das Ereignis E: „ein zufällig entnommener Puppenwagen hat keinen der beiden Fehler“ berechnen. Das Gegenereignis zu E lautet dann „ein zufällig entnommener Puppenwagen hat mindestens einen Fehler“.
Du hast folgende Wahrscheinlichkeiten gegeben:
Wahrscheinlichkeit bestimmen
Du sollst die Wahrscheinlichkeit für das Ereignis E: „ein zufällig entnommener Puppenwagen hat keinen der beiden Fehler“ berechnen. Das Gegenereignis zu E lautet dann „ein zufällig entnommener Puppenwagen hat mindestens einen Fehler“.
Du hast folgende Wahrscheinlichkeiten gegeben:


 Da 2,5% beide Fehler haben und bei 3% ein Oberflächenfehler auftritt, gilt außerdem
Da 2,5% beide Fehler haben und bei 3% ein Oberflächenfehler auftritt, gilt außerdem
 Jetzt kannst du die Wahrscheinlichkeit des Gegenereignisses ausrechnen:
Jetzt kannst du die Wahrscheinlichkeit des Gegenereignisses ausrechnen:
![\(\begin{array}[t]{rll}
P(\overline{E})&=&P(\text{nur Farbgestaltungsfehler}) + P(\text{nur Oberflächenfehler}) + P(\text{beide Fehler}) \\[5pt]
&=&0,01 + 0,005 + 0,025\\[5pt]
&=&0,04
\end{array}\)](https://mathjax.schullv.de/fe82b997ec12a01a2869b4c2e6b23ae832d511a31e0bce9be4ea50e58a703074?color=5a5a5a) Für die gesuchte Wahrscheinlichkeit gilt dann
Für die gesuchte Wahrscheinlichkeit gilt dann
 Mit einer Wahrscheinlichkeit von 96% hat ein zufällig ausgewählter Puppenwagen keinen der beiden Fehler.
Mit einer Wahrscheinlichkeit von 96% hat ein zufällig ausgewählter Puppenwagen keinen der beiden Fehler.
1.6  Ablehnungsbereich bestimmen
Du sollst den Ablehnungsbereich für die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens 4%“ auf einem Niveau von
Ablehnungsbereich bestimmen
Du sollst den Ablehnungsbereich für die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens 4%“ auf einem Niveau von  bestimmen.
bestimmen.
 Ein Puppenwagen ist fehlerhaft, wenn er mindestens einen der beiden Fehler aufweist. Sei die Zufallsvariable
Ein Puppenwagen ist fehlerhaft, wenn er mindestens einen der beiden Fehler aufweist. Sei die Zufallsvariable  die Anzahl der fehlerhaften Puppenwagen aus
die Anzahl der fehlerhaften Puppenwagen aus  .
Die Zufallsvariable
.
Die Zufallsvariable  kann als binomialverteilt angenommen werden, da ein Puppenwagen entweder fehlerhaft ist oder nicht. Es gibt also nur zwei mögliche Ausgänge des Zufallsexperiments. Außerdem sind die Puppenwagen unabhängig, ein Erfolg steht hier für einen fehlerhaften Puppenwagen. Die Zufallsvariable
kann als binomialverteilt angenommen werden, da ein Puppenwagen entweder fehlerhaft ist oder nicht. Es gibt also nur zwei mögliche Ausgänge des Zufallsexperiments. Außerdem sind die Puppenwagen unabhängig, ein Erfolg steht hier für einen fehlerhaften Puppenwagen. Die Zufallsvariable  ist also binomialverteilt mit
ist also binomialverteilt mit  .
Für den Ablehnungsbereich gilt demnacht:
.
Für den Ablehnungsbereich gilt demnacht:  .
Die Wahrscheinlichkeit für weniger als
.
Die Wahrscheinlichkeit für weniger als  fehlerhafte Puppenwagen soll weniger als 15% betragen.
fehlerhafte Puppenwagen soll weniger als 15% betragen.
 Du kannst
Du kannst  durch systematisches Probieren bestimmen. Berechne die Wahrscheinlichkeit für verschiedene Werte von
durch systematisches Probieren bestimmen. Berechne die Wahrscheinlichkeit für verschiedene Werte von  , das gesuchte
, das gesuchte  , ist das, für welches die Wahrscheinlichkeit gerade noch unterhalb von 0,15 liegt.
, ist das, für welches die Wahrscheinlichkeit gerade noch unterhalb von 0,15 liegt.
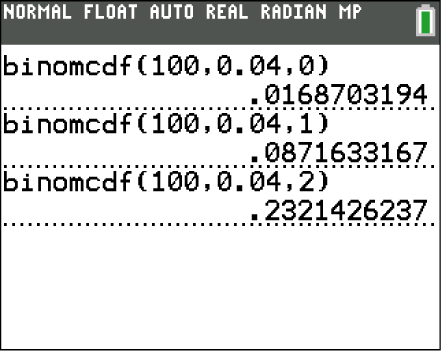 Du erhältst somit:
Du erhältst somit:  .
Der größtmögliche Ablehnungsbereich ist
.
Der größtmögliche Ablehnungsbereich ist  .
.
2nd  VARS (DISTR)
VARS (DISTR)  A: binomcdf
A: binomcdf

Aufgabe B 1
1.1  Länge der Strecke bestimmen
In der ersten Aufgabe sind zwei Funktion
Länge der Strecke bestimmen
In der ersten Aufgabe sind zwei Funktion  und
und  gegeben, diese begrenzen die Fläche der Seitenteile eines Puppenwagens. Du sollst zeigen, dass die Strecke
gegeben, diese begrenzen die Fläche der Seitenteile eines Puppenwagens. Du sollst zeigen, dass die Strecke  ungefähr 4,71 dm lang ist. Der Punkt
ungefähr 4,71 dm lang ist. Der Punkt  ist der Koordinatenursprung und
ist der Koordinatenursprung und  ist der Punkt, in dem
ist der Punkt, in dem  und
und  die
die  -Achse schneiden.
Die Länge der Strecke ist somit gerade die
-Achse schneiden.
Die Länge der Strecke ist somit gerade die  -Koordinate des Punkts
-Koordinate des Punkts  . Du musst also eine der folgenden Gleichungen lösen
. Du musst also eine der folgenden Gleichungen lösen
 oder
oder  Definiere dir die Funktion in deinem GTR und berechne die Nullstellen.
Definiere dir die Funktion in deinem GTR und berechne die Nullstellen.
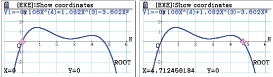 Die Strecke
Die Strecke  hat somit eine Länge von ungefähr 4,71 dm.
hat somit eine Länge von ungefähr 4,71 dm.
 Mindestlänge und -breite berechnen
Das Seitenteil wird aus einer rechteckigen Holzplatte ausgesägt. Du sollst nun die Mindestlänge und -breite für diese Holzplatte berechnen.
Die Mindestlänge hast du bereits berechnet, da diese der Länge der Strecke
Mindestlänge und -breite berechnen
Das Seitenteil wird aus einer rechteckigen Holzplatte ausgesägt. Du sollst nun die Mindestlänge und -breite für diese Holzplatte berechnen.
Die Mindestlänge hast du bereits berechnet, da diese der Länge der Strecke  entspricht.
Die Mindestbreite setzt sich aus dem maximalen Abstand der Funktion
entspricht.
Die Mindestbreite setzt sich aus dem maximalen Abstand der Funktion  zur
zur  -Achse und dem maximalen Abstand der Funktion
-Achse und dem maximalen Abstand der Funktion  zur
zur  -Achse zusammen. Berechne also von der Funktion
-Achse zusammen. Berechne also von der Funktion  den maximalen Funktionswert in
den maximalen Funktionswert in  und für
und für  den minimalen Funktionswert in
den minimalen Funktionswert in  . Dafür kannst du deinen GTR verwenden.
. Dafür kannst du deinen GTR verwenden.
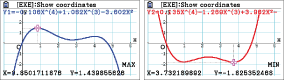 Der maximale Abstand der Funktion
Der maximale Abstand der Funktion  zur
zur  -Achse beträgt
-Achse beträgt
 .
Der maximale Abstand der Funktion
.
Der maximale Abstand der Funktion  zur
zur  - Achse beträgt
- Achse beträgt
 .
Für die Mindestbreite gilt somit:
.
Für die Mindestbreite gilt somit:
 Die Mindestbreite beträgt ungefähr 3,27 dm und die Mindestlänge beträgt ungefähr 4,71 dm.
Die Mindestbreite beträgt ungefähr 3,27 dm und die Mindestlänge beträgt ungefähr 4,71 dm.
G-Solve  ROOT
ROOT

G-Solve  MIN/MAX
MIN/MAX

1.2  Inhalt der zu lackierenden Fläche berechnen
Die Seitenfläche soll komplett lackiert werden. Du sollst die zu lackierende Fläche berechnen. Berechne zunächst den Inhalt der Innenseite bzw. Außenseite und dann den Inhalt der Randfläche.
1. Schritt: Flächeninhalt der Innenseite bzw. Außenseite berechnen
Die Fläche der Innenseite bzw. Außenseite wird durch die Funktionen
Inhalt der zu lackierenden Fläche berechnen
Die Seitenfläche soll komplett lackiert werden. Du sollst die zu lackierende Fläche berechnen. Berechne zunächst den Inhalt der Innenseite bzw. Außenseite und dann den Inhalt der Randfläche.
1. Schritt: Flächeninhalt der Innenseite bzw. Außenseite berechnen
Die Fläche der Innenseite bzw. Außenseite wird durch die Funktionen  und
und  begrenzt. Du kannst die Fläche zwischen diesen beiden Funktionen mit Hilfe ihrer Differenzenfunktion im Bereich
begrenzt. Du kannst die Fläche zwischen diesen beiden Funktionen mit Hilfe ihrer Differenzenfunktion im Bereich  berechnen:
berechnen:
 Dafür kannst du deinen GTR verwenden.
Dafür kannst du deinen GTR verwenden.
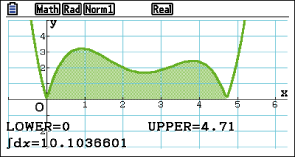 Du erhältst für den Inhalt einer Seitenfläche also
Du erhältst für den Inhalt einer Seitenfläche also  dm2.
2. Schritt: Randfläche berechnen
Um den Inhalt der Randfläche berechnen zu können, benötigst du zunächst den Umfang der Seitenfläche. Dieser Umfang setzt sich aus der Länge der Kurve
dm2.
2. Schritt: Randfläche berechnen
Um den Inhalt der Randfläche berechnen zu können, benötigst du zunächst den Umfang der Seitenfläche. Dieser Umfang setzt sich aus der Länge der Kurve  und der Länge der Kurve
und der Länge der Kurve  zusammen. Die Länge einer Kurve
zusammen. Die Länge einer Kurve  im Intervall
im Intervall ![\([a,b]\)](https://mathjax.schullv.de/c487989b0b629aea171018db737fb06843ac124c02828a0d3639596c70713937?color=5a5a5a) wird mit folgender Formel berechnet:
wird mit folgender Formel berechnet:
 Zeichne den Graphen zu der Wurzelfunktion und berechne das Integral für die Länge der Kurve jeweils für
Zeichne den Graphen zu der Wurzelfunktion und berechne das Integral für die Länge der Kurve jeweils für  und
und  .
.
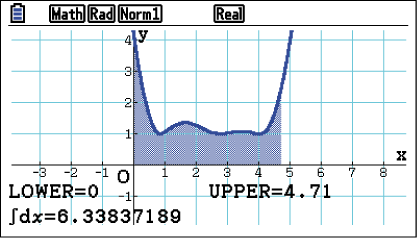
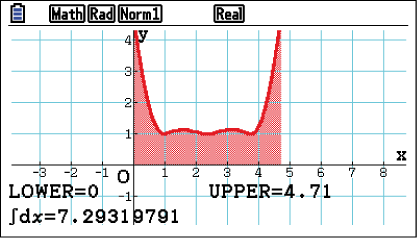 Die Kurvenlängen betragen
Die Kurvenlängen betragen
 dm
dm
 dm
Die Seitenfläche hat also einen Umfang von
dm
Die Seitenfläche hat also einen Umfang von
 Die Randfläche ist dann ein Rechteck mit Länge
Die Randfläche ist dann ein Rechteck mit Länge  dm und Breite
dm und Breite  cm
cm  dm. Nun kannst du den Inhalt
dm. Nun kannst du den Inhalt  dieser Fläche berechnen.
dieser Fläche berechnen.
 Der gesuchte Flächeninhalt berechnet sich dann wie folgt
Der gesuchte Flächeninhalt berechnet sich dann wie folgt
 Die zu lackierende Fläche ist ungefähr
Die zu lackierende Fläche ist ungefähr  dm2 groß.
dm2 groß.
G-Solv  F6
F6 






1.3  Maximale Breite des Zierstreifens
Du sollst die maximale Breite des Zierstreifens auf der Seitenfläche berechnen. Dieser Zierstreifen wird begrenzt von zwei Geraden mit einem Schnittwinkel mit der
Maximale Breite des Zierstreifens
Du sollst die maximale Breite des Zierstreifens auf der Seitenfläche berechnen. Dieser Zierstreifen wird begrenzt von zwei Geraden mit einem Schnittwinkel mit der  -Achse von
-Achse von  . Die gesuchte Breite ist also der Abstand zwischen diesen beiden Geraden. Stelle also die Funktionsgleichungen der beiden Geraden auf und berechne anschließend den Abstand dieser Geraden.
1. Schritt: Geradengleichungen aufstellen
Für den Steigungswinkel
. Die gesuchte Breite ist also der Abstand zwischen diesen beiden Geraden. Stelle also die Funktionsgleichungen der beiden Geraden auf und berechne anschließend den Abstand dieser Geraden.
1. Schritt: Geradengleichungen aufstellen
Für den Steigungswinkel  und die Steigung
und die Steigung  einer Funktion gilt folgender Zusammenhang
einer Funktion gilt folgender Zusammenhang
 Ist die Steigung positiv, so ist der Schnittwinkel mit der
Ist die Steigung positiv, so ist der Schnittwinkel mit der  -Achse gleich dem Steigungswinkel. Ist die Steigung jedoch negativ gilt
Steigungswinkel =
-Achse gleich dem Steigungswinkel. Ist die Steigung jedoch negativ gilt
Steigungswinkel = - Schnittwinkel
Der Steigungswinkel der beiden Geraden ist also
- Schnittwinkel
Der Steigungswinkel der beiden Geraden ist also  . Berechne die Steigung der beiden Geraden mit der oben angegebenen Formel.
. Berechne die Steigung der beiden Geraden mit der oben angegebenen Formel.
 Die Geraden haben dann folgende Form:
Die Geraden haben dann folgende Form:  und
und  .
Bestimme nun
.
Bestimme nun  so, dass die Gerade
so, dass die Gerade  den Graphen von
den Graphen von  von unten berührt und
von unten berührt und  so, dass die Gerade
so, dass die Gerade  den Graphen von
den Graphen von  von oben berührt.
Zwei Funktionen berühren sich in einem gemeinsamen Punkt, wenn sie dort dieselbe Steigung besitzen. Bestimme also zunächst die Stelle, an der die Funktion
von oben berührt.
Zwei Funktionen berühren sich in einem gemeinsamen Punkt, wenn sie dort dieselbe Steigung besitzen. Bestimme also zunächst die Stelle, an der die Funktion  bzw.
bzw.  eine Steigung von -0,27 hat, beachte dabei, dass die Stelle gesucht ist, sodass die Gerade innerhalb der Fläche verläuft. Für
eine Steigung von -0,27 hat, beachte dabei, dass die Stelle gesucht ist, sodass die Gerade innerhalb der Fläche verläuft. Für  muss gelten, dass die Gerade den Graphen von unten berührt, das bedeutet, dass der Graph der Funktion vorher eine größere negative Steigung hat als nach der Stelle mit Steigung -0,27. Für den Graphen von
muss gelten, dass die Gerade den Graphen von unten berührt, das bedeutet, dass der Graph der Funktion vorher eine größere negative Steigung hat als nach der Stelle mit Steigung -0,27. Für den Graphen von  gilt das Umgekehrte. Der Graph hat vorher eine kleinere negative Steigung als nach der Stelle mit Steigung -0,27.
Zeichne die Ableitung der Funktionen und die Gerade
gilt das Umgekehrte. Der Graph hat vorher eine kleinere negative Steigung als nach der Stelle mit Steigung -0,27.
Zeichne die Ableitung der Funktionen und die Gerade  , berechne dann den Schnittpunkt. Dafür kannst du deinen GTR verwenden.
, berechne dann den Schnittpunkt. Dafür kannst du deinen GTR verwenden.
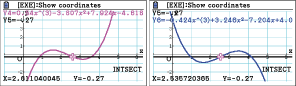 Du erhältst für
Du erhältst für  der zugehörige Funktionswert ist
der zugehörige Funktionswert ist  . Der Berührpunkt von
. Der Berührpunkt von  und dem Graphen von
und dem Graphen von  ist also
ist also  . Setze diese Werte in die Geradengleichung zu
. Setze diese Werte in die Geradengleichung zu  ein und berechne
ein und berechne  :
:
![\(\begin{array}[t]{rll}
0,3403&=&-0,27 \cdot 2,5357 + b_1\\[5pt]
0,3403&=&-0,684639 + b_1\quad \scriptsize \mid\;+0,684639 \\[5pt]
b_1 &\approx&1,02
\end{array}\)](https://mathjax.schullv.de/941ea6a275c147f2b1149f9bbcfb63fdf9fe11760eec0a1ee5cb60c9eea7896a?color=5a5a5a) Die Geradengleichung für
Die Geradengleichung für  lautet also
lautet also  .
Außerdem erhältst du für
.
Außerdem erhältst du für  der zugehörige Funktionswert ist
der zugehörige Funktionswert ist  . Der Berührpunkt von
. Der Berührpunkt von  und dem Graphen von
und dem Graphen von  ist also
ist also  . Setze diese Werte in die Geradengleichung zu
. Setze diese Werte in die Geradengleichung zu  ein und berechne
ein und berechne  :
:
![\(\begin{array}[t]{rll}
-1,3614&=&-0,27 \cdot 2,6110 + b_2\\[5pt]
-1,3614&=&-0,70497 + b_2\quad \scriptsize \mid\;+0,70497 \\[5pt]
b_2 &\approx&-0,66
\end{array}\)](https://mathjax.schullv.de/162c753eddbaf04653405ee2ae8c3def19a7a7a73f6b769d1dfb177272d67a82?color=5a5a5a) Die Geradengleichung lautet demnach
Die Geradengleichung lautet demnach  .
2. Schritt: Abstand zwischen den Geraden
Der Abstand zwischen den Geraden entspricht dem Abstand zwischen dem Berührpunkt
.
2. Schritt: Abstand zwischen den Geraden
Der Abstand zwischen den Geraden entspricht dem Abstand zwischen dem Berührpunkt  und der Gerade
und der Gerade  . Um diesen zu berechnen, stelle eine Lotgerade
. Um diesen zu berechnen, stelle eine Lotgerade  durch den Punkt
durch den Punkt  auf, welche orthogonal zu der Geraden
auf, welche orthogonal zu der Geraden  verläuft. Zwei Geraden sind orthogonal zueinander, wenn für die Steigungen folgendes gilt:
verläuft. Zwei Geraden sind orthogonal zueinander, wenn für die Steigungen folgendes gilt:
 Daher ist die Stiegung der Lotgeraden gegeben durch
Daher ist die Stiegung der Lotgeraden gegeben durch  . Berechne nun noch die
. Berechne nun noch die  -Achsenverschiebung
-Achsenverschiebung  wie oben durch Punktprobe mit
wie oben durch Punktprobe mit  :
:
![\(\begin{array}[t]{rll}
n_1: y&=& \frac{1}{0,27}x+ b &\quad \scriptsize \\[5pt]
0,3403&=&\frac{1}{0,27}\cdot2,5357+b &\quad \scriptsize \mid\;- \frac{1}{0,27}\cdot2,5357 \\[5pt]
-9,05118&=& b &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/737f5580adeb09277b0a9cb65a8931e681cec2e22a414831bc3a9cdddf20d15e?color=5a5a5a) Die Geradengleichung der Lotgerade lautet dann
Die Geradengleichung der Lotgerade lautet dann  .
.
Berechne nun den Lotfußpunkt, also den Schnittpunkt von und
und  . Der Abstand zwischen dem Lotfußpunkt
. Der Abstand zwischen dem Lotfußpunkt  und
und  ist dann der gesuchte Abstand.
ist dann der gesuchte Abstand.
![\(\begin{array}[t]{rll}
\frac{1}{0,27}x-9,05118&=& -0,27x - 0,66&\quad \scriptsize \mid\; +0,27x; +9,05118 \\[5pt]
\frac{1}{0,27}x+0,27x &=& 9,05118-0,66 &\quad \scriptsize \mid\; :(\frac{1}{0,27} + 0,27) \\[5pt]
x&=& 2,11168&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6301e383cbeb3d046ddffcecb57284d355a97cf39ddb5cb19adffa3dfe263b3e?color=5a5a5a) Die
Die  -Koordinate ist dann
-Koordinate ist dann  . Damit sind die Koordinaten des Lotfußpunktes
. Damit sind die Koordinaten des Lotfußpunktes  . Gesucht ist nun der Abstand zwischen
. Gesucht ist nun der Abstand zwischen  und
und  . Den Abstand zwischen zwei Punkten kannst du mit folgender Formel berechnen:
. Den Abstand zwischen zwei Punkten kannst du mit folgender Formel berechnen:
 Damit ergibt sich nun:
Damit ergibt sich nun:
![\(\begin{array}[t]{rll}
d&=& \sqrt{(2,11168-2,5357)^2+(-1,23015-0,3403)^2} &\quad \scriptsize \\[5pt]
&\approx& 1,63&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fb4556843d980bdc46ade83b1c55225a7c045008c947757d34edb3363081bf25?color=5a5a5a) Der Zierstreifen darf maximal
Der Zierstreifen darf maximal  dm breit sein.
dm breit sein.
G-Solv  F5: intersect
F5: intersect

Berechne nun den Lotfußpunkt, also den Schnittpunkt von
1.4  Länge der Metallstrebe berechnen
Um die Länge der Metallstrebe zu berechnen, stellst du zuerst die Gleichung der Geraden
Länge der Metallstrebe berechnen
Um die Länge der Metallstrebe zu berechnen, stellst du zuerst die Gleichung der Geraden  auf und berechnest dann den Abstand zwischen den Punkten
auf und berechnest dann den Abstand zwischen den Punkten  und
und  .
1. Schritt: Geradengleichung bestimmen
Die Gerade
.
1. Schritt: Geradengleichung bestimmen
Die Gerade  geht tangential in die Funktion
geht tangential in die Funktion  über, das bedeutet, dass diese im Punkt
über, das bedeutet, dass diese im Punkt  die gleiche Steigung haben.
die gleiche Steigung haben.
 Außerdem verläuft die Gerade durch den Punkt
Außerdem verläuft die Gerade durch den Punkt  . Damit kannst du die Geradengleichung aufstellen.
. Damit kannst du die Geradengleichung aufstellen.
![\(\begin{array}[t]{rll}
h(4,71)&=&0\\[5pt]
0&=&4,672 \cdot 4,71 + b\\[5pt]
0&=&22,00512 + b\quad \scriptsize \mid\; -22,00512\\[5pt]
b&=&-22,00512
\end{array}\)](https://mathjax.schullv.de/452dbf230128b620d3efbb53e525b4235c3225bf4cf0c89032d074b4f8aff706?color=5a5a5a) Die Geradengleichung von
Die Geradengleichung von  lautet:
lautet:  2. Schritt: Länge berechnen
Um die Länge der Metallstrebe berechnen zu können, bestimme zunächst die
2. Schritt: Länge berechnen
Um die Länge der Metallstrebe berechnen zu können, bestimme zunächst die  -Koordinate von Punkt
-Koordinate von Punkt  .
.
 Den Abstand
Den Abstand  zwischen zwei Punkten
zwischen zwei Punkten  und
und  berechnest du mit folgender Formel
berechnest du mit folgender Formel
 Die gesuchte Länge berechnet sich folgendermaßen
Die gesuchte Länge berechnet sich folgendermaßen
![\(\begin{array}[t]{rll}
d&=& \sqrt{(5,25-4,71)^2 + (2,52-0)^2} \\[5pt]
&\approx&2,58
\end{array}\)](https://mathjax.schullv.de/c1cb538ce3e938ba2d0f4670e2461fbc15da0b78befac2ecd62132f7851f8a6a?color=5a5a5a) Die Länge der Metallstrebe beträgt ungefähr
Die Länge der Metallstrebe beträgt ungefähr  dm.
dm.
1.5  Wahrscheinlichkeit bestimmen
Du sollst die Wahrscheinlichkeit für das Ereignis E: „ein zufällig entnommener Puppenwagen hat keinen der beiden Fehler“ berechnen. Das Gegenereignis zu E lautet dann „ein zufällig entnommener Puppenwagen hat mindestens einen Fehler“.
Du hast folgende Wahrscheinlichkeiten gegeben:
Wahrscheinlichkeit bestimmen
Du sollst die Wahrscheinlichkeit für das Ereignis E: „ein zufällig entnommener Puppenwagen hat keinen der beiden Fehler“ berechnen. Das Gegenereignis zu E lautet dann „ein zufällig entnommener Puppenwagen hat mindestens einen Fehler“.
Du hast folgende Wahrscheinlichkeiten gegeben:


 Da 2,5% beide Fehler haben und bei 3% ein Oberflächenfehler auftritt, gilt außerdem
Da 2,5% beide Fehler haben und bei 3% ein Oberflächenfehler auftritt, gilt außerdem
 Jetzt kannst du die Wahrscheinlichkeit des Gegenereignisses ausrechnen:
Jetzt kannst du die Wahrscheinlichkeit des Gegenereignisses ausrechnen:
![\(\begin{array}[t]{rll}
P(\overline{E})&=&P(\text{nur Farbgestaltungsfehler}) + P(\text{nur Oberflächenfehler}) + P(\text{beide Fehler}) \\[5pt]
&=&0,01 + 0,005 + 0,025\\[5pt]
&=&0,04
\end{array}\)](https://mathjax.schullv.de/0bb6d064f80171d5dd814ee406e671e26bd676775337132e596835de15adcb93?color=5a5a5a) Für die gesuchte Wahrscheinlichkeit gilt dann
Für die gesuchte Wahrscheinlichkeit gilt dann
 Mit einer Wahrscheinlichkeit von 96% hat ein zufällig ausgewählter Puppenwagen keinen der beiden Fehler.
Mit einer Wahrscheinlichkeit von 96% hat ein zufällig ausgewählter Puppenwagen keinen der beiden Fehler.
1.6  Ablehnungsbereich bestimmen
Du sollst den Ablehnungsbereich für die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens 4%“ auf einem Niveau von
Ablehnungsbereich bestimmen
Du sollst den Ablehnungsbereich für die Nullhypothese „Der Anteil der fehlerhaften Puppenwagen beträgt mindestens 4%“ auf einem Niveau von  bestimmen.
bestimmen.
 Ein Puppenwagen ist fehlerhaft, wenn er mindestens einen der beiden Fehler aufweist. Sei die Zufallsvariable
Ein Puppenwagen ist fehlerhaft, wenn er mindestens einen der beiden Fehler aufweist. Sei die Zufallsvariable  die Anzahl der fehlerhaften Puppenwagen aus
die Anzahl der fehlerhaften Puppenwagen aus  .
Die Zufallsvariable
.
Die Zufallsvariable  kann als binomialverteilt angenommen werden, da ein Puppenwagen entweder fehlerhaft ist oder nicht. Es gibt also nur zwei mögliche Ausgänge des Zufallsexperiments. Außerdem sind die Puppenwagen unabhängig, ein Erfolg steht hier für einen fehlerhaften Puppenwagen. Die Zufallsvariable
kann als binomialverteilt angenommen werden, da ein Puppenwagen entweder fehlerhaft ist oder nicht. Es gibt also nur zwei mögliche Ausgänge des Zufallsexperiments. Außerdem sind die Puppenwagen unabhängig, ein Erfolg steht hier für einen fehlerhaften Puppenwagen. Die Zufallsvariable  ist also binomialverteilt mit
ist also binomialverteilt mit  .
Für den Ablehnungsbereich gilt demnacht:
.
Für den Ablehnungsbereich gilt demnacht:  .
Die Wahrscheinlichkeit für weniger als
.
Die Wahrscheinlichkeit für weniger als  fehlerhafte Puppenwagen soll weniger als 15% betragen.
fehlerhafte Puppenwagen soll weniger als 15% betragen.
 Du kannst
Du kannst  durch systematisches Probieren bestimmen. Berechne die Wahrscheinlichkeit für verschiedene Werte von
durch systematisches Probieren bestimmen. Berechne die Wahrscheinlichkeit für verschiedene Werte von  , das gesuchte
, das gesuchte  , ist das, für welches die Wahrscheinlichkeit gerade noch unterhalb von 0,15 liegt.
, ist das, für welches die Wahrscheinlichkeit gerade noch unterhalb von 0,15 liegt.
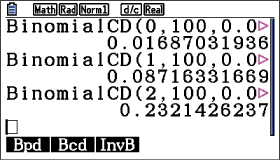 Du erhältst somit:
Du erhältst somit:  .
Der größtmögliche Ablehnungsbereich ist
.
Der größtmögliche Ablehnungsbereich ist  .
.
OPTN  STAT
STAT  DIST
DIST  BIN
BIN  Bcd
Bcd
