Teil A

In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Gegeben ist die Funktion $f$ mit $f(x)=\sqrt{2\cdot x+3}$ .
Der größtmögliche Definitionsbereich von $f$ ist:

	$\{x\mid x\in \mathbb{R};x\gt-6\}$
	$\{x\mid x\in \mathbb{R};x\geq-\frac{3}{2}\}$
	$\{x\mid x\in \mathbb{R};x\gt-\frac{3}{2}\}$
	$\{x\mid x\in \mathbb{R};x\lt-\frac{3}{2}\}$
	$\{x\mid x\in \mathbb{R};x\lt6\}$

1.2

Für jeden reellen Wert von $t$ ist eine Funktlon $f_{t}$ mit

$f_{t}(x)=\left\{\begin{array}{ll} t\cdot x- 4 \,\,\,\,\text{für} \ x\lt1\\ \ x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{für} \ x\geq 1 \end{array}\right.$ $(x\in \mathbb{R})$

gegeben.
Die Funktion $f_{t}$ ist an der Stelle $x_{0}=1$ stetig für:

	$t=-5$
	$t=-4$
	$t=1$
	$t=4$
	$t=5$

1.3

Gegeben sind die Ebenen $E$ und $F_{b}$ mit $E:6\cdot x-y-4\cdot z=12$
bzw.
$F_{b}:\ -3\cdot x+b\cdot y+2\cdot z=6\ (b\in \mathbb{R})\ .$

Für welchen Wert von $b$ stehen $E$ und $F_{b}$ senkrecht aufeinander?

	$b=-26$
	$b=-10$
	$b=0$
	$b=\dfrac{1}{2}$
	$b=26$

1.4

Welcher Punkt $B$ hat von der Ebene $E:\; x=4$ den gleichen Abstand wie der Punkt $A(1\mid 2\mid 3)$ von der Ebene $E?$

	$B(4\mid 2\mid-3)$
	$B(1\mid-2\mid3)$
	$B(0\mid-2\mid-3)$
	$B(-1\mid4\mid4)$
	$B(-2\mid 6\mid 5)$

1.5

Eine binomialverteilte Zufallsgröße $X$ hat den Erwartungswert $\mu = 20$ und die Standardabweichung $\sigma=4.$

Für die Parameter $n$ und $p$ von $X$ gilt:

	$n=20,\ p=\frac{1}{10}$
	$n=25,\ p=\frac{1}{5}$
	$n=40,\ p=\frac{1}{4}$
	$n=80,\ p=\frac{1}{4}$
	$n=100, p=\frac{1}{5}$

Für Aufgabe 1 erreichbare BE-Anzahl: 05

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ und $g$ mit $f(x)=\sin x$ bzw. $g(x)=x$ . Die Graphen von $f$ und $g$ haben in ihrem einzigen gemeinsamen Punkt $O(0\mid 0)$ die gleiche Steigung.

2.1

Ermittle den lnhalt der Fläche, die der Graph von $f$ , der Graph von $g$ und die Gerade mit der Gleichung $x=\pi$ einschließen.

Erreichbare BE-Anzahl: 03

2.2

Gib eine Gleichung einer Tangente an den Graphen von $f$ an, die die beiden folgenden Eigenschaften hat:

- Die Tangente verläuft parallel zum Graphen von $g$ .

- Die Tangente enthält nicht den Punkt $O$ .

Erreichbare BE-Anzahl: 02

Für jeden Wert von $a$ $(a\in \mathbb{R}, a\neq 0)$ ist eine Funktion $f_{a}$ gegeben mit $f_{a}(x)=a\cdot(x-2)^{3}$ und $x\in \mathbb{R}.$

3.1

Zeige, dass die in $\mathbb{R}$ definierte Funktion $F$ mit

$F(x)=\displaystyle \frac{1}{2}\cdot(x-2)^{4}+3$

eine Stammfunktion von $f_{2}$ ist.

Erreichbare BE-Anzahl: 01

3.2

Untersuche mithilfe von Skizzen, für welche Werte von $a$ sich unter den Stammfunktionen von $f_{a}$ solche befinden, die nur negative Funktionswerte haben.

Erreichbare BE-Anzahl: 04

In einem Koordinatensystem ist ein gerader Zylinder mit dem Radius $5$ und der Höhe $10$ gegeben, dessen Grundfläche in der $x-y$ -Ebene liegt. $M(8\mid5\mid10)$ ist der Mittelpunkt der Deckfläche.

4.1

Weise nach, dass der Punkt $P(5\mid1\mid0)$ auf dem Rand der Grundfläche des Zylinders liegt.

Erreichbare BE-Anzahl: 02

4.2

Unter allen Punkten auf dem Rand der Deckfläche hat der Punkt $S$ den kleinsten Abstand von $P$ , der Punkt $T$ den größten.
Gib die Koordinaten von $S$ an.
Bestimme die Koordinaten von $T$ .

Erreichbare BE-Anzahl: 03

Gegeben sind die Vektoren

$\overrightarrow{a_{t}}=\pmatrix{ t^{2}\\ t\\ -2 }$ mit $t\in \mathbb{R}$ und $\overrightarrow{b}=\pmatrix{ 1\\ -1\\ 1 }.$

5.1

Weise nach, dass die Vektoren $\overrightarrow{a_t}$ und $\overrightarrow{b}$ für jeden Wert von $t$ ein Parallelogramm aufspannen.

Erreichbare BE-Anzahl: 05

5.2

Ein Vektor $\overrightarrow{c}$ soll gemeinsam mit den Vektoren $\overrightarrow{a_t}$ und $\overrightarrow{b}$ einen Quader aufspannen.

Ermittle die Koordinaten eines solchen Vektors $\overrightarrow{c}$ .

Gib die Koordinaten des zugehörigen Vektors $\overrightarrow{a_t}$ an.

Erreichbare BE-Anzahl: 03

Für ein Spiel werden ein Tetraeder und ein Würfel verwendet. Die Seiten des Tetraeders sind mit den Zahlen $1$ bis $4$ durchnummeriert, die des Würfels mit den Zahlen $1$ bis $6$ . Ebenso wie beim Werfen des Würfels werden beim Werfen des Tetraeders alle Zahlen mit gleicher Wahrscheinlichkeit erzielt.
Zu Beginn des Spiels wird ein Einsatz von $5 \,\text{Euro}$ geleistet. Anschließend wird das Tetraeder einmal geworfen. Wird dabei die Zahl $3$ erzielt, wird das Tetraeder ein weiteres Mal geworfen, andernfalls einmal der Würfel. Nur dann, wenn bei genau einem der beiden Würfe die Zahl $3$ erzielt wird, erfolgt eine Auszahlung.

6.1

Zeige, dass die Wahrscheinlichkeit dafür, bei einmaliger Durchführung des Spiels mindestens einmal die Zahl $3$ zu erzielen, $\displaystyle \frac{3}{8}$ beträgt.

Erreichbare BE-Anzahl: 02

6.2

Bei vielfacher Durchführung des Spiels ist zu erwarten, dass sich Einsätze und Auszahlungen mit der Zeit ausgleichen.

Ermittle die Höhe der Auszahlung.

Erreichbare BE-Anzahl: 03

Lösung 1

1.1

$\begin{array}[t]{rll} 2 \cdot x +3&\geq&0 &\quad \scriptsize \mid -3\; \\[5pt] 2 \cdot x&\geq&-3 & \quad \scriptsize \mid :2\; \\[5pt] x&\geq&- \dfrac{3}{2} & \\[5pt] \end{array}$

Die richtige Antwort lautet : $\{ x \mid x \in\mathbb{R}; x\geq - \frac{3}{2}\}$

1.2

Damit die Funktion $f_t$ an der Stelle $x_0=1$ stetig ist, muss für $x\lt 1$ und $x\rightarrow 1$ gelten: $f_t(x) \rightarrow f_t(1) = 1.$

Es ist $5\cdot 1 -4 = 1,$ also ist die Bedingung für $t=5$ erfüllt und $f_t$ für $t=5$ stetig.

1.3

Die Ebenen stehen senkrecht aufeinander, wenn das Skalarprodukt der Normalenvektoren der Ebenen Null ergibt.

$\begin{array}[t]{rll} \pmatrix{6\\-1\\-4} \circ\pmatrix{-3\\b\\2} &=& 0 \\[5pt] 6 \cdot (-3)-b-8&=& 0 \\[5pt] -26-b&=& 0&\quad \scriptsize \mid\; + b \\[5pt] -26&=& b \end{array}$

Die richtige Antwort ist $b=-26.$

1.4

Die Ebene $E$ verläuft parallel zur $yz$ -Ebene. Der Abstand eines Punktes zu $E$ hängt also nur von seiner $x$ -Koordinate ab.

$A(1\mid 2\mid 3)$ hat zu $E$ daher den Abstand $4-1 = 3.$ Den gleichen Abstand hat $B(1\mid -2 \mid 3).$

Die richtige Antwort ist also $B(1\mid -2 \mid 3).$

1.5

Es müssen folgende Gleichungen erfüllt sein:

$n\cdot p = \mu$ und $\sqrt{n\cdot p \cdot (1-p)} = \sigma.$

Für $n=100$ und $p=\dfrac{1}{5}$ ist dies erfüllt.

Lösung 2

2.1

Die Integrationsgrenzen sind $x_u=0$ und $x_o= \pi.$

$\begin{array}[t]{rll} &\displaystyle\int_{0}^{\pi}(x - \sin(x))\;\mathrm dx \\[5pt] =& \left[\dfrac{1}{2}x^2 +\cos(x) \right]_{0}^{\pi} \\[5pt] =&\dfrac{1}{2} \pi ^2 -2 \end{array}$

2.2

Die gesuchte Tangente soll parallel zur Geraden $g$ verlaufen. $g$ ist bereits eine Tangente an den Graphen von $f,$ verläuft allerdings durch den Koordinatenursprung $O.$

Durch Verschiebung der Gerade $g$ um eine Periode von $f$ entlang der $x$ -Achse erhält man eine weitere Tangente an den Graphen von $f.$ Die Periode von $f$ beträgt $2\pi.$

$t: \quad y = x - 2\pi$

Hinweis: Neben der angegebenen Lösung gibt es unendlich viele weitere richtige Lösungen. Alle Lösungen der Form $t: \, y= x+k\cdot2\cdot \pi$ mit $k\in \mathbb{Z}\setminus \{0\}$ sind richtig.

Lösung 3

3.1

Damit $F$ eine Stammfunktion von $f_2$ ist, muss die erste Ableitung von $F$ wiederum $f_2$ sein.

$\(\begin{array}[t]{rll} F(x)&=& \dfrac{1}{2}(x-2)^4 +3\\[5pt] F$

3.2

Die Terme aller Stammfunktionen von $f_a$ lassen sich durch: $F_{a}(x)= \dfrac{a}{4} \cdot (x-2)^4 +b$ $(b\in \mathbb{R})$ darstellen.

Für $a\gt 0$ handelt es sich bei dem Graphen von $F_{a}$ um eine nach oben geöffnete Parabel. Dies ist in der Skizze anhand von $F_1$ beispielhaft dargestellt. Eine solche Funktion nimmt immer auch positive Funktionswerte an.

Für $a\lt 0$ handelt es sich bei dem Graphen von $F_{a}$ um eine nach unten geöffnete Parabel. Dies ist in der Skizze anhand von $F_{-1}$ beispielhaft dargestellt.
In diesem Fall kann der Graph mithilfe des Paramters $b$ so weit verschoben werden, dass er vollständig unterhalb der $x$ -Achse liegt und $F_a$ somit nur negative Funktionswerte annimmt.

Für $a\lt 0$ gibt es also Stammfunktionen von $f_a,$ die nur negative Funktionswerte annehmen.

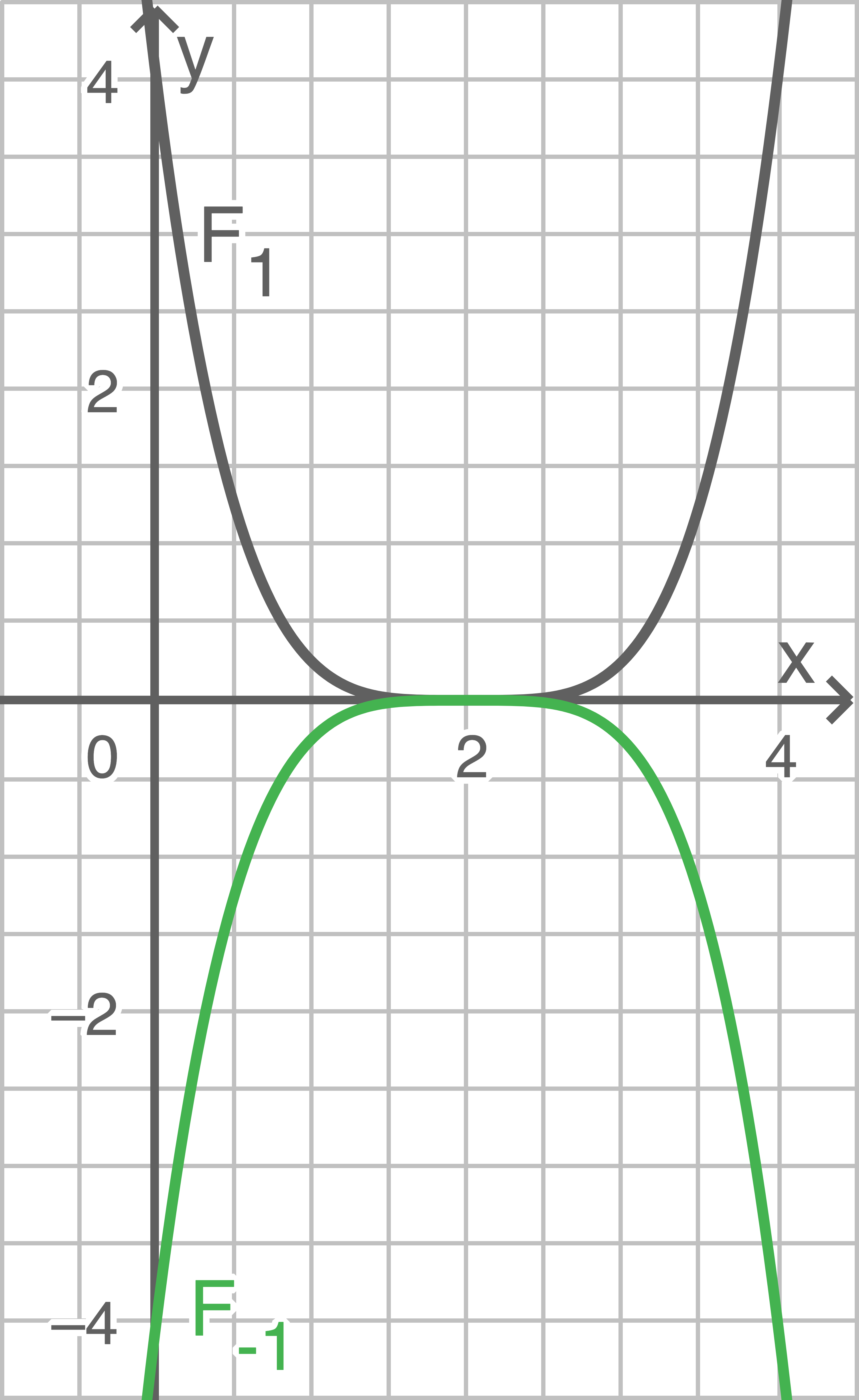
sachsen abi lk 2020 mathe funktionenschar v2

Lösung 4

4.1

Der Mittelpunkt der Grundfläche hat die gleichen $y$ - und $z$ -Koordinaten wie der Mittelpunkt $M$ der Deckfläche, liegt aber in der $xy$ -Ebene. Seine Koordinaten lauten also $M_G(8\mid 5\mid 0).$
Der Punkt $P(5 \mid 1 \mid 0)$ liegt auf dem Rand der Grundfläche, wenn der Abstand zum Mittelpunkt $M_G$ gleich $5$ ist.

$\begin{array}[t]{rll} \left|\overrightarrow{PM_G} \right| &=& \left|\pmatrix{3\\4 \\0} \right| \\[5pt] &=& \sqrt{3^2 + 4^2 + 0^2} \\[5pt] &=& 5 \end{array}$

Folglich liegt $P$ auf dem Rand der Grundfläche.

4.2

Der Punkt der Deckfläche mit dem kleinsten Abstand zu $P$ ist der Punkt, der genau horizontal über $P$ auf der Deckfläche liegt. Er muss die gleichen $x$ - und $y$ -Koordinaten besitzen. Da die Deckfläche parallel zur $xy$ -Ebene liegt, entspricht die $z$ -Koordinate von $S$ der von $M:$

$S(5\mid 1\mid 10)$

$T$ muss gegenüber von $S$ auf der Deckfläche liegen, die Richtung dorthin ist $2 \cdot \overline{SM}:$

$\overrightarrow{OT} = \overrightarrow{OS} + 2\cdot \overrightarrow{SM}$ $= \pmatrix{5\\1\\10} + 2\cdot \pmatrix{3\\4\\0}$ $= \pmatrix{11\\9\\10}$

$T(11 \mid 9 \mid 10)$

Lösung 5

5.1

$\overrightarrow{a_t} = \pmatrix {t^2 \\t \\-2}$ und $\overrightarrow{b}=\pmatrix {1\\-1\\1}$ spannen nur dann kein Parallelogramm auf, wenn sie voneinander linear abhängig sind.
Das ist der Fall, wenn es einen Faktor $c\in \mathbb{R}$ gibt, sodass $c\cdot \overrightarrow{a_t} = \overrightarrow{b}$ gilt.

Dafür müsste es ein $c$ geben, für das folgende drei Gleichungen erfüllt sind:

$\begin{array}{lrll} \text{I}\quad& c\cdot t^2 &=& 1 \\ \text{II}\quad& c\cdot t &=& -1 \\ \text{III}\quad& c\cdot (-2) &=& 1 \\ \end{array}$

Aus der dritten Gleichung folgt $c= -\frac{1}{2}.$ Das Einsetzen dieses Wertes in $\text{II}$ , ergibt $t=2.$ Für $t=2$ und $c=-\frac{1}{2}$ ist die erste Gleichung allerdings nicht erfüllt.
Also sind $\overrightarrow{a_t}$ und $\overrightarrow{b}$ für alle Werte von $t$ linear unabhängig und spannen somit in jedem Fall ein Parallelogramm auf.

5.2

Alle Seiten eines Quaders sind Rechtecke. Damit ein Quader entsteht, müssen also $\overrightarrow{a_t}$ und $\overrightarrow{b}$ zunächst senkrecht zueinander stehen. Das ist der Fall, wenn ihr Skalarprodukt $0$ ergibt:

Rechenweg anzeigen

$t_1 =-1, t_2 =2$

Sowohl $\overrightarrow{a_{-1}}$ als auch $\overrightarrow{a_2}$ spannen also mit $\overrightarrow{b}$ ein Rechteck auf.

Der dritte Vektor $\overrightarrow{c}$ muss ebenfalls senkrecht auf den Vektoren $\overrightarrow{a_{-1}},$ $\overrightarrow{b}$ bzw. den Vektoren $\overrightarrow{a_2},$ $\overrightarrow{b}$ stehen. Diese Bedingung lässt sich mit dem Kreuzprodukt bestimmen:

$\begin{array}[t]{rll} \overrightarrow{c_1} &=& \overrightarrow{a_{-1}} \times \overrightarrow{b}\\[5pt] &=& \pmatrix {1 \\-1 \\-2} \times \pmatrix {1\\-1\\1} \\[5pt] &=& \pmatrix{ (-1) \cdot 1 -(-1) \cdot (-2)\\ (-2)\cdot 1 -1\cdot 1 \\1\cdot(-1) -1\cdot (-1)} \\[5pt] &=& \pmatrix{-3\\-3\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{c_2} &=& \overrightarrow{a_{2}} \times \overrightarrow{b}\\[5pt] &=& \pmatrix {4 \\2 \\-2} \times \pmatrix {1\\-1\\1} \\[5pt] &=& \pmatrix{ 2 \cdot 1 -(-1) \cdot (-2)\\ (-2)\cdot 1 -1\cdot 4 \\4\cdot(-1) -1\cdot 2} \\[5pt] &=& \pmatrix{0\\-6\\-6} \end{array}$

Es gibt also zwei richtige Antwortmöglichkeiten:

Der Vektor $\overrightarrow{c} = \pmatrix{0\\-6\\-6}$ spannt mit $\overrightarrow{a_2} = \pmatrix{4\\2\\-2}$ und $\overrightarrow{b} = \pmatrix{1\\-1\\1}$ einen Quader auf.
Der Vektor $\overrightarrow{c} = \pmatrix{-3\\-3\\0}$ spannt mit $\overrightarrow{a_{-1}} = \pmatrix{1\\-1\\-2}$ und $\overrightarrow{b} = \pmatrix{1\\-1\\1}$ einen Quader auf.

Lösung 6

6.1

Zur visuellen Darstellung kann das folgende Baumdiagramm helfen. Dabei steht " $3$ " für eine gewürfelte $3$ und "n $3$ " für keine gewürfelte $3.$

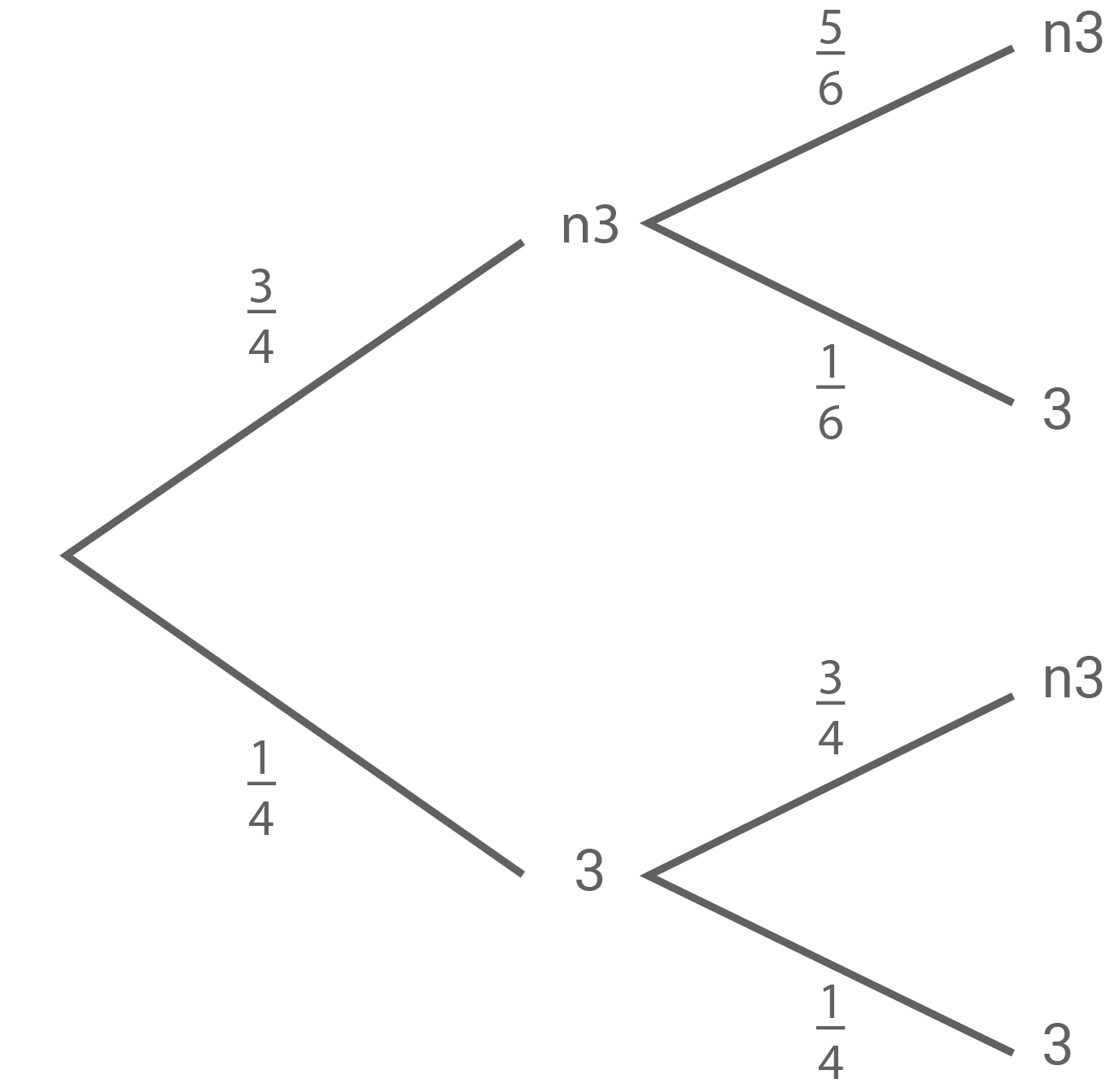Daraus ergibt sich mit den Pfadregeln:

$P(\text{mindestens eine 3})$ $=\dfrac{1}{4} \cdot \dfrac{1}{4}$ $+ \dfrac{1}{4} \cdot \dfrac{3}{4}$ $+\dfrac{3}{4} \cdot \dfrac{1}{6}$ $= \dfrac{3}{8}$

6.2

Die Wahrscheinlichkeit für eine Auszahlung ergibt sich durch:

$P(A) = P(\text{genau eine 3})$ $= \dfrac{1}{4}\cdot \dfrac{3}{4} + \dfrac{3}{4}\cdot \dfrac{1}{6}$ $= \dfrac{15}{48}$

Der zu erwartende Gewinn soll $0 \; €$ betragen. Im Fall einer Niederlage beträgt der Verlust $5€,$ also der Gewinn $-5€.$ Im Fall eines Erfolgs, beträgt die Auszahlung $x,$ der Gewinn also $x-5€.$

$\begin{array}[t]{rll} E(G) &=& x\cdot P(A) - 5€ \\[5pt] 0€ &=& x\cdot\dfrac{15}{48} -5€ &\quad \scriptsize \mid\; +5€ \\[5pt] 5€ &=& x\cdot \dfrac{15}{48} &\quad \scriptsize \mid\; \cdot \frac{48}{15}\\[5pt] 16€ &=& x \end{array}$

Es findet eine Auszahlung in Höhe von $16\,€$ statt.