Teil A

In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Der Anstieg des Graphen der Funktion $f$ mit $f(x)= \ln(2\cdot x)$ und $x\in D_f$ an der Stelle $x=1$ beträgt:

	$\frac{1}{\ln 2}$
	$1$
	$\ln 2$
	$\frac{1}{2}$
	$\frac{1}{4}$

1.2

Gegeben ist die Funktion $f$ mit $f(x)= \frac{27-x^2}{3-x}$ $(x\in D_f).$
Es gilt:

	Die Nullstelle von $f$ ist $x=3.$
	Der größtmögliche Definitionsbereich von $f$ ist $\mathbb{R}.$
	Der Graph von $f$ besitzt die waagerechte Asymptote mit der Gleichung $y=3.$
	Der Graph von $f$ besitzt die senkrechte Asymptote mit der Gleichung $x=3.$
	Der Schnittpunkt des Graphen von $f$ mit der $y$ -Achse hat die Koordinaten $(0\mid 3).$

1.3

Gegeben sind die Vektoren

$\overrightarrow{a}= \pmatrix{1\\ 2\\3}$ und $\overrightarrow{b} = \pmatrix{0\\1\\t}.$

Für welchen reellen Wert von $t$ sind die Vektoren $\overrightarrow{a}$ und $\overrightarrow{b}$ orthogonal zueinander?

	$t= -\frac{3}{2}$
	$t= -\frac{2}{3}$
	$t=0$
	$t= \frac{2}{3}$
	$t= \frac{3}{2}$

1.4

Ein Code besitzt die Form: Buchstabe_Buchstabe_Buchstabe_Ziffer.
Der Code besteht aus den Buchstaben A, B und C sowie einer der Ziffern 1,2 und 3.
Jeder der drei Buchstaben kommt genau einmal vor.
Wie viele verschiedene Codes sind damit möglich?

	4
	12
	18
	24
	81

1.5

Gegeben ist die vollständige Wahrscheinlichkeitsverteilung einer Zufallsgröße $X$ mit den positiven reellen Zahlen $a$ und $b.$

$X=x_i$	$P(X=x_i)$
1	a
2	a
3	b
4	a

Es gilt:

	$b=1-a$
	$b=-3\cdot a$
	$b=1-3 \cdot a$
	$P(X\leq 3) = 2\cdot a$
	$P(X\leq 2) = P(X=4)$

Für Aufgabe 1 erreichbare BE-Anzahl: 5

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)= \sin x.$ Die Abbildung zeigt den Graphen $G_f$ von $f$ sowie die Tangenten an $G_f$ in den dargestellten Schnittpunkten mit der $x$ -Achse.

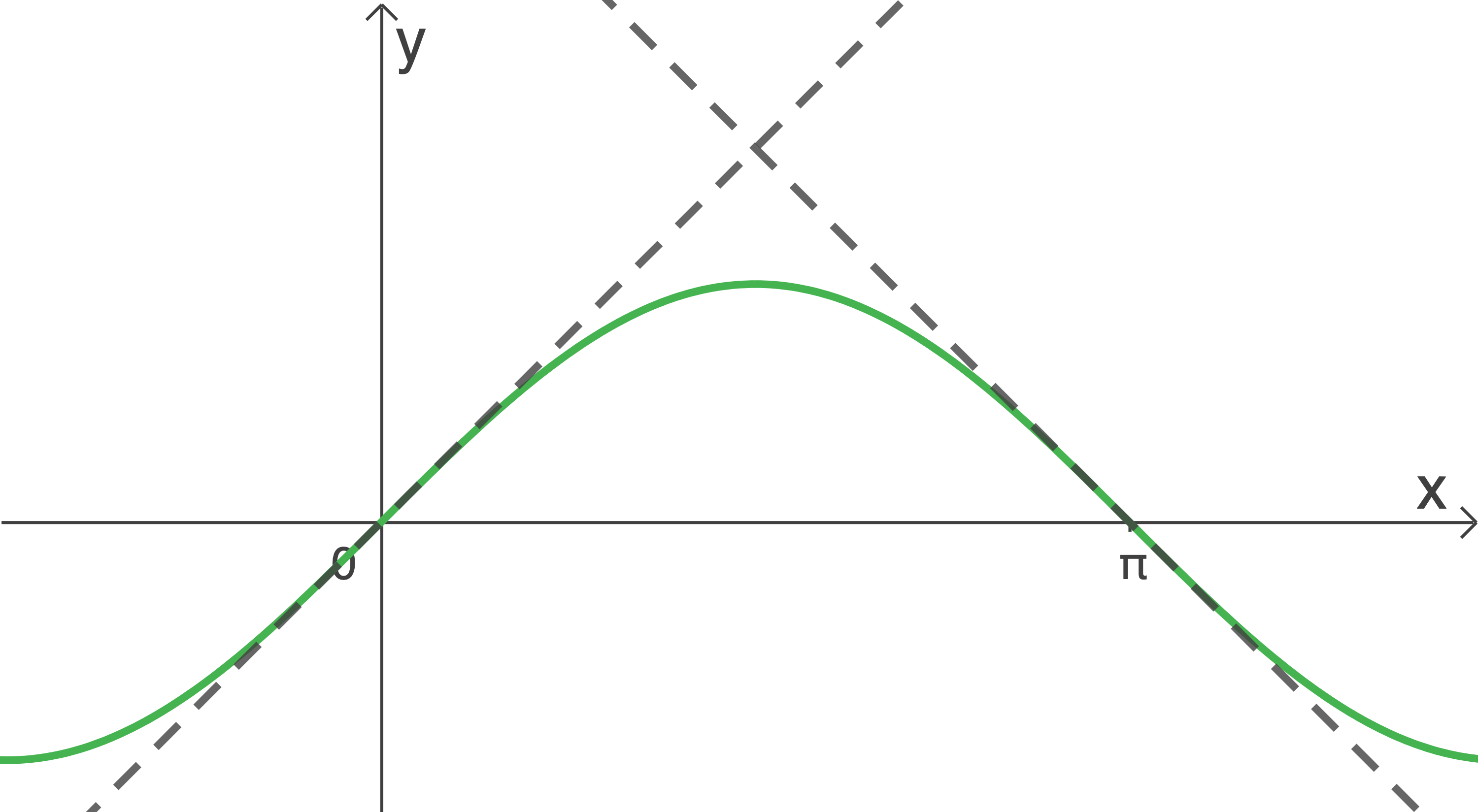
Graph einer sinusförmigen Funktion mit Achsenbeschriftung.

2.1

Zeige, dass diejenige der beiden Tangenten, die durch den Koordinatenursprung verläuft, die Steigung 1 hat.

(1 BE)

2.2

Berechne den Inhalt des Flächenstücks, das von $G_f$ und den beiden Tangenten eingeschlossen wird.

(4 BE)

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ und $g.$ Der Graph von $f$ ist symmetrisch bezüglich der $y$ -Achse, der Graph von $g$ ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt $(2\mid 1).$

3.1

Gib für die Graphen von $f$ und $g$ jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.

(2 BE)

3.2

Untersuche die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x)= f(x)\cdot (g(x))^3$ im Hinblick auf eine mögliche Symmetrie ihres Graphen.

(3 BE)

Gegeben sind der Punkt $P(-1\mid 7\mid 2)$ und die Ebene $E: x+3\cdot y = 0.$

4.1

Zeige, dass $P$ nicht in $E$ liegt.

(1 BE)

4.2

Bestimme die Koordinaten des Punkts, der entsteht, wenn $P$ an $E$ gespiegelt wird.

(4 BE)

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n=100$ und $p.$
Der Erwartungswert von $X$ ist 50.

5.1

Berechne die Standardabweichung von $X.$

(3 BE)

5.2

Die Wahrscheinlichkeit $P(X \geq 61)$ beträgt etwa 2 %.
Bestimme damit einen Wert für die Wahrscheinlichkeit $P(40 \leq X \leq 60).$

(2 BE)

Bei einem Spiel werfen zwei Spieler abwechselnd jeweils drei Würfel. Das Spiel endet, wenn ein Spieler die Augensumme 18 erzielt oder die Augensumme des vorausgegangenen Wurfs des anderen Spielers nicht übertrifft.
Beim ersten Wurf des Spiels erzielt ein Spieler die Augensumme 15.
Berechne die Wahrscheinlichkeit dafür, dass dieser Spieler die Würfel im selben Spiel noch einmal wirft.
Erläutere dein Vorgehen.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

1.1

$\(\begin{array}[t]{rll} f$

1.2

Die Funktion $f$ hat bei $x=3$ eine Definitionslücke und somit an dieser Stelle eine senkrechte Asymptote. Für den Definitionbereich gilt: $\mathbb{D}=\mathbb{R}\setminus {\{3\}}$

1.3

Die Vektoren $\overrightarrow a$ und $\overrightarrow b$ sind zueinander orthogonal, wenn ihr Skalarprodukt Null ergibt.

$\pmatrix{1\\2\\3} \circ \pmatrix{0\\1\\t} =0$

$\begin{array}[t]{rll} 1 \cdot 0+2\cdot 1+ 3\cdot t&=& 0&\quad \scriptsize \\[5pt] 2+3t&=& 0&\quad \scriptsize \mid -2\\[5pt] 3t&=& -2&\quad \scriptsize \mid :3 \\[5pt] t&=& -\dfrac{2}{3} \end{array}$

Für $t=-\dfrac{2}{3}$ sind die beiden Vektoren orthogonal zueinander.

1.4

Da jeder Buchstabe nur einmal vorkommt, gibt es sechs Möglichkeiten diese zu kombinieren:

$ABC, ACB, BAC, BCA, CAB, CBA$

Da weiterhin drei verschiedene Ziffern zur Verfügung stehen, existieren für jede Buchstabenkonstellation drei Varianten. Damit ergeben sich $6 \cdot 3 = 18$ Möglichkeiten.

1.5

Es gilt:

$P(X=1)+P(X=2)$ $+P(X=3)+P(X=4)=1$

Daraus folgt:

$\begin{array}[t]{rll} a+a+b+a&=& 1&\quad \scriptsize \\[5pt] 3a+b&=& 1&\quad \scriptsize \mid -3a\\[5pt] b&=& 1-3a&\quad \scriptsize \\[5pt] \end{array}$

Lösung 2

2.1

Die Steigung der Funktion $f$ im Koordinatenursprung wird mithilfe der ersten Ableitung an der Stelle $x=0$ bestimmt:

$\(f$

2.2

Vollständigen Rechenweg anzeigen

$2\cdot \displaystyle\int_{0}^{\frac{\pi}{2}}x-\sin(x)\;\mathrm dx = \dfrac{\pi^2}{4}-2$

Lösung 3

3.1

Der Graph von $f$ ist achsensymmetrisch zur $y$ -Achse, sodass dieser im Punkt $P(-2\mid 1)$ einen Hochpunkt hat.

Der Graph von $h$ ist punktsymmetrisch zum Koordinatenurprung, sodass dieser im Punkt $P(-2\mid-1)$ einen Tiefpunkt hat.

3.2

$h(-x)=f(-x)\cdot (g(-x))^3$ $=f(x)\cdot (-g(x))^3=-f(x)\cdot (g(x))^3$ $=-h(x)$

Die Funktion $h$ erfüllt die Gleichung $h(-x)=-h(x)$ , sodass der Graph von $h$ symmetrisch zum Koordinatenursprung ist.

Lösung 4

4.1

Wenn der Punkt $P$ nicht in der Ebene $E$ liegen soll, darf er nicht die Ebenengleichung erfüllen. Die Punktprobe liefert uns:

$-1+3\cdot 7\neq0$

Die Gleichung ist somit nicht erfüllt und der Punkt $P$ liegt nicht in der Ebene $E$ .

4.2

Zunächst muss eine Hilfsgerade $g$ , die senkrecht zur Ebene $E$ steht und durch den Punkt $P$ verläuft, aufgestellt werden:

$g: \overrightarrow x=\pmatrix{-1\\7\\2}+s\cdot \pmatrix{1\\3\\0}, \; s\in \mathbb{R}$

Dann wird der Schnittpunkt $S$ der Geraden $g$ mit der Ebene $E$ bestimmt:

$\begin{array}[t]{rll} -1+s+3\cdot (7+3s)&=& 0&\quad \scriptsize \\[5pt] -1+s+21+9s&=& 0&\quad \scriptsize \mid -20\\[5pt] 10s&=& -20&\quad \scriptsize \mid :10\\[5pt] s&=& -2&\quad \scriptsize \\[5pt] \end{array}$

$g: \overrightarrow x=\pmatrix{-1\\7\\2}+(-2)\cdot \pmatrix{1\\3\\0}$ $=\pmatrix{-1\\7\\2}+\pmatrix{-2\\-6\\0}=\pmatrix{-3\\1\\2}$

Die Gerade $g$ und die Ebene $E$ schneiden sich im Punkt $S(-3\mid 1\mid 2)$ .
Nun wird der Vektor $\overrightarrow {PS}$ berechnet:

$\overrightarrow {PS}=\pmatrix{-3\\1\\2}-\pmatrix{-1\\7\\2}=\pmatrix{-2\\-6\\0}$

Im letzten Schritt wird der Vektor $\overrightarrow {PS}$ zum Vektor $\overrightarrow {OS}$ addiert:

$\overrightarrow {OS}+\overrightarrow {PS}=\pmatrix{-3\\1\\2}+\pmatrix{-2\\-6\\0}$ $=\pmatrix{-5\\-5\\2}$

Die Koordinaten des Spiegelpunktes lauten $\(P$ .

Lösung 5

5.1

$\begin{array}[t]{rll} \mu&=& n\cdot p &\quad \scriptsize \\[5pt] 50&=&100\cdot p &\quad \scriptsize \mid :100\\[5pt] p&=&\dfrac{1}{2} \end{array}$

Damit ergibt sich für die Standardabweichung $\sigma = \sqrt{100\cdot 0,5\cdot 0,5}=5$ .

5.2

$P(40\leq X\leq60) \approx 100 \; \% - 2 \cdot 2 \; \%$ $= 96 \; \%$

Der Wert für die Wahrscheinlichkeit beträgt etwa $96\,\%$ .

Lösung 6

Damit der Spieler in diesem Spiel noch einmal die Würfel werfen darf, muss sein Gegenspieler die Augensumme $16$ oder $17$ erreichen.
Dafür kommen folgende Würfelkombinationen für die Augensumme $16$ in Frage:
einmal $4$ und zweimal $6$ , zweimal $5$ und einmal $6$
Für die Augensumme $17$ kommt nur eine Kombination in Frage:
einmal $5$ und zweimal $6$

Die Wahrscheinlichkeit, dass der Spieler noch einmal würfeln kann, beträgt:

$2 \cdot 3 \cdot \dfrac{1}{6^3}+3\cdot \dfrac{1}{6^3}=\dfrac{1}{24} \approx 4,17\,\%$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?