Wahlaufgaben
9
Wahlaufgabe Arithmetik/Algebra
9.1
Vereinfache den Term so weit wie möglich.

2 BE
9.2
Löse die Gleichung.

4 BE
9.3
Ein Shop für Fanartikel bietet einen Schal und ein Basecap zusammen zum gleichen Preis an wie zwei T-Shirts.
Ein Basecap kostet 14,95 Euro.
Ein Schal und ein T-Shirt kosten zusammen 44,90 Euro. Berechne den Preis für einen Schal und den Preis für ein T-Shirt.
Ein Basecap kostet 14,95 Euro.
Ein Schal und ein T-Shirt kosten zusammen 44,90 Euro. Berechne den Preis für einen Schal und den Preis für ein T-Shirt.
4 BE
10
Wahlaufgabe Stochastik
10.1
Beim Korrekturlesen eines neuen Romans mit 900 Seiten wurden die Rechtschreibfehler pro Seite gezählt.
Daraus ergab sich folgende Häufigkeitstabelle:
Berechne die relative Häufigkeit für die Seitenanzahl mit 0 Fehlern pro Seite in Prozent.
Daraus ergab sich folgende Häufigkeitstabelle:
| Fehler pro Seite | Seitenanzahl |
| 0 | 810 |
| 1 | 55 |
| 2 | 25 |
| 3 | 9 |
| mindestens 4 | 1 |
2 BE
10.2
Ein Glücksrad ist mit Zahlen beschriftet. Es wird zweimal gedreht.
Die Wahrscheinlichkeit für das Ereignis, dass zweimal eine gerade Zahl gedreht wird, beträgt Zeichne und beschrifte ein Glücksrad so, dass es diesem Ereignis entspricht.
Zeichne und beschrifte ein Glücksrad so, dass es diesem Ereignis entspricht.
Die Wahrscheinlichkeit für das Ereignis, dass zweimal eine gerade Zahl gedreht wird, beträgt
3 BE
10.3
Ein Kanuverleih hat zehn rote und sechs grüne Kanus. Davon werden zwei Kanus in zufälliger Reihenfolge ausgeliehen.
a)
Stelle den Sachverhalt in einem Baumdiagramm dar.
2 BE
b)
Ermittle die Wahrscheinlichkeit dafür, dass die beiden ausgeliehenen Kanus die gleiche Farbe haben.
3 BE
11
Wahlaufgabe Geometrie
11.1
Gegeben ist eine landwirtschaftliche Fläche  mit den folgenden Werten:
mit den folgenden Werten:

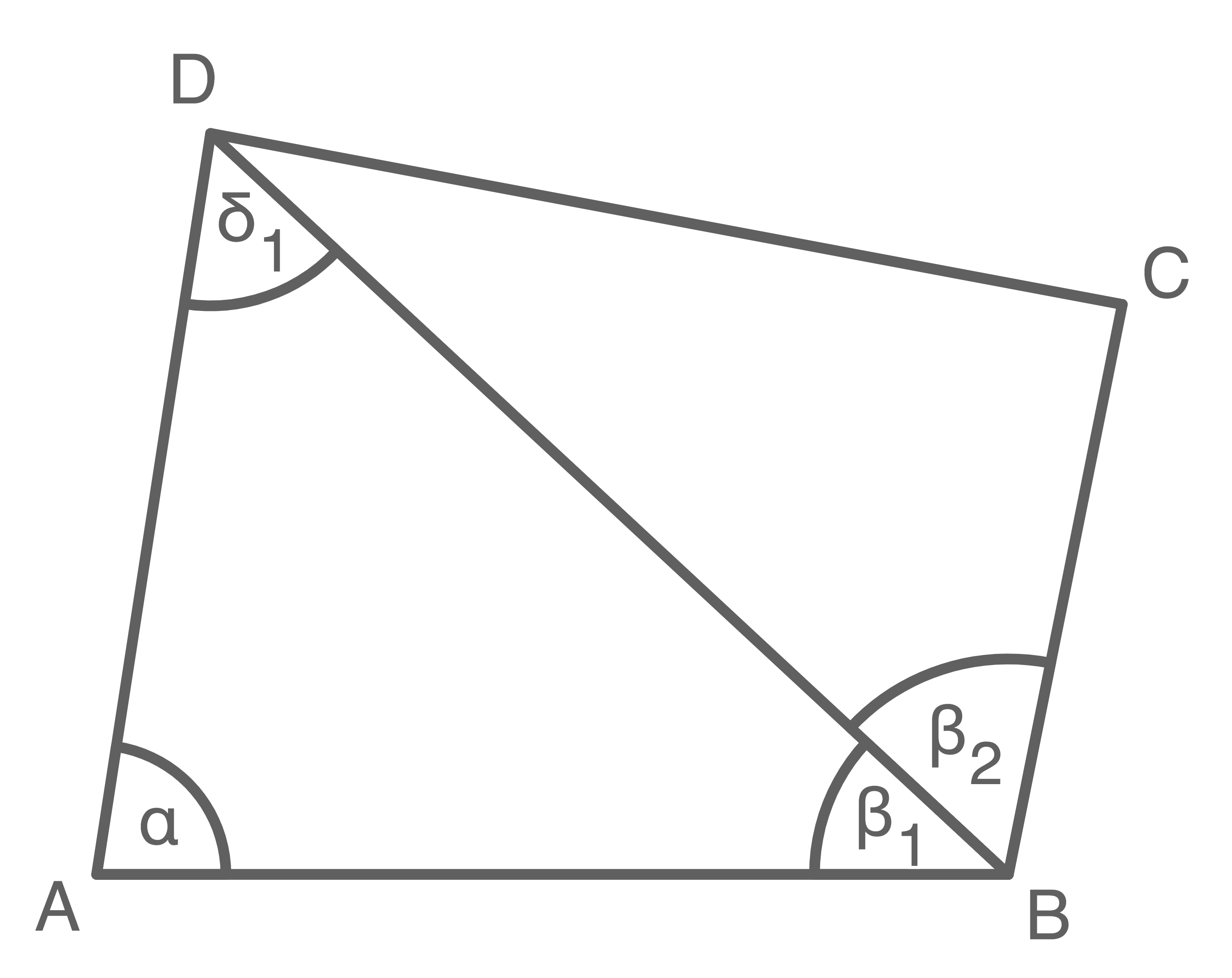 Berechne den Flächeninhalt des Dreiecks
Berechne den Flächeninhalt des Dreiecks  und gib diesen in Hektar an.
und gib diesen in Hektar an.

Skizze nicht maßstäblich
5 BE
11.2
Gegeben ist das unvollständige Körpernetz eines Prismas.
(Maße in cm)
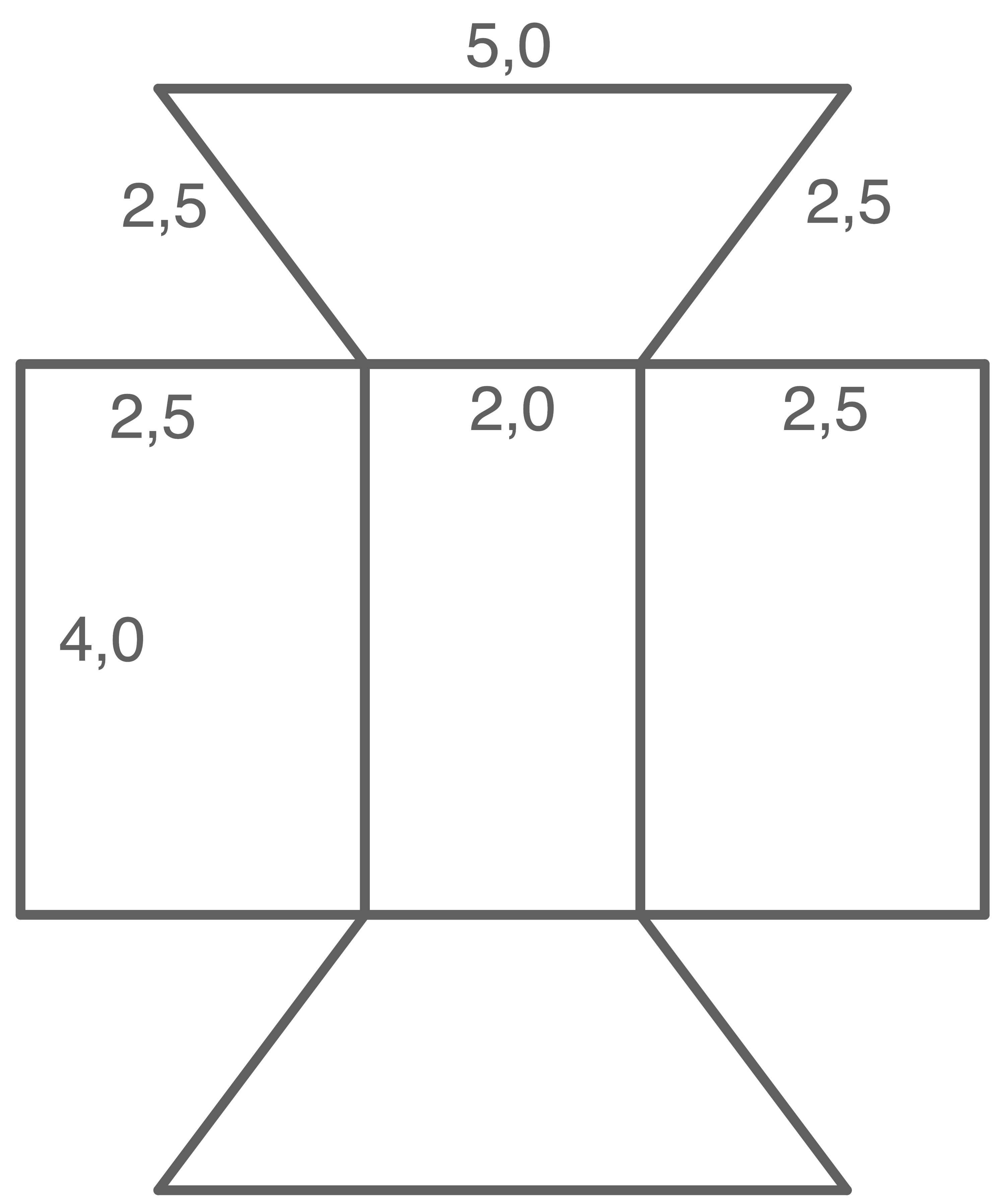
(Maße in cm)

Skizze nicht maßstäblich
a)
Berechne das Volumen dieses Prismas.
4 BE
b)
Stelle die fehlende Teilfläche des Körpernetzes dar.
1 BE
12
Wahlaufgabe Funktionen
12.1
In Heuschreckenschwärmen verdoppelt sich die Anzahl der Heuschrecken nach jeweils einer Woche.
Am 11. Juli 2022 schätzten die Fachleute die Anzahl der Heuschrecken in einem Heuschreckenschwarm auf Berechne die zu erwartende Anzahl der Heuschrecken in diesem Heuschreckenschwarm acht Wochen nach der Schätzung.
Berechne die zu erwartende Anzahl der Heuschrecken in diesem Heuschreckenschwarm acht Wochen nach der Schätzung.
Am 11. Juli 2022 schätzten die Fachleute die Anzahl der Heuschrecken in einem Heuschreckenschwarm auf
2 BE
12.2
Die Waldschlösschenbrücke ist eine Straßenbrücke in Dresden über der Elbe. Sie wird durch zwei Stahlbögen mit einer Spannweite von  getragen und erreicht dabei eine Höhe von
getragen und erreicht dabei eine Höhe von  über der Elbe.
über der Elbe.
 Mit einer Gleichung der Form
Mit einer Gleichung der Form  kann ein Stahlbogen der Brücke annähernd beschrieben werden.
kann ein Stahlbogen der Brücke annähernd beschrieben werden.
 Kraftfahrzeuge über die Brücke. Man erwartet, dass sich diese Anzahl in den nächsten Jahren auf etwa
Kraftfahrzeuge über die Brücke. Man erwartet, dass sich diese Anzahl in den nächsten Jahren auf etwa  Kraftfahrzeuge täglich erhöht.
Kraftfahrzeuge täglich erhöht.

a)
Berechne 
Derzeit fahren täglich etwa
3 BE
b)
Berechne, auf wie viel Prozent sich die Anzahl der Kraftfahrzeuge pro Tag erhöhen wird.
2 BE
12.3
Ordne den Aussagen  bis
bis  jeweils die zugehörige Funktionsgleichung zu.
jeweils die zugehörige Funktionsgleichung zu.
 Der Graph verläuft durch den Punkt
Der Graph verläuft durch den Punkt 
 Die Nullstelle ist
Die Nullstelle ist  .
.
 Der Graph ist punktsymmetrisch zum Koordinatenursprung.
Der Graph ist punktsymmetrisch zum Koordinatenursprung.
![\(\begin{array}[t]{rll}
\text{I}& y=x^3 & (x \in \mathbb{R})\\[5pt]
\text{II}& y=x^{-2} & (x \in \mathbb{R}, x \neq 0)\\[5pt]
\text{III}& y=2^x & (x \in \mathbb{R})\\[5pt]
\text{IV}& y=2 x-4 & (x \in \mathbb{R})\\[5pt]
\end{array}\)](https://mathjax.schullv.de/02ef2634db62ee64f8dd93c36410a61df64d74200f6f237516f30378c338e7e8?color=5a5a5a)
3 BE
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
9
Wahlaufgabe Arithmetik/Algebra
9.1
9.2
9.3
10
Wahlaufgabe Stochastik
10.1
10.2
10.3
a)
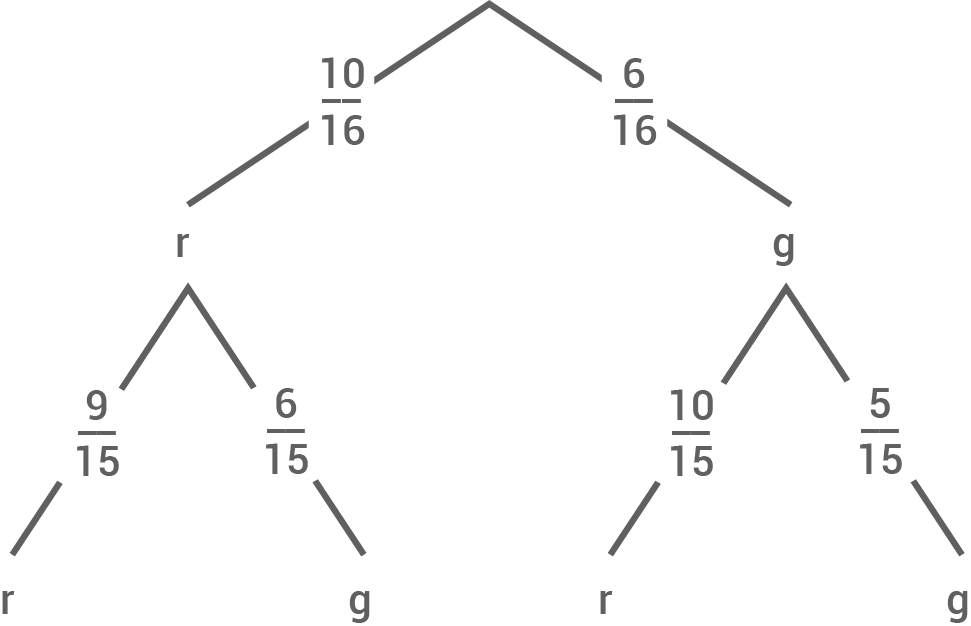
b)
Mit einer Wahrscheinlichkeit von  haben beide Kanus die gleiche Farbe.
haben beide Kanus die gleiche Farbe.
11
Wahlaufgabe Geometrie
11.1
Die Länge der Strecke  kann mit dem Sinussatz berechnet werden:
kann mit dem Sinussatz berechnet werden:
![\(\begin{array}[t]{rll}
\dfrac{\overline{BD}}{\sin\alpha}&=& \dfrac{\overline{AB}}{\sin\delta_1} \quad \scriptsize \mid\;\cdot \sin \alpha \\[5pt]
\overline{BD}&=& \dfrac{\overline{AB}}{\sin\delta_1}\cdot \sin \alpha \\[5pt]
\overline{BD}&=& \dfrac{530\,\text{m}}{\sin 55,6°}\cdot \sin 59,3° \\[5pt]
\overline{BD}&\approx& 552\,\text{m}
\end{array}\)](https://mathjax.schullv.de/f16fcc2752b974c38a3d8b50f80179a47c5c1a89222672a31bb2ecdfcf98cbd7?color=5a5a5a) Damit kann nun der Flächeninhalt des Dreiecks
Damit kann nun der Flächeninhalt des Dreiecks  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot \overline{BC}\cdot \overline{BD}\cdot \sin(\beta_2) \\[5pt]
&=& \dfrac{1}{2}\cdot 320\,\text{m}\cdot 552\,\text{m}\cdot \sin(72,3°) \\[5pt]
&\approx& 84\,000\,\text{m}^2 \\[5pt]
&=& 8,4\,\text{ha}
\end{array}\)](https://mathjax.schullv.de/b6e695441aa24bc234ce7861211ee367c9e1f13706c2f02ef724715fb9dcf557?color=5a5a5a)
11.2
a)
Es handelt sich um ein Prisma mit einem Trapez als Grundfläche und einer Höhe von  Höhe des Trapezes mit dem Satz des Pythagoras berechnen
Höhe des Trapezes mit dem Satz des Pythagoras berechnen
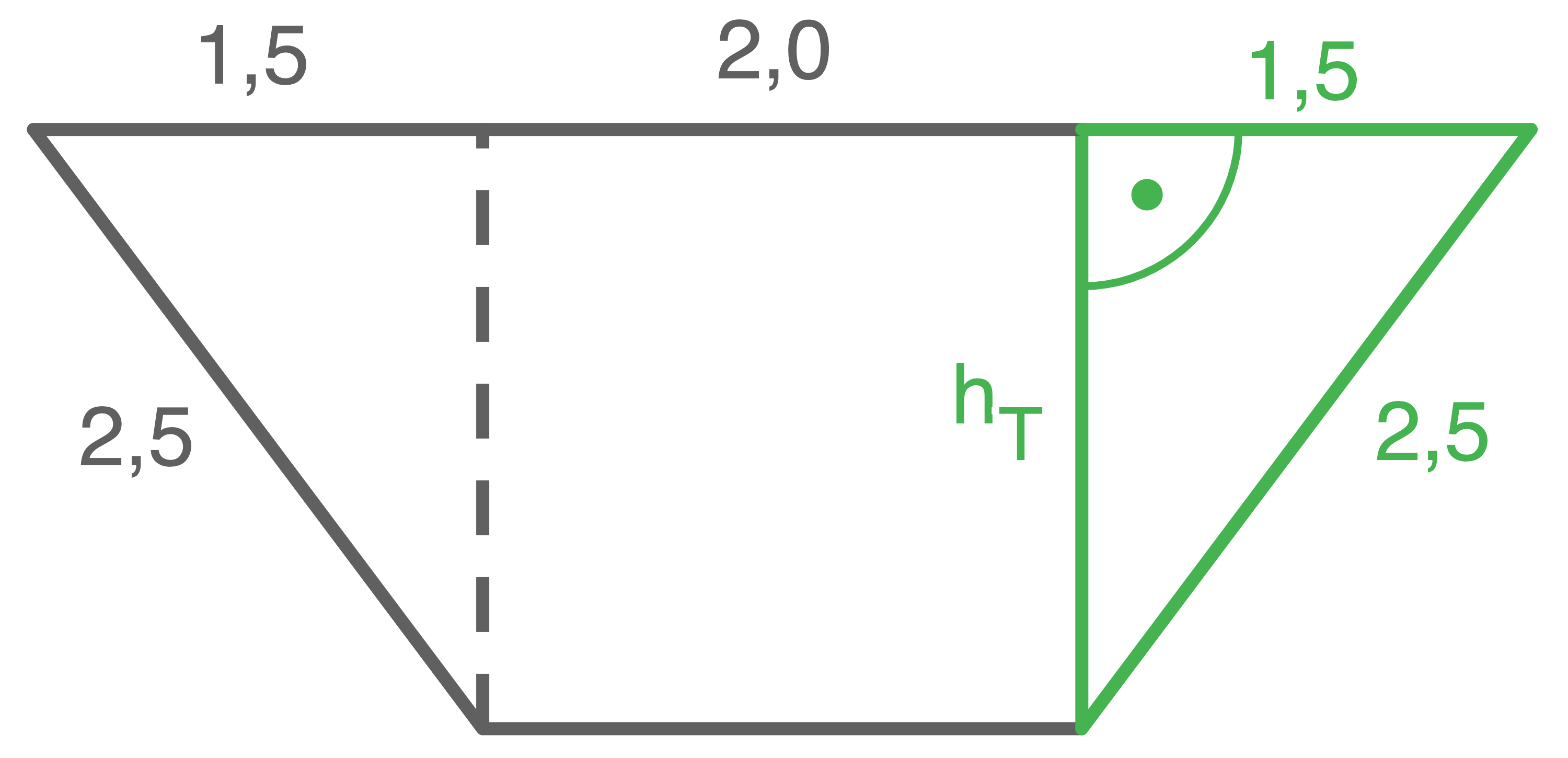 Flächeninhalt des Trapezes berechnen
Flächeninhalt des Trapezes berechnen
![\(\begin{array}[t]{rll}
G&=& \dfrac{5,0\,\text{cm}+2,0\,\text{cm}}{2}\cdot 2,0\,\text{cm} \\[5pt]
&=& 7,0\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/1210a5c43f62b461692c92ad27b2c0f3d729f2b60a7872f7a5b32a021f2c99ca?color=5a5a5a) Volumen des Prismas berechnen
Volumen des Prismas berechnen
![\(\begin{array}[t]{rll}
V&=& G\cdot h \\[5pt]
&=& 7,0\,\text{cm}^2\cdot 4,0\,\text{cm} \\[5pt]
&=& 28\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/3c6f9652c7cf99be31def7a818281074abafee6eb9ae0a49ea6f06fee4aeebd5?color=5a5a5a)

Hilfsskizze
b)
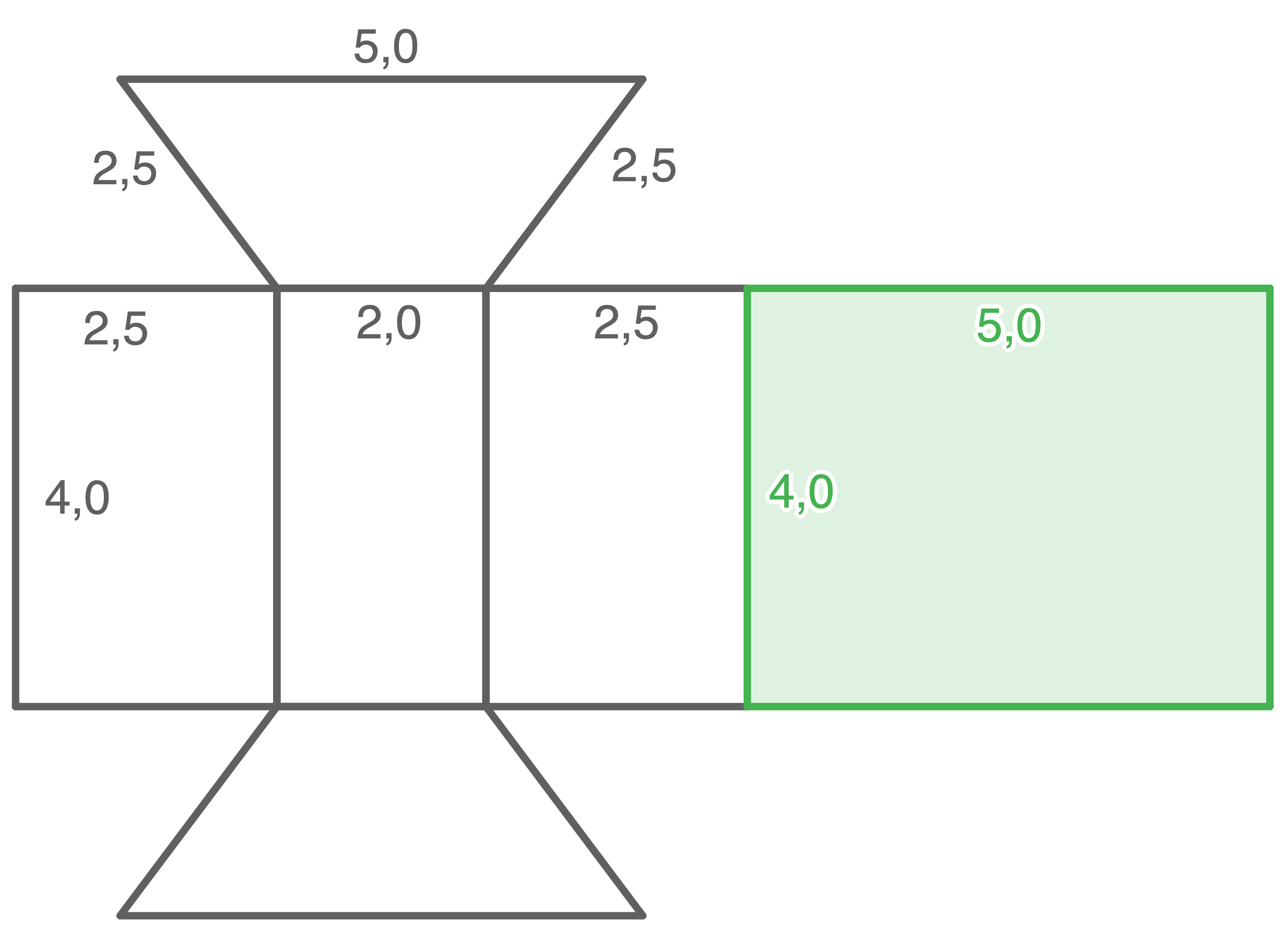
12
Wahlaufgabe Funktionen
12.1
12.2
a)
Es gilt  Außerdem sind die Koordinaten des Punkts, auf dem die Brücke die Höhe der Elbe erreicht, durch
Außerdem sind die Koordinaten des Punkts, auf dem die Brücke die Höhe der Elbe erreicht, durch  gegben. Einsetzen dieser Werte in die Gleichung liefert:
gegben. Einsetzen dieser Werte in die Gleichung liefert:
![\(\begin{array}[t]{rll}
0&=& a\cdot 74^2+26 \quad \scriptsize \mid\;-26 \\[5pt]
-26&=& a\cdot 74^2 \quad \scriptsize \mid\; :74^2 \\[5pt]
-0,0047&\approx& a
\end{array}\)](https://mathjax.schullv.de/9d0db3aef093972ffe0e9bc53be18c1918c035e0ded46a8395fadaf00d65b3ef?color=5a5a5a)
b)
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{45\,000\,\text{Autos}}{35\,000\,\text{Autos}}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 128,6\,\%
\end{array}\)](https://mathjax.schullv.de/f67e753b0dc735ff526b6bd6ef39964f2e7271ec63585e6920f1a7204294cebd?color=5a5a5a) Lösung mit Dreisatz
Die Anzahl an Kraftfahrzeugen pro Tag wird sich auf
Lösung mit Dreisatz
Die Anzahl an Kraftfahrzeugen pro Tag wird sich auf  erhöhen.
erhöhen.
12.3