Wahlaufgaben
8
Wahlaufgabe Geometrie
8.1
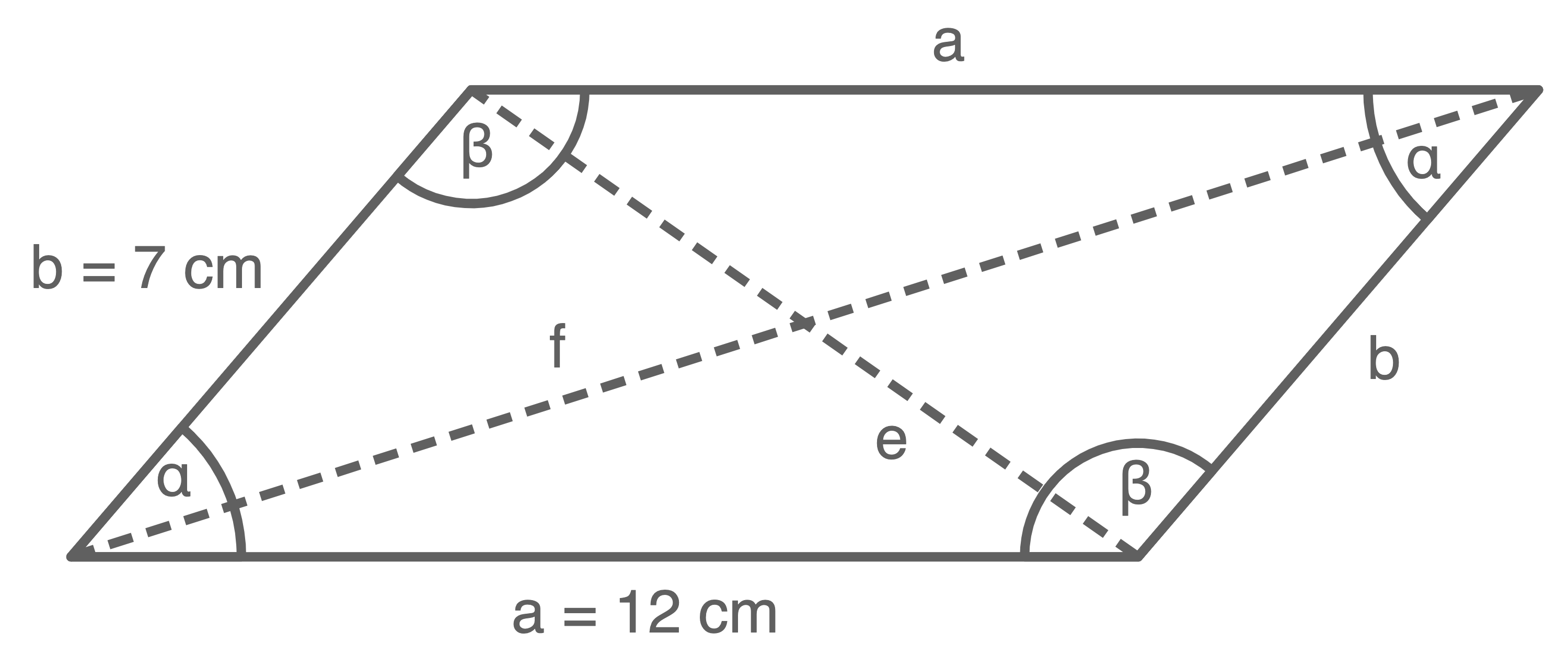
Ein Parallelogramm hat die Seitenlängen  und
und  Ein Innenwinkel ist
Ein Innenwinkel ist 
a)
Berechne die Länge einer Diagonalen des Parallelogramms.
2 BE
b)
Berechne den Flächeninhalt des Parallelogramms.
2 BE
c)
Begründe, dass der Flächeninhalt eines jeden Parallelogramms  immer kleiner als der Flächeninhalt des seitengleichen Rechtecks ist.
immer kleiner als der Flächeninhalt des seitengleichen Rechtecks ist.
2 BE
8.2
Auf einem Schild am Baggersee steht:

Seefläche:
Länge Rundweg um den See:
 Entscheide, ob der Burgsee annähernd kreisförmig ist.
Entscheide, ob der Burgsee annähernd kreisförmig ist.
Begründe rechnerisch.
Burgsee
größte Tiefe: Seefläche:
Länge Rundweg um den See:

Begründe rechnerisch.
4 BE
9
Wahlaufgabe Funktionen
9.1
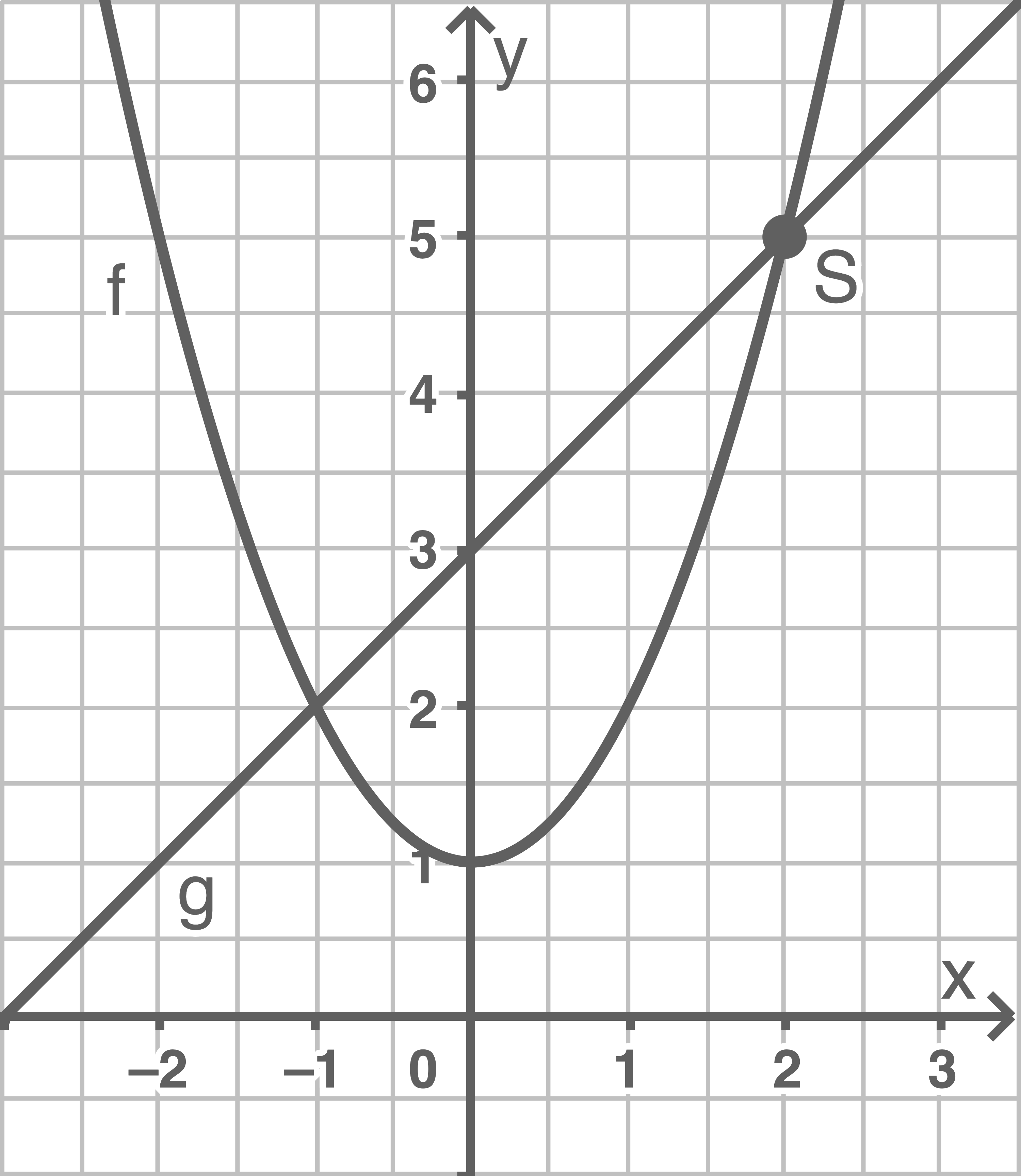
Die Graphen der Funktionen  und
und  mit
mit 
 schneiden sich.
schneiden sich.
Bestimme die Koordinaten des Schnittpunkts im ersten Quadranten.
Bestimme die Koordinaten des Schnittpunkts im ersten Quadranten.
3 BE
9.2
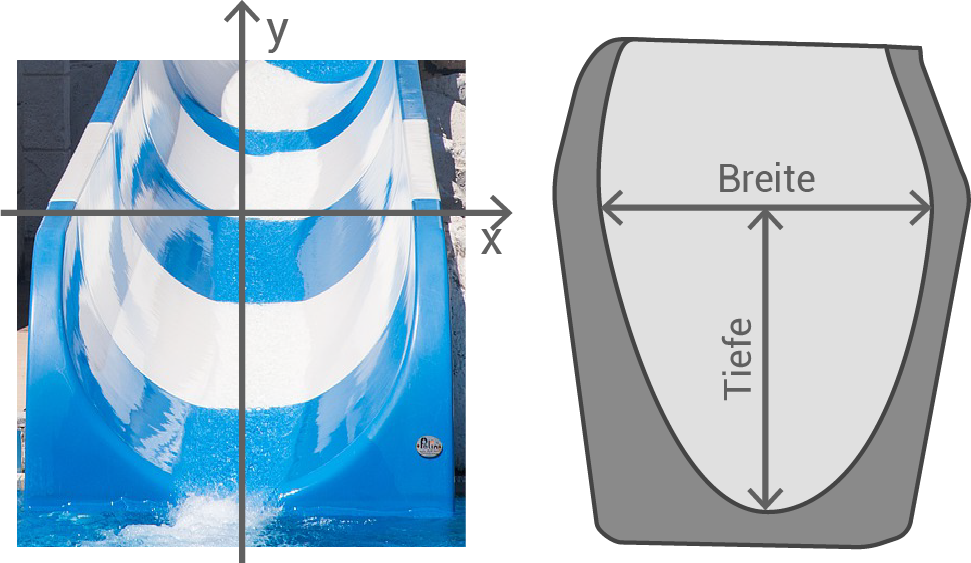
Der Querschnitt einer Wasserrutsche lässt sich näherungsweise durch den Graphen von
 mit
mit 
 beschreiben.
Eine Längeneinheit entspricht einem Dezimeter in der Realität.
beschreiben.
Eine Längeneinheit entspricht einem Dezimeter in der Realität.



a)
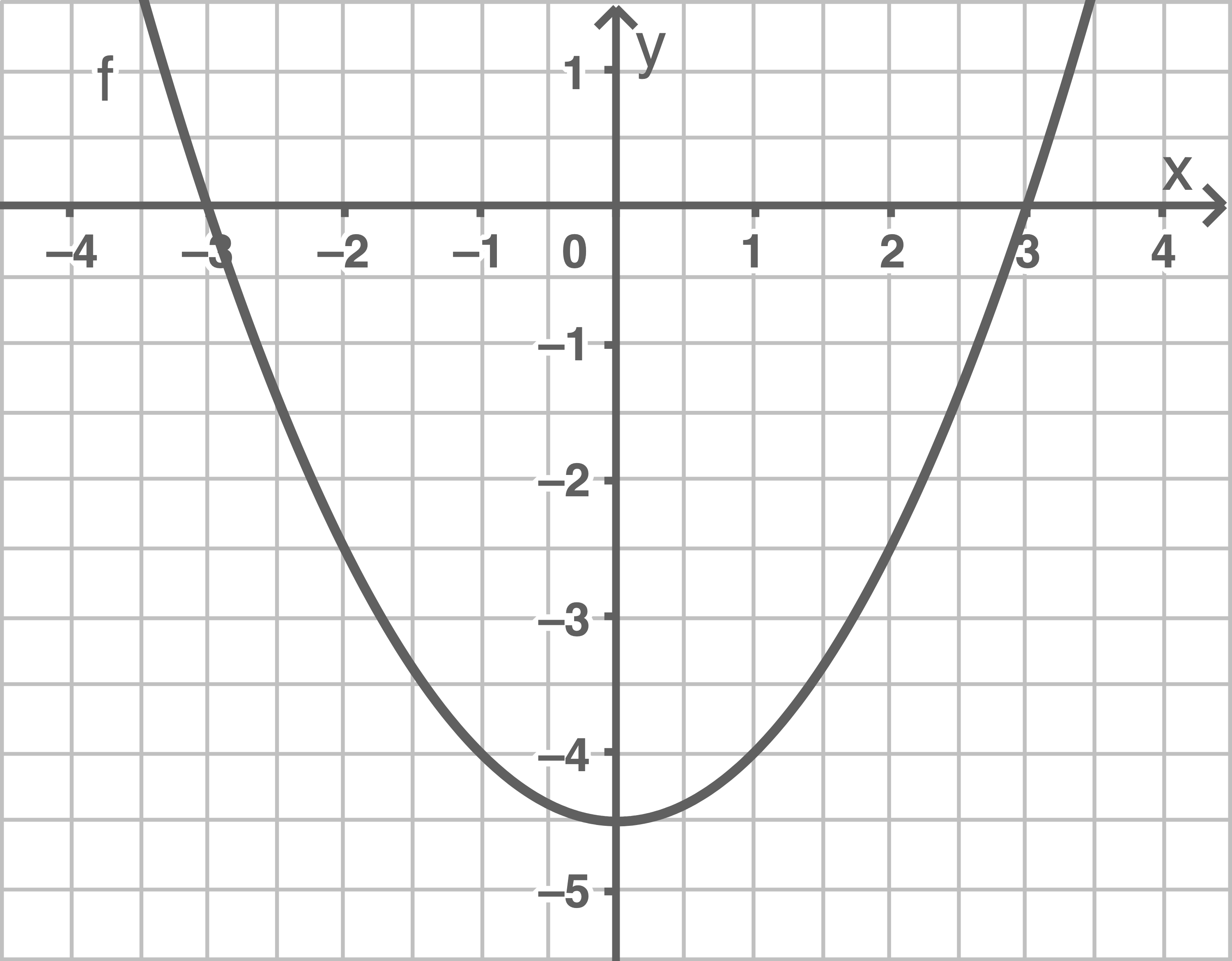
Stelle den Graphen von  in einem Koordinatensystem dar.
in einem Koordinatensystem dar.
3 BE
b)
Gib die Tiefe der Wasserrutsche an.
1 BE
c)
Berechne die Breite der Wasserrutsche.
3 BE
10
Wahlaufgabe Stochastik
10.1
Die Tabelle enthält die Verteilung der Noten einer Leistungskontrolle der Klasse 10a.
 nicht mehr lesbar.
nicht mehr lesbar.
Der Durchschnitt der Noten beträgt
Der Durchschnitt ändert sich dadurch nicht.
| Note | ||||||
|---|---|---|---|---|---|---|
| Anzahl der Schüler |
a)
Berechne den Durchschnitt dieser Noten.
In der Verteilung der Noten der Klasse 10b ist die Anzahl der Note
2 BE
Der Durchschnitt der Noten beträgt
| Note | ||||||
|---|---|---|---|---|---|---|
| Anzahl der Schüler |
b)
Ermittle die Anzahl der Schüler, die diese Leistungskontrolle geschrieben haben.
Zwei Schüler der Klasse 10b schreiben die Leistungskontrolle nach.
4 BE
Der Durchschnitt ändert sich dadurch nicht.
c)
Gib eine Möglichkeit für die Noten dieser Schüler an.
1 BE
10.2
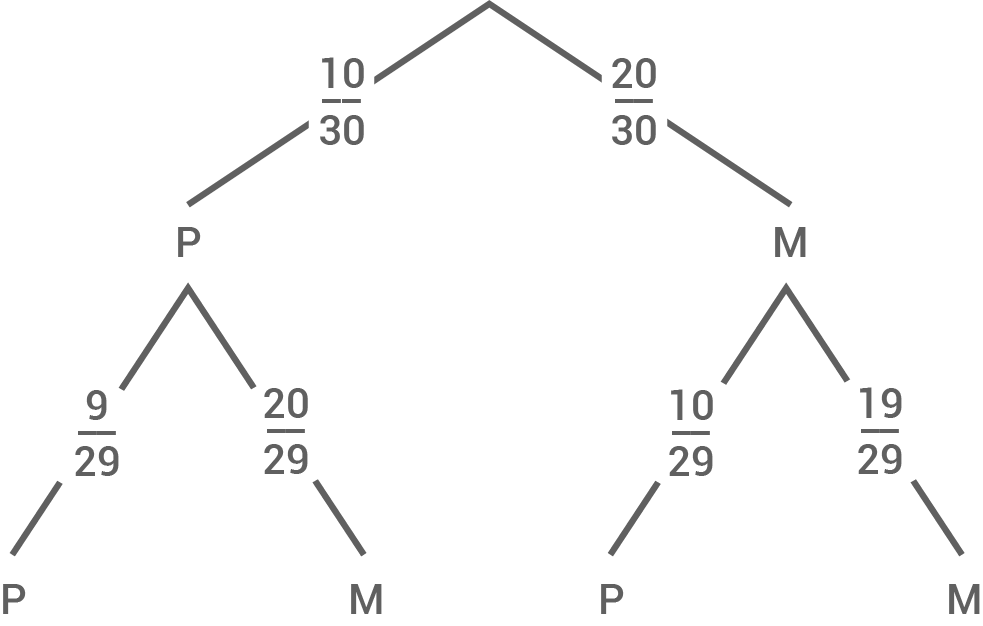
Auf einem Tablett sind 30 Pfannkuchen. Der Bäcker hat 10 Pfannkuchen mit Pflaumenmus und die restlichen mit Marmelade gefüllt. Jan wählt zufällig zwei Pfannkuchen.
Bestimme die Wahrscheinlichkeit dafür, dass Jan mindestens einen Pfannkuchen mit Pflaumenmus entnimmt.
3 BE
11
Wahlaufgabe Arithmetik/ Algebra
11.1
Berechne den Term.

1 BE
11.2
Löse die Gleichung.

4 BE
11.3
Das menschliche Haar wächst durchschnittlich  pro Tag.
pro Tag.
Eine Europäerin hat etwa Haare auf dem Kopf.
Haare auf dem Kopf.
Eine Europäerin hat etwa
a)
Berechne die gesamte Länge des Haarwuchses auf dem Kopf an einem Tag.
Gib das Ergebnis in Meter an.
Gib das Ergebnis in Meter an.
2 BE
b)
Bestimme die Anzahl der Jahre, die ein Haar wachsen müsste, um einen Meter lang zu werden.
3 BE
8.1
a)
b)
Die Diagonale  teilt das Parallelogramm in zwei gleich große Dreiecke. Der Flächeninhalt eines solchen Dreiecks kann wie folgt berechnet werden:
teilt das Parallelogramm in zwei gleich große Dreiecke. Der Flächeninhalt eines solchen Dreiecks kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot a\cdot b\cdot \sin \alpha \\[5pt]
&=& \dfrac{1}{2}\cdot 12\,\text{cm}\cdot 7\,\text{cm}\cdot \sin 55° \\[5pt]
&\approx& 34,4\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/c3449b7ac2fb80c95773a803d4da658eb5a6ff8ccdaaaef4ef23b112016d6d52?color=5a5a5a) Damit folgt für den Flächeninhalt des Parallelogramms:
Damit folgt für den Flächeninhalt des Parallelogramms:
![\(\begin{array}[t]{rll}
A&=& 2\cdot A_D \\[5pt]
&=& 2\cdot 34,4\,\text{cm}^2 \\[5pt]
&=& 68,8\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/1b443d249f4b3649929dfc527cf946d218c353f1c49c4696283a93f10cbc6956?color=5a5a5a)
c)
Flächeninhalt Rechteck:  Flächeninhalt Parallelogramm:
Flächeninhalt Parallelogramm:  mit
mit  Das Parallelogramm hat also einen Flächeninhalt von
Das Parallelogramm hat also einen Flächeninhalt von  Da für
Da für  der Wert von
der Wert von  immer kleiner als
immer kleiner als  ist, gilt:
ist, gilt:
 Damit ist gezeigt, dass der Flächeninhalt des Parallelogramms stets kleiner ist als der Flächeninhalt des seitengleichen Rechtecks.
Damit ist gezeigt, dass der Flächeninhalt des Parallelogramms stets kleiner ist als der Flächeninhalt des seitengleichen Rechtecks.
8.2
Wenn der Burgsee annähernd kreisförmig ist, muss die Länge  des Rundwegs ungefähr dem Umfang eines Kreises mit folgendem Radius entsprechen:
des Rundwegs ungefähr dem Umfang eines Kreises mit folgendem Radius entsprechen:
![\(\begin{array}[t]{rll}
u&=& 2 \cdot \pi \cdot r \\[5pt]
1\,150\,\text{m}&=& 2 \cdot \pi \cdot r \quad \scriptsize \mid\; :2\cdot \pi\\[5pt]
183\,\text{m}&\approx& r
\end{array}\)](https://mathjax.schullv.de/86bc4d8616bed6f933531b09de914945d548009de48ed67174a0ad5784d4c0e8?color=5a5a5a) Der Flächeninhalt eines möglichen Kreises beträgt dann:
Der Flächeninhalt eines möglichen Kreises beträgt dann:
![\(\begin{array}[t]{rll}
A&=& \pi\cdot r^2 \\[5pt]
&\approx& \pi\cdot (183\,\text{m})^2 \\[5pt]
&\approx& 105\,209\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/0612fca6a6b9e8f727c9734394712e61ab2c1f2b6365302e8d39c891a10d0d46?color=5a5a5a) Der berechnete Flächeninhalt und der Oberflächeninhalt des Sees liegen nahe beieinander. Es könnte sich also annähernd um eine Kreisform handeln.
Der berechnete Flächeninhalt und der Oberflächeninhalt des Sees liegen nahe beieinander. Es könnte sich also annähernd um eine Kreisform handeln.
9.1
Grafische Lösung
Der Schnittpunk im ersten Quadranten hat die Koordinaten 
| -2 | -1 | 0 | 1 | 2 | |
| 5 | 2 | 1 | 2 | 5 |
| -2 | -1 | 0 | 1 | 2 | |
| 1 | 2 | 3 | 4 | 5 |
9.2
a)
| -3 | 0 |
| -2 | -2,5 |
| -1 | -4 |
| 0 | -4,5 |
| 1 | -4 |
| 2 | -2,5 |
| 3 | 0 |
b)
Die  -Koordinate des Scheitelpunkts ist
-Koordinate des Scheitelpunkts ist  Da eine Längeneinheit in der Realität einem Dezimeter entspricht, ist die Wasserrutsche
Da eine Längeneinheit in der Realität einem Dezimeter entspricht, ist die Wasserrutsche  tief.
tief.
c)
Die Breite der Rutsche ist durch den Abstand der beiden Nullstellen gegeben.
![\(\begin{array}[t]{rll}
f(x)&=& 0 \\[5pt]
0,5x^2-4,5&=& 0 \quad \scriptsize \mid\;+4,5 \\[5pt]
0,5x^2&=& 4,5 \quad \scriptsize \mid\;\cdot 2 \\[5pt]
x^2&=& 9 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x&=& \pm 3
\end{array}\)](https://mathjax.schullv.de/a43e807bc579e8843f4e254b8c6b44f7047202a44b036b2b5f46ef6f91e3844d?color=5a5a5a) Die Nullstellen
Die Nullstellen  und
und  haben einen Abstand von
haben einen Abstand von  Die Wasserrutsche ist also
Die Wasserrutsche ist also  breit.
breit.
10.1
a)
Anzahl vergebener Noten:  Summe der Werte der vergebenen Noten:
Summe der Werte der vergebenen Noten: 
 Der Notendurchschnitt beträgt 2,7.
Der Notendurchschnitt beträgt 2,7.
b)
Um herauszufinden, wie viele Schüler die Leistungskontrolle geschrieben haben, muss die Anzahl  der Schüler bestimmt werden, die eine 3 geschrieben haben.
5 Schüler haben die Note 3 geschrieben. Für die Anzahl
der Schüler bestimmt werden, die eine 3 geschrieben haben.
5 Schüler haben die Note 3 geschrieben. Für die Anzahl  der Schüler folgt:
der Schüler folgt:
 22 Schüler haben die Leistungskontrolle geschrieben.
22 Schüler haben die Leistungskontrolle geschrieben.
c)
Der Schnitt bleibt unverändert, wenn die beiden Nachschreiber ebenfalls einen Notendurchschnitt von 2,5 erreichen. Dafür gibt es zwei Möglichkeiten. Es genügt jedoch, eine Möglichkeit anzugeben.
- Der eine Schüler schreibt eine 2 und der andere eine 3:
- Der eine Schüler schreibt eine 1 und der andere eine 4:
10.2
11.1
11.2
11.3
a)
Wachstum eines Haares an einem Tag: 
Anzahl der Haare:
![\(\begin{array}[t]{rll}
\ell&=& n\cdot \ell_1 \\[5pt]
&=& 1,2\cdot 10^5\cdot 0,3\,\text{mm}\\[5pt]
&=& 120\,000\cdot 0,3\,\text{mm}\\[5pt]
&=& 36\,000\,\text{mm}\\[5pt]
&=& 36\,\text{m}
\end{array}\)](https://mathjax.schullv.de/fb3c52f1027af69711ccf592e7781e897754870387c015dfb0f87aeca487b738?color=5a5a5a) Der gesamte Haarwuchs an einem Tag beträgt
Der gesamte Haarwuchs an einem Tag beträgt 
Anzahl der Haare:
b)
Haarlänge, die erreicht werden soll: 
Wachstum eines Haares: Berechnung der Zeit
Berechnung der Zeit  in Tagen:
in Tagen:
![\(\begin{array}[t]{rll}
t&=& \dfrac{\ell}{\ell_1} \\[5pt]
&=& \dfrac{1\,000\,\text{mm}}{0,3\,\frac{\text{mm}}{\text{d}}} \\[5pt]
&\approx& 3\,333,3\,\text{d}
\end{array}\)](https://mathjax.schullv.de/5f7f27fa9f6cc37d63396ab83066fe364498500c3521df4983aee8646aa0f8eb?color=5a5a5a) Umrechnung in Jahre:
Umrechnung in Jahre:
![\(\begin{array}[t]{rll}
t&\approx& \dfrac{3\,333,3}{365}\,\text{Jahre} \\[5pt]
&\approx& 9,1\,\text{Jahre}
\end{array}\)](https://mathjax.schullv.de/1434a1c954ae5c67164f5aed02cee05b590b23cfe3c75ea412e24b8cd976bddc?color=5a5a5a) Nach ungefähr 9 Jahren ist ein Haar einen Meter lang.
Nach ungefähr 9 Jahren ist ein Haar einen Meter lang.
Wachstum eines Haares: