Pflichtaufgaben 2-7
2
Der trockene Sommer 2018 führte zu Einbußen bei den Ernteerträgen.
In der Abbildung sind die Ernteerträge von Winterraps für mehrere Jahre dargestellt.
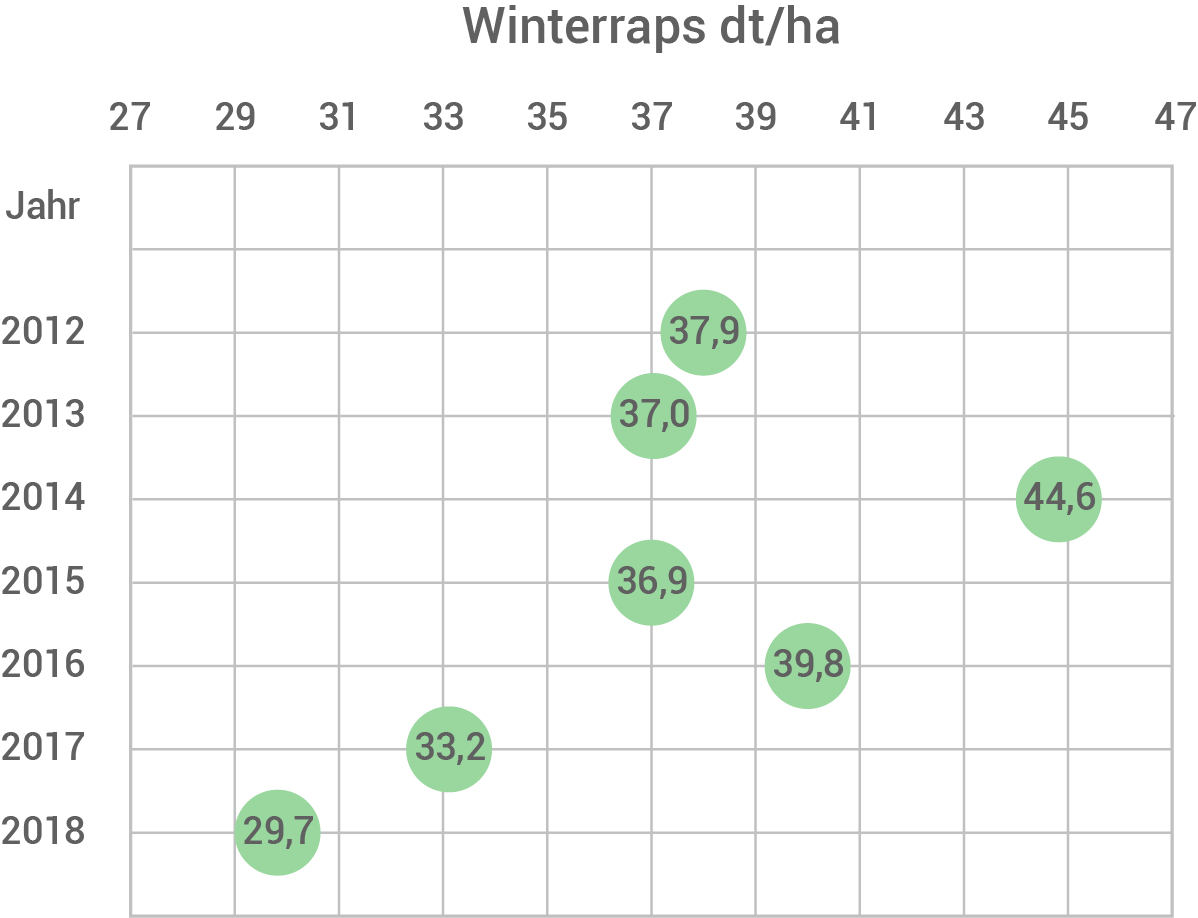
 und war damit
und war damit  geringer als der langjährige durchschnittliche Ertrag.
geringer als der langjährige durchschnittliche Ertrag.
In der Abbildung sind die Ernteerträge von Winterraps für mehrere Jahre dargestellt.

Nach: Wochenspiegel vom 29. September 2018, Seite 10.
a)
Berechne das arithmetische Mittel der Ernteerträge von Winterraps für die Jahre 2012 bis 2018.
2 BE
b)
Stelle die Ernteerträge von Winterraps der Jahre 2016 bis 2018 in einem Säulendiagramm auf kariertem Papier dar.
Sommergerste hat die Trockenheit von 2018 gut verkraftet. Der Ernteertrag betrug
3 BE
c)
Berechne den langjährigen durchschnittlichen Ertrag von Sommergerste.
2 BE
3
Gegeben ist das Dreieck  mit
mit 
 und
und 
a)
Berechne den Flächeninhalt des Dreiecks  .
.
3 BE
b)
Zeichne das Dreieck  im Maßstab
im Maßstab  auf unliniertem Papier.
auf unliniertem Papier.
3 BE
4
Gegeben sind die Funktionen  und
und 
 mit
mit 

(Eine Längeneinheit entspricht einem Zentimeter.)
 und
und  schneiden sich im Punkt
schneiden sich im Punkt 
Die Schnittpunkte der Funktionen mit der -Achse sind
-Achse sind  und
und 
(Eine Längeneinheit entspricht einem Zentimeter.)
a)
Stelle die Funktionen in ein und demselben Koordinatensystem grafisch dar.
Die Graphen der Funktionen
3 BE
Die Schnittpunkte der Funktionen mit der
b)
Zeichne das Dreieck  in die Darstellung und berechne dessen Flächeninhalt.
in die Darstellung und berechne dessen Flächeninhalt.
3 BE
5
Bei einem zweistufigen Zufallsexperiment mit Zurücklegen soll für ein Ereignis die Wahrscheinlichkeit  betragen.
Beschreibe ein zugehöriges Zufallsexperiment und gib dieses Ereignis an.
betragen.
Beschreibe ein zugehöriges Zufallsexperiment und gib dieses Ereignis an.
3 BE
6
Stromanbieter  berechnet für jede Kilowattstunde 27 Cent und einen jährlichen Grundpreis von
berechnet für jede Kilowattstunde 27 Cent und einen jährlichen Grundpreis von 
Der Stromanbieter berechnet für jede Kilowattstunde 32 Cent und
berechnet für jede Kilowattstunde 32 Cent und  jährlichen Grundpreis.
jährlichen Grundpreis.
Der Stromanbieter
a)
Familie Fuchs bezieht ihren Strom von Anbieter  und bezahlte im letzten Jahr
und bezahlte im letzten Jahr  Berechne die Anzahl der Kilowattstunden, die Familie Fuchs im letzten Jahr verbrauchte.
Berechne die Anzahl der Kilowattstunden, die Familie Fuchs im letzten Jahr verbrauchte.
2 BE
b)
Ermittle die Anzahl der Kilowattstunden, bei denen der Preis von beiden Anbietern gleich ist.
3 BE
7
Ein Kegel und eine Kugel haben jeweils gleich große Radien. Die Höhe des Kegels ist doppelt so groß wie sein Radius.
Weise nach, dass allgemein gilt:
Das Volumen der Kugel ist doppelt so groß wie das Volumen des Kegels.
Das Volumen der Kugel ist doppelt so groß wie das Volumen des Kegels.
3 BE
2
a)
Das arithmetische Mittel der Ernteerträge von Winterraps für die Jahre 2012 bis 2018 beträgt ungefähr 
b)
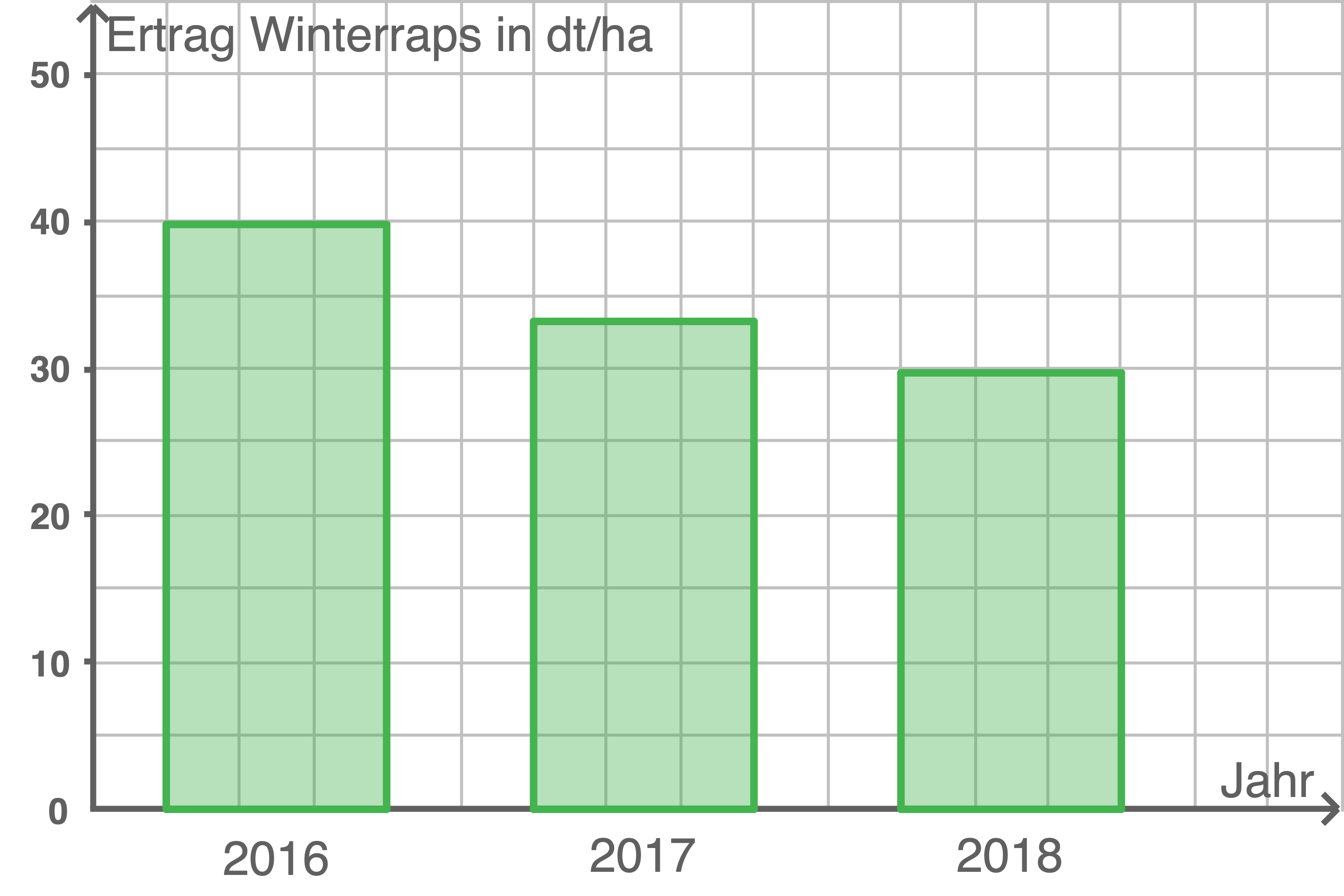
c)
Lösung mit Lösungsformel


![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&=& \dfrac{53,7\,\frac{\text{dt}}{\text{ha}}\cdot 100\,\%}{93\,\%} \\[5pt]
G&\approx& 57,7 \,\dfrac{\text{dt}}{\text{ha}}
\end{array}\)](https://mathjax.schullv.de/1a616b3554997d7b651fe2e0c15c86a0db311fc738712a2cab08f0723a1ae126?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rrcll}
& 93\,\%&\mathrel{\widehat{=}}& 53,7\,\dfrac{\text{dt}}{\text{h}} \\[5pt]
& 1\,\% &\mathrel{\widehat{=}}& \dfrac{53,7}{93}\,\dfrac{\text{dt}}{\text{h}} \\[5pt]
& 100\,\% &\mathrel{\widehat{\approx}}& 57,7 \,\dfrac{\text{dt}}{\text{h}} &
\end{array}\)](https://mathjax.schullv.de/cc98049234128dc4c795950867ed293bb4f114f56f9ef49eabff4952355dcac9?color=5a5a5a)



 Der langjährige durchschnittliche Ertrag von Sommergerste beträgt
Der langjährige durchschnittliche Ertrag von Sommergerste beträgt  .
.
3
a)
Planfigur:
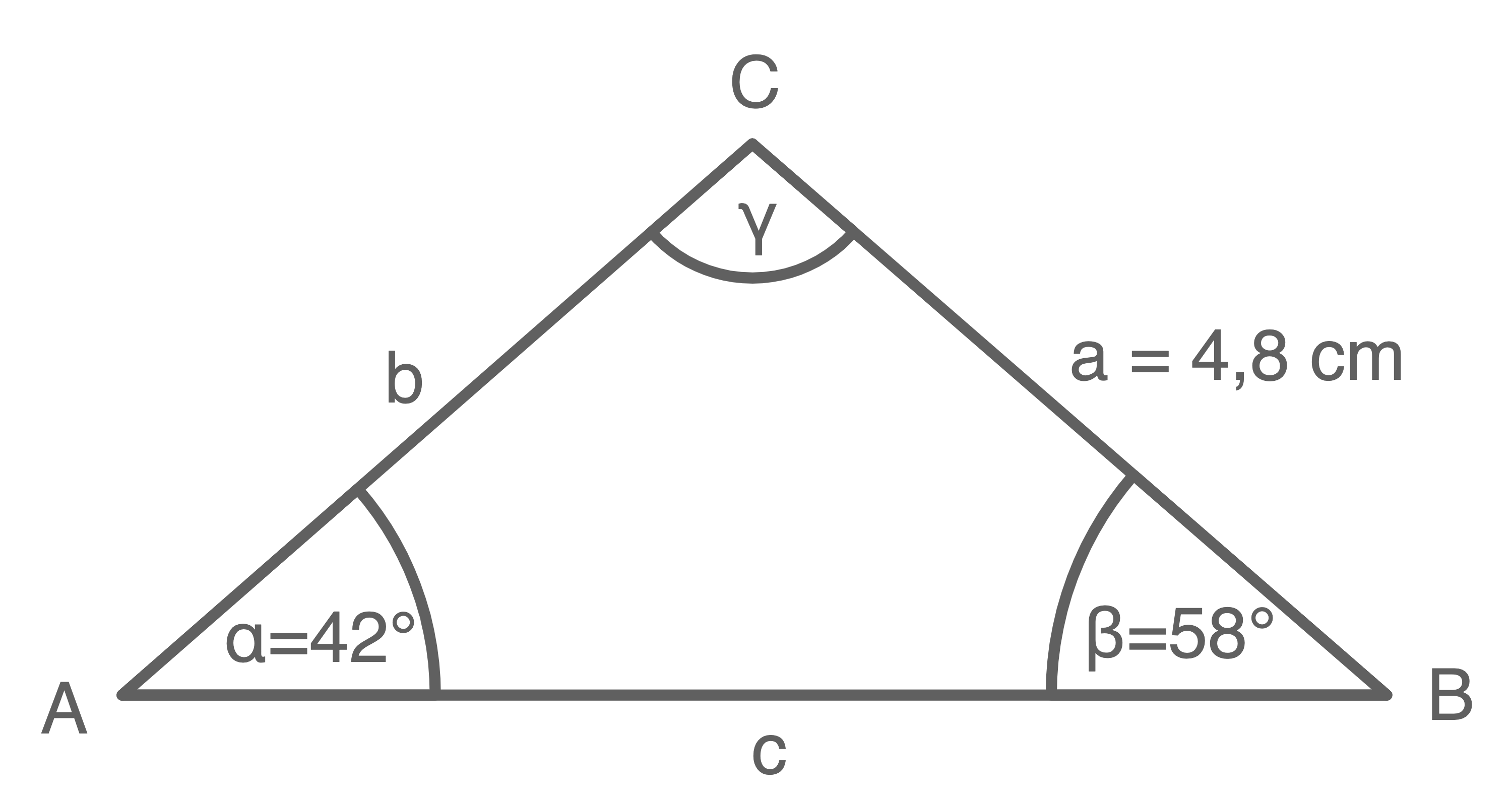 Mit dem Innenwinkelsummensatz im Dreieck folgt für den Winkel
Mit dem Innenwinkelsummensatz im Dreieck folgt für den Winkel 
 Die Seitenlänge
Die Seitenlänge  lässt sich mit dem Sinussatz berechnen:
lässt sich mit dem Sinussatz berechnen:
![\(\begin{array}[t]{rll}
\dfrac{a}{\sin \alpha}&=& \dfrac{b}{\sin \beta} \quad \scriptsize \mid\; \cdot \sin \beta \\[5pt]
\dfrac{a}{\sin \alpha}\cdot \sin \beta &=& b \\[5pt]
\dfrac{4,8\,\text{cm}}{\sin 42°}\cdot \sin 58° &=& b \\[5pt]
6,1\,\text{cm}&\approx& b
\end{array}\)](https://mathjax.schullv.de/6a7c020ee1f29e4b1f89a0eb78eed1419943952eefa0ccbe2f35f8a6883ced2b?color=5a5a5a) Damit lässt sich der Flächeninhalt des Dreiecks berechnen:
Damit lässt sich der Flächeninhalt des Dreiecks berechnen:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot a\cdot b\cdot \sin \gamma \\[5pt]
&\approx& \dfrac{1}{2}\cdot 4,8\,\text{cm}\cdot 6,1\,\text{cm}\cdot \sin 80° \\[5pt]
&\approx& 14,4\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/ca4b039018aa8ac2178133a294399ec7bc27cf61ad7336e53213cc8a1e70364d?color=5a5a5a) Das Dreieck
Das Dreieck  hat den Flächeninhalt
hat den Flächeninhalt 

b)
Das Dreieck wird nach dem Kongruenzsatz WSW konstruiert. Dazu wird die Strecke  gezeichnet und anschließend werden die Winkel
gezeichnet und anschließend werden die Winkel  und
und  (siehe Teilaufgabe a) abgetragen.
Berechnung der Länge der Seite
(siehe Teilaufgabe a) abgetragen.
Berechnung der Länge der Seite  im Maßstab 2:1:
im Maßstab 2:1:
![\(\begin{array}[t]{rll}
\dfrac{2}{1}&=& \dfrac{a}{4,8\,\text{cm}} \quad \scriptsize \mid\; \cdot 4,8\,\text{cm} \\[5pt]
9,6 \,\text{cm}&=& a
\end{array}\)](https://mathjax.schullv.de/e117d7b7d07682c862c4bca49515c08c5ffaf9deeb142547df44d0f0ff2891de?color=5a5a5a)
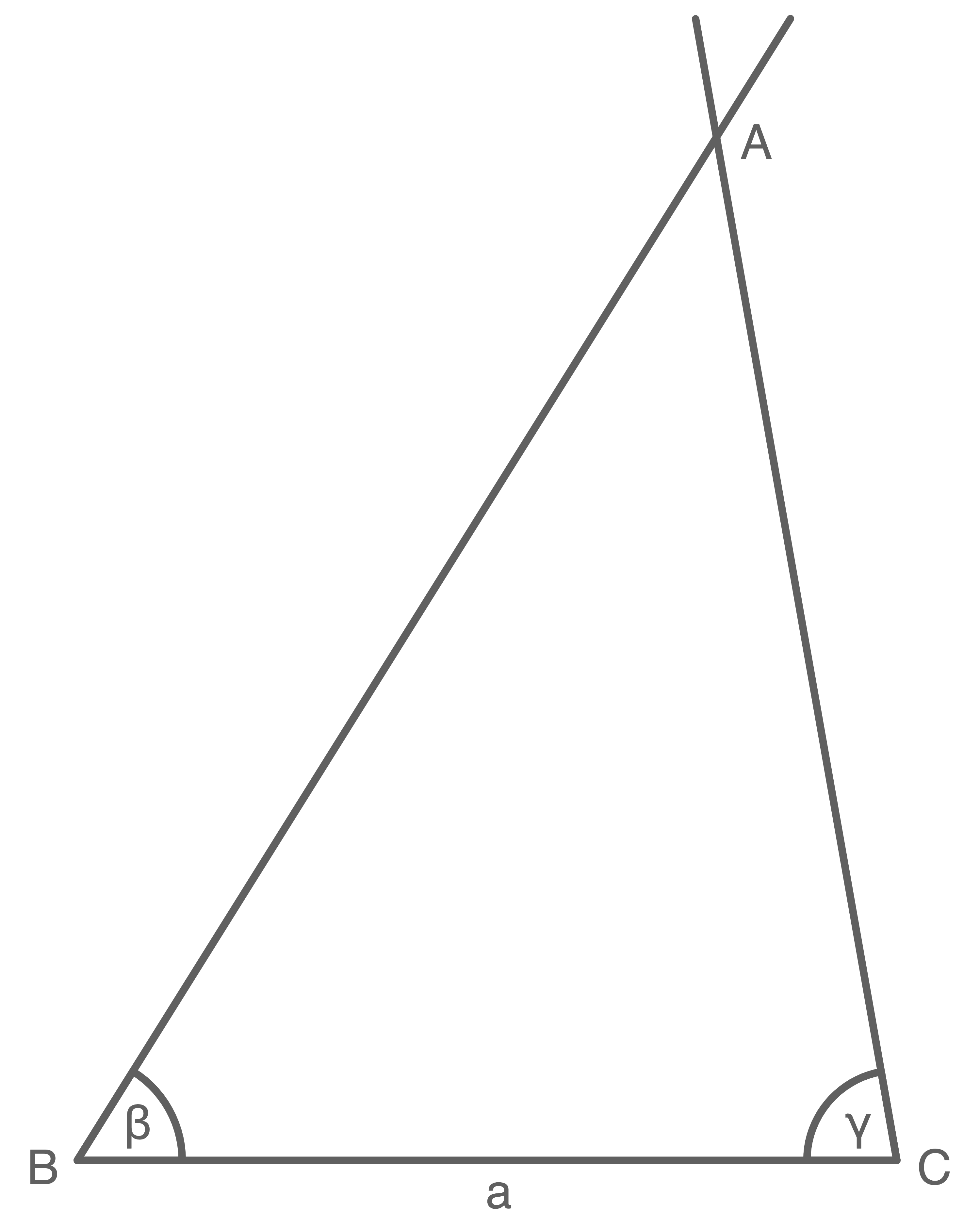 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

4
a)
Wertetabellen für beide Funktionen erstellen:
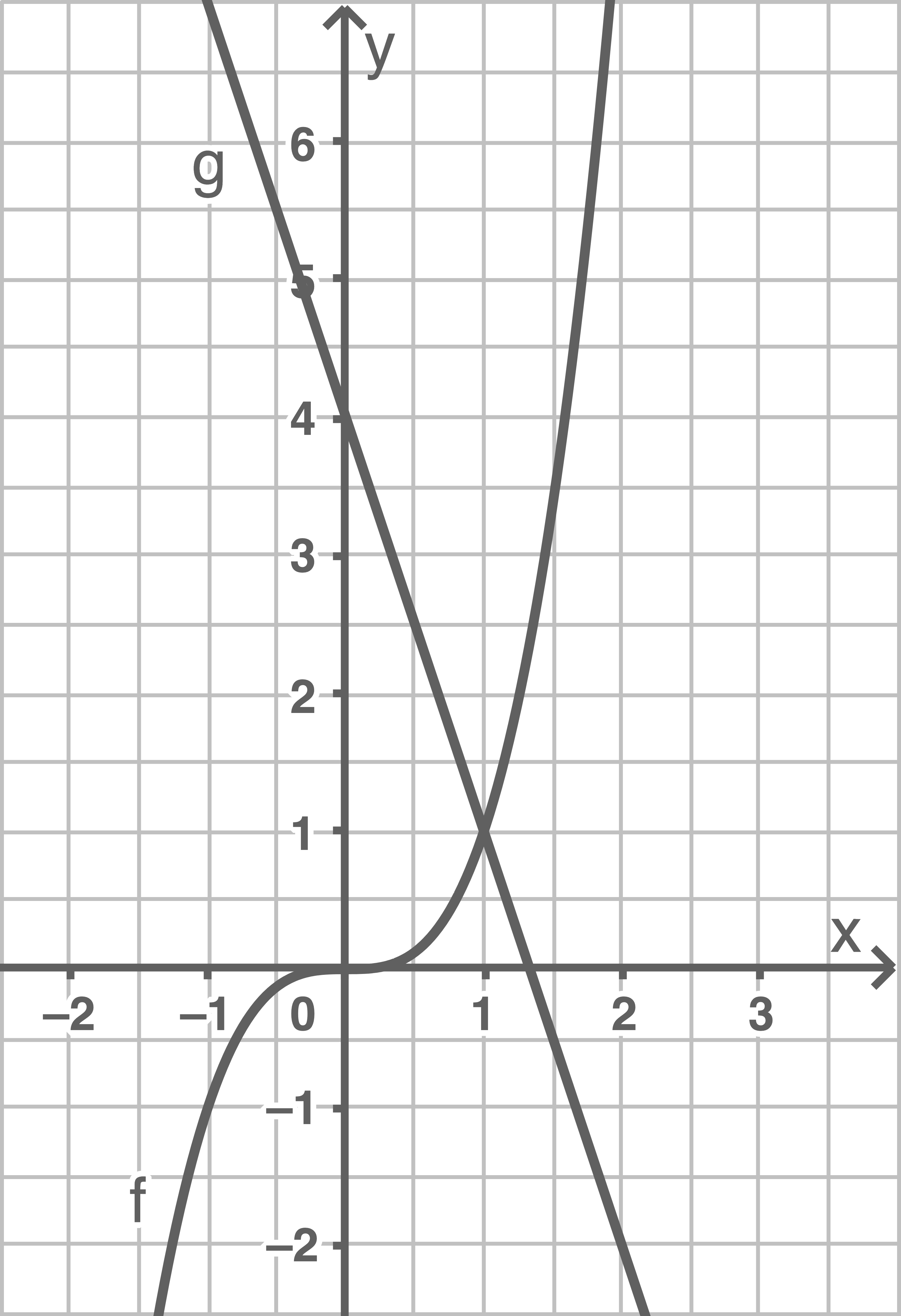
| -1 | -1 |
| -0,5 | -0,125 |
| 0 | 0 |
| 0,5 | 0,125 |
| 1 | 1 |
| 1,5 | 3,375 |
| 2 | 8 |
| -1 | 0 | 1 | 1,5 | |
| 7 | 4 | 1 | -0,5 |

b)
Dreieck einzeichnen
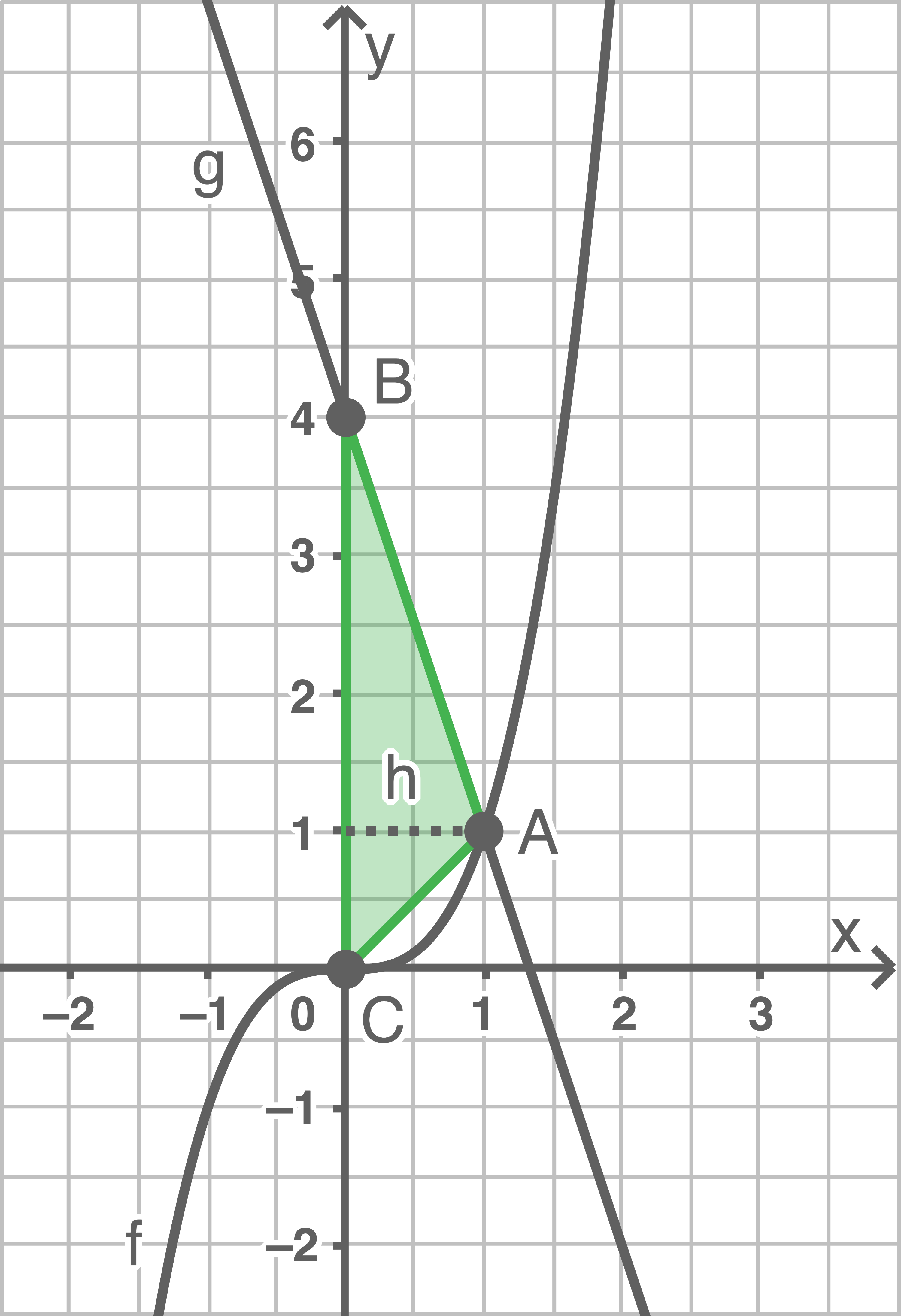 Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot \overline{BC}\cdot h \\[5pt]
&=& \dfrac{1}{2}\cdot 4\,\text{cm}\cdot 1\,\text{cm} \\[5pt]
&=& 2\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/7d8f12a4479a8fc3528ae3c589e3ea42634e314ff5eae6b667420e2986f79f62?color=5a5a5a) Der Flächeninhalt des Dreiecks
Der Flächeninhalt des Dreiecks  beträgt
beträgt 

5
Es handelt sich um ein zweistufiges Zufallsexperiment mit Zurücklegen. Daher muss für das gesuchte Ereignis  gelten:
gelten:
![\(\begin{array}[t]{rll}
P(E)&=& P(\text{Stufe 1})\cdot P(\text{Stufe 2}) \\[5pt]
\dfrac{9}{16}&=& \dfrac{a}{b}\cdot \dfrac{c}{b}
\end{array}\)](https://mathjax.schullv.de/7adaa3ee68bc1c70947a74a54b7ee90ba520960aa7ad84780455064fe5d99d4e?color=5a5a5a) Es gilt
Es gilt  und
und  Der Nenner jeder Stufe ist 4. Das passt zum Ziehen aus einer Urne mit 4 Kugeln.
Der Nenner jeder Stufe ist 4. Das passt zum Ziehen aus einer Urne mit 4 Kugeln.
Der Zähler jeder Stufe ist 3. Das passt dazu, dass 3 dieser 4 Kugeln für das Ereignis günstig sind. Ein mögliches Zufallsexperiment ist das folgende: Aus einer Urne mit 3 grünen und 1 roten Kugel werden zwei Kugeln mit Zurücklegen gezogen. „Es wird zweimal eine grüne Kugel gezogen.“
„Es wird zweimal eine grüne Kugel gezogen.“

Der Zähler jeder Stufe ist 3. Das passt dazu, dass 3 dieser 4 Kugeln für das Ereignis günstig sind. Ein mögliches Zufallsexperiment ist das folgende: Aus einer Urne mit 3 grünen und 1 roten Kugel werden zwei Kugeln mit Zurücklegen gezogen.
6
a)
b)
Gleichung Anbieter 
 Gleichung Anbieter
Gleichung Anbieter 
 Die Anzahl der Kilowattstunden, bei denen der Preis von beiden Anbietern gleich ist, kann mit dem Gleichsetzungsverfahren bestimmt werden:
Die Anzahl der Kilowattstunden, bei denen der Preis von beiden Anbietern gleich ist, kann mit dem Gleichsetzungsverfahren bestimmt werden:
![\(\begin{array}[t]{rll}
f(x)&=& g(x) \\[5pt]
0,27x+320&=& 0,32x+180 \quad \scriptsize \mid\, -180 \\[5pt]
0,27x+140&=& 0,32x \quad \scriptsize \mid\;-0,27x \\[5pt]
140&=& 0,05x \quad \scriptsize \mid\;: 0,05 \\[5pt]
2\,800&=& x \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d0238097d87c73edb45f2d9348333d5aebcdc1c8fa4f430e0d3f5ab3a1f28728?color=5a5a5a) Der Preis von beiden Anbietern ist gleich, wenn
Der Preis von beiden Anbietern ist gleich, wenn  verbraucht werden.
verbraucht werden.
7
Volumen der Kugel:
 Volumen des Kegels:
Volumen des Kegels:
![\(\begin{array}[t]{rll}
V_{\text{Ke}}&=& \dfrac{1}{3}\cdot \pi\cdot r^2\cdot h \quad \scriptsize \mid\; h=2r \\[5pt]
&=& \dfrac{1}{3}\cdot \pi\cdot r^2\cdot 2\cdot r \\[5pt]
&=& \dfrac{2}{3}\cdot \pi\cdot r^3
\end{array}\)](https://mathjax.schullv.de/66d464109b194dba5eb903bb5207b3b499cd5644a00d8014468effdb2d899b4a?color=5a5a5a) Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
2\cdot V_{\text{Ke}}&=& V_{\text{Ku}} \\[5pt]
2\cdot \dfrac{2}{3}\cdot \pi\cdot r^3&=& \dfrac{4}{3}\cdot \pi\cdot r^3 \\[5pt]
\dfrac{4}{3}\cdot \pi\cdot r^3&=& \dfrac{4}{3}\cdot \pi\cdot r^3
\end{array}\)](https://mathjax.schullv.de/1548b848ab46c9a936dcc7bfad205a7aeb58448a56817f7374c0e6549ed6051c?color=5a5a5a) Damit ist gezeigt, dass das Volumen der Kugel doppelt so groß ist wie das Volumen des Kegels.
Damit ist gezeigt, dass das Volumen der Kugel doppelt so groß ist wie das Volumen des Kegels.